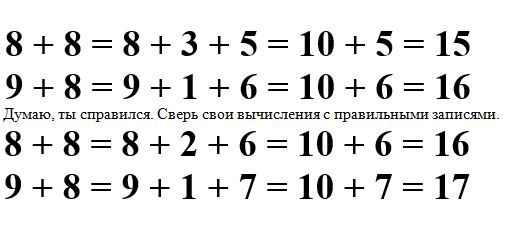План урока:
Общий приём сложения однозначных чисел с переходом через десяток
Сложение вида □ + 2, □ + 3
Сложение вида □ + 4
Сложение вида □ + 5
Сложение вида □ + 6
Сложение вида □ + 7
Сложение вида □ + 8, □ + 9
Таблица сложения
Всем привет и добрый день!
Прогоняй скорей ты лень.
Таблицы будем составлять –
Постарайся все понять.
Сегодня на нашем уроке мы попадем в загадочный математический город. Он называется «Состав числа». В этом городе расположены необычные дома. На каждом этаже живут пары чисел, которые отражают состав числа, соответствующего номеру дома.
Рассмотри внимательно эти домики и вспомни состав чисел.
А еще перед тем, как мы приступим к изучению новой темы, вспомни материал, который мы рассматривали на прошлом уроке о сложении разрядных чисел. Мишка рассказал Маше как найти результат в примерах типа 10 + 6. 10 – это 1 десяток, а 6 – это 6 единиц. При сложении получаем число,которое состоит из 1 дес. и 6 ед. – это 16.
Вспомнил этот материал? Тогда мы приступаем к изучению нового.
Общий приём сложения однозначных чисел с переходом через десяток
Итак, поговорим о сложении однозначных чисел. Ты уже знаешь, что обозначает это действие. Давай решим пример.
6 + 3 =
Посмотри, первое слагаемое в этом примере 6. Давай отсчитаем на счетах шесть косточек.
Второе слагаемое 3. Добавим три косточки.
Теперь пересчитаем все косточки вместе. Получим 9.
Значит, 6 + 3 = 9.
Это очень простой пример на сложение числа 6 с однозначными числами. Главная особенность таких примеров в том, что их результат не больше 10.
На счетах каждая палочка имеет по 10 косточек – ровно один десяток. Этого достаточно, чтобы решить любой пример на сложение в пределах 10.
Но сегодня мы будем учиться решать математические выражения другого вида. Сейчас мы разберем один пример и определим в чем заключается их особенность.
6 + 7 =
Первое слагаемое 6. Отсчитаем на счетах 6 косточек.
Второе слагаемое – 7. Нам нужно добавить 7 косточек, но у нас на палочке осталось только 4 косточки.
Оставшиеся косточки мы досчитаем на нижней палочке.
После присоединения 4 косточек на первой палочке мы собрали целый десяток (10 косточек вместе).
А теперь посмотрим, сколько косточек нам понадобилось добавить на второй палочке. Их 3.
Сложение слагаемых 6 и 7 происходит по такому алгоритму. Второе слагаемое 7 мы прибавляли частями: сначала 4, а потом еще 3. При этом первое число подбирается так, чтобы в сумме с первым слагаемым получилось 10. В результате мы получили число, которое состоит из 10 (это 1 десяток) и 3 – это 13.
Вот как весь процесс записывается в виде математического выражения.
Итак, мы можем описать порядок выполнения общего приема сложения однозначных чисел с переходом через десяток.
- Представить (иногда говорят «разложить») второе слагаемое в виде суммы удобных чисел.
- Одно из чисел подбирается так, чтобы дополнить первое слагаемое до целого десятка (1 дес.=10).
- Другое выбирается исходя из состава числа, которое является вторым слагаемым.
Используя этот прием, мы будем составлять таблицы сложения, чтобы находить правильный ответ не при помощи счет, что долго и не всегда удобно, а по памяти. Это в дальнейшем облегчит решение более сложных математических выражений.
Сложение вида □ + 2, □ + 3
Начнем с таблицы сложения с числом 2. Рассмотрим пример
9 + 2 =
Сначала нужно дополнить первое слагаемое – число 9 – до 10. Для этого представим второе слагаемое — число 2 в виде суммы двух удобных чисел.
Давай прогуляемся в город и найдем дом с номером 10.
На одном этаже с числом 9 живет 1. Значит первое число, которым мы представим второе слагаемое 2, будет 1.
Чтобы найти пару, посмотрим на дом под номером 2 (это наше второе слагаемое).
Посмотри, кто живет на одном этаже с числом 1?
Правильно, число 1. Это наше второе число.
А теперь все быстро посчитаем: 9 плюс 1 будет 10. Затем к 10 прибавим еще 1 – получим 11.
Вот и все. Мы составили таблицу сложения однозначного числа с числом 2.
Приступим к решению примеров, в которых вторым слагаемым является 3.
8 + 3 =
Нужно разложить второе слагаемое 3 на две части.
Будем дополнять первое слагаемое 8 до 10. Опять прогуляемся к домику с номером 10.
Кто живет на одном этаже с 8?
Правильно, 2. Запишем его под первой стрелкой от слагаемого 3.
Чтобы узнать пару, поищем домик с номером, который указывает на второе слагаемое – 3.
Кто сосед числа 2 по этажу?
Правильно, это 1. Запишем его под второй стрелкой.
Итак, мы представим наше второе слагаемое 3 как 2 и 1. Начинаем прибавлять. Сумма чисел 8 и 2 равна 10. Затем к 10 прибавить 1. Полученный результат – 11.
Решим еще один пример из таблицы сложения с числом 3.
9 + 3 =
Снова разложим второе слагаемое.
Посмотри на первое слагаемое в нашем примере. Это 9.
Как мы будем дополнять число 9 до 10? Вспомни, мы сегодня уже называли эту пару из состава числа 10.
Правильно, 10 можно представить, как 9 и 1.
Поэтому пишем под первой стрелкой 1.
Пару к нему подберем в домике с номером 3 – это наше второе слагаемое.
Здесь рядом с 1 живет 2. Запишем его под второй стрелкой.
Мы представили второе слагаемое 3 в виде суммы чисел 1 и 2. Найдем результат нашего выражения. Сумма чисел 9 и 1 равна 10. Считаем дальше: к 10 прибавить 2 будет 12.
В таблицах сложения однозначных чисел с числами 2 и 3 всего три примера. Мы нашли их результаты путем прибавления второго слагаемого по частям. Но может быть тебе будет проще выучить все наизусть.
Сложение вида □ + 4
Теперь перейдем к составлению таблицы сложения однозначных чисел с числом 4. Думаю, ты уже понял принцип решения примеров. Давай сразу определим, какие домики нам нужно посетить, чтобы справиться с заданием.
Правильно, нам нужен домик с номером 10, чтобы знать,как будем дополнять первое слагаемое до десятка.
Еще нам нужен домик с номером 4, чтобы вспомнить состав числа 4 – нашего второго слагаемого.
Посмотри на эти домики.
Итак, решим первый пример.
7 + 4 =
Раскладываем второе слагаемое.
Нужно дополнить первое слагаемое до 10. Посмотрим, кто живет рядом с числом 7.
Его сосед 3.
Найдем его пару. Посмотрим на состав числа 4. В домике с таким номером рядом с 3 живет 1.
Начинаем считать. 7 плюс 3 будет 10. А 10 и 1 получим 11.
7 + 4 = 7 + 3 + 1 = 10 +1 = 11
Следующий пример:
8 + 4 =
Представим второе слагаемое в виде суммы удобных чисел. Первое из них должно дополнять первое слагаемое 8 до десятка.
В домике с номером 10 рядом с 8 живет 2.
Определим пару в составе числа 4. В его домике рядом с 2 стоит 2. Ведь 4 это 2 и 2.
Выполняем сложение. 8 плюс 2 будет 10 и 10 плюс 2 будет 12.
8 + 4 = 8 + 2 + 2 = 10 + 2 = 12
Остался еще один пример:
9 + 4 =
Мы уже рассматривали случай дополнения слагаемого 9 до 10. Вспомни, как это сделать.
Определим нужный вариант состава числа 4. В домике под номером 4 рядом с 1 находится 3.
Находим результат. К 9 прибавить 1 будет 10. Теперь к 10 прибавим 3 и получим 13.
9 + 4 = 9 + 1 + 3 = 10 + 3 = 13
Вот и все. Мы решили все примеры из таблицы сложения однозначных чисел с числом 4.
Она выглядит следующим образом.
7 + 4 = 11
8 + 4 = 12
9 + 4 = 13
Сложение вида □ + 5
Надеюсь, ты понял, как нужно находить результат в примерах на сложение с переходом через десяток. Переходим к таблице сложения однозначных чисел с числом 5. Она содержит четыре примера. Предлагаю тебе подумать над их решением самостоятельно. Я дам тебе небольшие подсказки и помогу проверить правильность твоих вычислений.
Подумай, мимо каких домиков нужно прогуляться, чтобы решать примеры на сложение со слагаемым 5.
Вот какие домики выбрала я.
Домик с номером 10 поможет подобрать число, дополняющее первое слагаемое до целого десятка. Домик с номером 5 поможет найти нужный вариант из состава числа 5.
Вот тебе первый пример.
6 + 5 =
Попробуй подобрать удобные числа, на которые нужно разложить второе слагаемое.
Давай проверим, правильно ли ты подумал.
Итак, 4 дополнит первое слагаемое 6 до 10. А 4 и 1 – подходящий вариант состава числа 5.
Теперь сделай нужные вычисления.
Давай проверим, правильно ли ты все посчитал. 6 плюс 4 будет 10, а сумма чисел 10 и 1 равна 11.
6 + 5 = 6 + 4 + 1 = 10 + 1 = 11
Уверена, что ты посчитал все правильно. Идем дальше. Вот следующий пример.
7 + 5 =
Разложи второе слагаемое для выполнения сложения частями
Ты уже подобрал? Давай проверим.
Число 3 нужно тебе, чтобы дополнить первое слагаемое 7 до 10. А в домике с номером 5 рядом с 3 живет 2. 3 и 2 – это пара из состава числа 5.
Надеюсь, ты рассуждал так же.
Выполни сложение, прибавив сначала 3, а потом еще 2.
Какой результат ты получил? Давай сверим с моими подсчетами.
7 + 5 = 7 + 3 + 2 = 10 + 2 = 12
Сначала прибавим 7 и 3. Мы получим 10. А затем к 10 прибавим 2 будет 12.
Готов продолжить? Тогда вот еще один пример.
8 + 5 =
Начни решать его самостоятельно. У нас уже были случаи, когда слагаемое 8 нужно было дополнить до 10. Вспомни, как мы это делали. И соответствующую пару из состава числа 5 мы тоже уже называли.
Подумал? Посмотри, что должно было получиться.
Теперь быстро все посчитаем. Начинай, а результат проверим.
8 + 5 = 8 + 2 + 3 = 10 + 3 = 13
Остался последний пример.
9 + 5 =
Ты легко можешь дополнить 9 до 10, ведь мы уже несколько раз рассматривали этот случай. Осталось только уточнить, какую пару из состава числа 5 нужно использовать в нашем примере. Попробуй представить второе слагаемое в виде суммы двух удобных чисел и найди результат выражения самостоятельно. Я помогу тебе все проверить.
9 + 5 = 9 + 1 + 4 = 10 + 4 = 14
У тебя получился такой же ответ? Молодец!
Мы закончили составлять таблицу на сложение однозначных чисел с числом 5. Прочитай еще раз ее всю.
Сложение вида □ + 6
Теперь давай займемся составлением таблицы сложения однозначных чисел с числом 6. В нашем городке мы зайдем в домики с номерами 10 и 6.
В таблице сложения с числом 6 есть пример, результат которого ты можешь назвать, не совершая вычислительных действий. Посмотри и определи, как это сделать.
5 + 6 =
Догадался? Ты уже знаешь ответ? Давай проверим.
5 + 6 = 11
Этот результат мы знаем из таблицы сложения с числом 5: 6 + 5 = 11. Простой перестановкой слагаемых мы получим выражение уже из таблицы сложения 6, но результат останется тот же.
А вот остальные примеры из таблицы сложения однозначных чисел вида □ + 6 нужно решать самостоятельно.
6 + 6 =
Посмотри на наши домики и определи, как нужно представить второе слагаемое 6. После этого попробуй решить пример самостоятельно.
Если ты готов, то можно сделать проверку.
6 + 6 = 6 + 4 + 2 = 10 + 2 = 12
Чтобы дополнить первое слагаемое 6 до 10, необходимо прибавить к нему 4. В составе числа 6 есть пара 4 и 2. Получается, что к 6 прибавим 4 и получим 10, а затем к 10 прибавим 2 – будет 12.
Рассуждая аналогично попробуй решить остальные примеры из таблицы сложения однозначных чисел с переходом через десяток вида □ + 6.
Проверь правильность своих вычислений.
Объединим все решенные примеры из таблицы сложения однозначных чисел с переходом через десяток вида □ + 6.
Сложение вида □ + 7
Приступим к составлению таблицы сложения однозначных чисел с числом 7. Посмотри на примеры, которые нужно решить.
4 + 7 =
5 + 7 =
6 + 7 =
7 + 7 =
8 + 7 =
9 + 7 =
Определи, в каких выражениях результат можно найти путем применения переместительного свойства сложения.
Вот эти примеры.
4 + 7 = 7 + 4 = 11
5 + 7 = 7 + 5 = 12
6 + 7 = 7 + 6 = 13
Остальные примеры будем решать самостоятельно. Сделаем это возле домиков с номером 10 и номером 7.
Давай вместе порассуждаем над выражением
7 + 7 =
Я начну, а ты мне помогай. Чтобы получить 10 надо к 7 прибавить …
Правильно, надо прибавить 3.
Теперь дополним состав числа 7. 7 это 3 и …
Верно, это 3 и 4.
Значит будем прибавлять частями. Сначала 3, а потом 4.
Посчитаем. 7 плюс 3 будет 10 и 10 плюс 4 получим 14.
7 + 7 = 7 + 3 + 4 = 10 + 4 = 14
Выполним сложение еще в одном примере со слагаемым 7.
8 + 7 =
Определи,как мы заменим второе слагаемое 7.
Нам подходит следующая пара: 7 это 2 и 5.
Прибавим частями: 8 и 2 будет 10, а к 10 прибавим 5 получим 15.
8 + 7 = 8 + 2 + 5 = 10 + 5 = 15
Осталось решить последний пример.
9 + 7 =
Слагаемому 9 не хватает всего 1 до образования десятка. А когда мы у 7 заберем 1, то останется 6. Вот мы и определили два слагаемых для прибавления частями. Осталось все посчитать.
9 + 7 = 9 + 1 + 6 = 10 + 6 = 16
Мы закончили с составлением таблицы сложения однозначных чисел с числом 7. Еще раз прочитай все примеры и запомни результаты вычислений.
Сложение вида □ + 8, □ + 9
Сейчас мы завернем на последнюю улицу и остановимся в беседке возле домиков с номерами 8, 9 и 10.
Сначала рассмотрим примеры из таблицы сложения однозначных чисел с числом 8, которые можно решить с использованием переместительного свойства сложения.
Осталось решить всего два примера на сложение вида □ +8. Думаю ты уже хорошо усвоил алгоритм выполнения сложения с переходом через десяток. Поэтому предлагаю тебе «хитрое» задание. Я выполнила все вычисления, но допустила некоторые ошибки. Постарайся найти их и исправить.
Тебе нужно выучить только эти два примера из таблицы сложения со слагаемым 8.
В таблице сложения однозначных чисел с числом 9 примеров для заучивания нет совсем.Ведь в ней много примеров, результаты которых ты уже знаешь из других таблиц.
Тебе нужно выучить только эти два примера из таблицы сложения со слагаемым 8.
В таблице сложения однозначных чисел с числом 9 примеров для заучивания нет совсем.Ведь в ней много примеров, результаты которых ты уже знаешь из других таблиц.
Кроме этого у таблицы сложения однозначных чисел с числом 9 есть очень интересная особенность.
Рассмотрим ее на первом примере из таблицы: 2 + 9 = 11. Какое первое слагаемое?
Верно, 2.
А теперь посмотрим на сумму. Она равна 11. Следует обратить внимание на количество единиц в данном числе (это последняя цифра). Всего 1 единица.
1 является предыдущим к числу 2.
Итак, какой можно сделать вывод? При выполнении сложения с числом 9 мы получаем число, у которого 1 дес., а количество единиц на 1 меньше, чем другое слагаемое.
Давай проверим это правило еще на одном примере.
5 + 9 =
Первое слагаемое 5. Значить сумма должно быть равна числу, у которого 1 дес. и 4 единицы. Получается 14.
Проверь по таблице: 5 + 9 = 14. Все верно! Значит правило работает. Давай с его помощью решим последний пример в таблице сложения однозначных чисел с числом 9.
Как ты думаешь, сколько единиц должно иметь число, которое обозначает сумму данного выражения?
Верно, 8 единиц.
Значит в результате мы должны получить число, в котором 1 дес. и 8 ед. Это 18.
9 + 9 = 18
Таблица сложения
Мы рассмотрели все случаи сложения с переходом через десяток. Теперь можем составить общую таблицу.
Наша таблица сложения может иметь другой вид.
В таблице зеленым цветом отмечены примеры, результат которых находим путем использования переместительного закона сложения.
Ты можешь выбрать любой вариант таблицы, который больше подходит для заучивания. Чтобы ускорить процесс запоминания рекомендуется выполнять тренировочные задания.
Посмотри на картинку и запиши пропущенные числа.
Определи, в какое ведро должна попасть каждая рыбка.
Установи соответствие и соедини.
Результаты заучивания таблицы проверь в процессе выполнения тестовых заданий.
- Главная
- Справочники
- Справочник по математике для начальной школы
- Сложение
Познакомимся со сложением.
Рассмотрим числовой ряд.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Прибавляет число 2.
К какому числу он прибавляет число 2?
К числу 4.
Наш зайчик стоит на числе 4 и думает, в какую сторону ему идти.
Подскажи ему.
В какую сторону пойдёт зайчик?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает заяц?
2, потому что ему нужно прибавить 2.
На каком делении остановится заяц?
На числе 6.
Когда прибавляем, становится больше.
Чем правее, тем числа больше.
4 + 2 = 6
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Прибавляет число 5.
К какому числу он прибавляет число 5?
К числу 3. Мы поставили зайчика на число 3.
В какую сторону он пойдёт?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает зайчик? 5.
На каком делении он остановится? На числе 8.
3 + 5 = 8
Как называются числа при сложении?
Первое слагаемое и второе слагаемое.
Результат называется суммой.
Рассмотрите рисунок.
Представь части домика как слагаемые и сумму.
Как найти неизвестное слагаемое
Второе слагаемое неизвестно.
Рассмотри рисунок и догадайся, как его можно найти.
Нужно из суммы вычесть первое слагаемое.
Рассмотри рисунок.
Неизвестно первое слагаемое.
Как его можно найти?
Нужно из суммы вычесть второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Проверка сложения
Если из суммы двух слагаемых, вычесть одно из слагаемых, то получится второе слагаемое.
8 + 4 = 12
12 — 4 = 8
12 — 8 = 4
Именно эта связь между суммой и слагаемыми используют для проверки вычислений.
Например, 35 + 7 = 42.
Правильно ли произведено вычисление? Можно проверить так:
42 — 7 = 35, мы из суммы вычли одно из слагаемых и получили ВТОРОЕ слагаемое. Значит, вычисление произведено верно и пример решен правильно.
Перестановка слагаемых
Сделаем запись к рисунку.
3 + 2 = 5
Сделаем запись к этому рисунку.
2 + 3 = 5
Теперь рассмотрим обе записи к рисункам:
3 + 2 = 5
3 — первое слагаемое
2 — второе слагаемое
5 сумма
2 + 3 = 5
2 — первое слагаемое
3 — второе слагаемое
5 — сумма
Мы заметили, что сумма в обеих записях одинаковая, хотя слагаемые мы записывали по-разному.
Это переместительный закон сложения, который гласит:
От перестановки мест слагаемых сумма не меняется.
Сочетательный закон сложения
Рассмотрим пример: (37 + 29) + 1 = …. (читаем: к сумме чисел 37 и 29 прибавить
1) Какие числа удобно сложить сначала, чтобы получился удобный способ? Числа 29 и 1.
Сумму чисел 29 и 1 возьмем в скобки.
37 + (29 + 1) = … (читаем: к 37 прибавить сумму чисел 29 и 1)
Решаем. Сначала выполним действие в скобках.
29 + 1 = 30
37 + 30 = 67, значит,
(37 + 29) + 1 = 67
Вывод: два соседних слагаемых можно заменить их суммой.
Советуем посмотреть:
Табличное сложение
Письменное сложение в столбик
Правило встречается в следующих упражнениях:
1 класс
Страница 27,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 50,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 62,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 66,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 73,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 90,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 102,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 28,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 29. Урок 18,
Петерсон, Учебник, часть 1
Страница 75. Урок 38,
Петерсон, Учебник, часть 3
2 класс
Страница 34,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 33,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 52,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 62,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 39. Урок 20,
Петерсон, Учебник, часть 1
Страница 14. Урок 4,
Петерсон, Учебник, часть 2
Страница 38. Урок 15,
Петерсон, Учебник, часть 2
Страница 54. Урок 19,
Петерсон, Учебник, часть 3
3 класс
Страница 34,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 40,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 19,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 31,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 21,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 48,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 52,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 74,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 98,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 95. Урок 36,
Петерсон, Учебник, часть 1
4 класс
Страница 5,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 91,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 43,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 43. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 83. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 15,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 6. Урок 2,
Петерсон, Учебник, часть 1
5 класс
Задание 219,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Содержание
Определение действия сложение и компоненты сложения
Переместительный и сочетательный законы сложения
Правило прибавления слагаемого к сумме или суммы к слагаемому
Изменение суммы чисел с изменением слагаемых
Сложение однозначных чисел
Сложение многозначного и однозначного чисел
Сложение двух многозначных чисел в столбик
Сложение в столбик нескольких многозначных чисел
Пройти тест по теме «Сложение и вычитание натуральных чисел» можно по ссылке. Проверьте свои знания!
Как вы уже знаете, любое натуральное число представляет собой единицу или собрание нескольких единиц. Так вот, мы можем взять несколько чисел и объединить все единицы, которые их составляют, в одно большое собрание. Число, которое получилось в результате этого объединения, называется суммой.
Сумма чисел – это такое число, которое получается после объединения всех единиц других данных натуральных чисел.
Слагаемые – это числа, над которыми мы выполняем действие сложения. Иными словами, это те числа, количество единиц которых мы объединяем в новом числе.
Арифметическое действие – это нахождение нового числа при помощи двух или нескольких других данных чисел.
В курсе математики 5 класса изучаются основные арифметические действия – сложение, вычитание, умножение и деление.
Определение
Сложение – это арифметическое действие, которое выполняется для получения суммы нескольких чисел.
Или другими словами:
Сложение – это действие увеличения числа на количество единиц, содержащихся в другом числе.
Сумма – это результат действия сложения.
На записи действие сложения обозначается знаком + (плюс). То есть, если записано 3+2+5, то это означает, что нам нужно найти сумму этих трех чисел: 3, 2 и 5. Сумма записывается обычно справа от слагаемых после знака = (равно): 3+2+5 = 10.
Сумма чисел состоит (слагается, складывается, – можно говорить по-разному) из двух или более слагаемых. Понятно, что сумма всегда больше любого ее слагаемого.
Слагаемые – это не что иное, как состав числа, обозначающего сумму этих слагаемых.
Компоненты действия сложения для двух слагаемых:
Компоненты сложения для трех слагаемых:
Действие сложения можно выполнить всегда. Действительно, так как натуральный ряд бесконечен, то мы всегда можем любые числа этого ряда объединить в другое, какое угодно большое число.
Действие сложения всегда имеет единственный результат. Действительно, если мы, к примеру, отметим на координатном луче с началом в точке O и единичным отрезком 1 см отрезок OA длиной 5 см, а потом построим еще один отрезок AB длиной 7 см, то у нас получится только единственный отрезок OB длиной 12 см.
Рисунок 1. Сумма двух чисел на координатном луче.
Основные свойства суммы натуральных чисел
Есть два основных закона суммы, из которых следуют остальные ее свойства:
- переместительный закон сложения,
- сочетательный закон сложения.
Переместительный закон сложения
Сумма двух или нескольких чисел от изменения порядка сложения слагаемых не меняется.
Это значит, что значение суммы не зависит от порядка выполнения действия сложение.
Например, в каком бы порядке мы ни складывали числа 2, 3 и 5, результат неизменно будет 10:
Сочетательный закон сложения
Сумма нескольких чисел не поменяется, если некоторые слагаемые заменить их суммой.
Это значит, что мы можем группировать слагаемые как угодно, а также выполнять действия сложения в любом порядке.
Например, если в нашем примере мы заменим слагаемые 2 и 3 их суммой, то результат останется такой же, как и при обычном сложении слагаемых:
То же самое будет, если мы заменим слагаемые 3 и 5, или 2 и 5 их суммами:
или
или
Из этих законов вытекает правило прибавления слагаемого к сумме или суммы к слагаемому.
Правило
Для прибавления суммы некоторых чисел к числу или некоторого числа к сумме чисел, нужно сложить это число с одним из слагаемых суммы, а получившийся результат сложить последовательно с остальными слагаемыми.
Пример 1. Прибавление числа к сумме чисел:
Можно сразу вычислить сумму чисел в скобках и сложить ее с первым слагаемым:
325+(12+64+5) = 325+81 = 406
Также можно использовать правило прибавления слагаемого и суммы. Результат при этом не поменяется
325+12 = 337;
337+64 = 401;
401+5 = 406
или
325+64 = 389;
389+12 = 401;
401+5 = 406.
Пример 2. Прибавление суммы чисел к другому числу:
Можно сразу вычислить сумму чисел в скобках и сложить ее со вторым слагаемым
(54+240+189)+37 = 483+37 = 520
Или можно использовать правило прибавления суммы чисел к числу. Результат останется тот же.
54+37 = 91;
91+240 = 331;
331+189 = 520
или
240+37 = 277;
277+54 = 331;
331+189 = 520.
Изменение суммы чисел с изменением слагаемых
Чтобы понять, как изменится сумма чисел, если изменить одно или несколько ее слагаемых, нужно вспомнить, что сумма представляет собой собрание всех единиц, из которых состоят слагающие ее числа. Поэтому, легко можно понять, что:
При увеличении одного из слагаемых на какое-то число (на какое-то количество единиц), сумма тоже увеличится на это же число (на это же количество единиц).
При уменьшении одного из слагаемых на какое-то число (на какое-то количество единиц), сумма тоже уменьшится на это же число (на это же количество единиц).
Эти два свойства справедливы и в обратную сторону. То есть, если увеличить или уменьшить сумму на какое-то число, тогда для сохранения равенства нужно соответственно увеличить или уменьшить одно из слагаемых.
Если увеличить одно из слагаемых на какое-то число (на какое-то количество единиц), а другое уменьшить на это же число (на это же количество единиц), то в результате сумма не поменяется.
Простой пример увеличения суммы при увеличении слагаемого: у вас есть 700 рублей; 200 рублей лежит в левом кармане, а 500 – в правом. Вы нашли на улице 300 рублей и положили их в левый карман, после чего там стало 200+300=500 рублей. Таким образом, всего у вас оказалось 500+500=1000 рублей, то есть, сумма всех ваших денег увеличилась на 300 рублей.
Попробуйте самостоятельно придумать примеры для всех трех правил.
Сложение однозначных чисел
Сложение двух однозначных чисел выполняется так: одно число увеличивается на количество единиц другого числа. То есть, единицы одного числа присоединяются к единицам другого числа.
Например, для нахождения суммы 5+2 нужно к числу 5 присоединить 2 единицы. Тогда получим 5+2=7. А если нужно к числу 7 прибавить число 8, или другими словами, найти сумму 7+8, то после присоединения к 7 единиц числа 8 получим 1 десяток единиц и еще 5 единиц, то есть, число 15.
Сложение однозначных чисел – это первый и очень важный шаг в освоении этого арифметического действия. Если хорошо выучить все результаты сложения однозначных чисел между собой, тогда вы сможете намного быстрее складывать в уме любые числа.
Сложение многозначного числа с однозначным
Чтобы найти сумму многозначного числа и однозначного, можно действовать двумя способами. Оба они основаны на свойствах суммы чисел. Рассмотрим их на примерах.
Допустим, нам нужно найти сумму чисел 88 и 5.
Способ 1.
Представим число 88 в виде суммы 80+8 и прибавим к ней число 5. После этого, найдем сумму однозначных чисел 8 и 5, получится 13. Прибавим этот результат к числу 80. Число 13 – это 10+3, поэтому мы к 8 десяткам прибавляем 1 десяток, получаем 9 десятков, или число 90, а к нему прибавляем еще 3 (оставшиеся от числа 13), и получим 93.
То есть, мы проделываем такие действия:
88+5 = 80+8+5 = 80+13 = 80+10+3 = 90+3=93.
Способ 2.
Замечаем, что если к 88 прибавить 2, то получим полный десяток, то есть, число 90. Тогда представляем число 5 в виде суммы 2+3; число 2 складываем с 88, получаем замеченное нами ранее число 90. Добавляем к нему оставшееся число 3, и получаем результат 93.
То есть, ход вычисления был такой:
88+5 = 88+2+3 = 90+3 = 93.
Сложение в столбик многозначных чисел
Сумма многозначных чисел удобно вычисляется, если использовать так называемое сложение в столбик.
Сложение в столбик – это способ нахождения суммы чисел путем их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим).
Этот способ простой, и он помогает не запутаться во время вычисления, не допустить ошибки. Но, чтобы складывать быстро, как я и говорил раньше, вам нужно очень хорошо знать все попарные суммы однозначных чисел.
Итак, допустим, что нам нужно найти сумму : 5728+803
Запишем их друг под другом таким образом, чтобы совпадали соответствующие разряды обоих чисел, т.е. единицы под единицами, десятки под десятками и т.д. После этого, под вторым слагаемым проводим горизонтальную черту, а между слагаемыми ставим знак действия, т.е. плюс. У нас получилась такая запись:
Теперь нам нужно сложить между собой единицы каждого разряда, начиная с первого: сперва простые единицы, потом десятки единиц, потом сотни единиц и т.д. Результаты этих сложений записываем под чертой в том разряде, единицы которого мы складывали.
Начинаем с простых единиц: 8+3=11. У нас получилось число 11, то есть, 1 десяток и 1 единица. 1 единицу мы записываем под чертой в разряде единиц, а 1 получившийся десяток нужно будет дополнительно прибавить к сумме единиц разряда десятков. Чтобы не забыть совершить это действие, мы пишем над цифрами разряда десятков маленькую цифру 1 или ставим там точку.
Про подобное действие обычно говорят: «один пишем, один в уме» , то есть, оставляем в памяти, чтобы не забыть добавить при следующем действии.
Далее переходим к десяткам. У первого слагаемого 2 единицы разряда десятков, а у второго 0, поэтому: 2+0=2. Мы помним, что после сложения простых единиц у нас образовался дополнительно 1 десяток, поэтому к этому результату добавляем еще единицу: 2+1=3. У нас получилось 3 десятка, поэтому записываем цифру 3 под чертой в разряде десятков.
Следующими идут сотни: 7+8=15. Первым делом проверяем, не нужно ли нам дополнительно добавлять единицу? В нашем случае нет, потому что на предыдущем шаге при сложении десятков мы получили однозначное число. Поэтому, пишем под чертой в разряде сотен цифру 5. И у нас получилось дополнительно 10 сотен, то есть, 1 тысяча единиц. Значит, нам нужно отметить эту получившуюся 1 тысячу как дополнительную, поставив маленькую цифру 1 над цифрами разряда тысяч.
В разряде тысяч у первого слагаемого стоит цифра 5, а у второго ничего не стоит. Но мы помним, что при отсутствии разрядов в начале числа (слева) нули не пишутся, но подразумевается, что в этих разрядах по 0 единиц. Поэтому мы находим сумму 5+0=5, т.е. 5 единиц разряда тысяч и добавляем к ней дополнительную 1 единицу тысяч, полученную после сложения разрядов сотен. 5+1=6. Записываем эту цифру под чертой в разряде тысяч.
После нахождения суммы чисел методом сложения столбиком, записываем результат решения в исходном строчном примере:
5728+803 = 6531
Сложение в столбик нескольких многозначных чисел
Этим способом так же легко можно найти сумму нескольких многозначных чисел.
Рассмотрим пример: 12044+28609+1358
Сложив простые единицы, мы получим 21, то есть, 2 десятка и 1 единицу. Записываем под чертой в разряде единиц цифру 1, а 2 отмечаем «в уме».
Сложив десятки этих трех чисел, мы получим 4+0+5=9 единиц разряда десятков. Добавив 2 десятка единиц, которые у нас были «в уме», получаем 11, то есть, 10 десятков и ещё 1 десяток. Под чертой мы записываем цифру 1 в разряде десятков, а так как 10 десятков – это не что иное как 1 сотня, то мы отмечаем «единицу в уме», то есть, ставим над всеми тремя числами в разряде сотен маленькую цифру 1.
Теперь складываем 0 сотен первого числа, 6 сотен второго и 3 сотни третьего. Получается 9 сотен. Добавляем 1 сотню, которая была «в уме» после сложения всех десятков, и у нас выходит 10 сотен, то есть, 1 тысяча единиц. Значит, под чертой в разряде сотен мы пишем 0 (так как у нас не получилось ни одной единицы сотен, только десяток сотен), а над всеми числами в разряде тысяч отмечаем дополнительную 1 тысячу.
В разряде тысяч мы находим сумму 2+8+1, это будет 11 тысяч единиц, добавляем 1 тысячу, которая получилась после сложения сотен. Получаем 12 тысяч единиц, то есть, 10 тысяч и 2 тысячи. Цифру 2 пишем в разряде тысяч единиц под чертой, а единицу десятка тысяч (наши 10 тысяч единиц) отмечаем сверху в соответствующем разряде.
Нам осталось сложить десятки тысяч единиц: 1+2+0=3 десятка тысяч, и прибавить к результату 1 десяток тысяч, получившийся после прошлого шага. У нас вышло 4 десятка тысяч, поэтому в этом разряде под чертой мы пишем цифру 4.
Нам остается только записать результат в начальном примере:
12044+28609+1358
Хочу обратить внимание, что при сложении в столбик все шаги (сложение единиц каждого разряда) совершаются последовательно в одной записи. Я расписывал их отдельными только для лучшего понимания сути процесса сложения. И конечно же, не нужно выделять каждый разряд отдельным цветом. В случае рассмотренных выше примеров все решение выглядит так:
Загрузить PDF
Загрузить PDF
Если вы готовитесь к тестированию или просто хотите научиться быстро складывать числа, запомните, как суммировать целые числа от 1 до 

-
1
Определите арифметическую последовательность. Посмотрите на ряд чисел, которые вы хотите сложить. Чтобы воспользоваться формулой для суммирования целых чисел, убедитесь, что ряд чисел действительно является последовательностью, то есть каждое число возрастает на одну и ту же величину.[1]
- Например, ряд чисел 5, 6, 7, 8, 9 представляет собой последовательность, как и ряд 17, 19, 21, 23, 25.
- Ряд чисел 5, 6, 9, 11, 14 не является последовательностью, потому что числа возрастают на разные величины.
-
2
-
3
Найдите количество складываемых целых чисел. Чтобы суммировать целые числа от начального числа до
, необходимо найти общее количество складываемых чисел. Например, если вы хотите сложить целые числа от 1 до 200, общее количество чисел вычисляется так: 200+1 = 201.[2]
- Например, если нужно найти сумму целых чисел от 1 до 12, количество чисел: 12+1 = 13.
-
4
Найдите сумму целых чисел между двумя целыми числами, которые в расчете не участвуют. В этом случае вычтите 1 из
.[3]
- Например, чтобы найти сумму целых чисел между 1 и 100, вычтите 1 из 100 и получите 99.
Реклама
-
1
-
2
-
3
-
4
Пользуйтесь представленными формулами, чтобы найти сумму. Когда вы подставили нужно число в формулу, умножьте его на себя, прибавьте 1, 2 или 4 (в зависимости от формулы), а затем разделите результат на 2 или 4. [7]
- Пример 1: 100*101/2 = 10100/2 = 5050.
- Пример 2 (с четными числами): 20*22/4 = 440/4 = 110.
Реклама
Об этой статье
Эту страницу просматривали 191 897 раз.
Была ли эта статья полезной?
Порядок действий
- Порядок действий без скобок
- Порядок действий со скобками
- Дробная черта
Для правильного вычисления значений числовых выражений, в которых нужно произвести более одного действия, необходимо знать установленный порядок выполнения арифметических действий.
Порядок действий без скобок
Установленный порядок арифметических действий без скобок:
- Если выражение содержит только действия на сложение и вычитание, то они выполняются в порядке следования — слева направо:
- Если выражение содержит только действия на умножение и деление, то действия выполняются в порядке следования — слева направо:
- Если в выражении присутствуют и умножение с делением, и сложение с вычитанием, то сначала выполняются умножение и деление в порядке их следования (слева направо), а затем сложение и вычитание в порядке их следования (слева направо):
Порядок действий со скобками
Если выражение содержит скобки, то сначала выполняются все действия внутри скобок, а затем все действия, находящиеся за скобками.
В числовых выражениях со скобками порядок выполнения арифметических действий такой же, как и в выражениях без скобок.
Скобки применяются для обозначения действий, которые нужно произвести раньше остальных. Скобки не влияют на порядок остальных действий в выражении, остальные действия выполняются в указанном порядке.
Дробная черта
Дробная черта в выражении может быть заменена на знак деления, в этом случае, всё что было над и под дробной чертой надо взять в скобки. Например:
| 13 + 2 | = (13 + 2) : (10 — 7). |
| 10 — 7 |
Знак деления в выражении можно заменить дробной чертой только в том случае, если это не нарушает порядок действий. Например, выражение:
20 : 4(2 + 3)
нельзя заменить на
потому что такая замена нарушит порядок действий в данном выражении.
| 20 : 4(2 + 3) ≠ | 20 | ; |
| 4(2 + 3) |
| 20 | = 20 : (4(2 + 3)). |
| 4(2 + 3) |
Дробная черта в выражении заменяет скобки и означает, что надо вычислить отдельно выражение, стоящее в числителе, и отдельно выражение, стоящее в знаменателе, и первый результат разделить на второй.