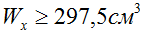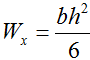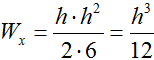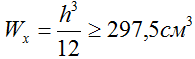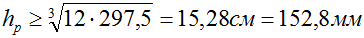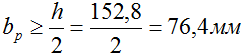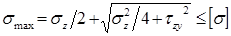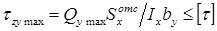Обычно в инженерной
практике проверку прочности балок
производят по нормальным наибольшим и
касательным напряжениям [2]. Нормальные
напряжения σ зависят от величины
изгибавшего момента, а касательные
τ – от величины поперечной силы.
Касательные напряжения в сечениях балки
обычно не играют существенной роли,
поэтому размеры сечения балок определяют
из условия прочности по нормальным
максимальным напряжениям:
,
где Мmax
–
наибольший (по абсолютной величине)
изгибающий момент, известный из эпюры
изгибающих моментов (
).
Сечение балки
подбирается по моменту сопротивления
относительно нейтральной оси:
.
(3.10)
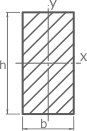
Для балки
прямоугольного сечения
.
Числовые значения
моментов сопротивления стандартных
профилей проката указаны в соответствующих
государственных стандартах на прокат,
а на балки двутавровые приведены в
таблицах приложения Г. Следует подбирать
номер профиля, имеющий большее стандартное
ближайшее значение. Допустимо принимать
и меньшее ближайшее значение WхСТ,
однако оно должно удовлетворять условию:
.
Момент сопротивления
при изгибе
Подходит швеллер
№ 8 (Wx=22,4
см3,
площадь сечения А=8,98 см2).
Определим
прямоугольное сечение (рисунок 3.10) при
Рисунок 3.10 –
Сечение швеллера и прямоугольное сечение
Площадь
прямоугольного сечения
A=bh=16,27
см2
≈
в 2 раза больше площади швеллера.
3.4 Совместное действие изгиба и кручения
Сочетание деформаций
изгиба и кручения испытывает большинство
валов, которые обычно представляют
собой прямые брусья круглого или
кольцевого сечения.
Возникающие от
изгиба нормальные напряжения достигают
максимального значения в волокнах,
наиболее удаленных от нейтральной оси:
,
где М — максимальный
изгибающий момент, Нм;
W
— осевой момент сопротивления сечения,
м3.
Для вала круглого
сечения
Максимальные
касательные напряжения при кручении
возникают в точках контура поперечного
сечения:
где Wp
— полярный момент сопротивления сечения
(Wp=2W),
м3;
Т
– крутящий момент, Нм.
Таким образом, при
сочетании изгиба и кручения опасными
будут точки (для конкретного поперечного
сечения), наиболее удаленные от нейтральной
оси.
Применив третью
теорию прочности, получим
.
Расчетная формула
для круглых валов принимает вид:
,
где М
экв.
– эквивалентный момент, Нм;
[σ]
– допускаемое
напряжение на растяжение для материала
вала, Па.
Если величина и
направление нагрузки во время работы
вращающегося вала остаются неизменными,
то напряжения изгиба в теле вала будут
изменяться во времени по симметричному
циклу – I циклу
нагружения (рисунок 3.11).
Рисунок 3.11 – График
изменения во времени напряжения изгиба
I
цикл
При действии на
вал нагрузок в разных плоскостях силы
раскладывают на две взаимно перпендикулярные
плоскости, за одну из которых выбирают
плоскость действия одной из сил.
Суммарный изгибающий
момент определится как геометрическая
сумма моментов, действующих во взаимно
перпендикулярных плоскостях
рассматриваемого сечения:
где Мiв
и Мiгор
– изгибающие
моменты в i
– м сечении,
действующие в вертикальной и в
горизонтальной плоскостях соответственно.
Эквивалентный
момент определится по формуле:
,
Диаметр вала в
опасном сечении
рассчитывается из условия прочности:
.
Примечание —
При решении задач все необходимые
вычисления следует сначала проделать
в общем виде, обозначая все данные и
искомые величины буквами, после чего
вместо буквенных обозначений подставить
их числовые значения и найти результат.
На расчетных эскизах размеры должны
быть проставлены теми же буквами, какие
имеются в расчетных формулах.
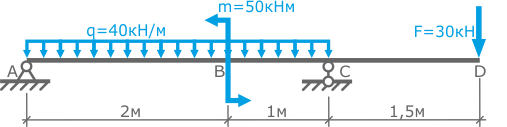
Пример 4.
Построить
эпюры изгибающих, крутящего, суммарного
изгибающего моментов и определить
диаметр вала (рисунок 3.12) в опасном
сечении.
Т = 0,2 кНм, F
= 2 кН, q
= 4 кН/м, a
= 0,2м, b
=1,2а = 0,24м,
с = 0,8а = 0,16м, [σ]
= 110МПа.
Решение:
Плоскость yz:
Плоскость хz:
Из условия прочности
наиболее нагруженного сечения А определим
диаметр вала.
Рисунок 3.12 —
Расчетная
схема и эпюры вала
ПРИЛОЖЕНИЕ А
ЗАДАЧА 1
Расчет бруса на
осевое растяжение (сжатие)
Сечение бруса
квадратное. Материал – сталь. Допускаемое
напряжение [σ]
= 100 МПа. Модуль продольной упругости Е
= 2·105
МПа. Исходные данные к расчету см. в
таблице + рисунок.
ИСХОДНЫЕ ДАННЫЕ
|
Вариант |
F1 |
F2 |
F3 |
l1 |
l2 |
l3 |
|
кН |
м |
|||||
|
1 |
32 |
18 |
24 |
0,7 |
0,4 |
0,8 |
|
2 |
28 |
16 |
12 |
0,6 |
0,5 |
0,7 |
|
3 |
22 |
8 |
26 |
0,5 |
0,6 |
0,9 |
|
4 |
19 |
24 |
15 |
0,8 |
0,6 |
0,5 |
|
5 |
30 |
12 |
16 |
0,4 |
0,9 |
0,6 |
|
6 |
27 |
15 |
10 |
0,6 |
0,7 |
0,8 |
|
7 |
24 |
14 |
8 |
0,3 |
0,8 |
0,7 |
|
8 |
26 |
16 |
11 |
0,7 |
0,9 |
0,4 |
|
9 |
25 |
12 |
18 |
0,5 |
0,5 |
0,9 |
|
10 |
31 |
26 |
14 |
0,7 |
0,3 |
0,5 |
|
11 |
18 |
15 |
12 |
0,6 |
0,6 |
0,8 |
|
12 |
23 |
25 |
12 |
0,8 |
0,4 |
0,7 |
|
13 |
16 |
8 |
12 |
0,4 |
0,7 |
0,9 |
|
14 |
18 |
10 |
14 |
0,6 |
0,5 |
0,8 |
|
15 |
22 |
12 |
14 |
0,5 |
0,6 |
0,7 |
|
16 |
20 |
9 |
12 |
0,7 |
0,4 |
0,8 |
|
17 |
24 |
16 |
12 |
0,9 |
0,3 |
0,6 |
|
18 |
18 |
10 |
14 |
0,8 |
0,2 |
0,7 |
|
19 |
25 |
18 |
14 |
0,7 |
0,6 |
0,9 |
|
20 |
19 |
11 |
10 |
0,8 |
0,5 |
0,6 |
|
21 |
30 |
13 |
10 |
0,4 |
0,8 |
0,5 |
|
22 |
27 |
15 |
12 |
0,6 |
0,9 |
0,4 |
|
23 |
22 |
11 |
10 |
0,7 |
0,7 |
0,6 |
|
24 |
20 |
9 |
10 |
0,5 |
0,9 |
0,7 |
|
25 |
24 |
12 |
14 |
0,7 |
0,4 |
0,9 |
|
26 |
19 |
10 |
11 |
0,8 |
0,3 |
0,6 |
|
27 |
25 |
13 |
13 |
0,4 |
0,7 |
0,8 |
|
28 |
21 |
16 |
12 |
0,5 |
0,5 |
0,7 |
|
29 |
22 |
20 |
10 |
0,8 |
0,6 |
0,8 |
|
30 |
23 |
15 |
11 |
0,7 |
0,3 |
0,9 |
Расчетные схемы
ПРИЛОЖЕНИЕ Б
ЗАДАЧА 2 РАСЧЕТ
ВАЛА НА КРУЧЕНИЕ
Сечение вала
круглое, сплошное и кольцевое. Допускаемое
напряжение кручения [τ]=25
МПа. Модуль сдвига G=8∙104
МПа
|
Вариант |
Т1, |
Т2, |
Т3, |
Т4, |
l1, |
l2, |
l3, |
l4, |
l5, |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
200 |
300 |
400 |
0,8 |
0,7 |
0,4 |
0,6 |
0,3 |
|
|
2 |
300 |
500 |
500 |
0,7 |
0,6 |
0,5 |
0,8 |
0,4 |
|
|
3 |
400 |
400 |
300 |
0,9 |
0,5 |
0,6 |
0,3 |
0,2 |
|
|
4 |
100 |
200 |
300 |
0,5 |
0,8 |
0,9 |
0,4 |
0,3 |
|
|
5 |
300 |
400 |
100 |
0,6 |
0,4 |
0,6 |
0,5 |
0,4 |
|
|
6 |
100 |
100 |
500 |
0,8 |
0,6 |
0,7 |
0,3 |
0,2 |
|
|
7 |
300 |
200 |
200 |
0,7 |
0,3 |
0,8 |
0,4 |
0,3 |
|
|
8 |
500 |
600 |
500 |
0,4 |
0,7 |
0,9 |
0,5 |
0,4 |
|
|
9 |
600 |
800 |
700 |
0,9 |
0,5 |
0,5 |
0,3 |
0,2 |
|
|
10 |
400 |
200 |
300 |
0,5 |
0,7 |
0,8 |
0,2 |
0,3 |
|
|
11 |
300 |
500 |
600 |
0,8 |
0,6 |
0,6 |
0,4 |
0,3 |
|
|
12 |
100 |
200 |
200 |
0,7 |
0,8 |
0,4 |
0,3 |
0,4 |
|
|
13 |
700 |
500 |
200 |
0,9 |
0,4 |
0,7 |
0,2 |
0,3 |
|
|
14 |
800 |
400 |
300 |
0,8 |
0,6 |
0,5 |
0,3 |
0,3 |
|
|
15 |
900 |
600 |
400 |
0,7 |
0,5 |
0,6 |
0,4 |
0,4 |
|
|
16 |
100 |
200 |
300 |
0,8 |
0,7 |
0,4 |
0,2 |
0,5 |
|
|
17 |
200 |
800 |
100 |
0,6 |
0,9 |
0,3 |
0,3 |
0,6 |
|
|
18 |
300 |
800 |
100 |
0,7 |
0,8 |
0,2 |
0,4 |
0,7 |
|
|
19 |
400 |
500 |
300 |
200 |
0,9 |
0,7 |
0,6 |
0,2 |
|
|
20 |
500 |
500 |
200 |
300 |
0,6 |
0,8 |
0,5 |
0,3 |
|
|
21 |
600 |
900 |
400 |
100 |
0,5 |
0,4 |
0,8 |
0,4 |
|
|
22 |
700 |
800 |
300 |
200 |
0,4 |
0,6 |
0,9 |
0,2 |
|
|
23 |
800 |
700 |
100 |
400 |
0,6 |
0,7 |
0,7 |
0,3 |
|
|
24 |
900 |
600 |
200 |
300 |
0,7 |
0,5 |
0,9 |
0,4 |
|
|
25 |
100 |
500 |
300 |
200 |
0,9 |
0,7 |
0,4 |
0,2 |
|
|
26 |
200 |
300 |
500 |
300 |
0,6 |
0,8 |
0,3 |
0,4 |
|
|
27 |
300 |
300 |
400 |
200 |
0,8 |
0,4 |
0,7 |
0,3 |
|
|
28 |
400 |
200 |
600 |
100 |
0,7 |
0,5 |
0,5 |
0,2 |
|
|
29 |
500 |
100 |
700 |
200 |
0,8 |
0,8 |
0,6 |
0,3 |
|
|
30 |
600 |
200 |
800 |
300 |
0,9 |
0,7 |
0,3 |
0,4 |
Расчетные схемы
ПРИЛОЖЕНИЕ В
ЗАДАЧА 3
РАСЧЕТ НА ПРОЧНОСТЬ ДВУХОПОРНОЙ БАЛКИ
ПРИ ИЗГИБЕ
Для данной балки подобрать сечения
двутавра и прямоугольника (h/b=2).
Допускаемое напряжения изгиба [σ]=160
МПа
|
Вариант |
М,K |
F, |
q, |
l1, |
l2, |
l3, |
l4, |
l5, |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
18 |
26 |
14 |
2 |
2 |
5 |
1 |
1 |
|
2 |
24 |
18 |
10 |
2 |
3 |
2 |
3 |
2 |
|
3 |
16 |
34 |
12 |
2 |
3 |
3 |
2 |
2 |
|
4 |
30 |
24 |
16 |
2 |
4 |
4 |
1 |
2 |
|
5 |
20 |
12 |
8 |
1,8 |
2,2 |
1 |
5 |
1 |
|
6 |
22 |
16 |
10 |
1,6 |
1 |
1,4 |
6 |
2 |
|
7 |
18 |
22 |
14 |
2,2 |
2 |
1,8 |
5 |
1 |
|
8 |
16 |
24 |
12 |
2,5 |
1 |
1,5 |
5 |
2 |
|
9 |
16 |
24 |
12 |
2,5 |
1 |
1,5 |
5 |
2 |
|
10 |
14 |
15 |
8 |
1,6 |
2 |
1,4 |
4 |
3 |
|
11 |
10 |
23 |
12 |
2 |
2 |
2 |
4 |
2 |
|
12 |
18 |
17 |
10 |
1,8 |
3 |
1,2 |
5 |
1 |
|
13 |
16 |
25 |
15 |
2 |
2 |
4 |
2 |
2 |
|
14 |
24 |
16 |
10 |
2 |
3 |
4 |
2 |
1 |
|
15 |
1 |
22 |
12 |
1,6 |
2,4 |
3,5 |
2,5 |
2 |
|
16 |
20 |
18 |
14 |
1,8 |
2,2 |
4,5 |
2,5 |
2 |
|
17 |
22 |
24 |
8 |
2 |
2 |
4 |
3 |
1 |
|
18 |
16 |
26 |
6 |
2 |
2 |
3,5 |
3,5 |
1 |
|
19 |
18 |
20 |
10 |
1,5 |
2,5 |
4,2 |
1,8 |
8 |
|
20 |
28 |
18 |
16 |
1,8 |
2,2 |
4,5 |
2,5 |
3 |
|
21 |
17 |
25 |
12 |
2 |
2 |
1 |
5 |
2 |
|
22 |
15 |
30 |
10 |
1,5 |
2,5 |
2 |
4 |
1 |
|
23 |
26 |
22 |
8 |
2 |
2 |
2 |
3 |
2 |
|
24 |
30 |
18 |
14 |
1,6 |
3,0 |
2 |
4 |
1 |
|
25 |
24 |
26 |
15 |
1,5 |
2,5 |
6 |
1 |
1 |
|
26 |
22 |
13 |
2,5 |
1,5 |
5 |
2 |
2 |
|
|
27 |
20 |
12 |
2,0 |
1,5 |
5,5 |
3 |
2 |
|
|
28 |
18 |
28 |
10 |
2,0 |
1,5 |
4,5 |
2 |
2 |
|
29 |
30 |
20 |
8 |
1,8 |
3,2 |
1 |
2 |
1 |
|
30 |
28 |
18 |
15 |
2 |
2,5 |
1,5 |
5 |
2 |
Расчетные схемы
задачи 3
ПРИЛОЖЕНИЕ Г
Сталь прокатная
– балки двутавровые (ГОСТ 8239-83)
h
– высота профиля;
b
– ширина;
d
– толщина;
t
– средняя толщина;
R
и r
– внутренний и наружный радиусы
скруглений;
J
– момент инерции;
W
– момент сопротивления;
i
– радиус инерции;
S
– статический момент полусечения
|
Номер профиля |
Масса |
Размеры, |
Площадь сечения, |
Jx, см4 |
Wx, см3 |
ix, см |
Sx, см3 |
Jy, см4 |
Wy, см3 |
iy, см |
|||||
|
h |
b |
d |
t |
R |
r |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
10 |
9,46 |
100 |
55 |
4,5 |
7,2 |
7 |
2,5 |
12 |
198 |
39,7 |
4,06 |
23 |
17,9 |
6,49 |
1,22 |
|
12 |
11,45 |
120 |
64 |
4,8 |
7,3 |
7,5 |
3 |
14,7 |
350 |
58,4 |
4,88 |
33,7 |
27,9 |
8,72 |
1,38 |
|
14 |
13,7 |
140 |
73 |
4,9 |
7,5 |
8 |
3 |
17,4 |
572 |
81,7 |
5,73 |
46,8 |
41,9 |
11,5 |
1,55 |
|
16 |
15,9 |
160 |
81 |
5,0 |
7,8 |
8,5 |
3,5 |
20,2 |
873 |
109,0 |
6,57 |
62,3 |
58,6 |
14,5 |
1,7 |
|
18 |
18,4 |
180 |
90 |
5,1 |
8,1 |
9,0 |
3,5 |
23,4 |
1290 |
143,0 |
7,42 |
81,4 |
82,6 |
18,4 |
1,88 |
|
18а |
19,9 |
180 |
100 |
5,1 |
8,3 |
9,0 |
3,5 |
25,4 |
1430 |
159,0 |
7,51 |
89,8 |
114,0 |
22,8 |
2,12 |
|
20 |
21,0 |
200 |
100 |
5,2 |
8,4 |
9,5 |
4,0 |
26,8 |
1840 |
184,0 |
8,28 |
104,0 |
115,0 |
23,1 |
2,07 |
|
20а |
22,7 |
200 |
110 |
5,2 |
8,6 |
9,5 |
4,0 |
28,9 |
2030 |
203,0 |
8,37 |
114,0 |
155,0 |
28,2 |
2,32 |
|
22 |
24,0 |
220 |
110 |
5,4 |
8,7 |
10,0 |
4,0 |
30,6 |
2550 |
232,0 |
9,13 |
131,0 |
157,0 |
28,6 |
2,27 |
|
22а |
25,8 |
220 |
120 |
5,4 |
8,9 |
10,0 |
4,0 |
32,6 |
2790 |
254,0 |
9,22 |
143,0 |
106,0 |
34,3 |
2,5 |
|
24 |
27,3 |
240 |
115 |
5,6 |
9,5 |
10,5 |
4,0 |
34,8 |
3460 |
289 |
9,97 |
163 |
198 |
34,5 |
2,37 |
|
24а |
29,4 |
240 |
125 |
5,6 |
9,8 |
20,5 |
4,0 |
37,5 |
3800 |
317 |
10,1 |
178 |
260 |
41,6 |
2,63 |
|
27 |
31,5 |
270 |
125 |
6,0 |
9,8 |
11,0 |
4,5 |
40,2 |
5010 |
371 |
11,2 |
210 |
260 |
41,5 |
2,54 |
|
27а |
33,9 |
270 |
135 |
6,0 |
10,2 |
11,0 |
4,5 |
43,2 |
5500 |
407 |
11,3 |
229 |
337 |
50,0 |
2,8 |
|
30 |
36,5 |
300 |
135 |
6,5 |
10,2 |
12,0 |
5 |
46,5 |
7080 |
472 |
12,3 |
268 |
337 |
49,9 |
2,69 |
|
30а |
39,2 |
300 |
145 |
6,5 |
10,7 |
12,0 |
5 |
49,9 |
7780 |
518 |
12,5 |
292 |
436 |
60,1 |
2,95 |
|
33 |
42,2 |
330 |
140 |
7,0 |
11,2 |
13,0 |
5 |
53,8 |
9840 |
597 |
13,5 |
339 |
419 |
59,1 |
3,79 |
|
36 |
48,6 |
360 |
145 |
7,5 |
12,3 |
14,0 |
6 |
61,9 |
13380 |
743 |
14,7 |
423 |
516 |
71,1 |
2,89 |
|
40 |
57,0 |
400 |
155 |
8,3 |
13,0 |
15,0 |
6 |
72,6 |
19062 |
953 |
16,2 |
545 |
667 |
86,1 |
3,08 |
|
45 |
66,5 |
450 |
160 |
9,0 |
14,2 |
16,0 |
7 |
84,7 |
27696 |
1231 |
18,1 |
708 |
808 |
101,0 |
3,09 |
|
50 |
78,5 |
500 |
170 |
10,0 |
15,2 |
17,0 |
7 |
100 |
39727 |
1589 |
19,9 |
919 |
1043 |
123,0 |
3,23 |
|
60 |
108,0 |
600 |
190 |
12,0 |
17,8 |
20,0 |
8 |
138 |
76806 |
2560 |
23,6 |
1491 |
1725 |
182,0 |
3,54 |
|
60б |
120,0 |
650 |
200 |
12,0 |
19,2 |
22,0 |
9 |
153 |
101400 |
3120 |
25,8 |
1800 |
2170 |
217,0 |
3,77 |
|
70 |
138,0 |
700 |
210 |
13,0 |
20,8 |
24,0 |
10 |
176 |
134600 |
3840 |
27,7 |
2230 |
2730 |
260,0 |
3,94 |
|
70а |
168,0 |
700 |
210 |
15,0 |
24,0 |
24,0 |
10 |
202 |
152700 |
4360 |
27,5 |
2550 |
3240 |
309,0 |
4,01 |
|
70б |
184,0 |
700 |
210 |
17,5 |
28,2 |
24,0 |
10 |
234 |
175770 |
5010 |
27,4 |
2940 |
3910 |
373,0 |
4,09 |
ПРИЛОЖЕНИЕ Д
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В этой статье рассмотрим, как подобрать двутавровое поперечное сечение при плоском изгибе.
Поперечное сечение при плоском изгибе, всегда подбирается по нормальным напряжениям, так как касательные напряжения при данном виде деформации, как правило, в несколько раз меньше, за исключением тех случаев, когда поперечные силы имеют большие значения.
Условие прочности для двутавра
Условие прочности при поперечном изгибе выглядит таким образом:
В неравенстве слева записано максимальное расчётное напряжение, а справа напряжение допустимое.
Максимальное расчётное напряжение можно найти двумя способами:
Как отношение максимального изгибающего момента к моменту сопротивления:
Либо по такой формуле, с использованием момента инерции:
где Мmax — максимальный изгибающий момент, y — расстояние от нейтральной линии до крайней точки сечения, J — момент инерции сечения.
Момент инерции и момент сопротивления связаны следующим образом:
Какую формулу удобнее использовать?
- Если в условии задачи вас просят найти максимальное напряжение, то используйте формулу с моментом сопротивления. То есть, по этой формуле вы сразу вычислите максимальные напряжения в крайних точках сечения.
- Если вам потребуется найти напряжение в любой другой точке сечения, например, в месте перехода полки в стенку, то используйте вторую формулу.
Подбор двутавра на практике
Ну что же, самое время перейти к практике. Например, посчитали вы балку, построили эпюры и нужно теперь подобрать двутавр удовлетворяющий условию прочности. Для этого вам необходимо:
Проанализировать эпюру изгибающих моментов и определить положение наиболее опасного сечения. Опасным можно считать то сечение, в котором изгибающий момент максимален. Скажем, у вас он будет равен 30 кНм.
Далее необходимо определить минимально допустимый момент сопротивления из условия прочности. Допустимое напряжение примем равным 160 МПа:
Нашли момент сопротивления. Далее по сортаменту двутавров (ГОСТ 8239-89) выбираем номер профиля, у которого момент сопротивления будет ближайшим большим к нашему расчётному. Это двутавр № 20а у которого момент сопротивления равен 203 см3.
Делаем проверочный расчет. Вычисляем напряжение с табличным значением момента сопротивления:
Так как получили напряжение меньшее, чем допустимое, можно сделать вывод, что подобранный двутавр удовлетворяет условию прочности.
Пример решения задачи по подбору минимальных размеров балки прямоугольного поперечного сечения, обеспечивающих её необходимую прочность.
Задача
Для заданной стальной балки подобрать размеры прямоугольного поперечного сечения по условию прочности.
Соотношение сторон сечения h=2b (h – высота, b – ширина).
Полученные размеры принять согласно ГОСТ 6636.
Допустимые напряжения для материала балки [σ]=160МПа.
Другие примеры решений >
Помощь с решением задач >
Решение
Предыдущие пункты решения задачи:
- Определение опорных реакций
- Построение эпюр внутренних поперечных сил и изгибающих моментов
- Расчет момента сопротивления сечения балки по условию прочности
Минимально необходимый расчетный момент сопротивления сечения балки составил
В случаях, когда система изгибающих нагрузок действующих на балку расположена в вертикальной плоскости сечение тоже следует располагать вертикально.
По справочнику находим формулу осевого момента сопротивления прямоугольного сечения
Используя заданное соотношение сторон (h=2b), уменьшим количество переменных в выражении
и запишем необходимое неравенство
откуда находим расчетную высоту прямоугольного сечения
Из заданного соотношения сторон определяем расчетную ширину сечения
Отметим, что полученные размеры являются минимально необходимыми для обеспечения прочности заданной балки.
При отсутствии дополнительных условий расчетные размеры можно округлить до целого значения в миллиметрах исключительно в большую сторону (h=153мм, b=77мм).
По ГОСТ 6636 нормальных линейных размеров выбираются ближайшие значения в сторону увеличения.
Следовательно, за окончательные размеры прямоугольного сечения балки принимаем: h=155мм, b=80мм.
После принятия размеров согласно ГОСТ заданное соотношение сторон может несколько измениться. Это нормально.
Оценка экономичности сечений >
Построение эпюры нормальных напряжений >
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Проверка прочности балки и подбор поперечных сечений
Балка проверяется на прочность по наибольшим нормальным напряжениям, возникающие в поперечном сечении балки, где на эпюре 
наибольший по абсолютному значению изгибающий момент. При поперечном изгибе в балке возникают и касательные напряжения, но они невелики, и при расчете на прочность учитываются только для двутавровых балок.
Условие прочности при изгибе по нормальным напряжениям: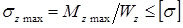 
,
где допускаемое напряжение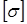 
принимается, как и при растяжении (сжатии) стержня из такого же материала.
Формула условия прочности при изгибе по нормальным напряжениям позволяет осуществить подбор сечения балки при заданном материале и максимальном абсолютном значении изгибающего момента. Требуемый момент сопротивления балки при изгибе определяется из условия: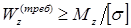 
.
При изменении положения сечения по отношению к действующей нагрузке прочность балки существенно изменяется, хотя площадь сечения и остается неизменной. Например, для балки прямоугольного поперечного сечения с отношением сторон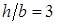 
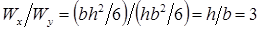
, расположенной таким образом, что высота прямоугольника h перпендикулярна нейтральной оси x, прочнее той же самой балки повернутой на 
, в три раза, так как 
. В выражении для осевого момента сопротивления балки прямоугольного поперечного сечения при изгибе в квадрате стоит тот ее размер, который перпендикулярен нейтральной оси. Следовательно, сечение балки необходимо располагать таким образом, чтобы силовая плоскость совпадала с той из главных центральных осей, относительно которой момент инерции минимален ( ось, относительно которой главный момент инерции поперечного сечения максимален, является нейтральной осью). Это обстоятельство лишний раз подчеркивает важность темы «Определение положения главных центральных осей инерции поперечного сечения стержня».
Проверка прочности двутавров
Для тонкостенных балок, например балок двутаврового профиля, проверка прочности производится следующим образом:
в наиболее удаленных от нейтральной оси точках прочность проверяется по формуле ;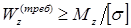
в точках, где полка соединяется со стенкой прочность определяется по главным напряжениям.
в точках, расположенных на нейтральной оси, прочность определяется по наибольшим касательным напряжениям:
Балка с профилем Н-образной формы – мерный отрезок фасонной металлопродукции, изготовленный способом прокатки или сварки. Подбор размеров поперечного сечения двутавра осуществляется в соответствии с таблицами сортамента (совокупности основных характеристик), представленными в соответствующих ГОСТах.
При одинаковой высоте стенки различные виды двутавра имеют разное соотношение высоты стенки и ширины полок, неодинаковую толщину этих элементов, и следовательно разную площадь сечения. Профиль, изготовленный способом горячей прокатки, может иметь параллельные или наклонные внутренние грани.
Как подобрать форму сечения двутавровой балки, в зависимости от назначения?
Горячекатаный металлопрокат с параллельными внутренними полками граней бывает следующих групп, согласно ГОСТу 26020-83:
- «Б» – нормальная. Диапазон номеров – 10-60. Толщина стенки составляет до 1/58 ее высоты. Металлопродукция применяется при монтаже перекрытий путепроводов, возведении мостов и эстакад.
-
«Ш» – широкополочная. Подразделяется на разрезную и неразрезную продукцию. Разрезные изделия, позволяющие получать две тавровые балки, применяют для укладки на один пролет, неразрезные – на один или несколько. Производство таких металлоизделий требует увеличенного (на 10-12%) расхода металла, что можно считать минусом. Плюсы: возможность установки в качестве самостоятельного элемента без дополнительных деталей, что существенно сокращает скорость проведения работ.
-
«К» – колонная. Особенность сечения этого вида двутавра – увеличенная толщина полок. Продукция выполняет функции несущих элементов строений, применяется для устройства больших пролетов, способна выдерживать значительные крановые нагрузки. В сортаменте это самые тяжелые и износостойкие профили.
Расчет сечения двутавровой балки по нагрузке
Для точного определения необходимого номера и типа Н-образного профиля используются сложные формулы. В расчетах учитывают длину изделия, тип закрепления, наличие или отсутствие ребер жесткости, количество опор, шаг между отрезками металлопроката, нагрузку на перекрытие или со стороны верхнего этажа, марку стали.
В упрощенном варианте нагрузку на перекрытие с учетом собственного веса двутаврового профиля без цементной стяжки принимают равной 350 кг/м2, с цементной стяжкой – 500 кг/м2 (средние значения). Шаг между металлическими балками обычно – 1 м, в некоторых случаях в целях экономии шаг увеличивают до 1,2 м.
Таблица для выбора номера Н-образного профиля, в зависимости от нагрузки, длины пролета и шага между изделиями
| Общая нагрузка, кг/м2 | Длина пролета | ||||||||
| 3 м при шаге | 4 м при шаге | 6 м при шаге | |||||||
| 1,0 м | 1,1 м | 1,2 м | 1,0 м | 1,1 м | 1,2 м | 1,0 м | 1,1 м | 1,2 м | |
| 300 | 10 | 10 | 10 | 10 | 12 | 12 | 16 | 16 | 16 |
| 400 | 10 | 10 | 10 | 12 | 12 | 12 | 20 | 20 | 20 |
| 500 | 10 | 12 | 12 | 12 | 12 | 12 | 20 | 20 | 20 |