Полярная система координат (полярные координаты)
Полярная система координат на плоскости — это совокупность точки , называемой полюсом, и полупрямой
, называемой полярной осью. Кроме того, задается масштабный отрезок для измерения расстояний от точек плоскости до полюса. Как правило, на полярной оси выбирается вектор
, приложенный к точке
, длина которого принимается за величину масштабного отрезка, а направление вектора задает положительное направление на полярной оси (рис.2.28,а).
Положение точки в полярной системе координат определяется расстоянием
(полярным радиусом) от точки
до полюса (т.е.
) и углом
(полярным углом) между полярной осью и вектором
. Полярный радиус и полярный угол составляют полярные координаты точки
, что записывается в виде
. Полярный угол измеряется в радианах и отсчитывается от полярной оси:
— в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;
— в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.
Полярный радиус определен для любой точки плоскости и принимает неотрицательные значения . Полярный угол
определен для любой точки плоскости, за исключением полюса
, и принимает значения
, называемыми главными значениями полярного угла. В некоторых случаях целесообразно считать, что полярный угол определен с точностью до слагаемых
, где
. В этом случае значениям
полярного угла для всех
соответствует одно и то же направление радиус-вектора.
С полярной системой координат можно связать прямоугольную систему координат
, начало
которой совпадает с полюсом, а ось абсцисс (точнее положительная полуось абсцисс) — с полярной осью. Ось ординат достраивается перпендикулярно оси абсцисс так, чтобы получилась правая прямоугольная система координат (рис.2.28,б). Длины базисных векторов определяются масштабным отрезком на полярной оси.
Наоборот, если на плоскости задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим полярную систему координат {связанную с данной прямоугольной).
Выведем формулы, связывающие между собой прямоугольные координаты точки
, отличной от точки
, и ее полярные координаты
. По рис.2.28,б получаем
(2.17)
Эти формулы позволяют найти прямоугольные координаты по известным полярным координатам. Обратный переход выполняется по формулам:
(2.18)
Последние два равенства определяют полярный угол с точностью до слагаемых , где
. При
из них следует, что
. Главное значение полярного угла
находится по формулам (рис.2.29):
Пример 2.9. В полярной системе координат :
а) изобразить координатные линии ;
б) изобразить точки с полярными координатами
. Найти главные значения полярных углов этих точек;
в) найти прямоугольные координаты точек .
Решение. а) Координатные линии представляют собой окружности соответствующих радиусов, а линии
и
— полупрямые (рис.2.30,а).
б) Построим точки и
(рис.2.30,б,в). Их координаты отличаются полярным углом, однако, имеют одно и то же главное значение
. Следовательно, это одна и та же точка, которая совпадает с точкой
, изображенной на рис.2.30,а.
в) Учитывая пункт «б», найдем прямоугольные координаты точки . По формулам (2.17) получаем:
то есть
Замечания 2.8
1. Главное значение полярного угла можно выбрать иначе, например, .
2. Расстояние между двумя точками и
(длина отрезка
) вычисляется по формуле
что следует из теоремы косинусов (рис.2.31).
3. Ориентированная площадь параллелограмма (рис.2.31), построенного на радиус-векторах
и
, находится по формуле
Она положительна, если (при этом ориентация пары радиус- векторов
и
правая), и отрицательна, если
(ориентация пары радиус-векторов
и
левая).
Пример 2.10. Даны полярные координаты и
точек
и
(рис.2.32). Требуется найти:
а) скалярное произведение ;
б) длину отрезка ;
в) внешнее произведение ;
г) площадь треугольника
;
д) координаты середины отрезка
в прямоугольной системе координат, связанной с данной полярной.
Решение. а) По определению скалярного произведения находим
б) Находим длину отрезка (см. пункт 2 замечаний 2.8):
в) Внешнее произведение находим как ориентированную площадь параллелограмма, построенного на векторах и
:
Площадь положительная, так как векторы и
образуют правую пару
.
г) Площадь треугольника находим как половину площади параллелограмма, построенного на радиус-векторах
и
.
Так как (см. пункт «в»), то
.
д) По формулам (2.17) находим прямоугольные координаты точек и
:
а затем координаты середины отрезка
(см. пункт 3 замечаний 2.1):
Пример 2.11. На координатной плоскости отмечена точка
. Найти:
а) полярные координаты точки , образа точки
при повороте радиус-вектора
на угол
вокруг начала координат (рис.2.33);
б) полярные координаты точки , образа точки
при инверсии плоскости относительно окружности единичного радиуса с центром в начале координат (см. пример б преобразований плоскости в разд. 2.2.4).
Решение. а) Найдем полярные координаты точки . По формулам (2.17), учитывая рис.2.29, получаем:
так как точка лежит в
четверти.
При повороте радиус-вектора вокруг полюса на угол
полярный радиус не изменяется, а полярный угол увеличивается. Следовательно, полярные координаты точки
:
,
, причем
— главное значение полярного угла
.
б) При инверсии относительно окружности радиуса полярные координаты
образа выражаются через полярные координаты
прообраза следующими формулами:
Поэтому, учитывая пункт «а», находим (для ):
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Содержание:
Полярные координаты. параметрические уравнения линии
Полярные координаты
Основная идея метода координат состоит в том, что положение точки на плоскости однозначно определяется с помощью двух чисел. Конкретный геометрический смысл этих чисел дает ту или иную систему координат. Наиболее важной после прямоугольной системы, исключительно употреблявшейся нами до сих пор, является полярная система координат, к рассмотрению которой мы и переходим.
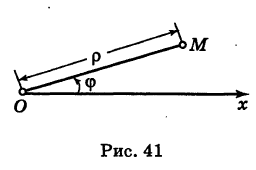
Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую Ох, называемую полярной осью (рис. 41).
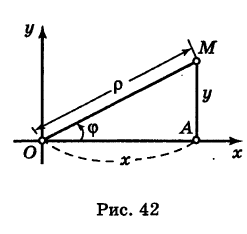
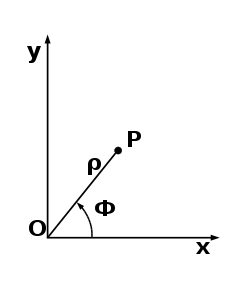
Пусть М — произвольная точка плоскости. Соединим точку М с полюсом О отрезком ОМ. Длина отрезка ОМ = р называется полярным радиусом точки М, а угол
Точка М с полярными координатами риф записывается следующим образом: М (р, ф), причем на первом месте ставится полярный радиус р, а на втором — полярный угол ф.
Что касается значений, принимаемых полярными координатами, то достаточно, очевидно, рассматривать значения р от 0 до 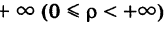
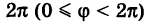
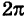
Связь между прямоугольными и полярными координатами
Рассмотрим переход от полярных координат к прямоугольным и обратно.
Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат Оху, а полярная ось является положительной полуосью Ох (рис. 42).
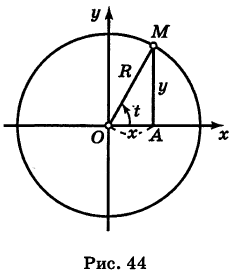
Тогда для произвольной точки М имеем
Считая угол ф острым, из прямоугольного треугольника АОМ находим
Полученные формулы справедливы для любого угла ф. Так выражаются прямоугольные координаты точки М через ее полярные координаты. Далее, из этого же прямоугольного треугольника АОМ получаем
Так выражаются полярные координаты точки через ее прямоугольные координаты.
Заметим, что при определении полярного угла ф по tg ф нужно учитывать знаки координат х и у.
Ранее мы видели, что линии могут быть заданы с помощью уравнений, связывающих их текущие прямоугольные координаты. Покажем теперь на простейшем примере, что линии могут определяться и уравнениями относительно полярных координат.
Пример:
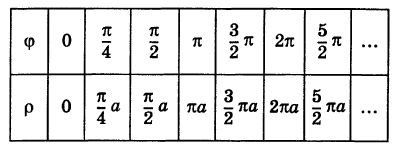
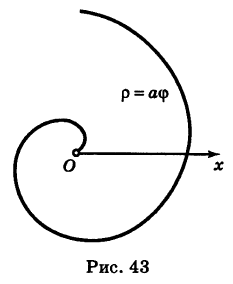
Рассмотрим кривую 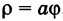
По этой таблице наносим точки и соединяем их линией, уточняя, если в этом есть необходимость, положение промежуточных точек (рис. 43).
Параметрические уравнения линии
Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты 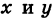
Пример:
Выведем параметрические уравнения окружности.
Пусть М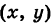
Это и есть параметрические уравнения окружности.
Чтобы получить обычное уравнение окружности, нужно исключить параметр t. Для этого возводим уравнения (1) в квадрат и складываем их:
Пример:
Выведем параметрические уравнения эллипса.
Эллипс с полуосями а и b можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса а, где коэффициент сжатия k = b/a. Пусть М (х, у) — точка эллипса, N (X, У) — соответствующая точка окружности (рис. 45), где
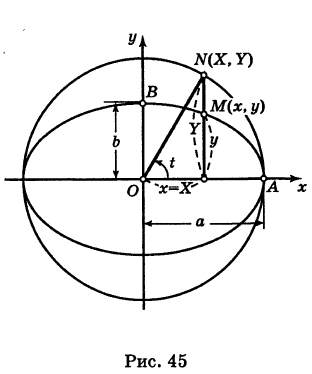
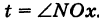
Таким образом, параметрические уравнения эллипса с полуосями а и b есть
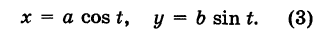
Имея параметрические уравнения линии, можно по точкам построить ее.
Пример:
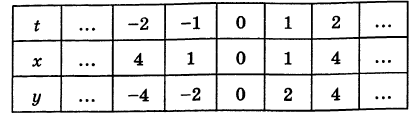
Построить кривую
Решение:
Составляем таблицу значений:
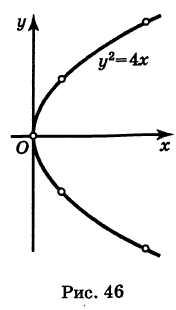
Эта кривая— парабола. В самом деле, исключив параметр t из уравнений (4), получим 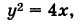
Параметрические уравнения циклоиды
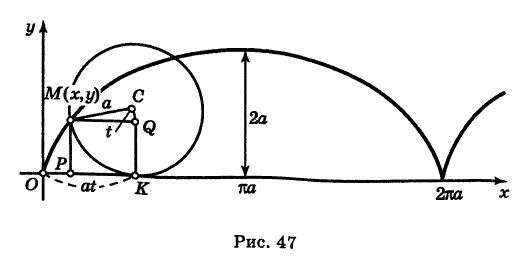
Определение: Циклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии (рис. 47).
Выведем параметрические уравнения циклоиды, приняв прямую за ось Ох, предполагая, что радиус катящейся окружности равен айв начальном положении движущаяся точка М совпадает с началом координат. За параметр t примем угол поворота (в радианах) подвижного радиуса МС окружности относительно вертикального радиуса КС, где К — точка касания окружности с осью Ох (рис. 47). Так как качение окружности происходит без скольжения, то, очевидно, имеем
Отсюда на основании рис. 47 для координат текущей точки М циклоиды получаем следующие выражения:
Таким образом, параметрические уравнения циклоиды есть
——-
Полярная система координат
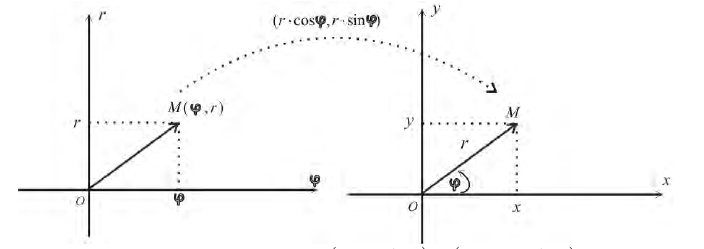
Определение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат Оху . Пусть М(х, у) – точка на плоскости, M ≠ 0. Полярными координатами точки М называются числа r − длина ее радиус-вектора (полярный
радиус) и ϕ − угол, образованный радиус-вектором с положительным направлением оси Ох (полярный угол), 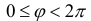
полюсом, а полуось Ох – полярной осью.
Замечание. Зависимость между прямоугольными (х, у) и полярными ( , ) r ϕ
координатами точки М задается в виде: 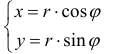
Рис.1. Полярные координаты точки.
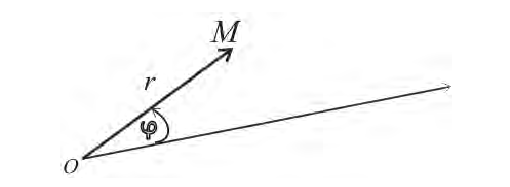
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя
прямоугольную систему координат:
Пример 1.
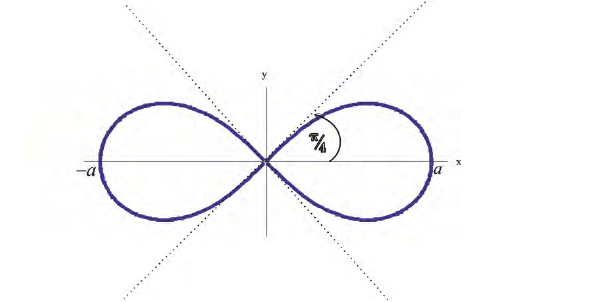
Построим на плоскости линию, заданную уравнением:
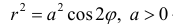
Решение.
Вычислим значения r при различных значениях ϕ :
Проводим лучи из начала координат под углами ϕ к оси Ох и на них откладываем
отрезки длины r , получим :
Рис.3. Лемниската
- Заказать решение задач по высшей математике
Пример 2.
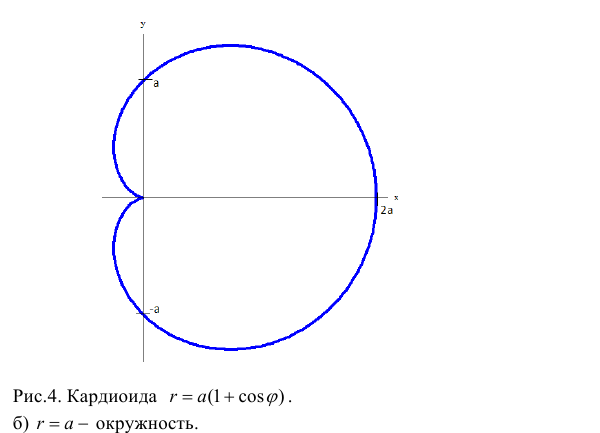
а) Построим кривую 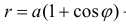
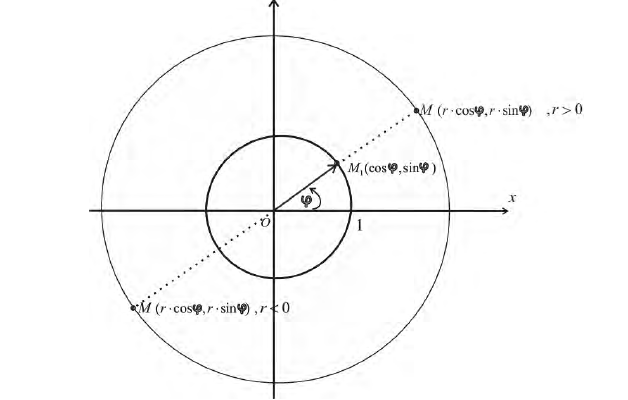
Замечание. Если в определении 1 отбросить требование 0 ≤ ϕ < 2π и не требовать r > 0, то формулы (1) будут задавать непрерывное отображение точек плоскости (O, r, ϕ) на точки плоскости (x, O, y).
При этом, если r > 0, то векторы 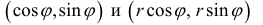
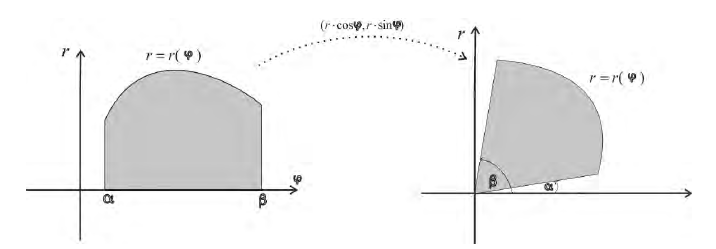
Тогда, с учетом (1), кривую r= r(ϕ) можно рассматривать как заданную параметрически в виде:
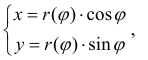
В этом случае на кривой 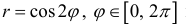
лепестка, когда 
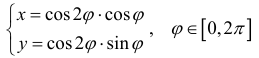
На кривой 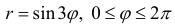
задается параметрически формулами:
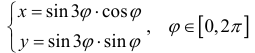
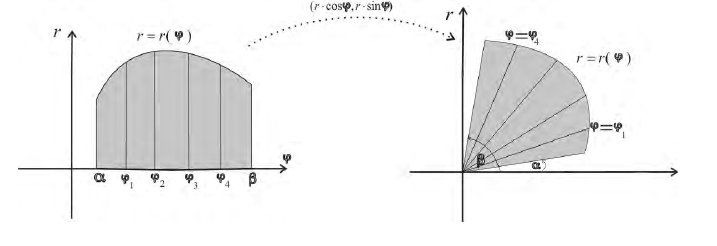
Пусть r = r(ϕ) – кривая в полярной системе координат, r (ϕ) – непрерывна при 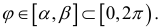
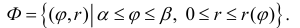
соответствует обычная криволинейная трапеция на плоскости (O, r, ϕ)
Разобьем фигуру Ф на n частичных фигур лучами 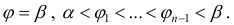
трапеции:
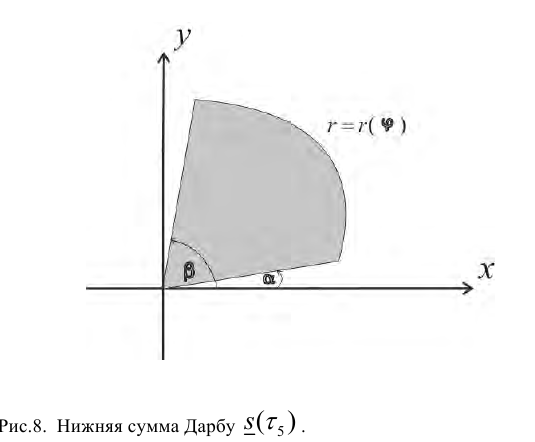
Рассмотрим, например, нижние суммы Дарбу:
Каждое слагаемое в нижней сумме 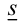
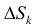
сектора радиуса 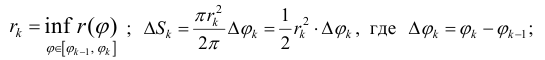
таким образом,
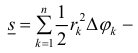
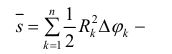
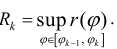
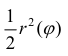
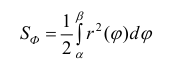
Пример 3.
Найти площадь ограниченную лемнискатой 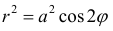
Решение.
По формуле (4):
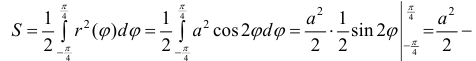
Поэтому
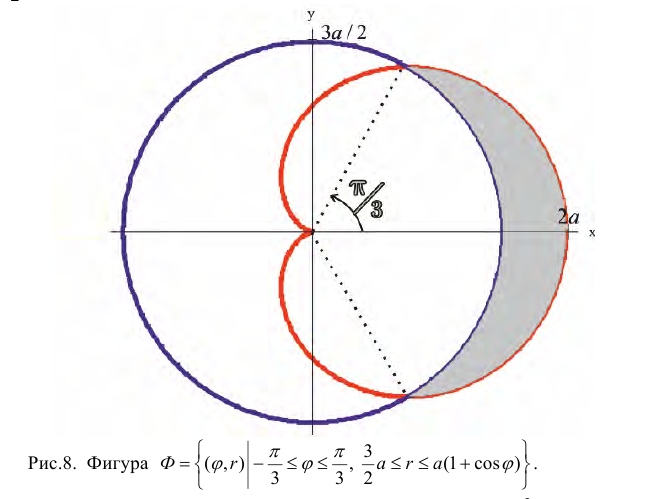
Пример 4.
Найти площадь фигуры ограниченной линиями: 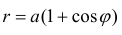
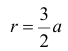
Решение. Найдем точки пересечения кривых: 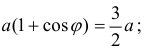
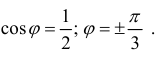
Пример 3.
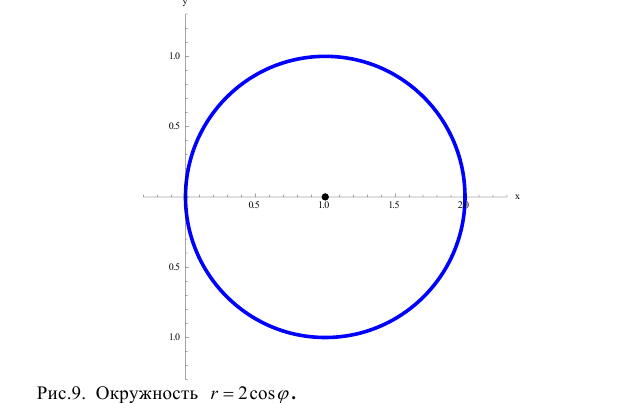
r=2cosϕ. Вычислим
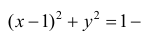
При изменении ϕ от 0 до 2 π окружность проходится дважды и оба раза против
часовой стрелки, поэтому (см. § 30) найденное значение интеграла задает
удвоенную площадь круга.
- Непрерывность функции
- Уравнения поверхности и линии в пространстве
- Общее уравнение плоскости
- Угол между плоскостями
- Интегрирование тригонометрических выражений
- Интегрирование иррациональных функций
- Прямоугольная система координат на плоскости и ее применение
- Линии второго порядка
Символ
М(
;
)
обозначает, что точка М имеет полярные
координаты
и
.
Полярный
угол
имеет
бесконечно много возможных значений
(отличающихся друг от друга на величину
вида
,
где n
—
целое положительное число). Значение
полярного угла, удовлетворяющее
неравенствам
,
называется главным.
В
случаях одновременного рассмотрения
декартовой и полярной систем координат
условимся: 1). Пользоваться одним и тем
же масштабом, 2). При определении полярных
углов считать положительным повороты
в том направлении, в каком следует
вращать положительную ось абсцисс,
чтобы кратчайшим путем совместить ее
с положительной осью ординат (таким
образом, если оси декартовой системы
находятся в обычном расположении, то
есть ось Ох направлена вправо, а ось Оу
— вверх, то и отсчет полярных углов должен
быть обычным, то есть положительными
следует считать те углы, которые
отсчитываются против часовой стрелки).
При
этом условии, если полюс полярной системы
координат совпадает с началом декартовых
прямоугольных координат, а полярная
ось совпадает с положительной полуосью
абсцисс, то переход от полярных координат
произвольной точки х к декартовым
координатам той же точки осуществляется
по формулам
,
.
В
этом же случае формулы
,
являются
формулами перехода от декартовых
координат к полярным.
При
одновременно рассмотрении в дальнейшем
двух полярных систем координат условимся
считать направление положительных
поворотов и масштаб для обеих систем
одинаковыми.
Полярная система координат
П
олярная
система координат
– система плоских координат образованная
направленным прямым лучом OX, называющимся
полярной осью. Чаще всего за полярную
ось принимают ось северного направления
какого-либо меридиана. Начало координат
— точка O — называется полюсом системы.
Положение
любой точки в полярной системе определяется
двумя координатами: радиусом-вектором
r
(или полярным расстоянием S) – расстоянием
от полюса до точки, и полярным углом
при точке O, образованным осью OX и радиусом
вектором точки и отсчитываемым от оси
OX по ходу часовой стрелки.
Под
полярным углом
в геодезии часто принимают дирекционный
угол
направления, с помощью которого определяют
координаты точек и расстояния между
ними.
П
ереход
от прямоугольных
координат
к полярным и обратно для случая, когда
начала обеих систем находятся в одной
точке и оси OX у них совпадают, выполняется
по формулам прямой
геодезической задачи:
tg
= Y/X,
= arctg(Y/X)
Полярная
система координат
— двумерная система координат, в которой
каждая точка на плоскости определяется
двумя числами — полярным углом и полярным
радиусом. Полярная система координат
особенно полезна в случаях, когда
отношения между точками проще изобразить
в виде радиусов и углов; в более
распространённой, декартовой
или прямоугольной системе координат,
такие отношения можно установить только
путём применения тригонометрических
уравнений.
Полярная
система координат задаётся лучом,
который называют нулевым или полярной
осью. Точка, из которой выходит этот луч
называется началом координат или
полюсом. Любая точка на плоскости
определяется двумя полярными координатами:
радиальной и угловой. Радиальная
координата (обычно обозначается r)
соответствует расстоянию от точки до
начала координат. Угловая координата,
также называется полярным углом или
азимутом
и обозначается
,
равна углу, на который нужно повернуть
против часовой стрелки полярную ось
для того, чтобы попасть в эту точку.[1]
Определённая
таким образом радиальная координата
может принимать значения от нуля
до бесконечности,
а угловая координата изменяется в
пределах от 0° до 360°. Однако, для удобства
область значений полярной координаты
можно расширить за пределы полного
угла, а также разрешить ей принимать
отрицательные значения, что отвечает
повороту полярной оси по часовой стрелке.
Графическое представление
Точка
в полярной системе координат.
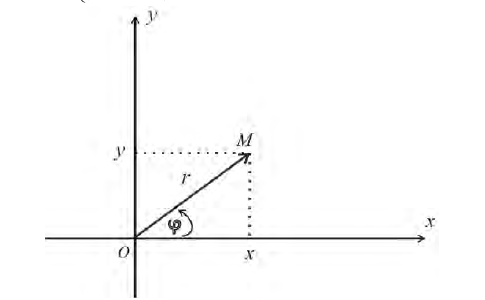
Каждая
точка в полярной системе координат
может быть определена двумя полярными
координатами, что обычно называются r
(радиальная координата) и
(угловая
координата, полярный угол, азимут, иногда
пишут θ или t).
Координата r
соответствует расстоянию до полюса, а
координата
равна
углу в направлении против часовой
стрелки от луча через 0° (иногда называется
полярной осью)[1].
Например,
точка с координатами
будет
выглядеть на графике как точка на луче,
который лежит под углом 60° к полярной
оси, на расстоянии 3 единиц от полюса.
Точка с координатами
будет
нарисована на том же месте, поскольку
отрицательное расстояние изображается
в положительную в противоположном
направлении (на 180°).
Одной
из важных особенностей полярной системы
координат является то, что одна и та же
точка может быть представлена бесконечным
количеством способов. Это происходит
потому, что для определения азимута
точки нужно повернуть полярную ось так,
чтобы он указывал на точку. Но направление
на точку не изменится, если осуществить
произвольное число дополнительных
полных оборотов. В общем случае точка
может
быть представлена в виде
или
,
где n
— произвольное целое
число[10].
Для
обозначения полюса используют координаты
.
Независимо от координаты
точка
с нулевым расстоянием от полюса всегда
находится на нём[11].
Для получения однозначных координат
точки, обычно следует ограничить значение
расстояния до неотрицательных значений
,
а угол
к
интервалу
или
(в
радианах
или
)[12].
Углы
в полярных координатах задаются либо
в градусах, либо в радианах, при этом
.
Выбор, как правило, зависит от области
применения. В навигации
традиционно используют градусы, в то
время как в некоторых разделах физики,
и почти во всех разделах математики
используют радианы[13].
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Пример с решением
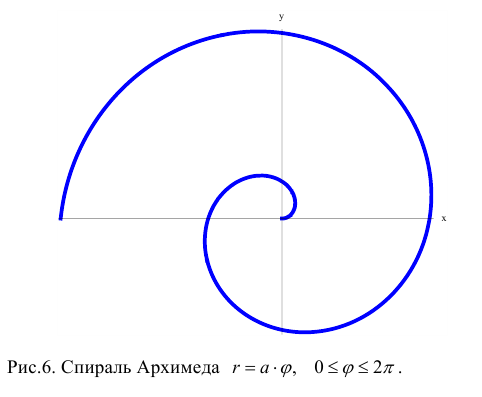
- Спираль Архимеда
- Гиперболическая спираль
- Вычисление площадей. Полярные координаты
- Примеры с решением
До сих пор для определения положения точки на плоскости мы пользовались ее прямоугольными координатами. Теперь мы рассмотрим другую важную систему координат — полярную.
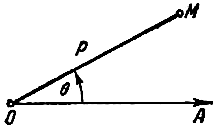
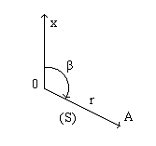
Эта система состоит из некоторой точки О (полюса) и проходящей через нее оси Ох (полярной оси). С помощью указанных Объектов можно определить положение любой точки М. Для этого соединим точку М с полюсом О и найдем угол 0, который луч ОМ образует с положительным направлением полярной оси Ох, и длину г этого луча **) ОМ (рис. 80).


Тот факт, что точка М имеет полярные координаты 

В дальнейших частях книги эта неясность будет устраняться сопровождающими пояснениями, а в данном параграфе мы введем обозначение М
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Полярная система координат имеет некоторые недостатки по сравнению с прямоугольной.
Прежде всего, аргументом полюса может считаться любое число. Так*),
суть различные обозначения одной и той же точки — полюса. Далее, и у любой другой точки плоскости имеется бесконечное множество аргументов, потому что прибавление, к аргументу точки угла
**) не меняет этой точки. Поэтому
,
представляют собой одну и ту же точку. Иногда рассматривают и отрицательные значения радиуса-вектора.
Например, под 



Иными словами, ту же точку можно задать, пользуясь положительным значением радиуса-вектора. Аналогичным образом, прибавив к аргументу 180°, мы всегда можем превратить отрицательный радиус-вектор в положительный. Имея это в виду, мы раз навсегда условимся считать радиус-вектор 

Возможно вам будут полезны данные страницы:
Пример с решением
Найти расстояние 


По теореме косинусов из треугольника 

Связь между полярными и прямоугольными координатами. Пусть на плоскости построены две системы координат: полярная и прямоугольная, причем полюс и полярная ось первой совпа-абсцисс второй. Возьмем на



Из формул (2) (или непосредственно из треугольника ОМА) следует, что 
Наконец, из (2) следует, что 



Спираль Архимеда
Мы знаем, что различные линии на плоскости определяются с помощью уравнений, которым должны удовлетворять прямоугольные координаты точек линии. Но совершенно то же будет справедливо, если говорить не о прямоугольных, а о полярных координатах точек. Прямую, эллипс, параболу, гиперболу удобнее изучать по их уравнениям в прямоугольных координатах. Однако для некоторых линий более удобным средством изучения служат их уравнения именно в полярных координатах. Такой линией является, например, спираль Архимеда.
Определение. Спиралью Архимеда называется линия, описываемая точкой, равномерно двигающейся по лучу, который сам равномерно вращается вокруг своего начала.
Мы будем предполагать, что в начальный момент точка М, описывающая спираль, находится в начале луча, упомянутого в определении.
Выведем уравнение спирали Архимеда. Для этого надо прежде всего выбрать определенную систему координат. Мы возьмем за полюс начало луча, по которому движется точка М, а за положительное направление полярной оси — начальное положение этого луча.
Обозначим соответственно через шит» скорость вращения луча и скорость ‘Движения точки М вдоль по лучу. Поскольку оба движения равномерны, [то 

Положение точки М мы будем определять ее полярными координатами 







Гиперболическая спираль
Определение. Гиперболическая спираль есть такая линия, что полярные координаты точки, движущейся по ней, изменяются обратно пропорционально друг другу. Иными словами, гиперболическая спираль есть линия, соответствующая уравнению 



Чтобы установить еще одно свойство гиперболической спирали, введем также прямоугольную систему координат, начало которой совпадает с полюсом, а ось абсцисс с полярной осью. Как мы знаем, для любой точки 

Значит, для точек, лежащих на спирали (5), окажется



к нулю, то согласно (5) точка 



Вычисление площадей. Полярные координаты
Пусть из центра круга радиуса 















Примеры с решением
Пример 1:
Найти площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда 
Здесь 




Пример 2:
Найти площадь F фигуры, ограниченной лемнискатой 
Еще в первой главе было показано, что в полярных координатах наша лемниската имеет уравнение 




Отсюда 
Лекции:
- Найти общее решение уравнения
- Значения случайной величины
- Площади поверхностей круглых фигур
- Интегралы для чайников
- Метод координат на прямой и его применение
- Метод Ньютона
- Упростить выражение: пример упрощения
- Ряд фурье функции
- Механический смысл производной
- Аналитическое решение уравнения

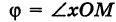
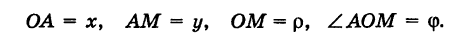
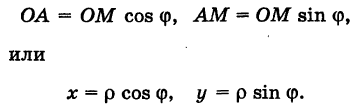
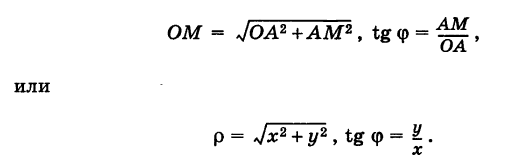
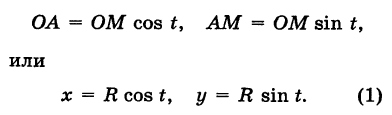
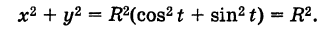

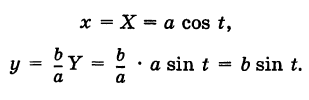
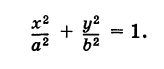

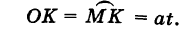
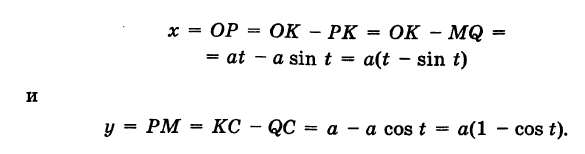
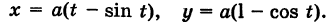
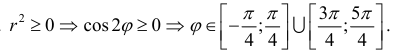
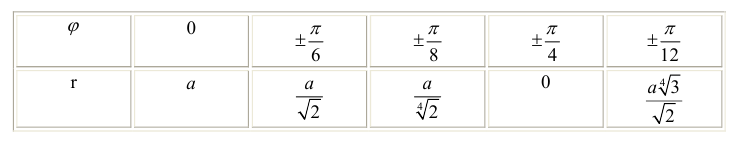
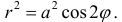
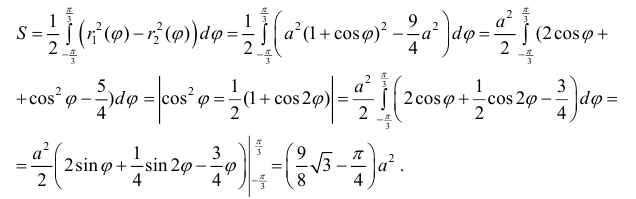
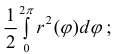
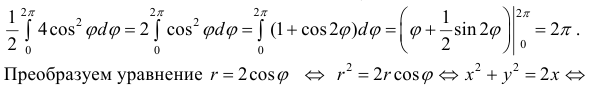

 суть различные обозначения одной и той же точки — полюса. Далее, и у любой другой точки плоскости имеется бесконечное множество аргументов, потому что прибавление, к аргументу точки угла
суть различные обозначения одной и той же точки — полюса. Далее, и у любой другой точки плоскости имеется бесконечное множество аргументов, потому что прибавление, к аргументу точки угла  **) не меняет этой точки. Поэтому
**) не меняет этой точки. Поэтому ,
,  представляют собой одну и ту же точку. Иногда рассматривают и отрицательные значения радиуса-вектора.
представляют собой одну и ту же точку. Иногда рассматривают и отрицательные значения радиуса-вектора. 



