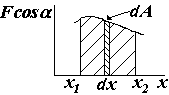Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
p = mv
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
10 г = 0,01 кг
Импульс равен:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Определение
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p1отн2 = m1v1отн2 = m1(v1 – v2)
p1отн2 — импульс первого тела относительно второго, m1 — масса первого тела, v1отн2 — скорость первого тела относительно второго, v1 и v2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
15 т = 15000 кг
p1отн2 = m1(v1 – v2) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙103 (кг∙м/с)
Изменение импульса тела
ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:
∆p = p – p0 = p + (– p0)
∆p — изменение импульса тела, p — конечный импульс тела, p0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар |
|
|
|
Конечная скорость после удара:
v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0. |
Абсолютно упругий удар |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p. |
Пуля пробила стенку |
|
|
|
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v) |
Радиус-вектор тела повернул на 180 градусов |
|
|
|
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0 |
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой: |
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
Или:
F∆t — импульс силы, ∆p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Определение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Реактивная сила:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Определение
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
Важно!
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
m2v2 = (m1 + m2)v
Отсюда скорость равна:
Задание EF17556
Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
1.Записать исходные данные.
2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.
4.Подставить известные значения и вычислить.
Решение
Запишем исходные данные:
• Модуль импульса частицы до столкновения равен: p1 = p.
• Модуль импульса частицы после столкновения равен: p2 = 2p.
• Угол между вектором начального и вектором конечного импульса: α = 90о.
Построим чертеж:
Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17695

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Алгоритм решения
1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.
2.Сделать вывод о том, как зависит характер движения от импульса.
3.На основании вывода и анализа графика установить характер движения тела на интервалах.
Решение
Импульс тела есть произведение массы тела на его скорость:
p = mv
Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.
На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.
Верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22730

Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса применительно к задаче.
3.Записать формулу кинетической энергии тела.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса камня: m1 = 3 кг.
• Масса тележки с песком: m2 = 15 кг.
• Кинетическая энергия тележки с камнем: Ek = 2,25 Дж.
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cosα=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22
Отсюда скорость равна:
v=√2Ekm1+m2
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22520

. Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
1.Сформулировать закон сохранения импульса и записать его в векторной форме.
2.Применить закон сохранения импульса к задаче.
3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′
1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:
Сделаем чертеж:
Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:
Выразим массу груза:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20.2k
Р
азделим
силы на внутренние и внешние:
— внутренние силы, действующие между
телами, включенными в систему (i,j
= 1,2,…, i
j),
F1,F2…-
внешние силы, действующие со стороны
других тел, не включенных в систему.
— теорема об изменении полного импульса
системы материальных точек
(II
закон Ньютона для системы материальных
точек), т.е. импульс системы может
измениться только под действием внешних
сил.
Вопрос 5. Центр масс(центр инерции). Уравнение движения центра масс.
Центром масс
(центром инерции) называется
воображаемая точка, в которой как бы
сосредоточена вся масса тела или системы
тел. Центр
тяжести
практически совпадает с центром масс.
Перепишем первое
уравнение, дифференцируя, найдем скорость
центра масс и получим:
.
—
уравнение
движения центра масс.
Тема 6. Закон сохранения импульса.
Вопрос 1. Замкнутая и незамкнутая системы в механике. Закон сохранения импульса.
Система, на которую
не действуют внешние силы или их действие
скомпенсировано, т.е. для которой
,
называется замкнутой
или
изолированной.
Для такой
системы можно записать:
и,
т.к.
,
следовательно,
— закон
сохранения импульса:
«В замкнутой системе полный импульс
материальных точек остается постоянным».
Пространство
однородно
– это означает, что все точки пространства
эквивалентны, т.е. равноправны. В
однородном пространстве нет каких-либо
особых точек, отличных от других. Если
некоторую систему тел перенести в другое
место пространства, а тела в ней поставить
в те же условия, в которых они находились
в прежнем положении, то это никак не
отразится на ходе всех последующих
явлений. Если взять замкнутую систему
тел, для которой полный импульс системы
равен некоторой величине, то и в любом
другом месте полный импульс будет
оставаться тем же самым. Иначе говоря,
закон
сохранения импульса
является следствием однородности
пространства.
Тема 7. Работа. Мощность. Энергия.
Вопрос 1. Определение элементарной работы, различные выражения.
-элементарная
работа, т.е. работа, совершаемая при
таком малом перемещении, в пределах
которого силу можно считать неизменной,
Fr
проекция силы на направление перемещения.
—
полная работа (это всегда интеграл).
,только
при
,
= 0 и S
=
r.
-работа
на конечном участке, выраженная через
проекции силы и изменения координат.
Н
а
приведенном графике для одномерного
движения
работа – площадь под кривой зависимости
проекции
силы от перемещения х.Работа
является положительной, если сила
действует в сторону перемещения
(перпендикулярная
сила работы не совершает).
Вопрос 2. Мощность, ее выражение через силу и скорость тела.
Мощность (Дж/с
= Вт) – по смыслу – это работа, совершаемая
за единицу времени.
Используя выражение
для работы, мощность можно выразить как
скалярное произведение вектора силы и
вектора скорости:
.
Вопрос 3. Кинетическая энергия и ее выражение через импульс тела.
Кинетическая
энергия –
это энергия, связанная с движением.
Выражение для кинетической энергии
можно получить, если найти работу,
которую должна совершить сила F,
чтобы сообщить неподвижному телу массой
m
скорость v.
Таким образом,
неподвижное тело за счет работы силы
приобрело скорость и кинетическую
энергию.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В статье обсуждается, как рассчитать импульс системы по импульсам каждого объекта.
Импульс системы определяется движением количества объектов, которыми обладает система. Одни из них движутся со своими скоростями внутри системы, другие покоятся. Следовательно, мы можем вычислить импульс системы, суммируя все импульсы объектов в системе.
Узнать больше о Momentum.
Вычислите импульс системы, содержащей движущиеся объекты, например объект А массой 5 кг, движущийся со скоростью 2 м/с, и объект В массой 3 кг, движущийся со скоростью 5 м/с.
Данный:
m1 = 5 кг
m2 = 3 кг
u1 = 2 м / с
u2 = 5 м / с
Найти: Псистема =?
Формула:
Σ Pсистема = P1+ Р2 +…
Решения:
Импульс системы рассчитывается путем сложения импульсов двух движущихся объектов.
Pсистема = P1 + Р2
Pсистема = м1u1 + м2u2
Подставляя все значения,
Pсистема = 5 х 2 + 3 х 5
Pсистема = 25
Импульс системы, состоящей из двух движущихся тел, равен 25 кг·м/с.
Узнать больше о Net Force
Каков импульс системы?
Импульс системы – это движение всей массы системы, включающей несколько объектов.
Когда система включает в себя движение многих объектов, понятие центр массы вводится. Это среднее положение всех объектов в системе, вес по отношению к их массе. Таким образом, импульс системы есть произведение полной массы и скорости центра масс.
(Кредит: Shutterstock)
Импульс системы равен P→см = Мв→cm
Где v→cm есть скорость центра масс.
Mv→cm = Мд/дтр→cm ……… .. (1)
Где r→cm это положение центра масс.
Формула центра масс такова,
r→cm = м1r→1/м2р→2
Уравнение (1) принимает вид
Mv→cm = Md/dt (m1r→1/м2р→2)
Mv→cm = м1д/дтр1→ +m2д/дтр2→ + …
Mv→cm = м1v1→ + м2v2→
Mv→cm = P→1+P→2
Р см = Р→1+P→2
Вот почему мы говорим, импульс системы есть вектор сумма всех импульсов каждого объекта в системе.
Подробнее о Как рассчитать моментум?
Мы видим три движущихся транспортных средства, таких как автомобиль массой 150 кг, движущийся со скоростью 50 км/ч, мотоцикл массой 80 кг, движущийся со скоростью 80 км/ч, и грузовик массой 250 кг, движущийся со скоростью 30 км/ч. Вычислите импульс системы, в которой автомобиль и мотоцикл движутся в одном направлении, а грузовик — в противоположном.
Данный:
m1 = 150 кг
m2 = 80 кг
m3 = 250 кг
v1 = 50 км / ч
v2 = 80 км / ч
v3 = 30 км / ч
Найти: Псистема =?
Формула:
P→cm= P→1+P→2 +…
Решения:
Импульс системы рассчитывается как
P→cm = P→1+P→2 +…
Pсистема = P1 + Р2 + Р3
Pсистема = м1v1+ м2v2 + (-м3v3)
Подставляя все значения,
Pсистема = 150 х 50 + 80 х 80 – 250 х 30
Pсистема = 7500 + 6400 – 7500
Pсистема = 6400 кг.км/час
Pсистема = 6400 х 1000/3600
Pсистема = 1777.7
Импульс системы, состоящей из движущегося автомобиля, мотоцикла и грузовика, равен 1777.7 кг.м/с.
Узнайте больше о начальном импульсе.
Как рассчитать полный угловой момент системы?
Полный угловой момент системы рассчитывается с использованием ее момента инерции и угловой скорости.
При расчете полного углового момента нам нужно предположить только объекты, движущиеся под углом в системе. Инерция вращения и угловая скорость объекта предлагают его угловой момент для расчета полного углового момента путем сложения всех угловых моментов объекта в системе.
Мы обсуждали только импульс объекта, который движется прямолинейно или линейно со скоростью v. В системе также присутствует объект, движущийся под углом со скоростью ω. Объект имеет линейный импульс (P) или угловой момент (L) в зависимости от движения.
Для линейное движение, линейный импульс объекта равен P = mv.
Для угловое движение, угловой момент объекта
L = Iω ………………(*)
Где я = момент инерции определяется как
«сумма массы объекта с системой с квадратом его расстояния от оси вращения системы ‘.
я = Σмiri2
я = мистер2.
Соотношение между угловая скорость ω и линейная скорость v равна ω = v/r
Подставляя значения I и ω в уравнение (*), получаем
L = v/r мр2
L → = р→ *мв→ or
L → = г→ * П→ ……………… (2)
Из приведенного выше соотношения между угловой момент и импульса, мы можем вычислить угловой момент для неорбитальных движущихся объектов внутри системы.
(Фото: Википедия)
Полный угловой момент системы представляет собой сумму углового момента каждого объекта в системе.
л = л1 + л2 + лN ………………. (3)
Второй закон движения Ньютона говорит
Σ F = d/dt P→
Дифференцируя уравнение (2) по t,
д/дт л→ = V→ * д/дт П→
д/дт л→ = г→* Σ Ф→ ……… .. (4)
Правая часть представляет собой формулу крутящего момента, которая также называетсямомент силыд., что заставляет тело вращаться вокруг неподвижной оси.
Σ = г→ * Σ Ф→ ……………… .. (5)
Используя уравнения (3), (4) и (5),
д/дт л→ =Σidli/дт = Σiτ→i
Приведенное выше уравнение выражает сумма крутящего момента на каждом объекте в системе дает чистый внешний крутящий момент Στ→ на систему, чтобы изменить ее полный угловой момент. Следовательно,
dL→/dt= Στ→
Но если нет крутящий момент, действующий на вращающийся объекты, Στ→ = 0 , тогда
dL→/дт = 0,
Так сохраняется угловой момент системы.
Это означает, что угловой момент отдельного объекта может измениться во время столкновения, но общий угловой момент системы останется прежним.
Для системы двух вращающихся тел
Lперед столкновением = лпосле столкновения
I1iω1i + Я2iω2i = Я1fω1f + Я2fω2f ………………….. (6)
Подробнее об угловой скорости.
Рассчитайте угловой момент системы, состоящей из двух конькобежцев с моментом инерции 5 кг·м2 и 8 кг·м2, которые скользят под углом со скоростью 10 и 15 рад/с соответственно, тяня их за руки. Кроме того, если они протягивают руки, чтобы уменьшить движение, первый фигурист скользит со скоростью 2 рад/с. Тогда какова скорость второго скольжения фигуриста?
Данный:
I1 = 5кг.м2
I2 = 8кг.м2
ω1i = 10 рад / с
ω2i = 15 рад / с
ω1f = 2 рад/с
Найти:
- Lобщий =?
- ω2f =?
Формула:
- Lобщий = л1 + L2
- I1iω1i + Я2iω2i = Я1fω1f + Я2fω2f
Решения:
Момент количества движения системы обоих конькобежцев рассчитывается как
Lобщий = л1 + L2
Lобщий = Я1iω1i + Я2iω2i
Подставляя все значения,
Lобщий = 5 х 10 + 8 х 15
Lобщий = 50 + 120
Lобщий = 170
Угловой момент системы конькобежцев 170кг.м.2/ S
Конечная скорость второго фигуриста рассчитывается по формуле закон сохранение момента импульса.
I1iω1i + Я2iω2i = Я1fω1f + Я2fω2f
Подставляя все значения,
5 х 10 + 8 х 15 = 5 х 2 + 8 х ω2f
170 = 10 + 8ω2f
8ч2f = 160
ω2f = 20
Скорость, с которой скользит второй фигурист после вытягивания рук, составляет 20 рад/с.
Узнайте больше об относительном движении.
Видеоурок 1: Закон сохранения импульса — Физика в опытах и экспериментах
Видеоурок 2: Физика — импульс и закон сохранения импульса
Лекция: Импульс системы тел
Чаще всего в практическом применении достаточно тяжело рассматривать движение исключительно одного тела, поэтому вводится понятие масса системы тел. Данная ФВ определяется суммой массы всех тел, что входят в данную систему.
Когда система тел достаточно объемная величина, принять её за материальную точку не очень удобно, поскольку любая материальная точка должна иметь свою координату. Чтобы
определить координату центра масс системы тел
, следует воспользоваться следующей
формулой
:
Если система тел двигается с некоторой скоростью, то для определения её импульса следует найти сумму всех импульсов тел данной системы.В школьной программе изучаются только процессы, происходящие в замкнутой системе.
Замкнутая система — это система, в которой тела взаимодействуют только друг с другом.

Если некоторые два тела системы двигались с некоторой скоростью, то сумма импульсов данных тел до взаимодействия равняется сумме импульсов после него.
Например, если на движущуюся тележку, массой 2 кг и скоростью 3 м/с, налетает и упруго соударяется вторая тележка, массой 4 кг и скоростью 1 м/с. После взаимодействия обе тележки начинают двигаться в противоположном направлении, причем первая имеет скорость 2 м/с, то по закону сохранения импульса, вторая тележка будет иметь скорость c учетом направления проекций:
m1v1 — m2v2 = m2v3 — m1v4,
v3 = (m1v1 — m2v2 + m1v4) / m2,
v3 = 1,5 м/с.
Все взаимодействия, происходящие в замкнутой системе, принято считать упругими. Это значит, в результате соударений тела не меняют своей формы и свойств. В реальном мире не существует абсолютно упругих взаимодействий. Изменения структуры тела происходят всегда.
Содержание книги
Предыдующая страница
§6. Законы сохранения в механике
В предыдущих параграфах мы фактически построили общую схему решения основной задачи динамики:
- — целый ряд физических законов дают возможность рассчитывать силы, действующие на тела;
- — второй закон Ньютона и известные силы позволяют получить уравнения, для определения ускорений тел;
- — методы кинематики позволяют, в принципе, рассчитать законы движения тел, по их известным ускорениям.
В данном параграфе мы рассмотрим фундаментальные физические законы сохранения энергии, импульса и момента импульса, также позволяющие получать уравнения для описания движения тел. Хотя эти законы нами будут получены на основании законов Ньютона, их обобщения имеют большую область применения, фактически именно законы сохранения являются фундаментом современной физики. В некоторых случаях в качестве исходных аксиом механики (и других разделов физики) используют законы сохранения, тогда законы Ньютона могут рассматриваться как «теоремы», являющиеся следствием законов сохранения.
Рассматриваемые ниже законы сохранения тесно связаны со свойствами симметрии пространства и времени. Симметрия в данном случае понимается в предельно широком смысле – наличие преобразований, оставляющих все свойства рассматриваемой системы неизменными. Согласно знаменитой теореме Эмми Нетер каждой сохраняющейся величине соответствуют некоторая симметрия, и наоборот наличие любого элемента симметрии приводит к появлению сохраняющейся физической величины
6.1 Импульс тела. Закон сохранения импульса.
Уравнение 2 закона Ньютона для материальной точки (или для твердого тела, движущегося поступательно) имеет вид
(~m vec a = vec F) , (1)
здесь m — масса тела, (~vec a = frac{Delta vec upsilon}{Delta t}) — ее ускорение, (~vec F) — сумма внешних сил, действующих на тело. Используя определение ускорения, уравнение (1) можно переписать в виде (~frac{Delta (m vec upsilon)}{Delta t} = vec F) . Векторная величина равная произведению массы тела на его скорость (~vec p = m vec upsilon) называется импульсом тела [1]. Тогда второй закон Ньютона может быть переформулирован следующим образом [2]: скорость изменения импульса тела равна сумме внешних сил, действующих на тело
(~frac{Delta vec p}{Delta t} = vec F) . (2)
На первый взгляд, эта новая формулировка закона полностью эквивалентна прежней. Но, она оказывается применимой в том случае, когда масса тела изменяется с течением времени. Данный вывод, не может быть подтвержден какими-либо теоретическими выкладками, обосновывается оно только результатами многочисленных экспериментов и экспериментально проверяемыми следствия из данного утверждения. Иными словами, уравнение (2) является обобщением экспериментальных данных.
В случае постоянной массы уравнения (2) и (1) полностью эквивалентны.
Часто произведение силы, на время ее действия (~vec F Delta t) называют импульсом силы. Используя это понятие, дадим еще одну эквивалентную формулировку второго закона Ньютона: изменение импульса тела равно импульсу суммарной внешней силы (~Delta vec p = vec F Delta t).
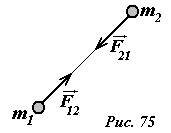
Рассмотрим теперь движение двух материальных точек, взаимодействующих только между собой (рис. 75), такую систему можно назвать изолированной, в том смысле, что нет взаимодействия с другими телами. По третьему закону Ньютона силы, действующие на эти тела, равны по величине и противоположны по направлению (~vec F_{12} = -vec F_{21}) . Эти силы можно выразить, используя второй закон Ньютона
(~vec F_{12} = m_1 vec a_1 ; vec F_{21} = m_2 vec a_2) .
Объединяя эти выражения, получим
(~m_1 vec a_1 + m_2 vec a_2 = vec 0) .
Перепишем данное соотношение, используя понятие импульса[~m_1 vec a_1 = m_1 frac{Delta vec upsilon_1}{Delta t} = frac{Delta (m_1 vec upsilon_1)}{Delta t} = frac{Delta vec p_1}{Delta t}] . Следовательно, (~frac{Delta vec p_1}{Delta t} + frac{Delta vec p_2}{Delta t} = vec 0) , или (~frac{Delta (vec p_1 + vec p_2)}{Delta t} = vec 0) . Если изменение какой-либо величины равно нулю, то эта физическая величина сохраняется. Таким образом, приходим к выводу: сумма импульсов двух взаимодействующих изолированных точек остается постоянным, независимо от вида взаимодействия между ними. Этот вывод можно обобщить на произвольную изолированную систему материальных точек, взаимодействующих между собой.
Ранее в качестве одного из следствий законов Ньютона, мы получили уравнение, описывающее движение центра масс системы материальных точек
(~m vec a_C = vec F) , (3)
где m — полная масса системы, (~vec a_C) — ускорение центра масс системы, (~vec F) — сумма внешних сил, действующих на систему, если система изолирована, то сумма внешних сил равна нулю, поэтому в таком случае (~m vec a_C = vec 0) . Вспомним определение центра масс системы. Радиус-вектор центра масс определяется по формуле
(~vec r_C = frac{m_1 vec r_1 + m_2 vec r_2 + m_3 vec r_3 + ldots}{m_1 + m_2 + m_3 + ldots}) .
Тогда произведение (~m vec a_C) можно представить в виде
(~(m_1 + m_2 + m_3 + ldots) vec a_C = m_1 vec a_1 + m_2 vec a_2 + m_3 vec a_3 + ldots = m_1 frac{Delta vec upsilon_1}{Delta t} + m_2 frac{Delta vec upsilon_2}{Delta t} + m_3 frac{Delta vec upsilon_3}{Delta t} + ldots = frac{Delta (m_1 vec upsilon_1 + m_2 vec upsilon_2 + m_3 vec upsilon_3 + ldots)}{Delta t} = frac{Delta vec P}{Delta t} = vec 0) , (4)
где (~vec P = m_1 vec upsilon_1 + m_2 vec upsilon_2 + m_3 vec upsilon_3 + ldots) — векторная сумма импульсов тел, входящих в систему, которую в дальнейшем будет называть импульс системы. Из полученного соотношения следует, что полный импульс замкнутой системы сохраняется, независимо от видов взаимодействий внутри системы. Это чрезвычайно важное утверждение носит название закона сохранения импульса.
Сделаем, два существенных замечания, касающихся проделанного вывода.
- Полный импульс системы материальных точек равен произведению массы системы на скорость центра масс системы. Действительно,
-
(~vec P = m_1 vec upsilon_1 + m_2 vec upsilon_2 + m_3 vec upsilon_3 + ldots = m frac{m_1 vec upsilon_1 + m_2 vec upsilon_2 + m_3 vec upsilon_3 + ldots}{m_1 + m_2 + m_3 + ldots} = m vec V_C) .
-
- Пусть система материальных точек не является замкнутой. Допустим, что сумма внешних сил действующих на систему не равна нулю (~vec F ne vec 0) , но проекция результирующей внешней силы на некоторую ось (например, X) равна нулю (F_x = 0) . Тогда уравнение (3) в проекции на эту ось будет иметь вид (m a_{Cx} = 0) , из которого следует, что проекция импульса системы на эту ось будет сохраняться. Итак, если сумма проекций внешних сил на некоторую ось равна нулю, то проекция импульса системы на эту ось сохраняется.
Так при движении системы материальных точек движет в поле тяжести земли, когда внешней силой является сила тяжести, направленная вертикально, будет сохраняться проекция импульса системы на любую горизонтальную ось.
Мы вывели закон сохранения импульса с помощью законов динамики Ньютона. Однако закон сохранения импульса является фундаментальным физическим законом. В теоретической физике показано, что он является следствием однородности [3] пространства, в котором происходят все физические явления. Если вы уверены в том, что результаты физического эксперимента одинаковы, независимо от того в каком месте этот опыт поставлен, то вы должны признать закон сохранения импульса.
Задания для самостоятельной работы.
- Движущийся кусок пластилина ударяется в стену и прилипает к ней. Куда «исчезает» импульс куска пластилина?
Примечания
- ↑ Также эту физическую величину называют количеством движения, однако, этот термин постепенно выходит из употребления.
- ↑ Заметим, что именно в такой форме закон был сформулирован И.Ньютоном.
- ↑ Однородность означает равноправие, одинаковость, всех точек пространства.
Следующая страница