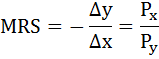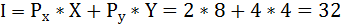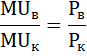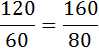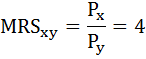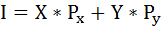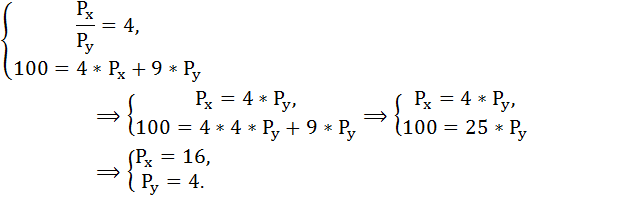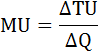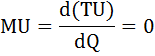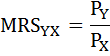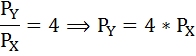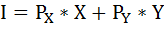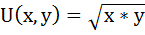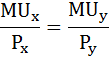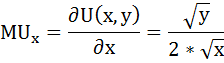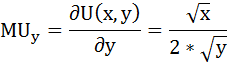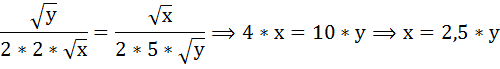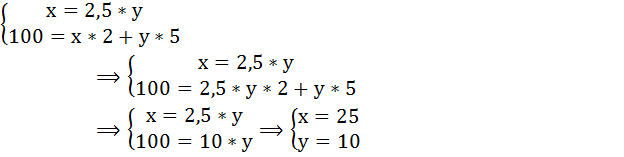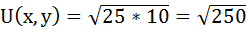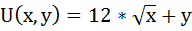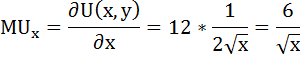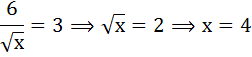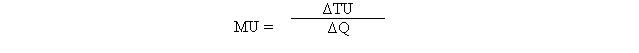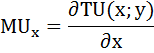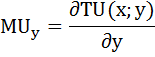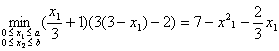Задача № 1 Расчёт дохода потребителя
Индивид покупает 8 единиц товара Х и 4 единицы товара Y. Найти его доход, если известно, что цена товара Х равна 2 ден. ед., а предельная норма замены равна 0,5.
Решение:
В точке оптимума выполняется равенство:
По условию MRS = 0,5 и Рх = 2. Следовательно, Ру = Рх / MRS = 2/0,5=4.
Найдём доход индивида, используя бюджетное ограничение:
где I – доход,
Рх и Ру – цены двух рассматриваемых благ,
Х и Y – их количества.
Задача № 2. Расчёт общей и предельной полезности
Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.
Решение:
Найдём общую полезность товара А.
Общая полезность N-й единицы товара = Предельная полезность N-й единицы товара + Общая полезность N-1-й единицы товара
TU(1)=MU(1)=20
TU(2)=MU(2) + TU(1)=15 + 20=35
TU(3)=MU(3) + TU(2)=12 + 35=47
TU(4)=MU(4) + TU(3)=8 + 47=55
TU(5)=MU(5) + TU(4)=6 + 55=61
Найдём предельную полезность товара В.
Предельная полезность N-й единицы товара=Общая полезность N-й единицы товара — Общая полезность N-1-й единицы товара
MU(1)=TU(1)=19
MU(2)= TU(2) — TU(1)=30 – 19 = 11
MU(3)= TU(3) — TU(2)=38 – 30 = 8
MU(4)= TU(4) — TU(3)=43 – 38=5
MU(5)= TU(5) — TU(4)=45 – 43=2
Найдём общую и предельную полезности товара С.
MU(1)=TU(1)=22
TU(2)=MU(2) + TU(1)=10 + 22=32
MU(3)= TU(3) — TU(2)=39 – 32=7
MU(4)= TU(4) — TU(3)=44 – 39=5
TU(5)=MU(5) + TU(4)=3 + 44=47
Заполним пропуски в таблице:
Задача № 3. Расчёт общей полезности
Предельная полезность первой единицы блага равна 420. При потреблении первых трёх единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза; предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 4 раза. Найти общую полезность блага при условии, что его потребление составляет 8 единиц.
Решение:
Распишем условие задачи следующим образом:
MU(1) = 420,
MU(2) = 420/2=210,
MU(3) = 210/2=105,
MU(4) = 105/4=26,25,
MU(5) = 26,25/4=6,5625,
MU(6) = 6,5625/4=1,640625,
MU(7) = 1,640625/4=0,410156,
MU(8) = 0,410156/4=0,102539.
Найдём общую полезность блага при условии, что его потребление составляет 8 единиц.
TU(8) = MU(8) + TU(7) = MU(8) + MU(7) + TU(6) =…=
= MU(8) + MU(7) + MU(6) + MU(5) + MU(4) + MU(3) + MU(2) + MU(1) =
= 420 + 210 + 105 + 26,25 + 6,5625 + 1,640625 + 0,410156 + 0,102539 = 769,96582
Задача № 4. Расчёт оптимального объёма потребления двух благ
В таблице представлены следующие данные о предельной полезности двух благ.
| Количество, кг | Конфеты | Виноград |
|---|---|---|
| 1 | 60 | 150 |
| 2 | 40 | 120 |
| 3 | 20 | 90 |
Цена 1 кг конфет 80 ден. ед., а цена 1 кг винограда 160 ден. ед.
Бюджет потребителя составляет 400 ден. ед.
Определить оптимальный объём потребления конфет и винограда.
Решение:
Оптимальный объём потребления конфет и винограда достигается тогда, когда отношение предельных полезностей равно отношению цен этих благ.
Среди перечисленных вариантов таким свойством обладает комбинация 2 кг винограда (MUв=120) и 1 кг конфет (MUк=60).
Предельная полезность винограда, разделённая на предельную полезность конфет равна отношению их цен:
Проверим соответствие этой комбинации бюджетному ограничению:
80*1 + 160*2 = 400
Бюджет полностью израсходован.
Задача № 5. Расчёт цен товаров Х и Y
Потребитель покупает 4 единицы блага Х и 9 единиц блага Y, имея доход 100 ден. ед. Найти цены товаров X и Y, если известно, что предельная норма замены товара Y товаром X (MRSxy) равна 4.
Решение:
Предельную норму замены товара Y товаром X(MRSxy) можно определить как отношение цены товара Х к цене товара Y:
Запишем бюджетное ограничение:
100 = 4*Px + 9*Py,
где
Px, Py – цены благ Х и Y соответственно.
Составим и решим систему уравнений:
Задача № 6. Расчёт оптимального объёма потребления
У студента Иванова в холодильнике сыр и колбаса нарезаны для удобства кусочками по 100 г. Общая полезность их потребления представлена в таблице. Определите количество съеденного им в день, если известно, что он в целом употребляет 700 г названных продуктов и при этом добивается максимума полезности.
| Количество, г | Колбаса (общая польза) | Сыр (общая польза) |
| 100 | 2000 | 1900 |
| 200 | 3900 | 3750 |
| 300 | 5700 | 5550 |
| 400 | 7400 | 7300 |
| 500 | 8000 | 9000 |
| 600 | 9500 | 10650 |
Решение:
Рассчитаем предельную полезность от потребления этих двух продуктов.
Предельная полезность в дискретном случае определяется по формуле:
где
ΔTU – приращение общей полезности (TU1 – TU0),
ΔQ – приращение количества потребляемого блага (Q1 – Q0).
Вычисления занесём в таблицу.
| Количество, г | Колбаса (общая польза) | Сыр (общая польза) | Предельная полезность колбасы | Предельная полезность сыра |
| 100 | 2000 | 1900 | 2000 | 1900 |
| 200 | 3900 | 3750 | 1900 | 1850 |
| 300 | 5700 | 5550 | 1800 | 1800 |
| 400 | 7400 | 7300 | 1700 | 1750 |
| 500 | 9000 | 9000 | 1600 | 1700 |
| 600 | 10500 | 10650 | 1500 | 1650 |
Известно, что в целом студент употребляет 700 г колбасы и сыра, то есть всего 7 кусочков, и при этом добивается максимума полезности.
Решение об оптимальном объёме потребления можно представить в виде таблицы, где на каждом шаге будем сравнивать предельную полезность каждого кусочка колбасы и сыра и выбирать наибольшую величину предельной полезности, что в сумме даст их максимум.
Итак, на первом шаге наибольшая предельная полезность, равная 2000 будет получена от потребления 1 кусочка/100 грамм колбасы. Дальше студенту без разницы, что употребить, так как первый кусочек сыра и второй кусочек колбасы приносят одинаковую полезность – 1900. Пусть, например, это будет сначала сыр, а затем колбаса. Но вот на четвёртом шаге наибольшую полезность принесёт второй кусочек сыра. Предельная полезность, полученная от его потребления 1850 больше, чем 1800 – предельная полезность третьего куска колбасы или третьего кусочка сыра. На пятом шаге студенту опять всё равно, что съесть первым, третий кусочек сыра или третий кусочек колбасы, так как полезность от дополнительного потребления этих продуктов одинакова. И наконец, седьмым кусочком должен стать сыр, поскольку предельная полезность четвёртого кусочка сыра (1750), больше чем предельная полезность четвёртого кусочка колбасы (1700).
Общая полезность от потребления 3 кусочков колбасы и 4 кусочков сыра будет максимальной и составит:
TU = 2000 + 1900 + 1900 + 1850 + 1800 + 1800 + 1750 = 13 000
Таким образом, студент Иванов получит максимум полезности при употреблении 3 кусочков (300 грамм) колбасы и 4 кусочков (400 грамм) сыра.
Задача № 7. Расчёт отимального объёма потребления
Определите оптимальный для потребителя объем блага Q, если известно, что функция полезности индивида от обладания этим благом имеет вид:
1) U(Q)= 1 – 5 × Q2
2) U(Q)= 5 + Q – Q2
3) U(Q) = Q2 – 5 × Q3
Как будут выглядеть функции предельной полезности? Проиллюстрируйте ответ.
Решение:
Оптимальный для потребителя объем блага Q будет определяться в точке, где потребитель получит максимум удовлетворения полезности. Задача сводится к нахождению экстремума функции полезности. Найдём производную функции полезности (предельную полезность MU) и приравняем её к нулю.
1) MU = –10 × Q = 0, следовательно, Q = 0;
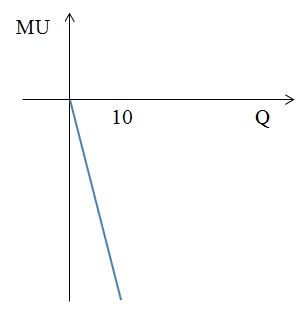
2) MU = 1 – 2 × Q = 0, следовательно, Q = 1/2;
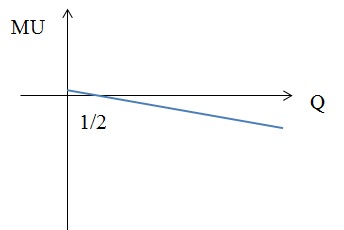
3) MU = 2 × Q – 15 × Q2 = 0, следовательно, Q = 0; Q = 2/15.
Задача № 8. Расчёт цен товаров X и Y
Индивид покупает 4 единицы блага X и 9 единиц блага Y, имея доход равный 100 денежным единицам. Найти цены товаров X и Y, если известно, что предельная норма замены X на Y равна 4.
Решение:
По условию задачи предельная норма замены благом Y блага X () равно 4. Это значит, что количество блага Х должно быть сокращено на 4 единицы в обмен на увеличение количества блага Y на единицу, при неизменном уровне удовлетворения потребителя.
Равновесие потребителя может быть представлено математически как:
— это предельная норма замещения, равная отношению цен благ Y и X. Данное условие оптимума потребителя следует понимать так. Соотношение, в котором потребитель при данных ценах способен замещать один товар другим, равно соотношению, в котором потребитель согласен замещать один товар другим, не изменяя уровень своего удовлетворения.
Отсюда
Далее воспользуемся формулой бюджетного ограничения:
где I – доход или бюджет потребителя.
100 = 4 × PX + 9 × PY
100 = 4 × PX + 9 × 4 × PX
100 = 40 × PX
PX = 2,5
PY = 4 × 2,5 = 10.
Ответ: PX = 2,5; PY = 10.
Задача № 9. Определение рационального выбора потребителя
Потребитель имеет функцию полезности:
и может на свой доход равный 100 единицам приобретать только эти два товара по ценам:
Px = 2
Py = 5
Определить рациональный выбор потребителя. Какой максимальный уровень полезности достижим?
Решение:
Рациональный выбор потребителя осуществляется в соответствии со вторым законом Госсена:
Предельная полезность товара х будет равна производной функции общей полезности по аргументу х:
Аналогично находим предельную полезность товара y:
Далее воспользуемся бюджетным ограничением:
Из условия задачи известно, что:
I = 100
Px = 2
Py = 5
Составим и решим систему уравнений:
При х = 25 и у = 10 общая полезность достигнет максимума:
Задача № 10. Расчёт оптимального объёма потребления
У Оксаны есть 30 рублей. Она хочет купить шоколадки «Шок» ценой 3 р. Полезность от этой покупки она оценивает функцией:
х – приобретённое количество шоколадок,
y – оставшаяся часть дохода.
Сколько купит шоколадок «Шок» рациональная Оксана?
Решение:
Рациональное поведение потребителя можно определить, как стремление максимизировать излишек потребителя. Потребитель будет покупать дополнительные единицы до тех пор, пока они приносят дополнительный избыток, т.е. пока цена, которую потребитель готов уплатить за единицу блага, превосходит реальную цену:
MU > P
Однако каждая последующая единица потребления обычно приносит уменьшающийся прирост полезности, т.е. при покупке благ «одно за другим» рано или поздно предельная полезность какого-то блага сравняется с его ценой:
MU = P
После того как предельная полезность сравняется с ценой, потребитель прекратит дальнейшие покупки: оптимальный объём потребления достигнут.
Найдём предельную полезность MU, как производную функции общей полезности по аргументу х:
Оптимальный объём потребления будет достигнут при МU = P:
Таким образом, рациональная Оксана купит 4 шоколадки, потратив на эту покупку 12 рублей.
Полезность данного
блага (набора
благ) — это степень
удовлетворения им той или иной потребности.
Полезность субъективна,
поскольку определяется индивидуальными
предпочтениями того или иного индивида.
Так, алкоголик высоко оценивает полезность
спиртного, которое объективно вредит
его здоровью.
Обычно оценивается полезность
не отдельного блага, но набора благ.
Дело в том, что удовлетворение потребителя
обычно зависит от того, вместе с какими
другими благами данное благо потребляется.
Так, полезность соли заметно возрастает,
если к ней в придачу имеется еще и мясо.
Напротив, полезность мясных блюд в
рамках «шведского стола» будет ниже
при наличии рыбных закусок.
Задача отдельного потребителя
состоит в том, чтобы при ограниченных
ресурсах приобрести набор благ, приносящий
ему наибольшее удовлетворение.
Увеличивая получаемую таким образом
полезность, потребитель максимизирует
свое благосостояние.
Функция полезности,
или функция
благосостояния,
потребителя — это выражение зависимости
общего уровня полезности набора благ ()
от объема потребления различных благ
(),
входящих в данный набор: .
Функция полезности –
функция, показывающая убывание предельной
полезности блага (MU) с ростом его
количества (Q):
Экономические блага.
Товар –
продукт труда, предназначенный для
обмена.
Товары – видимые
и осязаемые предметы, имеющие ценность,
товары можно складировать, они делимы.
Услуга –
труд, в виде деятельности, потребляемый
сразу, не делятся.
Экономические
блага –
желанные, но ограниченные по количеству
товары и услуги.
В
связи с их ограниченностью, каждое
экономическое благо имеет цену.
Цена
– денежное выражение стоимости.
Цена
блага зависит, в основном, от затрат на
его производство и доставку, а так же
от числа людей, желающих его иметь.
Желанность
и ценность благ зависит от их полезности,
т. е. способности удовлетворять
потребности.
Производство
благ требует использования ресурсов.
Классификация благ.
1. Ограниченные
и свободные.
К ограниченным относятся
такие блага, на которые в данный момент
спрос превышает предложение, поэтому
потребление приходится ограничивать
соответствующей ценой.
Песок в Сахаре – свободное
благо, т. к. даже при нулевой цене
предложение выше потребностей людей в
данный момент.
2. Используемые
и потребляемые.
Если благо используется
один раз и при этом исчезает, как благо,
называют потребляемым (продукты питания,
например).
3. Потребительские
(для дома) и капитальные (для производства
других благ).
4. Частные
и общественные блага
разделяются в зависимости от того,
удовлетворяет ли то или иное благо
потребности одного человека
или идет на пользу всем.
5. Нормальные
и подчиненные.
Спрос
на нормальные блага растет по мере
увеличения доходов, и уменьшается вместе
с последними. На подчиненные блага –
наоборот.
Общественным
благам присущи три принципа: во-первых,
их нельзя продать на рынке, они неделимы.
Во-вторых, к ним неприменим принцип
исключительности, т.е. ими нельзя
обеспечить одних и лишить других. Благом
может воспользоваться и те, кто за него
не платит (светофоры, освещение улиц,
маяки). В третьих, если благом обеспечить
хотя бы одного человека, то обеспечение
других не требует дополнительных затрат.
К
общественным благам относятся:
образование, здравоохранение, наука,
энергетика, общественный транспорт,
гидротехнические сооружения, водное
хозяйство, сооружения для спорта,
культуры и
отдыха, полиция, оборона, пожарная охрана
и общественное управление.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определите предельную полезность благ х и у, если функция полезности имеет вид:
1) U(x;y) = 2х + у;
2) U(x;y) = 2х2 + у;
3) U(x;y) = хβу1-β
Решение:
Предельную полезность блага х найдём как частную производную функции общей полезности по аргументу х:
1) MUx = (2х + у)’ = 2;
2) MUx = (2х2 + у)’ = 4x;
3) MUx = (хβу1-β)’ = βхβ-1у1-β = β(х/у)β-1
Аналогично найдём предельную полезность блага у, как частную производную функции общей полезности по аргументу у:
1) MUу = (2х + у)’ = 1;
2) MUу = (2х2 + у)’ = 1;
3) MUу = (хβу1-β)’ = (1 – β)хβу-β = (1 – β) × (х/у) β
Общая полезность
Общая полезность — удовлетворение, которое получают от потребления определенного набора товара или услуги.
Предельная полезность — это прирост общей полезности товарного набора при увеличении объема потребления данного товара на единицу.
Mu = (Tu1 — Tu0)/(Q1 — Q0)
Производная по количеству Q
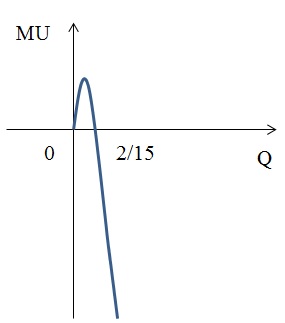
Mu = dTu/dQ
Как найти производную.
Например, TU = x*y. Mux = d(x*y)/dx = y; Muy = d(x*y)/dy = x
Например, TU = 10x2 + 2x + 2. Mux = d(10x2 + 2x + 2)/dx = 20x + 2
Функция полезности — функция, показывающая убывание полезности блага с ростом его количества:
Tu = f(Qi)
Условия равновесия потребителя
Условия равновесия потребителя можно выразить формулой:Mux / Muy = Px / Pyгде Px и Py — цены на товары X и Y.
Точка касания кривой безразличия с бюджетной линией означает равновесие потребителя.
Пример задачи на нахождение оптимального набора покупок
Пример задачи на нахождение оптимального набора товаров при заданной функции полезности
Кривая безразличия
Кривая безразличия — это множество точек на кривой, которые показывают различные комбинации двух экономических благ, имеющих одинаковую полезность для потребителя.
Предельная норма замещения (marginal rate of substitution — MRS) — количество, на которое потребление одного из двух благ должно быть увеличено (или уменьшено), чтобы полностью компенсировать потребителю уменьшение (или увеличение) потребления другого блага на одну дополнительную единицу:
MRSxy = ΔY / ΔXΔY = Y1 — Y0ΔX = X1 — X0илиMRSxy = Mux / Muy
Точка касания кривой безразличия с бюджетной линией означает оптимальный набор товаров потребителя.
Бюджетная линия
Бюджетная линия представляет собой прямую линию с отрицательным наклоном, графически отображающую множество наборов из двух товаров, требующих одинаковых затрат на их потребление. Она показывает, какие потребительские наборы можно приобрести за данную сумму денег.I = PxX + PyYгде I — доход потребителя;
Px — цена блага Х;
Py — цена блага Y;
X,Y — составляют соответственно купленные количества благ.
Пример. Функция полезности U(xy)=xy. Доход потребителя равен 80 ден. ед. Цены товаров x и y соответственно равны Px=2 руб. и Py=4 руб. Найдите равновесный набор.
Решение: Из условия равновесия потребителя: Mux / Muy = Px / Py получаем: Mux = d(x*y)/dx = y; Muy = d(x*y)/dy = x
Тогда: y / x = 2 / 4 = 1/2 или y = 1/2x
Для наших данных уравнение бюджетной линии запишем как: 80 = 2x + 4y = 2x + 4*1/2x = 4x
Откуда: x = 20 ед., y = 1/2*20 = 10 ед.
Ответ: потребитель приобретет 20 ед. товара x и 10 ед. товара y.
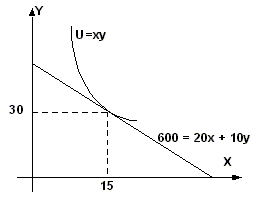
Пример решения определения оптимума потребителя
Потребитель тратит 600 рублей в месяц на приобретение двух товаров. Цена товара Х — 20 рублей, а товара Y — 10 рублей. Задана функция полезности потребителя U = ХY. Составить уравнение бюджетной линии. Найти предельную норму замещения. Определить оптимум потребителя. Представить графически. Если цена товара Х уменьшится на 5 руб., на сколько единиц изменится объем спроса данного товара всего?|Уравнение бюджетной линии:I = PxX + PyY 600 = 20X + 10Y
Предельная полезность товаров:
Mux = dU/dx = d(xy)/dx = yMuy = dU/dy = d(xy)/dy = x
Оптимум потребителя достигается при равенстве:
Mux / Muy = Px / PyMux / Muy = 20 / 10 = 2
Предельная норма замещения
MRSxy = Mux / Muy = 2
Выразим y через x.
Mux / Muy = y / x = 2y = 2x
Подставим в уравнение бюджетной линии:
600 = 20x + 10*2x = 20x + 20xоткуда X = 15; Y = 2x = 30
Точка касания кривой безразличия с бюджетной линией означает оптимальный набор товаров потребителя.
Проверка: 20 х 15 + 10 х 30 = 300 + 300 = 600.
При уменьшении цены товара X на 5 руб.
Px = 20 — 5 = 15
Найдем новый оптимум потребителя.
600 = 15X + 10Y = 15X + 20X = 35Xоткуда x = 17.14; y = 2x = 34.29
Спрос на товар Х увеличился на 2.14 (17.14 — 15)
Проверка: 15 х 17.14 + 10 х 34.29 = 257.1 + 342.9 = 600.
Пример нахождения цен товаров при оптимальном выборе покупателя
Утилитарное решение и решение, оптимальное по Нэшу
Определить утилитарное решение и решение, оптимальное по Нэшу, если функции полезности агентов равны u1 = х1 + 3, u2= 3х2 — 2 при х1 + x2 = 3 . Проверить независимость от масштаба для указанных ПКБ, если функция полезности первого агента была уменьшена в три раза.
Решение. Определим эгалитарное решение, для этого должно выполняться условие u1 = u2 или x1 + 3 = 3x2 — 2. Учитывая, что x2 = 3- x1, получаем x2 = 2, тогда x1 = 1. Вектор полезностей (4,4).
Утилитарное решение находим, максимизируя сумму полезностей агентов: x1 + 3 + 3x2 — 2 → max, подставив x1 вместо x2, получаем 4x2 + 1 → max. Рассматриваемая функция возрастает от x1 и достигает своего максимума при x1 = 3, тогда x2 = 0. Здесь вектор полезностей (1,1).
Независимость от масштаба
Определим эгалитарное решение, для этого должно выполняться условие u1 = u2 или x1/3 + 1 = 3x2 — 2. Учитывая, что x2 = 3- x1, получаем 10/3 x1 — 6 = 0, тогда x1 = 9/5, то x2 = 6/5. Вектор полезностей (8/5,8/5).
Множество допустимых распределений пары продуктов на неотрицательные количества определяется так:x1,x2 0, x1 + x1 = a, x2 = b.
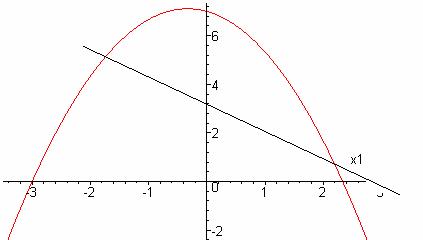
Максимизируя ФКП Нэша, мы выбираем эффективное распределение. Оптимальное распределение определяется как решение задачи:
Минимум достигается x1 = 2,17; x2 = 0,83.
Видим, что соблюдается условия:
а) 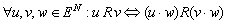
б)