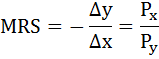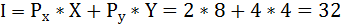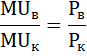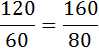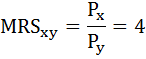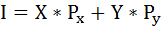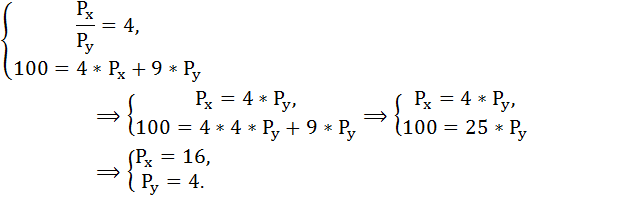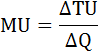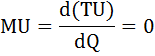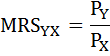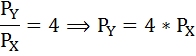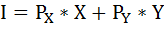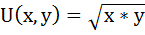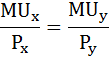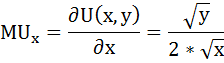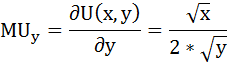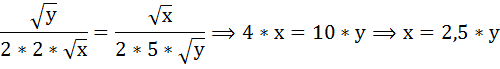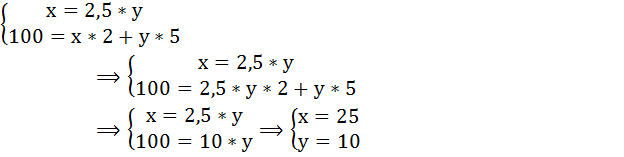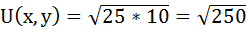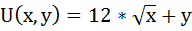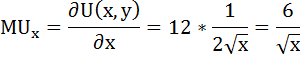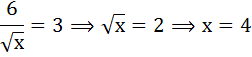Задача № 1 Расчёт дохода потребителя
Индивид покупает 8 единиц товара Х и 4 единицы товара Y. Найти его доход, если известно, что цена товара Х равна 2 ден. ед., а предельная норма замены равна 0,5.
Решение:
В точке оптимума выполняется равенство:
По условию MRS = 0,5 и Рх = 2. Следовательно, Ру = Рх / MRS = 2/0,5=4.
Найдём доход индивида, используя бюджетное ограничение:
где I – доход,
Рх и Ру – цены двух рассматриваемых благ,
Х и Y – их количества.
Задача № 2. Расчёт общей и предельной полезности
Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.
Решение:
Найдём общую полезность товара А.
Общая полезность N-й единицы товара = Предельная полезность N-й единицы товара + Общая полезность N-1-й единицы товара
TU(1)=MU(1)=20
TU(2)=MU(2) + TU(1)=15 + 20=35
TU(3)=MU(3) + TU(2)=12 + 35=47
TU(4)=MU(4) + TU(3)=8 + 47=55
TU(5)=MU(5) + TU(4)=6 + 55=61
Найдём предельную полезность товара В.
Предельная полезность N-й единицы товара=Общая полезность N-й единицы товара — Общая полезность N-1-й единицы товара
MU(1)=TU(1)=19
MU(2)= TU(2) — TU(1)=30 – 19 = 11
MU(3)= TU(3) — TU(2)=38 – 30 = 8
MU(4)= TU(4) — TU(3)=43 – 38=5
MU(5)= TU(5) — TU(4)=45 – 43=2
Найдём общую и предельную полезности товара С.
MU(1)=TU(1)=22
TU(2)=MU(2) + TU(1)=10 + 22=32
MU(3)= TU(3) — TU(2)=39 – 32=7
MU(4)= TU(4) — TU(3)=44 – 39=5
TU(5)=MU(5) + TU(4)=3 + 44=47
Заполним пропуски в таблице:
Задача № 3. Расчёт общей полезности
Предельная полезность первой единицы блага равна 420. При потреблении первых трёх единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза; предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 4 раза. Найти общую полезность блага при условии, что его потребление составляет 8 единиц.
Решение:
Распишем условие задачи следующим образом:
MU(1) = 420,
MU(2) = 420/2=210,
MU(3) = 210/2=105,
MU(4) = 105/4=26,25,
MU(5) = 26,25/4=6,5625,
MU(6) = 6,5625/4=1,640625,
MU(7) = 1,640625/4=0,410156,
MU(8) = 0,410156/4=0,102539.
Найдём общую полезность блага при условии, что его потребление составляет 8 единиц.
TU(8) = MU(8) + TU(7) = MU(8) + MU(7) + TU(6) =…=
= MU(8) + MU(7) + MU(6) + MU(5) + MU(4) + MU(3) + MU(2) + MU(1) =
= 420 + 210 + 105 + 26,25 + 6,5625 + 1,640625 + 0,410156 + 0,102539 = 769,96582
Задача № 4. Расчёт оптимального объёма потребления двух благ
В таблице представлены следующие данные о предельной полезности двух благ.
| Количество, кг | Конфеты | Виноград |
|---|---|---|
| 1 | 60 | 150 |
| 2 | 40 | 120 |
| 3 | 20 | 90 |
Цена 1 кг конфет 80 ден. ед., а цена 1 кг винограда 160 ден. ед.
Бюджет потребителя составляет 400 ден. ед.
Определить оптимальный объём потребления конфет и винограда.
Решение:
Оптимальный объём потребления конфет и винограда достигается тогда, когда отношение предельных полезностей равно отношению цен этих благ.
Среди перечисленных вариантов таким свойством обладает комбинация 2 кг винограда (MUв=120) и 1 кг конфет (MUк=60).
Предельная полезность винограда, разделённая на предельную полезность конфет равна отношению их цен:
Проверим соответствие этой комбинации бюджетному ограничению:
80*1 + 160*2 = 400
Бюджет полностью израсходован.
Задача № 5. Расчёт цен товаров Х и Y
Потребитель покупает 4 единицы блага Х и 9 единиц блага Y, имея доход 100 ден. ед. Найти цены товаров X и Y, если известно, что предельная норма замены товара Y товаром X (MRSxy) равна 4.
Решение:
Предельную норму замены товара Y товаром X(MRSxy) можно определить как отношение цены товара Х к цене товара Y:
Запишем бюджетное ограничение:
100 = 4*Px + 9*Py,
где
Px, Py – цены благ Х и Y соответственно.
Составим и решим систему уравнений:
Задача № 6. Расчёт оптимального объёма потребления
У студента Иванова в холодильнике сыр и колбаса нарезаны для удобства кусочками по 100 г. Общая полезность их потребления представлена в таблице. Определите количество съеденного им в день, если известно, что он в целом употребляет 700 г названных продуктов и при этом добивается максимума полезности.
| Количество, г | Колбаса (общая польза) | Сыр (общая польза) |
| 100 | 2000 | 1900 |
| 200 | 3900 | 3750 |
| 300 | 5700 | 5550 |
| 400 | 7400 | 7300 |
| 500 | 8000 | 9000 |
| 600 | 9500 | 10650 |
Решение:
Рассчитаем предельную полезность от потребления этих двух продуктов.
Предельная полезность в дискретном случае определяется по формуле:
где
ΔTU – приращение общей полезности (TU1 – TU0),
ΔQ – приращение количества потребляемого блага (Q1 – Q0).
Вычисления занесём в таблицу.
| Количество, г | Колбаса (общая польза) | Сыр (общая польза) | Предельная полезность колбасы | Предельная полезность сыра |
| 100 | 2000 | 1900 | 2000 | 1900 |
| 200 | 3900 | 3750 | 1900 | 1850 |
| 300 | 5700 | 5550 | 1800 | 1800 |
| 400 | 7400 | 7300 | 1700 | 1750 |
| 500 | 9000 | 9000 | 1600 | 1700 |
| 600 | 10500 | 10650 | 1500 | 1650 |
Известно, что в целом студент употребляет 700 г колбасы и сыра, то есть всего 7 кусочков, и при этом добивается максимума полезности.
Решение об оптимальном объёме потребления можно представить в виде таблицы, где на каждом шаге будем сравнивать предельную полезность каждого кусочка колбасы и сыра и выбирать наибольшую величину предельной полезности, что в сумме даст их максимум.
Итак, на первом шаге наибольшая предельная полезность, равная 2000 будет получена от потребления 1 кусочка/100 грамм колбасы. Дальше студенту без разницы, что употребить, так как первый кусочек сыра и второй кусочек колбасы приносят одинаковую полезность – 1900. Пусть, например, это будет сначала сыр, а затем колбаса. Но вот на четвёртом шаге наибольшую полезность принесёт второй кусочек сыра. Предельная полезность, полученная от его потребления 1850 больше, чем 1800 – предельная полезность третьего куска колбасы или третьего кусочка сыра. На пятом шаге студенту опять всё равно, что съесть первым, третий кусочек сыра или третий кусочек колбасы, так как полезность от дополнительного потребления этих продуктов одинакова. И наконец, седьмым кусочком должен стать сыр, поскольку предельная полезность четвёртого кусочка сыра (1750), больше чем предельная полезность четвёртого кусочка колбасы (1700).
Общая полезность от потребления 3 кусочков колбасы и 4 кусочков сыра будет максимальной и составит:
TU = 2000 + 1900 + 1900 + 1850 + 1800 + 1800 + 1750 = 13 000
Таким образом, студент Иванов получит максимум полезности при употреблении 3 кусочков (300 грамм) колбасы и 4 кусочков (400 грамм) сыра.
Задача № 7. Расчёт отимального объёма потребления
Определите оптимальный для потребителя объем блага Q, если известно, что функция полезности индивида от обладания этим благом имеет вид:
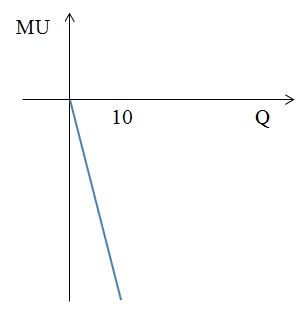
1) U(Q)= 1 – 5 × Q2
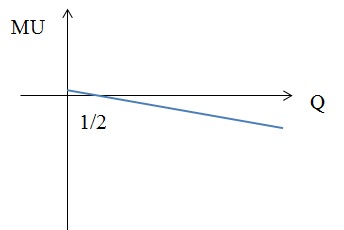
2) U(Q)= 5 + Q – Q2
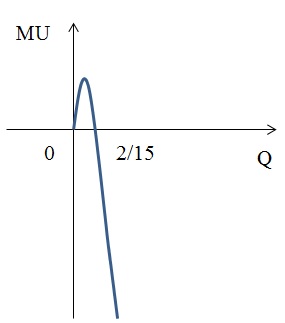
3) U(Q) = Q2 – 5 × Q3
Как будут выглядеть функции предельной полезности? Проиллюстрируйте ответ.
Решение:
Оптимальный для потребителя объем блага Q будет определяться в точке, где потребитель получит максимум удовлетворения полезности. Задача сводится к нахождению экстремума функции полезности. Найдём производную функции полезности (предельную полезность MU) и приравняем её к нулю.
1) MU = –10 × Q = 0, следовательно, Q = 0;
2) MU = 1 – 2 × Q = 0, следовательно, Q = 1/2;
3) MU = 2 × Q – 15 × Q2 = 0, следовательно, Q = 0; Q = 2/15.
Задача № 8. Расчёт цен товаров X и Y
Индивид покупает 4 единицы блага X и 9 единиц блага Y, имея доход равный 100 денежным единицам. Найти цены товаров X и Y, если известно, что предельная норма замены X на Y равна 4.
Решение:
По условию задачи предельная норма замены благом Y блага X () равно 4. Это значит, что количество блага Х должно быть сокращено на 4 единицы в обмен на увеличение количества блага Y на единицу, при неизменном уровне удовлетворения потребителя.
Равновесие потребителя может быть представлено математически как:
— это предельная норма замещения, равная отношению цен благ Y и X. Данное условие оптимума потребителя следует понимать так. Соотношение, в котором потребитель при данных ценах способен замещать один товар другим, равно соотношению, в котором потребитель согласен замещать один товар другим, не изменяя уровень своего удовлетворения.
Отсюда
Далее воспользуемся формулой бюджетного ограничения:
где I – доход или бюджет потребителя.
100 = 4 × PX + 9 × PY
100 = 4 × PX + 9 × 4 × PX
100 = 40 × PX
PX = 2,5
PY = 4 × 2,5 = 10.
Ответ: PX = 2,5; PY = 10.
Задача № 9. Определение рационального выбора потребителя
Потребитель имеет функцию полезности:
и может на свой доход равный 100 единицам приобретать только эти два товара по ценам:
Px = 2
Py = 5
Определить рациональный выбор потребителя. Какой максимальный уровень полезности достижим?
Решение:
Рациональный выбор потребителя осуществляется в соответствии со вторым законом Госсена:
Предельная полезность товара х будет равна производной функции общей полезности по аргументу х:
Аналогично находим предельную полезность товара y:
Далее воспользуемся бюджетным ограничением:
Из условия задачи известно, что:
I = 100
Px = 2
Py = 5
Составим и решим систему уравнений:
При х = 25 и у = 10 общая полезность достигнет максимума:
Задача № 10. Расчёт оптимального объёма потребления
У Оксаны есть 30 рублей. Она хочет купить шоколадки «Шок» ценой 3 р. Полезность от этой покупки она оценивает функцией:
х – приобретённое количество шоколадок,
y – оставшаяся часть дохода.
Сколько купит шоколадок «Шок» рациональная Оксана?
Решение:
Рациональное поведение потребителя можно определить, как стремление максимизировать излишек потребителя. Потребитель будет покупать дополнительные единицы до тех пор, пока они приносят дополнительный избыток, т.е. пока цена, которую потребитель готов уплатить за единицу блага, превосходит реальную цену:
MU > P
Однако каждая последующая единица потребления обычно приносит уменьшающийся прирост полезности, т.е. при покупке благ «одно за другим» рано или поздно предельная полезность какого-то блага сравняется с его ценой:
MU = P
После того как предельная полезность сравняется с ценой, потребитель прекратит дальнейшие покупки: оптимальный объём потребления достигнут.
Найдём предельную полезность MU, как производную функции общей полезности по аргументу х:
Оптимальный объём потребления будет достигнут при МU = P:
Таким образом, рациональная Оксана купит 4 шоколадки, потратив на эту покупку 12 рублей.
Если потребитель приобретает два и более наименования товаров и услуг, задача оптимального распределения семейного бюджета с целью максимизации совокупной полезности оказывается не такой простой. Рассмотрим сначала вариант потребления двух видов товаров, когда единственным ограничителем является фактор времени.
Пусть у студента есть возможность проводить свободные вечера на дискотеке или в спортзале. Допустим, что как занятия спортом, так и танцы бесплатны. Единственной альтернативной стоимостью танцевального вечера является упущенная возможность спортивной тренировки, и наоборот. В неделе всего 7 вечеров, которые предстоит распределить между двумя видами досуга таким образом, чтобы совокупная полезность была наибольшей.
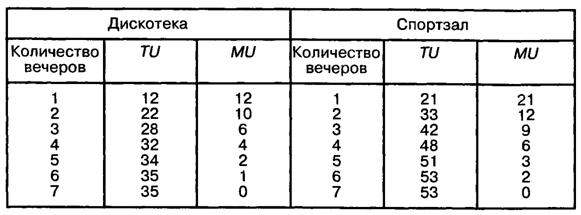
Предельная полезность каждого спортивного или танцевального вечера в течение недели приведена в табл. 1.
Таблица 1
Предельная полезность спортивного или танцевального вечера в течение недели
При заданных характеристиках распределение свободного времени будет происходить следующим образом. В первый вечер студент пойдет в спортзал, поскольку предельная полезность первого занятия спортом выше, чем предельная полезность первого посещения танцев. Полезность, полученная в первый вечер, составит 21 ютиль.
Во второй вечер студенту будет все равно, пойти ли на танцы, или в спортзал, потому что предельные полезности второго занятия спортом и первого посещения танцев равны 12. Предположим, что во второй вечер он пойдет для разнообразия на дискотеку, а в третий вечер — в спортзал. Таким образом, предельная полезность, полученная во второй день, составит 12, а совокупная полезность за 2 дня будет равна 21 + 12 = 33. Предельная полезность за третий вечер равняется также 12, а совокупная полезность за три дня составит 33 + 12 = 45.
В четвертый вечер студент пойдет на дискотеку, поскольку предельная полезность от второго ее посещения равна 10, тогда как предельная полезность от третьего посещения спортзала равна всего 9. Совокупная полезность за 4 дня составит 45 + 10 = 55.
Далее выбор между танцами и спортом будет осуществляться аналогичным образом, что в результате составит 4 вечера в спортзале и 4 вечера на дискотеке. Совокупная полезность будет при этом максимальной (80 ютилей).
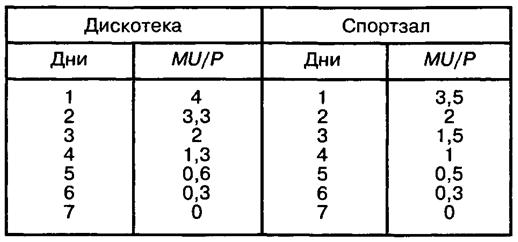
Далее рассмотрим ситуацию, когда и одна спортивная тренировка, и билет на танцы имеют свои цены соответственно 6 и 3 руб. Предположим одновременно, что отпущенный студентом на досуг бюджет равен 21 руб. в неделю. Каким образом ему следует распределить свое время и деньги, чтобы в пределах данного бюджета и при данных ценах получить максимально возможную полезность? Очевидно, что сопоставление полезности двух видов досуга должно вестись с учетом их цен, т.е. необходимо рассматривать полезность, получаемую на последний затраченный рубль. Для этого рассчитаем новый показатель, равный отношению предельной полезности к цене продукта (MU/P). В этом случае к нашей таблице прибавятся новые столбцы данных (табл. 2).
Таблица 2
Сопоставление полезности двух видов досуга с учетом их цен
С учетом бюджетного ограничения выбор потребителя будет осуществляться следующим образом. В первый вечер предпочтение будет отдано танцам, поскольку на затраченный рубль можно получить 4 ютиля полезности, тогда как на рубль занятий в спортзале — только 3,5 ютиля. Расходы составят 3 руб.
Во второй вечер студент отправится в спортзал (предельная полезность равна 3,5 ютилям на 1 руб. против 3,3 ютилей на 1 руб. на дискотеке). За первые два вечера студент израсходует 6 + 3 = 9 руб.
В третий вечер студент пойдет на дискотеку, так как 3,3 ютиля на 1 руб. выше, чем 2 ютиля на 1 руб. второго занятия в спортзале. Общая сумма расходов возрастет до 9 + 3 = 12 руб.
Четвертый и пятый вечера будут посвящены поочередно танцам и спорту, поскольку обеспечивают равную полезность на 1 руб. При этом общие расходы составят 12 + 6 + 3 = 21 руб. Таким образом, на шестой вечер студент исчерпал свой бюджет досуга, в седьмой вечер ему придется посидеть дома за учебниками. Если студент будет распределять свой недельный досуг так, как показано в настоящем примере, он израсходует свой бюджет наиболее рациональным образом и получит максимальную совокупную полезность в размере 61 ютиля.
Обратим внимание, что наилучшим образом бюджет используется в том случае, если уравниваются предельные полезности по каждому виду товара или услуги в расчете на последний израсходованный рубль. Действительно, если отношение предельной полезности к цене продукта А выше положительного эффекта от рубля, затраченного на продукт В, то потребитель будет увеличивать потребление именно товара А. И наоборот. Всякий раз предпочтение будет отдаваться тому или иному продукту до тех пор, пока полезный эффект от затраченного рубля по разноименным продуктам не станет равновеликим. Эту закономерность можно выразить следующей формулой, которая и будет формулой максимизации полезности для потребителя.
MUA / PA = MUB / PB = MUC / PC = …
Данное условие можно записать и в таком виде: по каждой паре товаров (услуг) отношение предельных полезностей должно равняться отношению их цен:
MUA / MUB = РА/РВ.
Отношение предельных полезностей двух товаров называется предельной нормой замещения в потреблении (MRS) и показывает, от какого количества единиц продукта В потребитель готов отказаться ради приобретения дополнительной единицы продукта А.
Например, если отношение предельной полезности товара X к предельной полезности товара У равно 4, это означает, что единица товара X имеет в глазах данного потребителя в 4 раза большую ценность и полезность, чем единица товара У. Если окажется, что рыночное соотношение цен этих товаров равно 5, это будет означать, что рынок позволяет за одну единицу товара X получить 5 единиц товара У.
Таким образом, в нашем примере потребитель выиграет, обменяв единицу продукта X на пять единиц товара У, предлагаемых ему рынком, поскольку сам потребитель был бы удовлетворен (т.е. не потерял бы в совокупной полезности) даже при обмене на четыре единицы товара У.
Можно сделать вывод, что рациональный потребитель предпочтет увеличивать потребление товара У до тех пор, пока отношение предельных полезностей двух товаров не сравняется с отношением их цен.
| < Предыдущая | Следующая > |
|---|
Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.
| Количество товара | А | В | С | |||
|---|---|---|---|---|---|---|
| TU | MU | TU | MU | TU | MU | |
| 1 | … | 20 | 19 | … | 22 | … |
| 2 | … | 15 | 30 | … | … | 10 |
| 3 | … | 12 | 38 | … | 39 | … |
| 4 | … | 8 | 43 | … | 44 | … |
| 5 | … | 6 | 45 | … | … | 3 |
Решение:
Найдём общую полезность товара А.
Общая полезность N-й единицы товара = Предельная полезность N-й единицы товара + Общая полезность N-1-й единицы товара
TU(1)=MU(1)=20
TU(2)=MU(2) + TU(1)=15 + 20=35
TU(3)=MU(3) + TU(2)=12 + 35=47
TU(4)=MU(4) + TU(3)=8 + 47=55
TU(5)=MU(5) + TU(4)=6 + 55=61
Найдём предельную полезность товара В.
Предельная полезность N-й единицы товара=Общая полезность N-й единицы товара — Общая полезность N-1-й единицы товара
MU(1)=TU(1)=19
MU(2)= TU(2) — TU(1)=30 – 19 = 11
MU(3)= TU(3) — TU(2)=38 – 30 = 8
MU(4)= TU(4) — TU(3)=43 – 38=5
MU(5)= TU(5) — TU(4)=45 – 43=2
Найдём общую и предельную полезности товара С.
MU(1)=TU(1)=22
TU(2)=MU(2) + TU(1)=10 + 22=32
MU(3)= TU(3) — TU(2)=39 – 32=7
MU(4)= TU(4) — TU(3)=44 – 39=5
TU(5)=MU(5) + TU(4)=3 + 44=47
Заполним пропуски в таблице:
| Количество товара | А | В | С | |||
|---|---|---|---|---|---|---|
| TU | MU | TU | MU | TU | MU | |
| 1 | 20 | 20 | 19 | 19 | 22 | 22 |
| 2 | 35 | 15 | 30 | 11 | 32 | 10 |
| 3 | 47 | 12 | 38 | 8 | 39 | 7 |
| 4 | 55 | 8 | 43 | 5 | 44 | 5 |
| 5 | 61 | 6 | 45 | 2 | 47 | 3 |
Примеры решений задач: функция полезности
В этом разделе вы найдете подробно решенные задачи, касающиеся функции полезности, задачи выбора потребителем набора благ при заданном бюджетном ограничении, максимизации полезности, заменяемости товаров и т.д.
Лучшее спасибо — порекомендовать эту страницу
Функция полезности: задачи с решениями
Задача 1. Функция полезности имеет вид: $TU=4xy$, где X и Y — количество товаров. Расходы потребителя на эти два товара в месяц равны 1200 р., цена товара X — 400 р., товара Y — 300 р. Определите оптимальный объем ежемесячных закупок двух данных товаров и соответствующее ему значение общей полезности.
Задача 2. Условия: потребитель расходует 200 руб. в неделю на покупку товаров А и В.
Цена (руб.) Кол-во покупаемых единиц товаров Общая полезность Предельная полезность
А 7 20 500 20
В 5 12 1000 30
Задание: Объяснить, как должен поступать потребитель, чтобы максимизировать получаемую полезность при данном бюджете.
Задача 3. Потребитель покупает три товара Х, Y, Z, цены которых соответственно равны Px=100 руб.; Py=70 руб.; Pz=50 руб.
Функции общей полезности разных благ: $F(TU(x))=3sqrt{Qx}$, $F(TU(y))=5sqrt{Qy}$, $F(TU(z))=5sqrt{Qz}$.
Определить:
1) каким образом потребитель может использовать денежный запас 500 рублей для достижения максимальной полезности при потреблении и рассчитать её количественно;
2) то же, если при покупке более, чем 2-х товаров Px снижается на 25%, а Py – на 50%
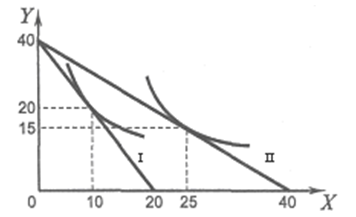
Задача 4. Допустим, потребитель имеет доход 200 ден. ед. На рисунке показаны две бюджетные линии (I и II) и соответствующие им кривые безразличия.
Определить координаты (P,Q) двух точек линии спроса данного потребителя на товар Х.
Задача 5. Общая полезность благ $alpha$ и $beta$ для некоего потребителя описывается уравнениями $U_alpha = q_alpha(15 — 0,5q_alpha)$, $U_beta = q_beta(30 — q_beta)$. Допустим, потребитель располагает бюджетом для покупки $alpha$ и $beta$ в размере 120 руб., цены на $alpha$ и $beta$ равны соответственно 5 и 10 руб. Определить количество $alpha$ и $beta$, максимизирующее полезность потребителя.
Задача 6. Потребитель тратит 7 долларов в день на товары X и Y. MU товара X для него равна $10 – x$, где $x$ — количество X в шт. MU товара Y: $21 – 2y$, где $y$ — количество Y в шт. Р 1 ед. товара X = 1 доллар, P 1 ед. Y = 1 доллар. Какое количество X и Y купит рациональный покупатель?
Задача 7. В таблице представлена предельная полезность для походов в магазин.
Имея 100 руб. 80 коп. потребитель купил 3 буханки хлеба по цене 8 руб. за буханку, 4 пакета молока по 11 руб. 20 коп. за пакет и 2 пачки сахара по 16 руб. за пачку. Достиг ли он максимума полезности? Ответ обосновать и в случае отрицательного ответа определить объем покупок, обеспечивающий максимум полезности при данном бюджете.
Задача 8. Построить кривую безразличия для двух абсолютно взаимозаменяемых товаров: пепси-колы и кока-колы, если их цены за литр равны 8 и 10 ден. ед. при бюджете на их потребление, равном 40 ден. ед.
Задача 9. Индивидуум имеет функцию полезности типа Неймана—Моргенштерна, а элементарная функция полезности строго возрастает и зависит только от одного аргумента (денег). Лотерея 6 долларов и 10 долларов с вероятностями 1/3 и 2/3 и лотерея 3 доллара и 9 долларов с вероятностями 2/3 и 1/3 для него эквивалентны. Что можно сказать о склонности данного индивида к риску?
Задача 10. Пусть функция полезности наборов из двух товаров $X=(x_1,x_2)$ имеет вид $u(x_1,x_2)=x_1^{1/7}x_2^{1/6}$.
• Найти набор товаров, который имеет такую же полезность, как набор $X_1=(5,3)$ и количество второго товара равно 1.
• Для набора $X_1=(5,3)$ найти предельные полезности первого и второго товаров.
• В наборе $X_1=(5,3)$ количество первого товара увеличивается на 0,1, а второго уменьшается на 0,2. Найти приближённое изменение полезности.
Задача 11. Функция полезности потребителя имеет вид $u(x_1,x_2)=(x_1-50)^{1/7}(x_2-40)^{1/6}$.
1. Найти равновесный спрос и его полезность, если рыночная цена первого товара $p_1=5$, рыночная цена второго товара $p_2=3$ и потребитель выделяет на приобретение товаров сумму $M=5000$ денежных единиц.
2. Найти функции спроса на оба вида товаров.
3. Найти спрос на оба товара при увеличении дохода на 30 денежных единиц и при уменьшении дохода на 60 денежных единиц.
Задача 12. Для потребителя с функцией полезности $U(x_1,x_2)=x_1^{1/3}x_2^{1/4}$
1) найдите функцию спроса на каждый товар;
2) найдите точку спроса при доходе $K=60$ и ценах $P=(2,4)$.
Задача 13. Решить прямую задачу потребителя (найти оптимальную потребительскую корзину). Дано: Функция полезности потребителя $U=sqrt{xy}$. Цена блага х равна 15, цена блага у равна 20, доход потребителя равен 300.
Найти: Оптимальный набор благ потребителя $(х, у)$.
Задача 14. Предельная полезность первой единицы блага равна 300. При потреблении первых трех единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза. Предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 5 раз. Найти совокупную полезность 5 единиц блага.
Консультируем по решению задач микроэкономики
Может быть интересно:
|
|
Теория потребительского выбора
Понятия полезности, потребительского выбора, общей и предельной полезности
Потребители распределяют свой доход по различным доступным для них товарам и услугам. Изучив поведение потребителя, можно лучше понять сущность законов спроса.
Цель потребителя – воспроизводство, возобновление и развитие своей жизнедеятельности на основе потребления определённой совокупности благ и услуг.
- безграничность;
- историчность (меняются во времени).
Средством удовлетворения потребностей служат экономические блага (товары и услуги).
Главным фактором, определяющим выбор рационального потребителя, является полезность. При этом он стремится к ее максимизации, затратив минимум средств.
Полезность – это свойство экономического блага удовлетворять потребности.
Потребительский выбор – это выбор такой достижимой для него комбинации продуктов, которая максимизировала бы удовлетворение его потребностей или извлекаемую им полезность.
где U – уровень полезности;
Qx, Qy, Qz – объёмы потребляемых продуктов или услуг за определённый период времени;
f – зависимость уровня полезности от количества потребляемых продуктов и услуг.
- общей (совокупной) полезности (TU);
- предельной полезности (MU).
В микроэкономике различают две версии рационального потребительского поведения: количественную и порядковую.
Сторонники количественного подхода к анализу полезности – видные экономисты ХIХ в. У. Джевонс, К. Менгер, Л. Вальрас и другие – предлагали для удобства исследования спроса измерять общую полезность от потребления блага в неких количественных показателях – «ютилях» (от англ. utility – полезность). В частных случаях для измерения полезности используют денежные единицы измерения, дополнительные баллы, бонусы и т.д.
Сегодня больше говорят не об измерении, а о сравнении полезностей, получаемых от потребления различных наборов благ. Этот подход называется порядковым (ординалистским).
Общая (совокупная) полезность (TU) – это общее удовлетворение или удовольствие, которое получает человек от потребления конкретного количества (скажем, 10-ти ед.) товара или услуги.
Предельная полезность (MU) – это дополнительное удовлетворение, извлекаемое потребителем из следующей (11-й) единицы продукта, то есть это изменение совокупной полезности, вызванное потреблением еще одной единицы продукта.
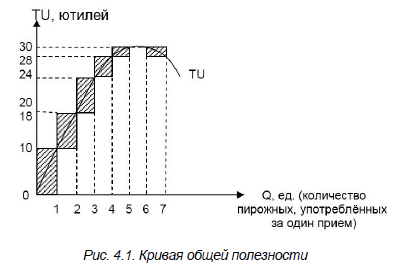
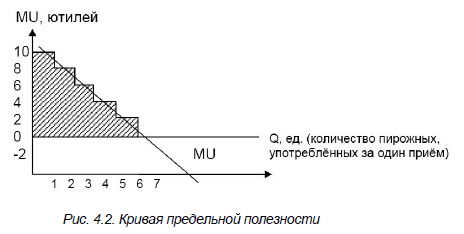
На графиках (рис. 4.1, рис. 4.2) и в табл. 4.1 – соотношение совокупной и предельной полезности.
При потреблении пяти единиц совокупная полезность возрастает, при потреблении 6-й единицы TU достигает максимальной величины, а затем начинает сокращаться.
Предельная полезность(MU) пирожных вплоть до 5-й единицы остается величиной положительной (поскольку ТU растёт всё более низкими темпами). К 6-й единице MU становится равной 0 (так как эта единица не изменяет величины TU). Затем, начиная с 7-й единицы, MU становится отрицательной величиной (поскольку TU сокращается) – дальнейшее потребление принесёт вред.
| Количество пирожных, употреблённых за один прием пищи, ед. | Совокупная полезность, ютилей | Предельная полезность, ютилей |
|---|---|---|
| 0 | 0 | |
| 1 | 10 | 10 |
| 2 | 18 | 8 |
| 3 | 24 | 6 |
| 4 | 28 | 4 |
| 5 | 30 | 2 |
| 6 | 30 | 0 |
| 7 | 28 | –2 |
По мере роста потребления MU сокращается, затем в точке, где TU максимальна, становится равной 0, а с уменьшением TU приобретает отрицательное значение. Как показано на графиках, MU – это изменение TU от наличия дополнительного пирожного. Каждый новый уровень TU можно определить, если добавить MU к предыдущему уровню TU.
Закон возрастающей общей полезности; 1-й и 2-й законы Госсена
Закон возрастающей общей полезности: по мере увеличения количества потребляемого продукта общая полезность возрастает, а прирост полезности от каждой ее порции убывает.
Предельная полезность определяется по формуле
1-й закон Госсена (или закон убывающей предельной полезности): при увеличении объёма потребляемого продукта добавочная полезность каждой последующей порции продукта убывает.
Минимум MU достигается в точке, когда TU6 = 30 (максимальна):
2-й закон Госсена, или правило максимизации полезности: рациональный потребитель максимизирует общую полезность, если каждая последняя денежная единица, затрачиваемая на приобретение продуктов или услуг, приносит одинаковую полезность:
MU1 / P1 = MU2 / P2 = … = MUn / Pn = λ,
где MU1; MU2; … MUn – предельные полезности потребляемых продуктов; P1; Р2; … Рn – цены на данные продукты; λ – предельная полезность денег.
Правило максимизации полезности отражает ситуацию потребительского равновесия.
Тогда MU = P·λ, где P·λ – предельные издержки потребителя.
Следовательно, если МС = Р·λ, то MU = MC.
Шкала, кривая и карта безразличия. Предельная норма замещения. Бюджетная линия. Условие равновесия потребителя
Основоположники порядковой теории – Слуцкий, Хикс, Парето – исходили из того, что полезность отдельных продуктов измерить нельзя, но можно расставить приоритеты, т.е. построить шкалу предпочтений (или шкалу безразличия).
| Комбинация продуктов А и В | Количество продукта А, ед. | Количество продукта В, ед. |
|---|---|---|
| J | 12 | 2 |
| K | 6 | 3 |
| L | 3 | 6 |
| M | 1 | 10 |
Потребителю безразлично, какой набор выбрать.
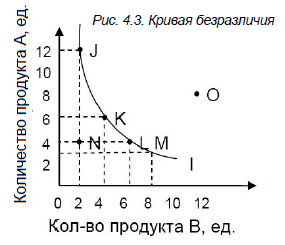
На основе шкалы безразличия (табл. 4.2) построим кривую безразличия (рис. 4.3).
Каждая точка на графике 4.3 – это одна из комбинаций двух продуктов А и В, выбор которой безразличен потребителю, так как обладает одинаковой совокупной полезностью.
На основе графика (см. рис. 4.3) можно сделать следующие выводы:
- наборы продуктов, соответствующие точкам J, K, L, M, имеют одинаковую полезность для потребителя (т.е. потребитель безразличен к этим наборам продуктов);
- набор продуктов, соответствующий точке N, менее предпочтителен для потребителя;
- набор продуктов, соответствующий точке O, более предпочтителен для потребителя.
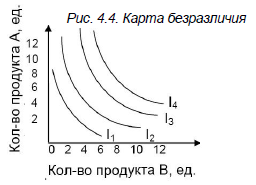
Если через точки N и O провести кривые, параллельные исходной кривой, то получим карту безразличия (рис. 4.4).
Карта безразличия представляет собой набор кривых безразличия (вкусы и предпочтения потребителей).
Каждая последующая кривая, дальше отстоящая от начала координат, соответствует большей величине совокупной полезности.
Комбинация А и В, представленная любой точкой на кривой I4, обладает большей полезностью, чем любая комбинация А и В, соответствующая любой точке на кривых I3, I2, I1.
Свойства кривых безразличия на карте безразличия следующие.
1. Кривые безразличия не пересекаются, так как один набор продуктов, который предпочтительнее другого набора, не может находиться с ним на одном уровне.
2. Кривые безразличия имеют отрицательный наклон, так как увеличение количества одного продукта сопровождается уменьшением количества другого, входящего в тот же набор продуктов.
3. Кривые безразличия вогнуты: чем менее вогнута кривая безразличия, тем ниже предельная норма замещения.
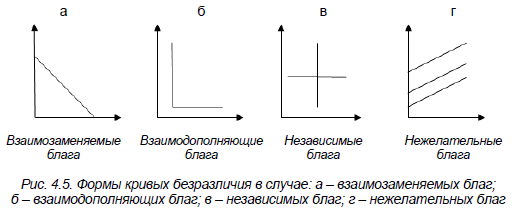
На рис. 4.5 представлены формы кривых безразличия.
Предельная норма замещения (marginal rate of substitution) – такое количество продукта А, которым потребитель согласен пожертвовать, чтобы приобрести дополнительную единицу продукта В, при их одинаковой общей полезности:
где MUA, MUB – предельные полезности товаров А и В.
Предельная норма замещения – производная в любой точке кривой безразличия:
Анализ потребительских предпочтений не показывает, какой из наборов продуктов купит покупатель. Следовательно, чтобы разобраться в этом, надо изучить покупательную способность потребителя. Для этого необходимо учитывать цены на продукты и доход потребителя.
Пусть A и B – то количество продукта, которое хотят приобрести покупатели. При этом цены на продукты равны РА и РВ соответственно, I – номинальный доход потребителя (величина постоянная). Тогда алгебраически бюджетное ограничение потребителя примет следующий вид:
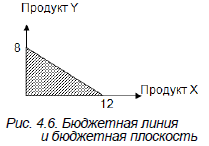
На основе данного тождества построим бюджетную плоскость (рис. 4.6).
На основе графика можно сделать следующие выводы:
- заштрихованная плоскость – бюджетные возможности покупателя;
- все точки, лежащие внутри бюджетного пространства, показывают доступность потребителю данных продуктов (однако, приобретая их, он не полностью использует свой доход);
- наборы продуктов, лежащие за бюджетной линией, предпочтительны для потребителя, но не доступны, так как его доход не позволяет их приобрести.
Бюджетная линия – линия, которая графически отражает набор продуктов, приобретение которых требует одинаковых затрат (различные комбинации двух продуктов, которые могут быть приобретены при данной величине денежного дохода).
Например, если продукт B стоит 1,5 долл., а продукт A – 1 долл., то при доходе 12 долл. можно купить комбинации продуктов А и В (табл. 4.3).
График (см. рис. 4.6) не ограничивается комбинациями целых единиц В и А, представленных в таблице.
| Кол-во единиц продукта B (по цене 1,5 долл. за ед.) | Кол-во единиц продукта А (по цене 1 долл. за ед.) | Совокупные расходы, долл. |
|---|---|---|
| 8 | 0 | 12 (12 + 0) |
| 6 | 3 | 12 (9 + 3) |
| 4 | 6 | 12 (6 + 6) |
| 2 | 9 | 12 (3 + 9) |
| 0 | 12 | 12 (0 + 12) |
Наклон бюджетной линии определяется величиной отношения цены товара А к цене товара В:
Уравнение бюджетной линии
где I – доход (бюджет) потребителя в единицу времени; РА, PB – цены соответствующих благ (заданные величины); A, B – переменные величины (потребитель выбирает значения A и B, которые доступны его бюджету).
Свойства бюджетной линии:
- при увеличении дохода бюджетная линия смещается вправо; при уменьшении дохода – влево;
- при уменьшении цен обоих продуктов бюджетная линия смещается вправо; при росте цен на продукты А и В – влево.
Таким образом, оптимальный выбор потребителя зависит от следующих факторов:
- степени предпочтения потребителя;
- цен на продукты;
- дохода, т.е. бюджетного ограничения.
Условие равновесия потребителя
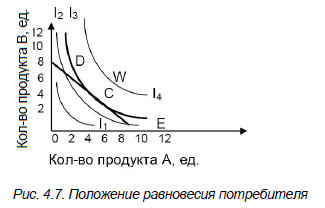
Положение равновесия потребителя можно определить путем совмещения бюджетной линии и карты безразличия (рис. 4.7).
Точка С – равновесная; точка качания бюджетной линии и наиболее высокой кривой безразличия I3. В этом случае потребитель, имеющий доход 12 долл., купит 4 ед. продукта B по цене 1,5 долл. и 6 ед. Х по цене 1 долл.
Точки E и D также показывают комбинации продуктов А и В, но этим точкам соответствуют меньшие совокупные полезности.
Точка W соответствует большей величине полезности, чем точка C, но находится выше бюджетной линии и, следовательно, недоступна для данного потребителя.
Таким образом, в точке С достигается оптимальная комбинация продуктов B и A.
Поскольку наклон кривой безразличия отражает предельная норма замещения (MRS), а наклон бюджетной линии равен PА /PB, оптимальное, или равновесное положение достигается при условии, что
Таким образом, набор из двух продуктов, соответствующий точке С, отражает ситуацию потребительского равновесия, в которой рациональный потребитель достигает максимума общей полезности (2-й закон Госсена).
- достигается максимум общей полезности;
- объединяются обе теории потребительского выбора (количественная и порядковая).
Изменение цены одного из продуктов приводит к смещению бюджетной линии и установлению нового равновесного положения.
Понятие потребительской ренты
Анализ кривой предельной полезности позволяет осмыслить и такую важнейшую категорию, как избыток потребителя (потребительская рента).
Смысл этой категории заключается в следующем: потребитель платит за каждую единицу товара одинаковую цену, равную предельной полезности последней, наименее ценной для него единицы.
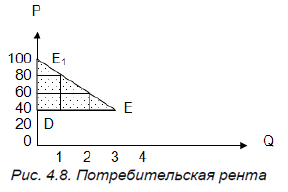
А это значит, что на каждой единице товара, предшествующей этой последней, потребитель получает некоторую выгоду (рис. 4.8).
Если бы потребитель приобретал только одну единицу товара, то он согласен был бы уплатить 80 долл. За 2-ю единицу (если бы было всего 2 ед. товара) потребитель заплатил бы 60 долл. Рыночная цена каждой из 2-х единиц при этом составила бы одну и ту же величину – 60 долл. (ведь цена устанавливается на уровне предельной – в данном случае 2-й единицы).
Индивидуальная оценка полезности 1-й ед. – 80 долл., 2-й – 60 долл., их сумма – 140 долл. Но по единой цене покупаются обе единицы, так что потребитель заплатит (60 + 60) всего 120 долл.; 3-ю ед. покупатель оценивает в 40 долл., и эта предельная полезность будет определять рыночную цену всех 3-х единиц. Следовательно, рыночная цена, уплаченная потребителем при покупке 3-х товаров, составит 40 + 40 + 40 = 120 долл. А ведь если суммировать индивидуальные оценки предельной полезности каждой из 3-х единиц, то получилось бы 80 + 60 + 40 = 180 долл. Итак, потребительская рента – это разница между той суммой денег, которую потребитель был бы согласен уплатить, и той суммой, которую он реально уплатил. На графике (см. рис. 4.8) потребительская рента – это заштрихованный треугольник DEE1. Чем ниже цена, тем больше величина потребительской ренты. При покупке 2-х единиц товара потребительская рента составит 140 – 120 = 20 долл.; при покупке 3-х единиц 180 – 120 = 60 долл.
Эффект дохода и эффект замещения
Изменение цены воздействует на потребляемый объём (объём спроса) двояко. Например, снижение цены какого-либо одного блага позволяет без изменения полезности высвободить часть бюджета для дополнительного приобретения обоих благ. Это явление получило название эффекта дохода.
Кроме того, снижение цены может привести к тому, что потребитель будет склонен изменить структуру потребления, отказываясь от покупки относительно подорожавшего блага и покупая на высвободившиеся средства относительно подешевевшее благо. Это эффект замещения.
Задача №59. Расчёт общей и предельной полезности
Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.
| Количество товара | А | В | С | |||
|---|---|---|---|---|---|---|
| TU | MU | TU | MU | TU | MU | |
| 1 | . | 20 | 19 | . | 22 | . |
| 2 | . | 15 | 30 | . | . | 10 |
| 3 | . | 12 | 38 | . | 39 | . |
| 4 | . | 8 | 43 | . | 44 | . |
| 5 | . | 6 | 45 | . | . | 3 |
Решение:
Найдём общую полезность товара А.
Общая полезность N-й единицы товара = Предельная полезность N-й единицы товара + Общая полезность N-1-й единицы товара
TU(2)=MU(2) + TU(1)=15 + 20=35
TU(3)=MU(3) + TU(2)=12 + 35=47
TU(4)=MU(4) + TU(3)=8 + 47=55
TU(5)=MU(5) + TU(4)=6 + 55=61
Найдём предельную полезность товара В.
Предельная полезность N-й единицы товара=Общая полезность N-й единицы товара — Общая полезность N-1-й единицы товара
MU(2)= TU(2) — TU(1)=30 – 19 = 11
MU(3)= TU(3) — TU(2)=38 – 30 = 8
MU(4)= TU(4) — TU(3)=43 – 38=5
MU(5)= TU(5) — TU(4)=45 – 43=2
Найдём общую и предельную полезности товара С.
Предельная полезность
Определение
Предельная полезность (англ. Marginal Utility, MU) – это дополнительное количество полезности, которое получает потребитель от потребления следующей единицы блага. При этом кардиналисты предлагают использовать ютиль в качестве условной единицы измерения полезности.
Формула
Если общая полезность (англ. Total Utility, TU) блага задана в виде функции от его количества q, то функция предельной полезности будет ее первой производной. В общем виде она может быть записана следующим образом:
Поскольку функция общей полезности TU(q) достигает своего максимума при MU(q) = 0, то количество блага, при котором потребитель максимизирует полезность можно рассчитать решив следующее уравнение:
Если общая полезность блага задана в виде числового ряда, то предельную полезность от потребления его n-ой единицы можно рассчитать по следующей формуле:
где TUn – это общая полезность от потребления n единиц блага, а TUn-1 – это общая полезность от потребления (n-1) единиц блага.
График
Чтобы лучше разобраться с функцией общей и предельной полезности, рассмотрим следующий пример. Предположим, что кривая общей полезности блага описывается функцией:
График этой функции представлен на рисунке ниже.
Функция предельной полезности будет первой производной от функции общей полезности, а именно:
Ее график приведен на рисунке ниже.
Следует отметить, что предельная полезность равна нулю в тот момент, когда потребитель полностью удовлетворил свою потребность в данном благе. В этот же самый момент общая полезность достигает своего максимума. Дальнейшее потребление данного блага будет обладать отрицательной предельной полезностью, поэтому рациональный потребитель прекратит потребление.
Чтобы найти максимум функции общей полезности для условия данного примера, необходимо решить следующее уравнение:
Таким образом, потребитель максимизирует свою полезность потребив 23,3 единицы блага.
Закон убывающей предельной полезности
Закон убывающей предельной полезности утверждает, что полезность каждой следующей потребленной единицы блага снижается по сравнению с предыдущей единицей. При этом общая полезность увеличивается до того момента, пока предельная полезность не станет равна нулю.
Ограничения закона
Следует отметить, что действие этого закона возможно при выполнении следующих ограничений.
- Потребитель принимает решение рационально.
- Цена одной единицы блага неизменна. Цена является важным фактором, который принимает во внимание рациональный потребитель при принятии того или иного решения. Поскольку потребление одного блага осуществляется за счет отказа от потребления других благ, изменение цены может повлиять на пересмотр полезности этих благ для потребителя. В этом случае закон убывания предельной полезности может перестать выполняться, поэтому неизменность цен является обязательным условием.
- Потребляемое благо однородно. Другими словами, каждая следующая единица потребляемого блага должна быть полностью идентична предыдущей.
- Потребление блага осуществляется непрерывно. Каждая следующая единица блага потребляется непосредственно сразу за предыдущей. Если возникает перерывы в потреблении предельная полезность блага может не уменьшаться.
Принимая решение рациональный потребитель действует следующим образом:
- максимизирует полезность;
- предпочитает получить как можно больше благ;
- имеет возможность сравнивать различные альтернативы (имеет доступ к необходимой информации);
- остается последовательным в своих предпочтениях.
Примеры решения задач
Задача 1
Данные о количестве и общей полезности потребляемого блага приведены в таблице.
- рассчитать предельную полезность;
- построить график кривой общей и предельной полезности.
Решение
(a) Чтобы рассчитать предельную полезность каждой следующей единицы потребляемого блага воспользуемся следующей формулой:
Дальнейшие расчеты производились аналогично, а их результаты сведены в таблицу.
(b) Построим график на основании данных из предыдущей таблицы.
Как мы можем видеть предельная полезность блага равна нулю при потреблении 11 единиц, при этом потребителем достигается максимальная общая полезность 275 ютилей.
Задача 2
Общая полезность блага для потребителя описывается следующей функцией:
- построить графики общей и предельной полезности;
- определить количество единиц потребляемого блага, при котором потребитель максимизирует полезность.
Решение
(a) График функции общей полезности выглядит следующим образом.
Функция предельной полезности является первой производной от функции общей полезности.
Ее график представлен на рисунке ниже.
(b) Поскольку функция общей полезности достигает максимума при MU(q) = 0, то нам необходимо решить следующее уравнение относительно переменной q.
Таким образом, потребитель максимизирует свою полезность потребив 20 единиц блага. При этом общая полезность составит 600 ютилей.
http://ecson.ru/economics/consumer-behaviour/zadacha-59.raschyot-obschey-i-predelnoy-poleznosti.html
http://allfi.biz/CFA/Level-1/microeconomics/predelnaja-poleznost/