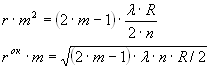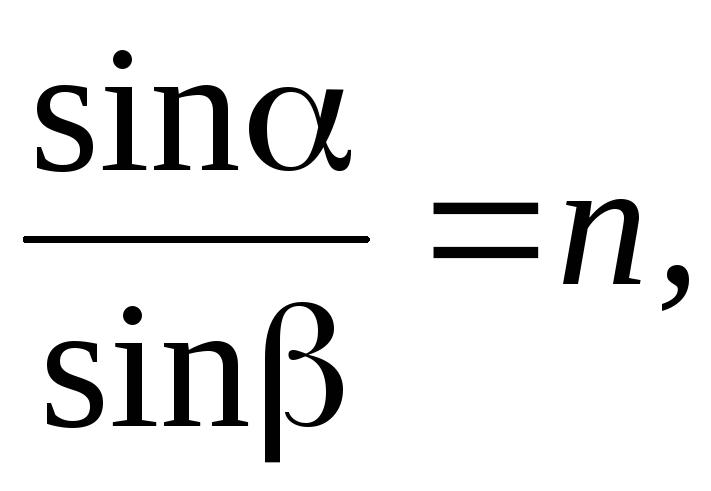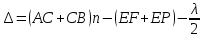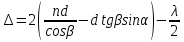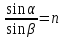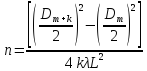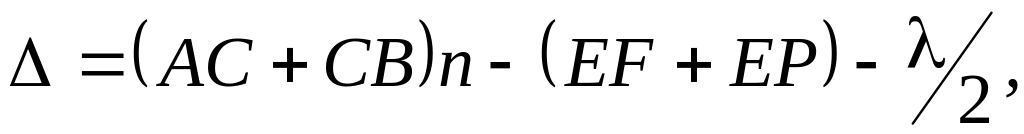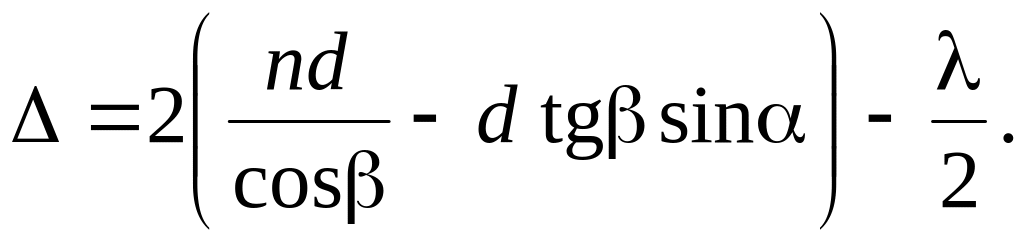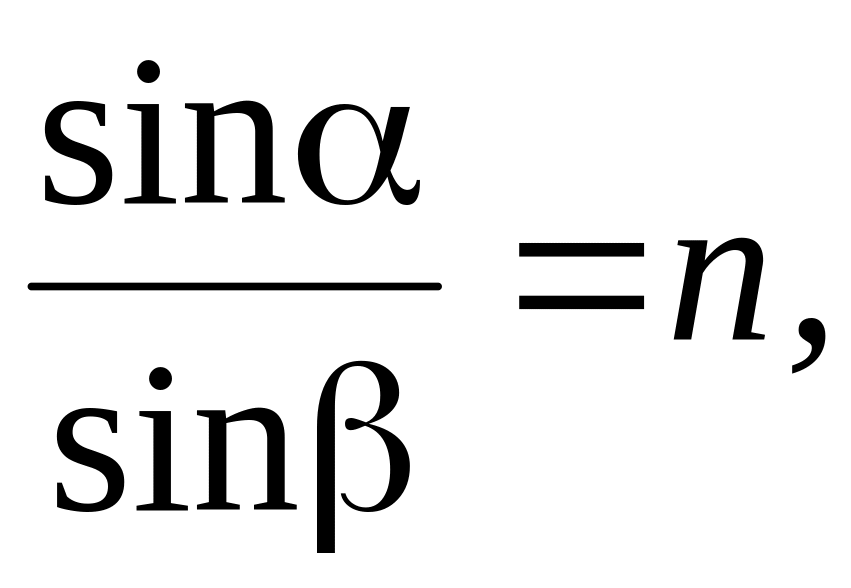Интерференцию света можно наблюдать
не только в лабораторных условиях с
помощью специальных установок и приборов,
но и в естественных условиях. Так,
легко наблюдать радужную окраску мыльных
пленок, тонких пленок нефти и минерального
масла на поверхности воды, оксидных
пленок на поверхности закаленных
стальных деталей (цвета побежалости).
Все эти явления обусловлены
интерференцией света в тонких прозрачных
пленках, возникающей в результате
наложения когерентных волн, возникающих
при отражении от верхней и нижней
поверхностей пленки.
Исследование интерференции в тонких
пленках позволяет определять ряд
практически важных величин
–толщину пленки,
её показатель преломления, температуру
нагрева под закалку деталей, длину
волны излучения и т.д.
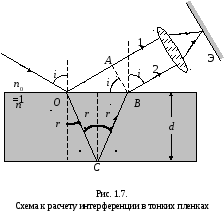
Схема возникновения интерференции
света в отраженном свете показана на
рис. 1.7. На пленку толщиной d
падает плоская монохроматическая
волна (λ0 =
соnst) под угломi. Предположим,
что по обе стороны от пленки с показателем
преломленияn находится
одна и та же среда (например, воздух
с показателем преломленияn0
=1).
Рассмотрим один луч, падающий на верхнюю
поверхность пленки. На поверхности
пленки в точке Опадающий
луч разделится на два: первый
(1) –отразится
от верхней поверхности пленки,
второй (2) –преломится. Преломленный луч, дойдя
до точкиС,частично
преломится в воздух, а частично
отразится и пойдет к точкеВ.
В этой точке он вновь
частично отразится в пленку и частично
преломится, выйдя в воздух под угломi.Лучи
1и 2,образовавшиеся в результате отражения
от верхней и нижней поверхностей пленки,
когерентны. Если на их пути поставить
собирательную линзу (глаз), то лучи
сойдутся в одной из точекМфокальной
плоскости, образуя на экране Э
интерференционную картину (интерференция
в отраженном свете).
Результат интерференции в точке Мопределится оптической разностью
хода лучей 1и
2.Оптическую разность хода эти лучи
набирают от точки Одо
плоскостиАВ ,являвшейся
фронтом вторичных (отраженных) лучей.
ФронтАВперпендикулярен лучам
1и 2.
Итак, оптическая разность хода лучей
1 и 2
,
(1.21)
где
п
–
показатель
преломления пленки; n0
–
показатель преломления воздуха, n0=
1;
а λ0/2
–
длина полуволны, потерянной при отражении
луча
1
в точке О
от
границы раздела с оптически более
плотной
средой
(n
>
n0).
Используя
выражение (1.21) для оптической разности
хода, условия максимумов и минимумов
интерференции, а также закон преломления,
получим:
,
(1.22)
где
k
= 0, 1, 2, … (в этом случае отраженные лучи
будут максимально усилены, т.е. наблюдается
максимум интерференции);
, (1.23)
(в этом случае наблюдается наибольшее
ослабление отраженных лучей – минимум
интерференции).
При освещении пленки белым светом она
окрашивается в какой-либо определенный
цвет, длина волны которого удовлетворяет
максимуму интерференции. Следовательно,
по цвету пленки можно оценивать её
толщину.
Интерференция наблюдается также и в
проходящем свете. Оптическая
разность хода (ΔL) для проходящего
света отличается от ее значения для
отраженного света на λ0/2.
Следовательно, максимуму интерференции
в отраженном свете для данной длины
волны соответствует минимум
интерференции в проходящем, т.е. в
отраженном и проходящем свете пленка
окрашивается в дополнительные (до
белого) цвета.
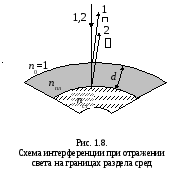
Возможность
ослабления отраженного света вследствие
интерференции в тонких пленках широко
используется в современных оптических
приборах (фотоаппаратах, биноклях,
перископах, микроскопах и т.д.) для
улучшения их качества. Способ получения
высокоотражающих покрытий и улучшения
качества оптических приборов получил
название «просветления оптики».
Прохождение света через каждую
преломляющую поверхность линзы,
например, через границу стекло
воздух, сопровождается отражением
~ 4 %падающего потока (при показателе
преломления стеклаn =
1,5).Так как современные объективы
содержат большое количество линз,
потери светового потока из-за отражений
велики. В результате интенсивность
прошедшего света ослабляется, и светосила
оптического прибора уменьшается. Кроме
того, отражение от поверхностей линз
приводит к возникновению бликов, что,
например, в военной технике, демаскирует
местонахождение прибора. Для
устранения указанных недостатков
осуществляют так называемое
просветление оптики. С этой целью на
поверхности линз наносят тонкие
пленки с показателем преломления,
меньшим показателя преломления материала
линз (1<
n < nст). При
отражении света от границ раздела
воздух пленка и пленка
стекло возникает интерференция
когерентных лучей 1и 2(рис. 1.8).
Толщину пленки d и показатели
преломления стеклаnсти пленкипплподбирают так, чтобы при
интерференции в отраженном свете лучи
1и 2гасили друг друга. Для этого их оптическая
разность хода должна удовлетворять
условию (1.17).Так как потери
полуволн происходят на обеих поверхностях
пленки, и свет падает нормально
(угол падения i = 0),
условие минимума в отраженном свете
запишется так:
, (1.24)
где
2d
·
nпл
—
оптическая разность хода лучей 1
и
2.
Толщину пленки выбирают минимальной
(k=
0).
Тогда
.
(1.25)
Так как
добиться одновременного гашения всех
длин волн спектра невозможно, то это
обычно делается для зеленого цвета (λ0
= 550нм), к которому
человеческий глаз наиболее чувствителен
(в спектре излучения Солнца эти лучи
имеют наибольшую интенсивность).
В отраженном свете объективы с
просветленной оптикой кажутся окрашенными
в красно-фиолетовый цвет. Это, разумеется,
несколько искажает цветопередачу в
изображении. Для улучшения характеристик
просветляющего покрытия его делают из
нескольких слоев, что «просветляет»
оптические стекла более равномерно по
всему спектру.
При изучении интерференции света в
тонких пленках различают полосы равного
наклона и равной толщины.
Из выражений (1.22, 1.23)следует, что для данныхλ0 ,
d,ипкаждому углу падения лучей
соответствует своя интерференционная
полоса. Интерференционные линии,
возникающие в результате наложения
лучей, падающих на плоскопараллельную
пластинку под одинаковыми углами,
называютсяполосами равного наклона.
Если пленка имеет переменную толщину
d≠ соnst,аλ0
, n и i
неизменны, то на экране возникает
система интерференционных полос,
называемыхполосами равной толщины.
Каждая из полос возникает за счет
отражения от мест пленки, имеющих
одинаковую толщину.
Классическим примером полос равной
толщины являются кольца Ньютона.Они наблюдаются при отражении света от
воздушного зазора, образованного
плоскопараллельной пластинкой и
соприкасающейся с ней плосковыпуклой
линзой с большим радиусом кривизныR
(рис. 1.9). В этом случае свет падает
нормально на плоскую поверхность линзы.
При наложении лучей, отраженных от
верхней и нижней поверхностей
воздушного клина, возникают интерференционные
полосы равной толщины, имеющие вид
концентрических окружностей (кольца
Ньютона).
В отраженном свете оптическая
разность хода (с учетом потери полуволныλ0/2 при отражении от
плоскопараллельной пластинки):
,
где
d
–
ширина зазора. Из рис. 1.9 следует, что
R2
= r2
+ (R
– d)2
,
где R –радиус кривизны линзы; r
–радиус кольца
Ньютона (все точки кольца соответствуют
одинаковой толщинеdзазора).
Учитывая, чтоd <<
R,получимd = r2/2R.
Следовательно,
.
(1.26)
Приравняв (1.26)к условиям
максимума и минимума (1.22)и (1.23),получим выражения
радиусов светлых и темных колец Ньютона
в отраженном свете:
для светлых
колец
,
(1.27)
для темных
колец
,k = 0, 1, 2, 3, … (1.28)
Система светлых и темных полос получается
только при освещении монохроматическим
светом. В белом свете интерференционная
картина изменяется: каждая светлая
полоса превращается в спектр.
Кольца Ньютона можно наблюдать и в
проходящем свете. При этом максимумы
интерференции в отраженном свете
соответствуют минимумам в проходящем
и наоборот.
Измеряя радиусы колец Ньютона, можно
определить λ0(зная радиус кривизны
линзы R )илиR(зная λ0 ).
Правильная
форма колец Ньютона легко искажается
при всяких, даже незначительных, дефектах
в обработке выпуклой поверхности линзы
и верхней поверхности пластины. Поэтому
наблюдение формы колец Ньютона позволяет
осуществить быстрый и весьма точный
контроль качества шлифовки линз и
плоских пластин, а также близость
поверхности линзы к сферической форме.
Последнее очень важно при изготовлении
стекол для очков и линз большого диаметра
для телескопов.
1.3.
Применение явления интерференции света.
Интерферометры
Интерференционная
картина очень чувствительна к разности
хода интерферирующих волн: ничтожно
малое изменение разности хода
вызывает
заметное смещение интерференционных
полос на экране. На этом основано
устройство интерферометров
–
приборов, служащих для точного
(прецизионного) измерения длин, углов,
показателей преломления и плотности
прозрачных сред и т.д. В промышленности
интерферометры широко используются
для контроля чистоты обработки
поверхностей металлических деталей (с
точностью до
0,01 мкм).
Все интерферометры основаны на одном
и том же принципе –
делении одного луча на два когерентных
–и различаются
лишь конструктивно.
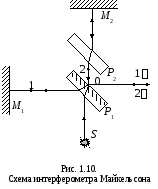
Интерферометр Майкельсона.
Упрощенная схема этого интерферометра
представлена на рис. 1.10. Монохроматический
свет от источникаS падает под углом
45°на плоскопараллельную стеклянную
пластинку Р1.Сторона пластинки, удаленная отS
,посеребренная и полупрозрачная,
разделяет луч на две части: луч
1 –отражается от посеребренного
слоя и луч 2
–проходит
через него. Луч 1 отражается
от зеркалаM1 и,возвращаясь обратно, вновь проходит
через пластинкуP1(луч
1‘).Луч 2идет к зеркалуМ2
,отражается от него, возвращается
обратно и отражается от пластинкиР1
в т. О (луч 2‘).Так как луч 1проходит
пластинкуР1 дважды, то
для компенсации возникающей разности
хода на пути луча 2ставится прозрачная пластинкаP2(точно такая же, как иP1).
Лучи 1′ и 2′когерентны, следовательно, наблюдается
интерференция, результат которой
будет зависеть от оптической разности
хода луча 1от точки
0до зеркалаМ1и луча
2от точки 0 до
зеркалаМ2.При
перемещении одного из зеркал на расстояние
λ0/4 разность хода обоих лучей
изменится на λ0/2 и произойдет
смена освещенности зрительного поля
(смена максимумов и минимумов).
Следовательно, по изменению интерференционной
картины можно судить о малом перемещении
одного из зеркал. Поэтому интерферометр
Майкельсона применяется для точных (~
10-9 м) измерений длин: сравнения
и проверки точности изготовления
технических эталонов длины, изменения
длины тела при
нагревании (интерференционный дилатометр).
Применяя интерферометр, Майкельсон
(американский физик) впервые сравнил
международный эталон метра с длиной
световой волны. Самый известный
эксперимент, выполненный Майкельсоном
(совместно с Морли) в 1887г., ставил целью обнаружить зависимость
скорости света от скорости движения
инерциальной системы координат. В
результате было установлено, что скорость
света одинакова во всех инерциальных
системах, что послужило экспериментальным
обоснованием для создания специальной
теории относительности Эйнштейна.
Советский
физик академик В.П. Линник использовал
принцип действия интерферометра
Майкельсона для создания микроинтерферометра
(комбинация интерферометра и микроскопа),
служащего для контроля чистоты обработки
поверхности металлических изделий.
Таким образом, интерферометр Линника
является прибором, предназначенным
для визуальной оценки, измерения и
фотографирования высот микронеровностей
поверхности вплоть до 14-го класса чистоты
поверхности.
Другим,
очень чувствительным оптическим прибором
является интерферометр Рэлея. Он
применяется для определения незначительных
изменений показателя преломления
прозрачных сред в зависимости от
давления, температуры, примесей,
концентрации раствора и т.д. Интерферометр
Рэлея позволяет измерять изменение
показателя преломления c очень высокой
точностью –Δn~ 10-6
.
ВОПРОСЫ ДЛЯ
САМОКОНТРОЛЯ
-
Что такое
свет с точки зрения современной волновой
теории? -
Какими
явлениями подтверждается волновая
природа света? -
Какие
физические величины характеризуют
световую волну? -
Перечислите
и дайте определение пространственных
характеристик световой волны. -
Сформулируйте
принцип Гюйгенса. -
Какой
световой луч называется монохроматическим? -
Что такое
«белый свет»? -
Приведите
примеры источников белого света;
монохроматического света. -
В чем
заключается явление интерференции
света? -
Необходимые
условия возникновения явления
интерференции света. -
Какие
световые лучи называются когерентными? -
Можно ли
наблюдать интерференцию от естественных
источников света (например, двух
лампочек)? Если нет, то почему? -
На каком
принципе основаны все методы получения
когерентных источников света?
Перечислите методы получения когерентных
источников света. -
В чем
заключается метод Юнга для получения
когерентных источников света? -
Что такое
геометрическая длина пути светового
луча, оптическая длина пути луча? -
Какие
величины являются определяющими для
результата интерференции от двух
когерентных источников света? -
Какова
зависимость разности фаз от оптической
разности хода двух интерферирующих
световых лучей? -
При каких
условиях наблюдаются максимумы и
минимумы интерференции света
(выразить через разность фаз и через
оптическую разность хода)? -
Чем
отличаются интерференционные картины,
полученные от источников монохроматического
и белого света? Чем объясняется это
различие? -
Как
изменяется фаза колебаний при отражении
луча: а) от среды оптически более плотной;
б) от среды оптически менее плотной?
Как это учитывается при определении
оптической разности хода двух когерентных
лучей? -
Какие
приборы называются интерферометрами? -
Какие
величины можно измерять с помощью
интерферометров? -
Чем
объясняется явление интерференции в
тонких пленках? -
Чем
объясняется окрашивание пленок при
наблюдении их в отраженном (проходящем)
естественном свете? -
Что такое
«просветление оптики»? Где
применяется это явление? -
Что такое
«кольца” Ньютона? -
Изобразите
схему получения «колец Ньютона». -
Какие
физические величины определяются
методом «колец Ньютона»? -
Какие
физические величины можно измерить,
наблюдая интерференцию света в
тонких пленках?
Соседние файлы в папке Физика
- #
- #
- #
- #
- #
1. Интерференция световых волн
1.1. Интерференция от двух источников
1.2. Определим положение m-ого интерференционного максимума. Определим ширину интерференционного максимума
1.3. Интерференция на тонкой плёнке
1.4. Интерференция на клине (полосы равной толщины)
1.5. Кольца Ньютона
2. Дифракция волн
2.1. Дифракция Фраунгофера на узкой длинной щели в непрозрачном экране
2.2. Дифракция света на одномерной дифракционной решётке
2.3. Разрешающая способность дифракционной решётки
2.4. Дифракция рентгеновских лучей
3. Поляризация света
3.1. Поляризованный и естественный свет
3.2. Закон Малюса
3.3. Поляризация при отражении от диэлектриков. Закон Брюстера
3.4. Двойное лучепреломления
3.5. Искусственная оптическая анизотропия
3.6. Вращение плоскости поляризации
1. Интерференция световых волн
Интерференцией волн называется явление усиления колебаний в одних и ослабление колебаний в других точках пространства в результате наложения двух или нескольких волн, приходящих в эти точки пространства.
Для наблюдения устойчивой во времени интерференционной картины необходимы условия, при которых частоты, поляризация и разность фаз интерферирующих волн, были бы постоянными в течение всего времени наблюдения.
Интерферируют когерентные, монохроматические волны.
Когерентные волны — волны одинаковой частоты, колебания в которых отличаются постоянной разностью фаз, не изменяющейся со временем.
1.1. Интерференция от двух источников
Свет от одного источника с помощью непрозрачного экрана с двумя отверстиями даёт возможность получить два когерентных источника волн (схема Юнга). Расстояние между источниками (В, С) равно l. Длина волны, излучаемая источниками λ, расстояние до экрана, где наблюдается интерференция. О – центр экрана.
Пусть в точке М – экрана происходит наложение когерентных волн. Получим условие усиления и ослабления волнами друг друга. Расстояние от В источника до точки М – d1, от С до точки М – d2. Колебания точки М, вызываемые первым. источником волн: , а колебания, вызываемые 2-ым источником:
, где А – амплитуда колебаний источников, ω – частота колебаний, k=2π/λ – βолновое число.
Результирующее колебание точки М:
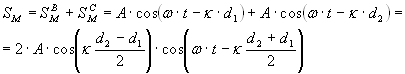
Амплитуда колебаний точки М:
AM=2Acos(k(d2-d1)/2) зависит от положения точки на экране и может быть равной 2А, если волны усиливают друг друга или нулю, если волны ослабляют друг друга.
Получим условие усиления или максимум интерференции. Чтобы АМ=2А, необходимо чтобы
|cos(k(d2-d1)/2)|=1
Это выполняется, если
;
.
Значит d2-d1=±mλ.
Пусть d2-d1=Δd – разность хода интерферирующих лучей, а ΔФ=2π(d2-d1)/λ=2πΔd/λ – разность фаз интерферирующих волн, тогда
ΔΤ=2π/λ (d2-d1) =2π/λ Δd – ρоотношение между разность фаз и разность хода волн.
Если d2-d1=Δd=± mλ, γде m=0,1…, то АМ=2А и, следовательно, в этих точках пространства (экрана) наблюдается максимум интерференции. Разность фаз волн при этом будет равна ΔФ=±2πmλ/λ=±2πm.
Условие ослабления или минимум интерференции
Ам=0,
|cos(k(d2-d1)/2)|=0.
Это выполняется, если (k(d2-d1)/2)=±(2m+1)λ/2; следовательно
Δd=±(2m+1)λ/2.
Волны ослабляют друг друга, если разность хода при этом
ΔΤ=±2πmλ /(2λ)(2m+1)=±(2m+1)π,
m – называется порядком интерференционного максимума или минимума. В центре экрана наблюдается максимум нулевого порядка: d2-d1=Δd=0.
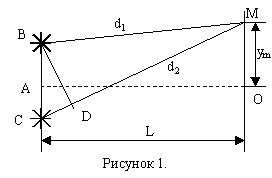
1.2. Определим положение m-ого интерференционного максимума. Определим ширину интерференционного максимума
Рисунок 1. В точке М наблюдается максимум m-ого порядка. Обозначим расстояние от центра экрана до точки М – ym. Воспользуемся геометрией рисунка 1. Отрезок CD=d2-d1. Треугольники BCD и AMO – подобны. Из подобия
.
Чтобы в точке наблюдался максимум m-ого порядка Δd=d2-d1=±mλ.
Ширина интерференционного максимума – расстояние между двумя соседними максимумами или минимумами.
Если положение m-ого максимума ym=mLλ/l, то положение (m+1)-го максимума ym+1=(m+1)Lλ/l. Тогда Δy= ym+1-ym=Lλ/l, γде Δy – ширина интерференционного максимума.
1.3. Интерференция на тонкой плёнке
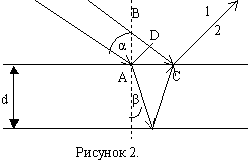
На тонкую плёнку толщиной d и показателем преломления n падает монохроматический свет с длиной волны λ. Угол падения α. Среда около плёнки – воздух. Определим условие наблюдения максимума и минимума интерференции на тонкой плёнке. Интерферирующие лучи показаны на рисунке 2. Часть первого луча проходит через плёнку, преломляясь на границе раздела, отражается от нижней границы плёнки и выходит в точке С. Часть второго луча отражается от верхней поверхности плёнки и в точке С интерферирует с лучом 1. Обозначим Δ – оптическую разность хода волны.
Оптическая разность хода волн 1 и 2:
Δ=n(AB+BC)-(DC+λ/2),
где n(AB+BC) – путь (оптический) первой волны,
(DC+λ/2) – путь второй волны. При отражении волны от поверхности плёнки, фаза волны меняется на π, т.к. отражение происходит от более плотной среды (nb=1);
n>nb.
Изменение фазы на π соответствует дополнительному ходу, равному λ/2.
Используя геометрию рисунка и законы преломления света, получим, что оптическая разность хода интерферирующихся волн равна:
или
,
где β – угол преломления. Запишем условие усиления волнами друг друга или максимума интерференции: Δ=+— mλ. Значит:
,
.
Толщина плёнки, при которой интерферирующие волны будут усиливать друг друга:
,
m – порядок интерференции (m=0,1,2…).
Если m=0, то
– это минимальная толщина плёнки, при которой плёнка будет окрашена цветом соответствующим данной длине волн λ. Условие ослабления при интерференции или минимум интерференции:
Δ=(2m+1)λ/2.
.
.
Толщина плёнки, при которой плёнка будет казаться тёмной, т.к. наблюдается ослабление волнами друг друга, равна:
, m=0,1,2…
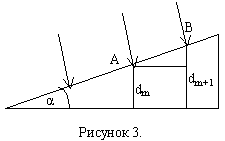
1.4. Интерференция на клине (полосы равной толщины)
Две поверхности, расположение под малым углом α, образуют систему получившую название клин. Клин имеет разную толщину, а поэтому при освещении поверхности клина монохроматическим светом на поверхности клина будут наблюдаться интерференционные максимумы и минимумы (смотри интерференцию на плёнке), т.к. в одних точках поверхности толщина клина соответствует условию наблюдению максимума, а в других – условию минимума.
Определим ширину интерференционной полосы.
Пусть в точке А поверхности клина возникает максимум m-ого порядка. Толщина клина — dm+1. В точке В возникает максимум (m+1)-го порядка. Толщина плёнки в этом месте — dm+1. Условие наблюдения максимума при толщине dm и dm+1:
2dmn=(2m+1)λ/2; 2dm+1n=(2m+3) λ/2.
Вычтем из второго уравнения первое:
.
dm+1-dm – разность толщины клина в местах наблюдения m-ого и (m+1)-го максимумов. На рисунке 3. Из прямоугольника:
AB=Δy=BD/sinα,
Δy – ширина интерференционной полосы
.
Если угол при вершине мал, то ,
, α[рад].
Ширина интерференционного минимума или расстояния между соседними минимумами равна ширине интерференционного максимума.
1.5. Кольца Ньютона
Частым случаем полос равной толщины являются кольца Ньютона, которые наблюдаются в схеме, изображённой на рисунке 4.
Плосковыпуклая линза с большим радиусом кривизны R выпуклой поверхностью лежит на плоской пластине и соприкасается с ней в точке О. Параллельный пучок света падает нормально на плоскую поверхность промежутка между линзой и пластиной. При наложении отраженных волн возникают интерференционные полосы равной толщины, имеющие вид колец. Вид этих колец в случае монохроматического света показан на рисунке 5.
В центре наблюдается минимум нулевого порядка (тёмное пятно). Центральный минимум окружён системой чередующихся окрашенных и тёмных колец, ширина и интенсивность которых постоянно убывает по мере удаления от центрального пятна.
Расчёт радиусом окрашенных и тёмных колец.
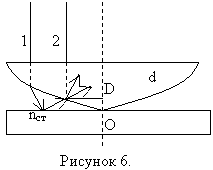
На рисунке 6 изображены интерферирующие волны, распространяются вдоль лучей 1 и 2.
Разность хода волн равна:
,
где d – толщина зазора между линзой и пластиной, где наблюдается интерференция, n – показатель преломления прослойки, λ/2 – потеря полволны при отражении 1-ой волны от стеклянной пластинки (при условии n<nстекла).
Для наблюдения максимума интерференции или окрашенного кольца:
,
где m-ого порядка окрашенного кольца (m=1,2,3…).
Значит,.
Для минимума интерференции , или
.
Радиус кольца определим, используя геометрию рисунка 4 OD=d. Из треугольника AO1D:
.
Пренебрегая d2, получим: .
Если подставим значения d, соответствующее минимуму интерференции, получим выражение для радиуса окрашенного кольца m-ого порядка.
Если между линзой и пластинкой воздушная прослойка, то n=1.
2. Дифракция волн
Огибание волнами препятствий или отклонение от прямолинейного распространения в оптически неоднородной среде получило название дифракции.
Дифракция возникает при прохождении световых волн через отверстия в непрозрачных экранах, вблизи границ непрозрачных тел и т.д.
Различаются два вида дифракции световых волн: дифракция Френеля, или дифракция в расходящихся лучах, и дифракция Фраунгофера, или дифракция в параллельных лучах.
В первом случае на препятствие падает сферическая или плоская волна, а дифракционная картина наблюдается на экране, который находится позади препятствия на конечном расстоянии от него.
Во втором случае на препятствие падает плоская волна, а дифракционная картина наблюдается на экране, который находится в фокальной плоскости собирающей линзы, установленной на пути прошедшего через препятствие света.
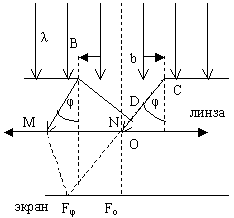
2.1. Дифракция Фраунгофера на узкой длинной щели в непрозрачном экране
Ширина щели BC=b, длина волны, падающего света λ. Свет падает на щель нормально к её поверхности так что колебания во всех точках щели совершаются в одной фазе. О – оптический центр линзы. Дифракционная картина наблюдается на экране, который установлен в фокальной плоскости линзы. φ – угол дифракции, или угол отклонения от прямолинейного распространения падающих волн, который может принимать значения от 0 до .
F0 – центр дифракционной картины, где интерферируют лучи, угол дифракции которых равен нулю. В F наблюдается центральный дифракционный максимум.
Параллельные лучи BM и CN, идущие от краёв щели под углом дифракции φ, собираются линзой в побочном фокусе Fφ.
Линза обладает тем свойством, что оптические пути лучей BM и DNFφ, где D – основание перпендикуляра, опущенного из точки В на направление луча CN, одинаковы.
Результат интерференции в точке Fφ экрана зависит от разности хода волн 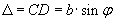
Число зон Френеля, укладывающихся в отверстие, равно:
.
Все зоны излучают свет в рассматриваемом направлении с одинаковой амплитудой, причём колебания, вызываемые в точке Fφ двумя соседними зонами противоположны по фазе.
Поэтому, если число зон Френеля в отверстии чётное
,
где k=1,2…,
то под углом дифракции, удовлетворяющем условию, наблюдается дифракционный минимум. k – порядок дифракционного минимума.
Если число зон Френеля нечётное
, где k=1,2…,
то под углом дифракции φ удовлетворяющему условию
наблюдается дифракционный максимум, соответствующий действию одной зоны Френеля (k — порядок дифракционного минимума).
Самый яркий центральный максимум наблюдается в главном фокусе линзы F0 (φ=0).
С ростом k ширина зон Френеля уменьшается и интенсивность максимумов быстро падает.
Амплитуда и интенсивность света в точке Fφ равны:
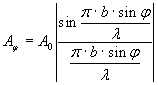
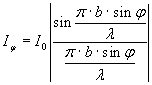
где А0 – амплитуда, I0 – интенсивность центрального максимума (φ=0).
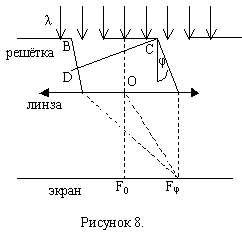
2.2. Дифракция света на одномерной дифракционной решётке
Одномерная дифракционная решётка представляет собой систему из большого число N одинаковых по ширине и параллельных друг другу щелей в экране, раздельных также одинаковыми по ширине непрозрачными промежутками.
На рисунке 8 показаны только две соседние щели решётки. Величина d=a+b, называется периодом решётки (a=KC – ширина непрозрачного промежутка, b=BK – ширина щели,
— ширина решётки). Если плоская монохроматическая волна с длиной λ падает на решётку нормально, то колебания во всех точках щели происходят в одинаковой фазе. Колебания, возбуждаемые в произвольной точке Fφ фокальной плоскости линзы каждой из щелей, совпадают по амплитуде, но отличаются по фазе. Для каждой пары соседних щелей сдвиг по фазе Δφ0 μежду этими колебаниями одинаков. Сдвиг по фазе зависит от разности хода волн, идущих от точек В и С под углом дифракции φ и длины волны λ.
,
где — разность хода,
D – основание перпендикуляра, опущенного из точки В на направление луча С.
.
Условие наблюдения главных максимумов: или
(k=1,2,3)
,
k – порядок интерференционного максимума.
Наибольший порядок спектра наблюдается под углом дифракции: ;
;
;
,
k может принимать только целые значения, поэтому результат, полученный от деления, нужно округлить до меньшего целого числа. Число максимумов наблюдаемых на экране . В центре экрана в точке F0 наблюдается центральный максимум (φ=0, k=0).
Условие наблюдения главных минимумов:
или
;
,
k – порядок главного минимума.
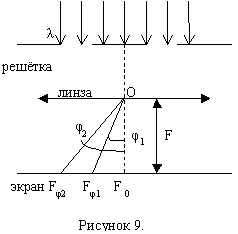
2.3. Разрешающая способность дифракционной решётки
Пусть на дифракционную решётку падает немонохроматический свет с длиной волны λ1 и λ2.
;
(близкие длины волн).
Период дифракционной решётке d, число щелей N. В спектре k-ого порядка на экране (рисунок 9) под углом φ1 наблюдается максимум для длины волны λ1, а под углом дифракции φ2 – максимум для волны с λ2. (Fφ1 θ Fφ2 – ρоответственно), максимумы для двух длин волн на экране пространственно разделены, если выполняется условие:
(формула Рэлея).
Это условие получило название разрешающей способности дифракционной решётки. λ можно принять равным λ1 или λ2.
2.4. Дифракция рентгеновских лучей
Кристаллическую решётку твёрдых тел можно рассматривать как пространственную дифракционную решётку, период которой значительно меньше длины волны видимого света (). Для видимого света кристаллы являются оптически однородной средой.
В тоже время для рентгеновских лучей кристаллы представляют естественные кристаллические решётки ().
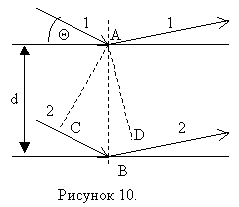
Дифракция рентгеновских лучей на кристаллах рассматривается как результат интерференции рентгеновского излучения, зеркально отражающегося от систем параллельных плоскостей, которые проходят через узлы кристаллической решётке. Расстояние d между двумя сетчатыми плоскостями называется межплоскостным расстоянием, а угол Θ между падающим лучом и плоскостью – угол скольжения. На рисунке 10 изображены две плоскости, которые проходят через углы кристаллической решётки (сетчатые или атомные плоскости).
На поверхности кристалла под углом скольжения Θ падает плоская волна с длиной λ. Рентгеновские лучи не преломляются в кристалле, т.к. показатель преломления для них равен единице (примерно). Разность хода интерферирующих волн (лучи 1 и 2), отражённых от двух параллельных плоскостей равна . Отражение наблюдается в направлениях, соответствующих дифракционным максимумам, которые удовлетворяют условию Вульфа-Брэгга:
, m=1,2,3…
m – порядок дифракционного максимума
,
Θ – σгол скольжения для наблюдения максимума удовлетворяет этому условию.
Угол скольжения, соответствующий первому дифракционному максимуму (m=1)
.
3. Поляризация света
3.1. Поляризованный и естественный свет
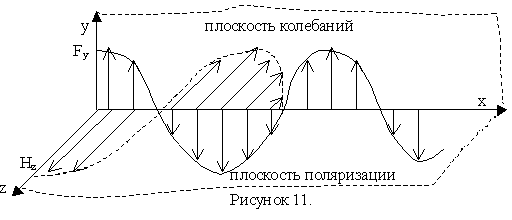
Из теории Максвелла следует, что свет является поперечной электромагнитной волной. Вектор напряжённости электрического поля (электрический или световой вектор) и вектор напряжённости магнитного поля (магнитный вектор) в световой волне колеблется в направлении перпендикулярном скорости распространения волны.
Линейно поляризованной волной называется волна, вектор которой не изменяют направление колебаний в пространстве.
Уравнение плоской монохроматической линейно-поляризованной волны, распространяющейся в направлении оси ОХ:
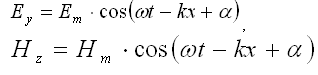
где ω – циклическая частота, — волновое число, υ – скорость распространения волны.
В каждой точке электромагнитного поля электрический вектор совершает гармонические колебания в плоскости XOY, которая называется плоскостью колебания.
Магнитный вектор колеблется в плоскости XOZ – в плоскости поляризации.
Световая волна со всевозможными одинаково вероятными направлениями колебаний электрического и магнитного векторов называется естественным светом.
В естественном свете плоскости поляризации меняют ориентацию в пространстве с течением времени.
Естественный свет можно представить в виде суперпозиции двух волн, которые поляризованы во взаимно-перпендикулярных плоскостях. Запишем уравнение естественного света только для электрического вектора волны:
;
,
где Ey, Ez – проекции электрического вектора на оси координат, α – сдвиг по фазе между колебаниями по Y и Z. Для естественного света Eoy=Eoz.
Частично поляризованным называется свет, если в нём есть преимущественное направление колебаний вектора
(Eoy>>Eoz) или (Eoz>>Eoy).
Частично поляризованный свет можно рассматривать как смесь одновременно распространяющихся в одном и том же направлении естественного и линейно поляризованного.
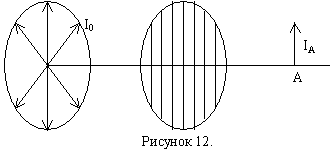
Поляризацией света называется выделение линейно поляризованного света естественного или частично поляризованного. Для этой цели используются специальные устройства, называемые поляризаторами.
Для определения характера и степени поляризации используют устройства, называемые анализаторами.
Поляризатор можно использовать в качестве анализатора.
Анализатор или поляризатор условно изображают в виде решётки, “прутья” которой параллельны направлению колебаний вектора в проходящем сквозь неё свете.
Если на такую решётку-анализатор падает естественный свет, то интенсивность проходящей волны не изменяется при вращении анализатора вокруг направления падающего луча вследствие того, что в естественном свете ни одно из направлений плоскости поляризации (плоскости колебаний) не является преобладающим.
,
где I0 – интенсивность падающего естественного света,
k – коэффициент прозрачности анализатора,
IА – интенсивность проходящего света.
На выходе из анализатора-поляризатора имеем линейно поляризованную волну.
Если падающий свет частично поляризован, то IA при вращении анализатора изменяется в зависимости от ориентации его главной плоскости (т.е. направления прутьев) по отношению к преимущественному направлению колебаний вектора в падающем свете.
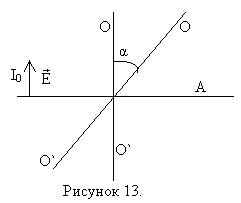
3.2. Закон Малюса
Пусть на анализатор падает линейно поляризованный свет интенсивностью I0. Оптическая ось анализатора О-О` (направление прутьев).
Определим интенсивность прошедшей волны в точке А, если анализатор повернуть на угол α вокруг направления распространения луча. Через анализатор пройдёт электрический вектор, величина . Т.к. интенсивность пропорциональна квадрату амплитуды, то
— это и есть закон Малюса.
3.3. Поляризация при отражении от диэлектриков. Закон Брюстера
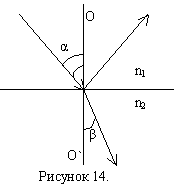
Направим на границу раздела двух диэлектриков (воздух, стекло) тонкий луч естественного света.
Часть световой волны отражается, а часть преломляется, распространяясь во второй среде. На рисунке: φ – угол падения луча, β – угол преломления, n2 – показатель преломления стекла, n1 — показатель преломления воздуха, n1=1.
Если на пути отражённого и преломлённого луча поставить анализатор, то можно исследовать поляризацию при отражении и преломлении.
Оказалось, что в общем случае отражённый и преломлённый лучи поляризованы частично. При некотором строго определённом для данной пары сред (диэлектриков) значение угла падения отражённый свет оказывается линейно поляризованным. Угол падения в этом случае называется углом Брюстера (φБ) или углом полной поляризации и определяется законом Брюстера:
,
где n21 – относительный показатель преломления среды.
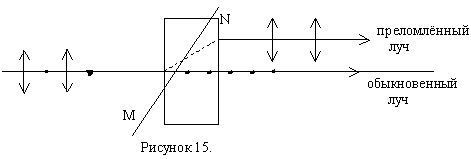
3.4. Двойное лучепреломление
В оптически анизотронных кристаллах наблюдается явление двойного лучепреломления, которое состоит в том, что луч света падающий на поверхность кристалла, раздваивается на два преломлённых луча.
MN – оптическая ось кристалла.
Оптическая ось кристалла – направление в оптически анизотронном кристалле, вдоль которого свет распространяется, не испытывая двойного лучепреломления. Главной плоскостью или главным сечением одностороннего кристалла называется плоскость, проходящая через падающий луч и пересекающую его оптическую ось.
В одноосном кристалле один из преломлённых лучей подчиняется обычным законом преломления света. Этот луч лежит в плоскости падения. Волну, распространяющуюся вдоль направления этого луча, называют обыкновенной волной и обозначают буквой О. Показатель преломления для этой волны n0.
Вдоль второго луча распространяется необыкновенная волна. Показатель преломления луча для неё nе. угол преломления для необыкновенного луча зависит от того, как ориентирована поверхность пластинки по отношению к оптической оси кристалла MN. Угол преломления равен нулю в двух случаях:
а) если поверхность пластинки перпендикулярна к оптической оси (свет распространяется вдоль оптической оси, не испытывая двойного лучепреломления).
б) если поверхность пластинки параллельна оптической оси (свет распространяется в пластинке перпендикулярно оптической оси).
Двойное лучепреломление можно объяснить тем, что падающая на оптически анизотронный кристалл световая волна возбуждает две волны, распространяющиеся в кристалле эти по разным направлениям. В однослойном кристалле эти волны называются обыкновенными и необыкновенными волнами. Обыкновенные и необыкновенные волны линейно поляризованы во взаимно-перпендикулярных плоскостях.
В обыкновенной волне вектор направлен перпендикулярно к главной плоскости кристалла. Электрический вектор
необыкновенной волны лежит в главной плоскости кристалла. Направления векторов
в обыкновенных и необыкновенных волнах условно показаны на рисунке точками на обыкновенном луче и поперечными чёрточками на необыкновенном. Предполагается, что оба луча и пересекающая их оптическая ось MN кристалла лежат в плоскости рисунка.
3.5. Искусственная оптическая анизотропия
1. Оптически изотропное прозрачное вещество становится анизотропным, если его подвергнуть механической деформации. Это явление называется фотоупругостью, при одностороннем растяжении или сжатии изотропного тела вдоль оси OX оно приобретёт оптические свойства одноосного кристалла, оптическая ось которого параллельна ОХ . Разность показателей преломления обыкновенного (no) и необыкновенного (nе) лучей в направлении перпендикулярном оси ОХ, пропорциональна нормальному напряжению .
n0-nе=к
где к- коэффициент пропорциональности, зависящий от свойств вещества.
2. Эффектом Керра называется возникновение оптической неоднородности у прозрачного изотропного диэлектрика, если его поместить во внешнее электрическое поле.
Под действием поля диэлектрик поляризуется и приобретает оптические свойства одноосного кристалла, оптическая ось которого совпадает по направлению с вектором напряженности внешнего поля.
Разность показателей преломления поляризованного диэлектрика для необыкновенного и обыкновенного лучей монохроматического света, распространяющегося перпендикулярно направлению вектора Е, удовлетворяет закону Керра.
nе-n0=Bв
где -длина волны в вакууме, Вв-постоянная Керра.
3. Эффектом Коттона-Мутона называется возникновение оптической анизотропии у некоторых изотропных вещество при помещении их в сильное внешнее магнитное поле.
В однородном магнитном поле вещество преображает оптические свойства одноосного кристалла, оптическая ось которого совпадает по направлению с вектором напряженности внешнего поля.
Разность показателей преломления вещества для необыкновенного и обыкновенного лучей монохроматического света при его распространении в направлении перпендикулярном вектору , пропорциональна
.
с- постоянная Коттона — Мутона, -длина волны в вакууме.
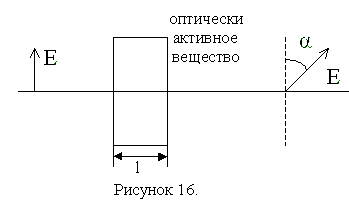
3.6. Вращение плоскости поляризации
При прохождении линейно поляризованного света через некоторые вещества, называемые оптически активными, плоскость поляризации света поворачивается вокруг направления распространения луча.
Оптически активны некоторые кристалла (кварц, киноварь и др.) чистые жидкости и растворы (скипидар, раствор сахара в воде и др.)
В оптически активных кристаллах и чистых жидкостях угол поворота плоскости поляризации пропорционален толщине
слоя вещества, через который проходит свет:
Коэффициент пропорциональности называется удельным вращением, или постоянной вращения.
Угол поворота плоскости поляризации при прохождении света пути в оптически активном растворе равен
С — объемно-массовая концентрация оптически активного вещества в растворе, D- плотность раствора, к=С/D- долевая концентрация по массе, — удельная вращения, зависит от природы оптически активного вещества.
Оптически неактивная среда под действием внешнего магнитного поля приобретает способность вращать плоскость поляризации света, распространяющегося вдоль направления поля.
Это явление называется эффектом Фарадея, или магнитным вращением плоскости поляризации.
где — угол поворота плоскости поляризации,
-напряженность магнитного поля,
— длина пути световой волны,
V — постоянная Верде.
Определение показателя преломления стекла интерференционным методом
Методические указания по выполнению лабораторной работы № 366
по курсу общей физики для подготовки студентов всех специальностей
Составитель А. А. Ильиных
Утверждены на заседании кафедры
Протокол № 1 от 31.08.2006
Рекомендованы к печати
Протокол № 3 от 20.09.2006
Электронная копия находится
в библиотеке главного корпуса
Лабораторная работа № 366
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ СТЕКЛА
1. Цель работы: Определение относительного показателя преломления стеклянной пластины.
2. Оборудование: оптическая скамья, гелий-неоновый лазер, толстая пластина, объектив.
3. Подготовка к работе: изучить по учебникам [1] §§ 31.1 – 31.5; [2] §§ 170–175.
4. Описание установки
Из лазера 1 (рис. 1) световой пучок падает на короткофокусный объектив 2 и, становясь расходящимся, освещает плоскопараллельную пластину 3.
О 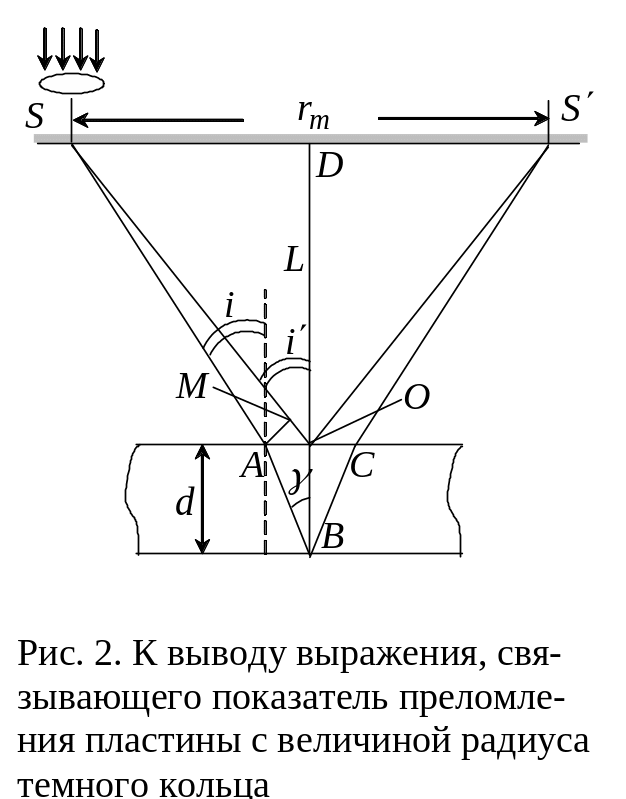
5. Теория эксперимента
Разность хода лучей 
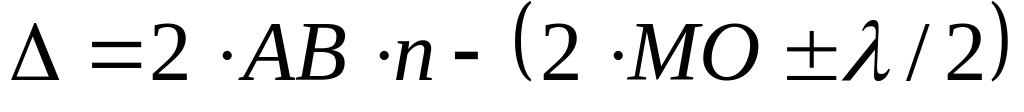
Здесь 
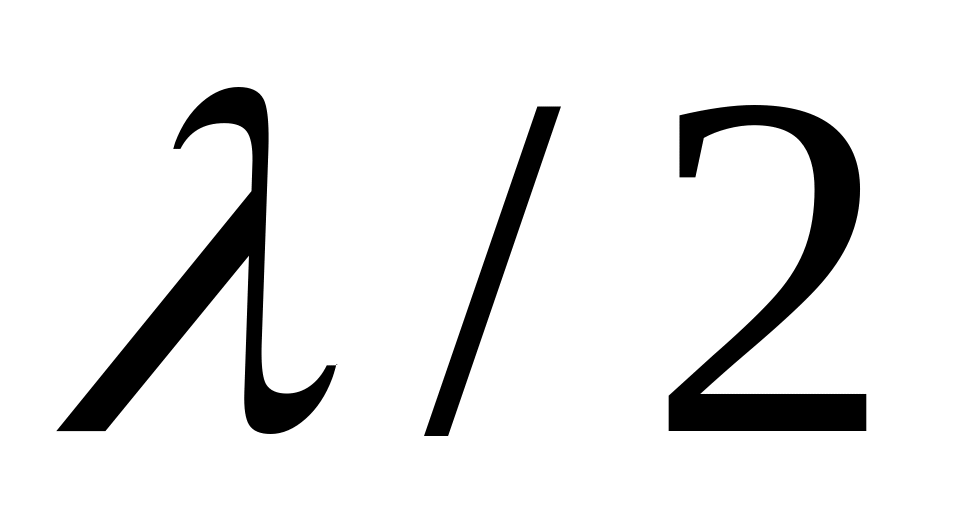

1) 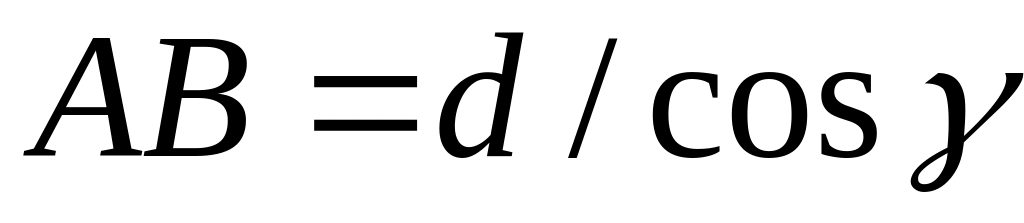
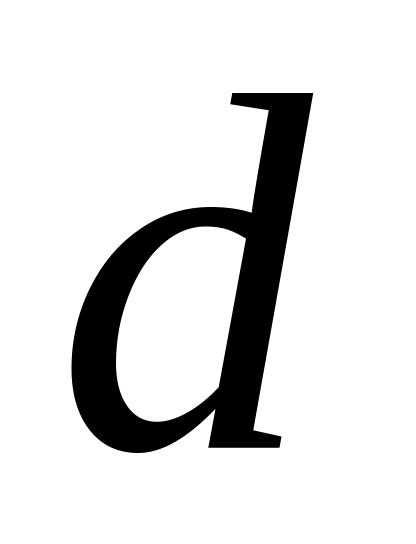
2) 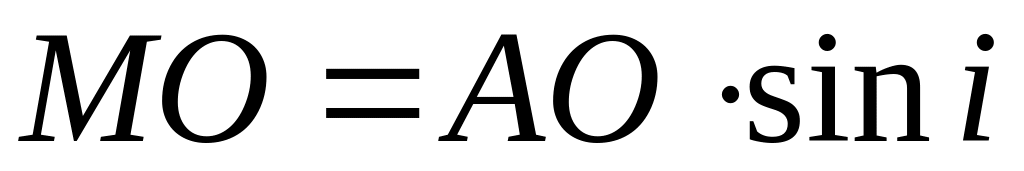
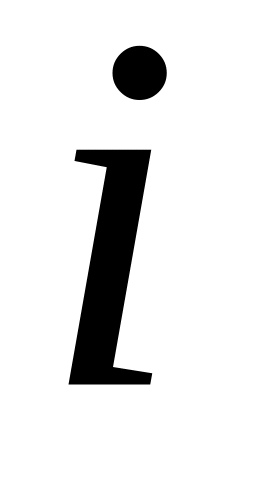
3) 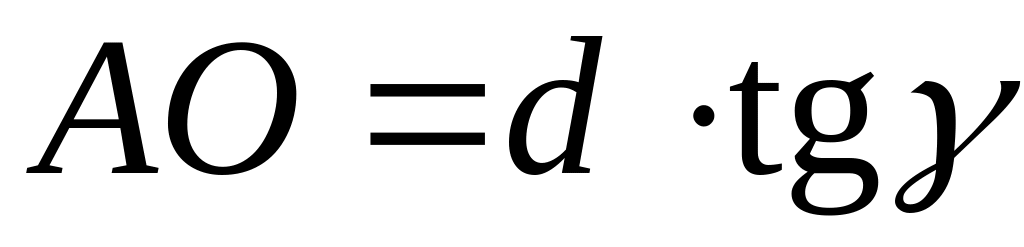
4) закон Снеллиуса 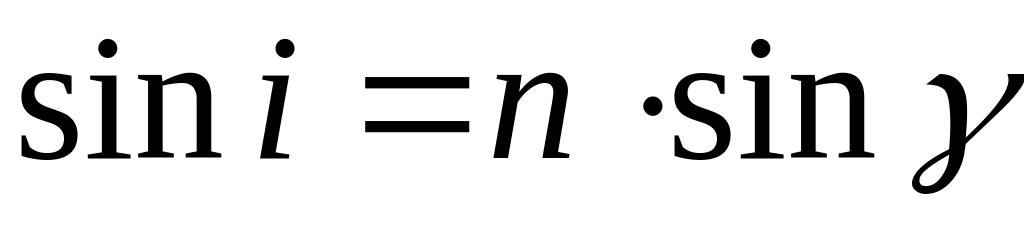
выражение (1) можно записать в виде

Темные кольца наблюдаются, если разность хода 
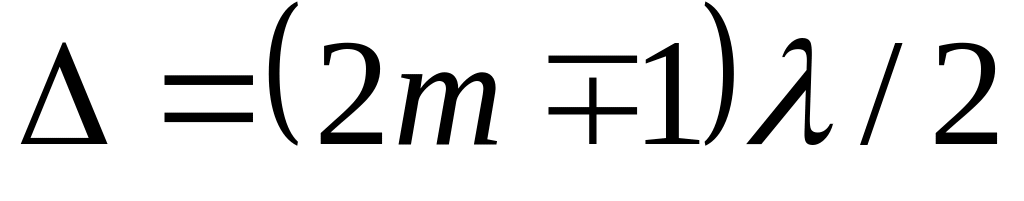
где 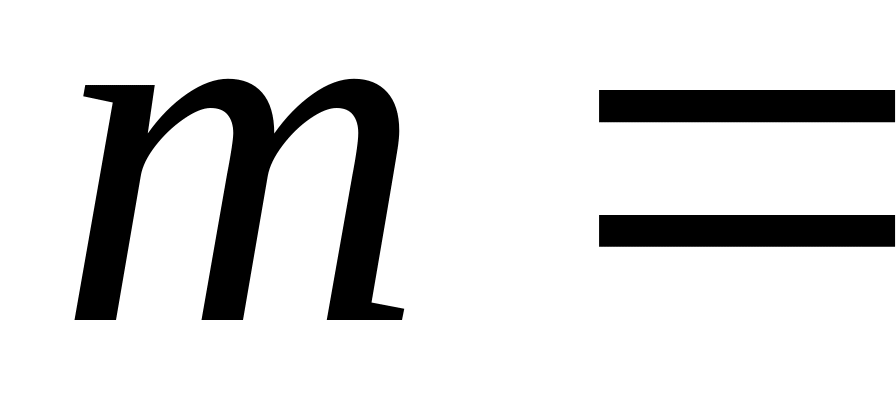
Таким образом, каждому кольцу соответствует свое значение 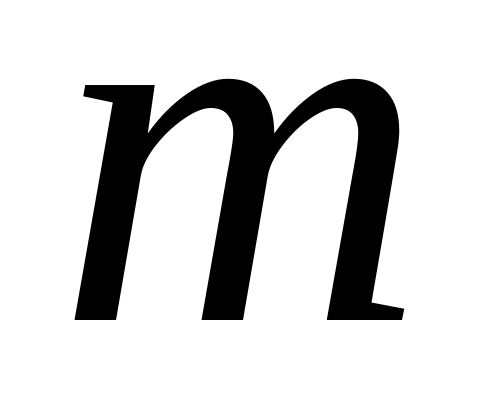
Сравнивая (2) и (3), условие наблюдения темных колец представим в виде

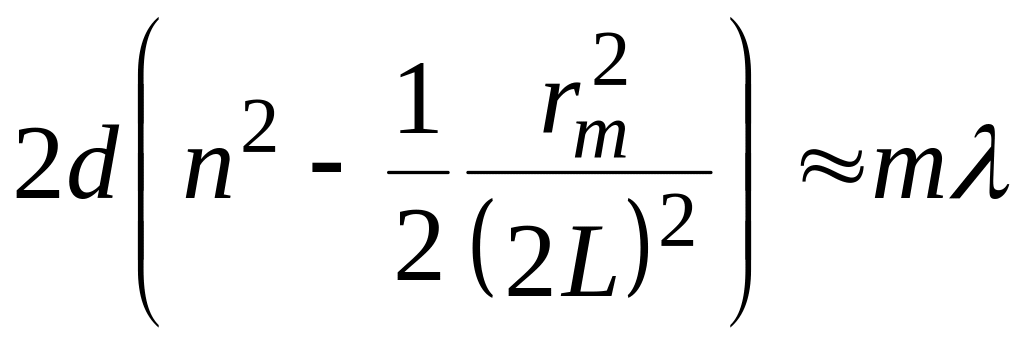
(Использовано то, что 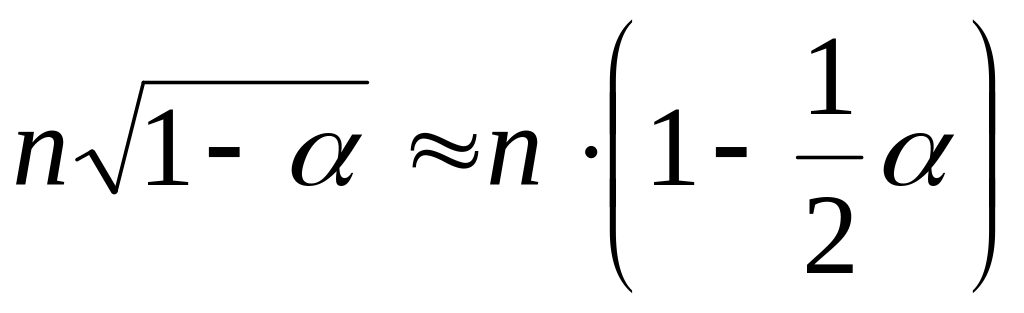

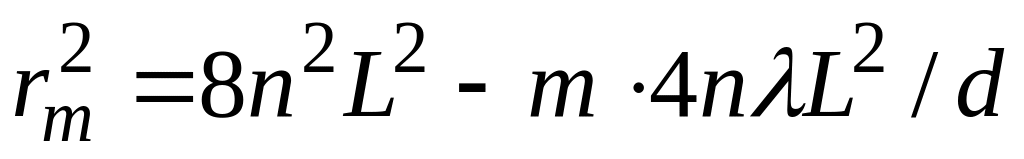
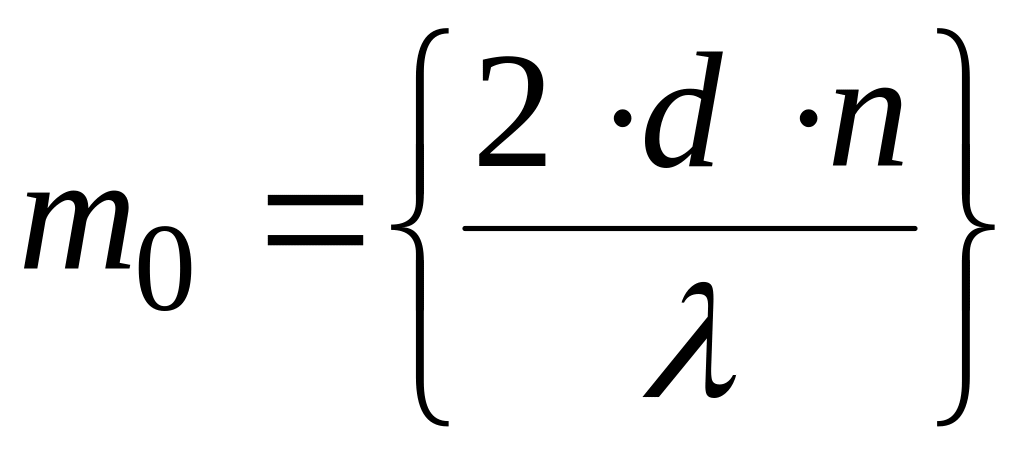
где 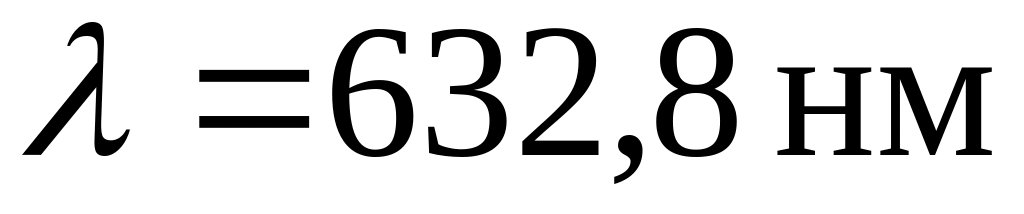
Для случая 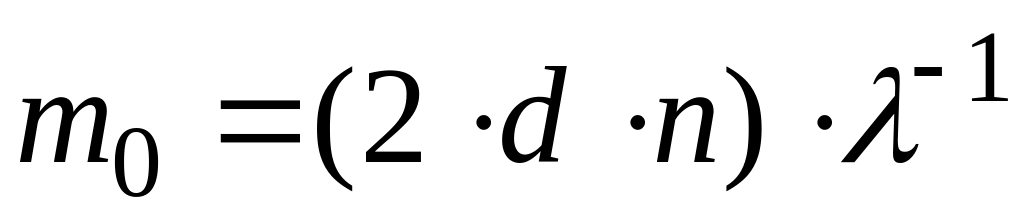
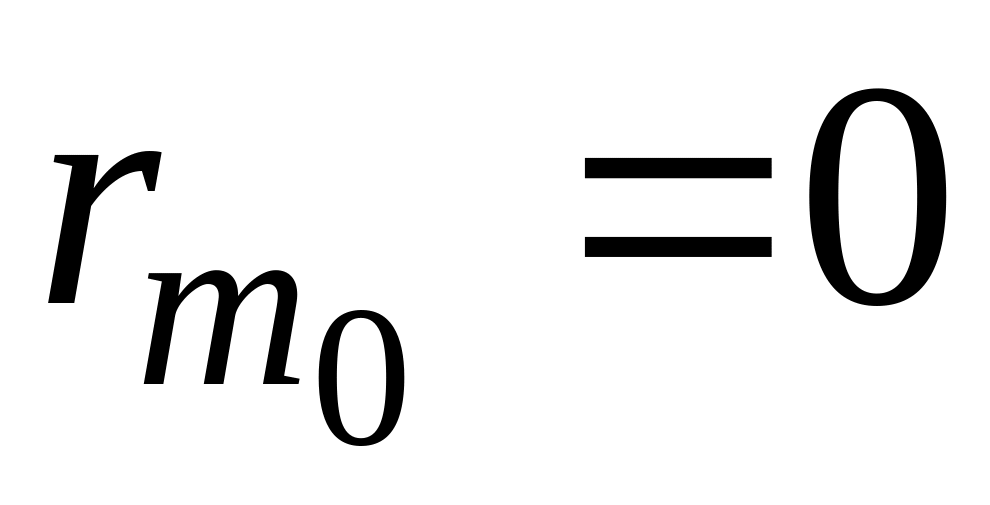

В силу особенностей установки в поле зрения находятся 5–6 темных колец.
Истинные порядки наблюдаемых минимумов неизвестны, поэтому целесообразно порядки интерференции наблюдаемых колец представить в виде 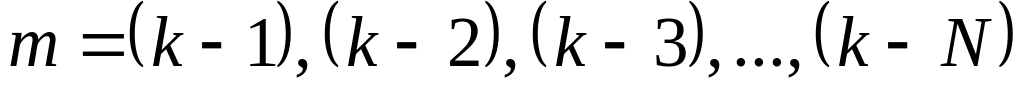
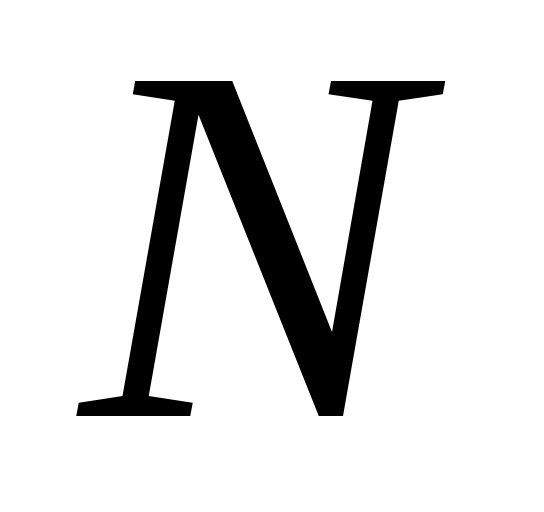

Запишем уравнение (5) для минимума 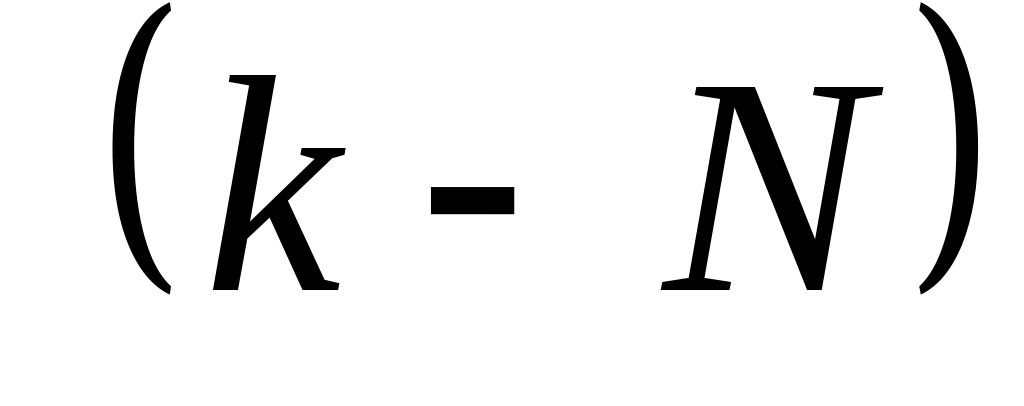
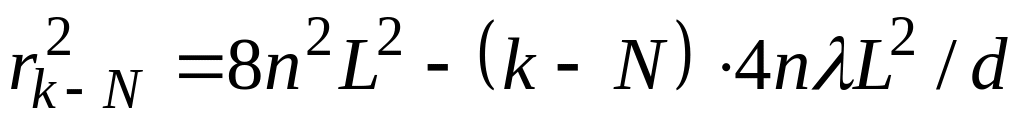
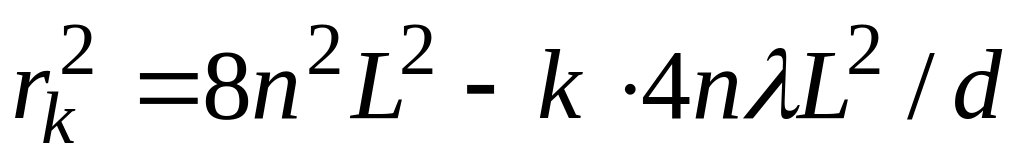
Вычитая уравнение (8) из уравнения (7) почленно, получим
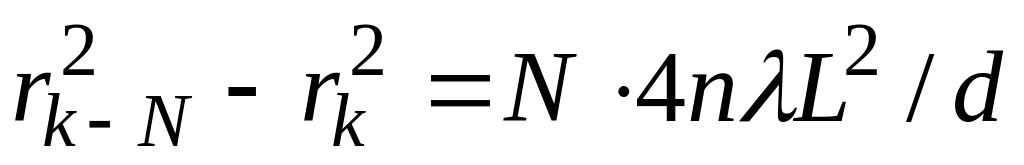
Квадрат радиуса кольца линейно зависит от порядка интерференции:
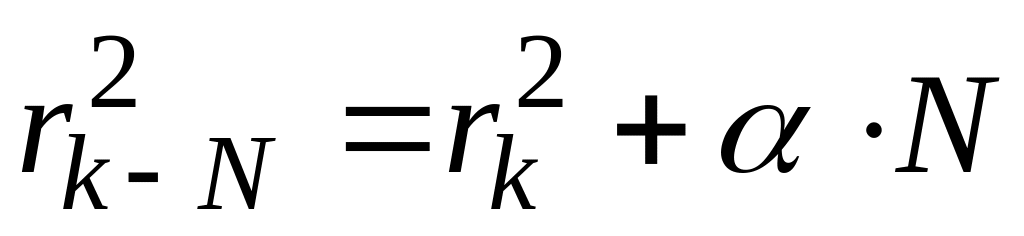
где 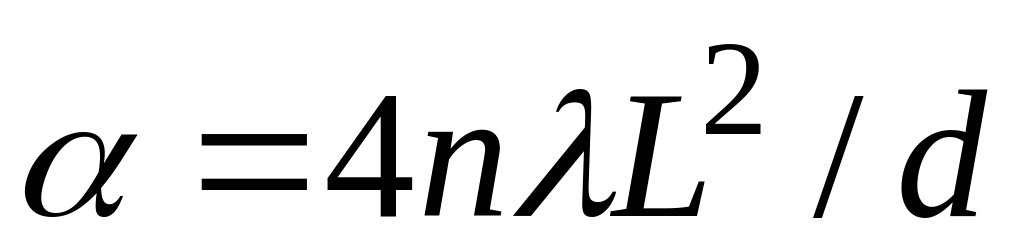
Введем сокращенные обозначения для радиусов темных колец: 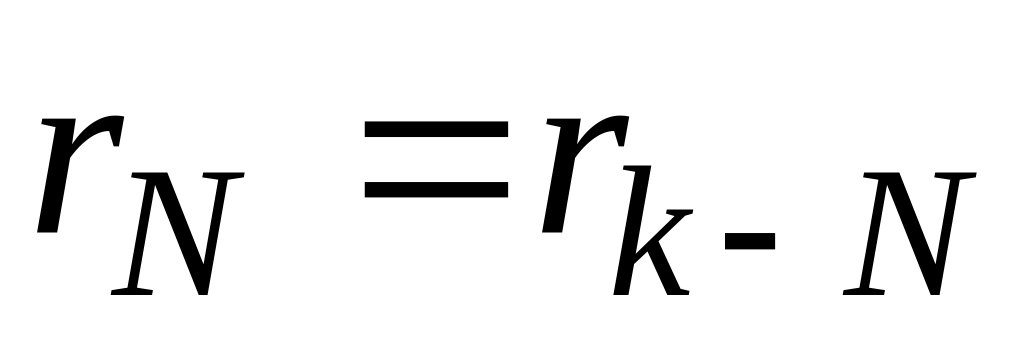
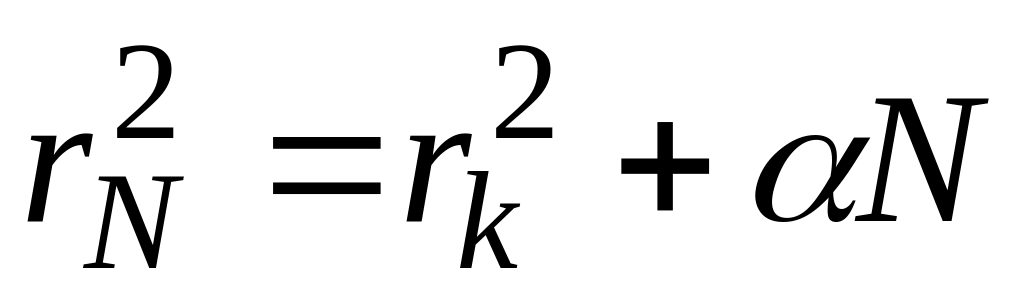
Результаты измерений радиусов колец можно представить графически как 
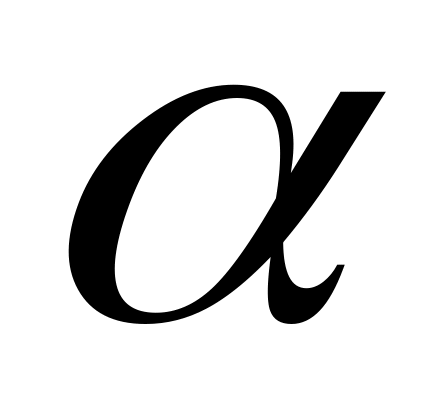
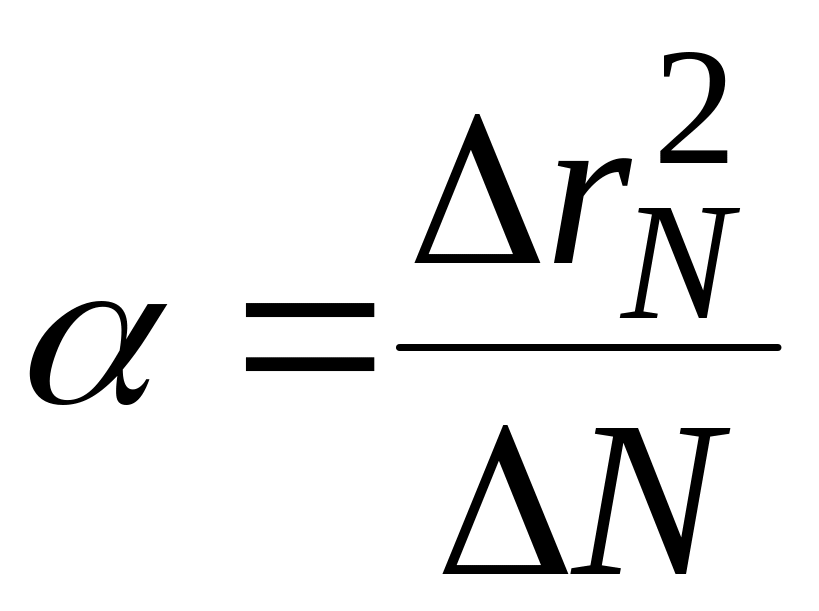
После чего показатель преломления можно определить, используя формулу (11)
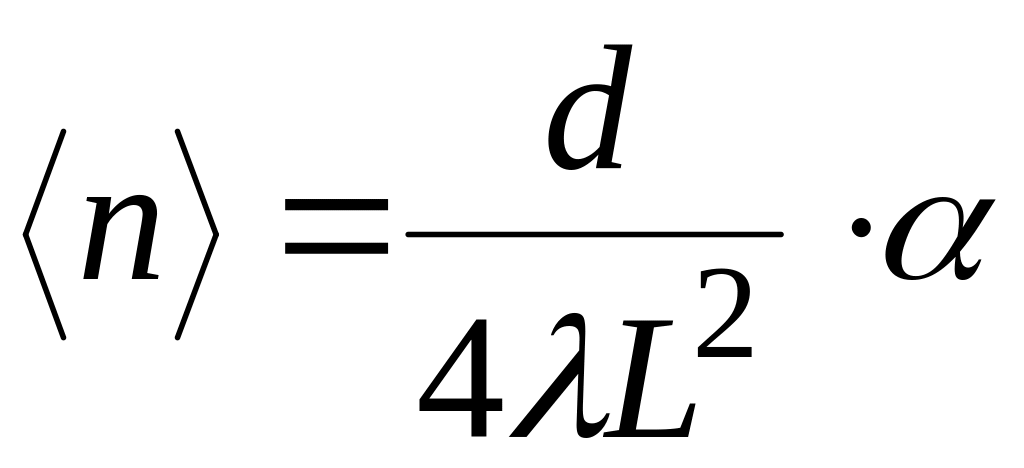
Источник
Работа 63. Определение показателя преломления стекла интерференционным методом
1. Цель работы
Целью работы является определение показателя преломления стекла по параметрам интерференционной картины, возникающей при отражении лазерного луча от плоскопараллельной стеклянной пластины.
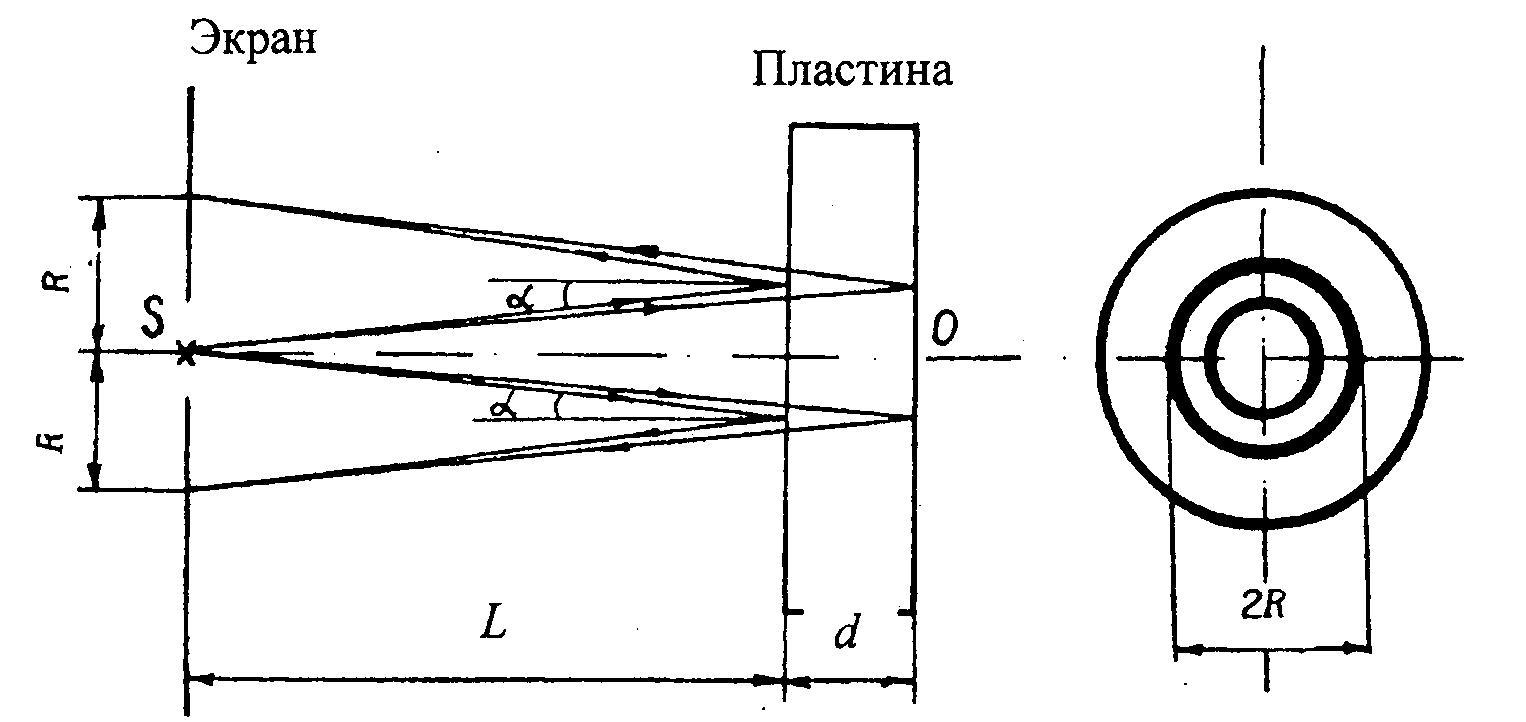
2. Краткая теория исследуемого явления
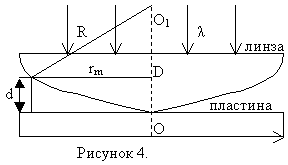
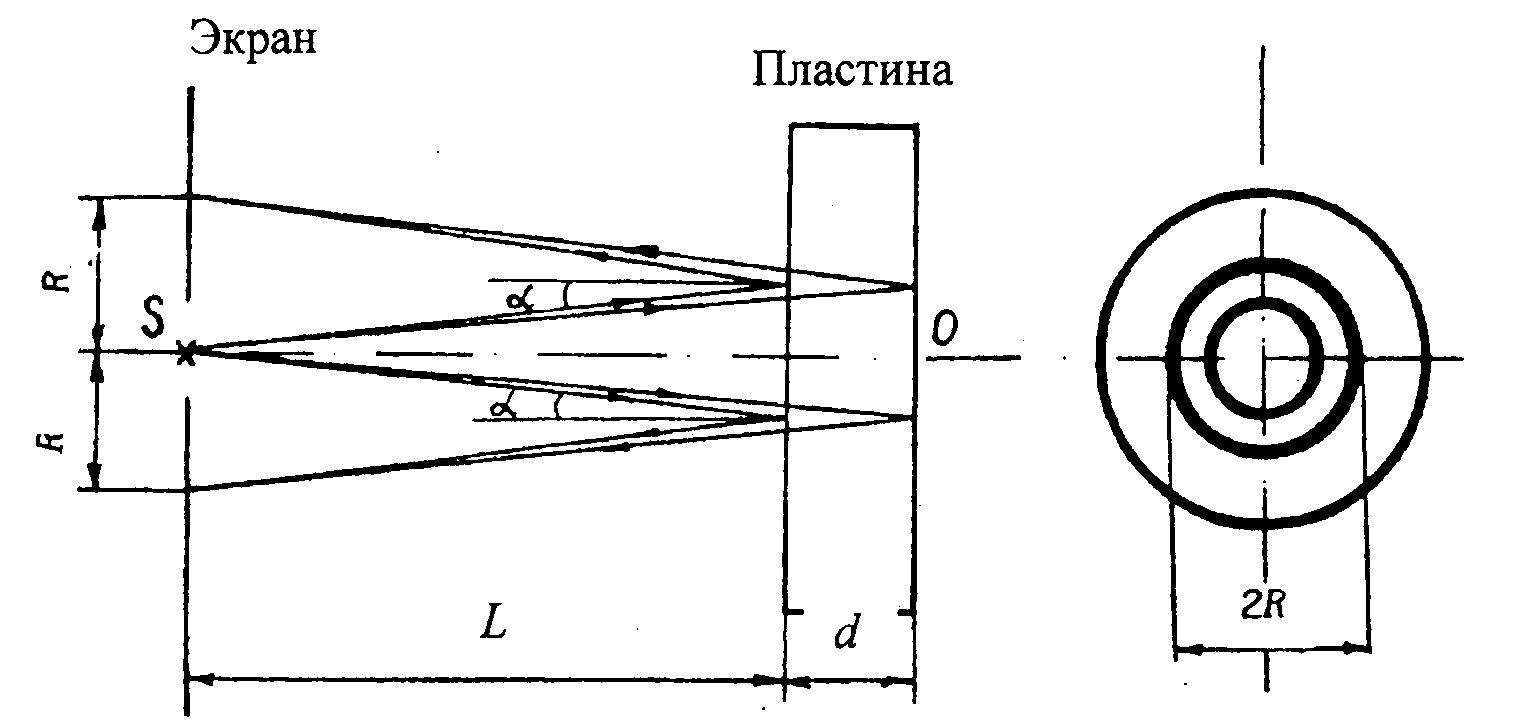
Рассмотрим расходящийся пучок монохроматических когерентных лучей, падающий на поверхность плоскопараллельной пластинки. Ось пучка перпендикулярна поверхности пластинки (рис. 1).
Лучи, отраженные от передней и задней поверхностей пластинки, сходятся на экране, где наблюдается интерференционная картина. Из рис. 1 видно, что любая пара интерферирующих лучей, идущих симметрично относительно нормали SO, имеет одинаковую разность хода. Следовательно, интерференционная картина на экране будет иметь вид концентрических колец.
Заметим, что для наблюдения интерференционной картины необходимо, чтобы складывающиеся колебания были когерентны. Если оптическая разность хода волн превышает длину когерентности, интерференция наблюдаться не будет. Излучение лазера обладает высокой монохроматичностью и, следовательно, большой длиной когерентности (порядка метра, а в случае одночастотных лазеров – и десятков метров).
В настоящей работе используется лазер для получения интерференции в сравнительно толстой (d = 5 мм) стеклянной пластинке.
При условии, что расстояние L между экраном и пластинкой значительно больше, чем толщина пластинки d, угол α между нормалью и лучом будет очень малой величиной (рис. 1).
3. Принцип метода измерения и рабочая формула
Плоскопараллельная стеклянная пластина освещается пучком параллельных когерентных лучей. В отраженном свете возникает интерференционная картина, которая визуализируется на экране, расположенном со стороны падения лучей, в виде тёмных и светлых концентрических колец. По размерам этих колец и определяют показатель преломления стекла, из которого изготовлена пластина.
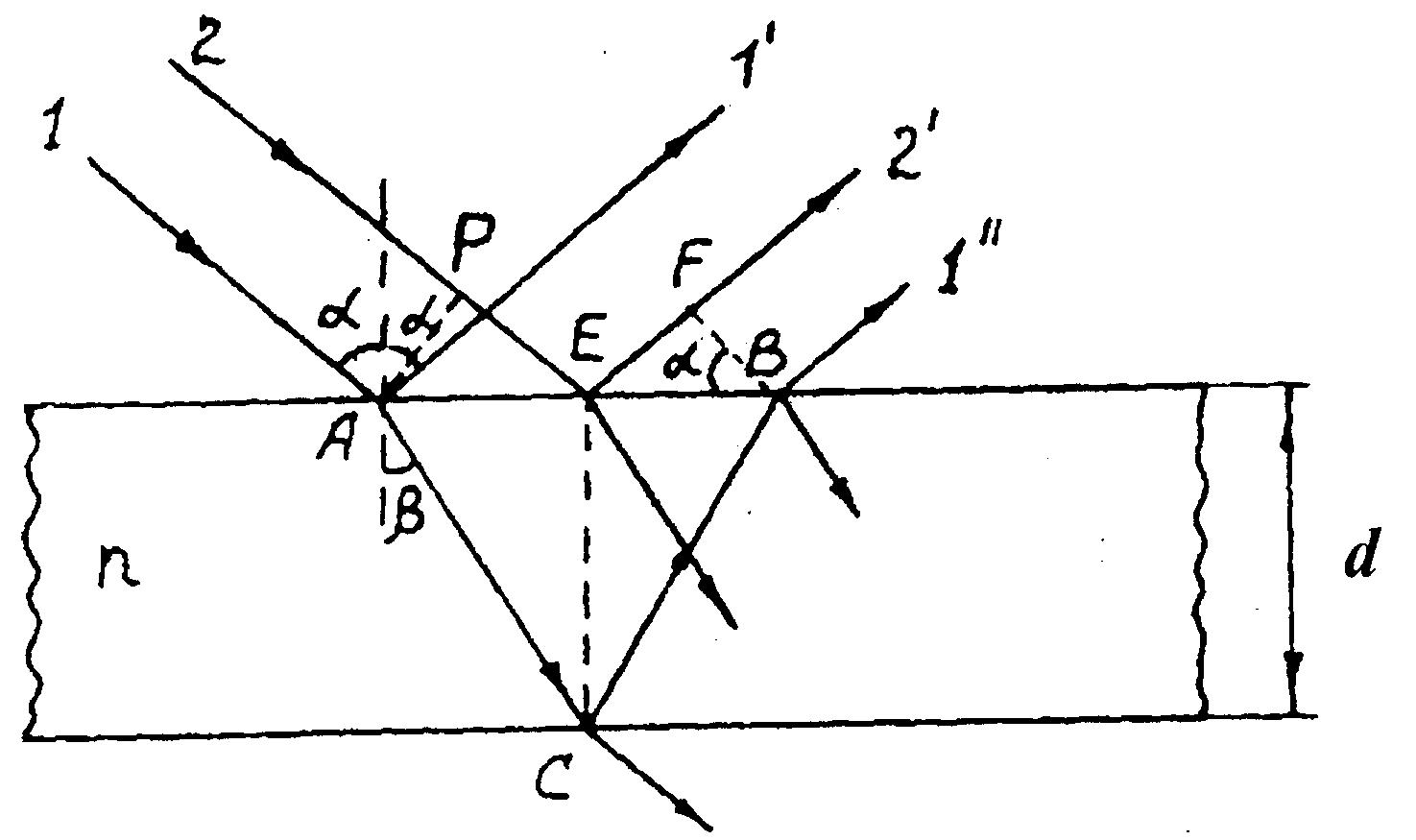
Предварительно определим условия образования темных и светлых интерференционных колец при отражении пучка параллельных когерентных лучей от плоскопараллельной пластинки (рис. 2).
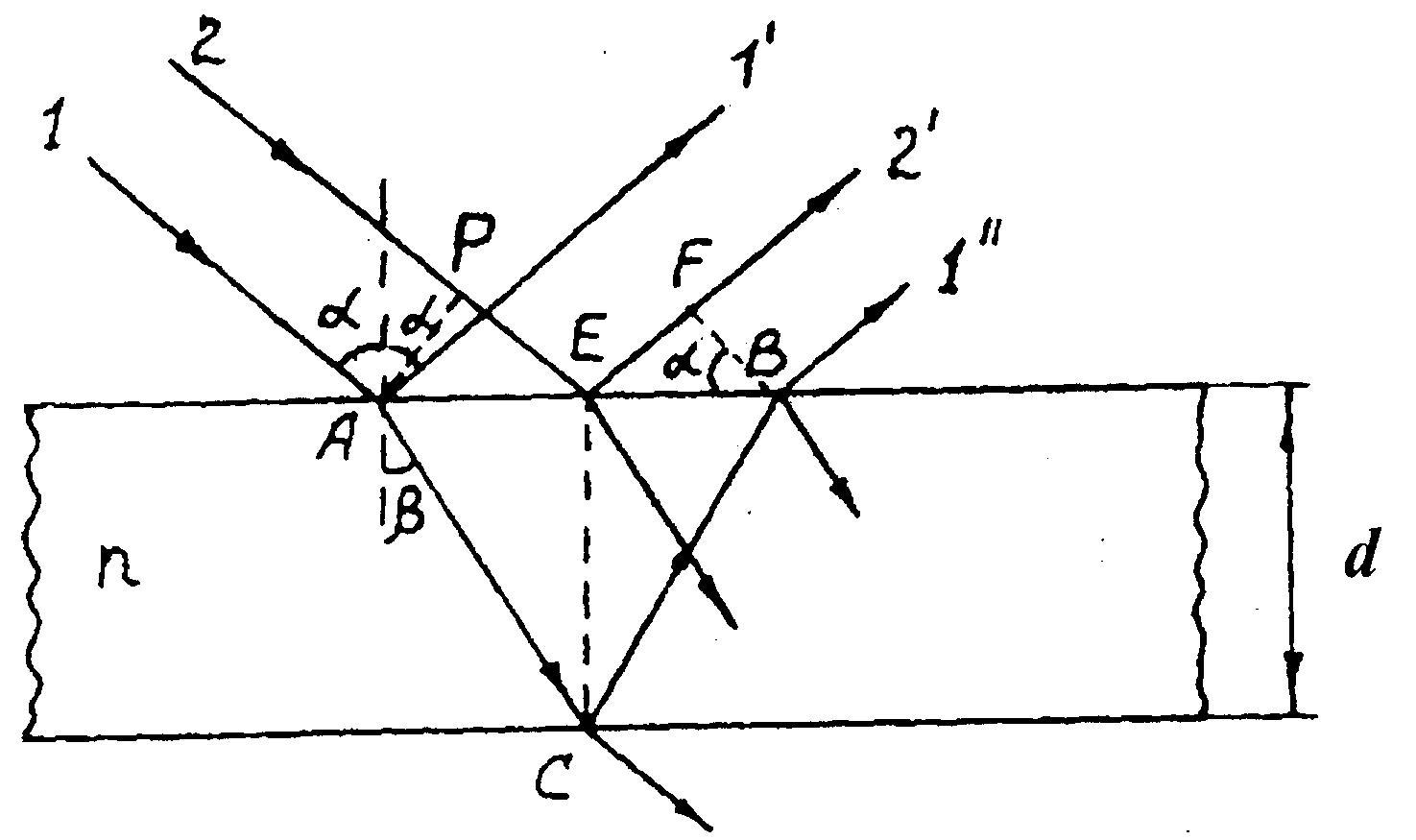
На поверхности пластинки световые лучи 1 и 2 разделятся на два луча – отраженный и преломленный от верхней поверхности пластинки. Разделение световых лучей происходит и на нижней поверхности пластинки. Обычно интенсивность отраженной волны много меньше интенсивности преломленной. Поэтому после многократных отражений и преломлений интенсивности волн резко убывают. При расчете интерференции в отраженном свете достаточно учитывать лишь лучи 2′ и 1″. Лучи 1′ и 2′ полностью идентичны, и их наложение мы не рассматриваем.
Из рис. 2 следует, что оптическая разность хода между этими лучами равна
где n – показатель преломления стекла.
Последнее слагаемое равенства данного учитывает изменение фазы колебаний светового вектора при отражении луча 2′ в точке E от оптически более плотной среды (показатель преломления стекла больше, чем показатель преломления воздуха) (см. рис. 2).
Из анализа рис. 2 получаем
Учитывая закон преломления света,
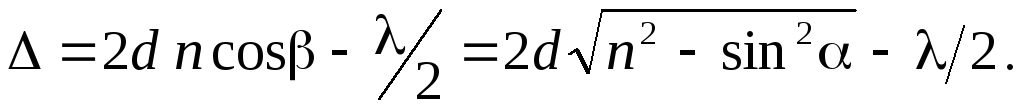
Вернемся к расчету интерференционной картины от расходящегося пучка когерентных лучей, освещающего поверхность плоскопараллельной пластинки.
Из рис. 1 видно, что
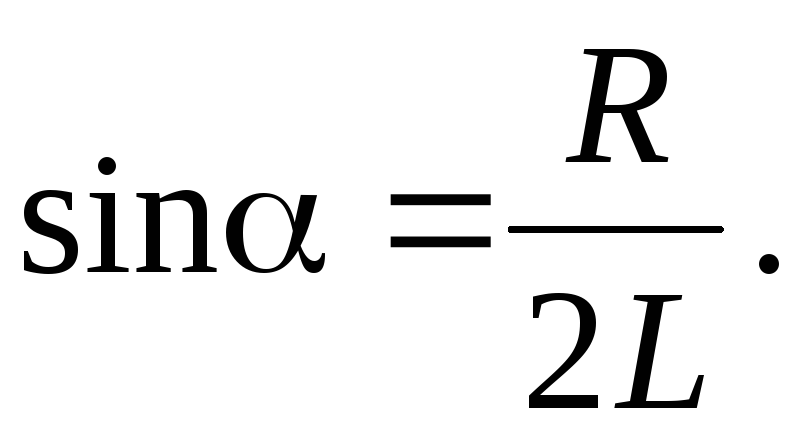
При образовании интерференционной картины минимум освещенности получается при условии, что оптическая разность хода лучей равна
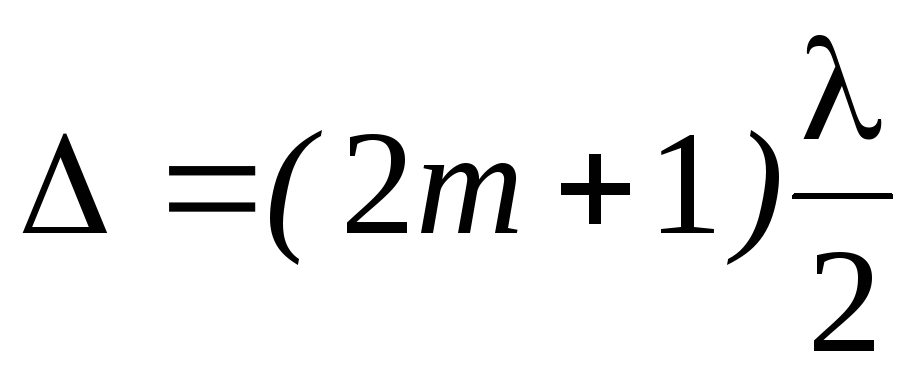
Приравнивая правые части равенств (1) и (3), с учетом (2), получим условие для расчета радиусов темных колец на экране

С учетом L >> R формулу (4) можно представить в приближенном виде
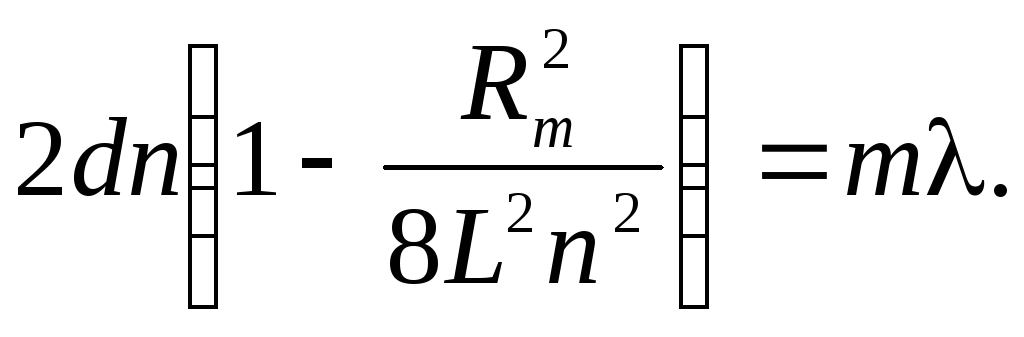
Равенство (5) для темного кольца порядка (m + k) может быть записано в виде
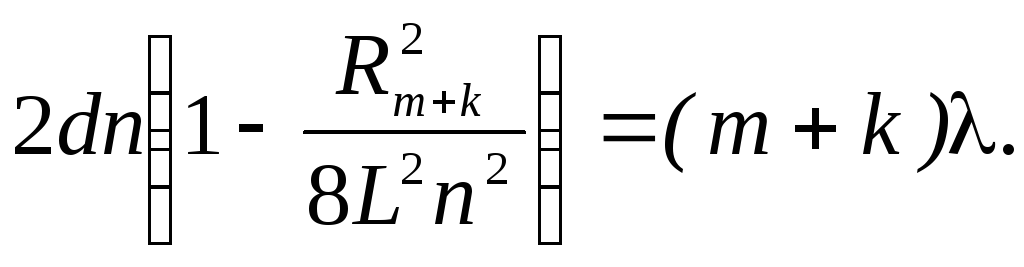
Из системы уравнений (5) и (6) находим показатель преломления стекла
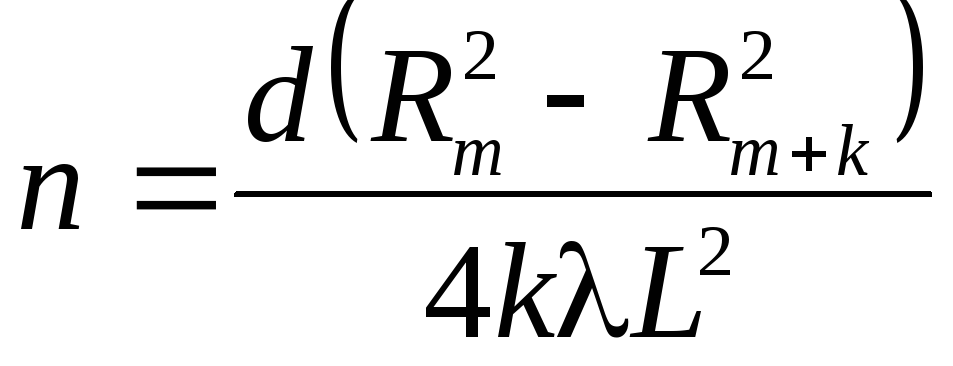
Равенство (7) справедливо и для светлых колец.
Источник
Оптика / лаб.раб.оптика для физиков / 3
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ СТЕКЛА ИНТЕРФЕРЕНЦИОННЫМ МЕТОДОМ
Цель работы: изучение полос равного наклона, возникающих при интерференции света, отраженного от плоскопараллельной стеклянной пластинки, и определение показателя преломления стекла.
Теоретические основы работы
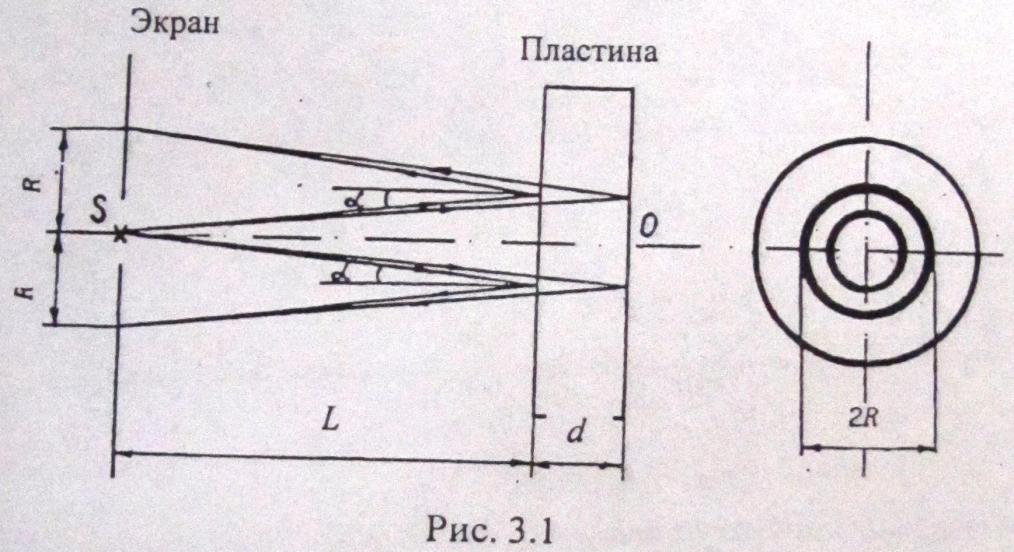
Рассмотрим расходящийся пучок монохроматических когерентных лучей, падающий на поверхность плоскопараллельной пластинки. Ось пучка перпендикулярна поверхности пластинки (рис. 3.1).
Лучи, отраженные от передней и задней поверхностей пластинки, сходятся на экране, где наблюдается интерференционная картина. Из рис. 3.1 видно, что любая пара интерферирующих лучей, идущих симметрично относительно нормали SO, имеет одинаковую разность хода. Следовательно, интерференционная картина на экране будет иметь вид концентрических колец.
При условии, что расстояние L между экраном и пластинкой значительно больше, чем толщина пластинки d, угол а между нормалью и лучом будет очень малой величиной (рис. 3.1).
Предварительно определим условия образования темных и светлых интерференционных колец при отражении пучка параллельных когерентных лучей от плоскопараллельной пластинки (рис. 3.2).
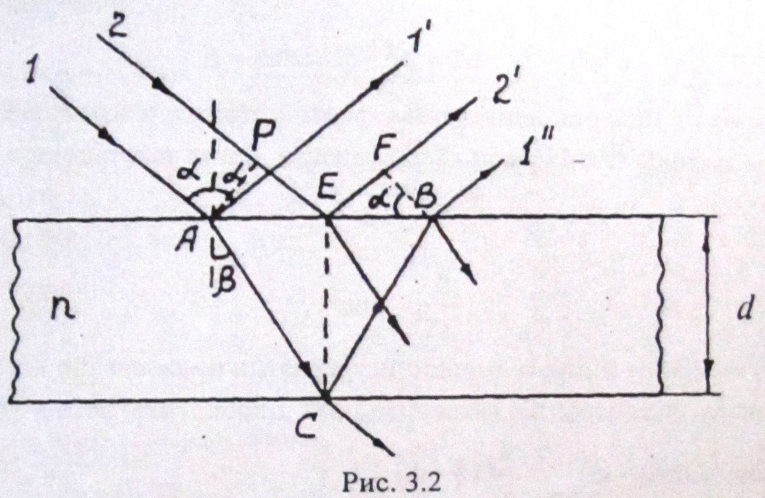
Из рис. 3.2 следует, что оптическая разность хода между этими лучами равна
Последнее слагаемое равенства (3.1) учитывает изменение фазы колебаний светового вектора при отражении луча 2′ в точке E от оптически более плотной среды (показатель преломления стекла больше, чем показатель преломления воздуха) (рис. 3.2).
Из анализа рис. 3.2 получаем
Учитывая закон преломления света

Вернемся к расчету интерференционной картины от расходящегося пучка когерентных лучей, освещающего поверхность плоскопараллельной пластинки.
Из рис. 3.1 видно, что

При образовании интерференционной картины минимум освещенности получается при условии, что оптическая разность хода лучей равна
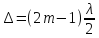
Приравнивая правые части равенств (3.1) и (3.3), с учетом (3.2), получим условие для расчета радиусов темных колец на экране
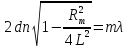
С учетом L» R формулу (3.4) можно представить в приближенном виде:
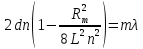
Равенство (3.5) для темного кольца порядка (т + к) может быть записано в виде:
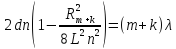
Из системы уравнений (3.5) и (3.6) находим показатель преломления стекла
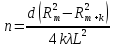
Равенство (3.7) справедливо и для светлых колец.
Описание экспериментальной установки
Экспериментальная установка изображена на рис. 3.3. Лазер 1 освещает параллельным пучком линзу, расположенную в центре экрана 2. Позади линзы находится плоскопараллельная пластинка 3. Расстояние между линзой и пластинкой больше фокусного расстояния линзы, поэтому на пластинку падает расходящийся пучок света. На экране наблюдается интерференционная картина в виде полос равного наклона. Все элементы оптической системы смонтированы на скамье 4.
Порядок выполнения работы
С помощью ручек управления предметного столика лазера совместить его луч с главной оптической осью линзы, вмонтированной в экран.
4. С помощью линейки или по шкале оптической скамьи измерить расстояние между плоскопараллельной пластинкой и экраном L. Результат записать в табл. 3.1.
Диаметр кольца Dm мм
Расстояние между экраном и пластинкой L мм
Обработка результатов измерений
Вычислить показатель преломления стекла
Оценить погрешность измерения показателя преломления.
Записать результат с учетом погрешности.
Сформулируйте основные законы геометрической оптики.
Выведите формулу для расчета оптической разности хода при интерференции на тонкой пленке.
При каких условиях возможно наблюдение интерференционной картины на пластинке?
В чем заключается сущность интерференции как физического явления?
Выведите формулы для максимумов и минимумов при интерференции на пленке.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник
Установка лабораторная «Измерение показателя преломления стекла интерференционным методом». ФПВ-05-2-1
Установка ФПВ-05-2-1 предназначена для изучения методов определения показателя преломления стекла.
Установка дает возможность получить интерференционную картину методом «полос равного наклона», по которой в дальнейшем вычисляетс
я показатель преломления стекла пластины.
Состав установки:
Лазер с источником питания;
Плоскопараллельной стеклянной пластины в оправе;
Экран с линзой и экран с миллиметровой шкалой в виде креста;
Устанавливаемых в рейтерах на оптической скамье.
На поверхности скамьи нанесена миллиметровая шкала.
Плоскопараллельная пластина крепится в оправе с узлом юстировки, который позволяет изменять угол наклона пластины по отношению оптической оси.
Основные технические характеристики:
Длина оптической скамьи, мм 1200
Высота оптической оси, над опорной плоскостью скамьи, мм 230
Цена деления линейки скамьи, мм 1
Клиновидность пластины, угловых сек., не более 5
Длина волны лазерного излучения, мкм не менее 0,5
Питание от сети переменного тока 220В 50Гц
Потребляемая мощность, ВА, не более 35
Габаритные размеры установки мм, не более 1300х300х400
Источник
Работа 63. Определение показателя преломления стекла интерференционным методом
1. Цель работы
Целью работы является определение показателя преломления стекла по параметрам интерференционной картины, возникающей при отражении лазерного луча от плоскопараллельной стеклянной пластины.
2. Краткая теория исследуемого явления
Рассмотрим расходящийся пучок монохроматических когерентных лучей, падающий на поверхность плоскопараллельной пластинки. Ось пучка перпендикулярна поверхности пластинки (рис. 1).
Лучи, отраженные от передней и задней поверхностей пластинки, сходятся на экране, где наблюдается интерференционная картина. Из рис. 1 видно, что любая пара интерферирующих лучей, идущих симметрично относительно нормали SO, имеет одинаковую разность хода. Следовательно, интерференционная картина на экране будет иметь вид концентрических колец.
Заметим, что для наблюдения интерференционной картины необходимо, чтобы складывающиеся колебания были когерентны. Если оптическая разность хода волн превышает длину когерентности, интерференция наблюдаться не будет. Излучение лазера обладает высокой монохроматичностью и, следовательно, большой длиной когерентности (порядка метра, а в случае одночастотных лазеров – и десятков метров).
В настоящей работе используется лазер для получения интерференции в сравнительно толстой (d = 5 мм) стеклянной пластинке.
При условии, что расстояние L между экраном и пластинкой значительно больше, чем толщина пластинки d, угол α между нормалью и лучом будет очень малой величиной (рис. 1).
3. Принцип метода измерения и рабочая формула
Плоскопараллельная стеклянная пластина освещается пучком параллельных когерентных лучей. В отраженном свете возникает интерференционная картина, которая визуализируется на экране, расположенном со стороны падения лучей, в виде тёмных и светлых концентрических колец. По размерам этих колец и определяют показатель преломления стекла, из которого изготовлена пластина.
Предварительно определим условия образования темных и светлых интерференционных колец при отражении пучка параллельных когерентных лучей от плоскопараллельной пластинки (рис. 2).
На поверхности пластинки световые лучи 1 и 2 разделятся на два луча – отраженный и преломленный от верхней поверхности пластинки. Разделение световых лучей происходит и на нижней поверхности пластинки. Обычно интенсивность отраженной волны много меньше интенсивности преломленной. Поэтому после многократных отражений и преломлений интенсивности волн резко убывают. При расчете интерференции в отраженном свете достаточно учитывать лишь лучи 2′ и 1″. Лучи 1′ и 2′ полностью идентичны, и их наложение мы не рассматриваем.
Из рис. 2 следует, что оптическая разность хода между этими лучами равна
где n – показатель преломления стекла.
Последнее слагаемое равенства данного учитывает изменение фазы колебаний светового вектора при отражении луча 2′ в точке E от оптически более плотной среды (показатель преломления стекла больше, чем показатель преломления воздуха) (см. рис. 2).
Из анализа рис. 2 получаем
Учитывая закон преломления света,
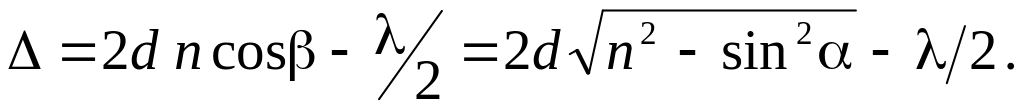
Вернемся к расчету интерференционной картины от расходящегося пучка когерентных лучей, освещающего поверхность плоскопараллельной пластинки.
Из рис. 1 видно, что
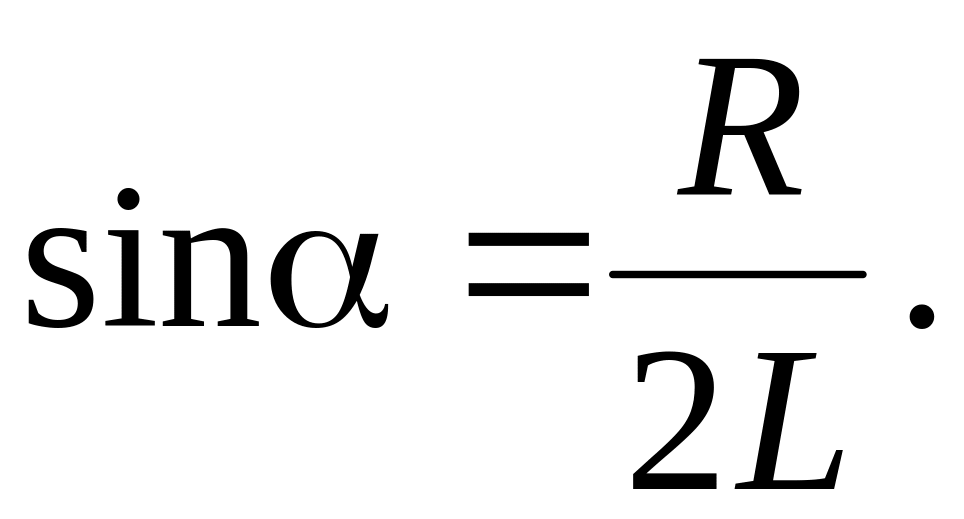
При образовании интерференционной картины минимум освещенности получается при условии, что оптическая разность хода лучей равна
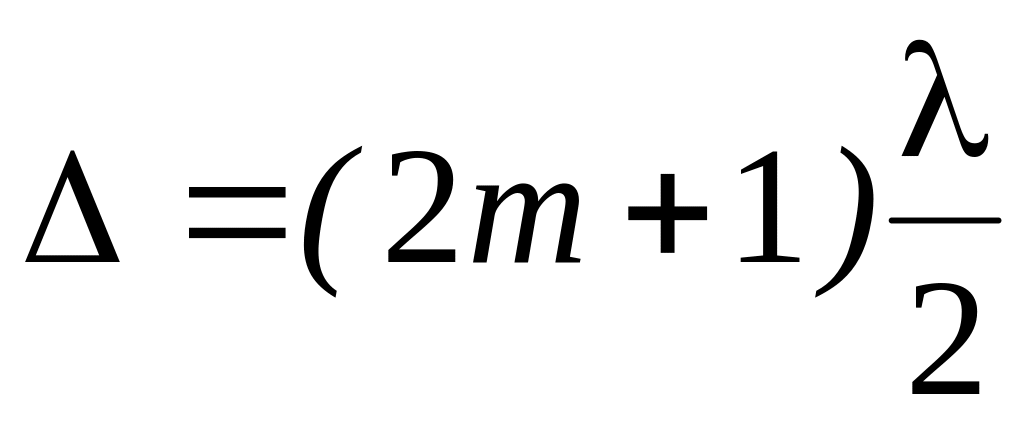
Приравнивая правые части равенств (1) и (3), с учетом (2), получим условие для расчета радиусов темных колец на экране

С учетом L >> R формулу (4) можно представить в приближенном виде
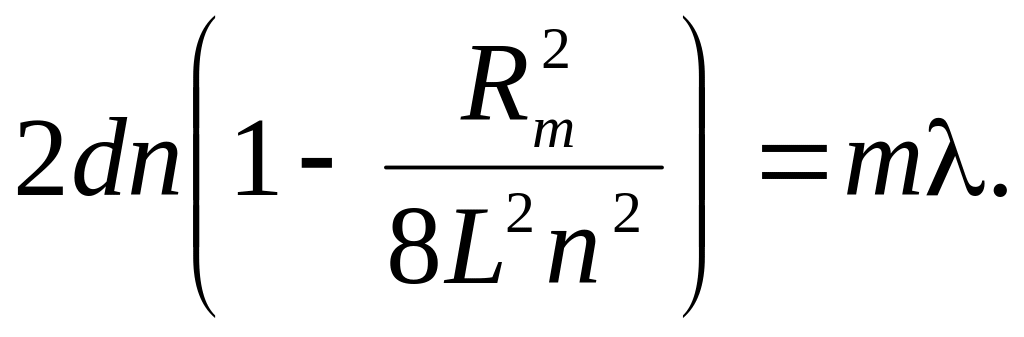
Равенство (5) для темного кольца порядка (m + k) может быть записано в виде
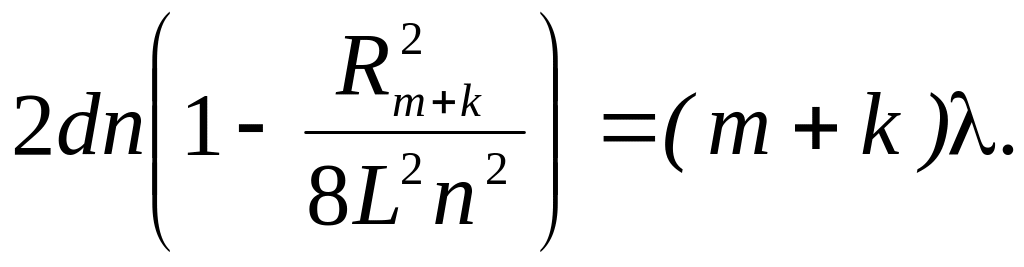
Из системы уравнений (5) и (6) находим показатель преломления стекла
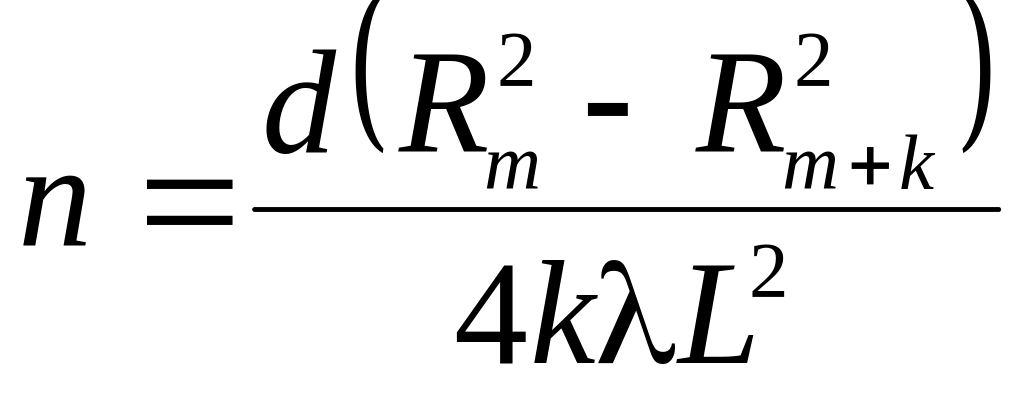
Равенство (7) справедливо и для светлых колец.
Источник