Измерение длины, площади, объема и времени
- Лабораторная работа №1. Измерение длины ребер, площади поверхности и объема прямоугольного параллелепипеда. Погрешность прямых и косвенных измерений
- Лабораторная работа №2. Измерение времени с помощью секундомера. Погрешность серии прямых измерений
п.1. Лабораторная работа №1. Измерение длины ребер, площади поверхности и объема прямоугольного параллелепипеда. Погрешность прямых и косвенных измерений
Цель работы
Научиться измерять длину с помощью линейки, определять площадь поверхности и объем прямоугольного параллелепипеда, находить абсолютные и относительные погрешности косвенных измерений.
Теоретические сведения
 |
Прямоугольный параллелепипед – это многогранник с шестью гранями, каждая из которых является прямоугольником. Прямоугольный параллелепипед имеет три измерения: длину, ширину и высоту. |
Пусть
длина (AD=BC=A_1 D_1=B_1 C_1=a)
ширина (AB=CD=A_1 B_1=C_1 D_1=b)
высота (AA_1=BB_1=CC_1=DD_1=c)
Площади верхней и нижней грани равны (S_1=ab), площади передней и задней граней равны (S_2=ac), площади левой и правой граней равны (S_3=bc).
Площадь поверхности прямоугольного параллелепипеда равна сумме площадей всех шести граней: $$ S_{пов}=2S_1+2S_2+2S_3=2(ab+ac+bc) $$ Объем прямоугольного параллелепипеда равен произведению всех трех измерений: $$ V=abc $$
Пусть измерения проводятся ученической линейкой с ценой деления (triangle=1 мм).
Тогда инструментальная погрешность измерений равна половине цены деления: $$ d=frac{triangle}{2}=0,5 мм $$ Абсолютная погрешность измерений при работе с линейкой равна инструментальной погрешности, поэтому для всех измерений: (triangle a=triangle b=triangle c=d=0,5 мм)
Относительные погрешности измерений (в долях, без процентов): $$ delta_a=frac{triangle a}{a}=frac da, delta_b=frac{triangle b}{b}=frac db, delta_c=frac{triangle c}{c}=frac dc $$ Выведем необходимые формулы.
Рассмотрим нижнюю грань. Её площадь (S_1=ab) является произведением двух длин.
Значит, относительная погрешность измерения площади равна сумме относительных погрешностей длин: $$ delta_{S1}=delta_a+delta_b $$ Аналогично для остальных граней: $$ delta_{S2}=delta_a+delta_c, delta_{S3}=delta_b+delta_c $$ Абсолютная погрешность измерения площади нижней грани: $$ triangle S_1=S_1cdotdelta_{S1}=abcdot(delta_a+delta_b)=abcdotleft(frac da+frac dbright)=abdcdotleft(frac ab+frac1bright)=abdcdotfrac{b+a}{ab}= d(a+b) $$ Аналогично для остальных граней: $$ triangle S_2=S_2cdotdelta_{S2}=d(a+c), triangle S_3=S_3cdotdelta_{S3}=d(b+c) $$ Абсолютная погрешность суммы измерений равна сумме абсолютных погрешностей. Получаем для площади поверхности: begin{gather*} triangle S_{пов}=2(triangle S_1+triangle S_2+triangle S_3)=2(d(a+b)+d(a+c)+d(b+c))=\ =2d(a+b+a+c+b+c)=4d(a+b+c) end{gather*}
Абсолютная погрешность определения площади поверхности прямоугольного параллелепипеда равна: $$ triangle S_{пов}=4d(a+b+c) $$ где (d) – инструментальная погрешность линейки, (a,b,c) — измеренные значения длины, ширины и высоты.
Найдем погрешность определения объема.
Объем равен произведению трех измерений, значит, относительная погрешность для объема равна сумме относительных погрешностей измерений: $$ delta_v=delta_a+delta_b+delta_c=frac da+frac db+frac dc=dleft(frac 1a+frac 1b+frac 1cright)=dcdotfrac{bc+ac+ab}{abc} $$ Абсолютная погрешность для объема: $$ triangle V=vcdotdelta_v=abccdot dcdotfrac{bc+ac+ab}{abc} = d(bc+ac+ab)=dcdotfrac{S_{пов}}{2} $$
Абсолютная погрешность определения объема прямоугольного параллелепипеда равна: $$ triangle V=dcdotfrac{S_{пов}}{2} $$ где (d) – инструментальная погрешность линейки, (S_{пов}) — площадь поверхности.
Приборы и материалы
Ученическая линейка, книга (или деревянный брусок).
Ход работы
1. Ознакомьтесь с теоретической частью работы, выпишите необходимые формулы.
2. Измерьте длину, ширину и высоту книги (бруска), (a,b,c).
3. Найдите площадь поверхности (S_{пов}) и объем (V).
4. Найдите абсолютные погрешности (triangle S_{пов}) и (triangle V).
5. Найдите относительные погрешности в процентах: $$ delta_{S_{пов}}=frac{triangle S_{пов}}{S_{пов}}cdot 100text{%}, delta_V=frac{triangle V}{V}cdot 100text{%} $$ 6. Дополнительное задание. Определите толщину одного листа книги, абсолютную и относительную погрешность этой величины.
7. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
Инструментальная погрешность линейки (d=frac{1 мм}{2}=0,5 мм)
Результаты измерений:
a=218 мм
b=147 мм
c=32 мм
Площадь поверхности: begin{gather*} S_{пов}=2(ab+ac+bc)=2(218cdot 147+218cdot 32+147cdot 32)=\ =2(32046+6976+4704)=87452 (мм^2) end{gather*} Объем: $$ V=abc=218cdot 147cdot 32=1025472 (мм^2) $$ Абсолютная погрешность определения площади поверхности (округляем до двух значащих цифр с избытком): $$ triangle S_{пов}=4d(a+b+c)=4cdot 0,5cdot (218+147+32)=2cdot 397=794 (мм^2)approx 800 (мм^2) $$ Полученную величину площади поверхности также округляем до сотен. Получаем: $$ S_{пов}=(87500pm 800) (мм^2) $$ Абсолютная погрешность определения объема: $$ triangle V=dcdotfrac{S_{пов}}{2}=0,5cdotfrac{87452}{2}=21863 (мм^3)approx 22000 (мм^3) $$ Полученную величину объема также округляем до тысяч. Получаем: $$ V=(1025000pm 22000) (мм^3) $$
Относительные погрешности (округляем до двух значащих цифр с избытком): begin{gather*} delta_{S_{пов}}=frac{triangle S_{пов}}{S_{пов}}cdot 100text{%}=frac{800}{87500}cdot 100text{%} approx 0,92text{%}\ delta_v=frac{triangle V}{V}cdot 100text{%}=frac{22000}{1025000}cdot 100text{%}approx 2,2text{%} end{gather*} Измеряем толщину книги между обложками: (h=23 мм)
Количество страниц в книге (N=688)
Количество листов в 2 раза меньше. Получаем толщину одного листа: $$ t=frac{h}{N/2}=frac{2h}{N}=frac{2cdot 23}{688}approx 0,0669 (мм)=66,9 (мк) $$ Количество листов – величина точная, без погрешностей.
Абсолютная погрешность для толщины листа зависит только от (triangle h): $$ triangle t=frac 2Ntriangle h=frac 2N d=frac{2}{688}cdot 0,5approx 0,0015 (мм)=1,5 (мк) $$ Толщина листа: $$ t=(66,9pm 1,5) мк $$ Относительная погрешность: $$ delta_t=frac{triangle t}{t}cdot 100text{%}=frac{1,5}{66,9}cdot 100text{%}approx 2,3text{%} $$
Выводы
На основании проделанной работы можно сделать следующие выводы.
Измерения проводились с помощью линейки с инструментальной погрешностью (d=0,5 мм).
Получена площадь поверхности книги $$ S_{пов}=(87500pm 800) мм^2, delta_{S_{пов}}approx 0,92text{%} $$ Объем книги: $$ V=(1025000pm 22000) мм^3, delta_Vapprox 2,2text{%} $$ Определяя толщину листа, мы использовали способ рядов и увеличили абсолютную точность измерений от 0,5 мм до 1,5 мк. Толщина листа: $$ t=(66,9pm 1,5) мк, delta_tapprox 2,3text{%} $$ С наибольшей точностью определена площадь поверхности, т.к. для нее относительная погрешность меньше всех.
С наименьшей относительной точностью определена толщина листа, зато абсолютная точность для этой величины очень высока – 1,5 микрона.
п.2. Лабораторная работа №2. Измерение времени с помощью секундомера. Погрешность серии прямых измерений
Цель работы
Научиться измерять время с помощью секундомера, определять абсолютную и относительную погрешность величины, полученной в серии прямых измерений.
Теоретические сведения
Математическим маятником называют груз небольших размеров, подвешенный на тонкой невесомой нерастяжимой нити.
Периодом колебаний математического маятника называют время, за которое он возвращается в исходную точку.
При отклонении математического маятника на малые углы (до 20°) период его колебаний (T) остается постоянной величиной. В действительности колебания постепенно затухают, но при достаточно длинной нити и тяжелом грузике, затухания происходят медленно.
Приборы и материалы
Секундомер, штатив, грузик на длинной нитке (не менее 50 см).
Ход работы
1. Закрепите нитку с грузиком в лапке штатива, как показано на рисунке.
2. Определите цену деления секундомера.
3. Отклоните грузик на небольшой угол, отпустите его и с помощью секундомера измерьте время, за которое маятник совершит 10 полных колебаний.
4. Повторите опыт 5 раз.
5. С помощью алгоритма определения истинного значения и абсолютной погрешности в серии измерений (см. §3 данного справочника) найдите точное значение и абсолютную погрешность времени 10 колебаний.
6. Найдите точное значение и абсолютную погрешность периода колебаний (T), рассчитайте относительную погрешность результата измерений.
7. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
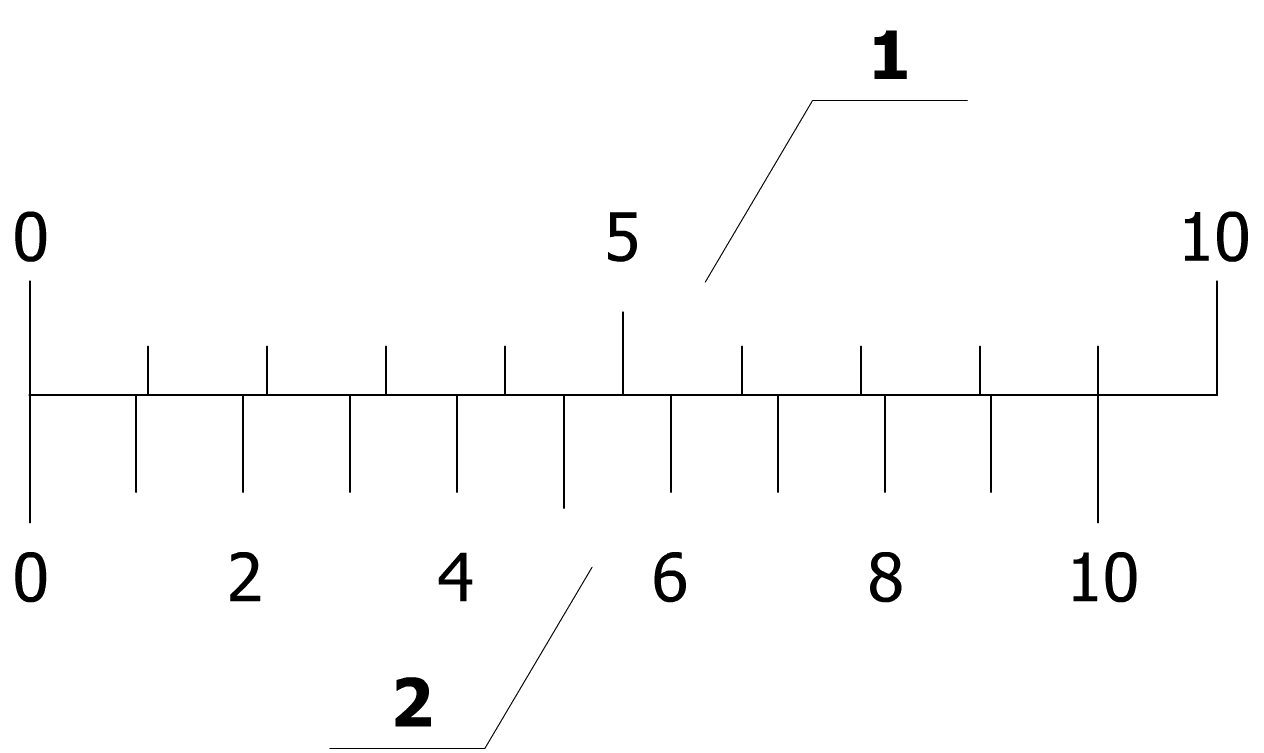
Определение цены деления секундомера
 |
Два ближайших пронумерованных деления на основной шкале: begin{gather*} a=5 с\ b=10 с end{gather*} Между ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления.
Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*} |
Инструментальная погрешность секундомера равна половине цены деления: (d=frac{triangle}{2}=0,1 c)
Измерения времени 10 колебаний
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t, c) | 15,3 | 14,9 | 15,2 | 15,5 | 15,1 | 76,0 |
| (triangle c) | 0,1 | 0,3 | 0 | 0,3 | 0,1 | 0,8 |
Найдем среднее время для 10 колебаний: begin{gather*} t_0=frac{15,3+14,9+15,2+15,5+15,1}{5}=frac{76,0}{5}=15,2 (c) end{gather*} Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_0): $$ triangle_1=|15,3-15,2|=0,1; triangle_2=|14,9-15,2|=0,3 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0,1+0,3+0+0,3+0,1}{5}=frac{0,8}{5}=0,16 (c) $$ Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,16right}=0,16 text{c} $$ Результат измерения времени 10 колебаний: begin{gather*} t=t_0pmtriangle t, t=(15,20pm 0,16) c end{gather*} Период колебаний в 10 раз меньше: $$ T=frac{1}{10}(t_0pmtriangle t), T=(1,520pm 0,016) c $$ Относительная погрешность измерений: $$ delta_T=frac{triangle T}{T_0}cdot 100text{%}=frac{0,016}{1,520}cdot 100text{%}approx 1,1text{%} $$
Выводы
На основании проделанной работы можно сделать следующие выводы.
Измерения проводились с помощью секундомера, для которого была определена цена деления (triangle=0,2 с) и соответствующая инструментальная погрешность (d=frac{triangle}{2}=0,1 с).
В данном случае абсолютная погрешность может быть заметно больше инструментальной, и поэтому для ее определения потребовалась серия экспериментов.
Полученный в серии из 5 экспериментов результат измерения времени 10 колебаний: $$ t=(15,20pm 0,16) c $$ Искомый период колебаний маятника: $$ T=(1,520pm 0,016) c, delta_T=1,1text{%} $$
Измерение линейных размеров тела правильной геометрической формы и расчет погрешностей при прямых измерениях
-
Измерить
длину апараллелепипеда 5 раз.
Результаты измерений записать в табл.
1.3.
Таблица 1.3
Измерительный инструмент:
Инструментальная погрешность:
-
№
п/пДлина
тела,а,
смАбсолютная
погрешность отсчета,
,
см1.
2.
3.
4.
5.
Среднее
значение
Вычислить
среднее значение длины
по формуле:
.
(1.19)
Рассчитать
абсолютную погрешность каждого отсчета*:
и т.д. (1.20)
Рассчитать
среднюю абсолютную погрешность отсчета:
.
(1.21)
Записать,
каким измерительным прибором проводились
измерения длины тела и его инструментальную
погрешность
Найти границу абсолютной погрешности
длины тела:
.
(1.22)
Записать
результат в форме:
.
(1.23)
-
Измерить
ширину bи высотус
параллелепипеда. Результаты измерений
занести в таблицы аналогичные табл.
1.3. Результаты представить в форме:
,
(1.24)
.
(1.25)
1
Примечание.Правила округления
-
Если старшая
отбрасываемая цифра меньше 5, то последняя
сохраняемая цифра не изменяется. -
Если старшая
отбрасываемая цифра больше или равна
5, то последняя сохраняемая цифра
увеличивается на единицу. -
Если при
округлении последняя сохраняемая цифра
оказалась нулем, то его следует писать,
даже если он стоит в разряде десятичных
дробей. -
Из правил
округления имеется существенное
исключение– при округлении
погрешностей последняя сохраняемая
цифра увеличивается на единицу, если
старшая отбрасываемая цифра 3 или больше
3. -
Физическая
величина округляется до первой
сомнительной цифры. Все цифры, стоящие
после сомнительной, отбрасываются. -
Абсолютная
погрешность округляется до одной
значащей цифры, относительная – до
двух значащих цифр. -
При
вычислении промежуточных результатов
следует брать на одну цифру больше. В
окончательном результате эта «запасная»
цифра отбрасывается.
ЗАДАНИЕ
6
Определение объема прямого прямоугольного параллелепипеда и расчет погрешностей при косвенных измерениях
Рассчитать
объем прямого прямоугольного
параллелепипеда по формуле:
.
(1.26)
Рассчитать
относительную погрешность объема:
.
(1.27)
Сравнить
вклад, который вносят погрешности
величин a, b,
cв относительную
погрешность объема. Сделать вывод.
Вычислить
абсолютную погрешность объема:
.
(1.28)
Записать
результат в форме:
.
(1.29)
Сделать
выводы по проведенному эксперименту.
ЗАДАНИЕ
7
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подборка по базе: КУРСОВАЯ РАБОТА.docx, курсовая работа 51^J Позныхов.docx, Лабораторная работа 1.pdf, Лабораторная работа 1 (GPSS).doc, Практическая работа Мои профессиональные установки педагога.docx, Практическая работа № 1_Смирнова ЛВ.docx, Корепанов А.П. ВУсБ-21.03.01.01- 23 Практическая работа.docx, практическая работа №1.doc, Практическая работа № 1.docx, Практическая работа №1 Тема_ «Особенности содержания обновленных
Отчёт о работе
| Работу выполнил: | |
| фамилия | Баянжаргал |
| имя | Бямбажаргал |
| отчество | |
| группа | 5Б11 |
Вариант
| 1 |
Краткое теоретическое содержание работы
| Нониус — это … | |
| вспомогательная шкала, устанавливаемая на различных измерительных приборах и инструментах, служащая для более точного определения количества долей делений основной шкалы. | |
| Точность нониуса определяется по формуле | |
| Β-α=β/m | |
| где | |
| y — | Расстояние между соседними штрихами масштаба |
| m — | Число делений нониуса |
Расчетные формулы
| Vп = | a*b*c |
| где | |
| a — | Стороны параллепида |
| b — | Стороны параллепида |
| c — | Стороны параллепида |
| Vц = | πd2/4*h |
| где | |
| D — | Диаметр цилиндра |
| h — | высота |
| π — | математическая постоянная (3.14) |
Схема установки
| Для измерения линейных величин в данной работе используются приборы: | |
| Штангенциркуль и микрометр | |
| основными частями которых являются шкала, называемая масштабом, и нониус:
где |
|
| 1 — | масштаб |
| 2 — | нониус |
| Точность нониуса для штангенциркуля, используемого в данной лабораторной работе, равна | |
| 0,1мм | |
| где | |
| y = | 0,5мм |
| m = | 50 |
| Длина L отрезка, измеряемая прибором, имеющим нониус, равна |
|
| k — | Целое число деления масштаба, измеряемого тела |
| n — | Ближайшие к делению масштаба деление нониуса |
| Нониус микрометрического винта (конический нониус) микрометра, используемого | ||
| в лабораторной работе, представляет собой барабан с | 50 | делениями. |
| Точность нониуса микрометра — | 0,01 | мм. |
Измерения
| Различают два вида измерений: | |
| а) прямые — | Измерения, полученные с помощь различных измерительных приборов |
| б) косвенные — | Измерения, полученные с помощью формул |
| Различают три вида ошибок: | |
| а) систематические — | Ошибки, сохраняющие величину и знак от опыта к опыту, проводящиеся в одинаковых условиях |
| б) приборные — | Ошибки, зависящие от точности измерения величины каким-либо прибором |
| в) случайные — | Ошибки, изменяющие свою величину или знак от опыта к опыту |
Результаты измерений линейных размеров тел
Таблица 1
| № | a (мм) | аi (мм) | b (мм) | bi (мм) | c (мм) | ci (мм) | |||
| 1 | 31,60 | 0,15 | 0,0225 | 19,10 | 0,48 | 0,2304 | 11,35 | -0,02 | 0,0004 |
| 2 | 31,85 | -0,1 | 0,01 | 19,90 | -0,32 | 0,1024 | 11,40 | -0,07 | 0,0049 |
| 3 | 31,70 | 0.05 | 0,0025 | 19,95 | -0,37 | 0,1369 | 11,35 | -0,02 | 0,0004 |
| 4 | 31,80 | -0,-5 | 0,0255 | 19,85 | -0,27 | 0,0729 | 11,30 | 0,03 | 0,0009 |
| 5 | 31,80 | -0,05 | 0,0025 | 19,10 | -0,48 | 0,2304 | 11,25 | 0,08 | 0,0064 |
| среднее значение |
31,75 | 19,58 | 11,33 |
Примечание: ,
,
,
,
где ,
,
— средние значения измеряемых величин a, b, c соответственно.
Таблица 2
| № | D (мм) | Di (мм) | h (мм) | hi (мм) | ||
| 1 | 22,90 | -0,12 | 0,0144 | 11,75 | -0,08 | 0,0064 |
| 2 | 22,50 | 0,28 | 0,784 | 11,65 | 0,02 | 0,0004 |
| 3 | 22,95 | -0,17 | 0,0289 | 11,60 | 0,07 | 0,0049 |
| среднее значение |
22,78 | 11,67 |
Примечание: ,
,
,
где ,
— средние значения измеряемых величин D, h соответственно.
Обработка результатов измерений
длины, ширины и высоты параллелепипеда.
Погрешности измерений
| Среднеквадратичная ошибка σx измеряемой величины x (длины, ширины либо высоты) параллелепипеда для случая 5-тикратного измерения величины рассчитывается по формуле | |
| Δσx = | |
| где | |
| Случайная погрешность Δxсл измеряемой величины x рассчитывается по формуле | |
| Δxсл = | |
| где | |
| σx — | 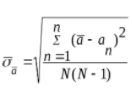 |
| tα,n — коэффициент Стьюдента для n = 5, α = 0.95 , tα,n = | 2,78 |
| Погрешность Δxои однократного измерения величины x рассчитывается по формуле | |
| Δxои = | |
| где | |
| α — | 0,95 |
| lx — | 0,05 |
| Общая погрешность Δx измеряемой величины x рассчитывается по формуле | |
| Δx = | |
| где | |
| Δxсл — | |
| Δxои — |
| Относительная погрешность δ определяемой величины объёма параллелепипеда Vп рассчитывается по формуле | |
| δ = | |
| Абсолютная погрешность ΔVп определяемой величины объёма параллелепипеда Vп рассчитывается по формуле | |
| ΔVп = |
| Δσa = | 44,72*10-3мм |
| Δaсл = | 124,32*10-3 |
| Δaои = | 0,02375мм |
| Δa = | 0,126568мм |
| Δσb = | 0,196596мм |
| Δbсл = | 0,546537мм |
| Δbои = | 0,02375мм |
| Δb = | 0,547053мм |
| Δσc = | 0,0254951мм |
| Δcсл = | 0,0708764мм |
| Δcои = | 0,02375мм |
| Δc = | 0,0747498мм |
| 7043.46445 | |
| δ = | 0,0289832 |
| ΔVп = | 204.1421388 |
Обработка результатов измерений диаметра и высоты цилиндра.
Погрешности измерений
| Среднеквадратичная ошибка σx измеряемой величины x (диаметра либо высоты) цилиндра для случая 3-хкратного измерения величины рассчитывается по формуле | |
| Δσx = | |
| где | |
| Случайная погрешность Δxсл измеряемой величины x рассчитывается по формуле | |
| Δxсл = | |
| где | |
| σx — | 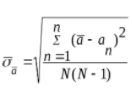 |
| tα,n — коэффициент Стьюдента для n = 3, α = 0.95 , tα,n = | 4,30 |
| Погрешность Δxои однократного измерения величины x рассчитывается по формуле | |
| Δxои = | |
| где | |
| α — | 0,95 |
| lx — | 0,05 |
| Общая погрешность Δx измеряемой величины x рассчитывается по формуле | |
| Δx = | |
| где | |
| Δxсл — | |
| Δxои — |
| Относительная погрешность δ определяемой величины объёма цилиндра Vц рассчитывается по формуле | |
| δ = | |
| Абсолютная погрешность ΔVц определяемой величины объёма цилиндра Vц рассчитывается по формуле | |
| ΔVц = |
| ΔσD = | 0,1424196мм |
| ΔDсл = | 0,612404мм |
| ΔDои = | 0,00475мм |
| ΔD = | 0,612422мм |
| Δσh = | 0,0441588мм |
| Δhсл = | 0,18988284мм |
| Δhои = | 0,00475мм |
| Δh = | 0,169942мм |
| 4753.877125 | |
| δ = | 0,0561779 |
| ΔVц = | 267.0628337 |
Окончательный результат
| (7040±200)мм | |
| (4760±270)мм |
Вывод
| Познакомиться с методами измерения линейных размеров объектов различной конфигурации (параллелепипедов и цилиндров), определения объема тела и вычисления погрешности.. |