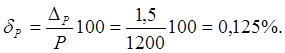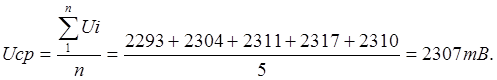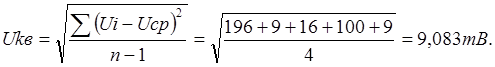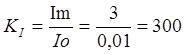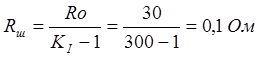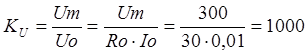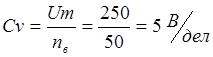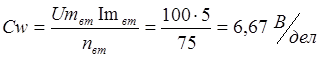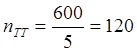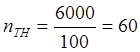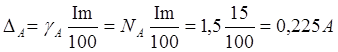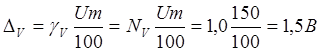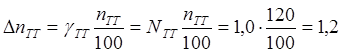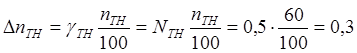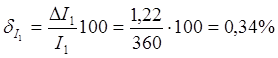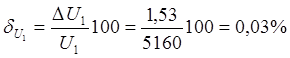Как найти погрешность измерения мощности

Лабораторная работа № 1.

Расчет погрешностей емкости с помощью коэффициента Стьюдента.

Расчет погрешности измерения мощности и сопротивления

Цели занятия:

1. Общеобразовательная – Умение решать задачи по теме погрешности.

2. Развивающая — Углубление знаний .

3. Воспитательная – Проверить сформированность качеств знаний.

Теоретическая часть

Отклонение результата измерения от истинного измеряемой величины называют погрешностью измерения.

Абсолютная погрешность измерения ΔА равна разности между результатом измерения Ах и истинным значением измеренной величины А:

ΔА = Ах – А (1)

Действительная относительная погрешность представляет собой отношение абсолютной погрешности измерения к действительному значению измеряемой величины, выраженное в процентах:

(2)

Номинальная относительная погрешность, равная отношению абсолютной погрешности к измеренному значению исследуемой величины,

т .е. к показанию прибора

(3)

Приведенная относительная погрешность измерения представляет собой отношение абсолютной погрешности измерения к максимальному значению измерительного прибора

(4)

Для приборов с двухсторонней шкалой А_макс определяется как сумма абсолютных величин положительного и отрицательного пределов измерения.

Если шкала начинается не с нуля, а с какого-то минимального значения, то А_макс равно разности между конечным и начальным значениями шкалы.

Случайными называются погрешности, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности нельзя исключить опытным путем, т. к. они возникают случайно. Для того, чтобы исключить случайные погрешности производят неоднократные измерения и определяют среднее арифметическое из полученных значений, определяемое как

,

где а₁, а₂, …, а_n – результаты отдельных измерений;

n – число измерений.

Для оценки точности результата измерений необходимо знать закон распределения случайных погрешностей, таким законом является нормальный закон Гаусса. Среднее квадратическое отклонение может быть выражено через случайные отклонения результатов наблюдения Р:

где Р₁ = а₁ – А_ср; Р₂ = а₂ – А_ср; Р_n = а_n – А_ср.

Этот способ определения доверительных интервалов справедлив толко для больших количеств измерений (20-30). Для небольшого количества измерений для определения доверительного интервала нужно пользоваться коэффициентами Стьюдента t_n, которые зависят от задаваемой доверительной вероятности Р и количества измерений n.

Для определения доверительного интервала среднюю квадратическую погрешность надо умножить на коэффициент Стьюдента. Окончательный результат измерения можно записать так:

А = Аср t_n

Контрольное задание

Задача 1. Для уменьшения влияния случайных погрешностей на результат измерения, емкость конденсатора С измерялась многократно в одинаковых условиях (таблица 1). Считая, что случайные погрешности имеют нормальный закон распределения, определить на основании заданного количества измерения (табл. 1, табл. 2):

• Действительное значение измеряемой емкости;

• Среднюю квадратическую и максимальную погрешности однократного измерения;

• Доверительный интервал для результата измерения при доверительной вероятности Р_д (табл.3).

• Имеется ли систематическая составляющая в погрешности измерения емкости и с какой доверительной вероятностью ее можно оценить, если принять в качестве действительного значения емкости значения С_ср (таб.1, таб.2).

Таблица 1

№№из мере ния	1	2	3	4	5	6	7	8	9	10
С, пФ	2430	2440	2435	2438	2439	2441	2438	2440	2441	2439
№№из мере ния	11	12	13	14	15	16	17	18	19	20
С, пФ	2500	2564	2550	2480	2450	2528	2440	2556	2562	2550

Таблица 2

№ вари анта	1	2	3	4	5	6	7	8	9	10
№№из мере ния	1-3	6-10	2-6	1-4	2-8	2-4	7-9	4-7	3-5	5-7
С0, пФ	2428	2429	2430	2432	2436	2424	2440	2441	2440	2442
Рд	0,89	0,9	0,99	0,95	0,85	0,94	0,97	0,9	0,96	0,98
№ вари анта	11	12	13	14	15	16	17	18	19	20
№№из мере ния	11-14	12-15	16-19	13-16	14-17	17-20	15-18	11-13	12-16	15-20

Примечание. Количество и номера наблюдений значений емкости для каждого варианта определяются данными таблицы 1 и 2, например для варианта 1 следует взять результаты измерений 1-3 табл.2.

Указания к решению

1. Для удобства выполнения и проверки расчетов по заданию целесообразно представить промежуточное вычисление в виде таблицы

Таблица 3

№№ пп	№№ наблюдения	Сi, пФ	Сi – Cср, пФ	(Сi – Cср)2, пФ
1 2 3 4
		Сумма Сi, пФ	Сумма Сi – Cср, пФ	Сумма (Сi – Cср)2, пФ

1. Далее определить среднеквадратическую погрешность :

1. По таблице (4) определить коэффициент Стьюдента.

2. В конце решения следует записать окончательный (с учетом округления) результат измерения в требуемой форме, например: С = 1231 12 пФ, Р

Задание 2._. Используя формулы (1-7 примера) произвести расчет абсолютной и относительной погрешностей измерения мощности и сопротивления. Расчет выполняется в соответствии с вариантами указанными в задании.

Задача 1. Для определения сопротивления резистора и мощности, выделяемой на этом сопротивлении, измерены напряжение и ток. Зная основные параметры измерительных приборов (амперметра и вольтметра), определить ошибку косвенных измерений мощности и сопротивления.

Пример. Определить абсолютную и относительную погрешности измерения мощности, выделяемой на резисторе, если известны показания вольтметра класс точности Кв = 2,5, номинальное значение Umax = 150 В, показание 120 В и амперметра – класс точности К_А = 1,0, номинальное значение шкалы 10 _МА, показания 6 _МА.

Решение:

1. Определяем мощность Р = U * I ( Вт)

2. Абсолютная ошибка измерения напряжения, В

1. Абсолютная ошибка измерения тока, _М А

1. В соответствии с таблицей абсолютная ошибка измерения мощности, Вт

Относительная ошибка

1. Формула для сопротивления R = U / I

2. 

3. Относительная погрешность

Примечание:

1. Для вычисления погрешностей измерения мощности используются формулы 1,2,3,4,

2. Для вычисления погрешностей измерения сопротивления используются формулы 2,3,5,6,7.

Формулы для выполнения контрольной работы и письменного экзамена по предмету «Электрические измерения»

1.Абсолютная погрешность измерения

ΔА = Ах – А

2. Действительная относительная погрешность

3 Номинальная относительная погрешность

4.Приведенная относительная погрешность

1. Сопротивление шунта

R_Ш = R_А / Р-1 (Ом)

6 .Добавочное сопротивление

R_ДОБ = R_V * ( Р-1) (Ом)

1. Коэффициент трансформации по току:

Кi = I ₁/ I₂

8 Коэффициент трансформации по напряжению:

К_U = U ₁ /U₂

9. Ток сети:

I_C = K_{i *} I (А)

1. Напряжение сети:

U_C = K_U* U (В)

1. Активная мощность сети:

P_C = K_i * K_U *P (Вт)

1. Реактивная мощность сети :

Q = U*I* sinφ (Вар)

1. Полная мощность сети:

S = U*I (ВА)

14. Полное сопротивление сети :

Z_C = U_C/ I_C (Ом)

15 Коэффициент мощности:

Cosφ = P_C / S_C

1. Номинальная постоянная счетчика:

С_НОМ = W _НОМ/ N_НОМ (Вт*с/об)

1. Действительная постоянная счетчика:

С = (U*I*t / N) (Вт*с/об)

18 Поправочный коэффициент:

К= С / С_НОМ

1. Относительная погрешность счетчика

Β = [(С_НОМ – С) /C_НОМ] * 100%

Введение

Основным назначением измерителей мощности ВЧ-сигналов является точное измерение абсолютных значений мощности и обеспечение точности на уровне эталонной системы. Будь то испытательная система в составе производственной линии, диагностический стенд или система для измерения параметров РЛС и средств мобильной связи в полевых условиях, измеритель мощности сохраняет за собой роль эталонного прибора, обеспечивающего прослеживаемость измерений к национальным эталонам. Это гарантирует возможность воспроизводимости измерений в другом месте и в другое время.

И хотя измерители мощности считаются наиболее точными приборами для измерения мощности, при их использовании неизбежно возникают погрешности. Многие производители измерителей мощности публикуют статьи и разрабатывают методики, помогающие анализировать погрешности, однако во всех этих материалах в большинстве случаев рассматривается лишь измерение средней мощности.

В этой статье описываются погрешности, связанные с измерением пиковой мощности. Также, для улучшения понимания этого вопроса, дано краткое описание методов измерения пиковой мощности и погрешностей измерения средней мощности.

Захват сигнала и выполнение измерений с помощью измерителя пиковой мощности

Входной интерфейс измерителя мощности состоит из чувствительного элемента, в качестве которого обычно используется диодный датчик (рисунок). Датчик преобразует мощность измеряемого сигнала в напряжение. В подсистеме захвата аналоговый сигнал напряжения фильтруется, дискретизируется и преобразуется из аналоговой формы в цифровую. На выход поступает цифровое представление входного аналогового сигнала.

Подсистема захвата имеет два сигнальных тракта: один из них измеряет только синусоидальные немодулированные сигналы (и средние значения), а второй выполняет широкополосные пиковые измерения.

Широкополосный тракт состоит из прецизионных широкополосных усилителей и дискретизатора с большим динамическим диапазоном. Огибающая сигнала отслеживается датчиком и с высокой скоростью дискретизируется непрерывно тактируемым АЦП (обычно с частотой 80 МГц и выше). Это позволяет получить оцифрованную форму огибающей мощности исследуемого сигнала в реальном масштабе времени. Для точной регистрации сигналов мощности с большим динамическим диапазоном обычно используются два параллельных АЦП со сдвигом по времени. При этом выполняется захват с упреждающим и задержанным запуском с последующим сохранением выборок. Захват контролируется системой запуска, которая определяет его временные характеристики. По завершении захвата все выборки передаются из памяти захвата в цифровой сигнальный процессор (ЦСП), который выполняет коррекцию и обработку измерений. ЦСП со встроенным ПО выполняет несколько видов обработки «сырых» оцифрованных результатов, полученных из блока захвата: коррекцию нуля/калибровку, коррекцию диапазона и полосы или математическую обработку измерений (вычисление пиковой и средней мощности, комплементарной интегральной функции распределения, трассировки).

Аналоговый тракт немодулированного сигнала измерителя мощности работает так же, как и традиционный измеритель средней мощности. Новое измерение выполняется после интегрирования хотя бы по одному периоду сигнала. Измерения фильтруются для подавления шумов и обеспечивают приемлемую скорость обновления — порядка 20/40/400 и более измерений в секунду.

Кроме того, прибор оборудован встроенным термодатчиком. Он измеряет температуру детектора и позволяет линеаризовать характеристику датчика в зависимости от его температуры.

Погрешности измерения средней мощности

В измерениях мощности, как и в любых других измерениях, существует множество источников погрешностей или ошибок. В большинстве случаев погрешность измерения складывается из трех основных составляющих: погрешности согласования датчика и источника сигнала, погрешности датчика и погрешности измерителя.

Погрешность согласования датчика и источника сигнала обычно дает самый большой вклад в общую погрешность и порождается сложением и вычитанием прямого и отраженного сигнала, что и создает стоячую волну напряжения в линии передачи. Это приводит к тому, что часть входной мощности не достигает датчика, а значит, не может быть измерена.

Вторым по значимости источником ошибок являются погрешности, связанные с датчиком мощности. Не вся мощность, достигающая датчика, будет измерена. Часть ее рассеивается в деталях датчика. Он измеряет только ту мощность, которая рассеивается на чувствительном элементе. Для коррекции неидеальной характеристики чувствительного элемента используется коэффициент калибровки.

Третий источник ошибок обусловлен погрешностями электронных компонентов измерителя мощности, такими как погрешность калибратора, погрешность коэффициента усиления усилителя и нелинейность цепей сигнального тракта. С появлением USB-датчиков мощности этот источник погрешности был исключен и считается теперь частью погрешности датчика, которая включает в себя нелинейность, погрешность коэффициента калибровки, температурную зависимость и погрешности, связанные с внутренними процессами калибровки.

При измерении сигналов малого уровня появляются дополнительные источники погрешности, такие как установка нуля, дрейф нуля и шум. Эти ошибки можно проанализировать и объединить с помощью метода GUM (руководство по расчету погрешностей измерения) для получения общей погрешности измерения (табл. 1). Метод GUM принят всеми основными государственными институтами метрологии и метрологическими лабораториями.

Таблица 1. Расчетная погрешность измерения USB-датчика пиковой и средней мощности Agilent U2021XA при уровне –10 дБм и частоте 1 ГГц при выполнении измерений средней мощности с автоматическим запуском

Источник погрешности	Значение,  ±%	Распределение вероятностей	Делитель	Стандартная погрешность (k = 1), %
Рассогласование источника-датчика (КСВ датчика = 1,2, КСВ источника = 1,25)	1,01	U-образное	√2	0,71
Шум измерения с автоматическим запуском (100 нВт)	0,1	Функция Гаусса	2	0,05
Дрейф нуля (100 нВт)	0,1	Функция Гаусса	2	0,05
Установка нуля (200 нВт)	0,2	Функция Гаусса	2	0,1
Погрешность калибровки датчика	4	Функция Гаусса	2	2
Комбинированная стандартная погрешность при k = 1	2,13
Расширенная погрешность при k = 2	4,25

Погрешности измерения пиковой мощности

В сущности, пиковая мощность — это средняя мощность за малый период времени. Приведенный выше пример расчета погрешностей измерения средней мощности в равной степени применим и к пиковой мощности. Основная разница заключается в шуме. Поскольку в измерениях пиковой мощности принимает участие только одна выборка, нужно использовать параметр «шум одной выборки». Если измерить среднюю мощность за определенный период времени (стробируемое измерение), то можно рассчитать шум за этот период времени. С ростом интервала измерения шум будет снижаться благодаря эффекту усреднения:

Для измерителя мощности с интервалом выборки 12,5 нс и шумом одной выборки 2,5 мкВт шум в интервале 5 мкс будет равен 125 нВт. При измерении пиковой мощности в том же интервале можно просто использовать шум одной выборки, который в данном случае равен 2,5 мкВт (табл. 2).

Таблица 2. Расчетная погрешность измерения USB-датчика пиковой и средней мощности Agilent U2021XA при уровне –10 дБм и частоте 1 ГГц при выполнении стробируемых измерений средней и пиковой мощности

Расчетная погрешность измерения пиковой мощности	Расчетная погрешность стробируемого измерения средней мощности в интервале 5 мкс
Источник погрешности	Значение, ±%	Распределение вероятностей	Делитель	Стандартная погрешность  (k = 1), %	Источник погрешности	Значение, ±%	Распределение вероятностей	Делитель	Стандартная погрешность (k = 1), %
Рассогласование источника-датчика (КСВ датчика = 1,2, КСВ источника = 1,25)	1,01	U-образное	√2	0,71	Рассогласование источника-датчика (КСВ датчика = 1,2, КСВ источника = 1,25)	1,01	U-образное	√2	0,71
Шум одной выборки при 12,5 нс (2,5 мкВт)	2,5	Функция Гаусса	2	1,25	Шум одной выборки в интервале 125 мкс (125 нВт)	0,125	Функция Гаусса	2	0,0625
Дрейф нуля (100 нВт)	0,1	Функция Гаусса	2	0,05	Дрейф нуля (100 нВт)	0,1	Функция Гаусса	2	0,05
Установка нуля (200 нВт)	0,2	Функция Гаусса	2	0,1	Установка нуля (200 нВт)	0,2	Функция Гаусса	2	0,1
Погрешность калибровки датчика	4	Функция Гаусса	2	2	Погрешность калибровки датчика	4,	Функция Гаусса	2	2
Комбинированная стандартная погрешность при k = 1	2,47	Комбинированная стандартная погрешность при k = 1	2,13
Расширенная погрешность при k = 2	4,93	Расширенная погрешность при k = 2	4,25

Заключение

Измерители и датчики мощности ВЧ-сигнала являются важными приборами, применяемыми для обеспечения отслеживаемости результатов измерений на уровне эталонной системы, что позволяет выполнять точные измерения абсолютной мощности ВЧ-сигналов. Методы, используемые для калибровки измерителей и датчиков мощности, хорошо известны и обычно основаны на методе GUM. Этот метод можно применять к измерениям средней и пиковой мощности. Основная разница между этими измерениями заключается в типе шума. В измерениях средней мощности используется шум несинхронных измерений с автоматическим запуском, тогда как в измерениях пиковой мощности или стробируемых измерениях средней мощности используется шум на одну выборку. Компания Agilent предлагает широкий выбор измерителей и датчиков пиковой и средней мощности. Для всех измерителей и датчиков мощности Agilent имеются калькуляторы погрешностей, которые можно загрузить со страницы www.agilent.com/find/uncertainty_calculators.

Задача 1

Для
определения мощности в цепи постоянного тока были измерены напряжение сети U вольтметром класса точности N_B
с пределом измерений U_m, ток I амперметром класса точности N_a
с пределом измерений I_m. Определить
мощность, потребляемую приёмником, а также относительную и абсолютную
погрешности её определения.

Дано:

Найти:

Решение:

1)  Найдем
мощность, потребляемую приемником

2)  Класс
точности определяет приведенную погрешность

3)  Найдем
абсолютную погрешность измерения тока и напряжения

,

.

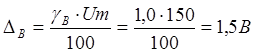
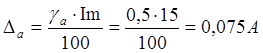
4)  Найдем
абсолютную погрешность измерения мощности при косвенном измерении

5)  Найдем
относительную погрешность измерения мощности

6)  Доверительный
интервал результата измерения с вероятностью .

Задача 2

Проведено пять
независимых наблюдений одного и того же напряжения U.
Найти результат измерения и доверительную вероятность того, что абсолютная
погрешность измерения не превышает по модулю DU. Систематической погрешностью можно пренебречь.

Дано:

Найти:

Решение:

1)  Определим
среднее арифметическое результатов измерения

2)  Определяем
среднее квадратичное результатов измерения

3)  Для
определения интервала и вероятности пользуются распределением Стьюдента, где
доверительный интервал равняется     , где

— коэффициент Стьюдента,

 — среднее квадратичное отклонение
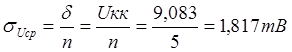
результата измерения.

4)  Находим
доверительный интервал

5)  Результат
измерения

Задача 3

Обмотка
магнитоэлектрического измерительного механизма имеет сопротивление R_O  и рассчитана на предельный длительный ток I_O, при котором подвижная часть получает
наибольшее отклонение. Каким образом на базе указанного измерительного
механизма сделать амперметр с пределом измерений I_m
и вольтметр с пределом измерений U_m?

Дано:

Найти: ,

Решение:

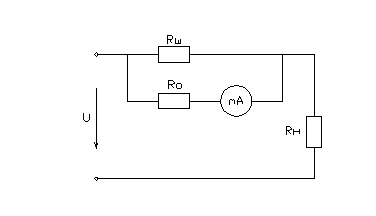
1)  Расчет
измерительной цепи амперметра

1.1 
Определяем коэффициент расширения пределов измерения по току

1.2     Определяем сопротивление
шунта

1.3 
 Схема измерительной цепи

2)  Расчет
цепи вольтметра

2.1 Определяем коэффициент
расширения пределов измерения по напряжению

2.2  Определяем добавочное
сопротивление

2.3 
Схема включения

Задача 4

Определить
цену деления измерительных приборов:

1) амперметра, имеющего на шкале n_a делений и предел измерения I_m;

2)вольтметра, имеющего n_в делений шкалы и предел измерения U_m;

3) ваттметра, имеющего n_ВТ делений шкалы и пределы измерений по току I_{m ВТ} и напряжению U_m
ВТ.

Дано:

Найти:

Решение:

1) Цена деления
амперметра

2) Цена деления
вольтметра

3) Цена
деления ваттметра

Задача 5

У вольтметра и
амперметра с пределами измерений U_m и I_m, включенных соответственно через измерительные
трансформаторы напряжения 6000/100 и тока 600/5, отчёт по шкале составил U₂ и I₂.
Определить напряжение и ток в сети, а также предел допускаемой абсолютной и
относительной погрешностей измерения, если известны класс точности приборов N_a и N_в и
измерительных трансформаторов N_тн и N_тт. Привести схему измерения.

Дано:

Найти:

Решение:

1) Определим
коэффициенты трансформации трансформатора напряжения и тока

2) Определим
ток и напряжение в сети

3) Определим
абсолютные погрешности амперметра и вольтметра

4) Определяем
абсолютные погрешности коэффициентов трансформации трансформатора тока и
напряжения

5) Результирующие
абсолютные погрешности измерения тока и напряжения равны

6)
Относительные погрешности измерения тока и напряжения

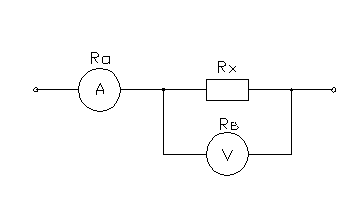
Задача 6

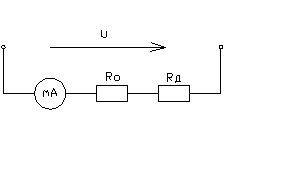
Определить
относительные погрешности измерения сопротивления R_x
в цепи постоянного тока с помощью амперметра и вольтметра при подключении их
двумя возможными способами. Сопротивление амперметра – R_a,
вольтметра – R_в. Сделать вывод о
целесообразности использования той или иной схемы.

Дано:

Найти: .

Решение:

Принципиальные
схемы

 

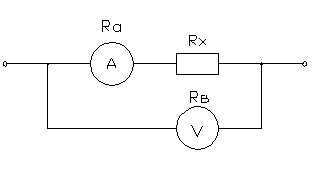
Схема
1                                              Схема 2

1)  Для
схемы включения 1.

1.1. 
Измеренное сопротивление.

1.2. 
Определяем абсолютную погрешность.

1.3. 
Определяем относительную погрешность.

Погрешность — измерение — мощность

Cтраница 3

В общем случае, когда результат измерения определяется алгебраической суммой показаний двух или трех ваттметров ( рис. 12.4, а и в, 12.5), для определения относительного значения погрешности измерения мощности необходимо определить абсолютные погрешности измерения мощности каждым ваттметром ( как для однофазной мощности) и их сумму разделить на результат измерения. При определении относительного значения погрешности метода для каждой из схем, представленных на рис. 12.4 и 12.5, необходимо определить мощность, которую потребляют вольтметры и цепи напряжения ваттметров, и разделить ее на результат измерения.
 [31]

Результат измерения мощности рассматриваемым способом может быть уточнен путем внесения поправки. После этого погрешность измерения мощности, как косвенного измерения, может быть определена через погрешности амперметра и вольтметра.
 [32]

Применение направленных ответвителей с градуированными аттенюаторами позволяет измерять методом терморезистора проходящую мощность практически любой величины. Погрешность измерения складывается из погрешности измерения мощности и неточности определения переходного ослабления направленного ответвителя.
 [33]

Применение направленных ответвителей с градуированными аттенюатэрами позволяет измерять методом терморезистора практически любую проходящую мощность. Погрешность измерения складывается из погрешности измерения мощности и неточности определения переходного ослабления направленного отвег-вителя.
 [35]

Если нужно знать значение вносимого ослабления в диапазоне частот, указанное измерение повторяют на нескольких частотах при постоянном выходном напряжении генератора. Погрешность измерения зависит только от погрешности измерения мощности. Измерение ослабления методом отношения напряжений выполняется в том же порядке.
 [37]

При напряжениях менее ПО В погрешность измерения мощности увеличивается, и тогда ее следует учитывать, вводя в результат соответствующие поправки.
 [39]

U, ( 7Ф, ил, 1, 7ф, / л — измеренные значения мощности, напряжений и токов. Погрешность измерения cos p состоит из погрешностей измерения мощности, напряжения и тока.
 [40]

Таким образом, равенство температур термистора говорит о равенстве рассеиваемых в нем мощностей, но при строгом подходе не говорит о равенстве полных мощностей — измеряемой и постоянного тока. Очевидно, если не учитывать рассматриваемого явления, возникает погрешность измерений мощности. Чтобы погрешности измерения не было, в термисторе должны полностью рассеиваться обе эти мощности или, по крайней мере, равные доли от каждой из полных мощностей.
 [41]

Интересной особенностью прибора является то, что вследствие равенства коэффициентов преобразования входного преобразователя / Свх Л / тс и обратного Р lrnc суммарная погрешность этих преобразователей равна нулю. Общая погрешность прибора определяется только погрешностью звеньев прямой цепи, уменьшенной в / СР раз, и погрешностью измерения мощности Р I-R. Таким образом, описанный прибор обладает очень высокой точностью. Проволочный термоанемометр R ( см. § 6 — 5) включен в одно из плеч измерительного моста. В измерительную диагональ моста включен усилитель, выходной ток / которого питает мост.
 [43]

Амплитуда видеоимпульсов при работе на квадратичном участке характеристики диода пропорциональна мощности измеряемых радиоимпульсов. Благодаря использованию нулевой точки вольт-амперной характеристики диода в режиме компенсации значительно уменьшается влияние температуры и разбросов характеристик от детектора к детектору на погрешность измерения мощности. Динамический диапазон, так же как и частотный, в основном определяется характеристиками применяемых диодов.
 [45]

Страницы:  

   1

   2

   3

   4

Лабораторная работа № 1.

Расчет погрешностей емкости с
помощью коэффициента Стьюдента.

Расчет погрешности измерения
мощности и сопротивления

Цели занятия:

1.     Общеобразовательная – Умение решать задачи по
теме погрешности.

2.     Развивающая —  Углубление знаний .

3.     Воспитательная – Проверить сформированность
качеств знаний.

Теоретическая часть

Отклонение результата измерения от истинного измеряемой
величины называют погрешностью измерения.

Абсолютная погрешность измерения ΔА равна разности
между результатом измерения Ах и истинным значением измеренной величины А:

ΔА = Ах – А                                                                                      
                          (1)

Действительная относительная погрешность  представляет собой отношение абсолютной
погрешности измерения к действительному значению измеряемой величины,
выраженное в процентах:

                                                                                                                  
       (2)

Номинальная относительная погрешность, равная отношению абсолютной погрешности к измеренному значению
исследуемой величины,

т
.е. к показанию прибора

                                                                      
                                               (3)

Приведенная относительная погрешность измерения представляет собой отношение абсолютной погрешности
измерения к максимальному значению измерительного прибора

                                                                                                          (4)

Для приборов с двухсторонней шкалой А_макс
определяется как сумма абсолютных величин положительного и отрицательного
пределов измерения.

Если шкала начинается не с нуля, а с какого-то минимального
значения, то А_макс равно разности между конечным и начальным
значениями шкалы.

Случайными называются
погрешности, изменяющиеся случайным образом при повторных измерениях одной и
той же величины. Случайные погрешности нельзя исключить опытным путем, т. к.
они возникают случайно. Для того, чтобы исключить случайные погрешности
производят неоднократные измерения и определяют среднее арифметическое из
полученных значений, определяемое как

 ,

где
а₁, а₂, …, а_n –
результаты отдельных измерений;

n
– число измерений.

            Для
оценки точности результата измерений необходимо знать закон распределения
случайных погрешностей, таким законом является нормальный закон Гаусса. Среднее
квадратическое отклонение может быть выражено через случайные отклонения
результатов наблюдения Р:

где
Р₁ = а₁ – А_ср; Р₂ = а₂ –
А_ср; Р_n = а_n – А_ср.

            Этот
способ определения доверительных интервалов справедлив толко для больших
количеств измерений (>20-30). Для небольшого количества измерений для
определения доверительного интервала нужно пользоваться коэффициентами
Стьюдента t_n, которые зависят от задаваемой
доверительной вероятности Р и количества измерений n.

            Для
определения доверительного интервала среднюю квадратическую погрешность  надо умножить на коэффициент Стьюдента.
Окончательный результат измерения можно записать так:

А
= Аср  t_n

Контрольное задание

Задача 1. Для уменьшения
влияния случайных погрешностей на результат измерения, емкость конденсатора С
измерялась многократно в одинаковых условиях (таблица 1). Считая, что случайные
погрешности имеют нормальный закон распределения, определить на основании
заданного количества измерения (табл. 1, табл. 2):

• Действительное
  значение измеряемой емкости;
• Среднюю
  квадратическую и максимальную погрешности однократного измерения;
• Доверительный
  интервал для результата измерения при доверительной вероятности Р_д
  (табл.3).
• Имеется
  ли систематическая составляющая в погрешности измерения емкости и с какой
  доверительной вероятностью ее можно оценить, если принять в качестве
  действительного значения емкости значения С_ср  (таб.1, таб.2).

Таблица
1

№№из мере ния	1	2	3	4	5	6	7	8	9	10
С, пФ	2430	2440	2435	2438	2439	2441	2438	2440	2441	2439
№№из мере ния	11	12	13	14	15	16	17	18	19	20
С, пФ	2500	2564	2550	2480	2450	2528	2440	2556	2562	2550

Таблица
2

№ вари анта	1	2	3	4	5	6	7	8	9	10
№№из мере ния	1-3	6-10	2-6	1-4	2-8	2-4	7-9	4-7	3-5	5-7
С0, пФ	2428	2429	2430	2432	2436	2424	2440	2441	2440	2442
Рд	0,89	0,9	0,99	0,95	0,85	0,94	0,97	0,9	0,96	0,98
№ вари анта	11	12	13	14	15	16	17	18	19	20
№№из мере ния	11-14	12-15	16-19	13-16	14-17	17-20	15-18	11-13	12-16	15-20

Примечание.
Количество и номера наблюдений значений емкости для каждого варианта
определяются данными таблицы 1 и 2, например для варианта 1 следует взять
результаты измерений 1-3 табл.2.

Указания к решению

1.     
Для удобства выполнения и проверки расчетов по
заданию целесообразно представить промежуточное вычисление в виде таблицы

Таблица
3

№№ пп	№№ наблюдения	Сi, пФ	Сi – Cср, пФ	(Сi – Cср)2, пФ
1 2 3 4
		Сумма Сi, пФ	Сумма Сi – Cср, пФ	Сумма (Сi – Cср)2, пФ

2.     
Далее определить среднеквадратическую погрешность :

3.     
По таблице  (4) определить коэффициент Стьюдента.

4.     
В конце решения следует записать окончательный  (с
учетом округления) результат измерения в требуемой форме, например: С = 1231 12 пФ, Р

Задание
2._. Используя
формулы (1-7 примера) произвести расчет абсолютной и относительной погрешностей
измерения мощности и сопротивления. Расчет выполняется в соответствии с
вариантами указанными в задании.

Задача 1. Для определения
сопротивления резистора и мощности, выделяемой на этом сопротивлении, измерены
напряжение и ток. Зная основные параметры измерительных приборов (амперметра и
вольтметра), определить ошибку косвенных измерений  мощности и сопротивления.

Пример. Определить абсолютную и
относительную погрешности измерения мощности, выделяемой на резисторе, если известны
показания вольтметра класс точности Кв = 2,5, номинальное значение Umax = 150 В, показание 120 В и амперметра – класс точности К_А =
1,0, номинальное значение шкалы 10 _МА, показания 6 _МА.

Решение:

1. Определяем
   мощность Р = U * I  ( Вт)
2. Абсолютная
   ошибка измерения напряжения, В

1. Абсолютная
   ошибка измерения тока, _М А

1. В
   соответствии с таблицей абсолютная ошибка измерения мощности, Вт

            Относительная
ошибка

1. Формула
   для сопротивления R = U / I
2. 
3. Относительная
   погрешность

  

Примечание:

1.     
Для  вычисления погрешностей измерения мощности
используются формулы 1,2,3,4,

2.     
Для вычисления погрешностей измерения сопротивления
используются формулы 2,3,5,6,7.

Формулы для выполнения
контрольной работы и письменного экзамена по предмету «Электрические измерения»

1.Абсолютная погрешность измерения

ΔА = Ах – А

2. Действительная относительная погрешность

          3    Номинальная относительная погрешность

          4.Приведенная относительная погрешность

5.     
Сопротивление шунта

R_Ш = R_А / Р-1  (Ом)

6 .Добавочное сопротивление

R_ДОБ = R_V * ( Р-1)  (Ом)

7       
Коэффициент трансформации по току:

Кi = I ₁/ I₂

8 Коэффициент трансформации по напряжению:

К_U = U ₁ /U₂

9. Ток сети:

I_C = K_{i *} I (А)

10   
Напряжение сети:

U_C = K_U* U (В)

11   
Активная мощность сети:

P_C = K_i * K_U *P (Вт)

12   
Реактивная мощность сети :

Q = U*I* sinφ (Вар)

13   
Полная мощность сети:

S = U*I (ВА)

14. Полное сопротивление
сети :

Z_C  = U_C/ I_C (Ом)

15 Коэффициент мощности:

Cosφ = P_C  / S_C

16   
Номинальная постоянная счетчика:

С_НОМ = W _НОМ/ N_НОМ (Вт*с/об)

17   
Действительная постоянная счетчика:

С = (U*I*t / N) (Вт*с/об)

18 Поправочный коэффициент:

К= С / С_НОМ

18   
Относительная погрешность счетчика

Β = [(С_НОМ – С) /C_НОМ] * 100%