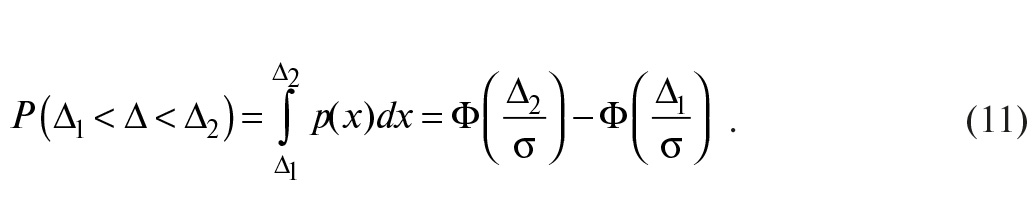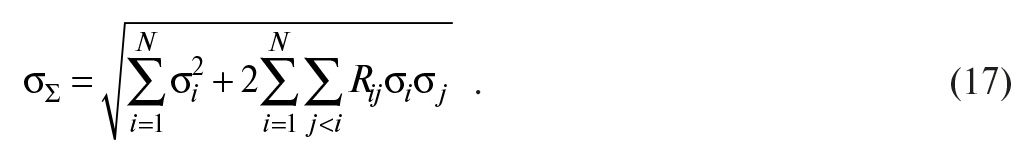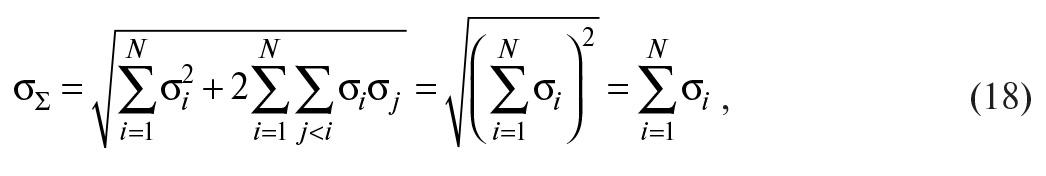Погрешность измерений
Неотъемлемой частью любого измерения является погрешность измерений. С развитием приборостроения и методик измерений человечество стремиться снизить влияние данного явления на конечный результат измерений. Предлагаю более детально разобраться в вопросе, что же это такое погрешность измерений.
Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерений представляет собой сумму погрешностей, каждая из которых имеет свою причину.
По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные
Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины. Она определяется выражением.
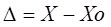
Поскольку истинное значение измеряемой величины остается неизвестным, на практике пользуются лишь приближенной оценкой абсолютной погрешности измерения, определяемой выражением
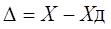
Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины:
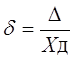
По закономерности появления погрешности измерения подразделяются на систематические, прогрессирующие, и случайные .
Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.
Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.
Систематические и прогрессирующие погрешности средств измерений вызываются:
- первые — погрешностью градуировки шкалы или ее небольшим сдвигом;
- вторые — старением элементов средства измерения.
Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.
Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.
По происхождению различают инструментальные и методические погрешности средств измерений.
Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.
Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.
Погрешности средств измерений.
Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины:
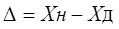
Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины:
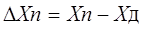
Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному
(действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).
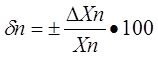
Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).
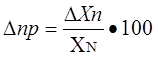
Предел допускаемой погрешности средств измерений – наибольшая без учета знака погрешность средства измерений, при которой оно может быть признано и допущено к применению. Данное определение применяют к основной и дополнительной погрешности, а также к вариации показаний. Поскольку свойства средств измерений зависят от внешних условий, их погрешности также зависят от этих условий, поэтому погрешности средств измерений принято делить на основные и дополнительные .
Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.
Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.
Погрешности средств измерений подразделяются также на статические и динамические .
Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.
Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.
Факторы влияющие на погрешность измерений.
Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений
Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.
Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.
Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.
Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.
Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.
Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.
Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.
Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.
Шумы — любой сигнал не несущий полезной информации.
Источник
Погрешности измерения датчиков КИП. Классы точности
Основной качественной характеристикой любого датчика КИП является погрешность измерения контролируемого параметра. Погрешность измерения прибора это величина расхождения между тем, что показал (измерил) датчик КИП и тем, что есть на самом деле. Погрешность измерения для каждого конкретного типа датчика указывается в сопроводительной документации (паспорт, инструкция по эксплуатации, методика поверки), которая поставляется вместе с данным датчиком.
По форме представления погрешности делятся на абсолютную, относительную и приведенную погрешности.
Абсолютная погрешность – это разница между измеренной датчиком величиной Хизм и действительным значением Хд этой величины.
Действительное значение Хд измеряемой величины это найденное экспериментально значение измеряемой величины максимально близкое к ее истинному значению. Говоря простым языком действительное значение Хд это значение, измеренное эталонным прибором, или сгенерированное калибратором или задатчиком высокого класса точности. Абсолютная погрешность выражается в тех же единицах измерения, что и измеряемая величина (например, в м3/ч, мА, МПа и т.п.). Так как измеренная величина может оказаться как больше, так и меньше ее действительного значения, то погрешность измерения может быть как со знаком плюс (показания прибора завышены), так и со знаком минус (прибор занижает).
Относительная погрешность – это отношение абсолютной погрешности измерения Δ к действительному значению Хд измеряемой величины.
Относительная погрешность выражается в процентах, либо является безразмерной величиной, а также может принимать как положительные, так и отрицательные значения.
Приведенная погрешность – это отношение абсолютной погрешности измерения Δ к нормирующему значению Хn, постоянному во всем диапазоне измерения или его части.
Нормирующее значение Хn зависит от типа шкалы датчика КИП:
- Если шкала датчика односторонняя и нижний предел измерения равен нулю (например, шкала датчика от 0 до 150 м3/ч), то Хn принимается равным верхнему пределу измерения (в нашем случае Хn = 150 м3/ч).
- Если шкала датчика односторонняя, но нижний предел измерения не равен нулю (например, шкала датчика от 30 до 150 м3/ч), то Хn принимается равным разности верхнего и нижнего пределов измерения (в нашем случае Хn = 150-30 = 120 м3/ч).
- Если шкала датчика двухсторонняя (например, от -50 до +150 ˚С), то Хn равно ширине диапазона измерения датчика (в нашем случае Хn = 50+150 = 200 ˚С).
Приведенная погрешность выражается в процентах, либо является безразмерной величиной, а также может принимать как положительные, так и отрицательные значения.
Довольно часто в описании на тот или иной датчик указывается не только диапазон измерения, например, от 0 до 50 мг/м3, но и диапазон показаний, например, от 0 до 100 мг/м3. Приведенная погрешность в этом случае нормируется к концу диапазона измерения, то есть к 50 мг/м3, а в диапазоне показаний от 50 до 100 мг/м3 погрешность измерения датчика не определена вовсе – фактически датчик может показать все что угодно и иметь любую погрешность измерения. Диапазон измерения датчика может быть разбит на несколько измерительных поддиапазонов, для каждого из которых может быть определена своя погрешность как по величине, так и по форме представления. При этом при поверке таких датчиков для каждого поддиапазона могут применяться свои образцовые средства измерения, перечень которых указан в методике поверки на данный прибор.
У некоторых приборов в паспортах вместо погрешности измерения указывают класс точности. К таким приборам относятся механические манометры, показывающие биметаллические термометры, термостаты, указатели расхода, стрелочные амперметры и вольтметры для щитового монтажа и т.п. Класс точности – это обобщенная характеристика средств измерений, определяемая пределами допускаемых основных и дополнительных погрешностей, а также рядом других свойств, влияющих на точность осуществляемых с их помощью измерений. При этом класс точности не является непосредственной характеристикой точности измерений, выполняемых этим прибором, он лишь указывает на возможную инструментальную составляющую погрешности измерения. Класс точности прибора наноситься на его шкалу или корпус по ГОСТ 8.401-80.
При присвоении прибору класса точности он выбирается из ряда 1·10 n ; 1,5·10 n ; (1,6·10 n ); 2·10 n ; 2,5·10 n ; (3·10 n ); 4·10 n ; 5·10 n ; 6·10 n ; (где n =1, 0, -1, -2, и т. д.). Значения классов точности, указанные в скобках, не устанавливают для вновь разрабатываемых средств измерений.
Определение погрешности измерения датчиков выполняют, например, при их периодической поверке и калибровке. С помощью различных задатчиков и калибраторов с высокой точностью генерируют определенные значения той или иной физической величины и сличают показания поверяемого датчика с показаниями образцового средства измерения, на которое подается то же самое значение физической величины. Причем погрешность измерения датчика контролируется как при прямом ходе (увеличение измеряемой физической величины от минимума до максимума шкалы), так и при обратном ходе (уменьшение измеряемой величины от максимума до минимума шкалы). Это связано с тем, что из-за упругих свойств чувствительного элемента датчика (мембрана датчика давления), различной интенсивности протекания химических реакций (электрохимический сенсор), тепловой инерции и т.п. показания датчика будут различны в зависимости от того, как меняется воздействующая на датчик физическая величина: уменьшается или увеличивается.
Довольно часто в соответствии с методикой поверки отсчет показаний датчика при поверке нужно выполнять не по его дисплею или шкале, а по величине выходного сигнала, например, по величине выходного тока токового выхода 4…20 мА.
У поверяемого датчика давления со шкалой измерения от 0 до 250 mbar основная относительная погрешность измерения во всем диапазоне измерений равна 5%. Датчик имеет токовый выход 4…20 мА. На датчик калибратором подано давление 125 mbar, при этом его выходной сигнал равен 12,62 мА. Необходимо определить укладываются ли показания датчика в допустимые пределы.
Во-первых, необходимо вычислить каким должен быть выходной ток датчика Iвых.т при давлении Рт = 125 mbar.
Iвых.т = Iш.вых.мин + ((Iш.вых.макс – Iш.вых.мин)/(Рш.макс – Рш.мин))*Рт
где Iвых.т – выходной ток датчика при заданном давлении 125 mbar, мА.
Iш.вых.мин – минимальный выходной ток датчика, мА. Для датчика с выходом 4…20 мА Iш.вых.мин = 4 мА, для датчика с выходом 0…5 или 0…20 мА Iш.вых.мин = 0.
Iш.вых.макс — максимальный выходной ток датчика, мА. Для датчика с выходом 0…20 или 4…20 мА Iш.вых.макс = 20 мА, для датчика с выходом 0…5 мА Iш.вых.макс = 5 мА.
Рш.макс – максимум шкалы датчика давления, mbar. Рш.макс = 250 mbar.
Рш.мин – минимум шкалы датчика давления, mbar. Рш.мин = 0 mbar.
Рт – поданное с калибратора на датчик давление, mbar. Рт = 125 mbar.
Подставив известные значения получим:
То есть при поданном на датчик давлении равном 125 mbar на его токовом выходе должно быть 12 мА. Считаем, в каких пределах может изменяться расчетное значение выходного тока, учитывая, что основная относительная погрешность измерения равна ± 5%.
То есть при поданном на датчик давлении равном 125 mbar на его токовом выходе выходной сигнал должен быть в пределах от 11,40 до 12,60 мА. По условию задачи мы имеем выходной сигнал 12,62 мА, значит наш датчик не уложился в определенную производителем погрешность измерения и требует настройки.
Основная относительная погрешность измерения нашего датчика равна:
Поверка и калибровка приборов КИП должна выполнятся при нормальных условиях окружающей среды по атмосферному давлению, влажности и температуре и при номинальном напряжении питания датчика, так как более высокие или низкие температура и напряжение питания могут привезти к появлению дополнительной погрешности измерения. Условия проведения поверки указываются в методике поверки. Приборы, погрешность измерения которых не уложилась в установленные методикой поверки рамки либо заново регулируют и настраивают, после чего они повторно проходят поверку, либо, если настройка не принесла результатов, например, из-за старения или чрезмерной деформации сенсора, ремонтируются. Если ремонт невозможен то приборы бракуются и выводятся из эксплуатации.
Если все же приборы удалось отремонтировать то они подвергаются уже не периодической, а первичной поверке с выполнением всех изложенных в методике поверки пунктов для данного вида поверки. В некоторых случаях прибор специально подвергают незначительному ремонту (с отметкой в паспорте) так как по методике поверки выполнить первичную поверку оказывается существенно легче и дешевле чем периодическую, из-за различий в наборе образцовых средств измерения, которые используются при периодической и первичной поверках.
Для закрепления и проверки полученных знаний рекомендую выполнить тестовое задание.
Источник
Погрешность
средства измерений
(англ. error (of indication) of a measuring instrument) –
разность между показанием средства
измерений и истинным (действительным)
значением измеряемой физической
величины.
Систематическая
погрешность средства измерений
(англ. bias error of a measuring instrument) – составляющая
погрешности средства измерений,
принимаемая за постоянную или закономерную
изменяющуюся. Примечание. Систематическая
погрешность данного средства измерений,
как правило, будет отличаться от
систематической погрешности другого
экземпляра средства измерений этого
же типа, вследствие чего для группы
однотипных средств измерений
систематическая погрешность может
иногда рассматриваться как случайная
погрешность.
Случайная
погрешность средства измерений
(англ. repeatability error of a measuring instrument) –
составляющая погрешности средства
измерений, изменяющаяся случайным
образом.
Абсолютная
погрешность средства измерений
– погрешность средства измерений,
выраженная в единицах измеряемой
физической величины.
Относительная
погрешность средства измерений –
погрешность средства измерений,
выраженная отношением абсолютной
погрешности средства измерений к
результату измерений или к действительному
значению измеренной физической величины.
Приведенная
погрешность средства измерений
(англ. reducial error of a measuring instrument) –
относительная погрешность, выраженная
отношением абсолютной погрешности
средства измерений к условно принятому
значению величины, постоянному во всем
диапазоне измерений или в части диапазона.
Примечания:
-
Условно
принятое значение величины называют
нормирующим значением. Часто за
нормирующее значение принимают верхний
предел измерений. -
Приведенную
погрешность обычно выражают в процентах.
Основная
погрешность средства измерений (англ.
intrinsic error of a measuring instrument) – погрешность
средства измерений, применяемого в
нормальных условиях.
Дополнительная
погрешность средства измерений (англ.
complementary error of a measuring instrument) – составляющая
погрешности средства измерений,
возникающая дополнительно к основной
погрешности вследствие отклонения
какой-либо из влияющих величин от
нормального ее значения или вследствие
ее выхода за пределы нормальной области
значений.
Статическая
погрешность средства измерений
– погрешность средства измерений,
применяемого при измерении физической
величины, принимаемой за неизменную.
Динамическая
погрешность средства измерений
– погрешность средства измерений,
возникающая при измерении изменяющейся
(в процессе измерений) физической
величины.
Погрешность
меры
– разность между номинальным значением
меры и действительным значением
воспроизводимой ею величины.
Стабильность
средства измерений
(англ. stability) – качественная характеристика
средства измерений, отражающая
неизменность во времени его метрологических
характеристик. Примечание. В качестве
количественной оценки стабильности
служит нестабильность средства измерений.
Нестабильность
средства измерений
– изменение метрологических характеристик
средства измерений за установленный
интервал времени. Примечания:
-
Для
ряда средств измерений, особенно
некоторых мер, нестабильность является
одной из важнейших точностных
характеристик. Для нормальных элементов
обычно нестабильность устанавливается
за год. -
Нестабильность
определяют на основании длительных
исследований средства измерений, при
этом полезны периодические сличения
с более стабильными средствами измерений.
Точность
средства измерений
(англ. accuracy of a measuring instrument) – характеристика
качества средства измерений, отражающая
близость его погрешности к нулю.
Примечание. Считается, что чем меньше
погрешность, тем точнее средство
измерений.
Класс
точности средств измерений
(англ. accuracy class) – обобщенная характеристика
данного типа средств измерений, как
правило, отражающая уровень их точности,
выражаемая пределами допускаемых
основной и дополнительных погрешностей,
а также другими характеристиками,
влияющими на точность. Примечания:
-
Класс
точности дает возможность судить о
том, в каких пределах находится
погрешность средства измерений одного
типа, но не является непосредственным
показателем точности измерений,
выполняемых с помощью каждого из этих
средств. Это важно при выборе средств
измерений в зависимости от заданной
точности измерений. -
Класс
точности средств измерений конкретного
типа устанавливают в стандартах
технических требований (условий) или
в других нормативных документах.
Предел
допускаемой погрешности средства
измерений
– наибольшее значение погрешности
средств измерений, устанавливаемое
нормативным документом для данного
типа средств измерений, при котором оно
еще признается годным к применению.
Примечания:
-
При
превышении установленного предела
погрешности средство измерений
признается негодным для применения (в
данном классе точности). -
Обычно
устанавливают пределы допускаемой
погрешности, то есть границы зоны, за
которую не должна выходить погрешность.
Пример.
Для 100-миллиметровой концевой меры длины
1-го класса точности пределы допускаемой
погрешности +/- 50 мкм.
Нормируемые
метрологические характеристики типа
средства измерений
– совокупность метрологических
характеристик данного типа средств
измерений, устанавливаемая нормативными
документами на средства измерений.
Точностные
характеристики средства измерений
– совокупность метрологических
характеристик средства измерений,
влияющих на погрешность измерения.
Примечание. К точностным характеристикам
относят погрешность средства измерений,
нестабильность, порог чувствительности,
дрейф нуля и др.
На точность датчиков
влияют такие характеристики как:
-
гистерезис,
-
мертвая
зона, -
параметры калибровки,
-
повторяемость
датчиков от партии к партии, -
воспроизводимость
погрешностей.
Предельно допустимые погрешности
обычно соответствуют самым худшим
рабочим характеристикам датчиков. При
более корректном проведении калибровки
(например, при проведении калибровки
на большем количестве точек),
калибровочная кривая проходит
ближе к реальным передаточным функциям,
что означает повышение точности
измерений. На практике пределы допустимых
погрешностей устанавливаются не вокруг
идеальной передаточной функции, а
относительно калибровочной кривой.
Допустимые пределы становятся меньше,
если они не включают в себя погрешности,
связанные с различиями датчиков от
партии к партии, а также когда они
относятся только к одному специально
откалиброванному датчику. Все это
повышает точность измерений, однако
значительно повышает стоимость, из-за
чего во многих ситуациях эти методы не
могут быть применены.
Погрешность датчиков
представляют:
-
непосредственно
в единицах измеряемой величины, -
в
процентах от значения максимального
входного сигнала, -
в
единицах выходного сигнала.
Например,
погрешность пьезорезистивного датчика
давления с диапазоном входных сигналов
100 кПа и диапазоном выходных сигналов
10 Ом можно определить как: ±0.5%, ±500 Па
или ±0.05 Ом.
Статистическая
ошибка измерений — современная
характеристика точности датчиков
учитывает влияние как систематических,
так и случайных погрешностей, и не
зависит от ошибок, допущенных
при определении передаточных
функций.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
-
-
May 8 2015, 14:46
Абсолютные ,относительные и приведенные погрешности измерений
Абсолютная погрешность – это разница между измеренной датчиком величиной Хизм и действительным значением Хд этой величины.
Действительное значение Хд измеряемой величины это найденное экспериментально значение измеряемой величины максимально близкое к ее истинному значению. Говоря простым языком действительное значение Хд это значение, измеренное эталонным прибором, или сгенерированное калибратором или задатчиком высокого класса точности. Абсолютная погрешность выражается в тех же единицах измерения, что и измеряемая величина (например, в м3/ч, мА, МПа и т.п.). Так как измеренная величина может оказаться как больше, так и меньше ее действительного значения, то погрешность измерения может быть как со знаком плюс (показания прибора завышены), так и со знаком минус (прибор занижает).
См.Абсолютная погрешность микрокомпьютерного расходомера скоростемера МКРС
Относительная погрешность – это отношение абсолютной погрешности измерения Δ к действительному значению Хд измеряемой величины.
Относительная погрешность выражается в процентах, либо является безразмерной величиной, а также может принимать как положительные, так и отрицательные значения.
См.Относительная погрешность ультразвукового уровнемера ЭХО-АС-01
Приведенная погрешность – это отношение абсолютной погрешности измерения Δ к нормирующему значению Хn, постоянному во всем диапазоне измерения или его части.
Нормирующее значение Хn зависит от типа шкалы датчика КИП:
- Если шкала датчика односторонняя и нижний предел измерения равен нулю (например, шкала датчика от 0 до 150 м3/ч), то Хn принимается равным верхнему пределу измерения (в нашем случае Хn = 150 м3/ч).
- Если шкала датчика односторонняя, но нижний предел измерения не равен нулю (например, шкала датчика от 30 до 150 м3/ч), то Хn принимается равным разности верхнего и нижнего пределов измерения (в нашем случае Хn = 150-30 = 120 м3/ч).
- Если шкала датчика двухсторонняя (например, от -50 до +150 ˚С), то Хn равно ширине диапазона измерения датчика (в нашем случае Хn = 50+150 = 200 ˚С).
Приведенная погрешность выражается в процентах, либо является безразмерной величиной, а также может принимать как положительные, так и отрицательные значения.
Довольно часто в описании на тот или иной датчик указывается не только диапазон измерения, например, от 0 до 50 мг/м3, но и диапазон показаний, например, от 0 до 100 мг/м3. Приведенная погрешность в этом случае нормируется к концу диапазона измерения, то есть к 50 мг/м3, а в диапазоне показаний от 50 до 100 мг/м3 погрешность измерения датчика не определена вовсе – фактически датчик может показать все что угодно и иметь любую погрешность измерения. Диапазон измерения датчика может быть разбит на несколько измерительных поддиапазонов, для каждого из которых может быть определена своя погрешность как по величине, так и по форме представления. При этом при поверке таких датчиков для каждого поддиапазона могут применяться свои образцовые средства измерения, перечень которых указан в методике поверки на данный прибор.
Отдельные значения параметров датчиков не позволяют объективно судить о работе в реальных условиях. Необходимо учитывать доверительный интервал, т.е. максимальное отклонение измеренной величины.
Точность и прецизионность являются первостепенными характеристиками датчика. Эти два параметра часто путают, хотя они принципиально различны. Точность — качественный признак, характеризующий степень близости результатов измерения к действительному значению. Прецизионность отражает повторяемость или воспроизводимость измерения.
Регламент ISO 3534-1:2006 определяет прецизионность как близость совпадения результатов независимых тестов, проведенных при оговоренных условиях, и связывает это понятие с воспроизводимостью и повторяемостью измерений. Под повторяемостью понимается прецизионность при повторяемых условиях, а под воспроизводимостью — прецизионность при воспроизводимых условиях.
Прецизионность, точность, повторяемость, воспроизводимость, изменчивость и неопределенность являются качественными понятиями, поэтому следует осторожно обходиться с ними. Прецизионность инструмента отражает количество значащих цифр в показании, как разрешение. Точность инструмента характеризует близость показания к реальной величине. Точное измерение не обязательно прецизионное. Часто инструменты прецизионные, но далеко не точные. Разница между этими понятиями наглядно показана на рисунке 1. Видно, что прецизионность измерения может меняться в зависимости от амплитуды сигнала.
|
|
|
Рис. 1. Разница между точностью и прецизионностью |
Понятие точности
Среди производителей датчиков наиболее распространены следующие методы определения характеристик: по измеренным параметрам и по доверительному интервалу. Первый способ предполагает количественное определение параметров датчика без попытки обобщения. Второй метод дает более близкий к реальному результат. Погрешность датчика выражается в виде полосы ошибки, ее также называют доверительным интервалом, в который попадают все точки измерений. Поскольку рабочие характеристики датчика, прописанные в технической документации, могут меняться только в указанном диапазоне, то все показания можно считать достоверными, т.е. полученные данные будут точными внутри указанной полосы ошибок. Отпадает необходимость долгого анализа, в процессе которого могут возникать новые ошибки. Суть данного метода проиллюстрирована рисунком 2.
|
|
|
Рис. 2. Оценка характеристик датчика с учетом их погрешности |
Однако многие производители указывают параметры погрешности отдельного датчика, если отсутствует какое-либо законодательное давление, заставляющее их указывать общую полосу ошибки. Например, взвешивающее оборудование подпадает под действие законодательной метрологии и проходит тщательный контроль мировых агентств по весу и измерениям. Международная организация законодательной метрологии требует, чтобы нагрузочные ячейки, используемые во взвешивающем оборудовании, предоставляли возможность контроля точности.
Как правило, в доверительный интервал включены такие параметры как нелинейность, гистерезис, неповторяемость, деформация при нагрузке, температурное смещение нуля и отклонение чувствительности. Таким образом, пользователь может быть уверен в том, что прецизионность измерений будет иметь указанный диапазон погрешности, если в нем учтены все интересующие параметры.
Если нет внешнего давления, производители неохотно используют данный метод спецификации параметров датчика, хотя он дает более наглядные характеристики работы датчика в конкретном приложении. Из коммерческих соображений производители имеют склонность представлять свою продукцию в лучшем свете, замалчивая о недостатках.
Широко распространенный метод оценки по параметрам позволяет сравнивать конкурирующие продукты напрямую, анализируя характеристики, указанные в технической документации. В процессе выбора датчика необходимо сравнивать параметры с учетом целевого применения, чтобы выбранный датчик отвечал требованиям конечного приложения.
Как правило, в техническом описании датчика указывается список потенциальных источников погрешности, не все из которых могут проявляться в конкретном приложении. На первый взгляд может показаться трудным разобраться в этом изобилии информации и решить, достаточно ли точен датчик для конкретного приложения.
В идеальном случае математическое соотношение, описывающее связь между измеряемой величиной и выходным сигналом во всем рабочем диапазоне, должно включать все источники погрешности, например, смещение нуля, нелинейность, гистерезис, повторяемость, отклонение параметров из-за изменения температуры, температурный гистерезис и долгосрочную стабильность. Обычно пользователи учитывают только один или два из этих факторов, сравнивая модели только по ним. Наиболее часто указывают нелинейность характеристики — максимальное отклонение выходного сигнала от прямой.
Если производитель приводит полином, описывающий действительное поведение датчика, то точность показаний может увеличиться на порядок. Для большинства датчиков зависимость квадратична, а в первом приближении выходной сигнал линеен. Таким образом, если заменить формулу, которую приводит производитель (y = ax + b) на y = ax2 + bx + c, точность повысится. Другой пример. Передаточная характеристика многих гравиметрических инерциальных датчиков угла имеет синусоидальный вид. Тем не менее в технической документации по-прежнему указывается линейное соотношение, поскольку при малых углах синус угла можно заменить самим углом.
Если источники ошибки нуля и причины отклонения чувствительности известны, погрешность измерения будет минимальной, поскольку учитываются фактические источники, а не предполагаемые. Часто погрешность указывается в виде доли от полной шкалы. При этом погрешность чувствительности обычно определяется как доля от полученного показания. Для ее уменьшения производится компенсация температурной зависимости. Датчик температуры устанавливается рядом с измерительным датчиком или прямо на нем. Для этой же цели некоторые производители устанавливают датчик температуры на плате.
Важно различать вклад погрешности смещения нуля и погрешности чувствительности. Сдвиг нуля из-за температуры — это абсолютная погрешность, выраженная в процентах от полной шкалы. В большинстве случаев шкала датчика не используется полностью, поэтому в пересчете на долю от показания погрешность может стать очень большой. Например, если используется только четверть шкалы, то ошибка установки нуля становится в 4 раза больше, чем заявлено в документации. То же самое происходит, когда пользователи выбирают датчик с большим, чем требуется, диапазоном работы «на всякий случай».
Эти примеры показывают, что точность и прецизионность можно увеличить за счет математической минимизации предсказуемых ошибок. Погрешность стабильности и несистемные ошибки, которые нельзя предсказать и повторить, представляют собой более сложное препятствие на пути повышения точности.
Непредсказуемые ошибки
Непредсказуемые ошибки, такие как долгосрочная стабильность, температурный гистерезис или неповторяемость, нельзя описать математически, чтобы повысить точность или прецизионность, поэтому с ними гораздо сложнее обращаться. В то время как температурный гистерезис и неповторяемость являются величинами, которые могут быть охарактеризованы количественно на стадии производства в контролируемых условиях, долгосрочная стабильность такого свойства не имеет. Она определяется с помощью различных статистических инструментов. Однако итоговое решение придется принимать в каждом случае отдельно с учетом того, насколько критично измерение. Единственным надежным способом избежать постепенного ухудшения характеристик датчика является периодическая плановая перекалибровка. Ниже приведены общие рекомендации по работе с датчиками:
– повторяемость — единственный важный параметр датчика. Без него не имеют смысла ни количество компенсации, ни коррекция результата;
– следует учитывать диапазон изменения температуры окружающей среды, внутри которого работает датчик. Как правило, основной вклад в погрешность, особенно в ошибку установки нуля, вносят именно температурные изменения;
– не следует преувеличивать диапазон работы датчика. Производитель указывает безопасные границы выхода за диапазон, этого достаточно. Если их расширять, то уменьшится величина сигнала, а погрешность из-за ухода нуля окажется еще больше, поскольку она рассчитывается исходя из диапазона измерения;
– не следует путать разрешение с точностью;
– если датчик предназначен для долгосрочной эксплуатации, нельзя забывать о стабильности характеристик во времени. Прогрессирующее ухудшение параметров может иметь катастрофические последствия. Необходимо периодически калибровать датчик. Обычно это делается раз в год, но этот интервал может быть изменен в зависимости от условий работы и возможных последствий от получения неточных данных;
– рассчитывать погрешность датчика следует по его техническим характеристикам. Причем в расчет стоит принимать только те параметры, которые имеют отношение к данному приложению.
Литература
1. Baker М. Choosing sensors: Specsmanship vs reality//www.eetimes.com.
Измерительные каналы систем автоматизации могут включать в себя несколько средств измерений различных типов, например датчики, измерительные преобразователи, модули аналогового и частотного ввода и вывода [1]. Погрешность такой системы желательно определять экспериментальным путём [2], однако это не всегда возможно или целесообразно. В таких случаях используют расчётный метод.
Исходные данные для расчёта
Исходными данными для расчёта погрешности измерительных каналов являются [3]:
-
метрологические характеристики средств измерений;
-
погрешность метода измерений (методическая погрешность);
-
характеристики влияющих величин (например, окружающая температура, влажность);
-
характеристики измеряемого сигнала.
ГОСТ 8.009-84 [4] для всех типов средств измерений устанавливает следующий комплекс метрологических характеристик, который указывается в эксплуатационной документации на средства измерений:
-
систематическая составляющая основной погрешности;
-
среднеквадратическое отклонение случайной составляющей основной погрешности;
-
дополнительная погрешность для каждой из влияющих величин;
-
динамическая погрешность.
Некоторые средства измерений обладают гистерезисом – для них, кроме перечисленных погрешностей, указывается случайная составляющая основной погрешности, вызванной гистерезисом.
Основная погрешность может быть указана без разделения её на части (на систематическую, случайную и погрешность от гистерезиса), и этот вариант является наиболее распространённым. Случайную составляющую указывают в случае, когда она больше 10% от систематической [4].
Дополнительная погрешность указывается в виде функции влияния внешнего фактора на основную погрешность или её составляющие: систематическую и случайную. Обычно эта функция представляет собой линейную зависимость, и тогда указывается только коэффициент влияния, например 0,05%/°С.
Динамическая погрешность указывается с помощью одной из следующих характеристик: импульсная, переходная, амплитудно-частотная и фазочастотная, амплитудно-фазовая характеристика, передаточная функция. Для минимально-фазовых цепей указывается только амплитудно-частотная характеристика, поскольку фазочастотная однозначно может быть получена из амплитудно-частотной характеристики.
Для расчёта методической погрешности могут быть указаны сопротивления проводов, среднеквадратическое значение или спектральная плотность помех в них, ёмкость, индуктивность и сопротивление источника сигнала, а также другие факторы, которые возникают при создании системы, включающей средства и объект измерений.
Характеристики измеряемого сигнала задаются в виде функции от времени или функции спектральной плотности. Для случайного входного сигнала задаётся спектральная плотность мощности или автокорреляционная функция. Во многих случаях для оценки погрешности бывает достаточно знания скорости нарастания входного сигнала.
Коэффициент корреляции
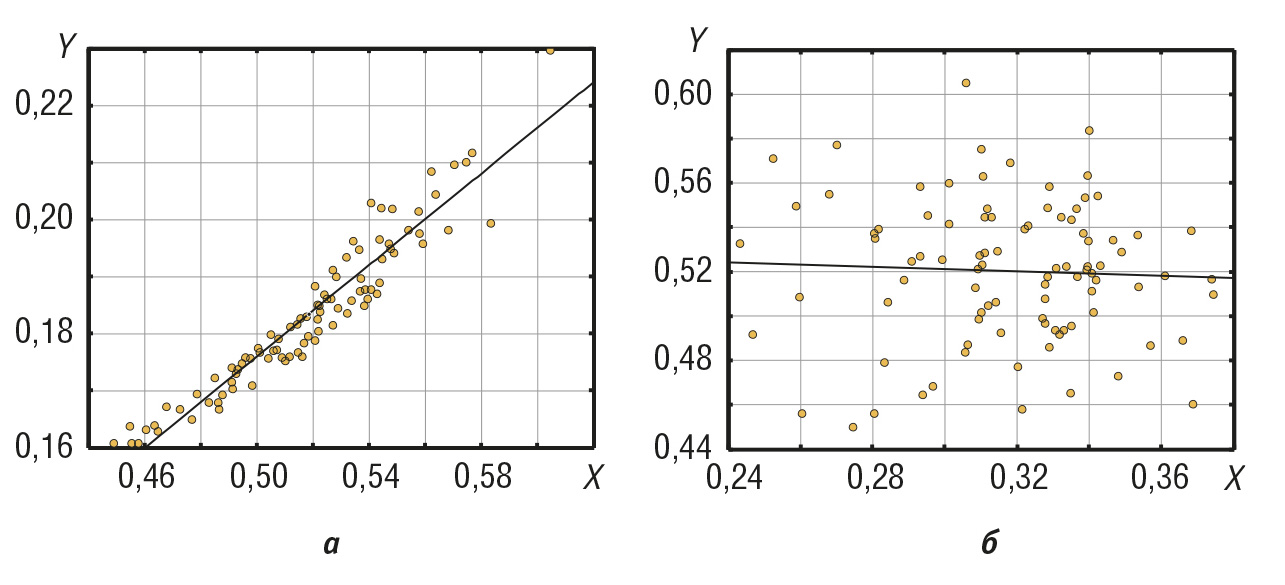
При расчёте погрешности измерительного канала возникает задача суммирования погрешностей средств измерений, которые являются случайными величинами. Способ суммирования будет различным в зависимости от того, являются ли случайные величины статистически зависимыми. Понятие статистической зависимости иллюстрирует рис. 1: если с ростом одной случайной величины X в среднем увеличивается (или уменьшается) и вторая (Y), то между этими величинами имеется статистическая зависимость. Для её количественного описания используются понятия ковариации или коэффициента корреляции.
Рассмотрим суммирование двух случайных погрешностей X и Y с нулевым математическим ожиданием (то есть центрированных случайных величин). Дисперсия суммы двух случайных величин по определению равна математическому ожиданию квадрата их суммы:
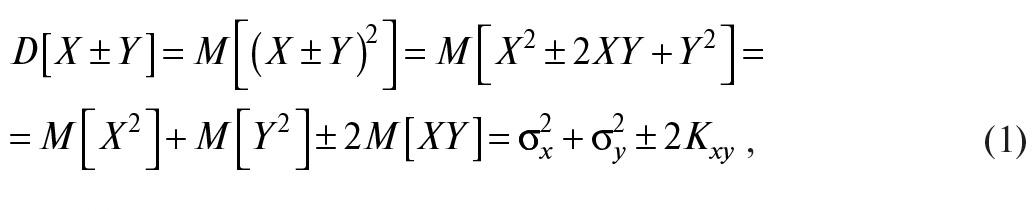
где D[•] и M[•] – операторы дисперсии и математического ожидания; σx, σy – среднеквадратические отклонения случайных величин X и Y. Величина

называется ковариацией («совместной вариацией») случайных величин X и Y.
Ковариацию дискретных случайных величин можно оценить по их дискретным значениям X = {x1,…xN} и Y = {y1,…yN} с помощью формулы среднего арифметического:

Коэффициентом корреляции Rxy называют отношение ковариации к произведению среднеквадратических отклонений σx и σy случайных величин X и Y:
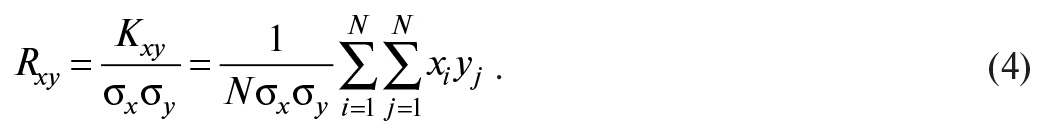
Когда случайные величины независимы, их коэффициент корреляции равен нулю (Rxy = 0), и такие величины называются некоррелированными. Если коэффициент корреляции равен единице (Rxy = 1), то между величинами X и Y имеется не статистическая, а функциональная зависимость.
Используя понятие среднеквадратического отклонения σx = √D[X], уравнение (1) можно записать в виде:
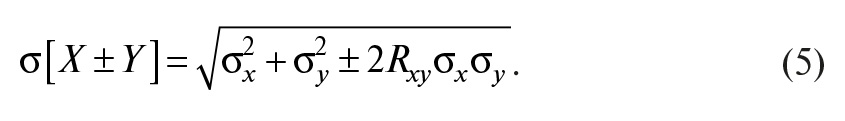
Здесь знак минус используется, когда случайные величины вычитаются, например, если находится разность напряжений двух измерительных каналов. При этом наличие корреляции между каналами частично уменьшает погрешность разности.
В случае когда случайные величины статистически независимы (Rxy = 0), выражение (5) упрощается:

Такое суммирование называют геометрическим, поскольку оно выполняется аналогично нахождению гипотенузы прямоугольного треугольника.
Если коэффициент корреляции Rxy = +1, то
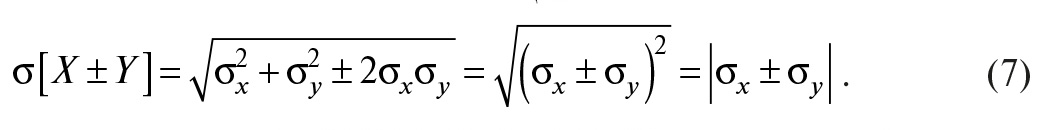
Если коэффициент корреляции равен Rxy = –1, то
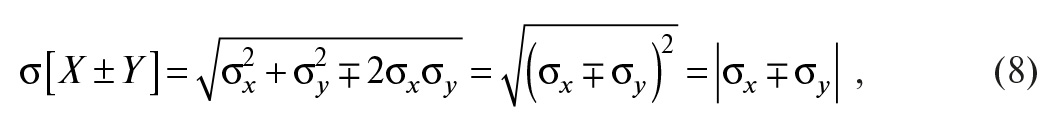
это означает, что при нахождении суммы случайных величин отрицательный коэффициент корреляции уменьшает итоговую погрешность, а при нахождении разности – увеличивает.
Если случайные величины не центрированы и имеют математические ожидания mx и my, то коэффициент корреляции можно оценить как
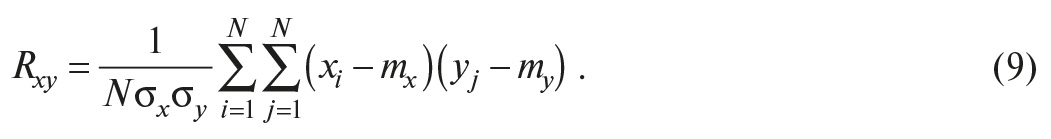
На рис. 1 показаны примеры статистической зависимости между случайными величинами при сильной (а) и слабой (б) корреляции. Точки на графике (значения случайной величины) могут группироваться очень близко к прямой линии, которая аппроксимирует эту зависимость, и тогда статистическая зависимость приближается к детерминированной. Степень отличия статистической зависимости от детерминированной характеризуют коэффициентом корреляции Rxy.
Прямая линия, проведённая таким образом, что сумма квадратов отклонений значений случайной величины от этой линии минимальна, называется линией среднеквадратической регрессии. Тангенс угла наклона этой линии называется коэффициентом регрессии. Уравнение линии регрессии можно получить методом наименьших квадратов; оно имеет вид [1]:
y = A(x – mx) + my,
где A – коэффициент регрессии. Коэффициент регрессии вычисляется через коэффициент корреляции Rxy и среднеквадратические отклонения σy и σx как

Коэффициент корреляции приобретает ясный физический смысл, если статистические переменные центрировать (вычесть математическое ожидание) и нормировать на величину среднеквадратического отклонения. Поскольку среднеквадратические отклонения нормированных величин равны единице, то коэффициент корреляции (9) становится равен тангенсу наклона линии среднеквадратической регрессии.
Статистическая зависимость между погрешностями средств измерений в общем случае нелинейная, однако этой нелинейностью обычно пренебрегают.
Точечные и интервальные оценки погрешности
Погрешности средств измерений и измерительных каналов средств автоматизации могут быть выражены двумя различными способами: с помощью точечных оценок и с помощью интервальных. К точечным оценкам относятся математическое ожидание погрешности и среднеквадратическое отклонение. В качестве интервальной оценки используют интервал погрешности, который охватывает все возможные значения погрешности измерений с вероятностью P. Она называется доверительной вероятностью, или надёжностью оценки погрешности.
Предел допускаемой погрешности можно рассматривать как точечную оценку или как интервальную для доверительной вероятности, равной единице.
Интервальная оценка является более гибкой, поскольку она позволяет указать погрешность измерений в зависимости от того, какая требуется вероятность реализации этой погрешности для конкретных условий эксплуатации средства измерений.
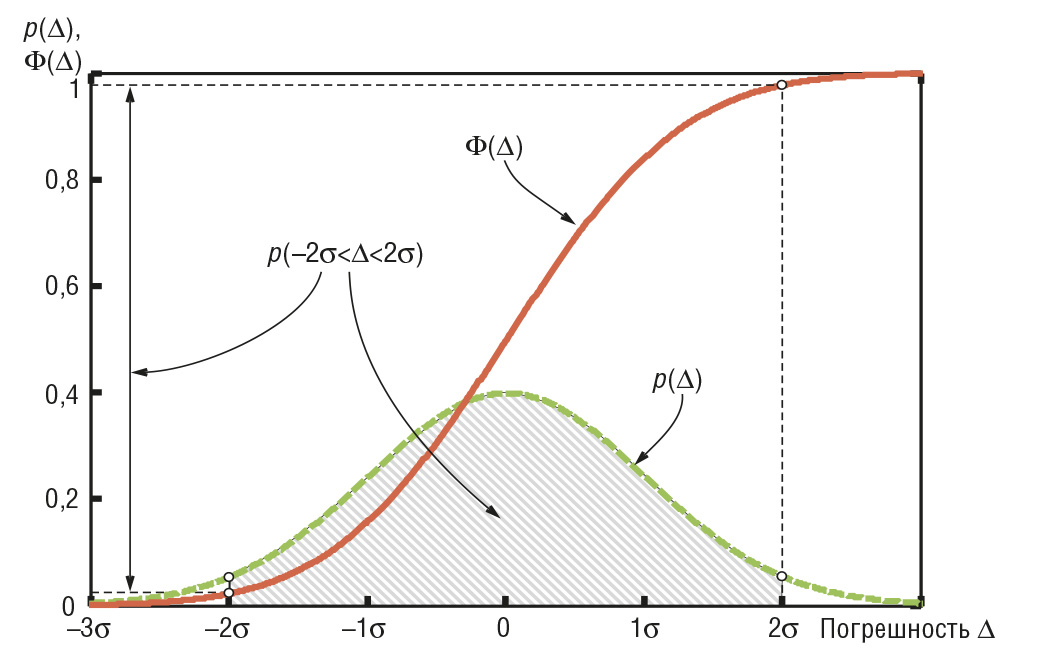
Смысл интервальной оценки погрешности иллюстрирует рис. 2. Здесь использованы следующие обозначения: ∆ – по-грешность измерения; р(∆) – плотность распределения по-грешностей; Φ(∆) – функция распределения погрешностей,
.jpg)
Для нормального закона распределения погрешностей (закона Гаусса) плотность распределения центрированной случайной величины ∆ описывается функцией
где σ – среднеквадратическая погрешность.
Если погрешность измерения ∆ находится внутри интервала ∆1 < ∆ < ∆2, то вероятность этого события вычисляется как
В наиболее типичном случае симметричных границ (–∆0 < ∆ < ∆0) получим
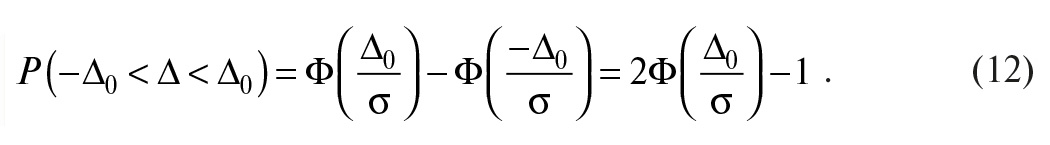
Здесь использовано свойство симметрии функции распределения для закона Гаусса.
Таким образом, если задан интервал –∆0 < ∆ < ∆0, который содержит в себе погрешность измеряемого параметра ∆, то вероятность того, что погрешность ∆ не выходит за границы интервала, можно найти по формуле (12) для нормального закона распределения. Вероятность P(–∆0 < ∆ < ∆0) называют также надёжностью оценки погрешности и обозначают символом γ:

Для вычисления функции распределения удобно использовать пакеты Mathcad, MATLAB. С их помощью из формулы (13) несложно найти величину доверительного интервала [–∆0, +∆0], если задана величина надёжности γ.
Для ∆0 = σ доверительная вероятность равна γ = 68,3%, для ∆0 = 2σ она уже равна γ = 95,3%, для ∆0 = 3σ составляет γ = 99,7% и для ∆0 = 4σ достигает γ = 99,994%.
Для увеличения надёжности оценки погрешности измерений или для сужения доверительного интервала при заданной надёжности можно использовать усреднение результатов многократных измерений. Поскольку оценка среднеквадратической погрешности результата усреднения σср равна [1], где σx – среднеквадратическая погрешность средства измерений, N – количество однократных измерений, то, подставив в (13) вместо σ величину σср, получим

Эта формула позволяет найти количество однократных измерений N, которое необходимо усреднить для получения требуемого доверительного интервала [–∆0, +∆0] при заданной надёжности γ или требуемой надёжности γ при заданном доверительном интервале [–∆0, +∆0]. Поскольку формула (14) задана в неявном виде, для нахождения требуемых неизвестных следует воспользоваться математическими пакетами для компьютерных вычислений.
Следует иметь в виду, что повышение точности путём усреднения результатов многократных измерений имеет множество ограничений [1].
Проблемой использования интервального метода оценки погрешности является необходимость знания закона распределения погрешностей.
Отметим, что доверительные интервалы, полученные из рассеяния множества измерений, никак не учитывают систематическую погрешность измерений. Интересные примеры из истории определения расстояния до Солнца, заряда электрона и др. приводятся в книге [5]. Ученые, которые делали эти выдающиеся измерения, указывали доверительные вероятности для оценки точности своих измерений. Однако ни одна из этих оценок не выдержала испытания временем: каждое новое, более точное измерение не укладывается в предсказанный ранее доверительный интервал. Это связано с тем, что систематическую погрешность или наличие ошибки в постановке эксперимента, в учёте факторов, о существовании которых мы не знаем, оценить невозможно, не имея более точного измерительного прибора.
Погрешность метода измерений
Для выполнения автоматизированных измерений используют датчики и измерительные преобразователи, измерительные модули ввода аналоговых сигналов, обработку результатов измерений на компьютере или в контроллере. При этом на погрешность результата измерений оказывают влияние следующие факторы:
-
сопротивление кабелей;
-
соотношение между входным импедансом средства измерений и выходным импедансом датчика;
-
качество экранирования и заземления, мощность источников помех;
-
погрешность метода косвенных, совместных или совокупных измерений;
-
наличие внешних влияющих факторов, если они не учтены в дополнительной погрешности средства измерений;
-
погрешность обработки результатов измерений программным обеспечением.
Все погрешности, которые не могут быть учтены в процессе сертификационных испытаний и внесены в паспорт средства измерений, а появляются в конкретных условиях применения, относятся к методическим. В отличие от них, инструментальные погрешности нормируются в процессе производства измерительного прибора и заносятся в его эксплуатационную документацию. Таким образом, если в состав смонтированной автоматизированной измерительной системы входят средства измерений с нормированными погрешностями, то погрешность, вызванная ранее перечисленными факторами, является методической. Если же выполняется сертификация всей измерительной системы, то методические погрешности могут быть учтены в погрешности всей системы, и тогда они переходят в разряд инструментальных.
Для расчёта или измерения методической погрешности трудно дать общие рекомендации. Каждый конкретный случай требует отдельного рассмотрения.
Погрешность программного обеспечения
Погрешность программного обеспечения (ПО) [6, 7] оценивается как разность между результатами измерений, полученными данным ПО и эталонным ПО. Под эталонным по-нимается программное обеспечение, высокая точность которого доказана многократными испытаниями и тестированием. Понятие эталонного ПО является условным и определяется соглашением между заказчиком аттестации и исполнителем. В качестве эталонного может быть использовано ра-нее аттестованное ПО.
К основным источникам погрешностей ПО относятся:
-
ошибки записи исходного текста программы и ошибки трансляции программы в объектный код;
-
ошибки в алгоритме решения измерительной задачи;
-
ошибки в таблицах для линеаризации нелинейных характеристик преобразования;
-
применение неустойчивых или медленно сходящихся алгоритмов при решении плохо обусловленных измерительных задач;
-
ошибки преобразования форматов данных;
-
ошибки округления и др.
Надёжность (достоверность) ПО обеспечивается средствами защиты от несанкционированных изменений, которые могут явиться причиной появления не учтённых при аттестации погрешностей.
Достоверность измерений
В процессе выполнения измерений могут появиться грубые ошибки (промахи), которые делают измерения недостоверными, несмотря на применение очень точных измерительных приборов. Здесь под достоверностью понимается степень доверия к полученным результатам. Достоверность может быть низкая при наличии погрешностей, о существовании которых экспериментатор не догадывается. Достоверность при использовании автоматизированных измерительных систем снижается с ростом их сложности и существенно зависит от квалификации персонала проектирующей и монтажной организаций.
Главным методом обеспечения достоверности является сопоставление результатов измерения одной и той же величины разными, не связанными друг с другом способами. Например, после монтажа системы измерения температуры в силосе элеватора следует сравнить показания автоматизированной системы и автономного контрольного термометра, чтобы убедиться в правильности показаний автоматизированной системы.
Приведём несколько примеров, иллюстрирующих случаи, когда, несмотря на применение точных средств измерений, получаются совершенно ошибочные данные, вводящие человека в заблуждение.
Пример 1. Для измерения температуры воздуха в теплице использован датчик температуры с погрешностью ±0,5°С. Однако датчик установлен таким образом, что в некоторые часы на него падают прямые лучи солнца, которые нагревают датчик, но не изменяют температуру воздуха. При этом погрешность измерения температуры воздуха может составить +5°С, что позволяет квалифицировать результат измерения как недостоверный.
Пример 2. Для измерения температуры в силосах элеватора установлены точные датчики и сделан тщательный монтаж, но расположенный на крыше элеватора ретранслятор сотовой связи оказался незамеченным, и не было принято достаточных мер для защиты от помех. При этом погрешность измерения температуры может составить ±10°С вслед-ствие помех, наведённых передатчиком в сигнальных кабелях системы.
Пример 3. В автоматизированной системе для измерения параметров продукции использован модуль ввода с погрешностью ±0,05%, однако при наладке системы программист по ошибке установил частоту помехоподавляющего режекторного фильтра не 50, а 60 Гц. Проведённые приёмо-сдаточные испытания системы не позволили выявить эту ошибку.
В результате погрешность измерений вследствие наведённой помехи с частотой 50 Гц может повыситься до ±10% вместо ожидаемых ±0,05%.
Пример 4. Во время выполнения измерений ваш коллега разговаривал по сотовому телефону. Наводка сигнала от передатчика сотового телефона может повысить погрешность измерений в несколько раз.
Пример 5. При монтаже системы заземлили экран сигнального кабеля с двух сторон. Проведённые приёмо-сдаточные испытания не позволили выявить эту ошибку. Погрешность может увеличиться в несколько раз по сравнению с ожидаемой.
Пример 6. В процессе эксплуатации системы нарушился контакт в цепи заземления, что привело к эпизодическому повышению уровня помех в измерительной цепи. В статье [8] описан пример, когда плохо затянутый болт в цепи заземления приводил к сбоям системы автоматики, причину которых искали несколько лет.
Пример 7. При расчёте погрешности средств измерений была проигнорирована динамическая погрешность, поскольку исходные данные для её расчёта не были указаны в эксплуатационной документации на средство измерения и не были выявлены в процессе приёмо-сдаточных испытаний ввиду сложности постановки эксперимента, отсутствия времени и приборов для контроля величины погрешности. Во время эксплуатации системы фактическая погрешность в несколько раз превысила расчётную.
В приведённых примерах сложно обнаружить наличие погрешности в процессе сдачи системы в эксплуатацию, она может появляться в особых условиях эксплуатации. Это приводит к снижению достоверности измерений, несмотря на высокую инструментальную точность использованных технических средств.
Общий подход к решению проблемы заключается в применении второй, независимой системы или методики измерений для обнаружения ошибок. Можно использовать также целый комплекс мер, включая подбор персонала, соблюдение графика поверки, тщательность выполнения типовых и сертификационных испытаний системы, соблюдение методики измерений и обслуживания измерительной системы.
Термин «достоверность» иногда используется во втором его значении – для указания вероятности того, что измеренное значение находится в заданном доверительном интервале [9] при условии, что все промахи и ошибки измерительной системы и методики измерений исключены. Количественным выражением достоверности в данном случае является доверительная вероятность [1]. Следует различать эти два значения одного и того же термина.
Методы суммирования погрешностей
Перед суммированием все погрешности делятся на следующие группы:
-
систематические и случайные;
-
в группе случайных – на коррелированные и некоррелированные;
-
аддитивные и мультипликативные;
-
основные и дополнительные.
Такое деление необходимо потому, что систематические и случайные погрешности, а также коррелированные и некоррелированные суммируются по-разному, а аддитивные по-грешности нельзя складывать с мультипликативными.
Если некоторые погрешности указаны в виде доверительных интервалов, то перед суммированием их нужно представить в виде среднеквадратических отклонений [1].
Дополнительные погрешности могут складываться с основными либо перед суммированием погрешностей, либо на заключительном этапе, в зависимости от поставленной задачи. Второй вариант часто предпочтительнее, поскольку он позволяет оценивать погрешность всего измерительного канала в зависимости от величины внешних влияющих факторов в конкретных условиях эксплуатации.
При последовательном соединении нескольких средств измерений погрешности, проходя через измерительный канал с передаточной функцией (функцией преобразования) f(x), могут усиливаться или ослабляться. Для учёта этого эффекта используют коэффициенты влияния, которые определяются как .
.jpg)
Все погрешности перед суммированием приводят к выходу (или входу) измерительного канала путём умножения (деления) на коэффициент влияния. В дальнейшем будем предполагать, что такое приведение уже выполнено.
Погрешности средств измерений являются случайными величинами, поэтому при их суммировании в общем случае необходимо учитывать соответствующие законы распределения. На практике пользуются более грубыми упрощёнными методами, разработанными математической статистикой.
Математическое ожидание погрешностей средств измерений, как правило, равно нулю. Если это не так, то его (в виде поправки) складывают с систематической составляющей погрешности. В средствах автоматизации введение поправки выполняется автоматически с помощью микроконтроллера, входящего в состав средств измерений. Математическое ожидание случайной составляющей всегда равно нулю, поскольку при нормировании метрологических характеристик его относят к систематической составляющей.
Наиболее полное определение итоговой погрешности измерительного канала состояло бы в нахождении функции распределения суммы нескольких погрешностей измерения. Однако функция распределения суммы случайных величин находится с помощью операции свёртки [10], что приводит к значительным практическим трудностям. Поэтому для оценки итоговой погрешности ограничиваются только суммированием дисперсий погрешностей.
Погрешности суммируют по однородным группам, затем находят общую погрешность, используя геометрическое суммирование для случайных погрешностей и алгебраическое для детерминированных.
Существует три способа суммирования погрешностей:
-
алгебраический (15)
где i – номер погрешности, N – их количество;
-
геометрический
где σi – среднеквадратическое значение i-й погрешности;
-
с учётом корреляции
В этой формуле j ≠ i потому, что члены с j = i уже учтены в сумме NΣi=1 σi2 , а граница j < i установлена для того, чтобы суммировать только члены, лежащие ниже диагонали корреляционной матрицы, поскольку вследствие её симметричности Rijσiσj + Rjiσjσi = 2Rijσiσj.
При Rij = +1 выражение (17) переходит в формулу алгебраического суммирования:
где σi складываются со своими знаками, то есть коррелированные погрешности с противоположными знаками частично взаимно компенсируются, если их коэффициент корреляции равен единице.
При Rij = –1 погрешности вычитают попарно в соответствии с (8):
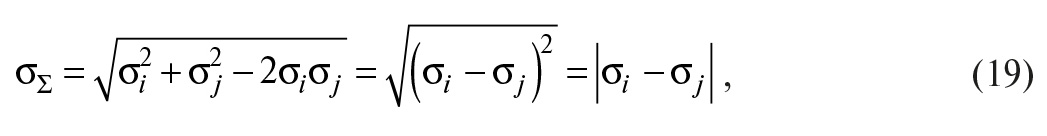
то есть при отрицательной корреляции погрешности частично компенсируются, если они имеют один и тот же знак.
Учитывая, что получить удовлетворительные оценки коэффициентов корреляции довольно трудно, используют следующий приём: при |Rij| ≥ 0,7 считают, что |Rij| = 1, при |Rij| < 0,7 полагают |Rij| = 0 [9, 10].
Систематические погрешности
В наиболее типовом случае систематические составляющие основных погрешностей средств измерений суммируются геометрически по формуле (16), поскольку они являются случайными величинами.
Формулы геометрического суммирования были получены для среднеквадратических погрешностей [1]. Поэтому, если комплекс метрологических характеристик средств измерений включает предел допускаемых значений систематической составляющей основной погрешности ∆os без указания среднеквадратического значения (по ГОСТ 8.009-84 [4]), то соответствующее ему среднеквадратическое значение находят в соответствии с рекомендациями РД 50-453-84 [11] по формуле

Эта формула справедлива, если нет оснований полагать, что функция распределения данной погрешности является несимметричной и имеет несколько максимумов.
Метрологическая инструкция МИ 2232-2000 [12] рекомендует иную формулу – половину предела допускаемой погрешности.
Выбор способа суммирования систематических составляющих основных погрешностей не является однозначным, и это связано с отсутствием полной информации о законе распределения. Дело в том, что причиной существования основной погрешности является как технологический разброс параметров электронных компонентов, так и нескомпенсированная нелинейность. Технологический разброс обычно является случайным, и на этом основании систематическая составляющая погрешности может рассматриваться как случайная величина на множестве средств измерений одного и того же типа. Поэтому в формулах для расчёта погрешностей она учитывается геометрически. Однако нелинейность передаточной характеристики средства измерений (нелинейность АЦП, нормирующих усилителей, термопар) у всех экземпляров приборов одного типа будет иметь примерно один и тот же вид, величину и знак. Например, погрешность, вызванная нелинейностью, в начале шкалы может быть положительной, в середине шкалы – отрицательной, у верхнего предела шкалы – опять положительной, и так для всех экземпляров приборов одного типа. Поэтому погрешности, обусловленные нелинейностью, должны суммироваться алгебраически.
В современных модулях аналогового ввода используется автоматическая калибровка, позволяющая уменьшить случайную компоненту систематической погрешности, и в этом случае преобладающей является детерминированная погрешность нелинейности.
Поскольку ГОСТ 8.009-84 [4] не предусматривает нормирование таких тонких нюансов поведения погрешностей, выбор способа суммирования начинает зависеть не от технических, а от политических факторов. Если фактическая погрешность окажется выше расчётной и это повлечёт за собой угрозу жизни людей, большой экономический ущерб, техногенную катастрофу и т. п. [12], то суммирование погрешностей выполняют алгебраически, причём используют не среднеквадратические отклонения, а пределы допустимых значений погрешности.
Если известен знак систематической погрешности, то его учитывают при суммировании.
Для наиболее ответственных применений следует использовать средства измерений, для которых указана погрешность без разделения на случайную и систематическую компоненты, поскольку в этом случае погрешность указана с доверительной вероятностью, равной единице. Если же ис-пользуются средства измерений, для которых указана случайная составляющая, то для них рассчитывают величину погрешности при доверительной вероятности, равной единице. Это условие существенно завышает требования к точности средства измерений.
Алгебраическое суммирование часто даёт слишком завышенную оценку погрешности. Поэтому МИ 2232-2000 [12] предусматривает промежуточный вариант между формулами геометрического и алгебраического суммирования:

где K – поправочный коэффициент, равный 1,2 для наиболее важных параметров устройств аварийной защиты и блокировки, контроля за соблюдением требований техники безопасности и экологической безопасности, контроля характеристик готовой продукции [12].
Для конкретных экземпляров приборов могут быть указаны не номинальные характеристики (имеющие одну и ту же величину для всех приборов данного типа), а индивидуальные. В этом случае систематическая погрешность является не случайной, а детерминированной величиной, поэтому должна учитываться в итоговой погрешности измерительного канала алгебраически.
Случайные составляющие погрешностей
Случайные составляющие основной погрешности средств измерений по ГОСТ 8.009-84 [4] задаются своими среднеквадратическими отклонениями, поэтому их суммирование выполняется непосредственно по формуле геометрического суммирования (16).
Если случайная погрешность является коррелированным случайным процессом [1] и задана в виде функции автокорреляции R(t) или спектральной плотности мощности S(f), то сначала находят среднеквадратическое значение случайной составляющей погрешности. Для этого используют формулу:

где fв – верхняя граничная частота полосы пропускания всего измерительного канала или цифрового фильтра, используемого при обработке полученных данных. Если задана функция автокорреляции, то спектральную плотность мощности находят по формуле, учитывающей корреляцию [1].
Случайная составляющая погрешности может быть уменьшена в несколько раз (в зависимости от величины фликкер-шума) путём усреднения результатов многократных измерений [1].
Дополнительные погрешности
Дополнительные погрешности задаются в виде функции влияния внешних факторов (температуры, влажности, напряжения питания) на основную погрешность измерения, или, в случае линейной функции влияния, они характеризуются коэффициентом влияния. Например, может быть задано, что основная погрешность увеличивается на +0,05% при изменении напряжения питания на +20%.
Если задан диапазон изменения влияющих величин, в качестве их математического ожидания для расчётов с помощью функции влияния берут их среднее значение [11].
Среднеквадратическое отклонение дополнительной погрешности для линейной функции влияния находят по формуле [11]:

где Kξ – коэффициент влияния внешнего фактора; ξ1, ξ2 – нижняя и верхняя границы изменения влияющей величины.
Дополнительная погрешность может увеличивать как систематическую, так и случайную составляющую основной погрешности. Для этого функции влияния задаются раздельно на каждую составляющую.
Если известно, что дополнительные погрешности нескольких средств измерений коррелируют (например, синхронно возрастают при увеличении напряжения питания в сети или температуры окружающей среды), то такие погрешности суммируют как коррелированные величины с учётом коэффициента корреляции в соответствии с (17) – (19).
Дополнительные погрешности считаются несущественными, если их сумма составляет менее 17% от наибольшего возможного значения инструментальной погрешности в рабочих условиях эксплуатации [4].
Динамические погрешности
Динамическая погрешность при известном входном сигнале является детерминированной. Она обычно приводит к занижению показаний измерительного прибора. Суммирование таких погрешностей выполняется алгебраически.
Подробнее об оценке динамической погрешности см. [1, 10].
Динамическая погрешность считается несущественной, если она составляет менее 17% от наибольшего возможного значения инструментальной погрешности в рабочих условиях эксплуатации [4].
Нахождение итоговой погрешности
После суммирования погрешностей по группам, как это было описано ранее, результат измерения обычно выражают в виде:

где x0 – измеренное значение; ∆ – сумма всех погрешностей, которые складывались алгебраически, то есть детерминированных погрешностей (детерминированные погрешности могут быть прибавлены к измеренной величине в качестве поправки); σ – сумма всех случайных погрешностей, которые складывались геометрически, в том числе с учётом корреляционных связей:
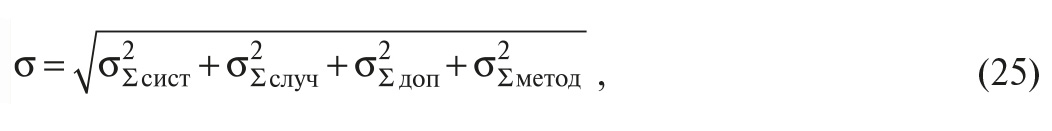
где σΣсист – сумма всех систематических погрешностей измерительного канала; σΣслуч – сумма всех случайных погрешностей; σΣдоп – сумма всех дополнительных погрешностей; σΣметод – сумма всех случайных составляющих методических погрешностей, включая погрешность программного обеспечения. Детерминированные составляющие методических погрешностей учитываются в слагаемом ∆.
Вместо среднеквадратического отклонения может быть указан предел допустимых значений. Однако должно быть явно указано, какая именно оценка погрешности использована, поскольку доверительные вероятности для предела допустимых значений (единица) и для среднеквадратического отклонения (0,68) существенно отличаются.
Случайная, систематическая и дополнительная погрешности могут быть указаны раздельно. МИ 1317-2004 [13] рекомендует «вместе с результатом измерений представлять характеристики его погрешности или их статистические оценки». Поэтому состав характеристик погрешности может быть выбран в каждом конкретном случае индивидуально, в зависимости от смысла решаемой задачи.
При выполнении многократных измерений результат должен также содержать указание на количество измерений, использованных при усреднении, и интервал времени, в течение которого были выполнены измерения [13].
Поскольку выражение для суммы дисперсий случайных величин (1) получено независимо от закона распределения, геометрическое суммирование погрешностей даёт правильное значение дисперсии независимо от законов распределения отдельных составляющих. Однако при этом ничего нельзя сказать о функции распределения суммарной погрешности, в том числе о надёжности (доверительной вероятности) полученного результата. Тем не менее, поскольку при суммировании пяти и более погрешностей закон распределения суммы близок к нормальному независимо от законов распределения отдельных слагаемых [10], то, зная среднеквадратическое отклонение итоговой погрешности, можно использовать нормальный закон распределения для указания доверительного интервала и доверительной вероятности результата измерений.
Нахождение погрешности измерительного канала в условиях недостатка исходных данных
При оценке погрешности измерительных каналов средств автоматизации следует по возможности использовать экспериментальный метод. Однако в случаях когда это невозможно или экономически нецелесообразно, делают расчёт по изложенной ранее методике. Типичной проблемой, которая при этом возникает, является отсутствие некоторых исходных данных. В этой ситуации метрологическая инструкция МИ 2232-2000 [12] рекомендует использовать следующие «значения по умолчанию»:
-
среднеквадратическое значение погрешности принимается равным половине предела допускаемых значений погрешности;
-
математическое ожидание основной и дополнительной погрешности принимается равным нулю;
-
корреляция между отдельными составляющими погрешности отсутствует;
-
случайная составляющая погрешности измерений является некоррелированной случайной величиной (белым шумом) или вырождается в систематическую погрешность;
-
функции распределения внешних влияющих величин предполагаются равномерными или нормальными;
-
считается, что инерционные свойства средств измерений не оказывают влияния на погрешность измерений. ●
Литература
-
Денисенко В.В. Компьютерное управление технологическим процессом, экспериментом, оборудованием. – М. : Горячая линия – Телеком, 2009. – 608 с.
-
МИ 2440-97. ГСИ. Методы экспериментального определения и контроля характеристик погрешности измерительных каналов измерительных систем и измерительных комплексов (взамен МИ 2313-94).
-
ГОСТ 23222-88. Характеристики точности выполнения предписанной функции средств автоматизации. Требования к нормированию. Общие методы контроля.
-
ГОСТ 8.009-84. Государственная система обеспечения единства измерений. Нормируемые метрологические характеристики средств измерений.
-
Тутубалин В.Н. Теория вероятностей и случайных процессов. Основы математического аппарата и прикладные аспекты. – М. : Изд-во МГУ, 1992. – 400 с.
-
МИ 2955-2005. ГСИ. Типовая методика аттестации программного обеспечения средств измерений и порядок её проведения.
-
МИ 2891-2004. ГСИ. Общие требования к программному обеспечению средств измерений.
-
Burleson J. Wiring and grounding to prevent power quality problems with industrial equipment // Textile, Fiber and Film Industry Technical Conference, 8–9 May 1991. – Pp. 5/1–5/6.
-
Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. – Л. : Энергоатомиздат, 1991. – 304 с.
-
Орнатский П.П. Теоретические основы информационно-измерительной техники. – 2-е изд. – Киев : Вища школа, 1983. – 455 с.
-
РД 50-453-84. Методические указания. Характеристики погрешности средств измерений в реальных условиях эксплуатации. Методы расчёта.
-
МИ 2232-2000. ГСИ. Обеспечение эффективности измерений при управлении технологическими процессами. Оценивание погрешности измерений при ограниченной исходной информации.
-
МИ 1317-2004. ГСИ. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров (взамен ГОСТ 8.011-72, МИ 1317-86).


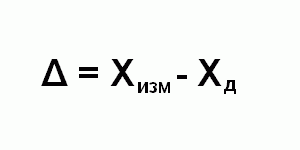
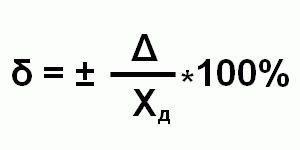
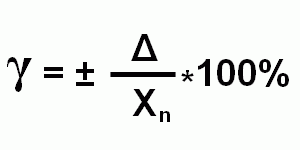






.jpg)