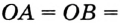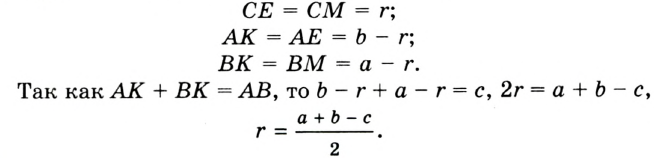Окружность
Привет, друг! Ниже собрана вся информация по окружности: что это такое, как найти ее величины, как круг связан с тригонометрией. Это поможет тебе еще лучше разобраться с этими темами, а также верно решать задачи! Время прочтения — 10 минут.
Что такое окружность?
Окружность — это множество всех точек на плоскости, находящихся на одинаковом расстоянии от данной точки, а ее радиусом называют отрезок, который соединяет любую её точку с центром (все радиусы окружности равны). У окружности также есть диаметр — отрезок, соединяющий две точки окружности и проходящий через её центр.
Выделяют также такое понятие как единичная окружность. Она представляет из себя такую окружность, центр которой располагается в начале координат, а ее радиус равен единице.
Есть еще один вид окружности — числовая. Это обычная единичная окружность, но с уже установленным соответствием между действительными числами и точками.
Как найти длину окружности
Зачастую в задачах просят найти длину окружности, как это сделать?
Так, для того чтобы найти длину окружности, нужно:
- Диаметр этой окружности умножить на , число ≈ 3,1415926535…
- Найти удвоенное произведение радиуса и числа
Формулы:
Где r — это радиус окружности, а d — ее диаметр, а число — это математическая константа (отношение длины окружности к длине ее диаметра)
Чему равен радиус окружности
Радиус окружности необходимо знать, чтобы решить многие задачи, поэтому давай вместе разберем, как его можно найти.
- Через площадь окружности : R=s, где S — площадь круга, — это математическая константа, которая объяснена выше.
- Через длину круга: R=P2, где P — длина круга.
- Через диаметр окружности: R=d2, где d — диаметр.
- Через диагональ вписанного треугольника: R=d2, где d=a2 b2.
- Через сторону описанного квадрата: R= a2, где а — сторона описанного квадрата.
- Через стороны и площадь вписанного треугольника: R=abc4S, где abc — стороны вписанного треугольника, а S — его площадь.
- Через площадь и полупериметр описанного треугольника: R=sp, где S — площадь треугольника, а p — полупериметр.
- Через площадь сектора и его центральный угол: R=360Spa, где S — площадь сектора круга, α — его центральный угол.
- Через сторону вписанного правильного многоугольника: R=a2sin(180N), где a — сторона правильного многоугольника (все его стороны равны), N — количество сторон многоугольника.
Окружность в тригонометрии
Окружность используется и в тригонометрии:
Что значат на рисунке все обозначение?
- Присутствует перевод градусов в радианы (и наоборот). В полном круге — 360 градусов ( радиан);
- Значение косинуса угла — на оси Х, а значение синуса — на У;
- Синус и косинус имеют значения от -1 до 1;
- На тригонометрическом круге видно, что косинус как и синус — периодические (один период равен 2).
Что еще важно знать?
Полный круг — 360 градусов.
Точка с координатами (1;0) — угол 0 градусов соответствует углу ноль градусов, а точка с координатами (-1;0) соответствует углу 180 градусов, точка с координатами (0;1) — в 90 градусов.
Косинус угла — абсцисса точки на единичной окружности, которая соответствует приведенному углу.
Синус угла — ордината точки на единичной окружности, которая соответствует приведенному углу.
Потому как окружность единичная, то для любого угла и синус, и косинус находятся в пределах от -1 до 1. Так:
Из этого можно выделить основное тригонометрическое тождество:
cos^2 a + sin^2 a = 1
По рисунку видно, что
,
Углы могут быть и больше 360 градусов. Например, угол 720 — это два полных оборота по часовой стрелке. Из этого можно сделать такой вывод:
Если же применять в этих формулах не градусы, а радианы, то:
Можно также по рисунку тригонометрической окружности определить тангенс угла и котангенс:
В результате, мы получаем таблицу:
Углы поворота
Угол поворота — это угол, образованный положительным направлением оси OX и лучом OA.
Их величина не имеет зависимости от радиуса приведенной окружности.
Угол в первом квадранте(четверти круга), имеет все положительные значения тригонометрических функций.
Во втором квадранте все функции (кроме sin и cos) — отрицательные.
В третьем квадранте значения всех функций (помимо tg и ctg) меньше 0.
В четвертом квадранте все функции (кроме cos и sec) с отрицательным значением.
Теорема синусов
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
На b сокращаем, синусы переносим в знаменатели:
bc sinα = ca sinβ
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
- Стороны треугольника, если даны два угла и одна сторона.
- Углы треугольника, если даны две стороны и один прилежащий угол.
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° — α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° — α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° — α) = 2R sinα
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
- sin120° = sin(180° — 60°) = sin60° = 3/√2;
- sin150° = sin(180° — 30°) = sin30° = 1/2;
- sin135° = sin(180° — 45°) = sin45° = 2/√2.
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Поэтому: ∠A + ∠C = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
sinγ = sin(180° — α)
Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
-
Согласно теореме о сумме углов треугольника:
∠B = 180° — 45° — 15° = 120°
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
>
Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:
Радиус описанной окружности
Удобно, когда все формулы, по которым можно найти радиус описанной окружности для треугольника, квадрата, многоугольника размещены на одной странице.
Формулы для нахождения радиуса описанной окружности треугольника (верны для треугольника любого вида):
где a, b, c — длины сторон треугольника, α, β, γ — противолежащие этим сторонам углы, S — площадь треугольника.
у остроугольного треугольника — внутри треугольника;
у прямоугольного — на середине гипотенузы;
у тупоугольного — вне треугольника, напротив тупого угла.
Радиус описанной окружности для прямоугольного треугольника
Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы:
Окружность, описанная около многоугольника
Если около многоугольника можно описать окружность, ее центр является точкой пересечения серединных перпендикуляров к сторонам многоугольника.
Радиус описанной около многоугольника окружности находят как радиус окружности, описанной около треугольника. Для этого берут любые три вершины многоугольника.
Например, для пятиугольника ABCDE можно взять любой из треугольников ABC, ABD, ABE, BCD, BCE, CDE, ACD, ACE, ADE, BDE.
Радиус окружности, описанной около правильного многоугольника
Формула радиуса описанной окружности для правильного многоугольника
где a — длина стороны многоугольника, n — количество его сторон.
Частные случаи — правильный треугольник, правильный четырехугольник (то есть квадрат), правильный шестиугольник.
Радиус описанной окружности правильного треугольника
Формула радиуса описанной окружности для правильного треугольника
Если без иррациональности в знаменателе —
У правильного треугольника радиус описанной окружности в два раза больше радиуса вписанной окружности:
Радиус описанной окружности квадрата
Формула радиуса описанной окружности для квадрата
Если без иррациональности в знаменателе —
Радиус описанной окружности правильного шестиугольника
Формула радиуса описанной окружности для правильного шестиугольника
http://skysmart.ru/articles/mathematic/teorema-sinusov
Окружность вписана в n-угольник, если она касается всех сторон этого n-угольника (рис. 8.106).
Окружность описана около n-угольника, если все вершины n-угольника лежат на окружности (рис. 8.107).
Свойства вписанной окружности
1. Окружность можно вписать в любой треугольник.
2. Окружность можно вписать в четырехугольник, если суммы длин его противолежащих сторон равны.
Например, на рисунке 8.106 
Так, окружность можно вписать в квадрат и в ромб, но нельзя вписать в параллелограмм и в прямоугольник.
Свойства описанной окружности
1. Окружность можно описать около любого треугольника.
2. Окружность можно описать около четырехугольника, если суммы его противолежащих углов равны.
Например, на рисунке 8.107 
Так, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.
Расположение центров окружностей, описанных около треугольника:
1) центр окружности расположен на пересечении серединных перпендикуляров к сторонам треугольника;
2) если треугольник остроугольный, то центр окружности расположен в этом треугольнике:
а) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника (центры вписанной и описанной окружностей совпадают (рис. 8.108);
б) в равнобедренном треугольнике центр окружности расположен на биссектрисе, проведенной из вершины треугольника к его основанию (рис. 8.109);
3) если треугольник прямоугольный, то центр окружности расположен на середине гипотенузы (рис. 8.110);
4) если треугольник тупоугольный, то центр окружности расположен вне треугольника (рис. 8.111).
Расположение центров окружностей, вписанных в треугольник:
1) центр окружности, вписанной в треугольник, расположен в этом треугольнике (рис. 8.112 – 8.115);
2) центром окружности является точка пересечения биссектрис треугольника;
3) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника.
Формулы для вычисления радиусов вписанной и описанной окружностей
Радиус окружности, описанной около многоугольника, как правило, обозначают 

1) для равностороннего треугольника со стороной 


2) для произвольного треугольника со сторонами 



3) для прямоугольного треугольника с катетами 



4) для квадрата со стороной 



5) для прямоугольника с диагональю 

6) для ромба с высотой 

7) для трапеции с высотой 

Если около трапеции можно описать окружность, то, проведя диагональ трапеции и рассмотрев один из полученных треугольников со сторонами 






Правильный шестиугольник состоит из шести правильных треугольников (рис. 8.117) и точка 
Пример 1. Найдите сторону квадрата, если известно, что разность между площадью квадрата и площадью вписанного в него круга равна 
Решение. Так как площадь круга радиуса 




А так как 





Ответ: 
Пример 2. Площадь прямоугольника равна 4, а разность длин его смежных сторон рана 3. Найдите радиус окружности, описанной около этого прямоугольника.
Решение. Площадь прямоугольника со смежными сторонами 


Пусть 

Получим: 




По теореме Пифагора найдем диагональ прямоугольника: 


Ответ: 
Пример 3. Найдите радиус окружности, вписанной в ромб, если его диагонали равны 6 и 8.
Решение. По теореме Пифагора найдем сторону ромба (рис. 8.119):



По формуле 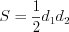

Но площадь ромба можно найти и по формуле 




Ответ: 2,4.
Пример 4. Найдите длину окружности, вписанной в правильный треугольник, если его площадь равна 
Решение. Площадь правильного треугольника со стороной 
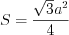
Зная площадь треугольника, найдем его сторону: 


По формуле 8.35 найдем радиус окружности, вписанной в этот треугольник: 
По формуле 8.30 найдем длину окружности: 
Ответ: 
Пример 5. Радиус окружности, описанной около равнобедренного прямоугольного треугольника равен 2. Найдите радиус окружности, вписанной в этот треугольник.
Решение. Радиус окружности, описанной около прямоугольного треугольника с гипотенузой 

Так как треугольник равнобедренный, то его катеты 




Радиус окружности, вписанной в прямоугольный треугольник, находят по формуле 8.39. В нашем случае 

Ответ: 
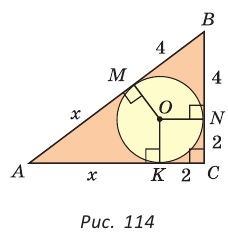
Пример 6. Один из катетов прямоугольного треугольника равен 8, а радиус окружности, вписанной в треугольник равен 3. Найдите площадь треугольника.
Решение. Рассмотрим прямоугольный треугольник 

Так как радиусы вписанной в треугольник окружности перпендикулярны сторонам треугольника в точках касания, то имеем квадрат 



Пусть отрезок 


Тогда по теореме Пифагора 



Найдем катет 

Найдем площадь треугольника: 

Ответ: 60.
Пример 7. Окружность, центр которой расположен на большей стороне треугольника, делит эту сторону на отрезки 4 и 8 и касается двух других его сторон, длина одной из которых равна 6. Найдите радиус окружности, вписанной в этот треугольник (рис.8.121).
Решение. Согласно свойству биссектрисы треугольника запишем: 

Радиус окружности, вписанной в треугольник, найдем по формуле 8.37.
В свою очередь по формуле Герона 


Тогда 
Ответ: 
Пример 8. В прямоугольную трапецию вписана окружность радиуса 3, которая в точке касания делит ее боковую сторону на отрезки 4 и 5. Найдите площадь трапеции.
Решение. Согласно условию задачи и рисунку 8.122, запишем: 

По свойству четырехугольника, описанного около окружности, получим: 


Согласно формуле 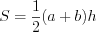

Ответ: 45.
Пример 9. Длины оснований равнобедренной трапеции относятся как 
Решение. Рассмотрим равнобедренную трапецию 
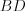
Радиус окружности, описанной около треугольника 


Зная, что 



Так как длина средней линии трапеции равна высоте трапеции, то 



Поскольку четырехугольник 


Согласно теореме Пифагора запишем:




По формуле 8.36 найдем радиус окружности, описанной около треугольника 


Согласно формуле 8.32 найдем площадь круга: 
Ответ: 
Пример 10. В правильный шестиугольник вписана окружность и около него описана окружность. Найдите площадь образовавшегося кольца, если сторона шестиугольника равна 
Решение. По формуле 8.45 найдем радиус окружности, описанной около правильного шестиугольника: 
По формуле 8.46 найдем радиус окружности, вписанной в этот шестиугольник. Так как 

Площадь круга находят по формуле 8.32. Тогда 

Найдем площадь кольца: 

Ответ: 
1. В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.
2. Не во всякий четырехугольник можно вписать окружность. Например, окружность можно вписать в ромб и квадрат, но нельзя вписать в параллелограмм и прямоугольник.
3. Не около всякого четырехугольника можно описать окружность. Например, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.
4. Не во всякую трапецию можно писать окружность и не около всякой трапеции можно описать окружность. Описать окружность можно только около равнобедренной трапеции.
5. Если многоугольник правильный (все его стороны и все его углы равны между собой), то в него всегда можно вписать окружность и около него всегда можно описать окружность. Причем, центры этих окружностей совпадают.
Длину окружности радиуса 

Площадь круга радиуса 

Описанная окружность — подробнее
Определение
Описанная окружность – такая окружность, что проходит через все три вершины треугольника, около которого она описана.
Свойства и центр описанной кружности
И вот, представь себе, имеет место удивительный факт:
Вокруг всякого треугольника можно описать окружность.
Почему этот факт удивительный?
Потому что треугольники ведь бывают разные!
И для всякого найдётся окружность, которая пройдёт через все три вершины, то есть описанная окружность.
Доказательство этого удивительного факта мы приведем чуть позже, а здесь заметим только, что если взять, к примеру, четырехугольник, то уже вовсе не для всякого найдётся окружность, проходящая через четыре вершины.
Вот, скажем, параллелограмм – отличный четырехугольник, а окружности, проходящей через все его четыре вершины – нет!
А есть только для прямоугольника:
Подробнее об этом смотри в статье о вписанных четырехугольниках!
Ну вот, а треугольник всякий и всегда имеет собственную описанную окружность! И даже всегда довольно просто найти центр этой окружности.
Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам этого треугольника.
Знаешь ли ты, что такое серединный перпендикуляр?
Серединный перпендикуляр — это прямая, проходящая через середину отрезка и перпендикулярная ему.
Прямая ( displaystyle a) – это серединный перпендикуляр к отрезку ( displaystyle AB).
А теперь посмотрим, что получится, если мы рассмотрим целых три серединных перпендикуляра к сторонам треугольника.
Вот оказывается (и это как раз и нужно доказывать, хотя мы и не будем), что все три перпендикуляра пересекутся в одной точке. Смотри на рисунок – все три серединных перпендикуляра пересекаются в одной точке ( displaystyle O).
Это и есть центр описанной около (вокруг) треугольника ( displaystyle ABC) окружности.
Как ты думаешь, всегда ли центр описанной окружности лежит внутри треугольника? Представь себе – вовсе не всегда!
Если треугольник тупоугольный, то центр его описанной окружности лежит снаружи!
Вот так:
А вот если остроугольный, то внутри:
Что же делать с прямоугольным треугольником?
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.
Здорово, правда?
Если треугольник – прямоугольный, то не надо строить аж три перпендикуляра, а можно просто найти середину гипотенузы – и центр описанной окружности готов!
Да ещё с дополнительным бонусом:
В прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы.
Раз уж заговорили о радиусе описанной окружности: чему он равен для произвольного треугольника? И есть ответ на этот вопрос: так называемая теорема синусов.
А именно:
В произвольном треугольнике:
( Large displaystyle frac{a}{sin angle A}=2R)
Ну и, конечно,
( displaystyle begin{array}{l}frac{b}{sin angle B}=2R\frac{c}{sin angle C}=2Rend{array})
Так что ты теперь всегда сможешь найти и центр , и радиус окружности, описанной вокруг треугольника.
То есть чтобы найти радиус описанной окружности, нужно знать одну (!) сторону и один (!) противолежащий ей угол.
Хорошая формула? По-моему, просто отличная!
Доказательство теоремы
Теорема. Вокруг всякого треугольника можно описать окружность, при том единственным образом.
Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.
Смотри, вот так:
Давай наберёмся мужества и докажем эту теорему.
Если ты читал уже тему «Биссектриса» разбирался в том, почему же три биссектрисы пересекаются в одной точке, то тебе будет легче, но и если не читал – не переживай: сейчас во всём разберёмся.
Доказательство будем проводить, используя понятие геометрического места точек (ГМТ).
Геометрическое место точек, обладающих свойством «( displaystyle X)» — такое множество точек, что все они обладают свойством «( displaystyle X)» и никакие другие точки этим свойством не обладают.
Ну вот, например, является ли множество мячей – «геометрическим местом» круглых предметов? Нет, конечно, потому что бывают круглые …арбузы.
А является ли множество людей, «геометрическим местом», умеющих говорить? Тоже нет, потому что есть младенцы, которые говорить не умеют.
В жизни вообще сложно найти пример настоящего «геометрического места точек». В геометрии проще. Вот, к примеру, как раз то, что нам нужно:
Серединный перпендикуляр к отрезку является геометрическим местом точек, равноудалённых от концов отрезка.
Тут множество – это серединный перпендикуляр, а свойство «( displaystyle X)» — это «быть равноудаленной (точкой) от концов отрезка».
Проверим? Итак, нужно удостовериться в двух вещах:
- Всякая точка на серединном перпендикуляре находится на одинаковом расстоянии от концов отрезка
- Всякая точка, которая равноудалена от концов отрезка – находится на серединном перпендикуляре к ему
Приступим:
Проверим 1. Пусть точка ( displaystyle M) лежит на серединном перпендикуляре к отрезку ( displaystyle AB).
Соединим ( displaystyle M) с ( displaystyle A) и с ( displaystyle B).Тогда линия ( displaystyle MK) является медианой и высотой в ( displaystyle Delta AMB).
Значит, ( displaystyle Delta AMB) – равнобедренный, ( displaystyle MA=MB) – убедились, что любая точка ( displaystyle M), лежащая на серединном перпендикуляре, одинаково удалена от точек ( displaystyle A) и ( displaystyle B).
Теперь 2. Почти точно так же, но в другую сторону. Пусть точка ( displaystyle M) равноудалена от точек ( displaystyle A) и ( displaystyle B), то есть ( displaystyle MA=MB).
Возьмём ( displaystyle K) – середину ( displaystyle AB) и соединим ( displaystyle M) и ( displaystyle K). Получилась медиана ( displaystyle MK). Но ( displaystyle Delta AMB) – равнобедренный по условию ( displaystyle (MA=MB)Rightarrow MK) не только медиана, но и высота, то есть – серединный перпендикуляр. Значит, точка ( displaystyle M) — точно лежит на серединном перпендикуляре.
Всё! Полностью проверили тот факт, что серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.
Это все хорошо, но не забыли ли мы об описанной окружности? Вовсе нет, мы как раз подготовили себе «плацдарм для нападения».
Рассмотрим треугольник ( displaystyle ABC). Проведём два серединных перпендикуляра ( displaystyle {{a}_{1}}) и ( displaystyle {{a}_{2}}), скажем, к отрезкам ( displaystyle AB) и ( displaystyle BC). Они пересекутся в какой-то точке, которую мы назовем ( displaystyle O).
А теперь, внимание!
Точка ( displaystyle O) лежит на серединном перпендикуляре ( displaystyle {{a}_{1}}Rightarrow OA=OB);
точка ( displaystyle O) лежит на серединном перпендикуляре ( displaystyle {{a}_{2}}Rightarrow OB=OC).
И значит, ( displaystyle OA=OB=OC) и ( displaystyle OA=OC).
Отсюда следует сразу несколько вещей:
Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 6. Описанная окружность. Многоугольники
Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства.
Около каких фигур можно, а вокруг каких нельзя описать окружность.
Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.
Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.
ЕГЭ 6. Вписанная окружность
В этом видео мы узнаем, что такое вписанная окружность, где находится её центр, и другие свойства.
В какие фигуры можно, а в какие нельзя вписать окружность. Научимся решать задачи на вписанную окружность.
Содержание:
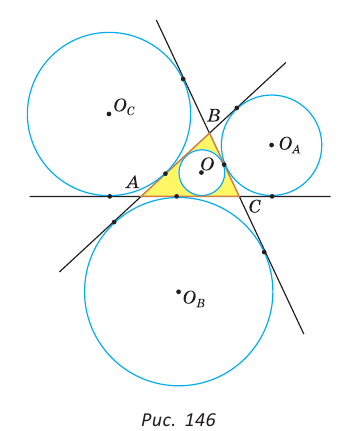
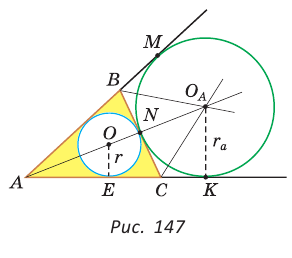
Окружность, которая касается стороны треугольника и продолжений двух других его сторон, называется вневписанной окружностью треугольника. На рисунке 146 изображен треугольник АВС и три его вневписанные окружности с центрами
Вневписанные окружности обладают рядом интересных свойств:
1. Центры вписанной и вневписанной окружностей лежат на биссектрисе соответствующего внутреннего угла треугольника.
2. 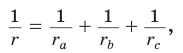
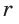
3. 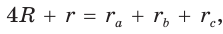
Попробуйте доказать некоторые из этих свойств.
Найдем радиус 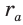
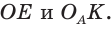
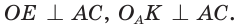
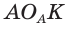
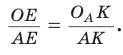
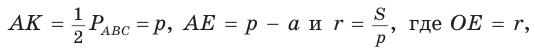
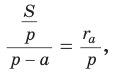
Пример:
Вычислим, используя данную формулу, радиус вневписанной окружности прямоугольного треугольника с катетами 3 и 4, которая касается гипотенузы:
Описанная и вписанная окружности треугольника
Определение. Окружность называется описанной около треугольника, если она проходит через все его вершины.
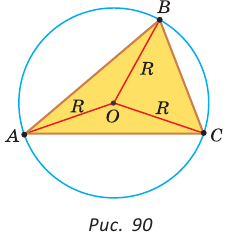
На рисунке 90 изображена окружность с радиусом R и центром 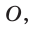
Так как ОА = ОВ = ОС = R, то центр описанной окружности равноудален от вершин треугольника.
Вместо слов «окружность, описанная около треугольника АВС», также говорят «окружность, описанная вокруг треугольника АВС», или «описанная окружность треугольника АВС».
Теорема (об окружности, описанной около треугольника).
Около любого треугольника можно описать окружность, причем только одну, ее центр находится в точке пересечения серединных перпендикуляров к сторонам треугольника.
Доказательство:
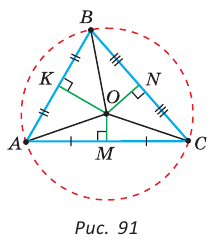
Рассмотрим произвольный треугольник АВС (рис. 91). Пусть О — точка пересечения серединных перпендикуляров к его сторонам. Проведем отрезки ОА, ОВ и ОС. По свойству серединного перпендикуляра ОА = ОС, ОС = ОВ. Так как точка О равноудалена от всех вершин треугольника АВС, то окружность с центром в точке О и радиусом ОА проходит через все вершины треугольника АВС, т. е. является его описанной окружностью. Единственность описанной окружности докажите самостоятельно.
Замечание. Так как все три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке, то для нахождения центра описанной окружности достаточно построить точку пересечения любых двух из них.
Определение. Окружность называется вписанной в треугольник, если она касается всех его сторон.
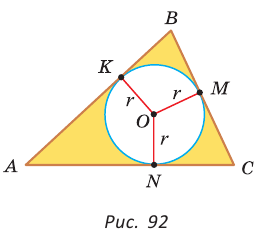
На рисунке 92 изображена окружность с центром О и радиусом 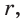
Так как 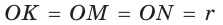
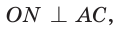
Вместо слов «окружность, вписанная в треугольник АВС», также говорят «вписанная окружность треугольника АВС».
Теорема (об окружности, вписанной в треугольник).
В любой треугольник можно вписать окружность, причем только одну, ее центр находится в точке пересечения биссектрис треугольника.
Доказательство:
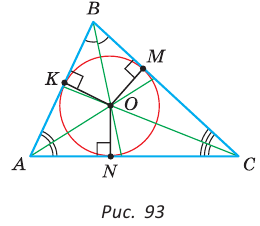
Рассмотрим произвольный треугольник АВС (рис. 93). Пусть О — точка пересечения его биссектрис. Проведем из точки О перпендикуляры ОК, ОМ и ON соответственно к сторонам АВ, ВС и АС. По свойству биссектрисы угла ОК = ON, ON = ОМ. Окружность с центром в точке О и радиусом ОК будет проходить через точки К, М и N и касаться сторон АВ, ВС и АС в указанных точках по признаку касательной.
Следовательно, эта окружность является вписанной в треугольник АВС. Единственность вписанной окружности докажите самостоятельно.
Замечание. Так как все три биссектрисы треугольника пересекаются в одной точке, то для нахождения центра вписанной окружности достаточно построить точку пересечения любых двух из них.
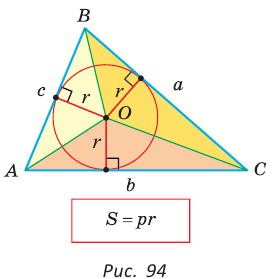
Теорема. Площадь треугольника можно найти по формуле 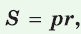
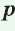
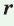
Доказательство:
Пусть дан треугольник АВС со сторонами 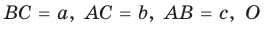
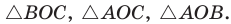
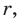
Теорема доказана.
Следствие:
Радиус окружности, вписанной в треугольник, можно найти по формуле
Одной из важнейших задач данной темы является задача нахождения радиуса описанной и радиуса вписанной окружностей данного треугольника.
Пример:
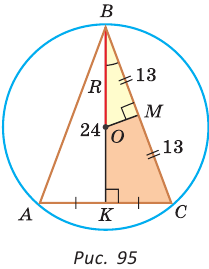
Найти радиус окружности, описанной около равнобедренного треугольника АВС, у которого АВ = ВС = 26 см, высота ВК = 24 см
(рис. 95).
Решение:
Способ 1 (метод подобия). Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника. Проведем серединные перпендикуляры к сторонам АС и ВС, которые пересекутся в точке О — центре описанной окружности. Так как в равнобедренном треугольнике высота, проведенная к основанию, является медианой, то ВК — серединный перпендикуляр к стороне АС. Пусть МО — серединный перпендикуляр к стороне ВС. Тогда ВМ = 13 см, ВО = R -— искомый радиус. Поскольку 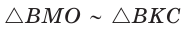
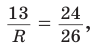
Способ 2 (тригонометрический метод). Из 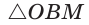
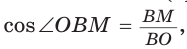
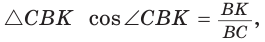
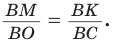
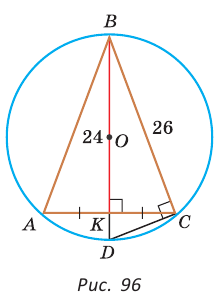
Способ 3* (среднее пропорциональное). Продлим высоту ВК до пересечения с описанной окружностью в точке D (рис. 96). Так как центр описанной окружности равнобедренного треугольника лежит на прямой ВК (см. способ 1), то BD = 2R — диаметр данной окружности. В прямоугольном треугольнике BCD 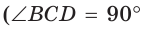
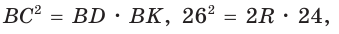
Ответ: 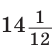
Замечание. Из решения ключевой задачи 1 следует свойство: «Центр окружности, описанной около равнобедренного треугольника, лежит на его высоте, проведенной к основанию, или на ее продолжении».
Верно и обратное утверждение: «Если центр окружности, описанной около треугольника, лежит на высоте треугольника или на ее продолжении, то этот треугольник равнобедренный».
Обратное утверждение докажите самостоятельно.
Полезно запомнить!
Если в ключевой задаче 1 боковую сторону обозначить 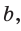
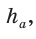
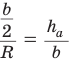
Отсюда следует удобная формула для нахождения радиуса окружности, описанной около равнобедренного треугольника:
Пример:
Найти радиус окружности, вписанной в равнобедренный треугольник АВС, у которого АВ = ВС = 10 см, АС = 12 см.
Решение:
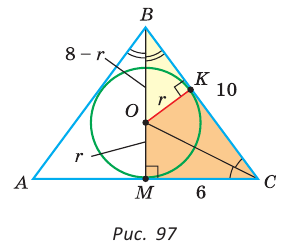
Способ 1 (метод подобия). Центр вписанной окружности находится в точке пересечения биссектрис треугольника. Проведем в треугольнике АВС биссектрисы из вершин В и С, которые пересекутся в точке О — центре вписанной окружности (рис. 97). Биссектриса ВМ, проведенная к основанию равнобедренного треугольника АВС, будет его высотой и медианой, луч СО — биссектриса угла С, 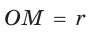
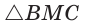
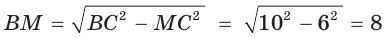
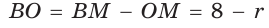
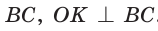
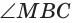
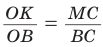
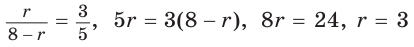
Способ 2 (тригонометрический метод). Из 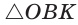
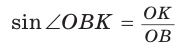
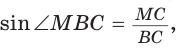
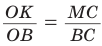
Способ 3 (свойство биссектрисы треугольника). СО — биссектриса 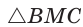
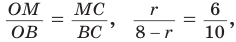
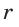
Способ 4 (формула 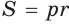
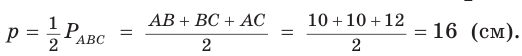
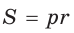
Ответ: 3 см.
Замечание. Из решения ключевой задачи 2 следует свойство: «Центр окружности, вписанной в равнобедренный треугольник, лежит на его высоте, проведенной к основанию».
Верно и обратное утверждение: «Если центр окружности, вписанной в треугольник, лежит на высоте треугольника, то этот треугольник равнобедренный».
Обратное утверждение докажите самостоятельно.
Пример:
Дан равносторонний треугольник со стороной а. Найти радиус R его описанной окружности и радиус 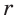
Решение:
Способ 1 (тригонометрический метод).Так как в равностороннем треугольнике биссектрисы являются и высотами, и медианами, то его биссектрисы лежат на серединных перпендикулярах к сторонам треугольника. Поэтому в равностороннем треугольнике центры описанной и вписанной окружностей совпадают.
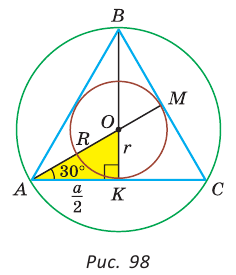
Рассмотрим равносторонний треугольник АВС со стороной а, у которого высоты AM и ВК пересекаются в точке О — центре описанной и вписанной окружностей (рис. 98). Тогда ОА = OB = R — радиусы описанной, 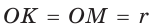
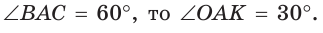
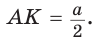
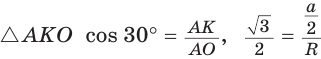
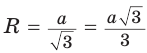
В 
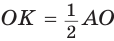
Способ 2 (свойство медиан). Поскольку AM и ВК — медианы треугольника АВС (см. рис. 98), то по свойству медиан 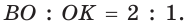
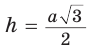
Ответ:
Полезно запомнить!
Поскольку радиус описанной окружности равностороннего треугольника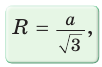
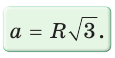
треугольника в 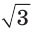
Чтобы найти радиус R описанной окружности равностороннего треугольника, нужно сторону 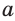
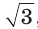
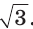
Прямоугольный треугольник и его описанная и вписанная окружности
Теорема. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а ее радиус равен половине гипотенузы, т. е. 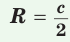
Доказательство:
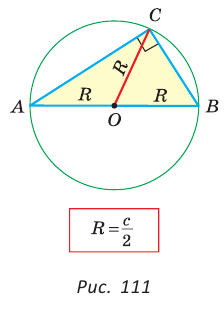
Проведем в прямоугольном треугольнике АВС медиану СО к гипотенузе АВ (рис. 111). Так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы, то ОС = ОА = ОВ.
Тогда середина гипотенузы — точка О — равноудалена от точек А, В и С и поэтому является центром описанной окружности треугольника АВС. Радиус этой окружности 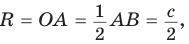
Теорема доказана.
Замечание. Также можно доказать, что серединные перпендикуляры к катетам прямоугольного треугольника пересекаются на середине гипотенузы.
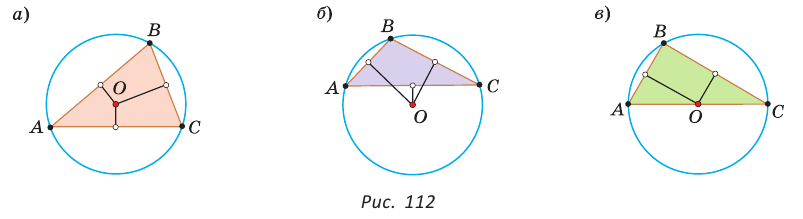
Отметим, что у остроугольного треугольника центр описанной окружности лежит внутри треугольника (рис. 112, а), у тупоугольного — вне треугольника (рис. 112, б), у прямоугольного — на середине гипотенузы (рис. 112, в). Обоснуйте первые два утверждения самостоятельно.
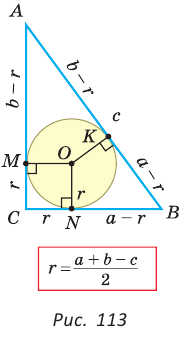
Теорема. Радиус окружности, вписанной в прямоугольный треугольник, можно найти по формуле 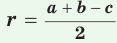
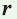
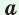
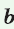
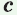
Доказательство:
Рассмотрим прямоугольный треугольник АВС с катетами 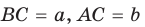
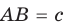
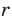
Проведем радиусы в точки касания и получим: 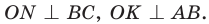
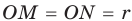
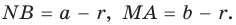
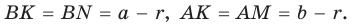
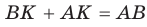
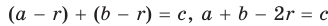
Теорема доказана.
Следствие: 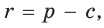
Доказательство:
Преобразуем формулу радиуса вписанной окружности:
Формула 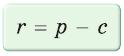
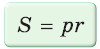
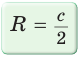
Пример. Дан прямоугольный треугольник, 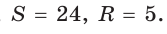
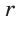
Решение:
Так как 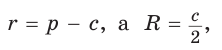
Из формулы 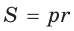
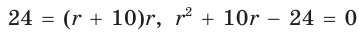
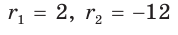
Ответ: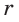
Пример:
Найти радиус окружности, описанной около прямоугольного треугольника, у которого один из катетов равен 6, а радиус вписанной окружности равен 2.
Решение:
Способ 1 (геометрический). Пусть в треугольнике АВС, где 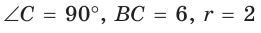
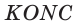
По свойству касательных
Тогда 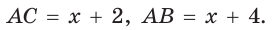
Следовательно,
Радиус описанной окружности
Способ 2 (алгебраический). Подставив в формулу 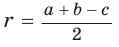
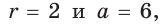
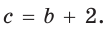
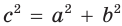
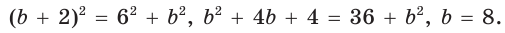
Ответ: 5.
Пример:
Гипотенуза прямоугольного треугольника 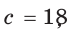
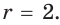
Решение:
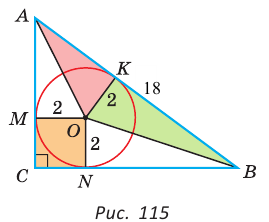
Способ 1 (геометрический). Пусть в 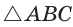
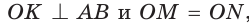
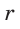
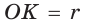
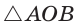
Отсюда 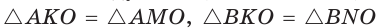
Площадь 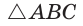
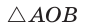
Способ 2 (алгебраический). Из формулы 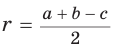
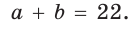
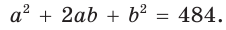
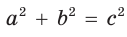
Способ 3 (алгебраический). Из формулы 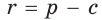
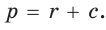
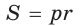
Ответ: 40.
Реальная геометрия:
Есть два листа ДСП (древесно-стружечной плиты). Один из них имеет форму равностороннего треугольника со стороной 1 м, другой — форму прямоугольного равнобедренного треугольника с катетами, равными 1 м (рис. 120). Из каждого листа необходимо вырезать по одному кругу наибольшего диаметра. Определите, из какого листа будет вырезан круг большего диаметра и каким в этом случае будет процент отходов, если известно, что площадь круга можно найти по формуле
Вписанные и описанные четырехугольники
Определение. Окружность называется описанной около многоугольника, если она проходит через все его вершины. При этом многоугольник называется вписанным в окружность.
Окружность называется вписанной в многоугольник, если она касается всех его сторон. При этом много угольник называется описанным около окружности.
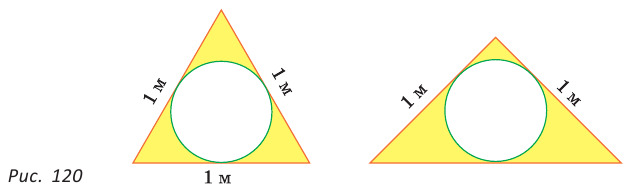
Пятиугольник ABCDE (рис. 121, а) является вписанным в окружность а четырехугольник MNPK (рис. 121, б) — описанным около окружности.
Центр описанной окружности многоугольника находится в точке пересечения серединных перпендикуляров к его сторонам, а центр вписанной — в точке пересечения биссектрис его углов.
Обоснуйте эти утверждения самостоятельно.
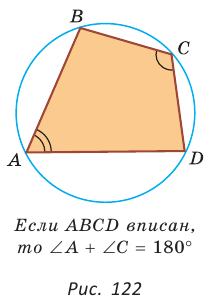
Теорема (свойство вписанного четырехугольника).
Сумма противоположных углов четырехугольника, вписанного в окружность, равна 180°.
Доказательство:
Пусть ABCD — четырехугольник, вписанный в окружность (рис. 122). Его углы А, В, С и D являются вписанными в окружность. Так как вписанный угол равен половине дуги, на которую он опирается, то 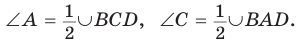
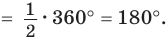
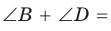
Теорема (признак вписанного четырехугольника).
Если сумма противоположных углов четырехугольника равна 
Доказательство:
Рассмотрим четырехугольник ABCD, у которого 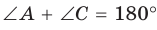
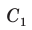
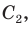
Тогда сумма 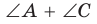
Замечание. Так как сумма углов четырехугольника равна 360°, то для того чтобы около четырехугольника можно было описать окружность, достаточно, чтобы сумма любой пары его противоположных углов была равна 180°.
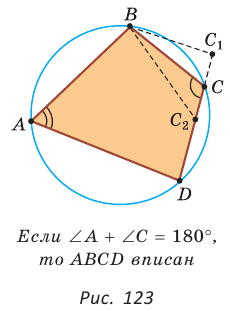
Следствия.
1. Около параллелограмма можно описать окружность, только если этот параллелограмм — прямоугольник (рис. 124, а). Центр этой окружности лежит в точке пересечения диагоналей прямоугольника.
2. Около ромба можно описать окружность, только если этот ромб — квадрат (рис. 124, б).
3. Около трапеции можно описать окружность, только если она равнобедренная (рис. 124, в).
Докажите эти следствия самостоятельно.
Теорема (свойство описанного четырехугольника ).
Суммы противоположных сторон описанного четырехугольника равны между собой.
Доказательство:
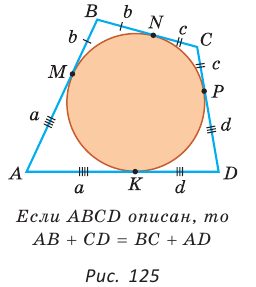
Пусть ABCD — описанный четырехугольник, М, N, Р и К — точки касания его сторон с окружностью (рис. 125). Так как отрезки касательных, проведенных к окружности из одной точки, равны между собой, то AM = АК = а, ВМ = BN = b, СР = CN = с, DP = DK = d. Тогда
откуда AD + ВС = AB + CD.
Теорема доказана.
Следствие:
Периметр описанного четырехугольника равен удвоенной сумме длин любой пары его противоположных сторон:
Теорема (признак описанного четырехугольника).
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Доказательство:
Пусть для выпуклого четырехугольника ABCD справедливо, что
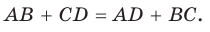
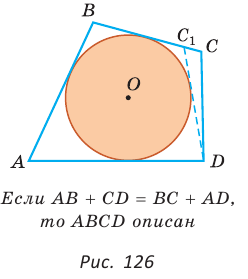
Проведем окружность, которая касается прямых AD, АВ и ВС (рис. 126). Такая окружность существует, ее центр находится в точке пересечения биссектрис углов А и В. Если окружность не касается стороны CD, то либо прямая CD не имеет с окружностью общих точек, либо является секущей. Рассмотрим первый случай. Проведем отрезок 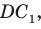
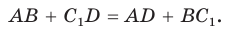
Отняв почленно от равенства (1) равенство (2), получим 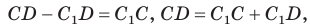
Рассмотрев случай, когда прямая DC — секущая, также придем к противоречию (сделайте это самостоятельно). Следовательно, данная окружность касается стороны CD и в четырехугольник ABCD можно вписать окружность. Теорема доказана.
Следствия.
1. В параллелограмм можно вписать окружность, только если этот параллелограмм — ромб. Центр этой окружности лежит в точке пересечения диагоналей ромба, а ее диаметр равен высоте ромба (рис. 127, а).
2. В прямоугольник можно вписать окружность, только если этот прямоугольник — квадрат (рис. 127, б).
3. Диаметр окружности, вписанной в трапецию, равен ее высоте (рис. 127, в).
Докажите эти следствия самостоятельно.
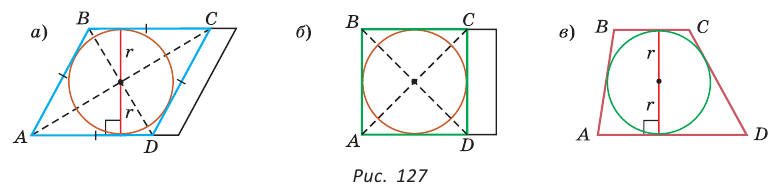
Для описанного многоугольника справедлива формула 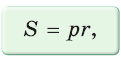
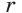
Доказательство аналогично приведенному в § 8 для треугольника. Выполните его самостоятельно, используя рисунок 128.
Пример:
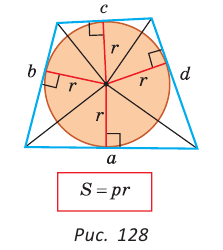
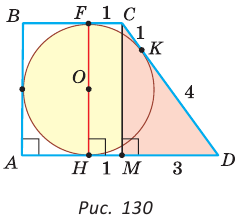
Найти радиус окружности, вписанной в ромб с периметром 24 см и острым углом, равным 45°.
Решение:
Способ 1 (решение прямоугольного треугольника). Пусть ABCD — ромб (рис. 129), О — центр вписанной в ромб окружности. Известно, что высота ВК ромба равна диаметру EF вписанной окружности, т. е. 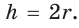
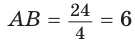
Из прямоугольного треугольника АВК находим. что 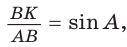
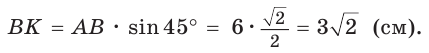
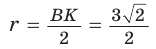
Способ 2 (метод площадей). Ромб — параллелограмм. По формуле площади параллелограмма 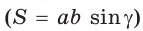
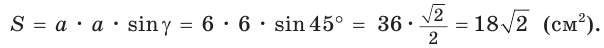
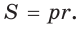
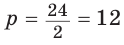
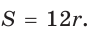
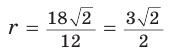
Ответ: 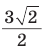
Пример:
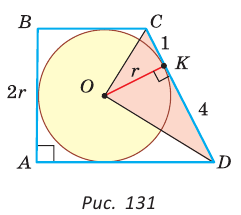
Окружность, вписанная в прямоугольную трапецию ABCD, где 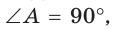
Решение:
Способ 1. Площадь трапеции находится по формуле 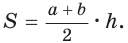
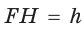
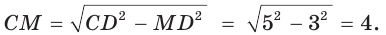
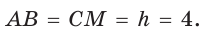
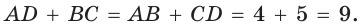
Способ 2*. Центр О вписанной окружности лежит на пересечении биссектрис углов 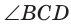
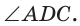
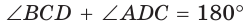
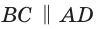
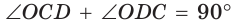
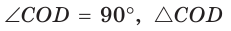
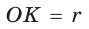
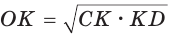
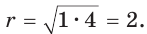
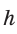
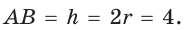
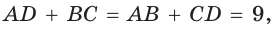
Ответ: 18.
Замечание. Полезно запомнить свойство: «Боковая сторона описанной трапеции видна из центра вписанной окружности под углом 90°».
Пример:
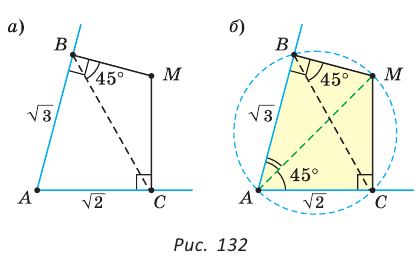
Внутри острого угла А взята точка М, из которой опущены перпендикуляры МВ и МС на стороны угла А, 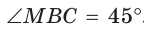
Решение:
Так как в четырехугольнике АВМС сумма углов В и С равна 180°, то около него можно описать окружность. Проведем в ней хорду AM (рис. 132, б). Поскольку 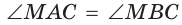
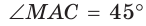
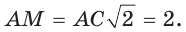
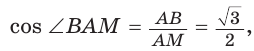
Ответ: 75°.
Окружность, вписанная в треугольник
Пример:
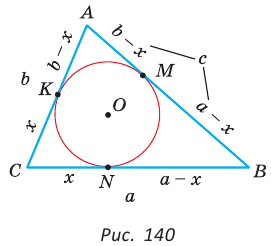
Окружность вписана в треугольник АВС со сторонами ВС = а, АС = Ь, АВ = с. Вывести формулу для нахождения длин отрезков, на которые точки касания окружности со сторонами делят каждую сторону треугольника.
Решение:
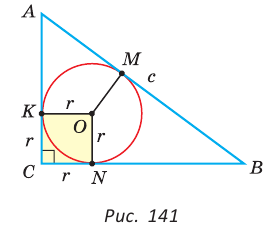
Пусть К, М и N — точки касания вписанной окружности соответственно со сторонами АС, АВ и ВС треугольника АВС (рис. 140). Известно, что отрезки касательных, проведенных из одной точки к окружности, равны между собой.
Тогда, если 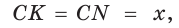
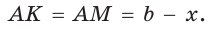
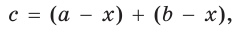
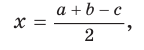
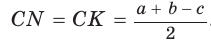
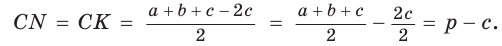
Ответ:
Замечание. Если 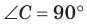
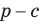
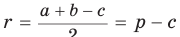
Описанная трапеция
Пример:
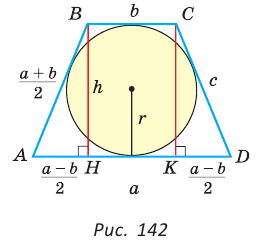
Найти площадь описанной равнобедренной трапеции с основаниями а и Ь.
Решение:
Площадь трапеции можно найти по формуле 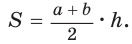
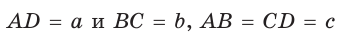
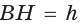
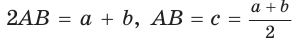
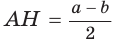
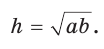
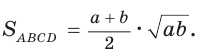
Замечание. Площадь описанной равнобедренной трапеции равна произведению среднего арифметического и среднего геометрического ее оснований.
Полезно запомнить!
Для описанной равнобедренной трапеции с основаниями 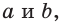
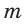
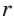
Дополнительные свойства и признаки вписанного четырехугольника
Теорема.
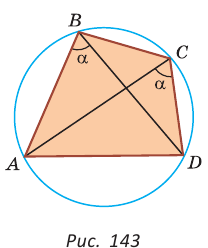
Около четырехугольника можно описать окружность тогда и только тогда, когда угол между его стороной и диагональю равен углу между противоположной стороной и другой диагональю.
Рис. 143
Доказательство:
1. Если четырехугольник ABCD вписан в окружность (рис. 143), то 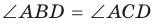
2. Докажем, что если в некотором четырехугольнике ABCD 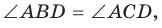
Опишем около треугольника ABD окружность.
В 8-м классе (В. В. Казаков. «Геометрия, 8», с. 186) было доказано свойство:
«Геометрическим местом точек плоскости, из которых данный отрезок AD виден под углом а, является объединение двух дуг окружностей: дуги ABD и ей симметричной относительно прямой AD, исключая точки 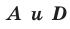
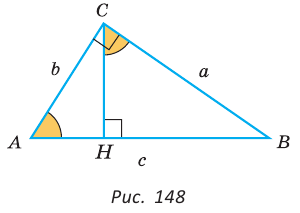
Обобщенная теорема Пифагора
В прямоугольном треугольнике 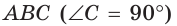
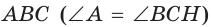
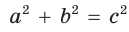
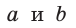
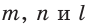
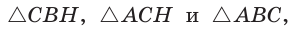
Действительно, из подобия указанных треугольников 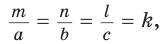
Пример:
Пусть 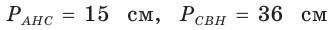
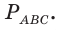
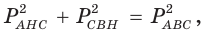
Ответ: 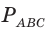
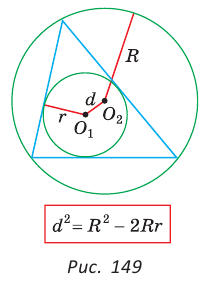
Формула Эйлера для окружностей
Для вписанной и описанной окружностей треугольника с радиусами 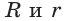
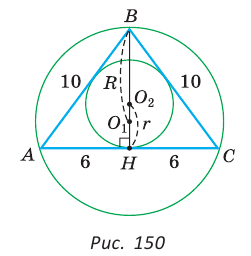
Проверим справедливость этой формулы на примере равнобедренного треугольника АВС, у которого АВ = ВС = 10, АС = 12 (рис. 150).
Вначале найдем расстояние между центрами указанных окружностей традиционным способом.
Проведем высоту ВН, длина которой будет равна 8 (пифагорова тройка 6, 8, 10). Центры описанной и вписанной окружностей — соответственно точки 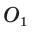
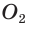
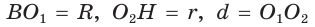
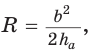
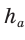
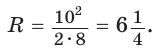
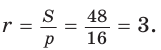
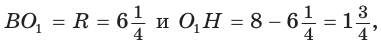
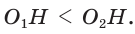
А теперь найдем d по формуле Эйлера:
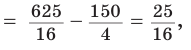
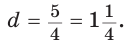
Запомнить:
- Центр описанной окружности треугольника (многоугольника) лежит в точке пересечения серединных перпендикуляров к его сторонам.
- Центр вписанной окружности треугольника (многоугольника) лежит в точке пересечения биссектрис его углов.
- Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы, а ее радиус равен половине гипотенузы:
- Радиус вписанной окружности прямоугольного треугольника находится по формуле
- Если четырехугольник вписан в окружность, то суммы его противоположных углов равны 180°. И обратно.
- Если четырехугольник описан около окружности, то суммы его противоположных сторон равны между собой. И обратно.
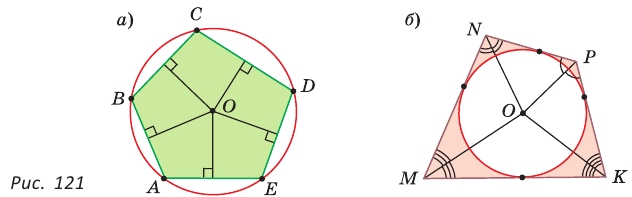
- Площадь треугольника и описанного многоугольника можно найти по формуле
где
— полупериметр,
— радиус вписанной окружности.
Справочная информация по описанной и вписанной окружности треугольника
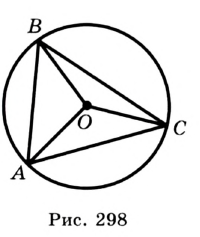
Определение. Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника.
На рисунке 298 изображена окружность, описанная около треугольника. В этом случае также говорят, что треугольник вписан в окружность. Очевидно, что центр описанной окружности треугольника равноудален от всех его вершин. На рисунке 298 точка 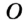
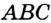
Теорема 21.1. Вокруг любого треугольника можно описать окружность.
Доказательство: Для доказательства достаточно показать, что для любого треугольника 
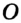
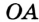
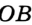
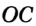
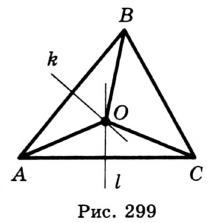
На рисунке 299 изображен произвольный треугольник 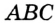
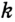
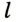
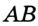
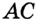

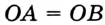
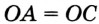
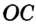

Заметим, что вокруг треугольника можно описать только одну окружность. Это следует из того, что серединные перпендикуляры 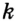
Следствие 1. Три серединных перпендикуляра сторон треугольника пересекаются в одной точке.
Следствие 2. Центр описанной окружности треугольника — это точка пересечения серединных перпендикуляров его сторон.
Определение. Окружность называют вписанной в треугольник, если она касается всех его сторон.
На рисунке 300 изображена окружность, вписанная в треугольник. В этом случае также говорят, что треугольник описан около окружности.
Точка 
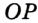
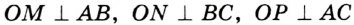
Теорема 21.2. В любой треугольник можно вписать окружность.
Доказательство: Для доказательства достаточно показать, что для любого треугольника 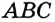
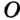
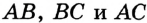
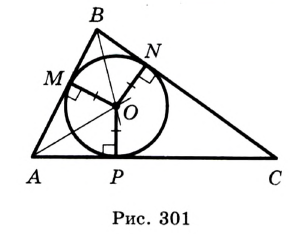
На рисунке 301 изображен произвольный треугольник 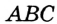


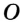





Заметим, что в треугольник можно вписать только одну окружность. Это следует из того, что биссектрисы углов 

Следствие 1. Биссектрисы углов треугольника пересекаются в одной точке.
Следствие 2. Центр вписанной окружности треугольника — это точка пересечения его биссектрис.
Пример:
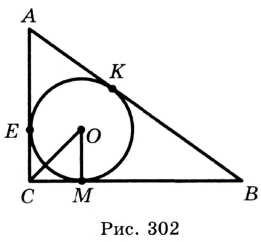
Докажите, что радиус окружности, вписанной в прямоугольный треугольник, определяется по формуле 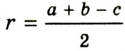
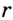
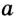
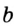
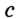
Решение:
В треугольнике 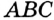
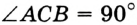
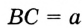
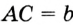
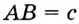
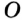
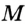
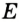
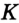
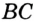
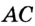
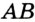
Отрезок 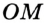
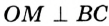
Так как точка 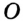
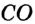
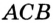
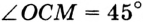
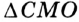
- Плоские и пространственные фигуры
- Взаимное расположение точек и прямых
- Сравнение и измерение отрезков и углов
- Первый признак равенства треугольников
- Треугольники и окружность
- Площадь треугольника
- Соотношения между сторонами и углами произвольного треугольника
- Окружность и круг
В тестовых задачах, не требующих развернутого ответа, принято использовать простые методы решения. В данном случае следует заметить, что радиус описанной окружности можно найти как половину диагонали ВD (это один из диаметров описанной окружности, длина которого выражается целым количеством клеток: 5; диаметр окружности в 2 раза больше ее радиуса).
Обосную этот способ.
Окружность называется описанной около многоугольника, если все вершины этого многоугольника лежат на окружности. В нашем случае все вершины А,В,С и D прямоугольника будут принадлежать описанной окружности, радиус которой требуется найти.
Заметим, что диагонали прямоугольника равны и точкой пересечения делятся пополам. Около прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусам (90+90).
Пусть АС и ВD пересекаются в точке О. Тогда ВО=ОD=АО=ОС (если диагонали равны, то их половины также будут равными). Поэтому точка О является центром описанной окружности, где равные отрезки — ее радиусы.
Поэтому нет необходимости находить радиус каким-то другим способом. Достаточно разделить на 2 длину диагонали ВD прямоугольника, как диаметра описанной окружности, равную 5 единицам.
Решение. 5:2=2,5.
Ответ: 2,5.












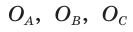
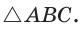
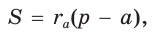
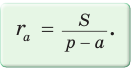
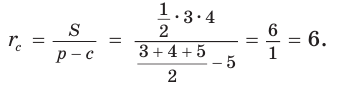
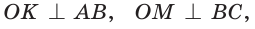
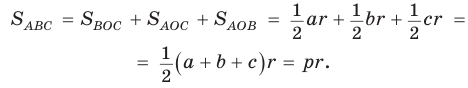
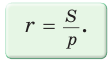
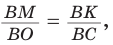
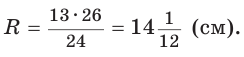
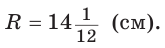
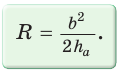
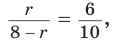
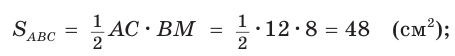
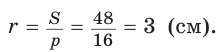
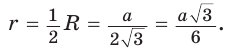
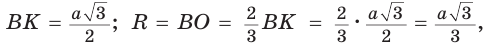
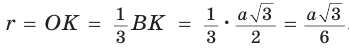
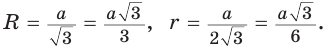
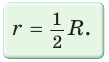
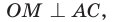
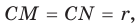
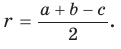
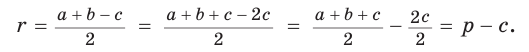
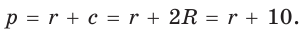
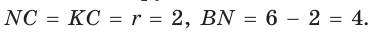
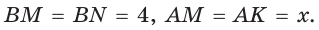
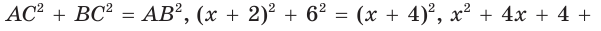
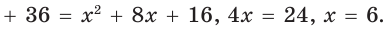
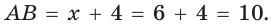
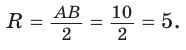
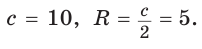
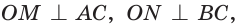
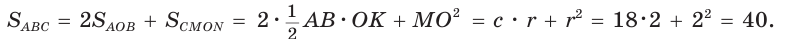
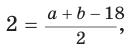
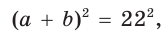
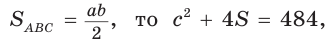
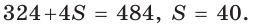
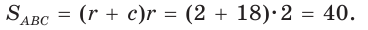
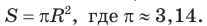

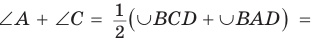
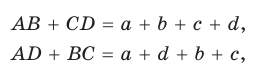
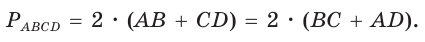
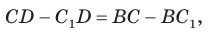
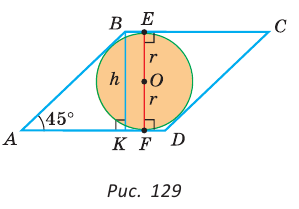
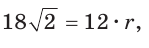
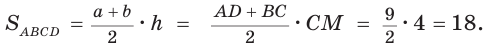
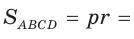
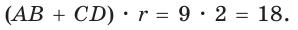
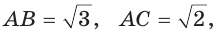
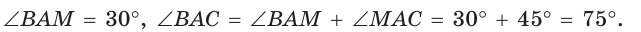
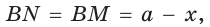
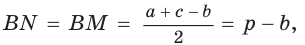
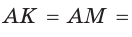
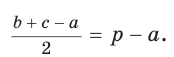
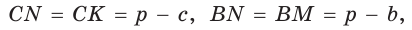
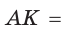
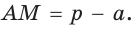
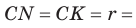
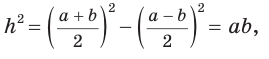
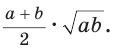
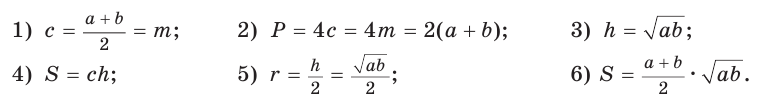
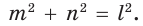
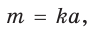
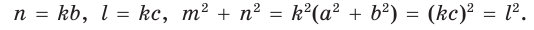
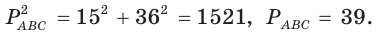
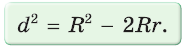
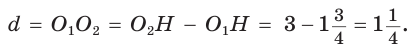
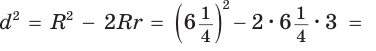
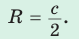
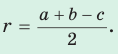
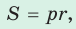 где
где 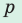 — полупериметр,
— полупериметр, 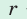 — радиус вписанной окружности.
— радиус вписанной окружности.