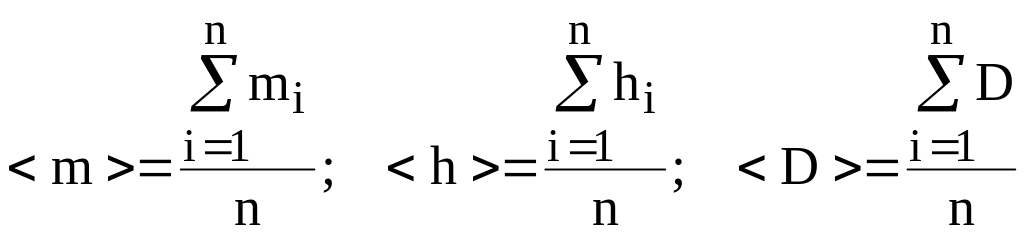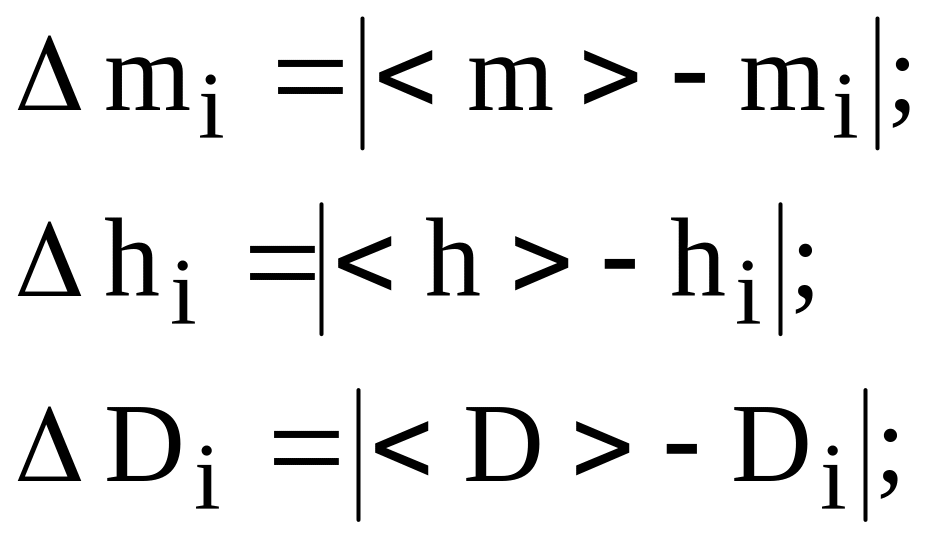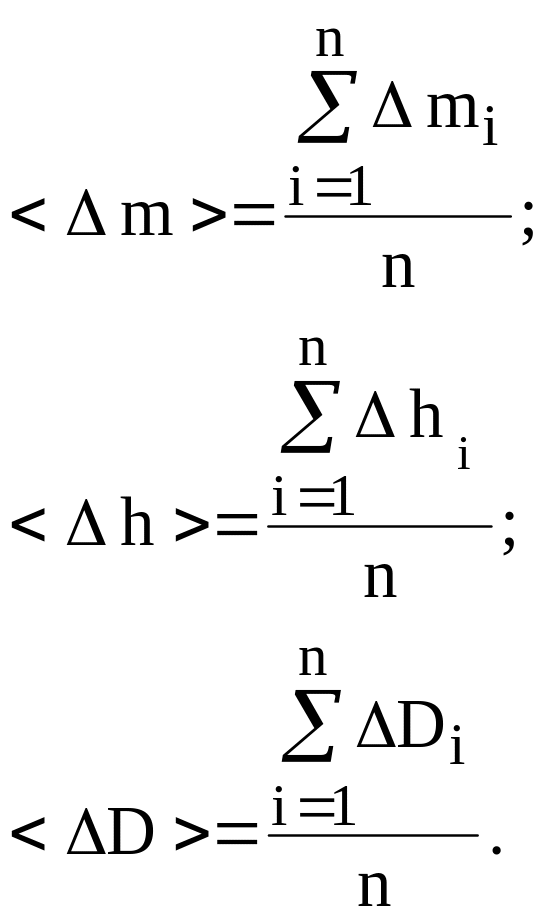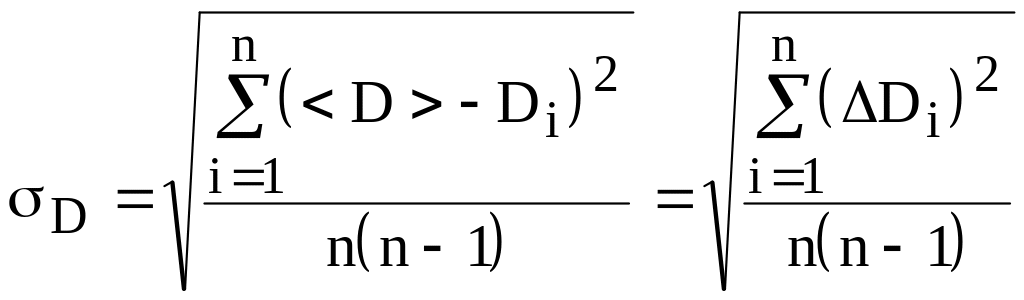Определение плотности твердого тела
Для определения плотности твердого тела используются гидростатические весы,
которые позволяют взвешивать тело как в воздухе, так и в жидкости.
Если
| ρ | плотность твердого тела, | кг/м3 |
|---|---|---|
| ρж | плотность жидкости, в которой тело взвешивается, | кг/м3 |
| G | вес тела в воздухе, | Ньютон |
| Gж | вес тела в жидкости, измеренный при полном его погружении в жидкость, | Ньютон |
то
[ ρ = ρ_{ж} frac{G}{G-G_{ж}} = frac{ρ_{ж}}{1-frac{G_{ж}}{G}} ]
Вычислить, определить плотность твердого тела по формуле (1)
Определение плотности твердого тела |
стр. 504 |
|---|
Любое физическое тело имеет некоторую массу. Определить массу тела можно с помощью весов — путем взвешивания. А также и более сложным способом — при взаимодействии двух тел, зная их скорости, и массу одного из них. Согласитесь, что первый способ — более легкий и практичный.
Тела имеют разные характеристики: разные размеры и формы, разные материалы, разные состояния и структуру (жидкие, твердые и газообразные), разные массы.
Сегодня мы познакомимся с такой характеристикой как плотность. Она покажет и объяснит нам, как может различаться масса тел одинаковой формы и размера.
Связь массы, объема и вещества, из которого состоит тело
Рассмотрим опыт, представленный на рисунке 1.
Возьмем два одинаковых цилиндра: они одинаковой формы и объема, но изготовлены из разных материалов.
Один сделан из алюминия, а другой из свинца. Поместим их на разные чаши весов.
В итоге, мы увидим, что масса цилиндра из алюминия будет почти в 4 раза меньше массы цилиндра из свинца.
Тела, имеющие равные объемы, но состоящие из разных веществ, имеют разные массы.
На рисунке изображены 2 тела массой $100 space г$: лед, железо и золото.
Здесь представлены тела одинаковой массы, но взгляните на их объем. Объем льда будет почти в 8,5 раз больше объема куска железа той же массы. А объем золота будет почти в 3 раза меньше объема железа.
Тела с равными массами, но состоящие из разных веществ, имеют разные объемы.
Определение плотности вещества
Вышерассмотренные свойства веществ, из которых состоят тела, объясняется тем, что разные вещества имеют разную плотность.
Рассмотрим два тела объемом $1 space м^3$ каждое. Если они будут состоять из разных веществ, то их массы тоже будут разными.
Итак, алюминий такого объема будет иметь массу 2700 кг, а свинец такого же объема ( $1 space м^3$) будет имеет массу 11 300 кг.
На рисунке 3 приведены другие примеры тел равного объема, но состоящих из разных веществ.
Плотность показывает, чему равна масса вещества, взятого в объеме $1 space м^3$ (или $1 space см^3$). Чтобы найти плотность вещества, нужно массу тела разделить на его объем.
По какой формуле можно рассчитать плотность вещества? Дадим определение.
Плотность — это физическая величина, которая равна отношению массы тела к его объему:
$плотность = frac{масса}{объем}$
или
$rho = frac{m}{V}$,
где $rho$ (“ро”) — плотность вещества, $m$ — масса тела, $V$ — объем тела.
Единицы измерения плотности
Какова единица плотности в СИ?
В СИ плотность вещества измеряется в килограммах на кубический метр ($1 frac{кг}{м^3}$).
Какие еще единицы плотности вам известны?
Часто используется другая единица измерения — граммы на кубический сантиметр ($1 frac{г}{см^3}$) (рисунок 4).
Иногда нам потребуется переводить плотность веществ, выраженную в $frac{кг}{м^3}$ в $ frac{г}{см^3}$.
Давайте выразим плотность мрамора ($2700 frac{кг}{м^3}$) в $frac{г}{см^3}$:
$$rho = 2700 cdot frac{1 space кг}{1 space м^3} = 2700 cdot frac{1000 space г}{1 space 000 space 000 space см^3} = frac{2700}{1000} cdot frac{г}{см^3} = 2.7 frac{г}{см^3}$$
Таблицы плотности некоторых тел и веществ
Плотность одного и того же вещества в твердом, жидком и газообразном состояниях различна.
Например, плотность воды составляет $1000 frac{кг}{м^3}$, льда — $900 frac{кг}{м^3}$, водяного пара — $0.590 frac{кг}{м^3}$ (рисунок 5).
Плотности различных твердых тел
| Твердое тело | $rho, frac{кг}{м^3}$ | $rho, frac{г}{см^3}$ | Твердое тело | $rho, frac{кг}{м^3}$ | $rho, frac{г}{см^3}$ |
|---|---|---|---|---|---|
| Осмий | 22 600 | 22,6 | Мрамор | 2700 | 2,7 |
| Иридий | 22 400 | 22,4 | Стекло | 2500 | 2,5 |
| Платина | 21 500 | 21,5 | Фарфор | 2300 | 2,3 |
| Золото | 19 300 | 19,3 | Бетон | 2300 | 2,3 |
| Свинец | 11 300 | 11,3 | Кирпич | 1800 | 1,8 |
| Серебро | 10 500 | 10,5 | Сахар | 1600 | 1,6 |
| Медь | 8900 | 8,9 | Оргстекло | 1200 | 1,2 |
| Латунь | 8500 | 8,5 | Капрон | 1100 | 1,1 |
| Сталь, железо | 7800 | 7,8 | Полиэтилен | 920 | 0,92 |
| Олово | 7300 | 7,3 | Парафин | 900 | 0,90 |
| Цинк | 7100 | 7,1 | Лед | 900 | 0,90 |
| Чугун | 7000 | 7,0 | Дуб сухой | 700 | 0,70 |
| Корунд | 4000 | 4,0 | Сосна сухая | 400 | 0,40 |
| Алюминий | 2700 | 2,7 | Пробка | 240 | 0,24 |
Плотности различных жидкостей
| Жидкость | $rho, frac{кг}{м^3}$ | $rho, frac{г}{см^3}$ | Жидкость | $rho, frac{кг}{м^3}$ | $rho, frac{г}{см^3}$ |
|---|---|---|---|---|---|
| Ртуть | 13 600 | 13,60 | Керосин | 800 | 0,80 |
| Серная кислота | 1800 | 1,80 | Спирт | 800 | 0,80 |
| Мед | 1350 | 1,35 | Нефть | 800 | 0,80 |
| Вода морская | 1030 | 1,03 | Ацетон | 790 | 0,79 |
| Молоко цельное | 1030 | 1,03 | Эфир | 710 | 0,41 |
| Вода чистая | 1000 | 1,00 | Бензин | 710 | 0,71 |
| Масло подсолнечное | 930 | 0,93 | Жидкое олово (при $400^{circ}$) | 6800 | 6,80 |
| Масло машинное | 900 | 0,90 | Жидкий воздух (при $-194^{circ}$) | 860 | 0,86 |
Плотности различных газов
| Газ | $rho, frac{кг}{м^3}$ | $rho, frac{г}{см^3}$ | Газ | $rho, frac{кг}{м^3}$ | $rho, frac{г}{см^3}$ |
|---|---|---|---|---|---|
| Хлор | 3,210 | 0,00321 | Угарный газ | 1,250 | 0,00125 |
| Углекислый газ | 1,980 | 0,00198 | Природный газ | 0,800 | 0,0008 |
| Кислород | 1,430 | 0,00143 | Водяной пар (при $100^{circ}$) | 0,590 | 0,00059 |
| Воздух (при $0^{circ}C$ | 1,290 | 0,00129 | Гелий | 0,180 | 0,00018 |
| Азот | 1,250 | 0,00125 | Водород | 0,090 | 0,00009 |
Примеры задач на расчет плотности вещества
Задача №1
В таблице 1 указана плотность сахара — $1600 frac{кг}{м^3}$. Что это значит? Какой здесь физический смысл?
Посмотреть ответ
Скрыть
Ответ:
Значение плотности показывает нам, какое количество вещества (его масса) будет находиться в объеме $1 space м^3$. Итак, это означает, что масса сахара объемом $1 space м^3$ будет равна $1600 space кг$.
Задача №2
Канистра объемом 30 л наполнена бензином. Масса полной канистры составляет 21,3 кг. Рассчитайте плотность бензина.
Переведем литры в кубические метры ($1 space л = 0.001 space м^3$):
$30 cdot 0.001 = 0.03 space м^3$.
Дано:
$V = 30 space л$
$m = 21.3 space кг$
$rho -?$
Показать решение и ответ
Скрыть
Решение:
По определению плотности:
$rho = frac{m}{V}$.
$rho = frac{21.3 space кг}{0.03 space м^3} = 710 frac{кг}{м^3}$.
Если мы сравним полученное значение с табличным, то получим подтверждение, что задача решена верно.
Ответ: $rho = 710 frac{кг}{м^3}$.
Задача №3
Деревянный брусок из березы имеет следующие размеры: длину 3 м, высоту 10 см, и ширину 50 см. Масса бруска составляет 75 кг. Найдите плотность березы.
Дано:
$а = 3 space м$
$b = 10 space см$
$c = 50 space см$
$m = 75 space кг$
$rho -?$
Показать решение и ответ
Скрыть
Решение:
Найдем объем бруска:
$V = a cdot b cdot c$,
$V = 3 space м cdot 0.1 space м cdot 0.5 space м = 0.15 space м^3$.
По определению плотности:
$rho = frac{m}{V}$.
$rho = frac{75 space кг}{0.15 space м^3} = 500 frac{кг}{м^3}$.
Ответ: $rho = 500 frac{кг}{м^3}$.
Больше задач с подробными решениями смотрите в отдельном уроке.
Упражнения
Упражнение №1
Плотность редкого металла осмия равна $22 space 600 frac{кг}{м^3}$. Что это означает?
Посмотреть ответ
Скрыть
Ответ:
Значение плотности показывает нам, какое количество вещества (его масса) будет находиться в объеме $1 space м^3$. Итак, это означает, что масса осмия объемом $1 space м^3$ будет равна $22 space 600 space кг$ или $22.6 space т$.
Упражнение №2
Пользуясь таблицами плотностей (таблицы 1, 2), определите, плотность какого вещества больше: цинка или серебра; бетона или мрамора; бензина или спирта.
Показать ответ
Скрыть
Плотность цинка составляет $7100 frac{кг}{м^3}$, а серебра — $10 space 500 frac{кг}{м^3}$. Получается, что плотность серебра больше плотности цинка.
Плотность бетона составляет $2300 frac{кг}{м^3}$, а мрамора — $2700 frac{кг}{м^3}$. Получается, что плотность мрамора больше плотности бетона.
Плотность бензина составляет $710 frac{кг}{м^3}$, а спирта — $800 frac{кг}{м^3}$. Получается, что плотность спирта больше плотности бензина.
Упражнение №3
Три кубика — из мрамора, льда и латуни — имеют одинаковый объем. Какой из них имеет большую массу, а какой — меньшую?
Показать ответ
Скрыть
Выразим массу из формулы плотности:
$rho = frac{m}{V}$,
$m = rho V$.
Объем кубиков у нас одинаковый. Значит, чем больше плотность вещества, из которого изготовлен кубик, тем больше его масса.
Плотность мрамора составляет $2700 frac{кг}{м^3}$, льда — $900 frac{кг}{м^3}$, а латуни — $8500 frac{кг}{м^3}$. У латуни наибольшая плотность, а у льда — наименьшая. Значит, кубик из латуни будет иметь наибольшую массу, а из льда — наименьшую.
Упражнение №4
Самое легкое дерево — бальза. Масса древесины этого дерева равна $12 space г$ при объеме в $100 space см^3$. Определите плотность древесины в $frac{г}{см^3}$ и $frac{кг}{м^3}$.
Дано:
$m = 12 space г$
$V = 100 space см^3$
$rho — ?$
Показать решение и ответ
Скрыть
Решение:
Мы не стали переводить единицы измерения в СИ. Сначала мы рассчитаем плотность этой древесины в $frac{г}{см^3}$, а затем переведем в $frac{кг}{м^3}$.
Рассчитаем плотность по известной нам формуле:
$rho = frac{m}{V}$,
$rho = frac{12 space г}{100 space см^3} = 0.12 frac{г}{см^3}$.
Теперь переведем полученное значение в $frac{кг}{м^3}$:
$rho = 0.12 frac{г}{см^3} = 0.12 frac{0.001 space кг}{0.01^3 space м^3} = 0.12 frac{10^{-3} space кг}{10^{-6} space м^3} = 0.12 cdot 10^3 frac{кг}{м^3} = 120 frac{кг}{м^3}$.
Ответ: $rho = 0.12 frac{г}{см^3} = 120 frac{кг}{м^3}$.
Упражнение №5
Кусочек сахара имеет размеры: $а = 2.5 space см$, $b = 1 space см$, $с = 0.7 space см$ (рис. 53). Его масса равна $0.32 space г$. Определите плотность сахара. Проверьте полученный результат по таблице 1.
Дано:
$а = 2.5 space см$
$b = 1 space см$
$с = 0.7 space см$
$m = 0.32 space г$
$rho — ?$
Показать решение и ответ
Скрыть
Решение:
Чтобы рассчитать плотность сахара, нужно знать его объем. Его мы можем вычислить перемножив друг на друга известные высоту, ширину и длину:
$V = a cdot b cdot c$.
Подставим в формулу плотности и рассчитаем ее:
$rho = frac{m}{V} = frac{m}{a cdot cdot b cdot c}$,
$rho = frac{0.32 space г}{2.5 space см cdot 1 space см cdot 0.7 space см} = frac{0.32 space г}{1.75 space см^3} approx 0.18 frac{г}{см^3}$.
Полученный результат не совпадает с табличным ($rho = 1.6 frac{г}{см^3}$). Расчеты произведены верно, значит ошибка или в условии задачи, или мы наблюдаем очень необычный сахар.
Ответ: $rho approx 0.18 frac{г}{см^3}$.
Задание
В вашем распоряжении имеются весы с разновесами, измерительный цилиндр с водой и металлический шарик на нити. Предложите, как определить плотность шарика.
Взвесим шарик, мы узнаем его массу. Чтобы определить его объем, мы можем использовать измерительный цилиндр с водой. Для этого нужно опустить шарик в воду, и посмотреть, до какого уровня теперь поднялась воды. Разность этого объема и первоначального объема жидкости будет равна объему шарику.
Зная его массу и объем, мы сможем рассчитать его плотность по формуле: $rho = frac{m}{V}$.
Цель работы: Научиться определять
плотность твердого тела.
Приборы и материалы:
- Весы с разновесами;
- Линейка ученическая;
- Твердые тела, плотность, которых надо
определять.
Теория.
Плотность – это физическая величина, которая
равна отношению массы тела к его объему: (1)
В СИ единицей плотности является килограмм на
кубический метр:
Очень часто плотность вещества выражается в
граммах на кубический сантиметр:
Например: Вода имеет плотность 1
гсм3; ртуть – 13600 гсм3; железо – 7, 8
гсм3; воздух – 0,0013 гсм3.
Пример: Плотность чугуна 7000 кгм3.
Выразите ее в гсм3.
Сначала килограммы переведем в граммы, а
кубические метры в кубические сантиметры: р =
7000кгм3 = 7000 *1000 кг106 см3 = 7 гсм3.
Плотность одного и того же вещества в твердом,
жидком и газообразном состояниях различна.
Работа №1. Определение плотности вещества
брусков.
Определить плотность брусков из древесины,
пластмассы и металлов.
Указания к работе.
- Напишите формулу (1) и обдумайте, что нужно
измерять для определения плотности вещества.
Составьте таблицу для занесения результатов
измерений и вычислений. - Измерьте массу тел.
- Измерьте размеры тел и определите их объем.
- Рассчитайте по формуле (1) плотность данных тел.
- Результаты измерений и вычислений занесите в
таблицу 1. - Сравните полученные результаты с данными из
таблиц плотностей. - Оцените погрешности вычислений физических
величин. - Ответьте на следующие вопросы:
— Плотность воды 1000 кгм3 . Что это
означает?
— Как можно определить наличие пустот в телах,
если известно из какого вещества они сделаны?
Таблица №1. Параметры брусков.
| Номер опыта | Брусок | Масса тела, г | Размеры брусков | Объем, V=авс, см3 | ||
| Длина а, см | Ширина в, см | Высота с, см | ||||
| 1. | ||||||
| 2. | ||||||
| 3. | ||||||
| 4. |
Таблица №2. Плотность вещества
брусков.
| Номер опыта | Брусок | Плотность вещества | Вещество | |
| гсм3 | кгсм3 | |||
| 1. | ||||
| 2. | ||||
| 3. | ||||
| 4. |
Работа №2. Определение плотности вещества
тела в форме параллелепипеда со сквозной
цилиндрической выемкой.
Определить плотность деревянного тела в форме
параллелепипеда со сквозной цилиндрической
выемкой.
Указания к работе.
- Напишите формулу (1) и обдумайте, что нужно
измерять для определения плотности вещества
твердого тела. - Измерьте массу тела.
- Измерьте размеры тела и определите его объем.
- Измерьте радиус и высоту воздушного цилиндра в
теле. Вычислить объем воздушного цилиндра. - Вычислите объем древесины.
- Рассчитайте плотность древесины по формуле (1).
- Результаты измерений и вычислений занесите в
таблицы № №1,2,3. - Определите сорт древесины по таблице
плотностей. - Оцените погрешности физических величин.
- Решите задачу (1): Кусок металла массой 461,5 г
имеет объем 65 см3. Что это за металл?
Таблица №1. Параметры бруска.
| Номер опыта | Длина а, | Ширина в, | Высота с, | Объем, V=авс |
| см | см | см | см3 | |
| 1. |
Таблица №2. Параметры воздушного
цилиндра.
| Радиус цилиндра, см | Объем цилиндра |
Таблица №3 Плотность вещества
твердого тела.
| Масса, г | Объем,см3 | Плотность, гсм3 | Сорт древесины |
Работа №3 Определение плотности вещества тела
в форме параллелепипеда с шестью
цилиндрическими выемками.
Указания к работе.
- Напишите формулу (1) и обдумайте, что нужно
измерять для определения плотности данного
твердого тела. - Измерьте массу тела.
- Измерьте размеры тела и определите его объем.
- Измерьте радиус и высоту воздушных цилиндров в
теле. Определите их суммарный объем. - Вычислите объем древесины.
- Рассчитайте плотность древесины по формуле (1).
- Результаты измерений и вычислений занесите в
таблицу №№ 1,2,3. - Оцените погрешности физических величин.
- Решите задачу (1): Три кубика – из мрамора, льда и
латуни имеют одинаковый объем. Какой из них имеет
большую массу, а какой меньшую.
Таблица №1 Параметры бруска.
| Длина, см | Ширина, см | Высота, см | Объем, см3 | |
Таблица №2. Параметры воздушных
цилиндров.
| Номер опыта № | Радиус цилиндра, см | Объем цилиндра, см | Сумма объемов воздушных цилиндров, см3 |
| 1. | |||
| 2. | |||
| 3. | |||
| 4. | |||
| 5. | |||
| 6 | |||
Таблица №3. Плотность вещества
тела.
| Масса | Объем, см3 | Плотность, гсм3 | Плотность, кгсм3 |
Задачи(1,2,5).
- Чугунный шар при объеме 125 см3 имеет массу
800 г. Сплошной или полый этот шар? - Картофелина массой 59 г. имеет объем 50 см3.
Определите плотность картофеля и выразите ее в
килограммах на кубический метр (кгм3). - Из какого металла изготовлена втулка
подшипника, если ее масса 3,9 кг, а объем 500 см3? - Точильный брусок, масса которого 300 г, имеет
размер 15*5*2 см. Определите плотность вещества, из
которого он сделан. - Определите массу мраморной плиты, размер
которой 1,0*0,8*0,1 м. - Как определить плотность неизвестной жидкости,
используя только стакан, воду и весы с
разновесом? - Как определить плотность неизвестной жидкости,
используя стакан и весы с разновесом из латуни? - Деталь, отлитая из меди, имеет массу М. Какую
массу m имела деревянная модель детали, если
известны плотности меди и дерева? - Начертите график зависимости плотности воды
данной массы от температуры. Температура воды
изменяется от 0 до 80 С. - Начертите график зависимости объема воды
данной массы от температуры. Температура воды
изменяется от 0 до 80 С.
Литература:
- Лукашик В.И. Сборник задач по физике 7-8 класс,
Москва, “Просвещение”, 1994. - Лукашик В.И. Физическая олимпиада. Москва,
“Просвещение”, 1999. - Мякишев Г.Я., Буховцев Б.Б. Физика 10 класс, Москва,
“Просвещение”, 2000. - Перышкин А.В. Физика, 7 класс, Москва, “Дрофа”,
2004. - Рымкевич А.П. Сборник задач по физике. Москва,
“Просвещение”. 2000.
Плотность тела и метод ее определения
Плотность —
это отношение массы тела к объему, в
котором эта масса распределена. Если
тело однородно, то плотность определяется
по формуле
,
где m
— масса тела, V-объем
тела. Для тела цилиндрической формы,
плотность определяется по формуле
(1)
где D—
диаметр цилиндра, h
высота цилиндра.
В
данной лабораторной работе предлагается
произвести расчет погрешностей измерений
по методу среднего арифметического.
Однако существуют и другие способы
расчета погрешностей
.
Среднее значение
массы, высоты и диаметра цилиндра
определяют по формулам
(2)
Находят абсолютные
погрешности каждого из измерений:
(3)
а затем значения
средних абсолютных погрешностей:
(4)
В том случае, если
значение средней абсолютной погрешности
измерения меньше погрешности прибора,
то при дальнейших расчетах берется
погрешность прибора. Например, для <h>,
берется погрешность штангенциркуля,
равная цене его деления.
В соответствии с
изложенной выше методикой расчета
погрешности косвенных измерений
осуществим расчет погрешности определения
плотности. Вначале логарифмируем
почленно левую и правую части равенства
(1), получим
Далее дифференцируя
почленно левую и правую части считая
ln4 постоянной величиной, имеем
Заменяем дифференциалы
величин их приращениями, в качестве
которых будем применять средние
абсолютные погрешности
Считая, что
погрешности отдельных прямых измерений
взаимно усиливают друг друга, заменяют
в правой части все знаки “ – “ на “ + “
(5)
Поскольку число
взято с определенной степенью точности,
его также можно считать измеренным. А
в качестве погрешности принять половину
единицы последнего разряда, который
определен в числе .
Так, при
= 3,14
= 0, 005. В правой части выражения (5) все
величины известны, поэтому можно
рассчитывать относительную погрешность
определения плотности
(6)
а затем и абсолютную
погрешность
(7)
Расчет плотности
следует проводить один раз, подставляя
среднее значение массы <m>, диаметра
<D> и высоты <h>.
Можно указать и
более точный метод расчета погрешностей
с помощью нахождения среднеквадратичных
ошибок:
-
Логарифмируем
выражение (1)
-
Дифференцируем
последнее выражение
и преобразуем его
к виду
(8)
где
(9)
<m>, <D>, <h>
— средние арифметические значения массы,
диаметра и высоты
m,
D,
h
– выборочные средние квадратичные
отклонения при измерении массы, диаметра
и высоты образца
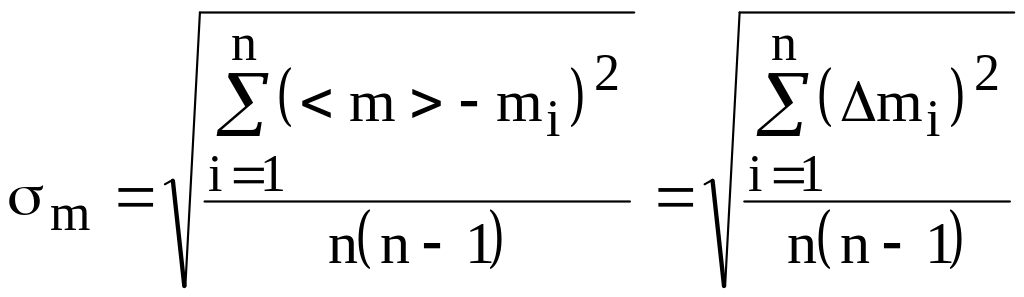
(10)
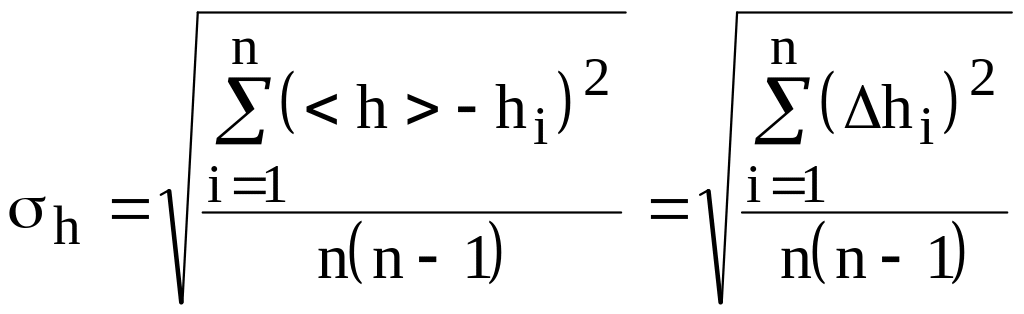
-
Из выражения (8)
определяем
(11)
-
Определяем величину
,
называемую доверительной случайной
погрешностью измерения плотности по
формуле
(12)
где коэффициент
называемый коэффициентом Стьюдента,
учитывает конечное число п
наблюдений и надежность (доверительную
вероятность р)
результата. Аппарат математической
статистики позволяет вычислять
коэффициенты
для любых р
и п.
Результаты таких вычислений приведены
в таблицах. Например, задаваясь
доверительной вероятностью р
= 0,8,
находим из таблицы, что для п
= 4 коэффициент
Стьюдента
.
Следовательно, в выбранном примере,
истинное значение плотности твердого
тела лежит в интервале
(13)
с вероятностью
р=0,8
Эта вероятность
означает, что из 4-х измерений 80% измеряемых
величин будет лежать в промежутке от
.
Выражения для
вычисления погрешностей нескольких
элементарных функций представлены в
таблице.
Таблица
|
№ п/п |
Вид функции |
Относительная |
|
1 |
2 |
3 |
|
1 |
У = а + в |
|
|
2 |
У = а — в |
|
|
3 |
У = а ∙ в ∙ с |
|
|
4 |
|
|
|
5 |
|
|
|
1 |
2 |
3 |
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
Примечание. При
вычислении погрешностей необходимо
учесть, что а, в и φ представляют собой
средние значения измеренных величин,
а также то, что
являются средними абсолютными ошибками
этих величин.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
| Плотность | |
 |
|
| Размерность | L−3 M |
|---|---|
| Единицы измерения | |
| СИ | кг/м³ |
| СГС | г/см³ |
| Примечания | |
| скалярная величина |
Пло́тность — скалярная физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму[1].
Для обозначения плотности обычно используется греческая буква ρ (ро) (происхождение обозначения подлежит уточнению), иногда используются также латинские буквы D и d (от лат. densitas — «плотность»).
Более точное определение плотности требует уточнение формулировки:
- Средняя плотность тела — отношение массы тела к его объёму. Для однородного тела она также называется просто плотностью тела.
- Плотность вещества — это плотность однородного или равномерно неоднородного тела, состоящего из этого вещества.
- Плотность тела в точке — это предел отношения массы малой части тела (
), содержащей эту точку, к объёму этой малой части (
), когда этот объём стремится к нулю[2], или, записывая кратко,
. При таком предельном переходе необходимо помнить, что на атомарном уровне любое тело неоднородно, поэтому необходимо остановиться на объёме, соответствующем используемой физической модели.
Поскольку масса в теле может быть распределена неравномерно, более адекватная модель определяет плотность в каждой точке тела как производную массы по объёму. Если учитывать точечные массы, то плотность можно определить как меру, либо как производную Радона—Никодима по отношению к некоторой опорной мере.
Содержание
- 1 Виды плотности и единицы измерения
- 2 Формула нахождения плотности
- 3 Зависимость плотности от температуры
- 4 Диапазон плотностей в природе
- 5 Плотности астрономических объектов
- 6 Плотности некоторых газов
- 7 Плотности некоторых жидкостей
- 8 Плотность некоторых пород древесины
- 9 Плотность некоторых металлов
- 10 Измерение плотности
- 11 См. также
- 12 Примечания
- 13 Литература
- 14 Ссылки
Виды плотности и единицы измерения
Исходя из определения плотности, её размерность представляет собой кг/м³ в СИ и г/см³ в системе СГС.
Для сыпучих и пористых тел различают:
- истинную плотность, определяемую без учёта пустот;
- удельную (кажущуюся) плотность, рассчитываемую как отношение массы вещества ко всему занимаемому им объёму. Истинную плотность из кажущейся получают с помощью величины коэффициента пористости — доли объёма пустот в занимаемом объёме. Для сыпучих тел удельная плотность называется насыпно́й плотностью.
Формула нахождения плотности
Плотность (плотность однородного тела или средняя плотность неоднородного) находится по формуле:
где m — масса тела, V — его объём;
формула является просто математической записью определения термина «плотность», данного выше.
- При вычислении плотности газов при нормальных условиях эта формула может быть записана и в виде:
- где М — молярная масса газа,
— молярный объём (при нормальных условиях приближённо равен 22,4 л/моль).
Плотность тела в точке записывается как
тогда масса неоднородного тела (тела с плотностью, зависящей от координат) рассчитывается как
Зависимость плотности от температуры
Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность в определённом диапазоне температур ведёт себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого значения.
При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Вода, кремний, висмут и некоторые другие вещества являются исключениями из данного правила, так как их плотность при затвердевании уменьшается.
Диапазон плотностей в природе
Для различных природных объектов плотность меняется в очень широком диапазоне.
- Самую низкую плотность имеет межгалактическая среда (2·10−31—5·10−31 кг/м³, без учёта тёмной материи)[3].
- Плотность межзвёздной среды приблизительно равна 10−23—10−21 кг/м³.
- Средняя плотность красных гигантов в пределах их фотосфер много меньше, чем у Солнца — из-за того, что их радиус в сотни раз больше при сравнимой массе.
- Плотность газообразного водорода (самого лёгкого газа) при нормальных условиях равна 0,0899 кг/м³.
- Плотность сухого воздуха при нормальных условиях составляет 1,293 кг/м³.
- Один из самых тяжёлых газов, гексафторид вольфрама, примерно в 10 раз тяжелее воздуха (12,9 кг/м³ при +20 °C)
- Жидкий водород при атмосферном давлении и температуре −253 °C имеет плотность 70 кг/м³.
- Плотность жидкого гелия при атмосферном давлении равна 130 кг/м³.
- Усреднённая плотность тела человека от 940—990 кг/м³ при полном вдохе, до 1010—1070 кг/м³ при полном выдохе.
- Плотность пресной воды при 4 °C 1000 кг/м³.
- Средняя плотность Солнца в пределах фотосферы около 1410 кг/м³, примерно в 1,4 раза выше плотности воды.
- Гранит имеет плотность 2600 кг/м³.
- Средняя плотность Земли равна 5520 кг/м³.
- Плотность железа равна 7874 кг/м³.
- Плотность металлического урана 19100 кг/м³.
- Плотность атомных ядер приблизительно 2·1017 кг/м³.
- Теоретически верхняя граница плотности по современным физическим представлениям это планковская плотность 5,1·1096 кг/м³.
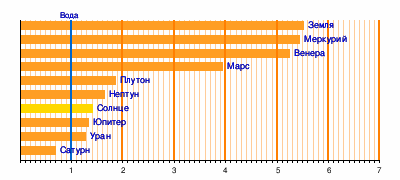
Плотности астрономических объектов
Средняя плотность небесных тел Солнечной
системы (в г/см³)[4][5][6]
- Средние плотности небесных тел Солнечной системы см. на врезке.
- Межпланетная среда в Солнечной системе достаточно неоднородна и может меняться во времени, её плотность в окрестностях Земли ~10−21÷10−20 кг/м³.
- Плотность межзвёздной среды ~10−23÷10−21 кг/м³.
- Плотность межгалактической среды 2×10−34÷5×10−34 кг/м³.
- Средняя плотность красных гигантов на много порядков меньше из-за того, что их радиус в сотни раз больше, чем у Солнца.
- Плотность белых карликов 108÷1012 кг/м³
- Плотность нейтронных звёзд имеет порядок 1017÷1018 кг/м³.
- Средняя (по объёму под горизонтом событий) плотность чёрной дыры зависит от её массы и выражается формулой:
- Средняя плотность падает обратно пропорционально квадрату массы чёрной дыры (ρ~M−2). Так, если чёрная дыра с массой порядка солнечной обладает плотностью около 1019 кг/м³, превышающей ядерную плотность (2×1017 кг/м³), то сверхмассивная чёрная дыра с массой в 109 солнечных масс (существование таких чёрных дыр предполагается в квазарах) обладает средней плотностью около 20 кг/м³, что существенно меньше плотности воды (1000 кг/м³).
Плотности некоторых газов
| Азот | 1,250 | Кислород | 1,429 |
| Аммиак | 0,771 | Криптон | 3,743 |
| Аргон | 1,784 | Ксенон | 5,851 |
| Водород | 0,090 | Метан | 0,717 |
| Водяной пар (100 °C) | 0,598 | Неон | 0,900 |
| Воздух | 1,293 | Радон | 9,81 |
| Гексафторид вольфрама | 12,9 | Углекислый газ | 1,977 |
| Гелий | 0,178 | Хлор | 3,164 |
| Дициан | 2,38 | Этилен | 1,260 |
Плотности некоторых жидкостей
| Бензин | 710 | Молоко | 1040 |
| Вода (4 °C) | 1000 | Ртуть (0 °C) | 13600 |
| Керосин | 820 | Эфир | 720 |
| Глицерин | 1260 | Спирт | 800 |
| Морская вода | 1030 | Скипидар | 860 |
| Масло оливковое | 920 | Ацетон | 792 |
| Масло моторное | 910 | Серная кислота | 1840 |
| Нефть | 550—1050 | Жидкий водород (−253 °C) | 70 |
Плотность некоторых пород древесины
| Бальса | 0,15 | Пихта сибирская | 0,39 |
| Секвойя вечнозелёная | 0,41 | Ель | 0,45 |
| Ива | 0,46 | Ольха | 0,49 |
| Осина | 0,51 | Сосна | 0,52 |
| Липа | 0,53 | Конский каштан | 0,56 |
| Каштан съедобный | 0,59 | Кипарис | 0,60 |
| Черёмуха | 0,61 | Лещина | 0,63 |
| Грецкий орех | 0,64 | Берёза | 0,65 |
| Вишня | 0,66 | Вяз гладкий | 0,66 |
| Лиственница | 0,66 | Клён полевой | 0,67 |
| Тиковое дерево | 0,67 | Бук | 0,68 |
| Груша | 0,69 | Дуб | 0,69 |
| Свитения (Махагони) | 0,70 | Платан | 0,70 |
| Жостер (крушина) | 0,71 | Тис | 0,75 |
| Ясень | 0,75 | Слива | 0,80 |
| Сирень | 0,80 | Боярышник | 0,80 |
| Пекан (кария) | 0,83 | Сандаловое дерево | 0,90 |
| Самшит | 0,96 | Эбеновое дерево | 1,08 |
| Квебрахо | 1,21 | Бакаут | 1,28 |
| Пробка | 0,20 |
Плотность некоторых металлов
Значения плотности металлов могут изменяться в весьма широких пределах: от наименьшего значения у лития, который легче воды, до наибольшего значения у осмия, который тяжелее золота и платины.
| Осмий | 22,61[7] | Родий | 12,41[8] | Хром | 7,19[9] |
| Иридий | 22,56[10] | Палладий | 12,02[11] | Германий | 5,32[12] |
| Плутоний | 19,84[13] | Свинец | 11,35[14] | Алюминий | 2,70[15] |
| Платина | 19,59[16] | Серебро | 10,50[17] | Бериллий | 1,85[18] |
| Тантал | 19,30[19] | Медь | 8,94[20] | Цезий | 1,84[21] |
| Золото | 19,30[14] | Никель | 8,91[22] | Рубидий | 1,53[23] |
| Уран | 19,05[24] | Кобальт | 8,86[25] | Натрий | 0,97[26] |
| Ртуть | 13,53[27] | Железо | 7,87[28] | Калий | 0,86[29] |
| Рутений | 12,45[30] | Марганец | 7,44[31] | Литий | 0,53[32] |
Измерение плотности
Для измерений плотности используются:
- Пикнометр — прибор для измерения истинной плотности
- Различные виды ареометров — измерители плотности жидкостей.
- Бурик Качинского и бур Зайдельмана — приборы для измерения плотности почвы.
- Вибрационный плотномер — прибор для измерения плотности жидкости и газа под давлением.
См. также
Видеоурок: плотность вещества
- Список химических элементов с указанием их плотности
- Удельный вес
- Удельная плотность
- Относительная плотность
- Объёмная плотность
- Конденсация
- Консистенция (лат. consistere — состоять) — состояние вещества, степень мягкости или плотности (твёрдости) чего-либо — полутвердых-полумягких веществ (масел, мыла, красок, строительных растворов и т. д.); наприм., глицерин имеет сиропообразную консистенцию.
- Консистометр — прибор для измерения в условных физических единицах консистенции различных коллоидных и желеобразных веществ, а также суспензий и грубодисперсных сред, к примеру, паст, линиментов, гелей, кремов, мазей.
- Концентрация частиц
- Концентрация растворов
- Плотность заряда
- Уравнение неразрывности
Примечания
- ↑ Существуют также поверхностная плотность (отношение массы к площади) и линейная плотность (отношение массы к длине), применяемые соответственно к плоским (двумерным) и вытянутым (одномерным) объектам.
- ↑ Подразумевается также, что область стягивается к точке, то есть, не только её объём стремится к нулю (что могло бы быть не только при стягивании области к точке, но, например, к отрезку), но также стремится к нулю и её диаметр (максимальный линейный размер).
- ↑ Агекян Т. А. Расширение Вселенной. Модель Вселенной // Звёзды, галактики, Метагалактика. 3-е изд. / Под ред. А. Б. Васильева. — М.: Наука, 1982. — 416 с. — С. 249.
- ↑ Planetary Fact Sheet (англ.)
- ↑ Sun Fact Sheet (англ.)
- ↑ Stern, S. A., et al. (2015). «The Pluto system: Initial results from its exploration by New Horizons». Science 350 (6258): 249–352. DOI:10.1126/science.aad1815.
- ↑ Krebs, 2006, p. 158.
- ↑ Krebs, 2006, p. 136.
- ↑ Krebs, 2006, p. 96.
- ↑ Krebs, 2006, p. 160.
- ↑ Krebs, 2006, p. 138.
- ↑ Krebs, 2006, p. 198.
- ↑ Krebs, 2006, p. 319.
- ↑ 1 2 Krebs, 2006, p. 165.
- ↑ Krebs, 2006, p. 179.
- ↑ Krebs, 2006, p. 163.
- ↑ Krebs, 2006, p. 141.
- ↑ Krebs, 2006, p. 67.
- ↑ Krebs, 2006, p. 151.
- ↑ Krebs, 2006, p. 111.
- ↑ Krebs, 2006, p. 60.
- ↑ Krebs, 2006, p. 108.
- ↑ Krebs, 2006, p. 57.
- ↑ Krebs, 2006, p. 313.
- ↑ Krebs, 2006, p. 105.
- ↑ Krebs, 2006, p. 50.
- ↑ Krebs, 2006, p. 168.
- ↑ Krebs, 2006, p. 101.
- ↑ Krebs, 2006, p. 54.
- ↑ Krebs, 2006, p. 134.
- ↑ Krebs, 2006, p. 98.
- ↑ Krebs, 2006, p. 47.
Литература
- Плотность — статья из Большой советской энциклопедии. — М.: «Советская Энциклопедия», 1975. — Т. 20. — С. 49.
- Плотность — статья из Физической энциклопедии. Т. 3, С. 637.
- Krebs R. E. The History and Use of Our Earth’s Chemical Elements: A Reference Guide. 2nd edition. — Westport: Greenwood Publishing Group, 2006. — xxv + 422 p. — ISBN 0-313-33438-2.
Ссылки
- Онлайн интерактивная таблица плотности веществ (рус.)
- Подробная таблица значений плотности распространенных жидкостей (рус.)