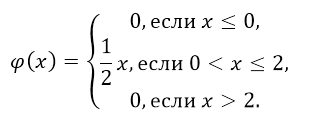Как найти плотность распределения непрерывной случайной величины - AvtoShod.ru

Плотность распределения вероятностей непрерывной случайной величины

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Краткая теория

Ранее
непрерывная случайная величина задавалась с помощью функции распределения. Этот
способ задания не является единственным. Непрерывную случайную величину можно
также задать, используя другую функцию, которую называют плотностью
распределения или плотностью вероятности (иногда ее называют дифференциальной
функцией).

Плотностью распределения вероятностей непрерывной случайной величины

называют функцию

– первую производную от функции распределения

Из этого определения следует, что
функция распределения является первообразной для плотности распределения.

Заметим, что для описания
распределения вероятностей дискретной случайной величины плотность
распределения неприменима.

Зная плотность распределения, можно
вычислить вероятность того, что непрерывная случайная величина примет значение,
принадлежащее заданному интервалу.

Вероятность того, что непрерывная
случайная величина

примет
значение, принадлежащее интервалу

равна
определенному интегралу от плотности распределения, взятому в пределах от

до

Геометрически полученный результат
можно истолковать так: вероятность того, что непрерывная случайная величина
примет значение, принадлежащее интервалу

, равна площади криволинейной трапеции, ограниченной
осью

, кривой распределения

и прямыми

В частности, если

– четная
функция и концы интервала симметричны относительно начала координат, то:

Зная плотность распределения

можно найти
функцию распределения

по формуле:

Свойства плотности распределения

Свойство 1.

Плотность
распределения – неотрицательная функция:

Свойство 2.

Несобственный
интеграл от плотности распределения в пределах от

до

равен единице:

Смежные темы решебника:

Дискретная случайная величина
Непрерывная случайная величина
Интегральная функция распределения вероятностей

Примеры решения задач

Пример 1

Задана
плотность распределения вероятностей f(x) непрерывной случайной
величины X. Требуется:

1)
определить коэффициент A;

2) найти
функцию распределения F(x);

3)
схематично построить графики F(x) и f(x);

4) найти
математическое ожидание и дисперсию X;

5) найти
вероятность того, что X примет значение из
интервала (α,β):

α=1; β=1.7

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

1)
Постоянный параметр

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Получаем:

2)
Функцию распределения

найдем из
формулы:

Учитывая
свойства

, сразу можем
отметить, что:

Остается
найти выражение для

, когда

принадлежит
интервалу

Получаем:

3) Построим графики

График плотности распределения

График функции распределения

4)
Математическое ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

5)
Вероятность того, что случайная величина примет значение из интервала

Пример 2

Плотность
распределения вероятности непрерывной случайной величины равна

, x∈(0,∞). Найти нормировочный множитель C,
математическое ожидание M(X) и дисперсию D(X).

Решение

Нормировочный множитель

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Плотность
вероятности:

Математическое
ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

Пример 3

Непрерывная
случайная величина

имеет плотность распределения:

Найти
величину a, вероятность P(X<0) и математическое
ожидание X.

Решение

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Постоянный
параметр

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Плотность
вероятности имеет вид:

Вероятность:

Математическое
ожидание находим по формуле:

Для
нашего примера:

Задачи контрольных и самостоятельных работ

Задача 1

Плотность
распределения непрерывной случайной величины X имеет вид:

Найти:

а)
параметр a;

б)
функцию распределения F(x);

в)
вероятность попадания случайной величины X в интервал (6.5; 11);

г)
математическое ожидание M(X) и дисперсию D(X);

Построить
график функций f(x) и F(x).

Задача 2

Задана
функция распределения непрерывной случайной величины:

Найти и
построить график функции плотности распределения вероятностей.

Задача 3

Случайная
величина X задана функцией распределения F(x).
Найти плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить график функции
F(x).

Задача 4

Задана
плотность вероятности f(x) или функции распределения
непрерывной случайной величины X. Найти a, M[X], D[X], P(α<x<β).

α=1,β=2

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 5

Непрерывная
случайная величина

задана плотностью распределения вероятностей.

Требуется
найти:

— функцию
распределения вероятностей;

—
математическое ожидание;

—
дисперсию;

— среднее
квадратическое отклонение;

— вероятность
того, что случайная величина отклонится от своего математического ожидания не
более, чем на одну четвертую длины всего интервала возможных значений этой
величины;

—
построить графики функции распределения и плотности распределения вероятностей.

Задача 6

Случайная
величина X равномерно распределена на интервале (2;7).
Составить f(x),F(x), построить графики. Найти
M(X),D(X).

Задача 7

Случайная
величина X~N(a,σ)

a=25;
σ=4; α=13; β=30; δ=0.1.

Требуется:

—
составить функцию плотности распределения и построить ее график;

— найти
вероятность того, что случайная величина в результате испытания примет
значение, принадлежащее интервалу (α; β);

— найти
вероятность того, что абсолютная величина отклонения значений случайной
величины от ее математического ожидания не превысит δ.

Задача 8

Плотность
вероятности непрерывной случайной величины ξ задана следующим выражением:

Найти
постоянную C, функцию распределения Fξ (x), математическое
ожидание и дисперсию Dξ случайной величины ξ.

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 9

Случайная
величина X задана функцией распределения вероятностей F(x).

Требуется:

1. Найти
функцию плотности распределения f(x).

2. Найти M(X).

3. Найти
вероятность P(α<X<β)

4.
Построить графики f(x) и F(x).

α=2, β=4.5

Задача 10

Найти
функцию плотности нормально распределенной случайной величины X и
постройте ее график, зная M(X) и D(X).

M(X)=-1; D(X)=8

Задача 11

Случайная
величина X задана интегральной F(x) или дифференциальной f(x)
функцией. Требуется:

а) найти
параметр C;

б) при
заданной интегральной функции F(x) найти дифференциальную функцию f(x), а при
заданной дифференциальной функции f(x) найти интегральную функцию F(x);

в)
построить графики функций F(x) и f(x);

г) найти
математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(x);

д)
вычислить вероятность попадания в интервал P(a≤x≤b)

е)
определить, квантилем какого порядка является точка xp;

ж)
вычислить квантиль порядка p

a=π/4; b=π/3; xp=π/2; p=0.75

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Источник

Александр Мельник

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Понятие плотности распределения вероятностей непрерывной случайной величины

Пусть $X$ — непрерывная случайная величина с функцией распределения вероятностей $F(x)$. Напомним определение функции распределения:

Определение 1

Функцией распределения называется функция $F(x)$ удовлетворяющая условию $F(x) = P(X⩽x)$.

Так как случайная величина является непрерывной, то, как нам уже известно, что функция распределения вероятностей F(x) будет непрерывной функцией. Пусть F(x) также дифференцируема на всей области определения.

Рассмотрим интервал (x,x+△x) (где △x — приращение величины x на нем).

Теперь устремляя значения приращения △x к нулю, получим:

Рисунок 1.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Таким образом, получаем:

Определение 2

Плотность распределения (плотность вероятности) φ(x) — это производная функции распределения непрерывной случайной величины.

Плотность распределения, как и функция распределения, — это одна из форм закона распределения случайной величины. Однако закон распределения может быть записан через плотность распределения только для непрерывных случайных величин.

Геометрический смысл плотности распределения вероятностей непрерывной случайной величины

Кривая распределения — это график функции φ(x) плотность распределения случайной величины (рис.2).

Рисунок 2. График плотности распределения. Автор24 — интернет-биржа студенческих работ

«Плотность распределения вероятностей непрерывной случайной величины» 👇

Геометрический смысл 1: Вероятность попадания непрерывной случайной величины в интервал (α,β) равна площади криволинейной трапеции, ограниченной графиком функции распределения φ(x) и прямыми x=α, x=β и y=0 (рис. 3).

Рисунок 3. Геометрическое изображение вероятности попадания непрерывной случайной величины в интервал (α, β). Автор24 — интернет-биржа студенческих работ

Геометрический смысл 2: Площадь бесконечной криволинейной трапеции, ограниченной графиком функции распределения φ(x), прямой y=0 и переменной прямой x есть ни что иное как функция распределения F(x) (рис. 4).

Рисунок 4. Геометрическое изображение функции вероятности F(x) через плотность распределения φ(x). Автор24 — интернет-биржа студенческих работ

Пример 1

Пусть функция распределения F(x) случайной величины X имеет следующий вид:

Рисунок 5.

а) Найти значение α.
б) Найти плотность распределения φ(x).
в) Построить кривую распределения.

Решение:

а) Так как необходимо найти плотность распределения, то случайная величина X является непрерывной. Тогда, при x=2, получим, что $αx^2=1$, то есть 4α=1, α=1/4.

То есть:

Рисунок 6.

б) Так как:

Рисунок 7.

то получим:

Рисунок 8.

в) Построим график функции φ(x).

Рисунок 9.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Непрерывные распределения вероятностей и их параметры

Общие свойства непрерывного распределения
Функция распределения непрерывной случайной величины
Числовые характеристики непрерывного распределения
Таблица непрерывных распределений, их параметров и числовых характеристик
Примеры

п.1. Общие свойства непрерывного распределения

Если случайная величина x может принимать любые значения в интервале (a;b), она называется непрерывной случайной величиной.
Функция (p(x)) от значения случайной величины, равная вероятности получения этого значения в испытании, называется плотностью распределения.
Свойства плотности распределения: begin{gather*} p(x)geq 0\ int_{-infty}^{+infty}p(x)dx=1 text{(условие нормировки)} end{gather*}

Например:
Пусть случайная величина равномерно распределена на отрезке (xin [a;b]), т.е. (p(x)=c=const). Из условия нормировки получаем: $$ int_{-infty}^{+infty}p(x)dx=int_{a}^{b}ccdot dx=ccdot x|_{a}^{b}=c(b-a)=1Rightarrow c=frac{1}{b-a} $$ Плотность равномерного непрерывного распределения: $$ p(x)= begin{cases} frac{1}{b-a}, xin [a;b]\ 0, xnotin [a;b] end{cases} $$

п.2. Функция распределения непрерывной случайной величины

Функцией распределения непрерывной случайной величины называют функцию, которая определяет вероятность, что значение случайной величины x не превышает граничное значение t: $$ F(t)=P(xleq t)=int_{-infty}^t p(x)dx $$ Вероятность для случайной величины попасть в интервал (cleq xleq d) определяется интегралом от плотности вероятности: $$ P(cleq xleq d)=int_{c}^d p(x)dx=F(d)-F(c) $$ и равна разности значений функции распределения на концах интервала.

Для непрерывной случайной величины график (F(x)) является монотонно возрастающей гладкой кривой. Область значений (F(x)in [0;1]).
Предел (F(x)) слева равен 0, предел справа равен 1: $$ lim_{xrightarrow -infty}F(x)=0; lim_{xrightarrow +infty}F(x)=1 $$ Например:
Найдем функцию распределения для равномерного распределения с плотностью: $$ p(x)= begin{cases} frac{1}{b-a}, xin [a;b]\ 0, xnotin [a;b] end{cases} $$ Для всех (xlt a) $$ F(x)=int_{-infty}^a p(x)dx=int_{-infty}^acdot dx=0 $$ Для всех (aleq xleq b) begin{gather*} F(t)=0+int_{a}^t p(x)dx=int_{a}^tfrac{1}{b-a}cdot dx=frac{1}{b-a}cdot x|_{a}^t=frac{t-a}{b-a}\ F(x)=frac{x-a}{b-a} end{gather*} Для всех (xgt b) begin{gather*} F(x)=F(b)+int_{b}^{+infty} p(x)dx=1+0=1 end{gather*} Получаем: $$ F(x)= begin{cases} 0, xlt a\ frac{x-a}{b-a}, xin [a;b]\ 1, xgt b end{cases} $$ Графики плотности распределения и функции распределения для равномерно распределенной непрерывной величины:

п.3. Числовые характеристики непрерывного распределения

Числовыми характеристиками непрерывного распределения являются математическое ожидание, дисперсия и среднее квадратичное отклонение (СКО).
Если для дискретных распределений числовые характеристики определяются через суммы (см. §62 данного справочника), то для непрерывных распределений для этого используются интегралы.

Математическое ожидание непрерывной случайной величины (x) с плотностью распределения (p(x)) равно интегралу: $$ M(X)=int_{-infty}^{+infty}xcdot p(x)dx $$

Дисперсия непрерывной случайной величины (x) с плотностью распределения (p(x)) равна интегралу: $$ D(X)=int_{-infty}^{+infty}(x-M(x))^2cdot p(x)dx=int_{-infty}^{+infty}x^2cdot p(x)dx-M^2(x) $$

Среднее квадратичное отклонение (СКО) непрерывной случайной величины – это корень квадратный от дисперсии: $$ sigma(X)=sqrt{D(X)} $$

Например:
Найдем числовые характеристики равномерного распределения. $$ p(x)= begin{cases} frac{1}{b-a}, xin [a;b]\ 0, xnotin [a;b] end{cases} $$ Мат. ожидание: begin{gather*} M(x)=int_{-infty}^{+infty} xcdot p(x)dx=int_{a}^{b} xcdotfrac{1}{b-a}dx=frac{1}{b-a}cdotfrac{x^2}{2}|_{a}^{b}=frac{b^2-a^2}{2(b-a)}=\ =frac{(b-a)(b+a)}{2(b-a)}=frac{a+b}{2} end{gather*} Т.е., среднее значение (центр тяжести) равномерного распределения – это середина отрезка.
Дисперсия: begin{gather*} D(x)=D(X)=int_{-infty}^{+infty}x^2cdot p(x)dx-M^2(x)=D(X)=int_{a}^{b}x^2cdotfrac{1}{b-a}dx-left(frac{a+b}{2}right)^2=\ =frac{1}{b-a}cdotfrac{x^3}{3}|_{a}^{b}-left(frac{a+b}{2}right)^2=frac{b^3-a^3}{3(b-a)}-frac{b^3-a^3}{3(b-a)}-frac{(a+b)^2}{4}=frac{a^2+ab+b^2}{3}-frac{a^2+2ab+b^2}{4}=\ =frac{a^2-2ab+b^2}{12}=frac{(b-a)^2}{12} end{gather*} СКО: $$ sigma(x)=sqrt{D(x)}=frac{b-a}{2sqrt{3}} $$

п.4. Таблица непрерывных распределений, их параметров и числовых характеристик

Название	Принятое обозначение	Плотность распределения	Мат. ожидание	Дисперсия
Непрерывное равномерное	(U(a,b))	begin{gather} p(x)=frac{1}{b-a}\ xinleft[a;bright] end{gather}	(frac{a+b}{2})	(frac{(b-a)^2}{12})
Нормальное (Гаусса)	(N(mu,sigma^2))	begin{gather} p(x)=frac{1}{sqrt{2pisigma^2}}e^{-frac{(x-mu)^2}{2sigma^2}}\ xinmathbb{R} end{gather}	(mu)	(sigma^2)
Экспоненциальное	(Exp(lambda))	begin{gather} p(x)=lambda e^{-lambda x}\ lambdagt 0, xgeq 0 end{gather}	(frac1lambda)	(frac{1}{lambda^2})

п.5. Примеры

Пример 1. Непрерывная случайная величина x задана плотностью распределения: $$ p(x)= begin{cases} Ax^2, xin [0;2]\ 0, xnotin [0;2] end{cases} $$ Найдите множитель A, функцию распределения, мат. ожидание, дисперсию и СКО случайной величины x. Постройте графики плотности распределения и функции распределения. Чему равна вероятность, что случайная величина окажется в интервале (frac12leq xleq 1)?

Находим множитель A из условия нормировки: begin{gather*} int_{-infty}^{+infty}p(x)dx=int_{0}^{2}Ax^2dx=1\ Acdotfrac{x^3}{3}|_{0}^{2}=frac{A}{3}(2^3-0)=frac{8A}{3}=1Rightarrow A=frac38\ p(x)= begin{cases} frac38 x^2, xin [0;2]\ 0, xnotin [0;2] end{cases} end{gather*} График плотности распределения:

Функция распределения (F(x)) для (xlt 0) равна 0, для (xgt 2) равна 1.
Найдем (F(x)) в интервале (xinleft[0;2right]): begin{gather*} F(t)=int_{0}^{t}p(x)dx=frac38int_{0}^{t}x^2dx=frac38cdotfrac{x^3}{3}|_{0}^{t}=frac{t^3}{8}Rightarrow F(x)=frac{x^3}{8}\ F(x)= begin{cases} 0, xlt 0\ frac{x^3}{8}, xin [0;2]\ 1, xgt 2 end{cases} end{gather*} График функции распределения:

Найдем математическое ожидание: begin{gather*} M(x)=int_{-infty}^{+infty}xcdot p(x)dx=int_{0}^{2}xcdotfrac38 x^2dx=frac38int_{0}^{2}x^3dx=frac38cdotfrac{x^4}{4}|_{0}^{2}=frac{3}{32}cdot 2^4=1,5 end{gather*} Найдем дисперсию: begin{gather*} D(x)=int_{-infty}^{+infty}x^2cdot p(x)dx-M^2(x)=int_{0}^{2}x^2cdotfrac38 x^2dx-1,5^2=frac38int_{0}^{2}x^4dx-1,5^2=\ =frac38cdotfrac{x^5}{5}|_{0}^{2}-1,5^2=frac{3}{40}cdot 2^5-1,5^2=2,4-2,25=0,15 end{gather*} Найдем СКО: $$ sigma(x)=sqrt{D(x)}=sqrt{0,15}approx 0,387 $$ Вероятность для x оказаться в интервале (frac12leq xleq 1) равна: $$ Pleft(frac12leq xleq 1right)=F(1)-Fleft(frac12right)=frac{1^3}{8}-frac{left(frac12right)^3}{8}=frac{7}{64} $$

Пример 2. Непрерывная случайная величина x задана функцией распределения: $$ F(x)= begin{cases} 0, xlt c\ frac{(x+2)^2}{4}, cleq xleq d\ 1, xgt d end{cases} $$ Найдите границы интервала c и d, плотность распределения, мат. ожидание, дисперсию и СКО случайной величины x. Постройте графики плотности распределения и функции распределения. Чему равна вероятность, что случайная величина окажется в интервале (-1leq xleq -frac12)

Границы интервала ищем из условий: begin{gather*} F(c)=frac{(c+2)^2}{4}=0Rightarrow c=-2\ F(d)=frac{(d+2)^2}{4}=1Rightarrow d=0 end{gather*} Получаем: begin{gather*} F(x)= begin{cases} 0, xlt -2\ frac{(x+2)^2}{4}, -2leq xleq 0\ 1, xgt 0 end{cases} end{gather*} График функции распределения:

Плотность распределения равна производной от функции распределения: $$ p(x)=F'(x) $$ Для (xlt -2cup xgt 0) получим (p(x)=0), т.к. производная от постоянной равна 0.
На значащем интервале: $$ p(x)=left(frac{(x+2)^2}{4}right)=frac{2(x+2)}{4}=frac{x+2}{2} $$ Получаем: begin{gather*} p(x)= begin{cases} frac{x+2}{2}, -2leq xleq 0\ 0, xlt -2cup xgt 0 end{cases} end{gather*} График плотности распределения:

Найдем математическое ожидание: begin{gather*} M(x)=int_{-infty}^{+infty}xcdot p(x)dx=int_{-2}^{0}xcdotfrac{x+2}{2}dx=frac12int_{-2}^{0}(x^2+2x)dx=frac12cdotleft(frac{x^3}{3}+x^2right)|_{-2}^{0}=\ =frac12left(0-left(frac{-8}{3}+4right)right)=-frac23 end{gather*} Найдем дисперсию: begin{gather*} D(x)=int_{-infty}^{+infty}x^2cdot p(x)dx-M^2(x)=int_{-2}^{0}x^2cdotfrac{x+2}{2}dx-left(-frac23right)^2=\ =frac12int_{-2}^{0}(x^3+2x^2)dx-frac49=frac12cdotleft(frac{x^4}{4}+frac{2x^3}{3}right)|_{-2}^{0}-frac49=frac12left(0-left(frac{16}{4}-frac{2cdot 8}{3}right)right)-frac49=\ =frac23-frac49=frac29 end{gather*} Найдем СКО: $$ sigma(x)=sqrt{D(x)}=frac{sqrt{2}}{3} $$ Вероятность для x оказаться в интервале (-1leq xleq -frac12) равна: $$ Pleft(-1leq xleq -frac12right)=Fleft(-frac12right)-F(-1)=frac{left(-frac12+2right)^2}{4}-frac{(-1+2)^2}{4}=frac{1,5^2-1^2}{4}=frac{9}{16} $$