Загрузить PDF
Загрузить PDF
Объем – это количество занимаемого телом пространства, а плотность равна массе тела, поделенной на его объем.[1]
Прежде чем вычислить плотность тела, необходимо найти его объем. Если тело имеет правильную геометрическую форму, его объем можно рассчитать при помощи простой формулы. Объем измеряется обычно в кубических сантиметрах (см3) или кубических метрах (м3). Используя найденный объем тела, легко рассчитать его плотность. Для измерения плотности служат граммы на кубический сантиметр (г/см3) или граммы на миллилитр (г/мл).
-
1
Определите форму тела. Знание формы позволит вам выбрать правильную формулу и провести измерения, необходимые для расчета объема.
-
Сфера представляет собой идеально круглый трехмерный объект, все точки поверхности которого отстоят на равном расстоянии от центра. Иными словами, сферическое тело похоже на круглый мяч.[2]
-
Конус – это трехмерная фигура, в основании которой лежит круг, а вершину составляет единственная точка, называемая вершиной конуса. Конус можно представить также в виде пирамиды с круглым основанием.[3]
-
Куб представляет собой трехмерную фигуру, составленную из шести одинаковых квадратных граней.[4]
-
Прямоугольный параллелепипед, называемый также прямоугольной призмой, похож на куб: он также имеет шесть граней, однако в этом случае они представляют собой прямоугольники, а не квадраты.[5]
-
Цилиндр – это трехмерная фигура, состоящая из одинаковых круглых концов, края которых соединены округлой поверхностью.[6]
-
Пирамида является трехмерной фигурой, в основании которой лежит многоугольник, который соединен с вершиной боковыми гранями.[7]
Правильной пирамидой называется такая пирамида, в основании которой лежит правильный многоугольник, все стороны и углы которого равны между собой.[8]
- Если тело имеет неправильную форму, его объем можно найти, полностью погрузив его в воду.
-
Сфера представляет собой идеально круглый трехмерный объект, все точки поверхности которого отстоят на равном расстоянии от центра. Иными словами, сферическое тело похоже на круглый мяч.[2]
-
2
Выберите для вычисления объема правильное уравнение. Для тела каждого типа существует своя формула, позволяющая рассчитать занимаемый им объем. Ниже приведены формулы для нахождения объема перечисленных выше фигур. Более подробные сведения и иллюстрации можно найти в статье Как находить объем.
- Сфера: V = (4/3) π r3, где r – радиус сферы, а π – константа, равная примерно 3,14.
- Конус: V = (1/3) π r2h, где r – радиус круглого основания, h – высота конуса, π – константа, равная приблизительно 3,14.
- Куб: V = s3, где s – длина ребра куба (стороны любой из его квадратных граней).
- Прямоугольный параллелепипед: V = l x w x h, где l – длина прямоугольной грани, w – ее ширина, h – высота параллелепипеда (призмы).
- Цилиндр: V= π r2h , где r – радиус круглого основания, h – высота цилиндра, π – константа, составляющая примерно 3,14.
- Пирамида: V= (1/3) b x h, где b – площадь основания пирамиды (l x w), h – высота пирамиды.
-
3
Произведите необходимые измерения. Они будут зависеть от того, с телом какого вида вы имеете дело. Для большинства тел простой формы понадобится измерить высоту; если у фигуры круглое основание, необходимо также определить его радиус, если же в основании лежит прямоугольник – его длину и ширину.
- Радиус круга равен половине его диаметра. Измерьте диаметр, приложив к середине круга линейку, после чего поделите полученный результат на 2.
- Радиус сферы измерить немного сложнее, однако и это не составит труда, если вы воспользуетесь методами, подробно изложенными в статье Как найти радиус шара.
- Длину, ширину и высоту тела можно определить, приложив к нему линейку в соответствующих местах и записав результаты измерений.
-
4
Вычислите объем. Выяснив форму тела, выберите подходящую формулу и измерьте входящие в нее величины. Подставьте в формулу измеренные значения и выполните необходимые математические действия. В результате вы получите объем тела.
- Помните о том, что ответ должен выражаться в кубических единицах независимо от того, какой системой единиц вы пользуетесь (метрической либо другой). После полученной величины обязательно напишите единицы, в которых она измеряется.
Реклама
-
1
Определите объем тела по количеству вытесняемой им воды. Тело может иметь неправильную форму, что затрудняет измерение его размеров и ведет к неточному определению объема. В этом случае прекрасно работает метод, заключающийся в определении объема воды, вытесняемой телом при полном погружении.[9]
- Данный метод можно применить и для нахождения объема тел правильной формы, чтобы избежать вычислений.
-
2
Наполните водой мерный цилиндр (мензурку). Это лабораторная емкость с метками на боковой поверхности, позволяющая измерять объем жидкостей. Выберите достаточно большой цилиндр, чтобы в него полностью поместился измеряемый объект. Необходимо наполнить цилиндр водой так, чтобы в нее можно было полностью погрузить объект, но при этом она не выливалась. Запишите начальный объем воды без измеряемого тела.
- Наблюдая первоначальный объем воды, наклонитесь так, чтобы ваши глаза находились на одном уровне с поверхностью жидкости, после чего запишите высоту, на которой расположено дно мениска. Мениск – это внешняя поверхность воды, которая искривляется при контакте с другими поверхностями (в нашем случае это стенки сосуда).[10]
- Наблюдая первоначальный объем воды, наклонитесь так, чтобы ваши глаза находились на одном уровне с поверхностью жидкости, после чего запишите высоту, на которой расположено дно мениска. Мениск – это внешняя поверхность воды, которая искривляется при контакте с другими поверхностями (в нашем случае это стенки сосуда).[10]
-
3
Аккуратно поместите в емкость измеряемое тело. Делайте это плавно, чтобы не уронить объект, поскольку в этом случае часть воды может выплеснуться из мерного цилиндра. Убедитесь в том, что тело полностью погрузилось в воду. Запишите новые показания уровня воды в емкости, вновь расположившись так, чтобы ваши глаза находились на одном уровне с мениском.
- Если при погружении тела часть воды выплеснулась, попробуйте повторить с самого начала, налив меньше воды или взяв больший мерный цилиндр.
-
4
Вычтите из окончательного уровня воды его первоначальное значение. Количество вытесненной предметом воды будет равняться его объему в кубических сантиметрах. Обычно объем жидкостей измеряют в миллилитрах, но один миллилитр как раз и равен одному кубическому сантиметру.[11]
- Например, если сначала уровень воды был 35 мл, а после опускания в нее предмета поднялся до 65 мл, объем этого предмета составляет 65 – 35 = 30 мл, или 30 см3.
Реклама
-
1
Определите массу предмета. Масса объекта соответствует количеству материи, из которой он состоит.[12]
Массу находят путем прямого взвешивания на весах, она измеряется в граммах или килограммах.- Возьмите точные измерительные весы и поместите на них предмет. Запишите показания весов в свой блокнот.
- Массу тела можно определить и при помощи чашечных весов. Положив объект на одну чашу, на вторую поместите гирьки с известными массами так, чтобы обе чаши уравновесили друг друга, расположившись на одинаковой высоте. В этом случае искомая масса предмета будет равна сумме масс использованных гирек.
- Перед взвешиванием проследите, чтобы предмет не был влажным, иначе погрешность измерений возрастет.
-
2
Определите объем тела. Если предмет имеет правильную форму, для определения его объема используйте одну из формул, приведенных выше. Если форма тела неправильна, измерьте объем, погрузив его в воду, как описано выше.
-
3
Вычислите плотность. Согласно определению, плотность равна массе, деленной на объем. Таким образом, поделите измеренную массу на вычисленный объем. В результате вы получите плотность тела, измеренную в г/см3.
- Например, вычислим плотность предмета объемом 8 см3 и массой 24 г.
- плотность = масса / объем
- d = 24 г / 8 см3
- d = 3 г/см3
Реклама
Советы
- Нередко предметы состоят из нескольких частей, имеющих правильные геометрические формы. В этом случае разделите составляющие элементы на группы, относящиеся к той или иной правильной форме, найдите объем каждого элемента, а затем сложите их вместе, определив тем самым общий объем всего предмета.
- Можно определить объем какого-либо предмета как путем вычислений, так и погружением в воду, после чего сравнить полученные результаты.
Реклама
Предупреждения
- Будьте внимательны: прежде чем приступать к вычислениям, обязательно переведите все измеренные величины в метрическую систему (систему единиц СИ).
Реклама
Об этой статье
Эту страницу просматривали 43 244 раза.
Была ли эта статья полезной?
Цель
работы:
Научиться рассчитывать погрешности
прямых и косвенных измерений, научиться
использовать рычажные весы и приборы
для измерений линейных размеров тел,
на примере определения плотности тел
правильной геометрической формы.
-
Теоретическое
введение
Плотностью
элементарной части тела называется
предел отношения элементарной массы
∆m
к элементарному объему ∆V,
при ∆V→
0:
[1]
Для
однородного тела ()
определение плотности сводится к
нахождению отношения его массы к объему:.
Внимание!
Для экспериментального определения
плотности тел правильной геометрической
формы (цилиндр и параллелепипед) в данной
работе необходимо предварительно
провести прямые измерения их линейных
размеров и массы, пользуясь
рекомендациями, приведенными во
введении §1.
Раздел: «Расчет погрешности прямых
измерений».
Доверительной
вероятностью (надежностью) P(∆x)
серии измерений называется вероятность
попадания истинного значения измеряемой
величины в данный интервал (выражается
в долях единицы или в процентах).
Интервал
(<x>±
∆x)
в который попадает истинное значение
искомой величины с заданной доверительной
вероятностью, называют доверительным
интервалом (интервалом надежности).
Определение
плотности цилиндра.
Плотность однородного
цилиндрического тела можно рассчитать
по формуле:
,
[2]
где
d
– диаметр цилиндра, h
– его высота.
Для нахождения
относительной погрешности косвенного
определения плотности цилиндра,
прологарифмируем расчетную формулу:
и возьмем
дифференциал. Заменив дифференциалы
приращениями, получим:
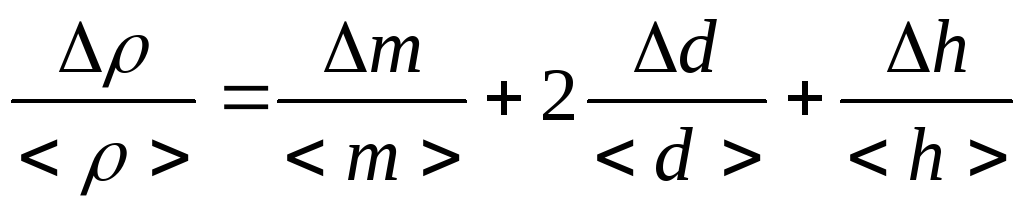
,
[3]
где
— средние значения массы, диаметра и
высоты, найденные в результате прямых
измерений, соответственно, а
—
относительные погрешности их прямых
измерений.
Среднее значение
плотности можно найти, подставляя в
расчетную формулу [2] средние значения
массы, диаметра и высоты:
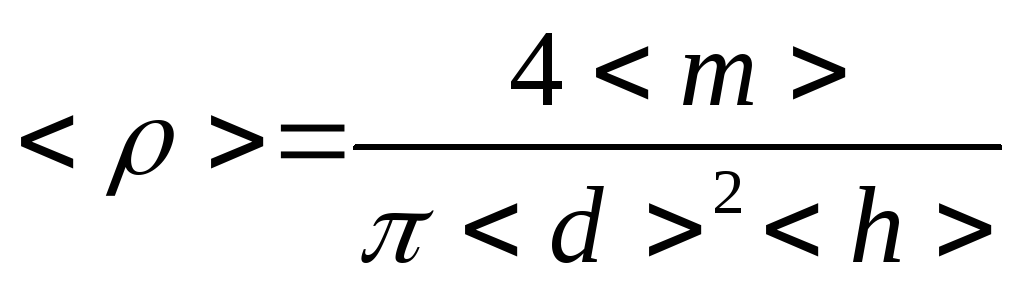
Определение
плотности параллелепипеда.
Плотность однородного
тела в форме параллелепипеда можно
рассчитать по формуле:
,
[5]
где
l
– длина тела , d
–ширина тела, h
– его высота. Действуя аналогично
предыдущему случаю, находим:
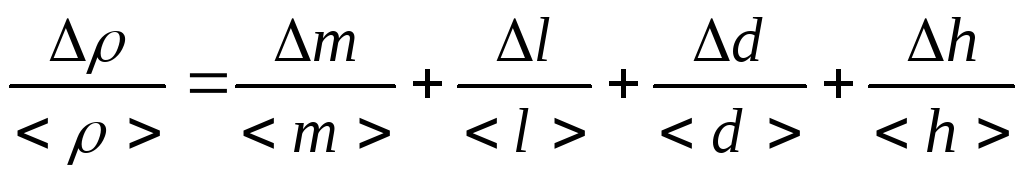
,
[6]
где
— средние значения массы, длины, ширины
и высоты, найденные в результате прямых
измерений, соответственно, а
—
относительные погрешности их прямых
измерений.
Среднее значение
плотности:
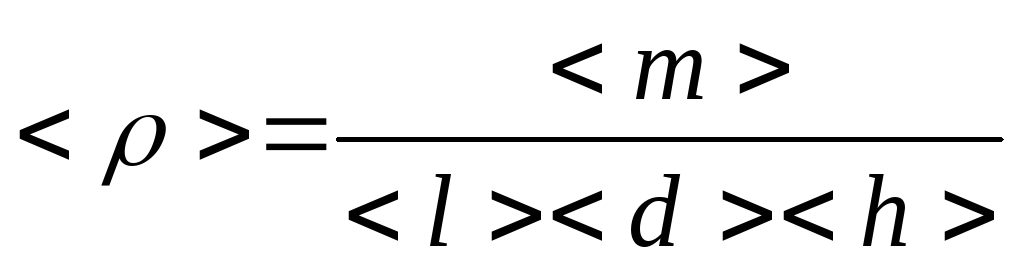
Интервал
надежности
при определении плотности во всех
случаях, можно вычислить по формуле:
[8]
где
— относительная погрешность определения
плотности, вычисляемая по формуле [3]
для цилиндра, или по формулу [6] для
параллелепипеда.
Результат
записывается в виде:
,
при р =
,
, [9]
где
величина надежности p
принимается равной наименьшей надежности
прямых измерений массы и линейных
размеров.
-
Выполнение
работы
Приборы и
принадлежности:
-
Тела для измерения
(цилиндр и параллелепипед) -
Весы и разновесы
-
Штангенциркуль
-
Микрометр
При
всех расчетах принять:
р
= 0,95
-
Ознакомиться с
устройством и принципом действия
штангенциркуля и микрометра, научиться
взвешивать тела с помощью рычажных
весов. -
Определить
инструментальные погрешности измерения
для каждой измеряемой величины и внести
в строку ∆и
в заголовке таблицы, под соответствующей
величиной. -
Провести прямые
измерения (не менее 3-х раз) всех линейных
размеров и массы тел, в указанных в
таблице единицах измерения, результаты
измерений заносить в верхнюю часть
таблицы, в строку, соответствующей
номеру опыта. -
Рассчитать,
по формуле:
,
средние арифметические значения всех
измеренных величин и занести в
соответствующую строку, в нижней части
таблицы, в соответствующем столбце. -
Рассчитать,
по формуле:
,
среднеквадратичные отклонения (СКО)
каждой величины и занести в соответствующую
строку, в нижней части таблицы, в
соответствующем столбце. -
Рассчитать,
по формуле:
,
случайную погрешность измерения каждой
величины и занести в соответствующую
строку, в нижней части таблицы, в
соответствующем столбце. -
Рассчитать,
по формуле:,
полную погрешность каждой величины и
занести в соответствующую строку, в
нижней части таблицы, в соответствующем
столбце. -
Рассчитать,
по формуле:
,
относительные ошибки измерения каждой
величины и занести в строку ε,
в нижней части таблицы, в соответствующем
столбце. -
По формулам [3],
[4], [8] (для цилиндра) или [6], [7], [8] (для
параллелепипеда) рассчитать среднюю
плотность и интервал надежности и
округленный результат записать в
строку ρ, в последней строке таблицы,
в соответствующем столбце. -
Сравнить полученные
значения плотности с табличными
значениями плотностей твердых тел, и
определить из какого вещества могут
быть изготовлены опытные образцы.
Таблица результатов
|
№ опыта |
Цилиндр |
Параллелепипед |
|||||
|
Величина |
m, |
d, |
h, |
m, |
l, |
d, |
h, |
|
∆и |
|||||||
|
1 |
|||||||
|
2 |
|||||||
|
3 |
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
, |
ρ |
ρ |
Контрольные
вопросы
-
Виды и источники
погрешностей измерения. -
Каковы инструментальные
погрешности линейки, штангенциркуля
и микрометра? -
Как
перевести плотность, выраженную в г/мм3
в кг/м3? -
Чем характеризуется
точность измерения? -
Что называют
доверительной вероятностью (надежностью)
и доверительным интервалом (интервалом
надежности) результата измерения? -
Как использовать
таблицу коэффициентов Стьюдента для
расчета доверительного интервала по
заданной надежности? -
Как рассчитать
погрешность прямого измерения массы
и линейных размеров тел? -
Как рассчитать
погрешность косвенного измерения
плотности цилиндра, параллелепипеда? -
Как округлять и
правильно записать результат измерений?
Литература
Введение
к данному пособию §1,
§3.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Найди верный ответ на вопрос ✅ «Вычислите плотность предмета имеющего форму прямоугольного параллелепипеда имеющего линейные размеры 0,5 дм, 20 см, 0,2 м если его масса …» по предмету 📙 Физика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more
Онлайн-калькулятор плотности, который поможет вам определить соотношение между плотностью, массой и весом объекта с помощью формулы плотности. В этом калькуляторе есть небольшая, но очень важная опция, где вы можете легко определить плотность объекта по категории и названию материала. Если вы хотите получить краткие сведения о том, как рассчитать плотность по формуле, продолжайте читать!
Кроме того, вы можете попробовать наш онлайн-калькулятор импульса, который поможет вам найти импульс движущегося объекта, а также определить массу объекта.
Читать дальше!
Что такое формула плотности?
Расчеты не слишком сложные, а очень простые. Просто введите значения в следующее уравнение плотности, чтобы легко вычислить любую из требуемых переменных:
р = м / В
Где,
V – объем & m – масса объекта.
Если вы хотите найти объем с помощью плотности и массы, калькулятор плотности использует формулу:
V = м / п
Чтобы найти массу с плотностью и объемом, рассмотрите следующую формулу:
т = р * V
Плотность можно определить как массу на единицу объема объекта. Со значениями введите единицы измерения, и этот калькулятор выполнит преобразование единиц измерения.
§ 2 Решение задач Какова масса подсолнечного масла в бутылке объемом 3 л, если плотность масла равна 930 кг/м3?
Запишем условие задачи. Нам известны объем бутылки (обозначается буквой V) 3 л, и плотность подсолнечного масла (обозначается буквой ρ) 930 кг/м3. Выразим объем бутылки в Международной системе единиц. 1 л = 0,001 м3, следовательно, 3 л составляют 0,003 м3.
Решение: Чтобы найти массу тела, нужно плотность умножить на объем: m = ρ · V. Подставим числовые значения величин: 930 кг/м3 · 0,003 м3 = 2,79 кг.
Сколько штук строительного кирпича размером 250 мм х 120 мм х 65 мм допускается перевозить на автомашине грузоподъемностью 4 т? Плотность кирпича 1800 кг/м3.
Запишем условие задачи и выразим данные в Международной системе единиц. Известны размеры кирпича: длина а = 250 мм = 0,25 м, ширина b= 120 мм = 0,12 м, высота с = 60 мм = 0,06 м, плотность кирпича ρ = 1800 кг/м3, грузоподъемность – наибольшая масса груза, которую может перевезти автомобиль – m = 4 т = 4000 кг. Найти количество кирпичей – обозначим латинской буквой N.
Решение: Количество кирпичей можно найти, поделив общую массу всех кирпичей на массу одного кирпича: N = m/m1. Чтобы найти массу одного кирпича, нужно плотность умножить на его объем: m1 = ρ · V. Кирпич имеет форму прямоугольного параллелепипеда, следовательно, его объем равен произведению длины, ширины и высоты кирпича. Подставим числовые значения известных величин и вычислим. Объем кирпича равен 0,0018 м3. Масса одного кирпича m1 равна 1800 кг/м3 , умножим на 0,0018 м3 , равно 3,24 кг. Тогда число кирпичей равно N 4000 кг, разделим на 3,24 кг и получим 1234, 567 штук или число целых кирпичей 1234 штуки.
Медный шар имеет массу 840 г при объеме 120 см3. Сплошной этот шар или полый? Плотность меди 8900 кг/м3.
Запишем условие задачи. Известна масса шара m 840 г, что в системе СИ составляет 0,84 кг, объем шара V=120 см3, в СИ 0,00 012 м3, плотность меди ρ = 8900 кг/м3. Определить, сплошной шар или содержит внутри пустое пространство?
Решение. Представим, что на рычажных весах лежат два медных шара, один сплошной, второй содержит внутри пустое пространство, то есть полый шар. Если у них массы одинаковы, то объем полого шара должен быть больше, чем объем сплошного шара (рис 1).
Определим, каков объем шара, состоящего полностью из меди. Если объем окажется равным 120 см3, то шар сплошной и пустот не содержит. Если же вычисленный объем окажется меньше 120 см3, значит, внутри есть полость.
Чтобы найти объем сплошного медного шара, массу шара разделим на его плотность. Для упрощения проведем вычисления в граммах и кубических сантиметрах.
Какая плотность воды?
Плотность воды между 0 ° C и 4 ° C обычно составляет 100 кг / м3, но она меняется в зависимости от температуры. При повышении температуры объем материала увеличивается. Согласно формуле, объем и плотность обратно пропорциональны друг другу, в конечном итоге плотность материала уменьшается. Плотность воды при различных температурах приведена в следующей таблице:
Стол
Ниже приведена таблица единиц, в которой плотность обычно выражается плотностями некоторых материалов.
Столы
Понятие объема тела
Объем является физическим свойством материи, которое определяет занимаемое ею пространство. В Международной системе единиц он измеряется в метрах кубических, но также часто используют другие единицы измерения: кубические сантиметры и литры.
В зависимости от состояния вещества применяют различные методы измерения объема:
- Для жидких тел используют специальные градуированные прозрачные емкости (цилиндры, пробирки, пипетки и другие).
- Для твердых тел, которые сохраняют свою форму, объем измеряется исходя из их линейных размеров с применением соответствующей математической формулы. Например, параллелепипеда объем равен произведению его длины, ширины и высоты.
- Газообразные тела не сохраняют свой объем, в отличие от жидкостей и твердых тел, поэтому он для газов всегда равен объему сосуда, в котором находится газ.
Как пользоваться калькулятором плотности:
Следуйте данным инструкциям по расчету с помощью этого онлайн-инструмента. С помощью этого калькулятора вы можете производить расчеты в простом и продвинутом режимах. Давайте взглянем!
Входы:
- Прежде всего, выберите во вкладке то, что вам нужно найти.
- Затем введите значения во все обозначенные поля в соответствии с выбранной опцией.
- Наконец, нажмите кнопку “Рассчитать”.
Выходы:
Как только вы заполните все поля, калькулятор покажет:
- Плотность объекта
- Масса объекта
- Объем объекта
- Корень кубический из объема
Заметка:
Есть дополнительное поле, где вы можете ввести категорию материала и название материала, этот калькулятор найдет плотность выбранного материала. Если вы не знаете значение объема, используйте предварительный вариант этого калькулятора для расчета объема, в противном случае используйте простой режим.
Масса сплошной детали
Главная > Вычисление масс > Масса сплошной детали
9.05.2013 // Владимир Трунов
Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала (см. таблицы плотностей): Объем сплошной детали — это… ее объем и больше ничего.
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр. Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
Масса параллелепипеда (бруска)
Объем параллелепипеда: , где — длина, — ширина, — высота. Тогда масса:
Масса цилиндра
Объем цилиндра: , где — диаметр основания, — высота цилиндра. Тогда масса:
Масса шара
Объем шара: , где — диаметр шара. Тогда масса:
Масса сегмента шара
Объем сегмента шара: , где — диаметр основания сегмента, — высота сегмента. Тогда масса:
Масса конуса
Объем любого конуса: , где — площадь основания, — высота конуса. Для круглого конуса: , где — диаметр основания, — высота конуса. Масса круглого конуса:
Масса усеченного конуса
Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : , где , . После никому не интересных алгебраических преобразований получаем: , где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса. Отсюда масса:
Масса пирамиды
Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды. Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды. Тогда масса пирамиды:
Масса усеченной пирамиды
Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями и : , где , . Исчеркав половину тетрадного листа, получаем: , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды. И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: . Тогда масса усеченной прямоугольной пирамиды:
или
Для пирамиды с квадратным основанием (, ) формула выглядит проще:
вычисление массы
-
Масса проволоки, прутка, проката
-
Масса кольца, звена
-
Масса полой детали
Похожие записи
Связь между объемом и массой для воды
Чтобы объем воды перевести в массу, следует воспользоваться приведенной выше формулой. Однако для чистой воды значение плотности составляет 1000 кг/м3, или 1 г/см3, или 1 кг/л. Это означает, что объем в массу и наоборот для этой субстанции легко переводить, для этого нужно лишь знать соответствие между единицами измерений этих физических величин. Например, 2 л воды имеют массу 2 кг, а 3,5 тонны воды занимают объем 3,5 м3.
Отметим, что плотность 1000 кг/м3 характерна только для чистой воды. Любые примеси и соли могут значительно изменить этот показатель, например плотность морской воды составляет 1027 кг/м3, то есть морская вода на 2,7 % плотнее пресной.
Физическая величина плотность
Наконец, прежде чем переходить к вопросу о том, как перевести объем в массу, рассмотрим плотность — величину, которая непосредственно касается указанного вопроса.
В таких науках, как химия и физика, под плотностью некоторой субстанции понимают количество массы, которая заключена в определенном объеме. Поскольку объем и масса являются скалярными величинами, то и плотность также — скаляр. Обычно плотность обозначают греческой буквой ρ (ро).
Согласно приведенному определению, математически можно записать: ρ = m/V, где m — масса тела в килограммах, V — объем в кубических метрах, который занимает это тело. Это означает, что плотность измеряется в единицах кг/м3.
Как найти массу в физике через объем и плотность?
Перейдем теперь непосредственно к решению поставленной задачи. Допустим необходимо измерить массу имеющегося алмаза. Сначала нужно измерить его объем, допустим, он равен 5000 см3. Разбираясь в том, как найти массу через объем, следует также определить плотность вещества. В данном случае можно обратиться к табличным данным и посмотреть, какая плотность характерна для алмаза. В таблице находим, что она равна 3,52 г/см3.
После того как все необходимые величины определены, следует использовать известную формулу, как найти массу через объем и плотность: m = V*ρ, где V — объем тела, ρ — плотность. Подставляя полученные значения для алмаза, получаем: m = 5000 (см3)*3,52 (г/см3) = 17600.0 г = 17,6 кг. Следует обратить внимание, что при умножении объема на плотность единицы измерения объема (см3 в примере) сокращаются и остаются только единицы измерения массы.
Плотность вещества
Наконец, отвечая на вопрос о том, как найти массу через объем и плотность, следует разобраться с последней характеристикой — плотностью тел. Плотность является неотъемлемой физической характеристикой материи, которая связывает массу и объем, то есть она определяет, какое количество массы вещества содержится в единице объема. В Международной системе единиц она выражается в виде килограммов на метр кубический, но часто используется и в граммах на сантиметр кубический.
Любое вещество обладает конкретным значением плотности, например, в одном литре воды содержится один килограмм массы, то есть ее плотность равна 1 кг/л или 1000 кг/м3.
Понятие плотности играет важную роль в природе. Так, вопрос плавучести тел в воде является исключительно вопросом сравнения плотности тела и воды. Тела, имеющие большую плотность, чем вода, тонут в ней, например, яйцо или камень.












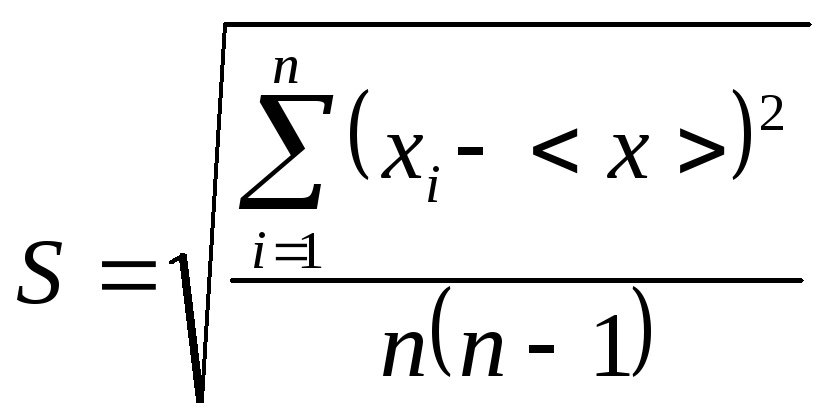 ,
,





