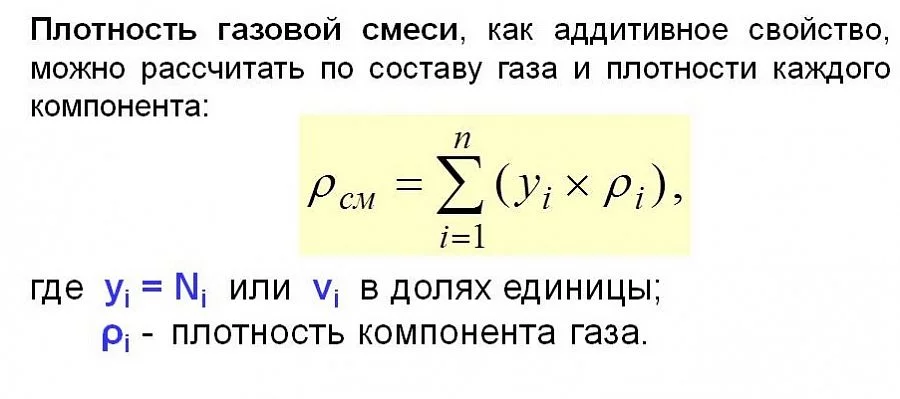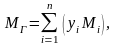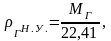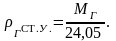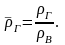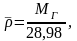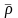Как найти плотность газа по формуле

Плотность — физическое свойство газа

Density is referred to as the ratio of the mass per unit of volume of a substance under specific conditions of pressure and temperature. Mathematically, it can be defined as mass divided by volume. It is generally represented by “ρ” or “D”. The density of a substance varies depending on its pressure and temperature. For example, the density of an ideal gas can be doubled as the pressure doubles or by halving its absolute temperature. That means the density of gas always increases as the pressure increases and decreases as the temperature increases. We can determine the molar mass of a substance if we know its density. Generally, the density of a substance is different for different materials. At standard conditions for temperature and pressure, osmium and iridium are the densest known elements.

Density (ρ) = m/V

Where “m” is the mass, and “V” is the volume.

The SI unit of density of a substance is kilogram per cubic meter (kg/m³). Some other units of measurement of density are kilogram per liter (kg/L), gram per milliliter (g/mL), tonne per cubic meter (t/m³), etc.

Density of Gas Formula

The formula to determine the density of a gas is given as follows:

Density of a gas (ρ) = PM/RT

Where,

“P” is the pressure of the gas,

“M” is the molar mass (g/mol),

“R” is the universal gas constant (R = 0.082 L⋅ atm⋅ K^−1⋅ mol⁻¹), and

“T” is the temperature of the gas (K)

Derivation For the Density of Gas formula 

The density of a gas is equal to the total mass of the gas to the total volume of the gas. To determine the molar mass of a gas, we have to consider the ideal gas equation.

From the ideal gas equation, we have

PV = nRT …………(1)

where,
“P” is the pressure of the gas,
“V” is the volume of the gas
“n” is the number of moles
“R” is the universal gas constant (R = 0.082 L⋅ atm⋅ K⁻¹⋅ mol⁻¹), and
“T” is the temperature of the gas

We know that, number of moles (n) = m/M 

where, 
“m” is the mass of the gas,
“M” is the molecular mass of the gas.

Now, substitute n = m/M in equation (1).

Thus, PV = mRT/M

P = mRT/MV ……….(2)

we know that density (ρ) = m/V. So, substitute the value of ρ in equation (2).

Thus, we get

P = ρ RT/M

ρ = PM/RT 

Thus, the ideal gas density formula is ρ = PM/RT.

Solved Examples on Gas Density

Example 1: What will be the density of a gas at 37 °C and a pressure of 5 atm and a molar mass of 84 g/mol?

Solution:

Given data:

Molar mass (M) = 84 g/mol

The pressure of the gas (P) =5 atm

The temperature of the gas (T) = 37 °C = 310 K

Universal gas constant (R) = 0.082 L⋅atm⋅K⁻¹⋅mol⁻¹

From the ideal gas density formula, we have

ρ = MP/RT

ρ = (84 × 5)/ (0.082 × 310)

ρ = 420/25.42 g/L

ρ = 16.522 g/L

Hence, the density of a gas is 16.522 g/L.

Example 2: Determine the density of a gas at 27 °C at a pressure of 7 atm and a molar mass of 54 g/mol. (R = 0.082 L⋅atm⋅K⁻¹⋅mol⁻¹)

Solution:

Given data:

Molar mass (M) = 54 g/mol

The pressure of the gas (P) =7 atm

The temperature of the gas (T) = 27 °C = 300 K

Universal gas constant (R) = 0.082 L⋅atm⋅K⁻¹⋅mol⁻¹

From the ideal gas density formula, we have

ρ= MP/RT

ρ= (54 × 7)/ (0.082 × 300)

ρ= 378/24.6 g/L

ρ= 15.37 g/L

Hence, the density of a gas is 15.37 g/L.

Example 3: Determine the density of carbon monoxide at 40 °C and a pressure of 730 Torr. (R = 0.082 L⋅atm⋅K⁻¹⋅mol⁻¹)

Solution:

Given data:

Molar mass of carbon monoxide (M) = 28 g/mol

Pressure (P) =730 Torr = 730/760 atm = 0.9605 atm

Temperature (T) = 40 °C = 313 K

Universal gas constant (R) = 0.082 L⋅atm⋅K⁻¹⋅mol⁻¹

From the ideal gas density formula, we have

ρ= MP/RT

ρ= (28 × 0.9605)/ (0.082 × 313)

ρ= 26.894/25.666 g/L

ρ= 1.0478 g/L

Hence, the density of carbon monoxide at 40 °C and a pressure of 730 Torr is 1.0478 g/L.

Example 4: If the density of a gas is 9.35 g/L at STP, then determine its density at 30 °C and a pressure of 700 mmHg.

Solution: 

Given data:

The density of a gas (ρ₁) = 9.35 g/L

We know that at STP pressure is equal to 0.987 atm and temperature is equal to 273.15 K.

So, P₁ = 0.987 atm

T₁ = 273.15 K

Let the density of the gas at 30 °C and pressure of 700mmHg be ρ₂.

P₂ = 700mmHg = 700 × 0.00131579 atm = 0.9210 atm

T₂ = 30 °C = 303K

From the ideal gas density formula, we have

ρ= MP/RT

As we are calculating the density of the same gas at different conditions, the mass of the gas remains the same.

ρ ∝ P/T

ρ₁/ρ₂ = (P₁/T₁)/ (P₂/T₂)

9.35/ρ₂ = (0.987/273.15)/ (0.9210/303)

9.35/ρ₂ = (0.987 × 303)/ (0.9210 × 273.15)

9.35/ρ₂ = (299.061/251.57)

ρ₂ = (9.35 × 251.57)/299.061

ρ₂ = 7.865 g/L

Hence, the density of the gas at 30 °C and pressure of 700mmHg is 7.865 g/L.

Example 5: What is the density of nitric oxide (NO) at a temperature of 51 °C and a pressure of 6 bar? (R = 0.082 L⋅atm⋅K⁻¹⋅mol⁻¹)

Solution:

Given data:

Density (ρ) = 3.42 g/L

Temperature (T) = 51 + 273 = 324 K

Pressure (P)= 6 bar = 6 × 0.9869 atm = 5.9215 atm

The molar mass of nitric oxide = 30 g/mol

Universal gas constant (R) = 0.082 L⋅atm⋅K⁻¹⋅mol⁻¹

From the ideal gas density formula, we have

ρ= MP/RT

ρ= (30 × 5.9215)/ (0.082 × 324)

ρ= 177.645/26.568 g/L

ρ= 6.686 g/L

Hence, the density of nitric oxide at 51 °C and a pressure of 6 bar is 6.686 g/L.

FAQs on Gas Density

Question 1: Define the density of the gas.

Answer:

Density is referred to as the ratio of the mass per unit of volume of a substance under specific conditions of pressure and temperature. Mathematically, it can be defined as mass divided by volume. It is generally represented by “ρ” or “D”. 

Density (ρ) = m/V

Where “m” is the mass, and “V” is the volume.

Question 2: What is the effect of pressure and temperature on the density of gas?

Answer:

The density of a substance varies depending on its pressure and temperature. For example, the density of an ideal gas can be doubled as the pressure doubles or by halving its absolute temperature. That means the density of gas always increases as the pressure increases and decreases as the temperature increases.

Question 3: What is meant by an ideal gas? Write down the ideal gas density formula.

Answer: 

The gas that strictly follows Boyle’s law, Charles’ law, and Avogadro’s law is known as an ideal gas. It is a hypothetical gas that is proposed to simplify the calculations. Many real gases behave qualitatively like an ideal gas under various conditions of temperature and pressure, where the gas molecules act as the ideal particles.

Ideal gas density formula

ρ = PM/RT

Where “P” is the pressure of the gas,

“M” is the molar mass (g/mol),

“R” is the universal gas constant (R = 0.082 L⋅ atm⋅ K⁻¹⋅ mol⁻¹), and

“T” is the temperature of the gas (K)

Question 4: What are units of measurement of density?

Answer: 

The SI unit of density of a substance is kilogram per cubic meter (kg/m³). Some other units of measurement of density are kilogram per liter (kg/L), gram per milliliter (g/mL), tonne per cubic meter (t/m³), etc.

Одним из важных
параметров газа является его молекулярная
масса,
которая определяется путем суммирования
масс атомов, входящих в молекулу.

Молекулярная масса
углеводородного газа, представляющего
собою смесь компонентов, при известном
объёмном составе, рассчитывается по
формуле:

(2.6)

где y_i
– объёмная
доля i—
го компонента в газовой смеси;

M_i
– молекулярная
масса i—
го компонента;

n
– число компонентов в смеси газов.

Под плотностью
углеводородного газа понимают его
массу, заключенную в 1 м³
при определенных условиях (нормальных
или стандартных), в системе СИ измеряется
в кг/м³.

_г
= m/V.

(2.7)

Под нормальными
условиями понимают условия, при которых
давление Р = 0,1 МПа, а температура Т = 273
К (0С);
под стандартными условиями – Р = 0,1 МПа,
Т = 293 К (20С).

Для всех газов
объем 1 киломоля постоянен и равен при
нормальных условиях – 22,41 м³,
при стандартных условиях – 24,05 м³.
Зная молекулярную массу газа, плотность
газа при нормальных условиях можно
вычислить по формуле:

(2.8)

при стандартных
условиях – по формуле:

(2.9)

На практике часто
пользуются относительной
плотностью газа,
равной отношению плотности газа к
плотности воздуха при определенных
условиях:

(2.10)

При расчетах
следует помнить, что плотность воздуха
при нормальных условиях
составляет
_в^н.у.
= 1,293
кг/м³,
при стандартных
_в^ст.у.
= 1,205
кг/м³.

Зная молекулярную
массу газа М_Г,
относительную плотность газа можно
также рассчитать по формуле:

(2.11)

где 28,98 –
молекулярная масса воздуха.

Задача 2.2. Даны
составы газов типичных газовых,
газоконденсатных и нефтяных месторождений.
Рассчитать молекулярную массу М_i
каждого компонента, входящего в состав
газа, молекулярную массу газа М_г,
плотность газа при нормальных (_г^н.у.)
и стандартных
условиях (_г^ст.у.),
а также относительную плотность по
воздуху

_г
(при нормальных
и стандартных условиях). Определить тип
газа (природный, попутный или газ
газоконденсатного месторождения).
Исходные данные для расчетов приведены
в таблицах 2.2 и 2.3.

Таблица 2.2 –
Компонентный состав газа

Таблица 2.3 – Атомные
массы компонентов

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Плотность и способы ее определения

Плотность равна отношению массы тела к объему, который оно занимает.

$mathrm {rho = frac {m}{V}}$, $mathrm {г/см^3}$

Где:

• m – масса вещества, г,
• V – объем данного вещества, $mathrm {см^3}$.

Данная формула применяется для определения плотности вещества в твердом состоянии.

Для газообразных веществ используют другую формулу: $mathrm {rho = frac {M_{в-ва}}{V_m}, г/л}$, где $mathrm {V_m}$ — молярный объем газа, при нормальных условиях равный 22,4 л/моль

Относительная плотность газов

Для того, чтобы перейти к определению относительной плотности газов, необходимо упомянуть о законе Авогадро, который заключается в том, что в равных объемах разных газов при одинаковых условиях содержится равное число молекул (число Авогадро $mathrm {N_A = 6,022 cdot 10^{23}}$

Из данного закона вытекают два следствия:

1. Один моль любого газа занимает равный объем при одинаковых условиях: $mathrm {V_m = frac {V}{n}}$.
2. Отношение плотностей разных газов относятся между собой как молярные массы этих газов.

$mathrm {rho_1 = frac {m_1}{V} = frac {n_{1}M_{1}}{n_{1}V_{m}} = frac {M_1}{V_m}}$

$mathrm {rho_2 = frac {m_2}{V} = frac {n_{2}M_{2}}{n_{2}V_{m}} = frac {M_2}{V_m}}$

$mathrm {frac {rho_1}{rho_2} = frac {M_1}{M_2} = D}$, где D – относительная плотность газа

Пример решения задачи

Необходимо определить плотность и относительную плотность оксида азота (II) по воздуху. При этом $mathrm {M_{NO} = 30 г/моль, V_{NO} = 22,4 л/моль}$

1) Определим плотность соединения с помощью формулы $mathrm {rho = frac {M_{NO}}{V_m} = frac {30 г/моль}{22,4 л/моль} = 1,34 г/л}$.

2) Рассчитаем относительную плотность газа по формуле: $mathrm {D_{возд.} = frac {M_{NO}}{M_{возд.}} = frac {30 г/моль}{29 г/моль} = 1,03 г/л}$.

Ответ: $mathrm {rho = 1,34 г/л}$, $mathrm {D_{возд.} = 1,03 г/л}$