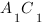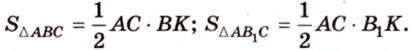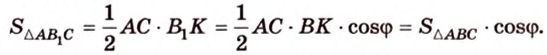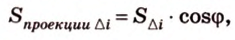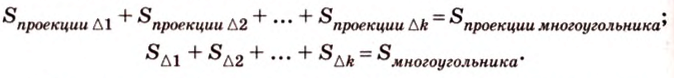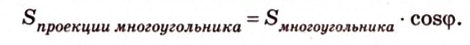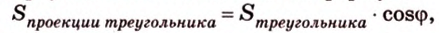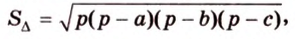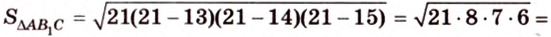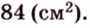19
Фев 2014
Категория: Справочные материалы
Площадь ортогональной проекции многоугольника
2014-02-19
2014-02-19
Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекций.
Докажем теорему для треугольника. Поскольку многоугольник разбивается на треугольники, сумма площадей которых есть площадь многоугольника, то и для многоугольника теорема будет верна.
Доказательство:
Пусть треугольник – проекция треугольника
на проецируемую плоскость.
Докажем, что
,
где – угол между плоскостями
Для этого разобьем треугольник на два треугольника c общей стороной
, параллельной прямой
пересечения плоскостей
. (Частный случай, когда одна из сторон треугольника
параллельна линии пересечения плоскостей
, можно рассмотреть отдельно (самостоятельно)).
Проекция треугольника – треугольник
. Причем
.
Пусть – перпендикуляр к
. Тогда по т. о трех перпендикулярах и
– перпендикуляр к
. Стало быть,
– угол между плоскостями треугольников (проецируемого и проекции).
Пусть – точка пересечения
и
,
– проекция т.
на плоскость
. Очевидно,
– высота треугольника
(
– высота треугольника
).
Из треугольника
Но и
Тогда
Имеем:
Аналогичные рассуждения – для пары треугольников и
:
(где – высота треугольника
,
– ее проекция)
Итак, суммируя площади треугольников и
соответственно, получаем
или
Что и требовалось доказать.
Пример.
Ребро куба равно 2 см. Через диагональ основания под углом к плоскости основания проведена плоскость, пересекающая боковое ребро. Найти площадь сечения.
Решение:
Пусть плоскость сечения проведена через диагональ и пересекает боковое ребро (
) в точке
.
По вышеуказанной теореме
где треугольник – проекция треугольника
на плоскость основания,
– угол между плоскостями
Ответ:
Применение теоремы можно также посмотреть, например, в этой задаче.
Автор: egeMax |
Нет комментариев
Печать страницы
Слайд 1
Подготовка к ЕГЭ – 2014 по математике. Нахождение площади сечения через площадь его ортогональной проекции. Задание С2 Учитель математики МБОУ СОШ № 143 г. Красноярска Князькина Т. В.
Слайд 2
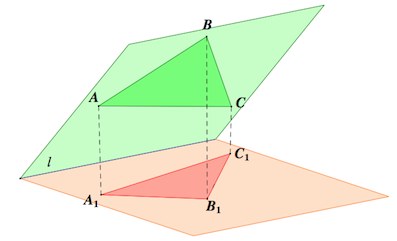
Рассмотрим решение такой задачи: В прямоугольном параллелепипеде , , . Сечение параллелепипеда проходит через точки B и D и образует с плоскостью ABC угол . Найдите площадь сечения . Ч асто бывает удобно находить площадь сечения через площадь его ортогональной проекции. Нахождение площади треугольника через площадь его ортогональной проекции легко иллюстрируется таким рисунком:
Слайд 3
CH- высота треугольника ABC , C ‘H – высота треугольника ABC ‘ , который является ортогональной проекцией треугольника ABC . Из прямоугольного треугольника CHC ‘ : Площадь треугольника ABC ‘ равна Площадь треугольника ABC равна Cледовательно , площадь треугольника ABC равна площади треугольника ABC ‘, деленной на косинус угла между плоскостями треугольника ABC и треугольника ABC ‘ , который является ортогональной проекцией треугольника ABC .
Слайд 4
Поскольку площадь любого многоугольника можно представить в виде суммы площадей треугольников, площадь многоугольника равна площади его ортогональной проекции на плоскость деленной на косинус угла между плоскостями многоугольника и его проекции . Используем этот факт для решения нашей задачи (см. слайд 2) План решения такой: А) Строим сечение. Б) Находим его ортогональную проекцию на плоскость основания. В) Находим площадь ортогональной проекции. Г) Находим площадь сечения.
Слайд 5
1. Сначала нам нужно построить это сечение. Очевидно, что отрезок BD принадлежит плоскости сечения и плоскости основания, то есть принадлежит линии пересечения плоскостей:
Слайд 6
Угол между двумя плоскостями – это угол между двумя перпендикулярами, которые проведены к линии пересечения плоскостей и лежат в этих плоскостях . Пусть точка O – точка пересечения диагоналей основания. OC – перпендикуляр к линии пересечения плоскостей , который лежит в плоскости основания :
Слайд 7
2. Определим положение перпендикуляра, который лежит в плоскости сечения. (Помним, что если прямая перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной. Ищем наклонную по ее проекции ( OC ) и углу между проекцией и наклонной). Найдем тангенс угла COC ₁ между OC ₁ и OC
Слайд 8
Следовательно, угол между плоскостью сечения и плоскостью основания больше, чем между OC ₁ и OC. То есть сечение расположено как-то так : K – точка пересечения OP и A ₁C₁, LM||B₁D₁ .
Слайд 9
Итак, вот наше сечение: 3. Найдем проекцию сечения BLMD на плоскость основания. Для этого найдем проекции точек L и M .
Слайд 10
Четырехугольник BL ₁M₁D – проекция сечения на плоскость основания. 4. Найдем площадь четырехугольника BL ₁M₁D . Для этого из площади треугольника BCD вычтем площадь треугольника L ₁CM₁ Найдем площадь треугольника L ₁CM₁ . Треугольник L ₁CM₁ подобен треугольнику BCD . Найдем коэффициент подобия .
Слайд 11
Для этого рассмотрим т реугольники OPC и OKK₁ : Следовательно, и площадь треугольника L₁CM₁ составляет 4/25 площади треугольника BCD (отношение площадей подобных фигур равно квадрату коэффициента подобия ). Тогда площадь четырехугольника BL₁M₁D равна 1-4/25=21/25 площади треугольника BCD и равна
Слайд 12
5. Теперь найдем 6 . И, наконец, получаем: Ответ : 112
Параллельное проецирование. Площадь проекции фигуры
В задачах по геометрии успех зависит не только от знания теории, но и от качественного чертежа.
С плоскими чертежами все более-менее понятно. А в стереометрии дело обстоит сложнее. Ведь изобразить надо трехмерное тело на плоском чертеже, причем так, чтобы и вы сами, и тот, кто смотрит на ваш чертеж, увидели бы то же самое объемное тело.
Как это сделать?
Конечно, любое изображение объемного тела на плоскости будет условным. Однако существует определенный набор правил. Существует общепринятый способ построения чертежей — параллельное проецирование.
Возьмем объемное тело.
Выберем плоскость проекции.
Через каждую точку объемного тела проведем прямые, параллельные друг другу и пересекающие плоскость проекции под каким-либо углом. Каждая из этих прямых пересекает плоскость проекции в какой-либо точке. А все вместе эти точки образуют проекцию объемного тела на плоскость, то есть его плоское изображение.
Как строить проекции объемных тел?
Представьте, что у вас есть каркас объемного тела — призмы, пирамиды или цилиндра. Освещая его параллельным пучком света, получаем изображение — тень на стене или на экране. Заметим, что в разных ракурсах получаются разные изображения, но некоторые закономерности все же присутствуют:
Проекцией отрезка будет отрезок.
Конечно, если отрезок перпендикулярен плоскости проекции — он отобразится в одну точку.
Проекцией круга в общем случае окажется эллипс.
Проекцией прямоугольника — параллелограмм.
Вот как выглядит проекция куба на плоскость:
Здесь передняя и задняя грани параллельны плоскости проекции
Можно сделать по-другому:
Какой бы ракурс мы ни выбрали, проекциями параллельных отрезков на чертеже тоже будут параллельные отрезки. Это один из принципов параллельного проецирования.
Рисуем проекции пирамиды,
цилиндра:
и шара:
Еще раз повторим основной принцип параллельного проецирования. Выбираем плоскость проекции и через каждую точку объемного тела проводим параллельные друг другу прямые. Эти прямые пересекают плоскость проекции под каким-либо углом. Если этот угол равен 90° — речь идет о прямоугольном проецировании. С помощью прямоугольного проецирования строятся чертежи объемных деталей в технике. В этом случае мы говорим о виде сверху, виде спереди и виде сбоку.
Иногда в задачах требуется найти площадь прямоугольной проекции фигуры.
Пусть S — площадь фигуры. Тогда площадь ее прямоугольной проекции равна S cosφ, где φ — угол между плоскостью фигуры и плоскостью проекции.
В следующей статье рассказано, как выбрать наиболее удачный ракурс для построения чертежей в задачах по стереометрии, а также о распространенных ошибках, которые могут помешать решению.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Параллельное проецирование. Площадь проекции фигуры» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
В последнее время в вариантах для подготовки к ЕГЭ по математике в Задании С2 часто стали появляться задачи на нахождение площади сечения. Рассмотрим решение такой задачи:
В прямоугольном параллелепипеде 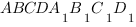
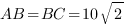
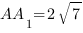
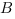
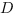

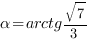
Как мы уже видели, часто бывает удобно находить площадь сечения через площадь его ортогональной проекции.
Нахождение площади треугольника через площадь его ортогональной проекции легко иллюстрируется таким рисунком: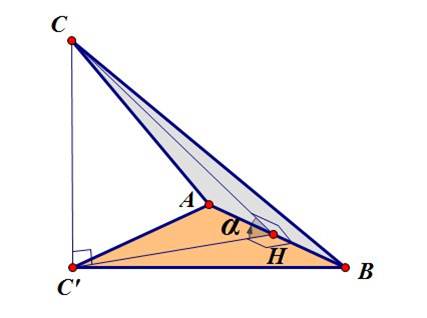







Площадь треугольника 

Площадь треугольника 

Cледовательно, площадь треугольника 




Поскольку площадь любого многоугольника можно представить в виде суммы площадей треугольников, площадь многоугольника равна площади его ортогональной проекции на плоскость деленной на косинус угла между плоскостями многоугольника и его проекции.
Используем этот факт для решения задачи:
В прямоугольном параллелепипеде 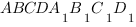
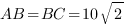
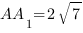
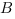
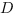

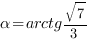
План решения такой:
А) Строим сечение.
Б) Находим его ортогональную проекцию на плоскость основания.
В) Находим площадь ортогональной проекции.
Г) Находим площадь сечения.
Итак.
1. Сначала нам нужно построить это сечение.
Очевидно, что отрезок 
Угол между двумя плоскостями — это угол между двумя перпендикулярами, которые проведены к линии пересечения плоскостей и лежат в этих плоскостях.



2. Определим положение перпендикуляра, который лежит в плоскости сечения. (Помним, что если прямая перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной. Ищем наклонную по ее проекции ( 




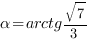


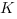


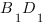
Итак, вот наше сечение:
3. Найдем проекцию сечения 

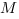
Четырехугольник 

4. Найдем площадь четырехугольника 

Найдем площадь треугольника 









Тогда площадь четырехугольника 


5. Теперь найдем 
6. И, наконец, получаем:
Ответ: 112
И.В. Фельдман, репетитор по математике.
Преподаватель который помогает студентам и школьникам в учёбе.
Ортогональное проецирование — определение и вычисление с примерами решения
Ортогональное проецирование:
Параллельное проецирование, направление которого перпендикулярно плоскости проекции, называется ортогональным проецированием. Проекция фигуры, образующаяся при ортогональном проецировании, называется ортогональной проекцией, или просто проекцией этой фигуры.
Поскольку ортогональное проецирование является особым видом параллельного проецирования, то для него выполняются все свойства последнего. Ортогональной проекцией прямой
Отметим, что прямые, перпендикулярные одной из параллельных плоскостей, перпендикулярны и остальным, поэтому ортогональное проецирование на одну из таких плоскостей будет ортогональным и на остальные плоскости. Очевидно, что ортогональные проекции фигуры на параллельные плоскости равны между собой.
Ортогональное проецирование также имеет только ему присущие свойства. Одно из них выражает теорема о площади ортогональной проекции многоугольника.
Площадь ортогональной проекции
Теорема 5
Площадь ортогональной проекции произвольного многоугольника на плоскость равна произведению площади самого многоугольника на косинус угла между плоскостью многоугольника и плоскостью проекции.
Доказательство:
Как пример многоугольника возьмем 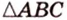
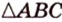
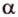
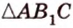
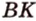
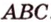
о трех перпендикулярах 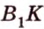
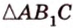
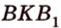
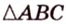
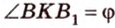
Учитывая, что 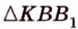
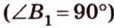
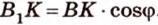
Итак, 
Чтобы доказать теорему для произвольного многоугольника, его разбивают на треугольники. Тогда для каждого треугольника и его проекции можно записать равенство
где 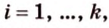
Получим в левой части равенства площадь проекции многоугольника, а в правой — площадь самого многоугольника, умноженную на косинус угла между их плоскостями. Отсюда
Т.е. и для этого случая теорема истинна.
Пример:
Ортогональной проекцией треугольника является треугольник со сторонами 13 см, 14 см и 15 см. Плоскость треугольника образует с плоскостью проекции угол 60°. Вычислите площадь данного треугольника.
Решение:
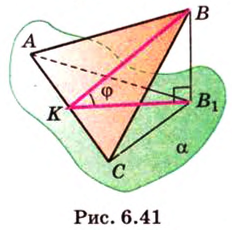
Воспользуемся рисунком 6.41. Известно, что площадь проекции треугольника вычисляют по формуле:
где 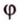
По формуле Герона найдем площадь 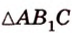
где 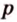
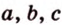
Тогда
Ответ: 168 см2.
- Декартовы координаты на плоскости
- Декартовы координаты в пространстве
- Геометрические преобразования в геометрии
- Планиметрия — формулы, определение и вычисление
- Параллельность прямых и плоскостей
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве