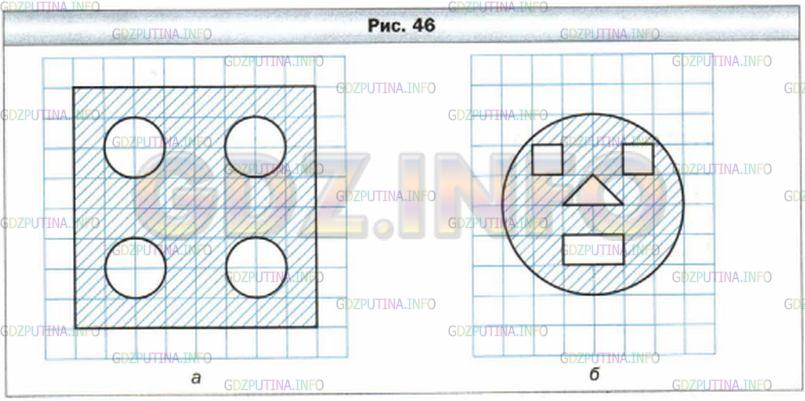
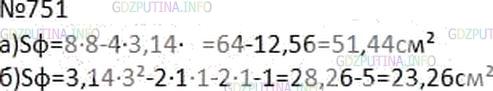Вычислите площадь закрашенной фигуры, изображенной на рисунке 45.
reshalka.com
Математика 6 класс Мерзляк. Номер №750
Решение а
S
к
в
а
д
р
а
т
а
=
a
2
=
2
2
=
2
∗
2
=
4
с
м
2
;
S
ф
и
г
у
р
ы
=
S
к
в
а
д
р
а
т
а
2
=
4
2
=
2
с
м
2
.
Решение б
S
к
в
а
д
р
а
т
а
=
a
2
=
2
2
=
2
∗
2
=
4
с
м
2
;
Если сложить 4 не закрашенные части то получится круг, тогда:
r
к
р
у
г
а
=
2
:
2
=
1
см;
S
к
р
у
г
а
=
π
r
2
=
3
,
14
∗
1
2
=
3
,
14
с
м
2
;
S
ф
и
г
у
р
ы
=
S
к
в
а
д
р
а
т
а
−
S
к
р
у
г
а
=
4
−
3
,
14
=
0
,
86
с
м
2
.
Решение в
Найдем площадь полукруга с диаметром 16 см:
r
к
р
у
г
а
=
d
:
2
=
16
:
2
=
8
с
м
;
S
п
о
л
у
к
р
у
г
а
=
π
r
2
2
=
3
,
14
∗
8
2
2
=
3
,
14
∗
64
2
=
3
,
14
∗
32
=
100
,
48
с
м
2
;
Если сложить 2 не закрашенные части то получится круг с диаметром 16 : 2 = 8 см, тогда:
r
к
р
у
г
а
=
d
:
2
=
8
:
2
=
4
с
м
;
S
к
р
у
г
а
=
π
r
2
=
3
,
14
∗
4
2
=
3
,
14
∗
16
=
50
,
24
с
м
2
;
S
ф
и
г
у
р
ы
=
S
п
о
л
у
к
р
у
г
а
−
S
к
р
у
г
а
=
100
,
48
−
50
,
24
=
50
,
24
с
м
2
.

ГДЗ (готовое домашние задание из решебника) на Номер №751 по учебнику Математика. 6 класс. Учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. Вентана-Граф. 2014г.
ГДЗ (готовое домашние задание из решебника) на Номер №751 по учебнику Математика. 6 класс. Учебник / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, под редакцией В.Е. Подольского. Вентана-Граф. 4 издание, дополненное. 2019г.
Условие
20142019г.
Вычислите площадь закрашенной фигуры (рис. 46), если длина стороны клетки равна 1 см.
Вычислите площадь закрашенной фигуры (рис. 46), если длина стороны клетки равна 1 см.
Решение 1
Решение 2
Решение 1
Решение 3
Решение 2
Решение 4
Решение 3
Популярные решебники
Ваше сообщение отправлено
и скоро будет рассмотрено
Я позволю себе также нетривиальный метод решения без использования теоремы Пифагора.
Дострою прямоугольник жёлтым цветом ABCD. Как мы видим на моём эскизе его площадь равна произведению клеток длинной стороны на клетки короткой стороны, точнее 4 х 3 = 12 клеток.
Далее я дострою голубой прямоугольник fBgh недостающего треугольника Bgh он занимает площадь 2 клетки или 1 х 2 = 2, но следует заметить, что недостающий треугольник занимает ровно половину от прямоугольника, а точнее 1 клетку или 2 : 2 = 1.
Осталось ещё немного. Я дострою малиновый прямоугольник CDeg недостающего треугольника Deg он занимает площадь в 6 клеток или 3 х 2 = 6, но следует заметить, что недостающий треугольник занимает ровно половину от прямоугольника а точнее 3 клетки или 6 : 2 = 3.
А теперь завершим расчёт:
Я отниму от площади большого прямоугольника ABCD 2 треугольника Bgh и Deg. Решаем:
12 — 1 — 3 = 8.
Мой ответ 8 клеток
Задача решена нетривиальным эксклюзивным методом с использованием не только логического, но и абстрактного мышления. Без квадратов катетов и квадрата гипотенузы.
- Категория: ГДЗ Математика учебник 6 класс Дорофеев, Шарыгин
Ответы к параграфу 8.3 Формулы. Вычисления по формулам
Задание № 651
Составьте формулы для вычисления периметров многоугольников, изображенных на рисунке 8.5,а−в.
Решение
а) P = 4x + 2a
б) P = 2a + b + c
в) P = 5m
Задание № 652
1) Чтобы найти площадь многоугольника, изображенного на рисунке 8.6, его можно разбить на прямоугольники и вычислить результат сложения площадей или достроить его до прямоугольника и вычислить результат вычитанием площадей. Вычислите площадь двумя способами.
2) Составьте формулы для вычисления площади фигуры (рис.8.7,а,б).
Решение
1) Способ 1.
S = 6 * (3 + 4) − 3 * (6 − 4) = 6 * 7 − 3 * 2 = 42 − 6 = 36 ($дм^2$) − площадь фигуры.
Способ 2.
S = 4 * 3 + 6 * 4 = 12 + 24 = 36 ($дм^2$) − площадь фигуры.2) Пример
а)
1) $a^2$ + x * y;
2) x * (a + y) − a * (x − a).
б)
1) $x^2$ + c * d;
2) с * (d + x) − x * (c − x).
Задание № 653
Площадь закрашенной части фигуры, изображенной на рисунке 8.8, вычисляется по формуле
$S=b^2−a^2$. Объясните, как получена эта формула. Найдите S, если:
а) b = 1 м, a = 0,7 м;
б) b = 2 м, a = 1,5 м.
Решение
1) $b*b=b^2$ − площадь большого квадрата;
2) $a*a=a^2$ − площадь малого квадрата;
3) $b^2−a^2$ − площадь заштрихованной части.
а)
при b = 1 м, a = 0,7 м:
$S=b^2-a^2=1^2-0,7^2=1-0,49=0,51({operatorname м}^2)$
б)
при b = 2 м, a = 1,5 м:
$S=b^2-a^2=2^2-1,5^2=4-2,25=1,75({operatorname м}^2)$
Задание № 654
1) Начертите куб. Обозначьте длину его ребра какой−нибудь буквой и составьте формулу объема куба.
2) Запишите формулы для вычисления объема фигуры, изображенной на рисунке 8.9,а,б.
Решение
1) a − длина ребра куба, тогда:
$V=a^3$ − формула объема куба.2) а) $V=a^3-x^3$
б) $V=a^3+b^3+c^3$
Как найти площадь закрашенной фигуры формула?
Для того, чтобы найти площадь, надо ширину умножить на длину, т. е. у квадрата 4м*4м=16 метров квадратных, а у прямоугольника 7м*5м=35 метров квадратных. Выходит, что площадь закрашенной фигуры метров квадратных).
Что такое площадь фигуры в математике?
Площадь плоской фигуры — аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.
Что такое площадь прямоугольника 4 класс?
Площадь прямоугольника равна произведению его длины и ширины. S = · b, где S — площадь, — длина, b — ширина прямоугольника. Периметр прямоугольника равен удвоенной сумме его длины и ширины. P = ( + b) · 2, где P — периметр, — длина, b — ширина прямоугольника.
Как можно вычислить площадь квадрата?
Формулы для вычисления площади квадрата
- Площадь квадрата равна квадрату длины его стороны. S = a2
- Площадь квадрата равна половине квадрата длины его диагонали. S = d2
Чему равна площадь квадрата?
Формула вычисления площади е. S = a*a = a2. Соотношение стороны и диагонали квадрата: d=a√2.
Как найти площадь квадрата зная все стороны?
Если известна длина стороны Умножаем ее на то же число или возводим в квадрат. S = a * a = a2 , где где S — площадь, a — сторона.
Как найти диагональ квадрата если нам известны его стороны?
Диагональ квадрата равна стороне квадрата, умноженной на корень из двух.
Как найти площадь квадрата если его диагональ равна 1?
Найдите площадь квадрата, если его диагональ равна 1. Ответ: 0,5.
Как найти площадь квадрата если известно его диагональ?
Диагонали квадрата равны между собой и используются в формуле площади квадрата через диагональ. То есть площадь квадрата равна квадрату длины диагонали поделенному на два.