Как найти площадь зак - AvtoShod.ru - решение различных проблем

Как найти площадь закрашенной фигуры формула?

Для того, чтобы найти площадь, надо ширину умножить на длину, т. е. у квадрата 4м*4м=16 метров квадратных, а у прямоугольника 7м*5м=35 метров квадратных. Выходит, что площадь закрашенной фигуры метров квадратных).

Что такое площадь фигуры в математике?

Площадь плоской фигуры — аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.

Что такое площадь прямоугольника 4 класс?

Площадь прямоугольника равна произведению его длины и ширины. S = · b, где S — площадь, — длина, b — ширина прямоугольника. Периметр прямоугольника равен удвоенной сумме его длины и ширины. P = ( + b) · 2, где P — периметр, — длина, b — ширина прямоугольника.

Как можно вычислить площадь квадрата?

Формулы для вычисления площади квадрата

Площадь квадрата равна квадрату длины его стороны. S = a2
Площадь квадрата равна половине квадрата длины его диагонали. S = d2

Чему равна площадь квадрата?

Формула вычисления площади е. S = a*a = a2. Соотношение стороны и диагонали квадрата: d=a√2.

Как найти площадь квадрата зная все стороны?

Если известна длина стороны Умножаем ее на то же число или возводим в квадрат. S = a * a = a2 , где где S — площадь, a — сторона.

Как найти диагональ квадрата если нам известны его стороны?

Диагональ квадрата равна стороне квадрата, умноженной на корень из двух.

Как найти площадь квадрата если его диагональ равна 1?

Найдите площадь квадрата, если его диагональ равна 1. Ответ: 0,5.

Как найти площадь квадрата если известно его диагональ?

Диагонали квадрата равны между собой и используются в формуле площади квадрата через диагональ. То есть площадь квадрата равна квадрату длины диагонали поделенному на два.

Источник

Найди площадь зак районной фигуры.

На этой странице находится вопрос Найди площадь зак районной фигуры?. Здесь же – ответы на него,
и похожие вопросы в категории Математика, которые можно найти с помощью
простой в использовании поисковой системы. Уровень сложности вопроса
соответствует уровню подготовки учащихся 1 — 4 классов. В комментариях,
оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
ними можно обсудить тему вопроса в режиме on-line. Если ни один из
предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
строке, расположенной вверху, и нажмите кнопку.

Источник

3 октября 2013

В этом уроке мы разберем еще одну задачу B5 на площади секторов из ЕГЭ по математике, однако будьте очень внимательны: на первый взгляд все считается очень просто. Но в самом конце решения многие ученики допускают очень обидную ошибку. Сейчас вы поймете, о чем идет речь. Итак, задача:

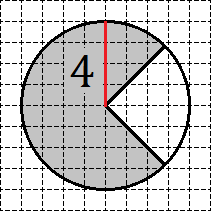
Задача. Найдите площадь S закрашенного сектора, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. В ответе укажите величину S/π.

Как решать такую задачу? В первую очередь, поскольку речь идет о площади сектора, нам нужно знать формулу площади круга:

S = πR²

где R — радиус круга. Следовательно, для решения нам потребуется найти этот самый радиус. В данной задаче все очень просто: проводим вертикальный радиус и считаем клеточки.

Отсюда сразу получаем, что радиус R = 4. Таким образом, площадь круга S равна:

S = π · 4² = 16π

Обратите внимание: нам очень повезло с радиусом. Потому что в настоящих задачах далеко не всегда верхняя точка окружности лежит в узлах координатной сетки. Однако где-то на окружности обязательно найдется точка с целочисленными координатами, которая точно будет лежать в узле сетки. Вот ее и надо использовать для вычисления радиуса. Давайте посмотрим, каким образом.

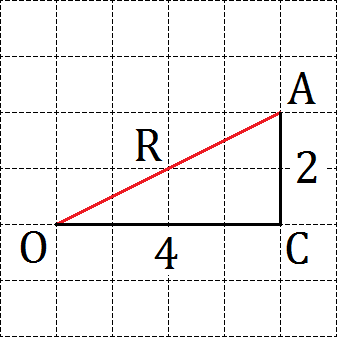
Для этого нам потребуется отдельная сетка. Отметим на ней центр окружности (точку O) и некую гипотетическую точку A, которая должна лежать на нашей окружности. Допустим, это будет выглядеть следующим образом:

Тогда отрезок OA будет радиусом этой окружности. Как его найти? Достроим до прямоугольного треугольника наш отрезок. Если двигаться вдоль линий координатной сетки, мы получим прямоугольный треугольник OAC с прямым углом C. Разумеется, полученная таким образом точка C не будет лежать на окружности — она лежит где-то внутри. Но этого нам и не требуется. Главное, что мы легко можем найти катеты: OC = 4, AC = 2.

Тогда мы можем найти радиус R (он же — отрезок OA) по теореме Пифагора:

R² = 4² + 2² = 16 + 4 = 20

И тогда получилось бы, что вместо 16π площадь всего круга равнялась бы 20π. В остальном решение было бы полностью аналогичным, поэтому возвращаемся к нашей исходной задаче. Мы только что нашли площадь круга, а нам надо найти площадь сектора. Давайте схематично перерисуем круг и разделим его на 8 равных частей, как пиццу (стандартная практика в задачах B5). Затем закрашиваем на получившемся рисунке те сектора, которые на исходном чертеже также были закрашены:

Получаем, что закрашенных кусочков было k = 6, а всего их изначально n = 8. Поскольку все части равные, мы можем найти площадь каждого маленького сектора, разделив общую площадь круга на 8:

S_sec = 16π/8 = 2π

А поскольку в закрашенном секторе таких кусочков k = 6, то искомая площадь будет равна

S = 6 · S_sec = 6 · 2π = 12π

Но в задаче B5 от нас требуется найти не просто площадь сектора, а величину S/π. Поэтому выполняем последний шаг. Подставляем и получаем:

12π : π = 12

Это и есть ответ. Так в чем же главная ошибка учеников, которые решают подобные задачи? Дело в том, что многие начинают считать площадь меньшего из секторов, изображенных на рисунке. Однако этот сектор не закрашен. В результате при правильных по существу расчетах многие ученики получают неправильный ответ. Согласитесь, обидная ошибка?

Поэтому рекомендация следующая: внимательно читайте условие задачи B5! Если требуется найти площадь закрашенного сектора, то именно закрашенный сектор и нужно искать. Даже если на чертеже он занимает большую часть круга. А если требуется найти площадь незакрашенного сектора, то об этом обязательно будет указано в условии. Поэтому прежде чем записывать ответ, еще раз проверьте, что от вас требуется: закрашенный сектор или незакрашенный? И тогда дополнительный балл на ЕГЭ по математике вам гарантирован.:)

Смотрите также:

Задача B5: площадь кольца
Задача B5: площадь сектора
Как сдать ЕГЭ по математике
Метод коэффициентов, часть 1
Задача B5: метод узлов
Сфера, описанная вокруг куба

Источник

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: $frac{AD+BC}{2}=frac{4+2}{2}=3.$

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла alpha равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна ${90}^{circ}.$ Тогда $angle alpha =frac{{90}^{circ}}{2}={45}^{circ}.$

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на $frac{sqrt{5}}{2}.$

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

${sin alpha }={sin angle AOB}=frac{4}{2sqrt{5}}=frac{2}{sqrt{5}}.$ Осталось умножить найденное значение синуса на $frac{sqrt{5}}{2}.$

$frac{2}{sqrt{5}}cdot frac{sqrt{5}}{2}=1$

Ответ: 1.

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где d_1 и d_2 — диагонали.

Получим:

Ответ: 12.

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: 12,5 .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: 10,5 .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна $frac{1}{2}cdot 3cdot 2=3.$

Площадь каждого из маленьких треугольников равна $frac{1}{2}cdot 1cdot 2=1.$

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как R=1 . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R=1 ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще $frac{1}{8}$ круга, то есть $frac{3}{8}$ круга.

Значит, нам надо умножить площадь круга на $frac{3}{8}$ . Получим:

$frac{3}{8}cdot 2,8 =1,05$

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна pi R^2 , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в ${frac{4}{3}}^2 = frac{16}{9}$ раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Ответ: 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Как считают объем и площадь здания

Объем и площадь здания жилого и общественного. Общая, расчетная, полезная…

Как считают объем и площадь здания

А. Объем и площадь здания жилого при проектировании
(из СП 54.13330.2011 Здания жилые многоквартирные)

Площадь жилого здания следует определять как сумму площадей этажей здания, измеренных в пределах внутренних поверхностей наружных стен.
В площадь этажа включаются площади балконов, лоджий, террас и веранд, а также лестничных площадок и ступеней с учетом их площади в уровне данного этажа. В площадь этажа не включается площадь проемов для лифтовых и других шахт, эта площадь учитывается на нижнем этаже.
Площади подполья для проветривания здания, неэксплуатируемого чердака, технического подполья, технического чердака, внеквартирных инженерных коммуникаций с вертикальной (в каналах, шахтах), и горизонтальной (в межэтажном пространстве) разводкой, а также тамбуров, портиков, крылец, наружных открытых лестниц и пандусов в площадь здания не включаются. Эксплуатируемая кровля при подсчете общей площади здания приравнивается к площади террас.
Площадь комнат, помещений вспомогательного использования и других помещений жилых зданий следует определять по их размерам, измеряемым между отделанными поверхностями стен и перегородок на уровне пола (без учета плинтусов).
Площадь неостекленных балконов, лоджий, а также террас следует определять по их размерам, измеряемым по внутреннему контуру (между стеной здания и ограждением) без учета площади, занятой ограждением.
Площадь размещаемых в объеме жилого здания помещений общественного назначения подсчитывается по правилам, установленным в СНиП 31-06.
Площадь застройки здания определяется как площадь горизонтального сечения по внешнему обводу здания на уровне цоколя, включая выступающие части, в том числе крыльца и террасы. Площадь под зданием, расположенным на опорах, а также проезды под ним включаются в площадь застройки.
Строительный объем жилого здания определяется как сумма строительного объема выше отметки ±0,000 (надземная часть) и ниже этой отметки (подземная часть).
Строительный объем определяется в пределах ограничивающих наружных поверхностей с включением ограждающих конструкций, световых фонарей и других надстроек, начиная с отметки чистого пола надземной и подземной частей здания, без учета выступающих архитектурных деталей и конструктивных элементов, козырьков, портиков, балконов, террас, объема проездов и пространства под зданием на опорах (в чистоте), проветриваемых подполий и подпольных каналов.

Б. Объем и площадь здания жилого для потребительской характеристики
(из СП 54.13330.2011 Здания жилые многоквартирные)

Площадь квартир определяют как сумму площадей всех отапливаемых помещений (жилых комнат и помещений вспомогательного использования, предназначенных для удовлетворения бытовых и иных нужд) без учета неотапливаемых помещений (лоджий, балконов, веранд, террас, холодных кладовых и тамбуров).
Площадь под маршем внутриквартирной лестницы на участке с высотой от пола до низа выступающих конструкций лестницы 1,6 м и менее не включается в площадь помещения, в котором размещена лестница.
При определении площади комнат или помещений, расположенных в мансардном этаже, рекомендуется применять понижающий коэффициент 0,7 для площади частей помещения с высотой потолка от 1,6 м — при углах наклона потолка до 45°, а для площади частей помещения с высотой потолка от 1,9 м — от 45° и более. Площади частей помещения с высотой менее 1,6 м и 1,9 м при соответствующих углах наклона потолка не учитываются. Высота помещения менее 2,5 м допускается не более чем на 50% площади этого помещения.
Общая площадь квартиры — сумма площадей ее отапливаемых комнат и помещений, встроенных шкафов, а также неотапливаемых помещений, подсчитываемых с понижающими коэффициентами, установленными правилами технической инвентаризации.
Площадь квартиры и другие технические показатели, подсчитываемые для целей статистического учета и технической инвентаризации, по завершению строительства уточняются по правилам, установленным в «Инструкции о проведении учета жилищного фонда в Российской Федерации», утвержденной Приказом N 37 от 04.08.98 Минземстроя России.

В. Объем и площадь здания общественного
(из СП 118.13330.2012 Для общественных зданий)

Общая площадь здания определяется как сумма площадей всех этажей (включая технический, мансардный, цокольный и подвальный).
В общую площадь здания включается площадь антресолей, галерей и балконов зрительных и других залов, веранд, наружных застекленных лоджий и галерей, а также переходов в другие здания.
В общей площади здания отдельно указывается площадь открытых неотапливаемых планировочных элементов здания (включая площадь эксплуатируемой кровли, открытых наружных галерей, открытых лоджий и т.п.).
Площадь многосветных помещений, а также пространство между лестничными маршами более ширины марша и проемы в перекрытиях более 36кв. м следует включать в общую площадь здания в пределах только одного этажа.
Площадь этажа следует измерять на уровне пола в пределах внутренних поверхностей (с чистой отделкой) наружных стен. Площадь этажа при наклонных наружных стенах измеряется на уровне пола. Площадь мансардного этажа измеряется в пределах внутренних поверхностей наружных стен и стен мансарды, смежных с пазухами чердака с учетом Г.5.
Полезная площадь здания определяется как сумма площадей всех размещаемых в нем помещений, а также балконов и антресолей в залах, фойе и т.п., за исключением лестничных клеток, лифтовых шахт, внутренних открытых лестниц и пандусов.
Расчетная площадь здания определяется как сумма площадей входящих в него помещений, за исключением:

коридоров, тамбуров, переходов, лестничных клеток, внутренних открытых лестниц и пандусов;
лифтовых шахт;
помещений, предназначенных для размещения инженерного оборудования и инженерных сетей.

В общую, полезную и расчетную площади здания не включаются площади подполья для проветривания здания на вечномерзлых грунтах, чердака, технического подполья (технического чердака) при высоте от пола до низа выступающих конструкций менее 1,8 м, а также наружных тамбуров, наружных балконов, портиков, крылец, наружных открытых лестниц и пандусов.
Площадь помещений здания определяется по их размерам, измеряемым между отделанными поверхностями стен и перегородок на уровне пола (без учета плинтусов). Площадь помещения мансардного этажа учитывается с понижающим коэффициентом 0,7 на участке в пределах высоты наклонного потолка (стены) при наклоне 30° — до 1,5 м, при 45° — до 1,1 м, при 60° и более — до 0,5 м.
Строительный объем здания определяется как сумма строительного объема выше отметки 0.00 (надземная часть) и ниже этой отметки (подземная часть).
Строительный объем надземной и подземной частей здания определяется в пределах ограничивающих поверхностей с включением ограждающих конструкций, световых фонарей, куполов и др., начиная с отметки чистого пола каждой из частей здания, без учета выступающих архитектурных деталей и конструктивных элементов, подпольных каналов, портиков, террас, балконов, объема проездов и пространства под зданием на опорах (в чистоте), а также проветриваемых подполий под зданиями на вечномерзлых грунтах и подпольных каналов.
Площадь застройки здания определяется как площадь горизонтального сечения по внешнему обводу здания по цоколю, включая выступающие части (входные площадки и ступени, веранды, террасы, приямки, входы в подвал). Площадь под зданием, расположенным на столбах, проезды под зданием, а также выступающие части здания, консольно выступающие за плоскость стены на высоте менее 4,5 м включаются в площадь застройки. Дополнительно указывается площадь застройки подземной автостоянки, выходящая за абрис проекции здания.
Торговая площадь магазина определяется как сумма площадей торговых залов, помещений приема и выдачи заказов, зала кафетерия, площадей для дополнительных услуг покупателям.

Вы смотрели статью «Как считают объем и площадь здания»

Источник

Как найти площадь закрашенной фигуры формула?

Что такое площадь фигуры в математике?

Что такое площадь прямоугольника 4 класс?

Как можно вычислить площадь квадрата?

Чему равна площадь квадрата?

Как найти площадь квадрата зная все стороны?

Как найти диагональ квадрата если нам известны его стороны?

Как найти площадь квадрата если его диагональ равна 1?

Как найти площадь квадрата если известно его диагональ?

Как считают объем и площадь здания

Объем и площадь здания жилого и общественного. Общая, расчетная, полезная…

Как считают объем и площадь здания

А. Объем и площадь здания жилого при проектировании (из СП 54.13330.2011 Здания жилые многоквартирные)

Б. Объем и площадь здания жилого для потребительской характеристики (из СП 54.13330.2011 Здания жилые многоквартирные)

В. Объем и площадь здания общественного (из СП 118.13330.2012 Для общественных зданий)

Не пропустите также:

А. Объем и площадь здания жилого при проектировании
(из СП 54.13330.2011 Здания жилые многоквартирные)

Б. Объем и площадь здания жилого для потребительской характеристики
(из СП 54.13330.2011 Здания жилые многоквартирные)

В. Объем и площадь здания общественного
(из СП 118.13330.2012 Для общественных зданий)