Загрузить PDF
Загрузить PDF
Определить площадь плоских фигур в квадратных сантиметрах (также обозначаемых как см2) достаточно просто. В самом легком случае, когда требуется рассчитать площадь квадрата или прямоугольника, она вычисляется произведением длины и ширины. Площадь других фигур (кругов, треугольников и так далее) можно определить с помощью целого ряда специальных математических формул. Также, если потребуется, можно без труда перевести площадь в квадратные сантиметры из других единиц измерения.
-
1
Определите длину измеряемой площади. У квадратов и прямоугольников по четыре стороны, расположенных под прямыми углами относительно друг друга. В случае с прямоугольниками, их противоположные стороны равны между собой, тогда как у квадратов равны все стороны. Измерьте одну из сторон квадрата или большую из сторон прямоугольника, чтобы определить ее длину в сантиметрах.[1]
-
2
Определите ширину измеряемой площади. Далее измерьте в сантиметрах любую из сторон, смежных с той, которую вы измерили в первую очередь. Эта сторона будет находиться под углом в 90 градусов к первой. Вторая мерка будет обозначать ширину квадрата или прямоугольника.[2]
- Так как у квадрата все стороны одинаковы, его длина будет равна ширине. Поэтому у квадрата можно изначально измерить только одну сторону.
-
3
Умножьте длину на ширину. Просто перемножьте длину и ширину фигуры, чтобы определить площадь квадрата или прямоугольника в квадратных сантиматрах.[3]
- Например, допустим, что длина прямоугольника составляет 4 см, а ширина – 3 см. В таком случае площадь фигуры рассчитывается следующим образом: 4 × 3 = 12 квадратных сантиметров.
- В случае с квадратом (по причине равных сторон) можно просто умножить саму на себя длину одной из его сторон (другими словами, возвести ее «в квадрат» или «во вторую степень»), чтобы определить площадь фигуры в квадратных сантиметрах.
Реклама
-
1
Найдите площадь круга по формуле: S = π × r2. Чтобы найти площадь круга в квадратных сантиметрах, необходимо знать расстояние в сантиметрах от центра круга до линии его окружности. Это расстояние называется радиусом окружности. Как только радиус будет известен, обозначьте его буквой r из вышеупомянутой формулы. Умножьте значение радиуса само на себя и на число π (3,1415926…), чтобы узнать площадь круга в квадратных сантиметрах.[4]
- Например, площадь круга с радиусом 4 см составит 50,27 квадратных сантиметра в результате перемножения 3,14 и 16.
-
2
Вычислите площадь треугольника по формуле: S = 1/2 b × h. Площадь треугольника в квадратных сантиметрах вычисляется умножением половины длины его основания b (в сантиметрах) на его высоту h (в сантиметрах). Основанием треугольника выбирается одна из его сторон, тогда как высота треугольника – это перпендикуляр, опущенный к основанию треугольника из противоположной к нему вершины. Площадь треугольника можно вычислить через длину основания и высоту по любой из сторон треугольника и противоположной к ней вершине.[5]
- Например, если длина основания треугольника составляет 4 см, а высота, проведенная к основанию – 3 см, площадь составит: 2 x 3 = 6 квадратных сантиметра.
-
3
Найдите площадь параллелограмма по формуле: S = b × h. Параллелограммы подобны прямоугольникам за одним исключением – их углы не обязательно равны 90 градусам. Соответственно, расчет площади параллелограмма производится аналогичным для прямоугольника способом: длина стороны основания в сантиметрах умножается на высоту параллелограмма в сантиметрах. За основание берут любую из сторон, а высота определяется длиной перпендикуляра к ней из противоположного тупого угла фигуры.[6]
- Например, если длина основания параллелограмма составляет 5 см, а его высота – 4 см, его площадь составит: 5 x 4 = 20 квадратных сантиметров.
-
4
Вычислите площадь трапеции по формуле: S = 1/2 × h × (B+b). Трапеция – это четырехугольник две стороны которого параллельны между собой, а остальные две – нет. Чтобы определить площадь трапеции в квадратных сантиметрах, необходимо знать три мерки (в сантиметрах): длину более длинной параллельной стороны B, длину более короткой параллельной стороны b и высоту трапеции h (определяемую как кратчайшее расстояние между ее параллельными сторонами по перпендикулярному к ним отрезку). Сложите между собой длины двух параллельных сторон, поделите сумму пополам и умножьте на высоту, чтобы получить площадь трапеции в квадратных сантиметрах.[7]
- Например, если более длинная из параллельных сторон трапеции равна 6 см, более короткая – 4 см, а высота – 5 см, площадь фигуры составит: ½ x (6+4) х 5 = 25 квадратных сантиметров.
-
5
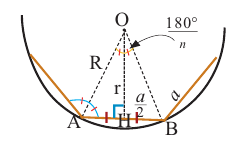
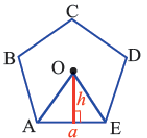
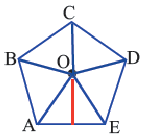
Найдите площадь правильного шестиугольника: S = ½ × P × a. Приведенная формула верна только для правильного шестиугольника с шестью равными сторонами и шестью одинаковыми углами. Буквой P обозначается периметр фигуры (или произведение длины одной стороны на шесть, что справедливо для правильного шестиугольника). Буквой a обозначается длина апофемы – расстояние от центра шестиугольника до середины одной из его сторон (точки, расположенной посередине между двумя соседними вершинами фигуры). Перемножьте периметр и апофему в сантиметрах и поделите результат на два, чтобы найти площадь правильного шестиугольника.[8]
- Например, если у правильного шестиугольника шесть равных сторон по 4 см (то есть его периметр P = 6 x 4 = 24 см), а длина апофемы равна 3,5 см, то его площадь составит: ½ x 24 x 3,5 = 42 квадратных сантиметра.
-
6
Вычислите площадь правильного восьмиугольника по формуле: S = 2a² × (1 + √2). Для расчета площади правильного восьмиугольника (с восемью равными сторонами и восемью одинаковыми углами) нужно знать только длину одной из сторон фигуры в сантиметрах (обозначенной в формуле буквой “a”). Подставьте соответствующее значение в формулу и вычислите результат.[9]
- Например, если длина стороны правильного восьмиугольника равна 4 см, то площадь этой фигуры составляет: 2 х 16 x (1 + 1,4) = 32 x 2,4 = 76,8 квадратных сантиметров.
Реклама
-
1
Переведите все мерки в сантиметры, прежде чем производить расчет площади. Чтобы сразу рассчитать площадь в квадратных сантиметрах, необходимо подставлять все параметры в формулу расчета площади также в сантиметрах (это касается, длины, высоты, апофемы и так далее). Поэтому, если ваши исходные данные выражены в других единицах измерения (например, в метрах), сначала их следует перевести в сантиметры. Ниже приведены соотношения наиболее популярных единиц измерения.
- 1 метр = 100 сантиметров
- 1 сантиметр = 10 миллиметров
- 1 дюйм = 2,54 сантиметра
- 1 фут = 30,48 сантиметра
- 1 сантиметр = 0,3937 дюйма
-
2
Чтобы перевести площадь из квадратных метров в квадратные сантиметры, ее следует умножить на 10000 (то есть площадь одного квадратного метра в сантиметрах), или на произведение 100 см на 100 см. Если вы знаете площадь фигуры в квадратных метрах, ее можно перевести в квадратные сантиметры умножением на 10000.[10]
- Например, 0,5 квадратного метра = 0,5 x 10000 = 5000 квадратных сантиметров.
-
3
Чтобы перевести в квадратные сантиметры площадь, выраженную в квадратных дюймах, умножьте ее на 6,4516. Как уже упоминалось, 1 дюйм равен 2,54 сантиметра, тогда как квадратный дюйм составляет 6,4516 квадратных сантиметров (или 2,54 x 2,54). Таким образом, если вам необходимо конвертировать в квадратные сантиметры площадь, равную 10 квадратным дюймам, следует умножить 10 на 6,4516, и у вас получится 64,5 квадратных сантиметров.[11]
- Также следует упомянуть, что в одном гектаре содержится 10000 квадратных метров, тогда как каждый квадратный метр равен 10000 квадратных сантиметров. Поэтому, чтобы выразить один гектар в сантиметрах, следует умножить 10000 на 10000 и получится 100 миллионов квадратных сантиметров.
Реклама
Об этой статье
Эту страницу просматривали 154 010 раз.
Была ли эта статья полезной?
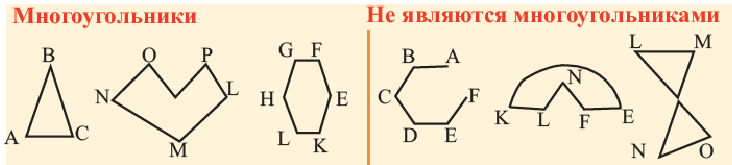
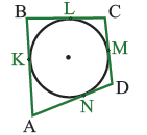
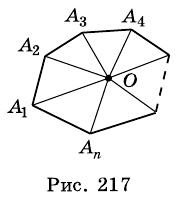
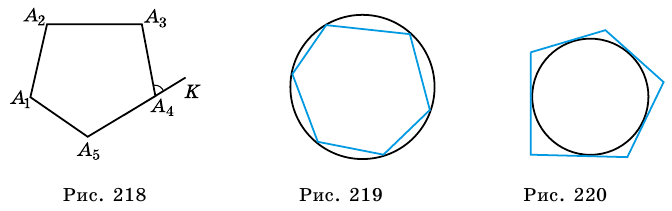
Многоугольником считается фигура,имеющая количество сторон больше или равное 3.
1)Площадь треугольника со сторонами a,b,c, и высотами h1,h2,h3,
площадь S =a*h1/2=b*h2/2=c*h3/2,
или по формуле Герона :
S= V p*(p-a)*(p-b)*(p-c),
где p — полупериметр.
Площадь четырехугольника:
1)площадь квадрата :S = a^2,
2)площадь прямоугольника :S = a *b,
3)площадь параллелограмма : S =a * h1 = b *h2,
4)площадь ромба S = a *h =d1*d2,
где a,b -стороны четырёхугольника,h1,h2-высоты,d1,d2-диагонали ромба.
5)площадь произвольного четырёхугольника определяется путем разбивки его по диагонали и нахождения площади каждого треугольника отдельно.
Площадь правильного многоугольника равна произведению полупериметра =n*a,на апофему h
S=(n*a)*h/2
где а-сторона многоугольника,n-число сторон,h-апофема.
План урока:
Понятие площади фигур
Сравнение площадей фигур
Квадратный сантиметр, дециметр, метр
Площадь прямоугольника
Преобразование величин
Здравствуйте, друзья! Давайте познакомимся. Я — Сова — Мудрая голова.
Масса моего мозга больше, чем у других птиц. Я, как все учителя, терпелива, замечаю все вокруг, слышу шорохи, обдумываю свои шаги. У многих народов меня считают символом знаний.
Сегодня на уроке мы познакомимся с различными способами сравнения и измерения геометрических фигур, а я поделюсь с вами своей мудростью.
Будь внимателен, дружок!
Начинаем наш урок.
Понятие площади фигур
Распределите фигуры на группы.
Какие фигуры вы видите?
Прямые и кривые линии, прямые и кривые, овалы, круг, прямоугольники, квадраты, треугольники.
Чем похожи данные фигуры?
Их можно начертить на плоскости.
Чем они отличаются?
Из бумаги можно вырезать только плоские фигуры, у которых кроме длин сторон, можно вычислить и новую величину — площадь.
Для чего это надо нам знать? Когда может пригодиться?
Величины нужны не только для решения математических задач, но и в жизни. Чтобы сделать поделку, надо определить, какое количество бумаги потребуется. При ремонте квартиры мы считаем, сколько купить рулонов обоев, чтобы оклеить стены комнаты. Величина понадобится при постройке дома, при изготовлении какой-либо продукции в промышленности. Даже в саду и огороде хозяйки считают, хватит ли места на грядке.
Как можно объяснить слово площадь? Значение понятий мы узнаем в толковых словарях.
Прочитайте, какой смысл нового термина в словаре С.И. Ожегова.
Первое объяснение:
Как называется главное место столицы нашей страны?
Красная площадь в Москве.
Вторая формулировка:
Общую и полезную площадь имеют разные помещения:
Квартира, в которой вы живете.
Классная комната, где вы учитесь.
Спортивный зал, столовая, бассейн школы.
Разные объекты, занимающие место на земле, можно встретить в любом городе.
Игровая площадка
Строительная площадка
Интересно, что некоторые люди заводят дома ушастых сов. Но держать птиц в клетке не рекомендуется: для них требуется более просторная комната, где они могли бы летать.
Жилая площадь квартиры
Любым диким животным лучше жить на воле. Сова – это хищная птица. Она питается грызунами, мышами, полевками, насекомыми и птицами. В этом отношении колоссальная польза от совы состоит в том, что за одно лето она может уничтожить около одной тысячи полевых мышей. Каждый грызун уничтожает более килограмма зерна на посевных площадях страны.
Поле с зерновыми культурами
Понятие площади фигуры:
В математике говорят — площадь фигуры. Это величина пространства, ограниченного замкнутым контуром (периметром фигуры).
Ее можно посчитать математическими методами. С этой целью еще в далекой древности была создана целая наука под названием геометрия. Она применялась для деления поля на земельные участки, но потом ее стали использовать для измерения различных фигур. Поэтому их называют геометрическими фигурами, их место на плоскости — площадью.
Сравнение площадей фигур
Мы можем площади плоских фигур сравнить на глазок. Посмотрите на иллюстрацию.
Картина на стене занимает меньше места, потому говорят, что ее площадь меньше, чем стена. Книги, тетради меньше площади крышки стола. Их как бы наложили сверху, и еще осталось место.
Перечислите способы сравнения фигур по площади.
Можно сравнить на глазок или накладывая предметы, фигуры друг на друга.
Расставьте в порядке уменьшения:
Если получилось так: 3, 1, 2, 4, то вы отлично справились.
Теперь сравните треугольник с кругом:
Круг меньше площади треугольника.
Сравнить можно с помощью любых мерок. На рисунке прямоугольники измеряли заданной меркой — треугольником.
В левый прямоугольник их поместилось 18, а в правый — 20. Делаем вывод, что площадь левой фигуры меньше, чем правой.
Хороший способ сравнения — это подсчет клеток.
Чтобы сравнить площади клетчатых фигур, надо пересчитать количество клеток:
Фигура 3 самая маленькая по площади – 6 клеток. Фигура 2 имеют большую площадь, чем 3. В ней 7 клеток. Площади фигур 1,4,5,6 равновеликие. Они равны 8 клеткам, по площади больше фигур 2 и 3.
Разностное сравнение площадей фигур — это нахождение разницы между большей и меньшей величиной.
Сравните площади фигур 3 и 1. Запишите результаты сравнения.
Проверьте себя:
8 – 6 = 2
Ответ: 2 клетки
Квадратный сантиметр, дециметр, метр
Какой меркой лучше измерить площадь фигуры квадрата и прямоугольника?
В 18 веке на Руси вводилась основная мера измерения площади — десятина и четь. Но поля крестьян были неровными, поэтому часто мерками служила урожайная копна. Народ изобретал особые мерки: выть, соха, обжа, коробь, веревка, жеребья. Сейчас мы не используем этих мер.
Начертите прямоугольник со сторонами 5см и 4см. Какими мерками можно измерить фигуру?
Посмотрите на рисунок, утенок измерил прямоугольник с помощью треугольников, ежонок — квадратами, а котенок — прямоугольниками.
Посчитаем, сколько единичных мерок находится в прямоугольнике. У животных получились разные величины: 40, 20, 10.
Всегда ли удобно определять площадь фигуры произвольными мерками?
Конечно, нет.
Вывод: значение величины зависит от выбранной мерки. Чтобы сравнить, нужно договориться об одинаковом способе измерения.
Всегда ли для определения площади фигуры подходит клетка?
Да.
Какого размера должна быть клетка?
Я предлагаю измерять как ежик, квадратами по 2 клеточки.
Измерьте длину и ширину этого квадратика. Что получилось?
Длина и ширина равна 1 см.
Единицей измерения площади еще 4-5 тысяч лет тому назад жители древнего города Вавилона считали квадрат, так как именно квадрат имеет превосходные признаки: четыре стороны равны межу собой, четыре прямых угла; можно провести ось и найти центр симметрии. Форма квадрата без изъянов, совершенна, поэтому его легко начертить и плотно покрыть фигуры любой формы.
Если у квадратика сторона 1см – площадь его равна квадратному сантиметру.
1 квадратный сантиметр сравним с ноготком взрослого человека.
Записывается площадь 1 квадратного сантиметра так:
S = 1 кв. см или S = 1 см2
Латинская буква «эс» обозначает площадь, двойка в правом верхнем углу — две величины: длину и ширину.
Начертите квадрат со стороной 10 сантиметров.
Квадратный дециметр (1 дм 2) — это квадрат со стороной 1 дм или 10 см.
Квадратный метр (1 м 2) — это квадрат со стороной 1 м или 10 дм. В квадратных метрах обозначается площадь в жилых помещениях, например: в комнатах, коридорах. Эта мерка подойдет для измерения дачного участка, спортивного зала, территории сквера.
А при строительстве школ важно учитывать, сколько квадратных метров должно быть в классе, если для одного ученика по санитарным правилам нужно 4 квадратных метра.
Вы хорошо справляетесь с заданиями. Спине, голове, всему телу нужен отдых. Встаньте на физкультурную минутку.
Физкультминутка
Поднимитесь, вверх потянитесь,
Вперед наклонитесь.
Ниже, ниже тянитесь,
Достаньте мизинцем до пятки.
Получилось? Тогда все в порядке.
Выпрямитесь, грудью вздохните,
Руки шире в стороны разведите.
Соедините в замок на лопатках.
Получилось? Тогда все в порядке.
Глазки зажмурьте, спокойно постойте.
Отдохнули? Теперь посчитайте площадки.
Площадь прямоугольника
Площади простых фигур, таких как квадратов и прямоугольников рассчитывать научились быстро. Для этого измеряют стороны прямоугольника.
Площадь прямоугольника находится по формуле: S = a ∙ b, где длину надо умножить на ширину фигуры.
Задание 1.
Постройте прямоугольник, длина которого 50 мм, а ширина 30 мм.
Можно ли длину и ширину данного прямоугольника выразить в сантиметрах?
Можно.
|
50 мм = 5 см |
30 мм = 3 см |
Найдите периметр прямоугольника. Р = (a + b) ∙ 2
Р = (5 + 3) ∙ 2 = 16 (см)
Ответ: 16 см
Имеет ли построенная вами фигура площадь?
Да. Прямоугольник имеет длину 5 см и ширину 3 см. Найдем, чему равна площадь прямоугольника по формуле S = a ∙ b.
S = 5 ∙ 3 = 15 см2
Ответ: площадь прямоугольника равна 15 кв.см.
Задание 2.
Чему равна площадь прямоугольника со сторонами 5 см и 4 см? Рассуждаем так. Нам известна длина и ширина прямоугольника. Площадь равна произведению этих величин.
S = 5 ∙ 4 = 20 см2
Ответ: 20 кв.см.
Задание 3.
Рассмотрите следующий рисунок:
Как называется данная геометрическая фигура?
Многоугольник.
Как найти площадь этого многоугольника?
Найти площади отдельных прямоугольников.
Найдите площадь этого многоугольника разными способами.
Первый способ.
Решение.
Измеряем стороны большого прямоугольника.
Длина равна 3 см, а ширина 3 + 1 = 4 (см).
1) 4 · 3 = 12 (см2) – площадь большого прямоугольника.
Длина маленького прямоугольника 3 см, а ширина 1 см. Перемножим эти величины.
2) 3 · 1 = 3 (см2) – площадь маленького прямоугольника.
Теперь из большей фигуры вырезаем два маленьких белых прямоугольника.
3) S = 12 – 3 – 3 = 6 (см2) – площадь многоугольника.
Второй способ.
Решение.
1) 3 · 1 = 3 (см2) – площадь верхнего прямоугольника.
2) 3 · 1 = 3 (см2) – площадь второго прямоугольника.
3) S = 3 + 3 = 6 (см2) – общая площадь многоугольника.
Ответ: S = 6 см2
Преобразование величин
По формуле S = a ∙ b квадратные сантиметры можно выразить в квадратных метрах. Давайте вспомним, что один метр равен сто сантиметрам.
1 м = 100 см
Мы выполним умножение сторон, и найдем квадратную величину.
Значит: 1 м2 = 100 ∙ 100 = 10000 см2
Задание 4.
Вычислите сколько кв.дм в 1 м2. Во сколько раз 1 кв. м. больше 1 кв. дм?
Как преобразовать квадратные дециметры в квадратные метры? Давайте рассуждать так. Квадрат со стороной 1 м разделим на 10 столбиков. В каждом таком столбике по 10 кв. дм, то есть всего в кв. м 10 десятков, или 100 дм2.
Второй вариант размышлений отталкивается от формулы. Умножаем длину на ширину. 10 дм на 10 дм, получится 100 дм2.
1 м2 = 10 ∙ 10 = 100 дм2
Ответ: в 1 кв. м содержится 100 кв.дм. 1 кв.м. в сто раз больше одного квадратного дециметра.
Задание 5.
Сколько кв. см в 1 кв. дм? Во сколько раз 1 кв. дм. больше 1 кв. см?
Выражаем квадратные дециметры в квадратных сантиметрах.
1 дм = 10 см
1 дм2 = 10 ∙ 10 = 100 см2
Ответ: 1 кв.дм равен 100 кв.см. 1 кв.дм в сто раз больше одного квадратного сантиметра.
Выполните упражнение:
Найдите, сколько квадратных дециметров в 8 м2, в 25 м2, в 45 м2 9 дм2
Мы знаем, что 1 м2 – это 100 дм2, то есть число м2 в 100 раз больше числа дм2, поэтому умножим 8 на 100, получим 800 дм2.
25 м2 : умножим 25 на 100 = 2500 дм2.
45 м2 9 дм2 : это 45 ∙ 100 + 9 = 3100 + 9 = 4509 мм2.
Наш урок подходит к концу.
Продолжите фразу:
сегодня я научился
было интересно
было трудно
Вы хорошо потрудились, поэтому сможете справиться с самостоятельными заданиями.
До новых встреч!
Содержание:
Изучив материал этой лекции, вы узнаете формулу, с помощью которой можно найти сумму углов выпуклого многоугольника.
- Вы расширите свои представления о такой знакомой вам величине, как площадь.
- Вы научитесь находить площадь параллелограмма, треугольника, трапеции.
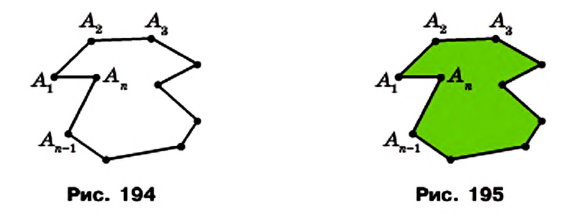
Определение многоугольников
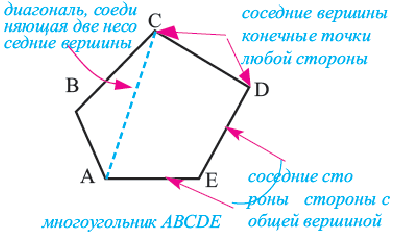
Рассмотрим фигуру, состоящую из точек
Фигура, образованная этими отрезками, ограничивает часть плоскости, выделенную на рисунке 195 зеленым цветом. Эту часть плоскости вместе с отрезками 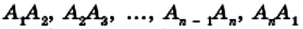
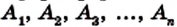
Стороны, являющиеся соседними отрезками, называют соседними сторонами многоугольника. Вершины, являющиеся концами одной стороны, называют соседними вершинами многоугольника.
Две соседние стороны многоугольника образуют угол многоугольника. Например, на рисунке 196 
Многоугольник называют по количеству его углов: треугольник, четырехугольник, пятиугольник и т. п.
Многоугольник обозначают по его вершинам. Например, на рисунке 197 изображен пятиугольник ABCDE. В обозначении многоугольника буквы, стоящие рядом, соответствуют соседним вершинам. Например, пятиугольник, изображенный на рисунке 197, можно обозначить еще и так: CDEAB, EABCD, EDCBA и т. д.
Периметром многоугольника называют сумму длин всех его сторон.
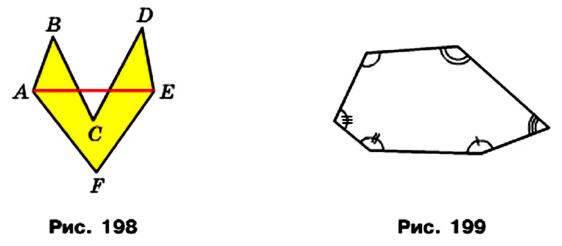
Отрезок, соединяющий несоседние вершины многоугольника, называют диагональю. Например, на рисунке 198 отрезок АЕ — диагональ шестиугольника ABCDEF.
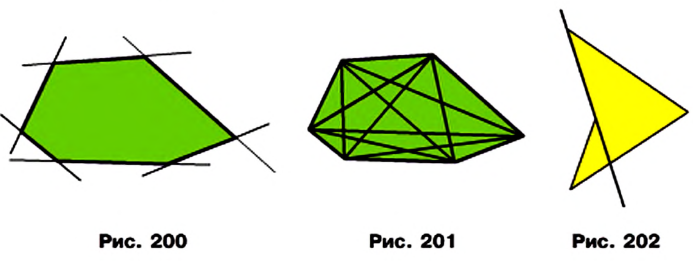
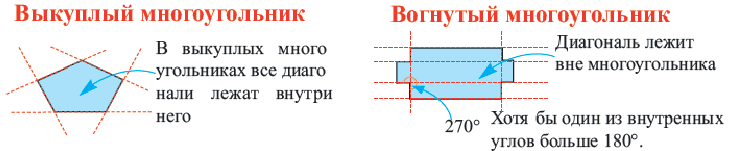
На рисунке 199 изображен многоугольник, все углы которого меньше развернутого. Такой многоугольник называют выпуклым. Из сказанного следует, что любой треугольник является выпуклым многоугольником. Заметим, что многоугольники, изображенные на рисунках 196-198, не являются выпуклыми.
Выпуклый многоугольник обладает такими свойствами:
- выпуклый многоугольник расположен в одной полуплоскости относительно любой прямой, содержащей его сторону (рис. 200);
- выпуклый многоугольник, отличный от треугольника, содержит любую свою диагональ (рис. 201).
Если многоугольник не является выпуклым, то он такими свойствами не обладает (рис. 198, 202).
Теорема 19.1. Сумма углов выпуклого n-угольника равна
Доказательство. Для случая n = 3 теорема была доказана в 7 классе (теорема 16.1).
Пусть 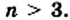
Докажем, что сумма всех его углов равна 180° (n-2).
Проведем все его диагонали, выходящие из вершины 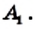
Отметим, что эта теорема справедлива и для любого многоугольника, не являющегося выпуклым.
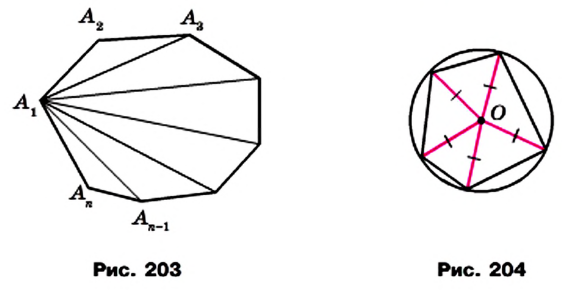
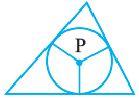
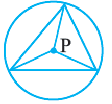
Определение. Окружность называют описанной около многоугольника, если она проходит через все его вершины.
На рисунке 204 изображена окружность, описанная около многоугольника. В этом случае также говорят, что многоугольник вписан в окружность.
Центр окружности, описанной около многоугольника, равноудален от всех его вершин. Следовательно, этот центр принадлежит серединным перпендикулярам всех сторон многоугольника, вписанного в окружность.
Около многоугольника можно описать окружность, если существует точка, равноудаленная от всех его вершин. Следовательно, если серединные перпендикуляры всех сторон многоугольника пересекаются в одной точке, то около такого многоугольника можно описать окружность.
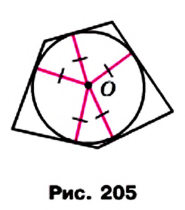
Определение. Окружность называют вписанной в многоугольник, если она касается всех его сторон.
На рисунке 205 изображена окружность, вписанная в многоугольник. В этом случае также говорят, что многоугольник описан около окружности.
Центр окружности, вписанной в многоугольник, равноудален от всех его сторон. Следовательно, этот центр принадлежит биссектрисам всех углов многоугольника, описанного около окружности.
Понятие площади многоугольника. Площадь прямоугольника
С такой величиной, как площадь, вы часто встречаетесь в повседневной жизни: площадь квартиры, площадь дачного участка, площадь поля и т. п.
Опыт подсказывает вам, что равные земельные участки имеют равные площади, что площадь квартиры равна сумме площадей всех ее помещений (комнат, кухни, коридора и т. д.).
Вы знаете, что площади земельных участков измеряют в сотках (арах) и гектарах; площади регионов и государств — в квадратных километрах; площадь квартиры — в квадратных метрах.
На этих практических знаниях о площади основывается определение площади многоугольника.
Определение. Площадью многоугольника называют положительную величину, которая обладает следующими свойствами:
- равные многоугольники имеют равные площади;
- если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников;
- за единицу измерения площади принимают единичный квадрат, то есть квадрат со стороной, равной единице измерения длины.
Измерить площадь многоугольника — это значит сравнить его площадь с площадью единичного квадрата. В результате получают числовое значение площади данного многоугольника. Это число показывает, во сколько раз площадь данного многоугольника отличается от площади единичного квадрата.
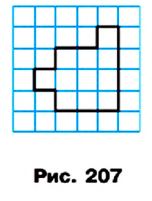
Например, если клетку вашей тетради принять за единичный квадрат, то площадь многоугольника, изображенного на рисунке 207, будет равна 11 квадратным единицам (кратко записывают: 11 ед.2).
Обычно для нахождения площади используют формулы, то есть вычисляют площадь многоугольника по определенным элементам (сторонам, диагоналям, высотам и т. д.). Некоторые из формул вы уже знаете. Например, вы неоднократно применяли формулу S = ab, где S — площадь прямоугольника, а и b — длины его соседних сторон.
Для доказательства этой формулы потребуется следующая лемма.
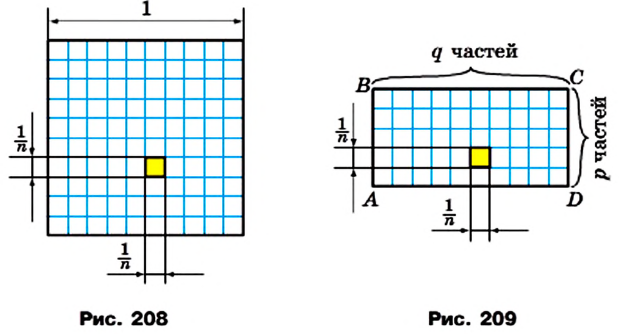
Лемма. Площадь квадрата со стороной 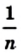
Доказательство. Рассмотрим единичный квадрат и разделим его на 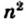
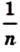
Из определения площади многоугольника (свойство 1) следует, что все эти квадраты имеют равные площади. По свойству 2 сумма площадей этих квадратов равна площади единичного квадрата, то есть 1 ед.2. Поэтому площадь каждого маленького квадрата равна
Теорема 20.1. Площадь прямоугольника равна произведению длин его соседних сторон.
Доказательство. На рисунке 209 изображен прямоугольник ABCD, длины соседних сторон которого равны a и b: АВ = а, ВС = b. Докажем для случая, когда а и b — рациональные числа, что площадь S прямоугольника вычисляют по формуле S = ab.
Числа а и b представим в виде обыкновенных дробей с одинаковыми знаменателями:
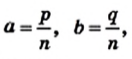
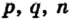
Разделим сторону АВ на р равных частей, а сторону ВС — на q равных частей. Через точки деления проведем прямые, параллельные сторонам прямоугольника. Тогда прямоугольник будет разделен на 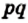
Согласно лемме площадь каждого квадрата равна 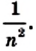
Рассмотрение случая, когда хотя бы одно из чисел а или b является иррациональным, выходит за рамки школьного курса геометрии.
Определение. Многоугольники, имеющие равные площади, называют равновеликими.
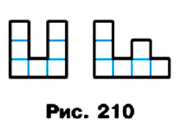
Из определения площади (свойство 1) следует, что все равные фигуры равновелики. Однако не все фигуры, имеющие равные площади, являются равными. Например, на рисунке 210 изображены два многоугольника, каждый из которых составлен из семи единичных квадратов. Эти многоугольники равновелики, но не равны.
Площадь параллелограмма
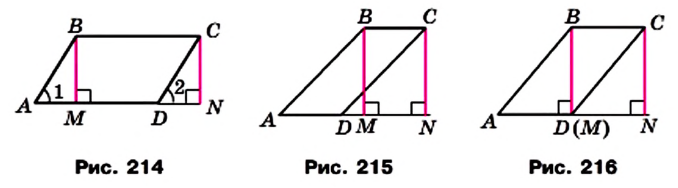
Теорема 21.1. Площадь параллелограмма равна произведению его стороны и высоты, проведенной к этой стороне.
Доказательство. На рисунке 214 изображены параллелограмм ABCD, площадь которого равна S, и его высота ВМ. Докажем, что S = ВС • ВМ.
Проведем высоту CN. Легко показать (сделайте это самостоятельно), что четырехугольник MBCN — прямоугольник. Покажем, что он равновелик данному параллелограмму.
Площадь параллелограмма равна сумме площадей треугольника АВМ и трапеции MBCD. Площадь прямоугольника равна сумме площадей указанной трапеции и треугольника DCN. Однако треугольники АВМ и DCN равны по гипотенузе и острому углу (отрезки АВ и CD равны как противолежащие стороны параллелограмма, углы 1 и 2 равны как соответственные при параллельных прямых АВ и DC и секущей AD). Значит, эти треугольники равновелики. Отсюда следует, что параллелограмм ABCD и прямоугольник MBCN равновелики.
По теореме 20.1 площадь прямоугольника MBCN равна произведению длин сторон ВС и ВМ. Тогда S = ВС • ВМ, где S — площадь параллелограмма ABCD.
Для завершения доказательства надо рассмотреть случаи, когда основание М высоты ВМ не будет принадлежать стороне AD (рис. 215) или совпадет с вершиной D (рис. 216). И в этом случае параллелограмм ABCD и прямоугольник MBCN будут равновеликими. Докажите этот факт самостоятельно.
Если обозначить длины стороны параллелограмма и проведенной к ней высоты соответственно буквами а и h, то площадь S параллелограмма вычисляют по формуле
Площадь треугольника
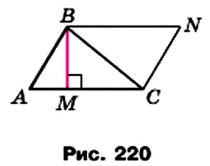
Теорема 22.1. Площадь треугольника равна половине произведения его стороны и проведенной к ней высоты.
Доказательство. На рисунке 220 изображены треугольник АВС, площадь которого равна S, и его высота ВМ. Докажем, что
Через вершины В и С треугольника проведем прямые, параллельные сторонам АС и АВ соответственно (рис. 220). Пусть эти прямые пересекаются в точке N. Четырехугольник ABNC — параллелограмм по определению. Треугольники АВС и NCB равны (докажите это самостоятельно). Следовательно, равны и их площади. Тогда площадь треугольника АВС равна половине площади параллелограмма ABNC. Высота ВМ треугольника АВС является также высотой параллелограмма
ABNC. Отсюда
Если воспользоваться обозначениями для высот и сторон треугольника АВС, то согласно доказанной теореме имеем:
где S — площадь треугольника.
Следствие. Площадь прямоугольного треугольника равна половине произведения его катетов.
Докажите эту теорему самостоятельно.
Пример №1
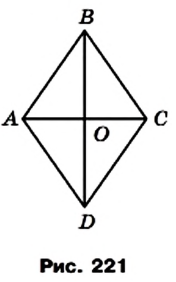
Докажите, что площадь ромба равна половине произведения его диагоналей.
Решение:
На рисунке 221 изображен ромб ABCD, площадь которого равна S. Его диагонали АС и BD пересекаются в точке О. Докажем, что
Поскольку диагонали ромба перпендикулярны, то отрезки АО и СО являются высотами треугольников BAD и BCD соответственно. Тогда можно записать:
Площадь трапеции
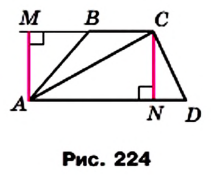
Теорема 23.1. Площадь трапеции равна произведению полусуммы ее оснований и высоты.
Доказательство. На рисунке 224 изображена трапеция ABCD (AD||BC), площадь которой равна S. Отрезок CN — высота этой трапеции. Докажем, что
Проведем диагональ АС и высоту AM трапеции. Отрезки AM и CN являются высотами треугольников АВС и ACD соответственно.
Имеем:
Если обозначить длины оснований трапеции и ее высоты соответственно буквами 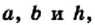
Следствие. Площадь трапеции равна произведению ее средней линии и высоты.
Равносоставленные и равновеликие многоугольники
Если некоторый многоугольник можно разрезать на части и составить из них другой многоугольник, то такие два многоугольника называют равносоставленными.
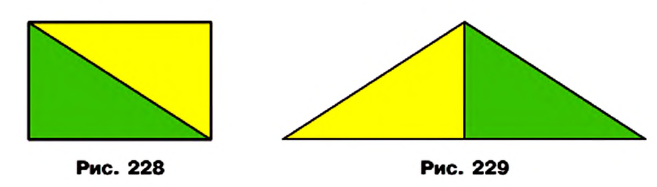
Например, если прямоугольник разрезать вдоль его диагонали (рис. 228), то получим два равных прямоугольных треугольника, из которых можно составить равнобедренный треугольник (рис. 229). Фигуры на рисунках 228 и 229 — равно составленные.
Очевидно, что равносоставленные многоугольники являются равновеликими. Этот факт применяют при доказательстве теорем и решении задач. Например, доказывая теорему 21.1, мы фактически разрезали параллелограмм на треугольник АВМ и трапецию MBCD, из которых составили прямоугольник MBCN (см. рис. 215).
Если треугольник разрезать вдоль средней линии, то из полученных треугольника и трапеции можно составить параллелограмм (рис. 230).
Легко установить (сделайте это самостоятельно), что такое разрезание треугольника приводит к еще одному доказательству теоремы о площади треугольника (теорема 22.1). Этой же цели служит разрезание треугольника на части, из которых можно составить прямоугольник (рис. 231).
Евклид в своей знаменитой книге «Начала» формулирует теорему Пифагора так:
«Площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах».
Если показать, что можно разрезать квадраты, построенные на катетах, на части и составить из этих частей квадрат со стороной, равной гипотенузе, то тем самым будет доказана теорема Пифагора.
На рисунке 232 показан один из возможных способов такого разрезания. Квадраты, построенные на катетах, разрезаны на части, площади которых равны 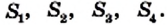
Из определения площади многоугольника следует, что равносоставленные многоугольники являются равновеликими. Но совсем неочевидной является такая теорема.
Теорема. Любые два равновеликих многоугольника являются равносоставленными.
Впервые этот факт доказал в 1832 г. венгерский математик Фаркаш Бойяи. Позднее немецкий математик Пауль Гервин нашел другое доказательство. Поэтому эту теорему называют теоремой Бойяи—Гервина.
Теорема Чевы
На сторонах ВС, СА и АВ треугольника АВС отметим произвольные точки 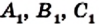
Если точки 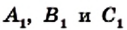
Если три прямые пересекаются в одной точке, то их называют конкурентными.
Теорема Чевы дает общий критерий конкурентности произвольных трех чевиан.
Теорема. Для того чтобы, чевианы 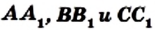
Доказательство. Докажем сначала необходимое условие конкурентности: если чевианы 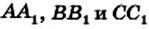
Воспользовавшись результатом ключевой задачи 757, можно записать (рис. 235):
Перемножив записанные равенства, получим равенство (*).
Докажем теперь достаточное условие конкурентности: если выполняется равенство (*), то чевианы 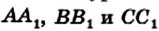
Пусть чевианы 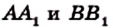
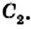
Сопоставляя это равенство с равенством (*), приходим к выводу, что 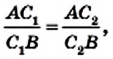
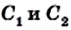
Напомню:
Сумма углов выпуклого n-угольника
Сумма углов выпуклого n-угольника равна 180° (n — 2).
Окружность, описанная около многоугольника
Окружность называют описанной около многоугольника, если она проходит через все его вершины.
Окружность, вписанная в многоугольник
Окружность называют вписанной в многоугольник, если она касается всех его сторон.
Площадь многоугольника
Площадью многоугольника называют положительную величину,
которая обладает следующими свойствами:
- равные многоугольники имеют равные площади;
- если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников;
- за единицу измерения площади принимают единичный квадрат, то есть квадрат со стороной, равной единице измерения длины.
Площадь прямоугольника
Площадь прямоугольника равна произведению длин его соседних сторон.
Равновеликие многоугольники
Многоугольники, имеющие равные площади, называют равновеликими.
Площадь параллелограмма
Площадь параллелограмма равна произведению его стороны и высоты, проведенной к этой стороне.
Площадь треугольника
Площадь треугольника равна половине произведения его стороны и проведенной к ней высоты.
Площадь прямоугольного треугольника
Площадь прямоугольного треугольника равна половине произведения его катетов.
Площадь трапеции
- Площадь трапеции равна произведению полусуммы ее оснований и высоты.
- Площадь трапеции равна произведению ее средней линии и высоты.
Ломанная линия и многоугольники
Ломаная линия состоит из таких нескольких последовательно-соединенных отрезков: конец первого является началом второго, конец второго является началом третьего и т.д. Если конечная точка последнего отрезка совпадает с начальной точкой первого отрезка, то ломаная называется замкнутой. Многоугольник — это фигура, образованная замкнутой ломаной линией, в которой смежные отрезки не лежат на одной прямой, а несмежные — не пересекаются.
- Многоугольник — это плоская фигура.
- Стороны состоят из конечного числа отрезков.
- Многоугольник это замкнутая фигура, делящая плоскость на 2 части: внутреннюю замкнутую область и внешнюю бесконечную область.
- Многоугольник обозначают буквами, указывающими его вершины.
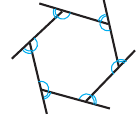
Многоугольники бывают выпуклые и вогнутые. Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой содержащей его сторону. Если не лежит в одной полуплоскости — вогнутым.
Многоугольник называется правильным, если у него все стороны все углы конгруэнтны.
В многоугольнике количество вершин, сторон и углов одинаковые. Многоугольник с 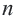
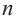
Соответственно количеству сторон, многоугольники называются треугольными, четырехугольными, пятиугольными, шестиугольными т.д. Из любой вершины выпуклого 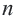
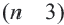
Внутренние и внешние углы многоугольника
Угол, образованный двумя сторонами, исходящими из данной вершины называется внутренним углом при данной’ вершине выпуклого многоугольника. Угол, смежный с внутренним углом многоугольника называется внешним. Сумма внутренних и внешних углов (взятых по одному при каждой вершине) многоугольника при любой вершине равна 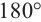
Теорема 1. Сумма внутренних углов выкуплого 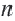
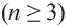
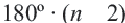
Следствие: Каждый внутренний угол правильного 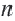
Теорема 2. Сумма внешних углов выкуплого многоугольника равен 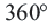
Следствие 2. Каждый внешний угол правильного 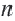
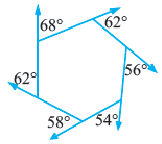
Пример №2
Один из внешних углов правильного многоугольника равен 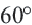
a) найдите градусную меру внутреннего угла многоугольника;
b) найдите число сторон многоугольника.
Решение: а) 
Внутренний угол:
b)
Многоугольники вписанные в окружность и описанные около окружности
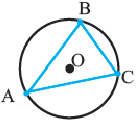
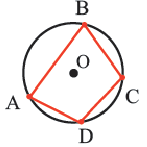
Определение 1. Многоугольник называется вписанным в окружность, если все его вершины лежат на окружности, а окружность называется описанной около многоугольника. На рисунке треугольник 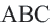
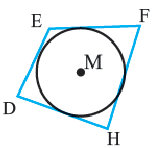
Определение 2. Многоугольник называется описанным около окружности, если все его стороны касаются окружности, а окружность называется вписанной в многоугольник. На рисунке четырехугольник 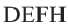
Окружность, вписанная в треугольник и описанная около нее
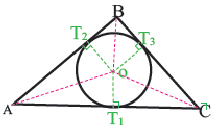
Теорема 1. В любой треугольник можно вписать окружность. Центром этой окружности будет точка пересечения биссектрис углов треугольника.
Теорема 2. Около любого треугольника можно описать окружность. Центром этой окружности будет точка пересечения серединных перпендикуляров к сторонам треугольника.
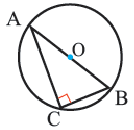
Теорема 3. Если в окружность вписан прямоугольный треугольник, то гипотенуза является диаметром этой окружности.
Обратная теорема. Если сторона треугольника, вписанного в окружность, является диаметром, то этот треугольник — прямоугольный.
Доказательство 1-ой теоремы (текстовое). Проведем биссектрисы углов 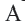
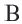
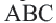

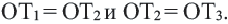

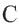

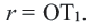
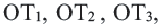
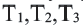
Доказательство 2-ой теоремы. Через середины сторон 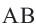
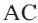
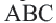

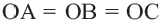
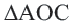

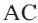

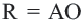
Замечание: Около данного треугольника можно описать только одну окружность. В данную окружность можно вписать бесконечное количество треугольников.
Свойства четырехугольников, вписанных в окружность и описанного около нее
В отличие от треугольников, не во всякий четырехугольник можно вписать или описать окружность.
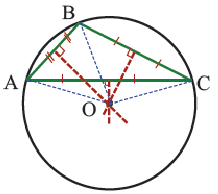
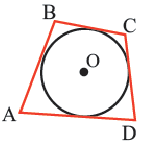
Теорема 4. В любом описанном четырехугольнике суммы противоположных сторон равны.
Обратная теорема. Если суммы противоположных сторон четырехугольника равны, то в этот четырехугольник можно вписать окружность.
Теорема 5. Сумма двух противоположных углов четырехугольника, вписанного в окружность, равна
Обратная теорема. Если сумма противоположных углов четырехугольника равна 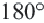
Доказательство теоремы 4: Пусть точки 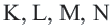
Если сложить почленно эти равенства, получим 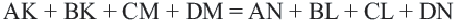
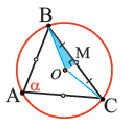
Отношение стороны треугольника, вписанного в окружность, к синусу противолежащего угла равно диаметру этой окружности:
Исследуйте данное доказательство для случая, когда центр окружности расположен внутри треугольника, обсудите и напишите в тетради.
В любой правильный многоугольник можно вписать и описать окружность. Центры этих окружностей совпадут. Биссектрисы углов правильного многоугольника пересекаются в точке 
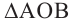
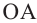
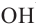
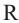
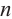
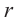
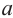
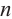
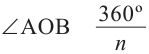
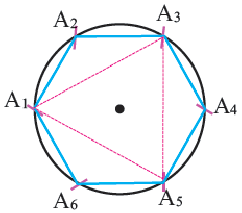
Задача на построение: Постройте правильный шестиугольник.
1. Нарисуйте отрезок 
2. Циркулем нарисуйте окружность, радиус которой равен длине этого отрезка.
3. Не меняя раствора циркуля, разбейте всю окружность на части одинаковой длины и отметьте их точками.
4. Соедините последовательно отмеченные точки. Получится правильный шестиугольник, вписанный в окружность.
Если соединить попарно некоторые вершины правильного шестиугольника 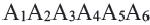
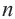
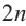
Площадь правильного многоугольника
Центр правильного многоугольника. Центр окружности, описанного около правильного многоугольника или вписанного в него, является центром правильного многоугольника. Центр правильного многоугольника находится на одинаковом расстоянии от всех вершин и всех сторон многоугольника.
Апофема правильного многоугольника. Перпендикуляр, проведенный из центра многоугольника к его стороне, называется апофемой. Апофема правильного многоугольника равна радиусу вписанной окружности.
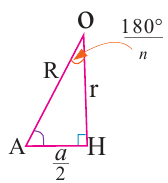
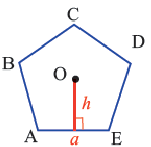
Выполните следующее упражнение по шагам и выведите формулу зависимости площади правильного многоугольника от апофемы.
1. Нарисуйте правильный пятиугольник 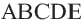
2. Из центра 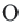

3. Соедините точки 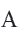
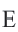
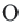
4. Выразите площадь треугольника 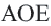
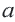
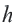
5. Соедините точки 
6. Обратите внимание на то, что площадь пятиугольника равна сумме площадей этих треугольников. Площадь пятиугольника:
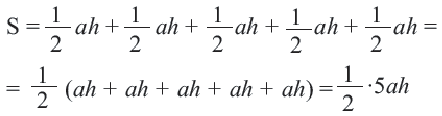
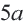
Площадь правильного многоугольника:
Соединив центр правильного 
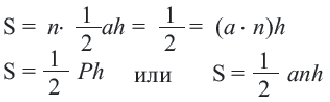
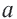

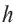
Пример №3
В окружность радиусом равным единице, вписан правильный пятиугольник. Найдите площадь пятиугольника. Решение:
Площадь многоугольника:
Нужно найти апофему 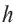
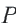
Центральный угол 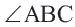
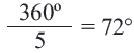
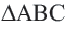
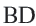
Тогда 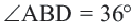

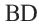
Сторона пятиугольника:

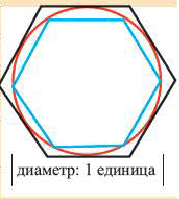
Историческое сведение. В 3-ем веке до н.э. Архимед — древнегреческий ученый, для того, чтобы определить численное значение 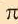
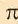
1. Принимая за единицу диаметр окружности, найдите периметр вписанного шестиугольника.
2. Покажите, что длина окружности с единичным диаметром равна 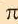
3. Нарисуйте радиус окружности. Найдите периметр описанного шестиугольника.
4. Напишите неравенство: 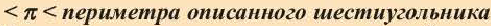
Увеличив число сторон многоугольника в 2 раза и продолжая вычисления для 12-ти, а затем для 96-ти угольного многоугольника Архимед, определил, что значения 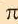
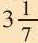
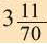
Паркетирование
Паркетированием называется покрытие площади фигурами до заполнения всей пустоты.
Если сумма углов при общей вершине многоугольника равна 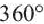
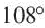
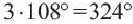
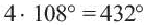
Справочный материал по многоугольникам
Многоугольник и его элементы.
Сумма углов выпуклого многоугольника. многоугольник, вписанный в окружность, и многоугольник, описанный около окружности.
Рассмотрим фигуру 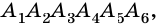
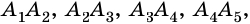
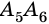
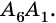
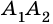
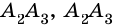

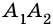
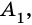

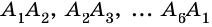
Очевидно, что количество вершин многоугольника равно количеству его сторон.
Сумму длин всех сторон многоугольника называют его периметром.
Наименьшее количество вершин (сторон) у многоугольника — три. В этом случае имеем треугольник. Еще одним отдельным видом многоугольника является четырехугольник.
Многоугольник, у которого 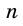
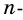
Две стороны многоугольника называют соседними, если они имеют общую вершину. Стороны многоугольника, не имеющие общей вершины, называют несоседними. Например, стороны 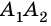
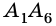
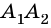
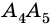
Две вершины многоугольника называют соседними, если они принадлежат одной стороне, а вершины многоугольника, не принадлежащие одной стороне, называют несоседними.
Например, вершины 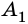
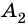
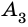
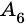
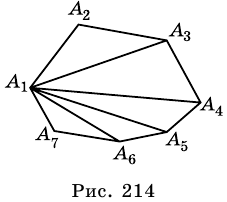
Отрезок, соединяющий две несоседние вершины многоугольника, называют диагональю многоугольника. На рисунке 214 изображены диагонали многоугольника 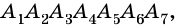
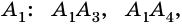
Пример №4
Сколько диагоналей имеет 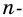
Решение:
Из каждой вершины 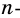

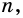
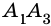
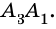
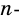
Ответ.
Углы, стороны которых содержат соседние стороны многоугольника, называют углами многоугольника. Пятиугольник 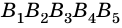
Если каждый из углов многоугольника меньше развернутого, то такой многоугольник называют выпуклым. Если хотя бы один угол многоугольника больше развернутого, то такой многоугольник называют невыпуклым.
Многоугольник 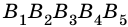
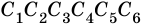
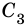
Теорема (о сумме углов выпуклого 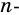
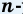
Доказательство:
Выберем во внутренней области многоугольника произвольную точку 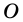
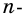
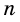
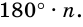
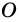
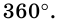
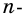
Углы выпуклого многоугольника называют еще его внутренними углами. Угол, смежный с внутренним углом многоугольника, называют внешним углом многоугольника. На рисунке 218 угол 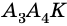
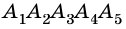
Очевидно, что каждый многоугольник имеет по два внешних угла при каждой вершине.
Пример №5
Докажите, что сумма внешних углов выпуклого 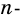
Решение:
Сумма внутреннего и внешнего углов при каждой вершине многоугольника равна 180°. Поэтому сумма всех внутренних и внешних углов 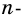
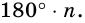
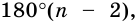
Многоугольник называют вписанным в окружность, если все его вершины лежат на окружности. Окружность при этом называют описанной около многоугольника (рис. 219).
Около многоугольника не всегда можно описать окружность. Если же это возможно, то центром такой окружности является точка пересечения серединных перпендикуляров к сторонам многоугольника (как и в случае треугольника).
Многоугольник называют описанным около окружности, если все его стороны касаются окружности. Окружность при этом называют вписанной в многоугольник (рис. 220).
Не в каждый многоугольник можно вписать окружность. Если же это возможно, то центром такой окружности является точка пересечения биссектрис внутренних углов многоугольника (как и в случае треугольника).
Многоугольник и его свойства
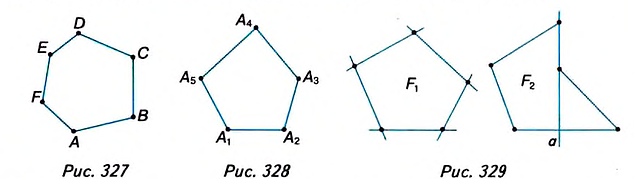
Вы уже знаете, что такое треугольник и четырёхугольник. Более общим является понятие многоугольника. На рисунке 327 вы видите многоугольник ABCDEF. Он состоит из отрезков АВ, ВС, CD, DE, EFy FA, размещённых таким образом, что смежные отрезки не лежат на одной прямой, а несмежные -не имеют общих точек. Отрезки, из которых состоит многоугольник, называются его сторонами, углы, образованные смежными сторонами, — углами, а вершины этих углов — вершинами многоугольника.
В зависимости от количества вершин (углов либо сторон) многоугольник называется треугольником, четырёхугольником, пятиугольником и т. д. Многоугольник с n вершинами называется n-угольником.
Многоугольник обозначают названиями его вершин, например шестиугольник ABCDEF (рис. 327), пятиугольник 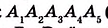
Ни одна из прямых, проходящих через стороны многоугольника 
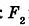
В дальнейшем мы будем рассматривать лишь выпуклые многоугольники.
Периметром многоугольника называется сумма длин всех его сторон. Его обозначают буквой Р.
Посмотрите на рисунок 330. В шестиугольнике ABCDEF отрезки AC, AD, АЕ соединяют вершину А с несоседними вершинами. Это — диагонали шестиугольника.
Диагональю n-угольника называется отрезок, который соединяет две несоседние его вершины.
Теорема (о сумме углов n-угольника).
Сумма углов n-угольника равна 180° • (n — 2).
Дано: 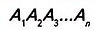
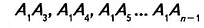
Доказательство. В заданном n-угольнике диагонали 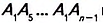
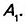
Угол, смежный с углом многоугольника (рис. 332), называется внешним углом многоугольника.
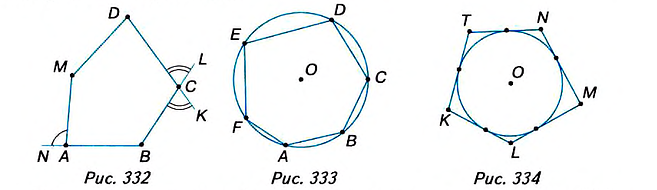
Многоугольники могут быть вписанными в окружность (рис. 333) или описанными около окружности (рис. 334). Попытайтесь дать определения и сравните их с указанными в учебнике.
Многоугольник все вершины которого лежат на окружности, называется вписанным, в эту окружность, а окружность — описанной около этого многоугольника.
Многоугольнику все стороны которого касаются окружности, называется описанным около этой окружности, а окружность — вписанной в этот многоугольник.
Стороны вписанного многоугольника и его диагонали — это хорды окружности. Каждый его угол является вписанным углом (рис. 335).
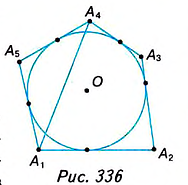
Стороны описанного многоугольника являются касательными к окружности, а его диагонали — секущими (рис. 336).
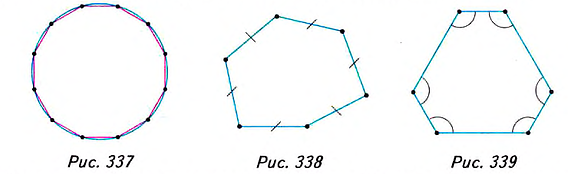
1. Геометрическая фигура называется простой, если её можно разбить на конечное количество треугольников. Многоугольник — это простая фигура (см. рис. 330 и 331), а окружность не является простой фигурой (рис. 337). Даже вписав в окружность многоугольник с очень большим количеством сторон, мы только приблизим его контур к окружности. Поэтому в геометрии длину окружности и площадь круга находят другими методами, чем периметр и площадь многоугольника.
2. У вас может возникнуть вопрос: Всегда ли из равенства сторон многоугольника следует равенство его углов и наоборот? Нет, это свойство лишь треугольника. Вы знаете пример четырёхугольника, в котором все стороны равны, а углы — не равны. Это ромб. В прямоугольнике все углы равны, а вот стороны — нет. Среди многоугольников с большим количеством вершин также можно выделить равносторонние многоугольники, в которых не все углы равны (рис. 338), и равноугольные многоугольники, в которых не все стороны равны
Понятие площади
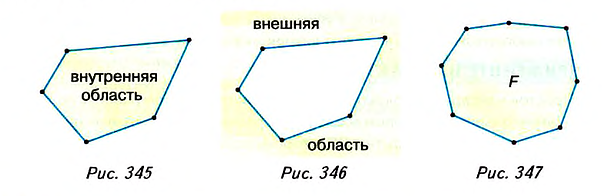
Многоугольник разбивает плоскость на две области — внутреннюю (рис. 345) и внешнюю (рис. 346).
Многоугольник вместе с его внутренней областью называется плоским многоугольником.
Каждый плоский многоугольник (например, многоугольник F на рис. 347) занимает часть плоскости. Если эту часть плоскости выразить некоторым числом, то получим площадь многоугольника. Далее будем говорить «площадь многоугольника», имея в виду, что многоугольник -плоский. Это относится и к другим плоским фигурам.
Площадь обозначают буквой S. Иногда указывают название фигуры, например 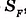
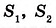
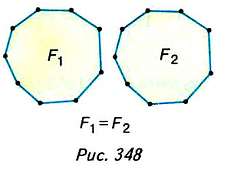
На рисунке 348 фигуры 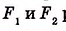
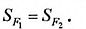
Единицы измерения площади кратко записываем так: 1 см2, а говорим: «один квадратный сантиметр». Говорить «сантиметр в квадрате» -неправильно!
Некоторые единицы измерения площади имеют специальные названия: ар (квадрат со стороной 10м), гектар (квадрат со стороной 100 м) и т. д.
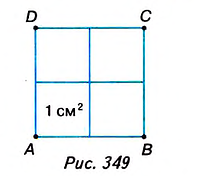
На рисунке 349 вы видите квадрат ABCD со стороной 2 см. Он состоит из четырёх квадратов площадью 1 см2, поэтому его площадь равна 4 см2.
Можем записать:
Ясно, что площадь любой фигуры выражается положительным числом. Изменится ли площадь квадрата ABCD, если за единицу измерения принять 1 мм2? Нет, площадь квадрата не изменится, но будет выражена иначе:
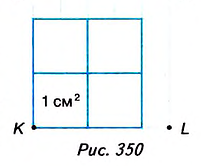
На рисунке 350 длина стороны квадрата KLMN равна 2,5 см. Он вмещает четыре квадрата площадью 1 см2 и ещё 9 маленьких квадратов площадью 0,25 см2. Поэтому 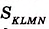
Ясно, что площадь любой фигуры равна сумме площадей частей, из которых она состоит.
Из предыдущих классов вы знаете, что площадь квадрата со стороной а можно вычислить иначе — по формуле площади квадрата:
Для квадратов ABCD и KLMN получим:
Поскольку 4 см2 < 6,25 см2, то можем записать:
Формулу площади квадрата будем считать основной, поэтому принимаем её без доказательства. Для других фигур формулы площади нужно выводить, исходя из основных свойств площади. Сформулируем их.
Основные свойства площади
- Площадь каждой фигуры больше нуля.
- Равные фигуры имеют равные площади.
- Площадь фигуры равна сумме площадей фигур, из которых она состоит.
- Единицей измерения площади является площадь квадрата со стороной, равной единице длины.
Основные свойства площади подсказывают способ выведения формул площади.
Для того чтобы вывести формулу площади многоугольника, нужно: либо разбить его на части, формулы площадей которых известны, либо дополнить его до такой фигуры, формула площади которой известна.
Теорема (о площади прямоугольника).
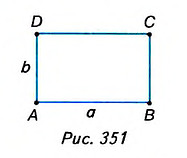
Площадь прямоугольника равна произведению его смежных сторон.
Дано: ABCD— прямоугольник (рис. 351),
AB=a,AD=b.
Доказать:
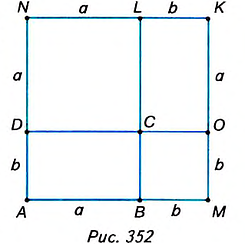
Доказательство. Достроим данный прямоугольник ABCD до квадрата AMKN со стороной о + b (рис. 352). Тогда S
С другой стороны, квадрат AMKNcociom из двух прямоугольников ABCD и OKLC и двух квадратов ВМОС и DNLC. Поэтому, по третьему свойству площади,
Прямоугольники ABCD и OKLC равны, поскольку равны смежные стороны а и b. Поэтому, по второму свойству площади, 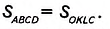
Далее получим:
Следствие. Площадь прямоугольного треугольника с катетами а и b равна половине произведения катетов.
Действительно, диагональ АС разбивает прямоугольник ABCD со сторонами а и b (рис. 353) на два равных прямоугольных треугольника ABC и ADC с катетами а и b. Поэтому
Пример №6
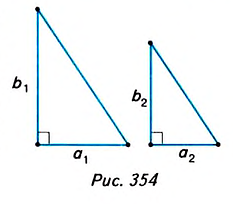
Докажите, что отношение площадей подобных прямоугольных треугольников равно квадрату их коэффициента подобия.
Решение:
Пусть один из заданных прямоугольных треугольников (рис. 354) имеет катеты 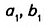
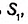
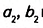
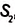
Докажем, что
Поскольку треугольники подобны, то 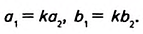
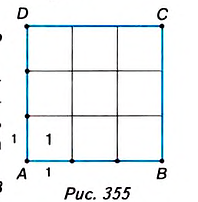
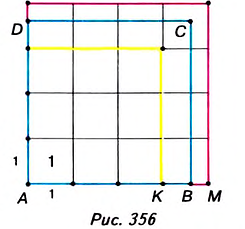
У вас может возникнуть вопрос: Как доказать, что площадь квадрата равна квадрату его стороны? Пусть сторона квадрата ABCD равна а. Возможны два случая: сторону АВ можно разбить на целое число п единичных отрезков (рис. 355); на стороне АВ можно разместить л единичных отрезков, но остаётся ещё отрезок, который короче единичного (рис. 356).
Рассмотрим первый случай (рис. 355). Разобьём сторону АВ на п единичных отрезков (на рисунке их три), тогда о — n • 1 — n. Аналогично разобьём сторону AD. Через точки деления проведём прямые, перпендикулярные АВ и AD. Эти прямые разбивают квадрат ABCD на 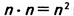
Поэтому 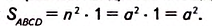
Рассмотрим второй случай (рис. 356). Пусть на отрезке АВ помещается n единичных отрезков и остаётся ещё отрезок длиной меньше 1. Это означает, что отрезок АК из п единичных отрезков меньше отрезка АВ, а отрезок AM из n + 1 единичных отрезков — больше этого отрезка. Получаем неравенство: n < а < n + 1.
Чтобы точнее оценить площадь заданного квадрата, разделим единичный отрезок на т равных частей. Тогда длина каждой части будет равна 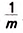
Пусть на отрезке АК их помещается 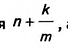
Число а будет лежать в пределах 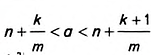
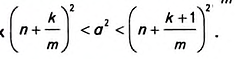
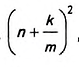
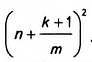
При увеличении количества точек деления число т станет как угодно большим. Площадь квадрата ABCD и квадрат числа а будут лежать в пределах, разность которых как угодно мала:
А это возможно лишь в случае, если
3. Символ S для обозначения площади фигуры происходит от латинского слова superficils, что означает «поверхность».
Параллелограмм и его площадь
Вы уже знаете формулы площадей трёх фигур -квадрата, прямоугольника и прямоугольного треугольника. Выведем формулу площади параллелограмма.
Теорема (о площади параллелограмма).
Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне.
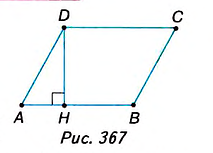
Дано: ABCD — параллелограмм (рис. 367), DH— высота, АВ= a, DH= 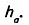
Доказать: 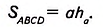
Доказательство. Проведём из вершины С высоту СМ= DH = 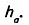

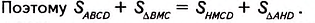
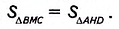
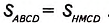
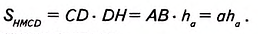
Пример №7
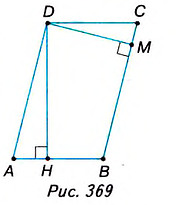
В параллелограмме стороны равны 8 см и 6,4 см, а высота, проведённая к большей стороне, — 6 см. Найдите высоту параллелограмма, проведённую к меньшей его стороне.
Решение:
Пусть ABCD— данный параллелограмм (рис. 369), в котором ab =6,4 см, ВС — 8 см, DM= 6 см.
Требуется найти высоту DH.
Площадь параллелограмма ABCD можно выразить двумя способами: либо как произведение стороны ВС на высоту DAf, либо как произведение стороны АВ на высоту DH.
Для того чтобы найти длину неизвестной стороны или высоту параллелограмма, выразите площадь двумя способами: через одну из двух смежных сторон параллелограмма и высоту, проведённую к ней, и через другую смежную сторону и соответствующую ей высоту. Составьте и решите уравнение относительно искомой величины.
Можно ли найти площадь ромба по стороне и высоте, проведённой к ней? Можно, поскольку ромб — частный вид параллелограмма.
Вы знаете, как находить площадь прямоугольного треугольника по его катетам. Воспользуемся этим, чтобы вывести ещё одну формулу площади ромба.
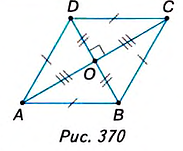
Теорема (о площади ромба по его диагоналям).
Площадь ромба равна половине произведения его диагоналей.
Дано: ABCD — ромб (рис. 370), АС и BD — диагонали,
Доказать:
Доказательство. В ромбе ABCD все стороны равны. Его диагонали АС и BD взаимно перпендикулярны и в точке пересечения делятся пополам. Поэтому они разбивают ромб на четыре равных прямоугольных треугольника ABO, СВО, CDO и ADO с катетами
Поскольку площадь ромба равна сумме площадей этих треугольников, то
Следствие. Площадь квадрата равна половине квадрата его диагонали.
Утверждение следует из того, что квадрат — это частный вид ромба и имеет равные диагонали, пусть d. Следовательно,
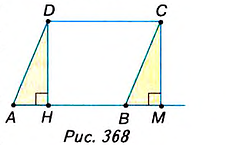
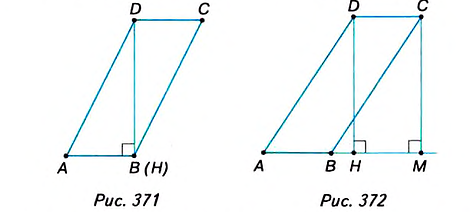
1. У вас может возникнуть вопрос: Зависит ли формула площади параллелограмма ABCD от расположения высоты DH (рис. 368)? Нет, не зависит. В расположении точки H возможны три случая. Один из них рассмотрен в учебнике. Ещё два случая: точка Н находится либо в вершине В параллелограмма (рис. 371), либо на продолжении его стороны АВ (рис. 372).
Во втором случае (рис. 371) параллелограмм ABCDсостоит из двух равных прямоугольных треугольников ABD u CDB, поэтому
В третьем случае (рис. 372) доказательство аналогично изложенному в учебнике. Проведите это самостоятельно.
2. Для фигур, имеющих равные площади, используют специальное название — равновеликие. Например, параллелограмм ABCD и прямоугольник HMCD на рисунке 372 являются равновеликими. Понятно, что два равных многоугольника всегда равновелики, но не любые два равновеликих многоугольника равны.
Два многоугольника называются равносоставленными, если их можно разбить на одинаковое количество попарно равных многоугольников, в частности треугольников. Таковы, например, параллелограмм ABCD и прямоугольник
HMCD на рисунке 368, поскольку каждый состоит из общей для них трапеции и равных прямоугольных треугольников ADH и ВСМ.
Между равновеликими и равносоставленными фигурами существует такая связь: равносоставленные многоугольники являются равновеликими (из определения о равносоставленных многоугольниках); равновеликие многоугольники являются равносоставленными. Последнее утверждение известно, как «теорема Больяи — Гервина», доказанная в XIX в. Интересно, что Фаркаш Больяи (1775 — 1856, Венгрия), доказавший теорему, был отцом Яноша Больяи (1802 — 1860) — одного из творцов неевклидовой геометрии. Янош Больяи.
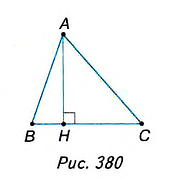
Треугольник и его площадь
Вы уже знаете, как вычислить площадь прямоугольного треугольника по его катетам. Возникает вопрос: Как найти площадь любого треугольника по его стороне и высоте, проведённой к этой стороне?
Теорема (о площади треугольника).
Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне.
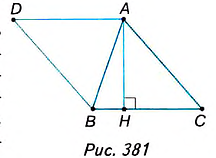
Дано: 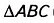
Доказать:
Доказательство. На стороне АВ заданного треугольника ABC построим равный ему треугольник BAD (рис. 381). Образованный четырёхугольник ADBC— параллелограмм, поскольку, по построению, AD = ВС, BD = АС. В нём сторона ВС= а, высота АН=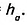
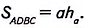
Следовательно:
Пример №8
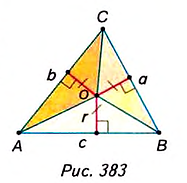
Докажите, что площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
Решение:
Пусть ABC — данный треугольник (рис. 382), в котором ВС= а, АС— b, АВ= с, 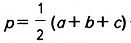
Докажем, что
Соединим отрезками вершины треугольника ABC с центром О вписанной в него окружности (рис. 383). Получаем три треугольника — ВОС, АОС и АОВ. В каждом из них радиус вписанной окружности r является высотой, проведённой к стороне, равной соответственно a, b или с.
Поэтому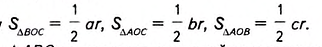
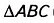
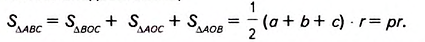
1. Способы вычисления площади треугольника (а также прямоугольника и трапеции) были известны ещё в Древнем Египте. Сведения об этом дошли до нас на папирусах. Среди них наиболее известные — папирус Ринда (около 1800 г. до н. э.), содержащий 84 задачи с решениями (страница из этого папируса на рис. 384), и так называемый московский папирус (около 1600 г. до н. э.), он содержит 25 задач с решениями. Чтобы найти площадь треугольника, древние египтяне основание треугольника делили пополам и умножали на высоту. А для определения площади равнобедренного треугольника использовали полупроизведение его боковых сторон.
2. Геометрические расчёты по точным формулам проводились и в древнем Вавилоне. Сведения сохранились на клинописных табличках (образец вы видите на рис. 385). Дошедшие до нас тексты свидетельствуют, что вавилоняне знали и использовали в практических задачах пропорциональность параллельных отрезков. Например, они умели вычислять длину отрезков AW, СМ и ВМ (рис. 386) в треугольнике ABC по его стороне АС= 30, разности S, — S2 = 42 площадей трапеции и треугольника, на которые разбивается данный треугольник параллельной прямой MN, и разности ВМ — СМ = 20. Сейчас для решения этой задачи нам пришлось бы составлять систему уравнений.
Трапеция и её площадь
Вы знаете, чтобы вывести формулы площадей прямоугольника, параллелограмма или треугольника, надо составить из этих фигур такие, площади которых умеете находить. Воспользуемся этим способом и выведем формулу площади трапеции.
Теорема (о площади трапеции).
Площадь трапеции равна произведению полусуммы её оснований на высоту.
Дано: ABCD— трапеция (рис. 397),
AB и CD — основания, СН— высота, АВ=о, CD=b, CH=h. а + b
Доказать:
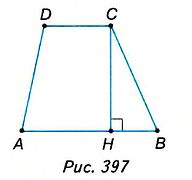
Доказательство. Проведём в трапеции диагональ АС (рис. 398). Она разбивает трапецию на два треугольника ABC и ADC. Высота h трапеции является высотой треугольника ABC, проведённой к стороне АВ = а, и равна высоте треугольника ADC, проведённой к стороне CD = b. Площадь трапеции равна сумме площадей этих треугольников, поэтому
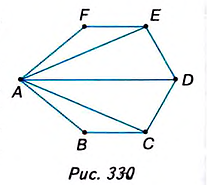
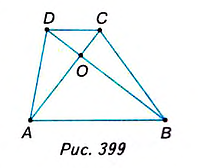
Пример №9
Диагонали АС и BD трапеции ABCD пересекаются в точке О (рис. 399). Докажите, что треугольники AOD и ВОС имеют равные площади.
Решение:
Рассмотрим треугольники ABD и ABC. В них сторона АВ— общая, а высоты, проведённые к этой стороне, равны высоте трапеции. Поэтому 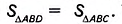
Следовательно, площади треугольников AOD и ВОС равны как разности равных площадей.
Для того чтобы установить, что неравные фигуры имеют равные площади, нужно доказать, что площади этих фигур равны либо сумме равных площадей, либо разности равных площадей.
1. У вас может возникнуть вопрос: Существует ли трапеция, средняя линия которой делит её площадь пополам?
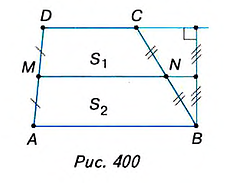
Существование фигуры с заданными свойствами можно доказать, если привести пример такой фигуры. Однако не всегда этот путь — самый простой. История свидетельствует о том, что иногда на поиски примера, подтверждающего существование некоторого математического объекта, учёные затрачивали многие годы. Чтобы упростить поиск, проводят предварительные аналитические расчёты. Именно это мы и сделаем, чтобы ответить на поставленный вопрос. Пусть трапеция ABCD (рис. 400) имеет основания а и b и высоту h. Средняя линия MN разбивает её на две трапеции с равными высотами 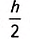
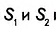
Найдём отношение площадей 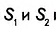
Равенство площадей 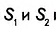
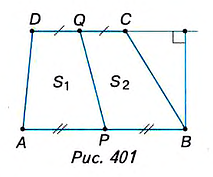
Интересно, что отрезок, соединяющий середины оснований трапеции (иногда его называют второй средней линией трапеции), делит площадь трапеции пополам. Докажите это самостоятельно, используя рисунок 401.
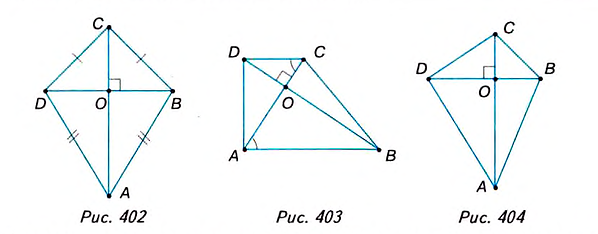
2. Изучая четырёхугольники, вы узнали о дельтоиде (рис. 402). Этот четырёхугольник, как и ромб, имеет взаимно перпендикулярные диагонали. Существуют трапеции со взаимно перпендикулярными диагоналями (рис. 403), а также произвольные четырёхугольники с аналогичным свойством (рис. 404). И ромб, и дельтоид, и указанная трапеция являются частными видами четырёхугольников со взаимно перпендикулярными диагоналями.
Докажите самостоятельно, что площадь четырехугольника со взаимно перпендикулярными диагоналями равна половине произведения этих диагоналей. Эта формула справедлива и для ромба, и для дельтоида, и для трапеции.
- Площадь многоугольника
- Правильные многоугольники
- Вписанные и описанные многоугольники
- Площадь прямоугольника
- Площади фигур в геометрии
- Площади поверхностей геометрических тел
- Вычисление площадей плоских фигур
- Преобразование фигур в геометрии
Download Article
Download Article
Calculating the area of a polygon can be as simple as finding the area of a regular triangle or as complicated as finding the area of an irregular eleven-sided shape. If you want to know how to find the area of a variety of polygons, just follow these steps.
Area Help
-
1
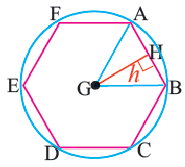
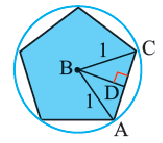
Write down the formula for finding the area of a regular polygon. To find the area of a regular polygon, all you have to do is follow this simple formula: area = 1/2 x perimeter x apothem.[1]
Here is what it means:-
Perimeter = the sum of the lengths of all the sides[2]
- Apothem = a segment that joins the polygon’s center to the midpoint of any side that is perpendicular to that side[3]
-
Perimeter = the sum of the lengths of all the sides[2]
-
2
Find the apothem of the polygon. If you’re using the apothem method, then the apothem will be provided for you. Let’s say you’re working with a hexagon that has an apothem with a length of 10√3.
Advertisement
-
3
Find the perimeter of the polygon. If the perimeter is provided for you, then you’re nearly done, but it’s likely that you have a bit more work to do. If the apothem is provided for you and you know that you’re working with a regular polygon, then you can use it to find the perimeter. Here’s how you do it:[4]
- Think of the apothem as being the «x√3» side of a 30-60-90 triangle. You can think of it this way because the hexagon is made up of six equilateral triangles. The apothem cuts one of them in half, creating a triangle with 30-60-90 degree angles.
- You know that the side across from the 60 degree angle has length = x√3, the side across from the 30 degree angle has length = x, and the side across from the 90 degree angle has length = 2x. If 10√3 represents «x√3,» then you can see that x = 10.
- You know that x = half the length of the bottom side of the triangle. Double it to get the full length. The bottom side of the triangle is 20 units long. There are six of these sides to the hexagon, so multiply 20 x 6 to get 120, the perimeter of the hexagon.
-
4
Plug the apothem and the perimeter into the formula. If you’re using the formula area = 1/2 x perimeter x apothem, then you can plug in 120 for the perimeter and 10√3 for the apothem. Here is what it will look like:[5]
- area = 1/2 x 120 x 10√3
- area = 60 x 10√3
- area = 600√3
-
5
Simplify your answer. You may need to state your answer in decimal instead of square root form. Just use your calculator to find the closest value for √3 and multiply it by 600. √3 x 600 = 1,039.2. This is your final answer.[6]
Advertisement
-
1
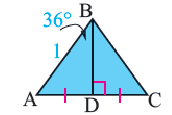
Find the area of a regular triangle. If you want to find the area of a regular triangle, all you have to do is follow this formula: area = 1/2 x base x height.
- If you have a triangle with a base of 10 and a height of 8, then the area = 1/2 x 8 x 10, or 40.
-
2
Find the area of a square. To find the area of a square, just square the length of one side. This is really the same thing as multiplying the base of the square by its height, because the base and height are the same.
- If the square has a side length of 6, then the area is 6 x 6, or 36.
-
3
Find the area of a rectangle. To find the area of a rectangle, simply multiply the base times the height.
- If the base of the rectangle is 4 and the height is 3, then the area of the rectangle is 4 x 3, or 12.
-
4
Find the area of a trapezoid. The find the area of a trapezoid, you just have to follow this formula: area = [(base 1 + base 2) x height]/2.
- Let’s say you have a trapezoid with bases that have a length of 6 and 8 and a height of 10. The area is simple [(6 +
x 10]/2, which can be simplified to (14 x 10)/2, or 140/2, which makes for an area of 70.
- Let’s say you have a trapezoid with bases that have a length of 6 and 8 and a height of 10. The area is simple [(6 +
Advertisement
-
1
Write down the coordinates of the vertices[7]
of the irregular polygon. Determining the area for an irregular polygon can be found when you know the coordinates of the vertices.[8]
-
2
Create an array. List the x and y coordinates of each vertex of the polygon in counterclockwise order. Repeat the coordinates of the first point at the bottom of the list.[9]
-
3
Multiply the x coordinate of each vertex by the y coordinate of the next vertex. Add the results. The added sum of these products is 82.
-
4
Multiply the y coordinate of each vertex by the x coordinate of the next vertex. Again, add these results. The added total of these products is -38.
-
5
Subtract the sum of the second products from the sum of the first products. Subtract -38 from 82 to get 82 — (-38) = 120.
-
6
Divide this difference by 2 to get the area of the polygon. Just divide 120 by 2 to get 60 and you’re all done.
Advertisement
Add New Question
-
Question
How can I calculate the area of an irregular polygon?
David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
Academic Tutor
Expert Answer
Divide the polygon into several triangles. Then, calculate the area of each triangle by multiplying the base by half of the height. Add the different areas together to find the total area of the polygon.
-
Question
How do I calculate the area of an octagon?
Cut it into smaller shapes, such as triangles or other quadrilaterals using angles. Find the area of each smaller shape, then add the areas together to find the area of the whole shape.
-
Question
How do I find the area of a 4-sided shape?
Assuming it’s not a square or rectangle, you would have to subdivide the figure into smaller sections consisting of squares, rectangles, triangles, and other shapes whose areas can be easily calculated. Then add those areas together.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
If you list the points in a clockwise order instead of counterclockwise, you will get the negative of the area. Hence this can be used as a tool to identify the cyclic path or sequence of a given set of points forming a polygon.
-
This formula computes area with orientation. If you use it on a shape where two of the lines cross like a figure eight, you will get the area surrounded counterclockwise minus the area surrounded clockwise.
Advertisement
References
About This Article
Article SummaryX
A polygon is any kind of closed, 2-dimensional shape with at least 3 straight sides and no curves. If a polygon is regular—that is, all of its sides are the same length—you can easily find the area given the side length and the apothem. The apothem is the distance from the exact center of the polygon to the center of any of the sides. If you know the apothem and the side length, simply use the formula area = ½ x perimeter x apothem. You can find the perimeter by adding together the lengths of all the sides, or multiplying the length of a side by the number of sides. For example, say you have a hexagon with an apothem that has a length of 3 units, and each side has a length of 7 units. Multiply 7 by 6 (the number of sides in the hexagon) to find the perimeter of 42 units. Multiply 42 x 3 x ½ to get an area of 63 square units. Some types of polygons have their own special formulas that you can use to find the area. For instance, to calculate the area of a triangle, use the formula ½ x base x height. For a rectangle, all you need to do is multiply length times width. Since the length and width are the same for a square, simply square the length of one of the sides to calculate the area. If your shape is a trapezoid, add together the lengths of the two parallel sides, then multiply the sum by the height of the trapezoid. Divide the result by 2 to get the area. In other words, use the formula area = (base1 + base2) x h x ½. When you’re dealing with an irregular polygon, things get a little trickier. The easiest way to find the area of an irregular polygon is to plot it on a graph and find the coordinates of each of the vertices, or corners. Create a table with the x-coordinate of each vertex in one column, and the y-coordinate of each vertex in the next column. Multiply the x-coordinate of each vertex by the y-coordinate of the vertex below it in the table and add all the products together. Then go back the other way, and multiply each y-coordinate by the x-coordinate below it. Add together those products as well. Subtract the sum of the second set of products from the sum of the first set, then divide the difference by 2 to find the area of the polygon. If you need to calculate the area of an irregularly-shaped polygon, keep reading to learn how!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,468,760 times.
Reader Success Stories
-
Olexiy Korshunov
Aug 14, 2019
«The calculation of the area of an irregular polygons is very intelligibly written and is easily implemented for…» more











































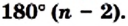
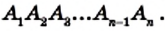
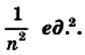
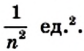
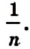
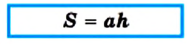
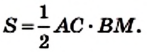
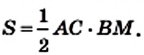
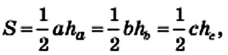
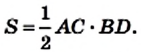
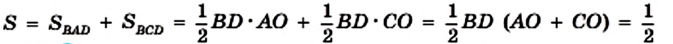
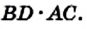
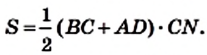
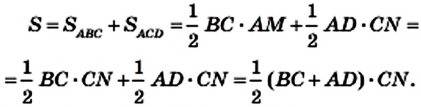
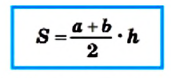


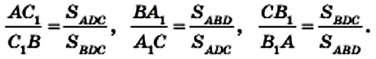
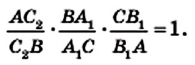

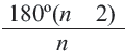
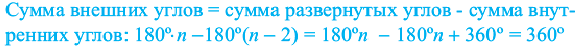

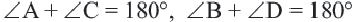
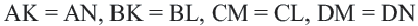
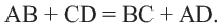
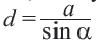

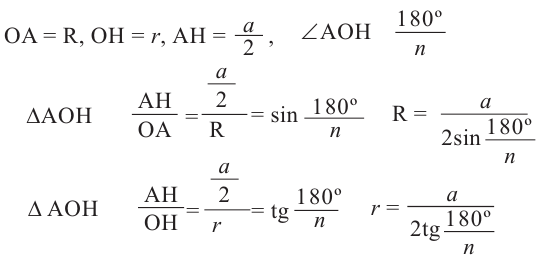


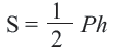

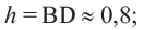
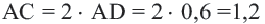
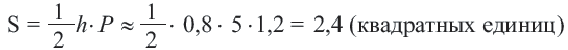

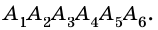
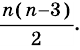
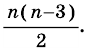
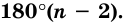
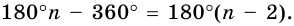
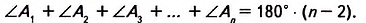
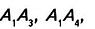
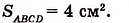
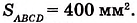
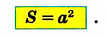
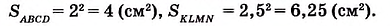
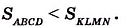
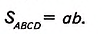
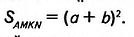
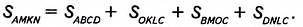
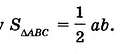
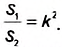
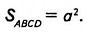
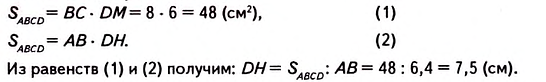
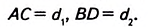
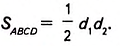
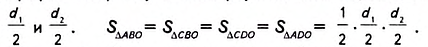
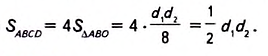
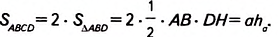
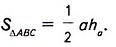
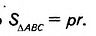
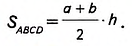
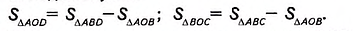
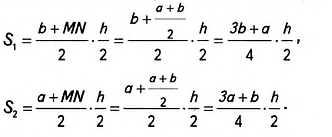
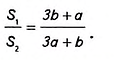









 x 10]/2, which can be simplified to (14 x 10)/2, or 140/2, which makes for an area of 70.
x 10]/2, which can be simplified to (14 x 10)/2, or 140/2, which makes for an area of 70.





