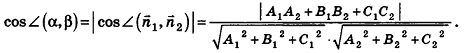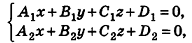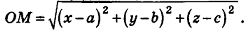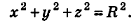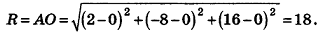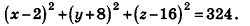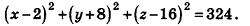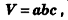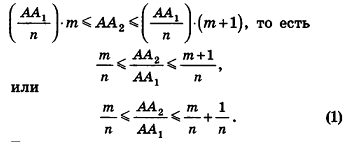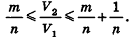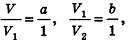
Шаровым сегментом называется часть шара, отсеченная от него плоскостью.
Формулы:
— площадь боковой поверхности
— площадь основания
— формула объема
Сегмент шара
Точность вычисления
Знаков после запятой: 5
Площадь боковой поверхности
Шаровой слой — часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар.
Формулы:
— площадь боковой поверхности
— объем
Шаровой слой
Точность вычисления
Знаков после запятой: 5
Площадь боковой поверхности
Площадь поверхности усеченной сферы. Как найти площадь и объем шара. Как найти площадь сферы
Многие из нас любят играть в футбол или, по крайней мере, почти каждый из нас
слышал про эту знаменитую спортивную игру. Всем известно,
что в футбол играют мячом.
Если спросить прохожего, форму какой геометрической фигуры имеет мяч, то часть
людей скажут, что форму шара, а часть, что формы сферы. Так кто же
из них прав? И в чем разница между сферой и шаром?
Важно!
Шар
— это пространственное тело. Внутри шар
чем-либо заполнен. Поэтому у шара можно найти объем.
Примеры шара в жизни: арбуз и стальной шарик.
Шар и сфера, подобно кругу и окружности, имеют центр, радиус и диаметр.
Важно!
Сфера
— поверхность шара. У сферы можно найти площадь поверхности.
Примеры сферы в жизни: волейбольный мяч и шарик для игры в настольный
теннис.
Как найти площадь сферы
Запомните!
Формула площади сферы:
S = 4π
R 2
Для того, чтобы найти площадь сферы, необходимо вспомнить,
что такое степень числа .
Зная определение степени,
можно записать формулу площади сферы следующим образом.
S = 4π
R 2 =
4π
R · R;
Закрепим полученные знания и решим задачу на площадь сферы.
Зубарева 6 класс. Номер 692(а)
Условие задачи:
- Вычислите площадь сферы, если её радиус равен
1 =
3 ·
=
=
/ (4 · 3)
= ) =
= ) =
= =
=
88
= 1 - R 3 = 1
- R = 1 м
Важно!
Уважаемые родители!
При окончательном расчете радиуса
не надо заставлять ребенка считать кубический корень. Учащиеся
6-го класса еще не проходили и не знают определение корней в математике.
В 6 классе при решении такой задачи используйте метод перебора.
Спросите ученика, какое число, если его умножить 3 раза на самого себя даст
единицу.
Шаром называют уйма всех точек в пространстве, простирающемся от точки-центра на расстоянии определенного радиуса R. Радиус в свою очередь – это отрезок, соединяющий центр шара
с всякий точкой его поверхности.
Вам понадобится
- – формула поверхности площади шара;
- – формула объема шара;
- – навыки арифметического счета.
Инструкция
1.
В повседневной жизни нередко появляется надобность вычислить площадь
шаровой поверхности либо его части, дабы рассчитать, скажем, расход материала. Вычислив объем шара
, вы можете через удельный вес рассчитать массу вещества, составляющего содержимое сферы. Для того дабы обнаружить площадь
и объем шара
, довольно знать его радиус либо диаметр. По формулам, которые сегодняшние школьники выводят в 11 классе общеобразовательной школы, вы легко можете рассчитать эти параметры.
2.
Скажем, диаметр футбольного мяча, согласно каждым требованиям ФИФА, должен быть в пределах 21,8-22,2 см. Усредните для простоты счета до 22 см. Следственно, радиус (R) будет равен (22:2) – 11 см. Чай увлекательно узнать, какова площадь
поверхности футбольного мяча?
3.
Возьмите формулу площади поверхности шара
: Sшара
= 4ттR2Подставьте в приведенную формулу значение радиуса футбольного мяча – 11 см.S = 4 x 3.14 x 11х11 .
4.
Позже проведения несложных математических действий вы получаете итог: 1519.76. Таким образом, площадь
поверхности футбольного мяча составляет 1 519.76 квадратных сантиметров.
5.
Сейчас рассчитайте объем мяча. Берите формулу расчета объема шара
: V = 4/3ттR3Подставляйте вновь же значение радиуса футбольного мяча – 11 см.V = 4/3 x 3.14 x 11 х 11 х 11.
6.
Позже подсчетов, скажем, на калькуляторе вы получаете: 5576.89.Оказывается, объем воздуха в футбольном мяче составляет 5 576.89 кубических сантиметров.
Шар – это простейшая объемная геометрическая фигура, для указания размеров которой довольно каждого одного параметра. Границы этой фигуры принято называть сферой. Объем пространства, ограничиваемого сферой, дозволено вычислить как с поддержкой соответствующих тригонометрических формул, так и подручными средствами.
Инструкция
1.
Используйте классическую формулу объема (V) сферы, если из условий знаменит ее радиус (r) – возведите радиус в третью степень, умножьте на число Пи, а итог увеличьте еще на треть. Записать эту формулу дозволено так: V=4*?*r?/3.
2.
Если есть вероятность измерить диаметр (d) сферы, то поделите его напополам и используйте как радиус в формуле из предыдущего шага. Либо обнаружьте одну шестую часть от возведенного в куб диаметра, умноженного на число Пи: V=?*d?/6.
3.
Если вестим объем (v) цилиндра, в тот, что вписана сфера, то для нахождения ее объема определите, чему равны две трети от вестимого объема цилиндра: V=?*v.
4.
Если вестима средняя плотность (p) материала, из которого состоит сфера, и ее масса (m), то этого тоже довольно для определения объема – поделите второе на первое: V=m/p.
5.
Воспользуйтесь какими-нибудь мерными емкостями в качестве подручных средств для измерения объема сосуда сферической формы. Скажем, наполните его водой, измеряя с подмогой мерной емкости число заливаемой жидкости. Полученное значение в литрах переведите в кубические метры – эта единица принята в интернациональной системе СИ для измерения объема. В качестве показателя перевода из литров в кубометры используйте число 1000, потому что один литр приравнен к одному кубическому дециметру, а их в всякий кубический метр вмещается ровно тысяча штук.
6.
Используйте правило измерения, противоположный описанному в предыдущем шаге, если тело в форме сферы невозможно наполнить жидкостью, но дозволено погрузить в нее. Заполните мерный сосуд водой, подметьте ярус, погрузите измеряемое сферическое тело в жидкость и по разнице ярусов определите число вытесненной воды. После этого переведите полученный итог из литров в кубометры так же, как это описано в предыдущем шаге.
Видео по теме
Ремонт, переезд, покраска объекта – все это затребует вычисления площади. Не проступок припомнить школьную программу.
Инструкция
1.
Припомним, что такое площадь. Площадь — это мера плоской фигуры по отношению к стандартной фигуре. Либо правильная величина, численное значение которой владеет следующими свойствами: Если фигуру дозволено разбить на части, которые будут являться примитивными фигурами, то площадь такой фигуры будет равна сумме площадей ее частей Площадь квадрата со стороной, которая равна единице измерения, равна единице Равные фигуры владеют равными площадямиИз этих правил следует, что площадь это не определенная величина, то есть площадь дает только условную колляцию какой-нибудь фигуре. Когда нужно обнаружить площадь произвольной фигуры, то надобно вычислить, сколько квадратов со стороной (которая равняется единице), эта фигура в себя может вместить.
2.
Пример: Возьмем фигуру – прямоугольник, такой, в котором квадратный сантиметр укладывается в шесть раз. Тогда площадь такого прямоугольника будет равняться – 6 см2. Если взять больше трудную фигуру, скажем, трапецию, то получится что: Если трапеция такой величины, что квадратный сантиметр укладывается в нее только два раза, а третья часть не влезает целиком и остается маленький треугольник. Дабы измерить площадь этого оставшегося треугольника необходимо применить к нему доли квадратного сантиметра, дозволено взять миллиметр. Правда, данный метод для трудных фигур не дюже комфортный. Следственно для вычисления площади различных фигур существуют разные формулы. Если надобно вычислить площадь определенной фигуры, то дозволено взять учебник по геометрии и припомнить материал, тот, что когда-то проходили в школе.Так, формула площади куба: площадь куба равна числу граней умноженное на площадь грани, т.е. 6 * a2
Видео по теме
Все планеты ясной системы имеют форму шара
. Помимо того, шарообразную либо близкую к таковой форму имеют и многие объекты, сделанные человеком, включая детали технических устройств. Шар, как и всякое тело вращения, имеет ось, которая совпадает с диаметром. Впрочем это не исключительное главное качество шара
. Ниже рассмотрены основные свойства этой геометрической фигуры и метод нахождения ее площади.
Инструкция
1.
Если взять полукруг либо круг и провернуть его вокруг своей оси, получится тело, называемое шаром. Иными словами, шаром именуется тело, ограниченное сферой. Сфера представляет собой оболочку шара
, и ее сечением является окружность. От шара
она отличается тем, что является полой. Ось как у шара
, так и у сферы совпадает с диаметром и проходит через центр. Радиусом шара
именуется отрезок, проложенный от его центра до всякий внешней точки. В противоположность сфере, сечения шара
представляют собой круги. Форму, близкую к шарообразной, имеет множество планет и небесных тел. В различных точках шара
имеются идентичные по форме, но неодинаковые по величине, так называемые сечения – круги различной площади.
2.
Шар и сфера – взаимозаменяемые тела, в различие от конуса, невзирая на то, что конус также является телом вращения. Сферические поверхности неизменно в своем сечении образуют окружность, самостоятельно от того, как именно она вращается – по горизонтали либо по вертикали. Коническая же поверхность получается лишь при вращении треугольника по его оси, перпендикулярной основанию. Следственно конус, в различие от шара
, и не считается взаимозаменяемым телом вращения.
3.
Самый огромный из допустимых кругов получается при сечении шара
плоскостью, проходящей через центр О. Все круги, которые проходят через центр О, пересекаются между собой в одном диаметре. Радиус неизменно равен половине диаметра. Через две точки A и B, располагающиеся в любом месте поверхности шара
, может проходить безграничное число кругов либо окружностей. Именно по этой причине через полюса Земли может быть проведено неограниченное число меридианов.
4.
При нахождении площади шара
рассматривается, раньше каждого, площадь
сферической поверхности.Площадь шара
, а вернее, сферы, образующей его поверхность, может быть рассчитана на основании площади круга с тем же радиусом R. От того что площадь
круга есть произведение полуокружности на радиус, его дозволено рассчитать дальнейшим образом:S = ?R^2Так как через центр шара
проходят четыре основных огромных круга, то, соответственно площадь
шара
(сферы) равна:S = 4 ?R^2
5.
Данная формула может быть пригодна в том случае, если вестим либо диаметр, либо радиус шара
либо сферы. Впрочем, эти параметры приведены в качестве условий не во всех геометрических задачах. Существуют и такие задачи, в которых шар вписан в цилиндр. В этом случае, следует воспользоваться теоремой Архимеда, суть которой заключается в том, что площадь
поверхности шара
в полтора раза поменьше полной поверхности цилиндра:S = 2/3 S цил., где S цил. –площадь
полной поверхности цилиндра.
Видео по теме
Шаром называют простейшую объемную фигуру геометрически положительной формы, все точки пространства внутри границ которой удалены от ее центра на расстояние, не превышающее радиуса. Поверхность, образуемая большинством максимально удаленных от центра точек, именуется сферой. Для количественного выражения меры пространства, заключенного внутри сферы, предуготовлен параметр, тот, что именуется объемом шара.
Инструкция
1.
Если требуется измерить объем шара не теоретически, а только подручными средствами, то сделать это дозволено, скажем, определив объем вытесненной им воды. Данный метод применим в том случае, когда есть вероятность разместить шар в какую-нибудь соизмеримую ему емкость – мензурку, стакан, банку, ведро, бочку, бассейн и т.д. В этом случае перед помещением шара подметьте ярус воды, сделайте это вторично позже полного его погружения, а после этого обнаружьте разность между отметками. Традиционно мерная емкость заводского производства имеет деления, показывающие объем в литрах и производных от него единицах – миллилитрах, декалитрах и т.д. Если полученное значение нужно перевести в кубические метры и кратные ему единицы объема, то исходите из того, что один литр соответствует одному кубическому дециметру либо одной тысячной доле кубометра.
2.
Если знаменит материал, из которого изготовлен шар, и плотность этого материала дозволено узнать, скажем, из справочника, то определить объем дозволено взвесив данный предмет. Примитивно поделите итог взвешивания на справочную плотность вещества изготовления: V=m/p.
3.
Если радиус шара вестим из условий задачи либо его дозволено измерить, то для вычисления объема дозволено применять соответствующую математическую формулу. Умножьте учетверенное число Пи на третью степень радиуса, а полученный итог поделите на тройку: V=4*?*r?/3. Скажем, при радиусе в 40см объем шара составит 4*3,14*40?/3 = 267946,67см? ? 0,268м?.
4.
Измерить диаметр почаще бывает проще, чем радиус. В этом случае нет необходимости разделять его напополам для применения с формулой из предыдущего шага – класснее упростить саму формулу. В соответствии с преобразованной формулой умножьте число Пи на диаметр в третьей степени, а итог поделите на шестерку: V=?*d?/6. Скажем, шар диаметром в 50см должен иметь объем в 3,14*50?/6 = 65416,67см? ? 0,654м?.
Задачи на вычисление площади круга зачастую встречаются в школьном курсе геометрии. Дабы обнаружить площадь
круга, нужно знать длину диаметра
либо радиуса окружности, в которую он заключен.
Вам понадобится
- – длина диаметра окружности.
Инструкция
1.
Окружность — фигура на плоскости, состоящая из множества точек, удалённых на одинаковое расстояние от другой точки, называемой центром. Круг — плоская геометрическая фигура, представляет собой уйма точек, заключённых в окружность, которая является рубежом круга. Диаметр — это отрезок, соединяющий две точки на окружности и проходящий через её центр. Радиус — это отрезок, соединяющий точку на окружности и с её центром. ? — число «пи», математическая константа, непрерывная величина. Она показывает отношение длины окружности к длине её диаметра
. Вычислить точное значение числа? невозможно. В геометрии пользуются примерным значением этого числа: ? ? 3,14
2.
Площадь круга равна произведению квадрата радиуса на число и вычисляется по формуле: S=?R^2, где S — площадь
круга, R — длина радиуса окружности.
3.
Из определения радиуса следует, что он равен половине диаметра
. Следственно, формула приобретает вид: S=?(D/2)^2, где D — длина диаметра
окружности. Подставьте в формулу значение диаметра
, вычислите площадь
круга.
4.
Площадь круга измеряется в единицах площади — мм2, см2, м2 и т.п. В каких единицах выражается полученная вами площадь
круга, зависит от того, в каких единицах был дан диаметр окружности.
5.
Если вам нужно вычислить площадь
кольца, воспользуйтесь формулой: S=?(R-r)^2, где R, r – радиусы внешней и внутренней окружностей кольца соответственно.
Полезный совет
Существует Интернациональный день числа «пи», тот, что отмечается 14 марта. Точное время наступления триумфальной даты — 1 час 59 минут 26 секунд, согласно цифрам числа — 3,1415926…
Видео по теме
Обратите внимание!
Увлекательно: объем шара с диаметром, превышающим в три раза диаметр иного шара, огромнее суммарного объема 3 таких шаров в 9 раз.
Полезный совет
Дабы развить у детей увлечение к математическим вычислениям, предлагайте в качестве примеров для расчета окружающие предметы: мяч, арбуз, клубок бабушкиной пряжи. Это наглядно и потому увлекательно.
Имея при себе всего одну формулу и зная изначально, чему равен диаметр или радиус, можно с лёгкостью вычислить площадь поверхности шара. Формула будет иметь вид S =4πR2
, где число «пи» умножается на 4, затем на радиус шара в квадратной степени. Но перед непосредственными вычислениями следует сразу разобраться в терминах.
Трактовка значений
Это следует знать:
- Шар
– геометрический объект, получившийся в результате вращательных полукруговых движений вокруг центра. Любая точка поверхности шара находится на одинаковом расстоянии от центра. - Сфера
– не то же самое, что шар. Если тот является объёмным объектом и включает в себя внутреннее пространство, то сфера – это лишь поверхность данного объекта и имеет только свою площадь. Иными словами – нельзя сказать, что сфера имеет такой-то объём, в отличие от шара. - Число «пи»
— это постоянное число, равное отношению длины окружности к её диаметру. В сокращённом виде его принято обозначать числом, равным 3,14. Но на самом деле, после тройки идёт больше тысячи цифр! - Радиус шара равен ½ его диаметру
. Точный диаметр можно вычислить с использованием нескольких плоских и ровных предметов. Нужно лишь зажать шар между этими предметами, которые зажимают шар и расположены перпендикулярно друг к другу, а затем измерить получившийся диаметр. - Квадратная степень
обозначается в виде двойки и означает то, что это число надо умножить на само себя один раз. Если бы степень числа была в виде тройки, то умножать на само себя нужно было бы два раза. Записав выражение на бумаге, можно понять, почему используются именно двойка и тройка, а не единица и двойка. - Объём
– величина, обозначающая размер в пространстве, занимающее объектом. От диаметра зависит объём шара. Формула будет равна четырём трети, умноженным на число «пи» и вновь умноженным на его радиус в кубе. - Площадь
– величина, обозначающая размер поверхности объекта, но не внутреннего пространства.
Занимательные факты
Это интересно:
- У числа «пи» есть собственные фан-клубы по всему миру. Члены общества пытаются запомнить как можно больше знаков из этого числа, а также пытаются разгадать вселенские тайны, сокрытые в числе.
- Площадь суши Земли составляет всего 29,2 % от её общей поверхности. Точное число площади сложно назвать из-за неравномерного рельефа Земли, такие как впадины и горы.
- Знания о формуле площади шара можно применять и в быту. Также этими знаниями можно подавлять соперника в споре.
Продемонстрировав объём своих знаний в области геометрии, можно изначально заставить вас уважать, а ремонтникам и продавцам можно дать понять, что вас просто так не обмануть.
Применение формулы
Рассмотрим на примере, как вычислить площадь круглого шара
, диаметр которого равен 50 см. Следуя формуле, нужно 50 разделить на два (чтобы получить радиус), возвести полученное число в квадрат и умножить всё это дело сначала на 4, затем на 3,14. В итоге получим число в 7 850 квадратных сантиметров.
Формула вычисления площади
применяется не только среди учителей в школе и научных сотрудников в лаборатории. Данная формула может пригодиться обычному маляру. Ведь если шар большой, а краски мало, то возникает вопрос – хватит ли ему этой смеси, чтобы покрасить весь объект. И это далеко не единственный бытовой случай, где может пригодиться формула.
Формула вычисления объёма
может пригодиться и строительной бригаде, что делает ремонт. И неважно, какой это объект – промышленное здание, небольшой дом или обычная квартира. Этим и отличаются профессионалы – они умеют применять свои знания на практике.
Но как быть, если не представляется возможным измерить объект?
Такой вопрос может возникнуть в случае огромных размеров объекта или его недосягаемости. В этом случае могут помочь электронные технологии, в основе работы которых лежит сканирование пространства определёнными частотами и лазерами. С современными технологиями необязательно знать все формулы наизусть. Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор.
Принято считать, что первый, кто нашёл и вывел формулу объёма и площади шара,
был Архимед
. Это величайший древнегреческий учёный, живший за 300 лет до нашей эры. Он был не только математиком, но и физиком, и инженером. Он один из первых людей, кто попытался «оцифровать» окружающий нас мир. Его теоремы и труды используются по сей день.
Именно Архимед определил границы числа «пи»
и обозначил их, не имея никаких современных гаджетов. Сам Архимед очень гордился найденной формулой, с помощью которой вычисляется объём шара. Его потомки в честь этого изобразили на его могильном камне цилиндр и шар.
Если бы каким-то чудом он переродился в наше время, то он сразу же смог бы преобразить этот мир и вывести его на новый уровень.
Видео
На примере этого видео вам будет легко понять, как найти площадь поверхности шара.
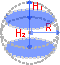
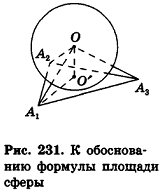
Мы даем здесь очень простой, хотя и не совсем строгий вывод формулы для площади сферической поверхности; по своей идее он очень близок к методам интегрального исчисления. Итак, пусть дан некоторый шар радиуса R. Выделим на его поверхности какую-либо малую область (рис. 412) и рассмотрим пирамиду или конус с вершиной в центре шара О, имеющие эту область своим основанием; строго говоря, мы лишь условно говорим о конусе или пирамиде, так как основание не плоское, а сферическое. Но при малых размерах основания по сравнению с радиусом шара оно будет весьма мало отличаться от плоского (так, например, при измерении не очень большого земельного участка пренебрегают тем, что он лежит не на плоскости, а на сфере).
Тогда, обозначая через площадь этого участка — основание «пирамиды», найдем ее объем как произведение одной трети высоты на площадь основания (высотой служит радиус шара):
Если теперь всю поверхность шара разложить на очень большое число N таких малых областей , тем самым объем шара на N объемов «пирамид», имеющих эти области своими основаниями, то весь объем представится суммой
где последняя сумма равна полной поверхности шара:
Итак, объем шара равен одной трети произведения его радиуса на площадь поверхности. Отсюда для площади поверхности имеем формулу
Последний результат формулируется так:
Площадь поверхности шара равна учетверенной площади его большого круга.
Приведенный вывод пригоден и для площади поверхности сектора шара (имеем в виду только основание, т. е. сферическую поверхность, или «шапочки»; см. рис. 409). И в этом случае объем сектора равен одной трети произведения радиуса шара на площадь его сферического основания:
откуда находим для площади шапочки формулу
Шаровым поясом (см. рис. 408) называют сферическую поверхность шарового слоя. Чтобы вычислить площадь поверхности шарового пояса, находим разность поверхностей двух сферических шапочек:
где — высота слоя. Итак, площадь поверхности шарового пояса для данного шара зависит только от высоты соответствующего слоя, но не от его положения на шаре.
Задача. Боковая поверхность конуса, описанного вокруг шара, имеет площадь, равную полуторной площади поверхности шара. Найти высоту конуса, если радиус шара равен .
Решение. Введем для удобства угол а между высотой и образующей конуса (рис. 413). Найдем для высоты, радиуса основания и образующей конуса выражения
Площадь поверхности шарового сегмента
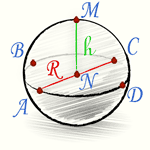
Часть шара, [шар, сфера] осекаемая от него какой-нибудь плоскостью, называется шаровым или сферическим сегментом. Основанием шарового сегмента называется круг ABCD. Высотой шарового сегмента называется отрезок NM, т.е. длина перпендикуляра, восстановленного из центра N основания до пересечения с поверхностью шара. Точка M называется вершиной шарового сегмента.
Площадь поверхности шарового сегмента равняется произведению его высоты на окружность большого круга шара.
[ S = 2 pi R h ]
(R — радиус большого круга шара, h=NM — высота шарового сегмента)
Формулы шара, сферы
Вычислить, найти площадь поверхности шарового сегмента по формуле (1)
Площадь поверхности шарового сегмента |
стр. 318 |
|---|
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности сегмента шара, а также разберем пример решения задачи для демонстрации их практического применения.
- Определение сегмента шара
-
Формулы для нахождения площади сегмента шара
- Площадь основания
- Площадь сферической поверхности
- Площадь полной поверхности
- Пример задачи
Определение сегмента шара
Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью. На чертеже ниже закрашен зеленым цветом.
- R – радиус шара;
- r – радиус основания сегмента;
- h – высота сегмента; это длина перпендикуляра от центра его основания (точка O2) до точки на поверхности шара.
Связь между радиусом основания сегмента, его высотой и радиусом шара:
Формулы для нахождения площади сегмента шара
Площадь основания
Основанием шарового сегмента является круг, площадь (S) которого находится по стандартной формуле (в расчетах число π округляется до 3,14):
Sосн. = πr 2
Примечание: если известен диаметр круга (d), чтобы найти радиус (r), нужно первое разделить на второе, то есть: r = d/2.
Площадь сферической поверхности
Чтобы найти площадь (S) сферической/внешней поверхности шарового сегмента, необходимо знать его высоту и радиус самого шара.
Sсфер. пов. = 2πRh
Площадь полной поверхности
Чтобы найти площадь (S) полной поверхности сегмента шара, необходимо сложить площади его основания и внешней поверхности.
Sполн. = Sосн. + Sсфер. пов. = π (2Rh + r 2)
Пример задачи
Дан шар радиусом 6 см. Найдите полную площадь шарового сегмента, если известно, что его высота равняется 2,4 см, а радиус основания – 4,7 см.
Решение
Воспользуемся формулами, приведенными выше, подставив в них известные по условиям задачи значения.
Sосн. = 3,14 ⋅ (4,7 см) 2 = 69,3626 см 2
Sсфер. пов. = 2 ⋅ 3,14 ⋅ 6 см⋅ 2,4 см = 90,432 см 2
Sполн. = Sосн. + Sсфер. пов. = 69,3626 см 2 + 90,432 см 2 = 159,7946 см 2
Содержание:
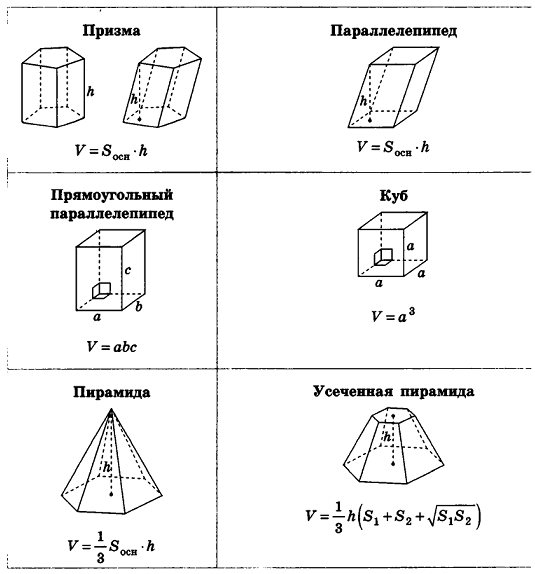
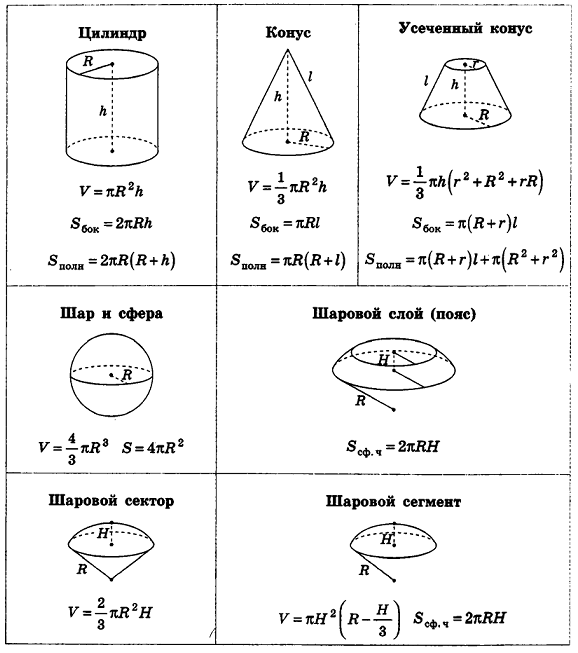
Площади поверхностей геометрических тел:
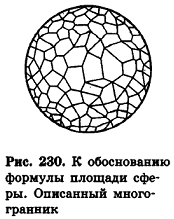
Под площадью поверхности многогранника мы понимаем сумму площадей всех его граней. Как же определить площадь поверхности тела, не являющегося многогранником? На практике это делают так. Разбивают поверхность на такие части, которые уже мало отличаются от плоских. Тогда находят площади этих частей, как будто они являются плоскими. Сумма полученных площадей является приближенной площадью поверхности. Например, площадь крыши здания определяется как сумма площадей кусков листового металла. Еще лучше это видно на примере Земли. Приблизительно она имеет форму шара. Но площади небольших ее участков измеряют так, как будто эти участки являются плоскими. Более того, под площадью поверхности тела будем понимать предел площадей полных поверхностей описанных около него многогранников. При этом должно выполняться условие, при котором все точки поверхности этих многогранников становятся сколь угодно близкими к поверхности данного тела. Для конкретных тел вращения понятие описанного многогранника будет уточнено.
Понятие площади поверхности
Рассмотрим периметры
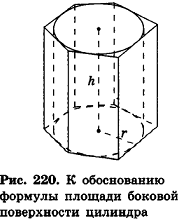
Применим данные соотношения к обоснованию формулы для площади боковой поверхности цилиндра.
При вычислении объема цилиндра были использованы правильные вписанные в него призмы. Найдем при помощи в чем-то аналогичных рассуждений площадь боковой поверхности цилиндра.
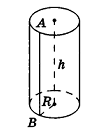
Опишем около данного цилиндра радиуса R и высоты h правильную n-угольную призму (рис. 220).
Площадь боковой поверхности призмы равна
где 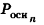
При неограниченном возрастании n получим:
так как периметры оснований призмы стремятся к длине окружности основания цилиндра, то есть к
Учитывая, что сумма площадей двух оснований призмы стремится к 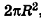
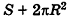
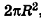
Итак, площадь боковой поверхности цилиндра вычисляется по формуле
где R — радиус цилиндра, h — его высота.
Заметим, что эта формула аналогична соответствующей формуле площади боковой поверхности прямой призмы
За площадь полной поверхности цилиндра принимается сумма площадей боковой поверхности и двух оснований:
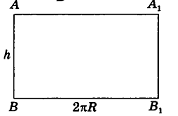
Если боковую поверхность цилиндра радиуса R и высоты h разрезать по образующей АВ и развернуть на плоскость, то в результате получим прямоугольник 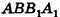
Очевидно, что сторона 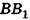
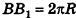
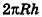
Пример:
Параллельно оси цилиндра на расстоянии d от нее проведена плоскость, отсекающая от основания дугу 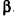
Решение:
Пусть дан цилиндр, в основаниях которого лежат равные круги с центрами 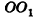
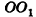
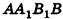
Пусть хорда АВ отсекает от окружности основания дугу 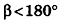
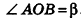
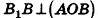
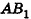
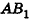
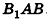
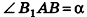
В равнобедренном треугольнике 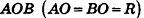
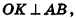
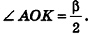
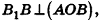
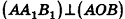
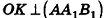
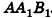
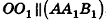
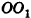
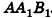
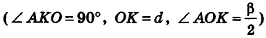
откуда 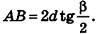
Итак,
В случае, когда
Аналогично предыдущему, и в этом случае получаем тот же результат для площади боковой поверхности.
Ответ:
Площадь поверхности конуса и усеченного конуса
Связь между цилиндрами и призмами полностью аналогична связи между конусами и пирамидами. В частности, это касается формул для площадей их боковых поверхностей.
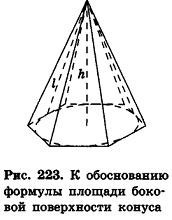
Опишем около данного конуса с радиусом основания R и образующей I правильную л-угольную пирамиду (рис. 223). Площадь ее боковой поверхности равна
где 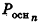
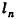
При неограниченном возрастании n получим:
так как периметры оснований пирамиды стремятся к длине окружности основания конуса, а апофемы 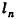
Учитывая, что площадь основания пирамиды стремится к 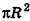
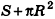
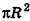
где R — радиус основания, I — образующая.
За площадь полной поверхности конуса принимается сумма площадей его основания и боковой поверхности:
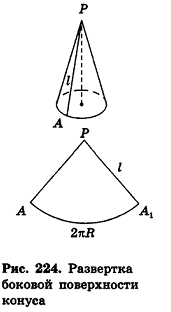
Если боковую поверхность конуса разрезать по образующей РА и развернуть на плоскость, то в результате получим круговой сектор 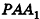
Очевидно, что радиус сектора развертки равен образующей конуса I, а длина дуги 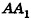
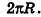
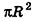
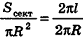
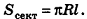
Учитывая формулу для площади боковой поверхности конуса, нетрудно найти площадь боковой поверхности усеченного конуса.
Рассмотрим усеченный конус, полученный при пересечении конуса с вершиной Р некоторой секущей плоскостью (рис. 225).
Пусть 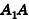
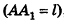
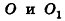
Из подобия треугольников
следует, что
Тогда получаем
Таким образом,
Итак, мы получили формулу для вычисления площади боковой поверхности усеченного конуса: 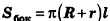
Отсюда ясно, что площадь полной поверхности усеченного конуса равна
Такой же результат можно было бы получить, если найти площадь развертки боковой поверхности усеченного конуса или использовать правильные усеченные пирамиды, описанные около него. Попробуйте дать соответствующие определения и провести необходимые рассуждения самостоятельно.
Связь между площадями поверхностей и объемами
При рассмотрении объемов и площадей поверхностей цилиндра и конуса мы видели, что существует тесная взаимосвязь между этими фигурами и призмами и пирамидами соответственно. Оказывается, что и сфера (шар), вписанная в многогранник, связана с величиной его объема.
Определение:
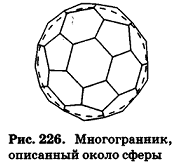
Сфера (шар) называется вписанной в выпуклый многогранник, если она касается каждой его грани.
При этом многогранник называется описанным около данной сферы (рис. 226).
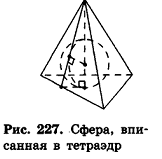
Рассмотрим, например, сферу, вписанную в тетраэдр (рис. 227).
Плоскости, содержащие грани тетраэдра, являются касательными к вписанной сфере, а точки касания лежат в гранях тетраэдра. Заметим, что по доказанному в п. 14.2 радиусы вписанной сферы, проведенные в точку касания с поверхностью многогранника, перпендикулярны плоскостям граней этого многогранника.
Для описанных многоугольников на плоскости было доказано, что их площадь равна произведению полупериметра на радиус вписанной окружности. Аналогичное свойство связывает объем описанного многогранника и площадь его поверхности.
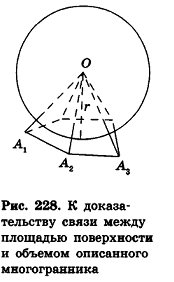
Теорема (о связи площади поверхности и объема описанного многогранника)
Объем описанного многогранника вычисляется по формуле
где 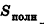
Доказательство:
Соединим центр вписанной сферы О со всеми вершинами многогранника 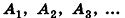
где 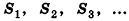
Теорема доказана.
Оказывается, что в любой тетраэдр можно вписать сферу, и только одну. Но не каждый выпуклый многогранник обладает этим свойством.
Рассматривают также сферы, описанные около многогранника.
Определение:
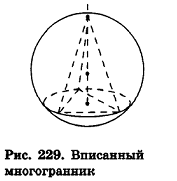
Сфера называется описанной около многогранника, если все его вершины лежат на сфере.
При этом многогранник называется вписанным в сферу (рис. 229).
Также считается, что соответствующий шар описан около многогранника.
Около любого тетраэдра можно описать единственную сферу, но не каждый многогранник обладает соответствующим свойством.
Площадь сферы
Применим полученную связь для объемов и площадей поверхностей описанных многогранников к выводу формулы площади сферы.
Опишем около сферы радиуса R выпуклый многогранник (рис. 230).
Пусть S’ — площадь полной поверхности данного многогранника, а любые две точки одной грани удалены друг от друга меньше чем на е. Тогда объем многогранника равен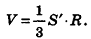
По неравенству треугольника 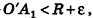
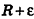
Итак, объем V данного многогранника больше объема шара радиуса R и меньше объема шара радиуса 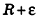
Отсюда получаем
Если неограниченно уменьшать размеры граней многогранника, то есть при е, стремящемся к нулю, левая и правая части последнего неравенства будут стремиться к 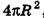
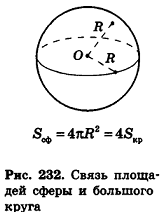
Итак, площадь сферы радиуса R вычисляется по формуле
Доказанная формула означает, что площадь сферы равна четырем площадям ее большого круга (рис. 232).
Исходя из аналогичных рассуждений, можно получить формулу для площади сферической части шарового сегмента с высотой Н:
Оказывается, что эта формула справедлива и для площади сферической поверхности шарового слоя (пояса):
где Н — высота слоя (пояса).
Справочный материал
Формулы объемов и площадей поверхностей геометрических тел
Историческая справка
Многие формулы для вычисления объемов многогранников были известны уже в Древнем Египте. В так называемом Московском папирусе, созданном около 4000 лет назад, вероятно, впервые в истории вычисляется объем усеченной пирамиды. Но четкие доказательства большинства формул для объемов появились позднее, в работах древнегреческих ученых.
Так, доказательства формул для объемов конуса и пирамиды связаны с именами Демокрита из Абдеры (ок. 460-370 гг. до н. э.) и Евдокса Книдского (ок. 408-355 гг. до н. э.). На основании их идей выдающийся математик и механик Архимед (287-212 гг. до н. э.) вычислил объем шара, нашел формулы для площадей поверхностей цилиндра, конуса, сферьГг
Дальнейшее развитие методы, предложенные Архимедом, получили благодаря трудам средневекового итальянского монаха и математика Бонавентуры Кавальери (1598-1647). В своей книге «Геометрия неделимых» он сформулировал принцип сравнения объемов, при котором используются площади сечений. Его рассуждения стали основой интегральных методов вычисления объемов, разработанных Исааком Ньютоном (1642 (1643)-1727) и Готфридом Вильгельмом фон Лейбницем (1646-1716). Во многих учебниках по геометрии объем пирамиды находится с помощью * чертовой лестницы» — варианта древнегреческого метода вычерпывания, предложенного французским математиком А. М. Лежандром (1752-1833).
На II Международном конгрессе математиков, который состоялся в 1900 году в Париже, Давид Гильберт сформулировал, в частности, такую проблему: верно ли, что любые два равновеликих многогранника являются равносоставленными? Уже через год отрицательный ответ на этот вопрос был обоснован учеником Гильберта Максом Деном (1878-1952). Другое доказательство этого факта предложил в 1903 году известный геометр В. Ф. Каган, который в начале XX века вел плодотворную научную и просветительскую деятельность в Одессе. В частности, из работ Дена и Кагана следует, что доказательство формулы объема пирамиды невозможно без применения пределов.
Весомый вклад в развитие теории площадей поверхностей внесли немецкие математики XIX века. Так, в 1890 году Карл Герман Аман-дус Шварц (1843-1921) построил пример последовательности многогранных поверхностей, вписанных в боковую поверхность цилиндра («сапог Шварца»). Уменьшение их граней не приводит к приближению суммы площадей этих граней к площади боковой поверхности цилиндра. Это стало толчком к созданию выдающимся немецким математиком и физиком Германом Минков-ским (1864-1909) современной теории площадей поверхностей, в которой последние связаны с объемом слоя около данной поверхности.
Учитывая огромный вклад Архимеда в развитие математики, в частности теории объемов и площадей поверхностей, именно его изобразили на Филдсовской медали — самой почетной в мире награде для молодых математиков. В 1990 году ею был награжден Владимир Дрин-фельд (род. в 1954 г.), который учился и некоторое время работал в Харькове. Вот так юные таланты, успешно изучающие геометрию в школе, становятся в дальнейшем всемирно известными учеными.
Уравнения фигур в пространстве
Напомним, что уравнением фигуры F на плоскости называется уравнение, которому удовлетворяют координаты любой точки фигуры F и не удовлетворяют координаты ни одной точки, не принадлежащей фигуре F. Так же определяют и уравнение фигуры в пространстве; но, в отличие от плоскости, где уравнение фигуры содержит две переменные х и у, в пространстве уравнение фигуры является уравнением с тремя переменными х, у и z.
Выведем уравнение плоскости, прямой и сферы в пространстве. Для получения уравнения плоскости рассмотрим в прямоугольной системе координат плоскость а (рис. 233) и определим свойство, с помощью которого можно описать принадлежность произвольной точки данной плоскости. Пусть ненулевой вектор 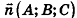
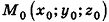
Так как 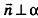
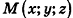
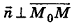
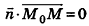
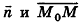
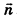
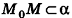
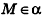
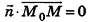
Теорема (уравнение плоскости в пространстве)
В прямоугольной системе координат уравнение плоскости имеет вид 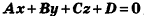
Доказательство:
Запишем в координатной форме векторное равенство 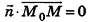
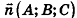
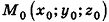
Следовательно,
После раскрытия скобок и приведения подобных членов это уравнение примет вид:
Обозначив числовое выражение в скобках через D, получим искомое уравнение, в котором числа А, В и С одновременно не равны нулю, так как 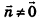
Покажем теперь, что любое уравнение вида Ах + Ву +Cz+D = 0 задает в пространстве плоскость. Действительно, пусть 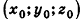
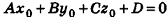
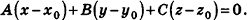
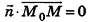
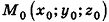
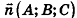
Обратим внимание на то, что в доказательстве теоремы приведен способ составления уравнения плоскости по данным координатам произвольной точки плоскости и вектора нормали.
Пример:
Напишите уравнение плоскости, которая перпендикулярна отрезку MN и проходит через его середину, если М{-1;2;3), N(5;-4;-1).
Решение:
Найдем координаты точки О — середины отрезка MN:
Значит, О (2; -1; l). Так как данная плоскость перпендикулярна отрезку MN, то вектор 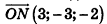
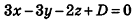
И наконец, так как данная плоскость проходит через точку О(2;-l;l), то, подставив координаты этой точки в уравнение, получим:
Таким образом, уравнение 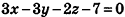
Ответ:
Заметим, что правильным ответом в данной задаче является также любое уравнение, полученное из приведенного умножением обеих частей на число, отличное от нуля.
Значения коэффициентов А, В, С и D в уравнении плоскости определяют особенности расположения плоскости в системе координат. В частности:
- если
, уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а);
- если один из коэффициентов А, В и С равен нулю, a
, плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали
перпендикулярен оси Ох, а плоскость By + Cz + D = Q параллельна оси Ох (рис. 234, б)
- если два из коэффициентов А, В и С равны нулю, а
, плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали
перпендикулярен плоскости Оху, а плоскость Cz+D = 0 параллельна плоскости Оху (рис. 234, в);
- если два из коэффициентов А, В и С равны нулю и D = 0, плоскость совпадает с одной из координатных плоскостей: например, при условиях
и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).
Предлагаем вам самостоятельно составить полную таблицу частных случаев расположения плоскости Ax + By+Cz+D = 0 в прямоугольной системе координат в зависимости от значений коэффициентов А, В, С и D.
Пример: (о расстоянии от точки до плоскости)
Расстояние от точки 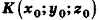
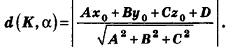
Решение:
Если 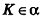
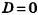
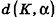
Если 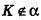
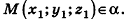
Тогда 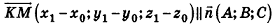
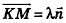
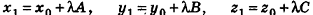
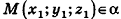
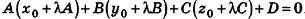
Таким образом,
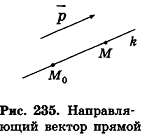
Рассмотрим теперь возможность описания прямой в пространстве с помощью уравнений.
Пусть в пространстве дана прямая k (рис. 235). Выберем ненулевой вектор 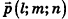
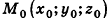
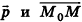
Представим это векторное равенство в координатной форме. Если ни одна из координат направляющего вектора не равна нулю, из данного равенства можно выразить t и приравнять полученные результаты:
Эти равенства называют каноническими уравнениями прямой в пространстве.
Пример:
Напишите уравнение прямой, проходящей через точки А(1;-3;2) и В(-l;0;l).
Решение:
Так как точки А и В принадлежат данной прямой, то 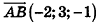
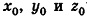
Ответ:
Заметим, что ответ в этой задаче может иметь и другой вид: так, в числителях дробей можно использовать координаты точки В, а как направляющий вектор рассматривать любой ненулевой вектор, коллинеарный 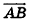
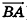
Вообще, если прямая в пространстве задана двумя точками 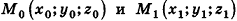
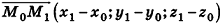
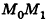
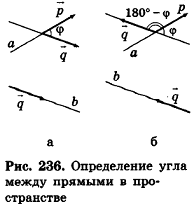
С помощью уравнений удобно исследовать взаимное расположение прямых и плоскостей в пространстве. Рассмотрим прямые 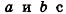
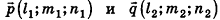
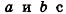
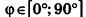
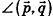
Так как cos(l80°-ф) = -coscp, имеем 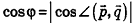
Отсюда, в частности, следует необходимое и достаточное условие перпендикулярности прямых 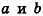
Кроме того, прямые 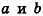
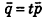
Проанализируем теперь отдельные случаи взаимного расположения двух плоскостей в пространстве. Очевидно, что если 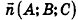
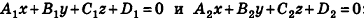
- совпадают, если существует число t такое, что
, или, если числа
ненулевые
- параллельны, если существует число t такое, что
, или, если координаты
ненулевые,
(на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где
).
В остальных случаях данные плоскости 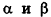
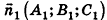
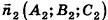
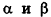
В частности, необходимое и достаточное условие перпендикулярности плоскостей 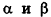
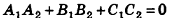
Заметим также, что прямая в пространстве может быть описана как линия пересечения двух плоскостей, то есть системой уравнений
где векторы 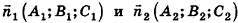
Пример:
Напишите уравнение плоскости, которая проходит через точку М(4;2;3) и параллельна плоскости x-y + 2z-S = 0.
Решение:
Так как искомая плоскость параллельна данной, то вектор нормали к данной плоскости 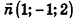
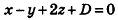
Ответ: x-y+2z-8 = 0.
Аналогично уравнению окружности на плоскости, в пространственной декартовой системе координат можно вывести уравнение сферы с заданным центром и радиусом.
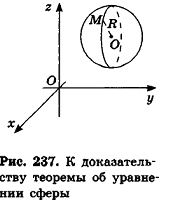
Теорема (уравнение сферы)
В прямоугольной системе координат уравнение сферы радиуса R с центром в точке 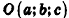
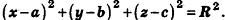
Пусть 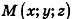
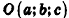
Так как OM=R, то есть ОМ2 = R2, то координаты точки М удовлетворяют уравнению 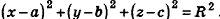
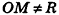
Следствие
Сфера радиуса R с центром в начале координат задается уравнением вида
Заметим, что фигуры в пространстве, как и на плоскости, могут задаваться не только уравнениями, но и неравенствами. Например, шар радиуса R с центром в точке 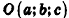
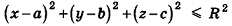
Пример:
Напишите уравнение сферы с центром А (2;-8; 16), которая проходит через начало координат.
Решение:
Так как данная сфера проходит через точку 0(0;0;0), то отрезок АО является ее радиусом. Значит,
Таким образом, искомое уравнение имеет вид:
Ответ:
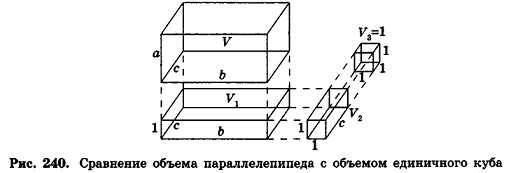
Доказательство формулы объема прямоугольного параллелепипеда
Теорема (формула объема прямоугольного параллелепипеда)
Объем прямоугольного параллелепипеда равен произведению трех его измерений:
где 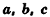
Доказательство:
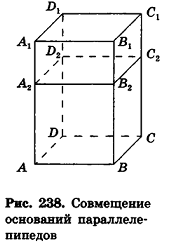
Докажем сначала, что объемы двух прямоугольных параллелепипедов с равными основаниями относятся как длины их высот.
Пусть 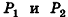
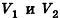
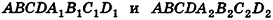
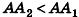
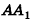
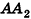
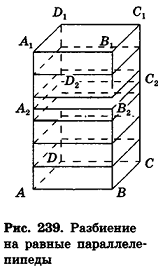
проведем через точки деления параллельные основанию ABCD (рис. 239). Они разобьют параллелепипед 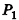
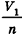
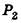
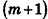
Таким образом, 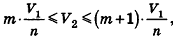
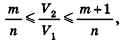
Сравнивая выражения (1) и (2), видим, что оба отношения 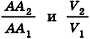
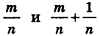
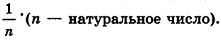
Допустим, что это не так, то есть 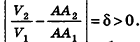
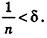
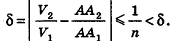
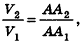
Рассмотрим теперь прямоугольные параллелепипеды с измерениями 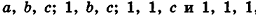
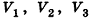
По аксиоме объема V3 =1. По доказанному 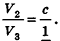
Теорема доказана.
* Выберем 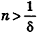
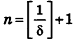
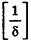
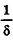
- Вычисление площадей плоских фигур
- Преобразование фигур в геометрии
- Многоугольник
- Площадь многоугольника
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Четырехугольник
- Площади фигур в геометрии















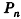
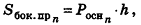
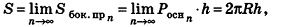
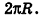
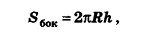
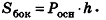
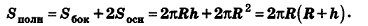

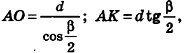
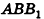
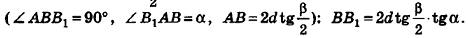
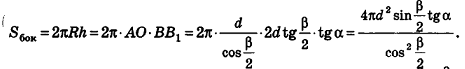
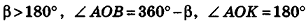
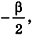
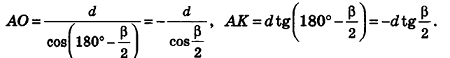
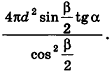
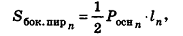
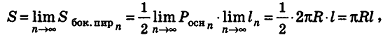
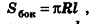
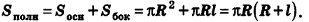
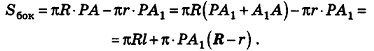
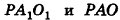
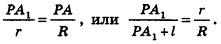
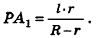
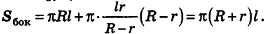
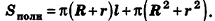
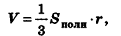
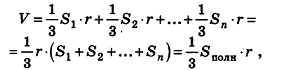
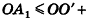
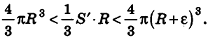
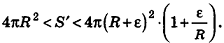
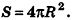
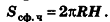






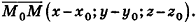
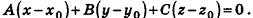
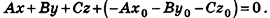
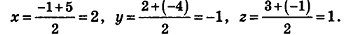
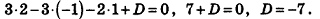
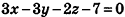
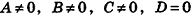 , уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а);
, уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а);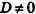 , плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали
, плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали 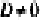 , плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали
, плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали 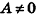 и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).
и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).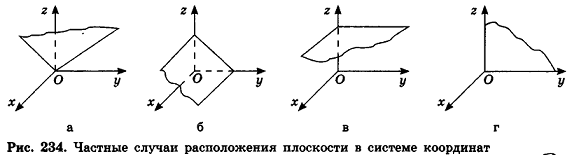
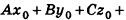
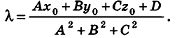
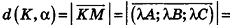
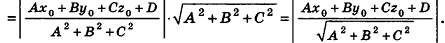
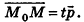
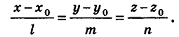
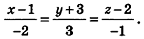
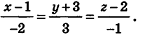
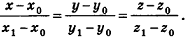
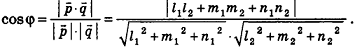
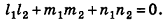
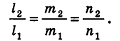
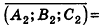
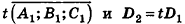 , или, если числа
, или, если числа 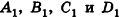 ненулевые
ненулевые 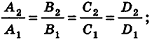
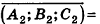
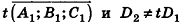 , или, если координаты
, или, если координаты 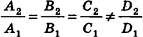 (на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где
(на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где 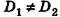 ).
).