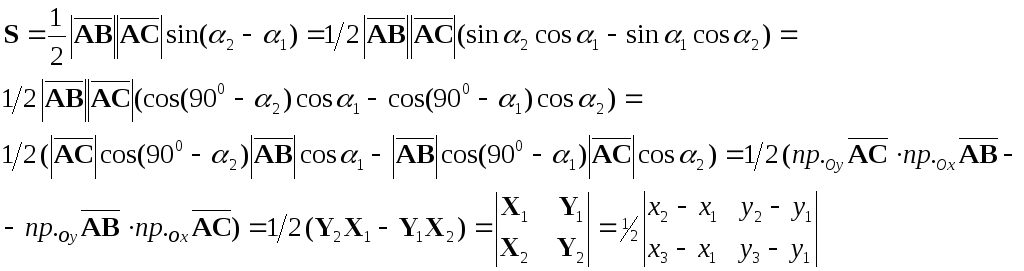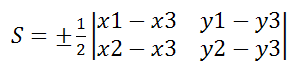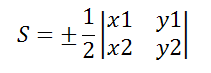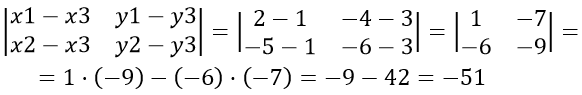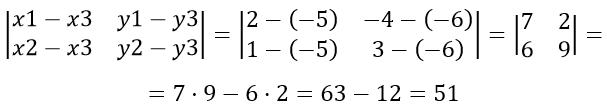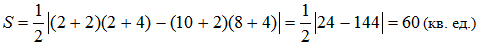Треугольник
– одна из самых распространенных фигур
и надо уметь вычислять площадь треугольника
средствами аналитической геометрии.
Пусть
даны вершины треугольника А(х1,
у1),
В(х2,
у2),
С(х3,у3).
Надо найти формулу, которая бы выражала
площадь S
треугольника АВС
через координаты его вершин.
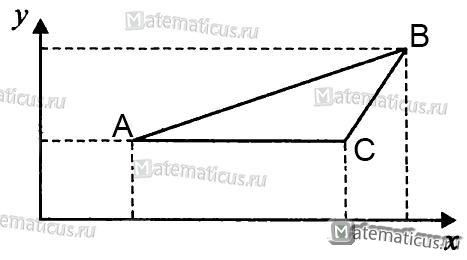
О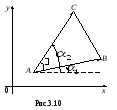
стороныАВ
и АС
треугольника как векторы, имеющие общее
начало в точке А
и следующие координаты
,
.
Пусть угол между вектороми осью Ох равен
,
угол между вектороми осьюОх
равен
,
а угол между самими векторамии
равен
(рис. 3.10).
Из
элементарной геометрии известно, что
площадь S
треугольника равна половине произведения
длин двух сторон треугольника на синус
угла между ними:
.
Если воспользуемся формулой синуса
разности двух углов и определением
проекции вектора на ось (2.2), то получим
Этот
определитель может оказаться как
положительным, так и отрицательным
(если
>
),
поэтому
Итак,
в 3-й лекции мы познакомились с некоторыми
важными понятиями аналитической
геометрии. В основе последней лежит
метод координат, введенный в науку
французским математиком и философом
Р. Декартом, а главная ее идея заключается
в возможности представлять геометрические
объекты в виде алгебраических уравнений
и переводить геометрические задачи на
язык алгебры.
Лекция 4. Введение в анализ
Обратимся теперь
к математике непрерывных величин.
Величиною будем называть все то, что
может быть выражено числом. Будем
рассматривать величины, которые
выражаются только действительными
числами: натуральными, целыми,
рациональными, иррациональными.
Величины
могут быть постоянными и переменными.
Среди постоянных будем различать
абсолютные постоянные, например,
отношение длины окружности к ее диаметру
(число );
отношение
диагонали квадрата к его стороне ()
идругие,
и постоянные в условиях данной задачи,
например, высота данной пирамиды
равна 30 см; площадь данной трапеции
равна 24 кв. см и тому подобное. Обозначать
постоянные величины будем большими и
малыми начальными
буквами латинского алфавита: А, В, С, …,
а, b,
с, …
Переменная
величина – величина, которая принимает
различные числовые
значения. Например, температура воздуха
в каждой точке пространства
меняется в течение суток, проходя
бесконечное множество значений
от наименьшего до наибольшего. Переменные
величины будем обозначать конечными
буквами латинского алфавита X,
Y,
Z,
…
, х, у, z,
…
4.1. Функция
Если
каждому значению переменной величины
х,
принадлежащему
некоторой области, по определенному
правилу (закону) ставится в соответствие
одно и только одно определенное значение
другой переменной
величины у,
то
говорят, что у
является
функцией
от
х и
обозначают
так: у
= f(x),
причем х
называют
независимой переменной или аргументом,
а у
называют
зависимой переменной или функцией.
Символ f
указывает вид зависимости у
от
х.
Иногда
пишут и так у
= у(х).
Функции
могут зависеть от одного, двух, трех и
более аргументов. Например,
площадь круга зависит только от величины
радиуса, площадь прямоугольника
от двух переменных – длины и ширины,
объем параллелепипеда
– от трех переменных: длины, ширины,
высоты, цена продукта
– от многих переменных.
Основные
способы
задания функции:
табличный,
графический
и аналитический, (в виде формулы).
Различают
следующие основные
элементарные функции;
—
степенная;
—
показательная;
—
логарифмическая;
—
тригонометрические;
—
обратные
тригонометрические.
Из
этих функций при помощи арифметических
операций можно составить
множество элементарных функций. Например,
,
,
и т.д.
Функция
от функции вида
называетсясложной
функцией, где
является промежуточным аргументом.
Выражение
функциональной зависимости между
несколькими переменными
через вспомогательную переменную –
параметр, называется параметрической
функцией:,
,где
t
– параметр. Например,
,
-параметрическое
уравнение эллипса –замкнутой
симметричной относительно осей координат
кривой – равномерно растянутой
(сжатой) вдоль одной из осей координат
окружности.
Соседние файлы в папке математика
- #
- #
- #
- #
- #
- #
Пусть точки A(x1;y1), B(x2;y2), C(x3;y3) – вершины треугольника, тогда площадь треугольника выражается формулой
В формуле правая сторона — это определитель второго порядка.
Площадь треугольника является положительной величиной и поэтому перед определителем берём знак «плюс», в случае, если значение положительно, и минус в противном случае, то есть отрицательно.
Примечание
Если вершина C треугольника совпадает с началом координат, то есть x3=y3=0, то формула площади треугольника примет види вычисляется как определитель второго порядка
Пример
Найти площадь треугольника с вершинами A(2;-4), B(-5;-6) и C(1;3)
Решение
Пусть примем A за первую вершину, B — за вторую и C — за третью, тогда находим:
,так как получился отрицательный знак, следовательно перед определителем берём знак «минус»
[S = ( — frac{1}{2})cdot( — 51) = 25,5]
Если вершины треугольника переобозначим немного в другом порядке, допустим, первой вершиной A, второй вершиной C и третьей вершиной B, тогда получим выражение:
В этом случае, необходимо взять знак «плюс« и получим снова площадь треугольника S=25,5
3647
Площадь треугольника с вершинами A(x1;y1) B(x2;y2) C(x3;y3) определяется по формуле
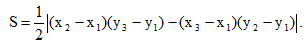
Пример 4. Определить площадь треугольника с вершинами A(-2;4), B(2;8); C(10;2).
Решение. Используя формулу (5), получаем
Добавлять комментарии могут только зарегистрированные пользователи.
Регистрация Вход
mat:geom:triangle-area
Содержание
Площадь треугольника

-
R — радиус описанной окружности
-
r — радиус вписанной окружности
-
p — полупериметр, $p = frac{a+b+c}{2}$
-
Площадь треугольника равна половине произведения двух его сторон и синуса угла между ними.
-
Площадь треугольника равна произведению сторон, деленному на 4 радиуса описанной окружности.
-
Площадь треугольника по трем высотам легко выводится из формулы Герона
-
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.

$$ begin{align} mbox{По высоте: } ; & S = frac12 a cdot h_a \[10pt]
mbox{По произведению сторон: } ; & S = frac{abc}{4R} \[10pt]
mbox{По полупериметру: } ; & S = p cdot r \[10pt]
mbox{По двум сторонам: } ; & S = frac12 cdot a cdot b cdot sin{gamma} \[12pt]
mbox{Формула Герона: } ; & S = sqrt {p(p-a)(p-b)(p-c)} \[12pt]
mbox{По высотам: } ; & S = frac{1}{sqrt {(frac1{h_a}+frac1{h_b}+frac1{h_c})(-frac1{h_a}+frac1{h_b}+frac1{h_c})(frac1{h_a}-frac1{h_b}+frac1{h_c})(frac1{h_a}+frac1{h_b}-frac1{h_c})}} \[12pt]
mbox{По высотам и радиусу: } ; & S = frac{r}{sqrt3} (h_a+h_b+h_c) \[12pt]
mbox{По трем углам: } ; & S = 2R^2 sin{alpha} cdot sin{beta} cdot sin{gamma}
end{align} $$
$
$
Формула Герона
Интерактивная модель и калькулятор
Формула Герона для треугольника — это частный случай формулы Брахмагупты для четырехугольника, вписанного в окружность (одну из сторон положить равной 0):
$S={sqrt {(p-a)(p-b)(p-c)(p-d)}}$
где p — полупериметр четырехугольника
Треугольник является предельным случаем вписанного четырёхугольника при устремлении длины одной из сторон к нулю.
Формула Пика
Площадь треугольника, нарисованного на клетчатой бумаге.
Если треугольник нарисован на клетчатой бумаге и все его вершины находятся в углах сетки, то площадь его можно вычислять по формуле Пика:
$$S = V+frac{G}{2}-1,$$
где $V$ — количество узлов сетки, находящихся внутри треугольника, $G$ — количество узлов сетки, находящихся на границе треугольника.

Подробнее — см. ниже Теорема Пика.

Целочисленные площади

Задача
Вычислить площадь Бермудского треугольника.
Бермудский Треугольник — широко известная аномальная зона. Расположен он в границах между Бермудскими островами, Майями во Флориде и Пуэрто-Рико.
Расстояние между вершинами треугольника в милях
| Norfolk | Bermuda | 850 |
| Bermuda | Santiago | 810 |
| Norfolk | Santiago | 894 |
В расчетах игнорировать кривизну поверхности Земли.
Задача
Может ли треугольник со сторонами больше километра иметь площадь, меньшую 1 мм²?
Теорема Пика. Нахождение площади решётчатого многоугольника
http://e-maxx.ru/algo/pick_grid_theorem
Многоугольник без самопересечений называется решётчатым, если все его вершины находятся в точках с целочисленными координатами (в декартовой системе координат).
Пусть дан некоторый решётчатый многоугольник, с ненулевой площадью.
Обозначим его площадь через $S$; количество точек с целочисленными координатами, лежащих строго внутри многоугольника — через $I$; количество точек с целочисленными координатами, лежащих на сторонах многоугольника — через $B$.
Тогда справедливо соотношение, называемое формулой Пика:
$$S = I -B/2 + 1$$
В частности, если известны значения $I$ и $B$ для некоторого многоугольника, то его площадь можно посчитать за $O(1)$, даже не зная координат его вершин.
Это соотношение открыл и доказал австрийский математик Георг Александр Пик (Georg Alexander Pick) в 1899 г.
Доказательство
Доказательство производится в несколько этапов: от самых простых фигур до произвольных многоугольников:
-
Единичный квадрат. В самом деле, для него S=1, B=4, I=0, и формула верна.
-
Произвольный невырожденный прямоугольник со сторонами, параллельными осям координат. Для доказательства формулы обозначим через $a$ и $b$ длины сторон прямоугольника. Тогда находим: $S=ab$, $I=(a-1)(b-1)$, $B=2(a+b)$. Непосредственной подстановкой убеждаемся, что формула Пика верна.
-
Прямоугольный треугольник с катетами, параллельными осям координат. Для доказательства заметим, что любой такой треугольник можно получить отсечением некоторого прямоугольника его диагональю. Обозначив через C число целочисленных точек, лежащих на диагонали, можно показать, что формула Пика выполняется для такого треугольника, независимо от значения C.
-
Произвольный треугольник. Заметим, что любой такой треугольник может быть превращён в прямоугольник приклеиванием к его сторонам прямоугольных треугольников с катетами, параллельными осям координат (при этом понадобится не более 3 таких треугольников). Отсюда можно получить корректность формулы Пика для любого треугольника.
-
Произвольный многоугольник. Для доказательства триангулируем его, т.е. разобьём на треугольники с вершинами в целочисленных точках. Для одного треугольника формулу Пика мы уже доказали. Дальше, можно доказать, что при добавлении к произвольному многоугольнику любого треугольника формула Пика сохраняет свою корректность. Отсюда по индукции следует, что она верна для любого многоугольника.
Задача
Обобщение на высшие размерности
К сожалению, эта столь простая и красивая формула Пика плохо обобщается на высшие размерности.
(подробнее по ссылке на источник)
Как можно найти I и B на практике?
$B = gcd(abs(x_0-x_1),abs(y_0-y_1)) — 1$, где $gcd$ — наибольший общий делитель, $(x_0;y_0), (x_1;y_1)$ — точки, соединённые стороной многоугольника.
тут интересно находить не площадь, а количество точек внутри, потому что другого алгоритма я не видел для подсчета этого количества.
Литература:
Учебники:
Площадь треугольника по высоте, проведенной к стороне — Геометрия 8 класс
Геометрия 9 класс Мерзляк, параграф 1 — формула Герона, по произведению сторон, через радиус вписанной и описанной окружности
· Последние изменения: 2020/02/21 17:21 —
kc
§2. Площадь треугольника. Метод площадей
В школьном курсе геометрии доказано несколько формул площади треугольника. Напомним их.
Пусть `A`, `B` и `C` — углы треугольника`ABC`; `a`, `b` и `c` — противолежащие этим углам стороны; `h_a`, `h_b` и `h_c` — высоты к этим сторонам; `r` — радиус вписанной окружности;`R` — радиус описанной окружности; `2p=(a+b+c)` — периметр треугольника; `S` — площадь треугольника
| `S=1/2ah_a=1/2bh_b=1/2ch_c`, | (1) |
| `S=1/2 ab sinC=1/2acsinB=1/2bcsinA`, | (2) |
| `S=pr`, | (3) |
| ``S=sqrt(p(p-a)(p-b)(p-c))` — формула Герона, | (4) |
| `S=(abc)/(4R)`. | (5) |
При вычислении площади из этих формул следует выбрать ту, которая в условиях конкретной задачи приводит к более простому решению.
Для примера, рассмотрим два треугольника:
`DeltaABC:` `AB=13`, `BC=14`, `AC=15`;
`DeltaKML:` `KL=sqrt(13)`, `LM=sqrt(14)`, `KM=sqrt(15)`;
Надо найти площадь и радиус описанной окружности.
Для треугольника `ABC` удобен ход решения такой:
`p=1/2(AB+BC+AC)=21`, по формуле Герона
`S_(ABC)=sqrt(21*6*7*8)= ul(84)` и по формуле (5)
`R=(abc)/(4S)=(13*14*15)/(4*84)=65/8=ul(8,125)`.
Для треугольника `KLM` вычисленная по формуле Герона затруднительны, более простой путь — найти косинус, например, угла `M`. По теореме косинусов
`13=14+15-2sqrt(14)*sqrt(15)cosM iffcosM=8/(sqrt(14)*sqrt(15))`,
тогда `sinM=sqrt(1-64/(210))=(sqrt(146))/(sqrt(14)*sqrt(15))` и по формуле (2):
`S_(KML)=1/2KM*LMsinM=1/2*(sqrt(14)*sqrt(15)*sqrt(146))/(sqrt(14)*sqrt(15))=(sqrt(146))/2`,
тогда `R=(KL)/(2sinM)=ul((sqrt(13)*sqrt(14)*sqrt(15))/(2*sqrt(146)))=(sqrt(13)*sqrt7*sqrt(15))/(2*sqrt(73))` (точно также по формуле 5).
Сравнение площадей треугольников обычно опирается на одно из следующих утверждений:
$$ 2.{1}^{○}$$. Площади треугольников с одинаковой высотой относятся как длины соответствующих оснований. В частности, если точка `D` лежит на основании `AC` (рис. 6а), то
`(S_(DBC))/(S_(ABC))=(DC)/(AC)`.
$$ 2.{2}^{○}$$. Площади треугольников с общим углом относятся как произведения сторон, заключающих этот угол (см. рис. 6б):
`(S_(KBL))/(S_(ABC))=(BK*BL)/(BA*BC)`.
$$ 2.{3}^{○}$$. Площади подобных треугольников относятся как квадраты их
сходственных сторон, т. е. если `Delta ABC~DeltaA_1B_1C_1`, то `(S_(A_1B_1C_1))/(S_(ABC))=((A_1B_1)/(AB))^2`.
Все эти утверждения легко доказываются с использованием соответственно формул площади (1) и (2).
Обратим внимание на важное свойство медиан треугольника.
Три медианы треугольника разбивают его на `6` треугольников с общей вершиной и равными площадями.
Известно, что три медианы треугольника пересекаются в одной точке и делятся в отношении `2:1`, считая от вершины. Пусть `O` — точка пересечения медиан треугольника `DeltaABC` площади `S` (рис. 7а). Надо доказать, что площади всех шести треугольников с верш иной в точке `O`, составляющих треугольник `ABC`, равны между собой, т. е. равны `1/6S`.
Докажем, например, для треугольника `BOM`, что `S_(BOM)=1/6S_(ABC)`.
Точка `M` — середина стороны `BC` (рис. 7б), по утверждению $$ 2.{1}^{○}$$ о сравнении площадей `S_(ABM)=1/2S`. Медиана `BN`, пересекая медиану `AM` в точке `O` (рис. 7в), делит её в отношении `AO:OM=2:1`, т. е. `OM=1/3AM`. По тому же утверждению $$ 2.{1}^{○}$$ площадь треугольника `BOM` составляет `1//3` площади треугольника `ABM`, т. е.
`S_(BOM)=1/3(1/2S)=1/6S`.
Дан треугольник `ABC`. Точка `D` лежит на стороне `AB`, `AD:DB=1:2`, точка `K` лежит на стороне `BC`, `BK:KC=3:2` (рис. 8а). Отрезки `AK` и `CD` пересекаются в точке `O`. Найти отношение площади четырёхугольника `DBKO` к площади треугольника `ABC`.
1. Обозначим `S_(ABC)=S`, `S_(DBKO)=sigma` и `S_(ADO)=a`. По утверждению $$ 2.{1}^{○}$$ имеем `S_(ABK)=a+sigma=3/5S` (так как `BK:BC=3:5`). Площадь `a` треугольника `ADO` найдём как часть площади треугольника `ADC`, зная, что `S_(ADC)=1/3S` (так как `AD:AB=1:3`).
2. Через точку `D` проведём прямую `DL«||«AK`. По теореме о пересечении сторон угла параллельными прямыми (`/_ABC`, `DL«||«AK`) имеем `(BL)/(LK)=(BD)/(AD)`, откуда `LK=y`.
По той же теореме (`/_DCB`, `OK«||«DL`) получим `(DO)/(DC)=(LK)/(LC)`, `DO=1/3DC`.
3. Теперь находим `S_(ADO):S_(ADC)=DO:DC`, `a=1/3(1/3S)=1/9S`.
(Можно по теореме Менелая для треугольника `BCD` и секущей `CD:`
`(BK)/(KC)*(CO)/(OD)*(DA)/(AB)=1 iff 3/2*(CO)/(OD)*1/3=1 iff CO=2OD=>OD=1/3DC`).
Находим площадь: `sigma=3/5S-a=(3/5-1/9)S=22/45S`.
`22/45`.
Найти площадь треугольника, две стороны которого равны `3` и `7`, а медиана к третьей стороне равна `4` (рис. 9).
Пусть `AB=3`, `BC=7`, `AM=MC` и `BM=4`. Достроим треугольник `ABC` до параллелограмма, для этого на прямой `BM` отложим отрезок `MD=BM` и соединим точки: `A` с `D` и `C` с `D`. Противоположные стороны параллелограмма равны: `(DC=AB)` и равны площади треугольников `ABC` и `DBC` (общее основание `BC` и равные высоты из вершин `A` и `D`).
В треугольнике `DBC` известны все три стороны: `BC=7`, `DC=3`, `BD=2BM=8`.
Находим его площадь по формуле Герона: `p=9`, `S_(BCD)=6sqrt3`.
Значит и `S_(ABC)=6sqrt3`.
В решении этой задачи дополнительным построением получен треугольник, площадь которого равна площади заданного и легко вычисляется по данным задачи. Приведём ещё одну задачу, где сначала вычисляется площадь дополнительно построенной фигуры, а затем легко находится искомая площадь.
Найти площадь треугольника, если его медианы равны `3`, `4` и `5`.
Пусть `O` — точка пересечения медиан треугольника `ABC` (рис. 10) и пусть `m_a=AM=3`, `m_b=BN=4` и `m_c=CP=5`.
По свойству медиан `AO=2/3m_a`, `CO=2/3m_c` и `ON=1/3m_b`. В треугольнике `AOC` известны две стороны `AO` и `CO` и медиана третьей стороны `ON`. Площадь этого треугольника найдём как в предыдущей задаче.
Достроим треугольник `AOC` до параллелограмма `AOCD`, `S_(AOC)=S_(DOC)`, в треугольнике `DOC` известны три стороны:
`DO=2ON=2/3m_b`, `OC=2/3m_c`, `DC=AO=2/3m_a`.
Площадь треугольника `DOC` вычисляем по формуле Герона `S_1=S_(AOC)=S_(DOC)=8/3`. Сравним теперь площадь треугольника `ABC` (обозначим её `S`) с площадью треугольника `AOC`. Из теоремы 2 о медианах и площадях следует `S_(AOC)=S_(AON)+S_(NOC)=2*1/6S=1/3S`.
Итак, `S=3`, `S_1=8`.
В следующей задаче докажем лемму об отношении площади треугольника к площади другого треугольника, построенного из медиан первого.
Найти отношение площади `S` треугольника к площади `S_0` треугольника, составленного из медиан первого.
Рассмотрим рис. 10. В построенном треугольнике `OCD` стороны таковы: `OC=2/3m_c`, `OD=2/3m_b`, `CD=2/3m_a`. Очевидно, что треугольник со сторонами `m_a`, `m_b`, `m_c` подобен (по третьему признаку) треугольнику со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`.
Из решения предыдущей задачи следует, что `S_(OCD)=S_1=1/3S` (здесь `S` — площадь треугольника `ABC`). Кроме того, площади подобных треугольников относятся как квадраты сходственных сторон, поэтому `(S_1)/(S_0)=(2/3)^2`. Таким образом, имеем `S_0=9/4S_1=3/4S`, т. е.
`S_(m_am_bm_c)=3/4S_(abc)`.
Из рассуждений в решении Примера 9 следует, что всегда существует треугольник со сторонами, равными медианам данного треугольника, поскольку всегда существует подобный ему треугольник со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`. Кроме того, становится ясным план построения треугольника по трём отрезкам, равным его медианам: сначала строится треугольник `OCD` (см. рис. 10) со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`, затем точка `N` — середина отрезка `OD`, потом точка `A` (из `AN=NC`) и точка `B` (из `OB=OD`). Это построение осуществимо, если существует треугольник `OCD`, т. е. если существует треугольник со сторонами `m_a`, `m_b`, `m_c`. Итак, вывод: три отрезка могут быть медианами некоторого треугольника тогда и только тогда, когда из них можно составить треугольник.
Около окружности радиуса `sqrt3` описан треугольник. Найти его площадь, если одна из его сторон точкой касания делится на отрезки `9` и `5`.
Пусть `AP=9`, `PC=5` (рис. 11) и пусть `BM=x`. По свойству касательных `AM=AP`, `CN=CP` и `BN=BM`, поэтому стороны треугольника таковы: `AC=14`, `AB=9+x`, `BC=5+x`, тогда `p=14+x`. (Заметим, что `p=AC+BM`!). По формулам площади (3) и (4) имеем: `S=pr=(14+x)sqrt3` и `S=sqrt((14+x)x*5*9)`. Приравниваем правые части, возводим в квадрат, приводим подобные члены, получаем `x=1`. Вычисляем площадь треугольника:
`S=pr=(14+1)*sqrt3=15sqrt3`.
Приём, применённый в решении этой задачи, когда площадь фигуры выражается двумя различными способами, часто используется в задачах на доказательство.
Проведём два примера, в каждом выведем полезную формулу.
В треугольнике `ABC` угол `C` равен `varphi`, `AC=b`, `BC=a` (рис. 12). Доказать, что биссектриса `CD` равна `(2ab)/(a+b) cos varphi/2`.
Обозначим `CD=x`. Очевидно, что `S_(ABC)=S_(ACD)+S_(DCB)`. По формуле (2) `S_(ABC)=1/2 ab sin varphi`, `S_(ACD)=1/2 bx sin varphi/2`, `S_(BDC)=1/2 ax sin varphi/2`. Таким образом, имеем: `1/2 ab sin varphi=1/2(a+b)x sin varphi/2`. Используем формулу синуса двойного угла `sin varphi=2sin varphi/2 cos varphi/2`, получим:
`x=(2ab)/(a+b)cos varphi/2`.
называется окружность, касающаяся одной из сторон треугольника и продолжений двух других сторон. Таких окружностей, очевидно, три (рис. 13). Их радиусы обычно обозначаются `r_a`, `r_b`, `r_c` в зависимости от того, какой стороны окружность касается.
Вневписанная окружность касается стороны `a=BC` треугольника `ABC` (рис. 14). Доказать, что `S_(ABC)=r_a(p-a)`, где `2p=a+b+c`.
Центр окружности `I_a` лежит на пересечении биссектрисы угла `A` и биссектрис внешних углов при вершинах `B` и `C`. Легко видеть, что если `D`, `F` и `E` — точки касания, то `I_aD=I_aF=I_aE=r_a`.
Считаем площадь `S_0` четырёхугольника `ABI_aC`:
`S_0=S_(ABC)+S_(BCI_a)` и `S_0=S_(ABI_a)+S_(ACI_a)`, откуда
`S_(ABC)=S_(ABI_a)+S_(ACI_a)-S_(BCI_a)=1/2 cr_a+1/2br_a-1/2ar_a=`
`=r_a (c+b-a)/2=r_a(2p-2a)/2=r_a(p-a)`.
Итак,