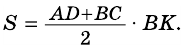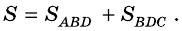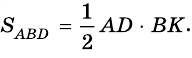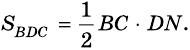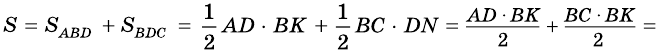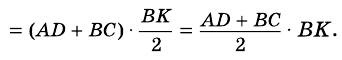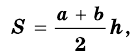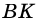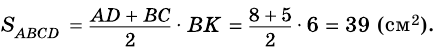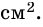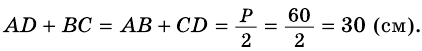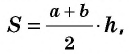18. Площади геометрических фигур
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Площадь трапеции
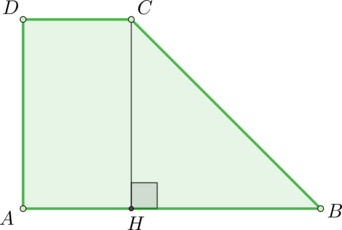
Найдите площадь прямоугольной трапеции, основания которой равны (6) и (2), большая боковая сторона составляет с основанием угол (45^circ).
Проведем высоту (CH).
Так как (angle HBC=45^circ), то (angle HCB=45^circ). Следовательно, (triangle HBC) равнобедренный и (HB=HC).
(ADCH) – прямоугольник, следовательно, (AH=DC=2). Тогда (CH=HB=6-2=4). Тогда площадь трапеции равна [S=dfrac{AB+DC}2cdot CH=dfrac{2+6}2cdot 4=16]
Ответ: 16
Основания прямоугольной трапеции равны (12) и (4). Ее площадь равна (64). Найдите острый угол этой трапеции. Ответ дайте в градусах.
Проведем высоту (CH).
(ADCH) – прямоугольник, следовательно, (AH=DC=4). Тогда (HB=12-4=8). Площадь трапеции равна [64=dfrac{AB+DC}2cdot CH=dfrac{4+12}2cdot CHquadRightarrowquad
CH=8] Заметим, что мы получили, что (CH=HB=8). То есть (triangle
CHB) равнобедренный, значит, углы при основании равны, то есть (angle HCB=angle HBC). Так как сумма острых углов в прямоугольном треугольнике равна (90^circ), то (angle B=angle
HBC=90^circ:2=45^circ).
Ответ: 45
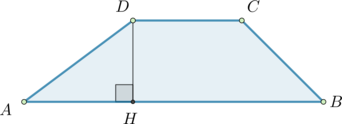
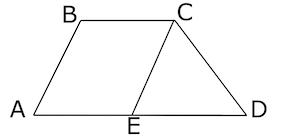
Основания трапеции равны (18) и (6), боковая сторона, равная (7), образует с одним из оснований угол (150^circ). Найдите площадь трапеции.
Пусть (AD=7), тогда (angle ADC=150^circ). По свойству трапеции (angle DAB=180^circ-150^circ=30^circ). Проведем (DHperp
AB).
Рассмотрим (triangle ADH). Катет, лежащий против угла (30^circ), равен половине гипотенузы, следовательно, (DH=AD:2=3,5). Тогда площадь трапеции равна [S=dfrac{AB+DC}2cdot DH=dfrac{18+6}2cdot 3,5=42]
Ответ: 42
Основания трапеции равны (27) и (9), боковая сторона равна (8). Площадь трапеции равна (72). Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ дайте в градусах.
Пусть (AD=8). Проведем (DHperp AB).
Тогда площадь трапеции равна [72=dfrac{AB+DC}2cdot DH=dfrac{27+9}2cdot DHquadRightarrowquad
DH=4] Рассмотрим прямоугольный (triangle ADH). Так как катет (DH) равен половине гипотенузы (AD), то угол (DAH) равен (30^circ).
Ответ: 30
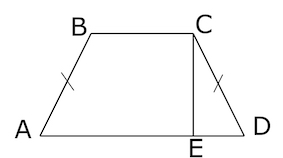
Основания равнобедренной трапеции равны (14) и (26), а ее боковые стороны равны (10). Найдите площадь трапеции.
Проведем высоту (BH). По свойству равнобедренной трапеции (AH=(AD-BC):2=(26-14):2=6).
Тогда из прямоугольного треугольника (ABH): [BH=sqrt{AB^2-AH^2}=sqrt{10^2-6^2}=8] Тогда площадь трапеции: [S=dfrac{AD+BC}2cdot BH=dfrac{26+14}2cdot 8=160]
Ответ: 160
Основания равнобедренной трапеции равны (7) и (13), а ее площадь равна (40). Найдите боковую сторону трапеции.
Проведем высоту (BH).
Площадь трапеции равна [40=dfrac{AD+BC}2cdot BH=dfrac{7+13}2cdot BHquadRightarrowquad BH=
4] Рассмотрим прямоугольный (triangle ABH). По свойству равнобедренной трапеции (AH=(AD-BC):2=(13-7):2=3). Следовательно, [AB=sqrt{AH^2+BH^2}=5]
Ответ: 5
Основания равнобедренной трапеции равны (14) и (26), а ее периметр равен (60). Найдите площадь трапеции.
Проведем высоту (BH). По свойству равнобедренной трапеции (AH=(AD-BC):2=(26-14):2=6).
Так как периметр трапеции равен (60), а боковые стороны равны, то [AB=dfrac{60-14-26}2=10] Тогда из прямоугольного треугольника (ABH): [BH=sqrt{AB^2-AH^2}=sqrt{10^2-6^2}=8] Тогда площадь трапеции: [S=dfrac{AD+BC}2cdot BH=dfrac{26+14}2cdot 8=160]
Ответ: 160

УСТАЛ? Просто отдохни
Всего: 183 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Тип 17 № 39
i
Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 2. Найдите площадь трапеции.
Основания трапеции равны 18 и 12, одна из боковых сторон равна а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
Основания трапеции равны 18 и 10, одна из боковых сторон равна а угол между ней и одним из оснований равен 120°. Найдите площадь трапеции.
Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а синус угла между ней и одним из оснований равен Найдите площадь трапеции.
Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а косинус угла между ней и одним из оснований равен Найдите площадь трапеции.
Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а тангенс угла между ней и одним из оснований равен Найдите площадь трапеции.
Какие из следующих утверждений верны?
1) Если площади фигур равны, то равны и сами фигуры.
2) Площадь трапеции равна произведению суммы оснований на высоту.
3) Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.
4) Если две смежные стороны параллелограмма равны 4 и 5, а угол между ними равен 30°, то площадь этого параллелограмма равна 10.
Если утверждений несколько, запишите их номера в порядке возрастания.
Какие из следующих утверждений верны?
1) Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.
2) Площадь трапеции равна произведению суммы оснований на высоту.
3) Площадь трапеции не превосходит произведения средней линии на высоту.
4) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне.
Какие из следующих утверждений верны?
1) Площадь многоугольника, описанного около окружности, равна произведению его периметра на радиус вписанной окружности.
2) Если диагонали ромба равна 3 и 4, то его площадь равна 6.
3) Площадь трапеции меньше произведения суммы оснований на высоту.
4) Площадь прямоугольного треугольника меньше произведения его катетов.
Если утверждений несколько, запишите их номера в порядке возрастания.
Какие из следующих утверждений верны?
1) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны.
2) В равнобедренном треугольнике имеется не менее двух равных углов.
3) Площадь трапеции не превосходит произведения средней линии на высоту.
4) Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.
Основания равнобедренной трапеции равны 8 и 18, а периметр равен 56.
Найдите площадь трапеции.
На клетчатой бумаге с размером клетки 1см × 1см изображена трапеция. Найдите её площадь. Ответ дайте в квадратных сантиметрах.
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(1 вар)
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар.6)
Основания равнобедренной трапеции равны 8 и 18, а её периметр равен 52. Найдите площадь трапеции.
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(1 вар)
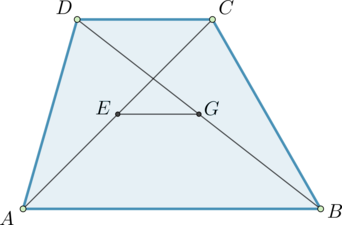
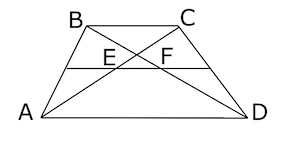
Диагонали AC и BD трапеции ABCD пересекаются в точке O. Площади треугольников AOD и BOC равны соответственно и
Найдите площадь трапеции.
Источник: ГИА-2013. Математика. Тренировочная работа №2.(4 вар)
Найдите площадь трапеции, изображённой на рисунке.
В трапеции проведен отрезок, параллельный основаниям и делящий ее на две трапеции одинаковой площади. Найдите длину этого отрезка, если основания трапеции равны см и
см.
Источник: ГИА-2012. Математика. Диагностическая работа №2 (2 вар.)
Всего: 183 1–20 | 21–40 | 41–60 | 61–80 …
25
Июл 2013
Категория: 01 Геометрия
01. Трапеция
2013-07-25
2022-09-11
Задача 1. Основания равнобедренной трапеции равны и
Боковые стороны равны
Найдите синус острого угла трапеции.
Решение: + показать
Задача 2. Большее основание равнобедренной трапеции равно Боковая сторона равна
Синус острого угла равен
Найдите меньшее основание.
Решение: + показать
Задача 3. Основания равнобедренной трапеции равны и
Тангенс острого угла равен
. Найдите высоту трапеции.
Решение: + показать
Задача 4. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.
Решение: + показать
Задача 5. Найдите среднюю линию трапеции, если ее основания равны и
Решение: + показать
Задача 6. Средняя линия трапеции равна а меньшее основание равно
Найдите большее основание трапеции.
Решение: + показать
Задача 7. Основания трапеции равны и
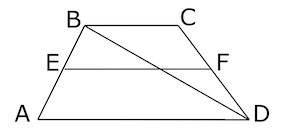
Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Решение: + показать
Задача 8. Основания трапеции равны и
Найдите отрезок, соединяющий середины диагоналей трапеции.
Решение: + показать
Задача 9. В равнобедренной трапеции основания равны и
острый угол равен
. Найдите ее периметр.
Решение: + показать
Задача 10. Основания трапеции равны и
боковая сторона равна
Площадь трапеции равна
Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ дайте в градусах.
Решение: + показать
Задача 11. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного отсекает треугольник, периметр которого равен
Найдите периметр трапеции.
Решение: + показать
Задача 12. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины и
Найдите среднюю линию этой трапеции.
Решение: + показать
Задача 13. Основания трапеции относятся как а средняя линия равна
Найдите меньшее основание.
Решение: + показать
Задача 14. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна Найдите ее среднюю линию.
Решение: + показать
Задача 15. Найдите площадь прямоугольной трапеции, основания которой равны и
большая боковая сторона составляет с основанием угол
Решение: + показать
Задача 16. Основания равнобедренной трапеции равны и
а ее периметр равен
Найдите площадь трапеции.
Решение: + показать
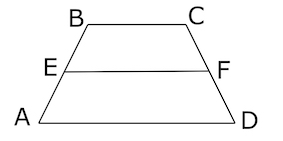
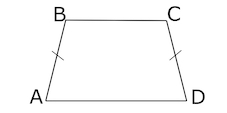
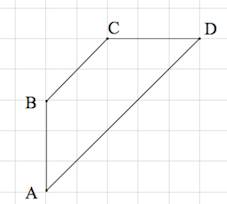
Задача 17. Найдите среднюю линию трапеции , если стороны квадратных клеток равны
.
Решение: + показать

Автор: egeMax |
комментариев 14
Печать страницы
Задачи пригодятся для отработки материала по теме, сдесь же имеются задачи для домашней работы.
Скачать:
Предварительный просмотр:
Площадь трапеции.
- В трапеции основания равны 6 см и 10 см, а высота равна полусумме длин оснований. Найдите площадь трапеции.
- В прямоугольной трапеции основания равны 6 см и 10см, меньшая боковая сторона- 5 см. Чему равна площадь трапеции?
- В равнобедренной трапеции ABCM большее основание AM=20 см, высота BH отсекает от AM отрезок AH=6 см, ∠BAM=45°. Найдите площадь трапеции.
- В трапеции ABCM одно из оснований в 3 раза меньше другого, а высота составляет 75% большего основания, площадь трапеции равна 72 см². Найдите основания и высоту трапеции.
- В трапеции ABCD BC и AD-основания, BC÷AD=4÷5. Площадь треугольника ACD=35 см². Найдите площадь трапеции.
Домашнее задание.
- Найдите площадь трапеции ABCD, если основания AD и BC равны соответственно 12 см и 8 см, боковая сторона AB=6 см, ∠A=30°.
- В треугольнике ABC стороны AB и BC равны соответственно 14 см и 18 см. Сторона AB продолжена за точку A на отрезок AM=AB. Сторона BC продолжена за точку C на отрезок KC, равный половине BC. Найдите площадь треугольника MBK, если площадь треугольника ABC равна 126 см².
Площадь трапеции.
- В трапеции основания равны 6 см и 10 см, а высота равна полусумме длин оснований. Найдите площадь трапеции.
- В прямоугольной трапеции основания равны 6 см и 10см, меньшая боковая сторона- 5 см. Чему равна площадь трапеции?
- В равнобедренной трапеции ABCM большее основание AM=20 см, высота BH отсекает от AM отрезок AH=6 см, ∠BAM=45°. Найдите площадь трапеции.
- В трапеции ABCM одно из оснований в 3 раза меньше другого, а высота составляет 75% большего основания, площадь трапеции равна 72 см². Найдите основания и высоту трапеции.
- В трапеции ABCD BC и AD-основания, BC÷AD=4÷5. Площадь треугольника ACD=35 см². Найдите площадь трапеции.
Домашнее задание.
- Найдите площадь трапеции ABCD, если основания AD и BC равны соответственно 12 см и 8 см, боковая сторона AB=6 см, ∠A=30°.
- В треугольнике ABC стороны AB и BC равны соответственно 14 см и 18 см. Сторона AB продолжена за точку A на отрезок AM=AB. Сторона BC продолжена за точку C на отрезок KC, равный половине BC. Найдите площадь треугольника MBK, если площадь треугольника ABC равна 126 см².
По теме: методические разработки, презентации и конспекты
- Мне нравится
Преподаватель который помогает студентам и школьникам в учёбе.
Площадь трапеции — определение и вычисление с примерами решения
Теорема (о площади трапеции). Площадь трапеции равна произведению полусуммы ее оснований на высоту.
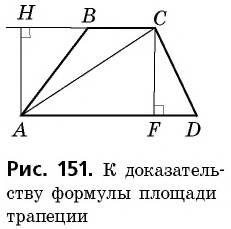
Доказательство:
Пусть
Докажем, что площадь 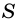
1) Диагональ 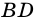
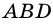
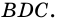
2) 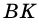
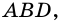
3) Проведем в трапеции высоту 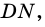
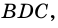
4) 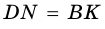
В общем виде формулу площади 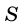
где 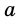
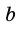
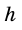
Следствие. Площадь трапеции равна произведению ее средней линии на высоту.
Пример:
В трапеции 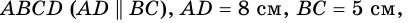
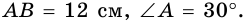
Решение:
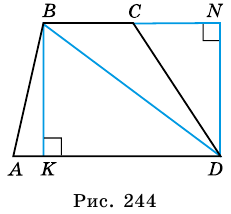
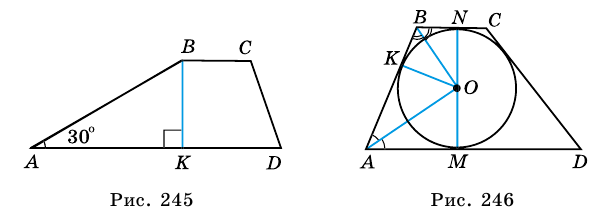
1) Проведем в трапеции 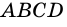
(рис. 245). В 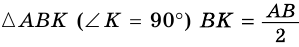
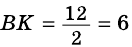
2)
Ответ. 39
Пример:
Периметр трапеции 60 см, а одна из боковых сторон точкой касания вписанной окружности делится на отрезки 9 см и 4 см. Найдите площадь трапеции.
Решение:
1) Так как трапеция является описанной около окружности (рис. 246), то
2) Центр вписанной окружности — точка 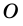
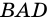
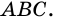
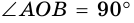
3) Точка 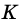
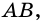
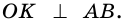
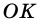
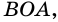
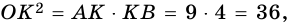
4) 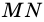
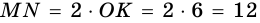
5) Следовательно,
Ответ. 180
Площадь трапеции
Часто для вычисления площади некоторого многоугольника его разбивают на несколько треугольников и находят искомую площадь как сумму площадей этих треугольников. Именно такой подход можно применить для вывода формулы площади трапеции.
Теорема (формула площади трапеции) Площадь трапеции равна произведению полусуммы ее оснований на высоту:
где 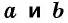
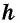
Доказательство:
Пусть дана трапеция 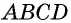
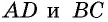
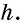
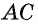
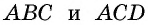
Проведем высоты этих треугольников 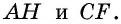
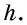
Теорема доказана.
Следствие
Площадь трапеции равна произведению средней линии на высоту.
- Центральные и вписанные углы
- Углы и расстояния в пространстве
- Подобие треугольников
- Решение прямоугольных треугольников
- Прямоугольник и его свойства
- Ромб и его свойства, определение и примеры
- Квадрат и его свойства
- Трапеция и ее свойства