Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
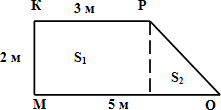
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
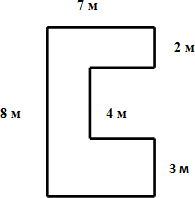
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников
ABC и

Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
На мой взгляд, задача учителя – не только научить, а развить познавательный интерес у учащегося. Поэтому, когда возможно, связываю темы урока с практическими задачами.
На занятии учащиеся под руководством учителя составляют план решения задач на нахождение площади «сложной фигуры» (для расчеты сметы ремонта), закрепляют навыки решения задач на нахождение площади; происходит развитие внимания, способности к исследовательской деятельности, воспитание активности, самостоятельности.
Работа в парах создает ситуацию общения между теми, кто имеет знания и теми, кто их приобретает; в основе такой работы лежит повышение качества подготовки по предмету. Способствует развитию интереса к процессу учения и более глубокому усвоению учебного материала.
Урок не только систематизирует знания обучающихся, но и способствует развитию творческих, аналитических способностей. Применение задач с практическим содержанием на уроке позволяет показать востребованность математических знаний в повседневной жизни.
Цели урока:
Образовательные:
- закрепление знаний формул площади прямоугольника, прямоугольного треугольника;
- анализ заданий на вычисление площади “сложной” фигуры и способов их выполнения;
- самостоятельное выполнение заданий для проверки знаний, умений, навыков.
Развивающие:
- развитие приёмов умственной и исследовательской деятельности;
- развитие умения слушать и объяснять ход решения.
Воспитательные:
- воспитывать у учащихся навыки учебного труда;
- воспитывать культуру устной и письменной математической речи;
- воспитывать дружеское отношение в классе и умение работать в группах.
Тип урока: комбинированный.
Оборудование:
- Математика: учебник для 5 кл. общеобразоват. учреждений/ Н.Я. Виленкин, В.И. Жохов и др., М.: «Мнемозина», 2010.
- Карточки для групп учащихся с фигурами для вычисления площади сложной фигуры.
- Чертёжные инструменты.
План урока:
- Организационный момент.
- Актуализация знаний.
а) Теоретические вопросы (тест).
б) Постановка проблемы. - Изученного нового материала.
а) поиск решения проблемы;
б) решение поставленной проблемы. - Закрепление материала.
а) коллективное решение задач;
Физкультминутка.
б) самостоятельная работа. - Домашнее задание.
- Итог урока. Рефлексия.
Ход урока
I. Организационный момент.
Урок мы начнём вот с таких напутствующих слов:
Математика, друзья,
Абсолютно всем нужна.
На уроке работай старательно,
И успех тебя ждёт обязательно!
II. Актуализация знаний.
а) Фронтальная работа с сигнальными карточками (у каждого ученика карточки с числами 1, 2, 3, 4; при ответе на вопрос теста ученик поднимает карточку с номером правильного ответа).
1. Квадратный сантиметр – это:
- площадь квадрата со стороной 1 см;
- квадрат со стороной 1 см;
- квадрат с периметром 1 см.
2. Площадь фигуры, изображённой на рисунке, равна:
- 8 дм;
- 8 дм2;
- 15 дм2.
3. Справедливо ли утверждение, что равные фигуры имеют равные периметры и равные площади?
- да;
- нет.
4. Площадь прямоугольника определяется по формуле:
- S = a2;
- S = 2 • (a + b);
- S = a • b.
5. Площадь фигуры изображённой на рисунке, равна:
- 12 см;
- 8 см;
- 16 см.
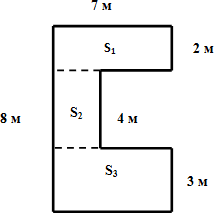
б) (Постановка проблемы). Задача. Сколько надо краски, чтобы покрасить пол, который имеет следующую форму (см. рис.), если на 1 м2 расходуется 200 г краски?
III. Изучение нового материала.
Что же мы должны узнать, чтобы решить последнюю задачу? (Найти площадь пола, который имеет вид «сложной фигуры».)
Учащиеся формулируют тему и цели урока (если необходимо учитель помогает).
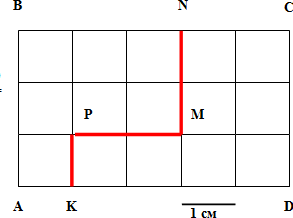
Рассмотрим прямоугольник ABCD. Проведём в нем линию KPMN, разбив прямоугольник ABCD на две части: ABNMPK и KPMNCD.
Чему равна площадь ABCD? (15 см2)
Чему равна площадь фигуры ABMNPK? (7 см2)
Чему равна площадь фигуры KPMNCD? (8 см2)
Проанализируйте полученные результаты. (15= = 7 + 
Вывод? (Площадь всей фигуры равна сумме площадей её частей.)
S = S1 + S2
Как можно применить это свойство для решения нашей задачи?(Разобьём сложную фигуру на части, найдём площади частей, затем площадь всей фигуры.)
S1 = 7 • 2 = 14 (м2)
S2 = (7 – 4) • (8 – 2 – 3) = 3 • 3 = 9 (м2)
S3 = 7 • 3 = 21 (м2)
S = S1 + S2 + S3 = 14 + 9 + 21 = 44 (м2)
Давайте составим план решения задач на нахождение площади «сложной фигуры»:
- Разбиваем фигуру на простые фигуры.
- Находим площади простых фигур.
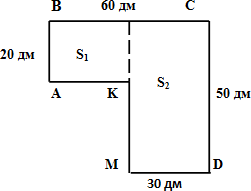
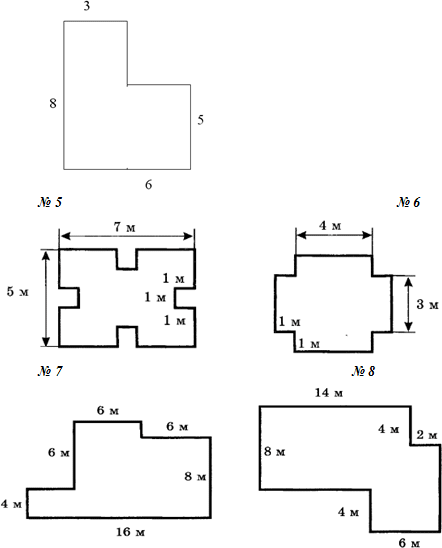
а) Задача 1. (коллективное решение на доске и в тетрадях.) Сколько потребуется плитки, чтобы выложить площадку следующих размеров:
Решение:
S = S1 + S2
S1 = (60 – 30) • 20 = 600 (дм2)
S2 = 30 • 50 = 1500 (дм2)
S = 600 + 1500 = 2100 (дм2)
Есть ли другой способ решения? (Рассматриваем предложенные варианты.)
Ответ: 2100 дм2.
Задача 2. (коллективное решение на доске и в тетрадях.) Сколько требуется м2 линолеума для ремонта комнаты, имеющей следующую форму:
Решение:
S = S1 + S2
S1 = 3 • 2 = 6 (м2)
S2 = ((5 – 3) • 2) : 2 = 2 (м2)
S = 6 + 2 = 8 (м2)
Ответ: 8 м2.
Физкультминутка.
А теперь, ребята, встали.
Быстро руки вверх подняли.
В стороны, вперед, назад.
Повернулись вправо, влево.
Тихо сели, вновь за дело.
б) Самостоятельная работа (обучающего характера).
Учащиеся разбиваются на группы (№ 5–8 более сильные). Каждая группа – ремонтная бригада.
Задание бригадам: определите, сколько надо краски, чтобы покрасить пол, имеющий форму фигуры, изображённой на карточке, если на 1 м2 требуется 200 г краски.
Вы эту фигуру строите своей тетради и записывая все данные, приступаете к выполнению задания. Можете обсуждать решение (но только в своей группе!). Если какая-то группа справляется с заданием быстро, то ей – дополнительное задание (после проверки самостоятельной работы).
Задания для групп:
V. Домашнее задание.
п. 18, № 718, № 749.
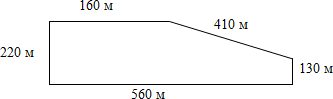
Дополнительное задание. План-схема Летнего сада (Санкт-Петербург). Вычислить его площадь.
VI. Итоги урока.
Рефлексия. Продолжи фразу:
- Сегодня я узнал…
- Было интересно…
- Было трудно…
- Теперь я могу…
- Урок дал мне для жизни…
Давайте вспомним, как найти площадь прямоугольника. Чтобы найти
площадь прямоугольника, надо длину умножить на ширину.
Вот формула для нахождения площади прямоугольника:
S = a · b
В этой формуле латинской буквой S обозначается площадь, буквами a и b – стороны прямоугольника.
Выполним задание, в котором надо найти площадь
прямоугольника со сторонами 5 см и 3 см.
Решение. Итак, чтобы найти площадь
прямоугольника, надо его длину умножить на ширину.
Произведение чисел 5 и 3 равно 15. Значит, площадь прямоугольника
равна 15 квадратным сантиметрам. Не забудьте, что площадь измеряется именно в
квадратных единицах. В данной задаче это квадратные сантиметры. Также важно
помнить, что длина и ширина должны быть выражены в одинаковых единицах длины.
3 · 5 =
15 (см2)
Ответ: площадь прямоугольника равна 15 см2.
Теперь давайте найдём площадь квадрата со стороной 4 см.
Решение. У этого квадрата каждая
сторона равна 4 см, поэтому умножим 4 на 4 и получится, что площадь квадрата
равна 16 квадратным сантиметрам.
4 · 4 =
16 (см2)
Ответ: площадь квадрата равна 16 см2.
Ну а сейчас перейдём к решению задач, в которых нам надо будет
найти площадь сложных фигур.
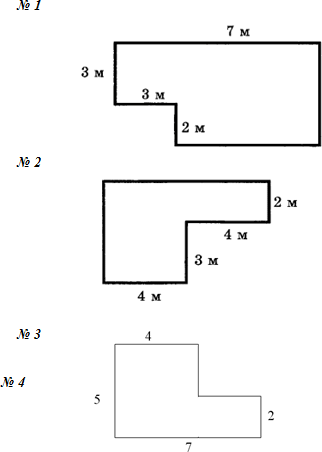
Найдите площадь фигуры, изображённой на рисунке.
Эта фигура не является ни прямоугольником, ни квадратом. Но мы
можем разделить эту фигуру на два прямоугольника, например, вот таким образом.
А площади прямоугольников мы легко можем найти с помощью
известной формулы.
Напомним, что противоположные стороны прямоугольника равны.
Итак, стороны первого прямоугольника равны 5 см и 4 см.
5 · 4 =
20 (см2) – площадь первого прямоугольника
Найдём площадь второго прямоугольника.
Ширина этого прямоугольника равна 2 см.
7 – 4 = 3 (см) – длина второго прямоугольника
3 · 2 = 6
(см2) – площадь второго прямоугольника
Мы нашли площади прямоугольников, из которых состоит сложная
фигура. Чтобы найти площадь этой фигуры, надо сложить найденные площади.
20 + 6 = 26
(см2) – площадь сложной фигуры
Ответ: площадь фигуры, изображённой на рисунке, равна 26 см2.
Площадь этой сложной фигуры найти другим способом. Можно разделить
её на два прямоугольника вот таким образом.
Найдём площадь первого прямоугольника.
Одна его сторона равна 4 см.
5 – 2 = 3 (см) – длина стороны первого прямоугольника
4 · 3 =
12 (см2) – площадь первого прямоугольника
Теперь найдём площадь второго прямоугольника.
7 · 2 =
14 (см2) – площадь второго прямоугольника
12 + 14 =
26 (см2) – площадь сложной фигуры
Ответ: площадь фигуры, изображённой на рисунке, равна 26 см2.
Решим следующую задачу.
Найдём площадь ещё одной фигуры, изображённой на рисунке.
Чтобы найти площадь этой фигуры, тоже разделим её на простые
фигуры. Сделаем это вот таким образом.
Получилось 3 прямоугольника.
Найдём площадь первого прямоугольника.
7 · 2 =
14 (см2) – площадь первого прямоугольника
Найдём площадь второго прямоугольника.
7 – 4 = 3 (см) – длина одной стороны второго прямоугольника
8 – 2 – 3 = 3 (см) – длина другой стороны второго прямоугольника
Получается, что это квадрат, так как длина всех его сторон равна 3
см.
3 · 3 = 9
(см2) – площадь квадрата
И найдём площадь последнего прямоугольника.
Его ширина равна 3 см. Длина равна 7 см.
3 · 7 =
21 (см2) – площадь третьего прямоугольника
Таким образом, мы нашли площади всех трёх фигур, на которые
разделили данную сложную фигуру. Площадь этой сложной фигуры найдём как сумму
площадей трёх фигур.
14 + 9 + 21 =
44 (см2) – площадь сложной фигуры
Ответ: площадь фигуры, изображённой на рисунке, равна 44 см2
Отметим, что площадь этой фигуры можно было бы найти, разделив её
на простые фигуры и вот таким образом:
И решим ещё одну задачу.
Найдите площадь незаштрихованной фигуры.
На рисунке изображён прямоугольник со сторонами 9 см и 5 см.
Внутри этого прямоугольника расположен ещё один прямоугольник со сторонами 5 см
и 3 см. Давайте найдём площадь каждого из них.
9 · 5 =
45 (см2) – площадь большего прямоугольника
5 · 3 =
15 (см2) – площадь меньшего прямоугольника
А как найти площадь незаштрихованной фигуры? Площадь этой фигуры
найдём, если из площади большего прямоугольника вычтем площадь меньшего
прямоугольника.
45 – 15 =
30 (см2) – площадь незаштрихованной фигуры
Ответ: площадь незаштрихованной фигуры равна 30 см2.
Определение площади сложной фигуры с помощью теории вероятностей
Время на прочтение
3 мин
Количество просмотров 22K
Зачем определять площадь сложной фигуры?
Да мало ли зачем. Например, возникла необходимость определить площадь территории на карте. Конечно, можно посмотреть в справочнике или поискать в интернете, но иногда и территории бывают нестандартными — допустим, вы озаботились проблемами лесов в пойме Амазонки и хотите ежемесячно измерять площадь зелёных пятен на фотографиях со спутника. Если вы ботаник (в хорошем смысле слова), то вам может понадобиться измерить площадь листовой поверхности разных сортов одного растения. Или, к примеру, более прозаичная задача — нужно зашпатлевать кусок стены, а банки шпатлёвки хватает только на 1 кв. м. — нужно выяснить, покупать одну банку или раскошелиться на две.
В чём сложность нахождения площади?
Конечно, если фигура представляет собой прямоугольник, круг или, что хуже, эллипс, то проблема решается с помощью Google и калькулятора. Но где бы найти формулу, да попроще, для нахождения площади, скажем, такого рисунка?
Теория вероятностей, Ваш выход!
Сразу оговорюсь, что теория вероятностей по своей сути не подразумевает точного решения задач. Так будет и в этом случае — если вам нужна космическая точность, то предлагаю копать в сторону методов имитационного моделирования. Если же погрешность в пределах 2-5% вас вполне устраивает, то будет достаточно того же калькулятора, базовых навыков программирования и умения считать до ста.
Суть метода
Суть метода проста до банальности. Допустим, мы пасмурным деньком выложили капустный листочек (см. ремарку про биолога выше) на прямоугольный поддон, а поддон выставили под накрапывающий дождик. А потом засекли определённое время (к примеру, пять минут) и посчитали, сколько капелек упало на поддон, а сколько непосредственно на лист. Если принять во внимание, что дождь обычно капает равномерно, то получается простая пропорция — лист во столько раз меньше поддона, во сколько раз на него упало меньше капель дождя, чем на весь поддон.
Возвращаемся к нашей фигуре
Итак, как же определить площадь той розовой пятерни? Да очень просто — заключить фигуру в прямоугольные границы и проставить случайным образом много точек. Чем больше, тем лучше (в соответствии с законом больших чисел). А потом подсчитать количество точек, попавших на фигуру.
Я намеренно не обсуждаю вопросы реализации такого алгоритма, потому что вариантов масса. Можно просто закрыть глаза и наугад тыкать шариковой ручкой, а можно действовать более научно — с помощью языков программирования. Например, код на PHP занял у меня не больше 15 строчек, а в результате получилось вот что:
Точки общим числом 300, разумеется, проставлены с помощью генератора случайных чисел. Для удобства подсчета точек я разбил изображение на 36 секторов — теперь нужно подсчитать количество точек, попавших на изображение, в каждом секторе, а результаты сложить. Сведём данные в таблицу (ячейка таблицы соответствует сектору на картинке):
| 0 | 4 | 8 | 4 | 0 | 0 |
| 0 | 7 | 5 | 6 | 0 | 4 |
| 3 | 6 | 13 | 7 | 8 | 5 |
| 1 | 10 | 10 | 13 | 7 | 2 |
| 0 | 2 | 3 | 7 | 10 | 2 |
| 0 | 0 | 2 | 5 | 3 | 0 |
Теперь у нас есть все данные для того, чтобы вычислить площадь розовой пятерни:
площадь описанного прямоугольника — 20 см х 20 см = 400 кв. см;
количество точек в прямоугольнике — 300;
количество точек внутри фигуры (сумма значений из таблицы) — 157;
площадь фигуры — 209,33 кв. см.
И насколько это точно?
Действительно, осталось определиться с точностью данного метода. Конечно, всё зависит от количества точек, и здесь нужно соблюдать золотую середину — десяти для нашего примера было бы явно недостаточно, а от тысячи слишком рябило бы в глазах. Поэтому попробуем определить погрешность для трёхсот точек и описанного квадрата со стороной 20 см. Для этого возьмём фигуру, площадь которой нам известна заранее. Например, такую:
Проставляем точки:
Результаты заносим в таблицу:
| 0 | 6 | 11 | 8 | 5 | 0 |
| 9 | 15 | 8 | 5 | 13 | 2 |
| 11 | 8 | 5 | 14 | 13 | 5 |
| 10 | 11 | 8 | 8 | 4 | 4 |
| 2 | 14 | 9 | 10 | 4 | 1 |
| 0 | 3 | 5 | 6 | 0 | 0 |
Рассчитываем площадь фигуры:
площадь описанного прямоугольника — 20 см х 20 см = 400 кв. см;
количество точек в прямоугольнике — 300;
количество точек внутри фигуры (сумма значений из таблицы) — 237;
площадь фигуры — 316 кв. см.
Нетрудно посчитать, что реальная площадь круга с радиусом 10 см составляет 314,16 кв. см. Таким образом, погрешность метода составила 0,59%, чего в большинстве случаев достаточно для прикладного использования.
Описание презентации по отдельным слайдам:
-
1 слайд
Математика, друзья,
Абсолютно всем нужна.
На уроке работай старательно,
И успех тебя ждёт обязательно! -
2 слайд
Какие геометрические фигуры изображены?
-
-
4 слайд
ПРЯМОУГОЛЬНИК
b
a
S=a·b -
5 слайд
ПРЯМОУГОЛЬНИК
Найдите площадь прямоугольника
7см
5см
S=5·7=35см2 -
6 слайд
ПРЯМОУГОЛЬНИК
Найдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1 см X 1 см. Ответ дайте в квадратных сантиметрах.
S=4·5=20 см24
5 -
-
8 слайд
КВАДРАТ
Найдите площадь квадрата
7см
S=7·7=72=49см2 -
9 слайд
КВАДРАТ
Найдите площадь квадрата, изображенного на клетчатой бумаге с размером клетки 1 см X 1 см. Ответ дайте в квадратных сантиметрах.
S=4·4=16 см24
-
10 слайд
ТРЕУГОЛЬНИК
b
a
S=(a·b):2 -
11 слайд
ТРЕУГОЛЬНИК
7см
6см
S=(6·7):2=21см2 -
12 слайд
ТРЕУГОЛЬНИК
S=(4·6):2=12см2
6
4
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см X 1 см. Ответ дайте в квадратных сантиметрах. -
13 слайд
S=a·b
S=(a·b):2
S=a·a=a2ПРЯМОУГОЛЬНИК
КВАДРАТ
ТРЕУГОЛЬНИК
a
b
a
a
b -
14 слайд
Сколько потребуется м2 линолеума для ремонта комнаты, имеющей следующую форму:
3м
5м
4м -
15 слайд
Тема урока: Площадь сложной фигуры
-
16 слайд
Сколько потребуется м2 линолеума для ремонта комнаты, имеющей следующую форму:
3м
5м
4м
I способ
II способ -
17 слайд
Сколько потребуется м2 линолеума для ремонта комнаты, имеющей следующую форму:
3м
5м
4м
2м
4м
S1=4·3=12 м2S2=(4·2):2=4 м2
начало -
18 слайд
Сколько потребуется м2 линолеума для ремонта комнаты, имеющей следующую форму:
3м
S=S1+S2=12+4=16 м2
4м
S1=12м2S2=4м2
начало
-
19 слайд
План решения задач на нахождение площади «сложной фигуры»:
I способ
1) Разбить фигуру на простые фигуры.
2) Найти площади простых фигур.
3) Найти сумму площадей простых фигурначало
-
20 слайд
Сколько потребуется м2 линолеума для ремонта комнаты, имеющей следующую форму:
3м
5м
4м
S1=4·5=20 М22м
4м
S2=(4·2):2=4 М2начало
-
21 слайд
Сколько потребуется м2 линолеума для ремонта комнаты, имеющей следующую форму:
S1=20М2
S2=4М2
начало
-
22 слайд
Сколько потребуется м2 линолеума для ремонта комнаты, имеющей следующую форму:
S=S1-S2=20-4=16 М2
S1=20М2S2=4М2
S=16 М2
начало -
23 слайд
План решения задач на нахождение площади «сложной фигуры»:
II способ
1)Достроить фигуру до прямоугольника.
2)Найти площади прямоугольника и площадь дополняющих простых фигур.
3)Найти разность площади прямоугольника и суммы площадей простых фигурначало
-
24 слайд
Площадь «сложной фигуры»
I способ
1) Разбить фигуру на простые фигуры.
2) Найти площади простых фигур.
3) Найти сумму площадей простых фигурII способ
1) Достроить фигуру до прямоугольника.
2)Найти площадь прямоугольника и площадь дополняющих простых фигур.
3)Найти разность площади прямоугольника и суммы площадей простых фигур -
25 слайд
Найдите площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
4 см
4 см
4 см
5 см
1. S1=
2. S2=
3. S=
Ответ: 26 см2
4·4=
(4·5):2=
16+10=26см2
S1+S2=
S1
S2
16 см2
10 см2 -
26 слайд
Найдите площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
-
27 слайд
Найдите площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
10+4=14см2
2 см
5 см
2 см
4 см
1. S1=
2. S2=
3. S=
Ответ: 14 см2
5·2=
(4·2):2=
S1+S2=
S1
S2
10 см2
4 см2
4 см
3 см
3 см
2 см
1. S1=
2. S2=
3. S=
Ответ: 9 см2
(3·4):2=
(3·2):2=
S1+S2=
S1
S2
6 см2
3 см2
6+3=9см2 -
28 слайд
Найдите площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
2 см
5 см
2 см
4 см
1. S1=
2. S2=
3. S=
Ответ: 14 см2
5·2=
(4·2):2=
10+4=14см2
S1+S2=
S1
S2
10 см2
4 см2 -
29 слайд
Найдите площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
6+3=9см2
4 см
3 см
3 см
2 см
1. S1=
2. S2=
3. S=
Ответ: 9 см2
(3·4):2=
(3·2):2=
S1+S2=
S1
S2
6 см2
3 см2 -
30 слайд
Продолжи фразу:
Сегодня я узнал________________________________________Было трудно__________________________________________
Теперь я могу__________________________________________