Как найти площадь шара вписанного в пирамиду - AvtoShod.ru

Чтобы легко справиться с решением задач на шар, вписанный в пирамиду, полезно разобрать небольшой теоретический материал.

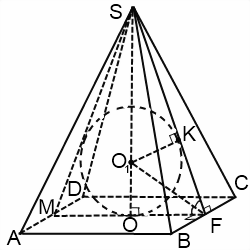
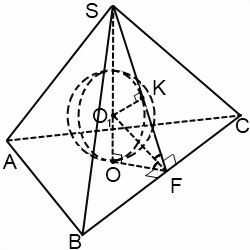
Шар вписан в пирамиду (или сфера вписана в пирамиду) — значит, шар (сфера) касаются каждой грани пирамиды. Плоскости, содержащие грани пирамиды, являются касательными плоскостями шара. Отрезки, соединяющие центр шара с точками касания, перпендикуляры к касательным плоскостям. Их длины равны радиусу шара. Центр вписанного в пирамиду шара — точка пересечения бисекторных плоскостей двугранных углов при основании (то есть плоскостей, делящих эти углы пополам).

Чаще всего в задачах речь идет о шаре, вписанном в правильную пирамиду. Шар можно вписать в любую правильную пирамиду. Центр шара в этом случае лежит на высоте пирамиды. При решении задачи удобно провести сечение пирамиды и шара плоскостью, проходящей через апофему и высоту пирамиды.

Если пирамида четырехугольная или шестиугольная, сечение представляет собой равнобедренный треугольник, боковые стороны которого — апофемы, а основание — диаметр вписанной в основание окружности.

Если пирамида треугольная или пятиугольная, достаточно рассмотреть лишь часть этого сечения — прямоугольный треугольник, катеты которого — высота пирамиды и радиус вписанной в основание пирамиды окружности, а гипотенуза — апофема.

В любом случае, в итоге приходим к рассмотрению соответствующего прямоугольного треугольника и других связанных с ним треугольников.

Итак, в прямоугольном треугольнике SOF катет SO=H — высота пирамиды, катет OF=r — радиус вписанной в основание пирамиды окружности, гипотенуза SF=l — апофема пирамиды. O1- центр шара и, соответственно, окружности, вписанной в треугольник, полученный в сечении (мы рассматриваем его часть). Угол SFO — линейный угол двугранного угла между плоскостью основания и плоскостью боковой грани SBC. Точки K и O — точки касания, следовательно, O1K перпендикулярен SF. OO1=O1K=R — радиусу шара.

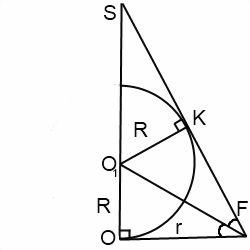
Прямоугольные треугольники OO1F и KO1F равны (по катетам и гипотенузе). Отсюда KF=OF=r.

Прямоугольные треугольники SKO1 и SOF подобны (по острому углу S), откуда следует, что

$[frac{{OF}}{{K{O_1}}} = frac{{SO}}{{SK}}, Rightarrow frac{r}{R} = frac{H}{{l - r}}.]$

В треугольнике SOF применим свойство биссектрисы треугольника:

$[frac{{SF}}{{S{O_1}}} = frac{{OF}}{{O{O_1}}}, Rightarrow frac{l}{{H - R}} = frac{r}{R}.]$

Из прямоугольного треугольника OO1F

$[tgangle OF{O_1} = frac{{O{O_1}}}{{OF}} = frac{R}{r}.]$

При решении задач на шар, вписанный в правильную пирамиду, будет полезным еще одно рассуждение.

$[frac{l}{{H - R}} = frac{r}{R}, Rightarrow Rl = (H - R)r, Rightarrow ]$

$[R = frac{{rH}}{{l + r}}.]$

Теперь найдем отношение объема пирамиды к площади ее поверхности:

$[frac{V}{{{S_{n.n/}}}} = frac{{frac{1}{3}{S_{ocn}} cdot H}}{{{S_{ocn}} + {S_{bok}}}} = frac{1}{3} cdot frac{{prH}}{{pr + pl}} = ]$

$[ = frac{1}{3} cdot frac{{rH}}{{r + l}} = frac{1}{3}R.]$

Таким образом, радиус вписанного шара выражается через объем пирамиды и ее полную поверхность:

$[R = frac{{3V}}{{{S_{n.n.}}}}.]$

Все эти рассуждения верны не только для правильной пирамиды, но и для пирамиды, основание высоты которой совпадает с центром вписанной в основание окружности (то есть для пирамиды, у которой все двугранные углы при основании равны).

Источник

В данной публикации представлены формулы, с помощью которых можно найти радиус шара (сферы), вписанного в правильную пирамиду: треугольную, четырехугольную, шестиугольную и тетраэдр.

Формулы расчета радиуса шара (сферы)
- Правильная треугольная пирамида
- Правильная четырехугольная пирамида
- Правильная шестиугольная пирамида

Формулы расчета радиуса шара (сферы)

Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.

Правильная треугольная пирамида

На рисунке:

a – ребро основания пирамиды, т.е. это равные отрезки AB, AC и BC;
DE – высота пирамиды (h).

Если известны значения этих величин, то найти радиус (r) вписанного шара/сферы можно по формуле:

Частный случай правильной треугольной пирамиды – это правильный тетраэдр. Для него формула нахождения радиуса выглядит следующим образом:

Правильная четырехугольная пирамида

На рисунке:

a – ребро основания пирамиды, т.е. AB, BC, CD и AD;
EF – высота пирамиды (h).

Радиус (r) вписанного шара/сферы рассчитывается так:

Правильная шестиугольная пирамида

На рисунке:

a – ребро основания пирамиды, т.е. AB, BC, CD, DE, EF, AF;
GL – высота пирамиды (h).

Радиус (r) вписанного шара/сферы вычисляется по формуле:

Источник

11.185_ Найти площадь поверхности шара, вписанного в пирамиду

	26.11.2013, 17:08
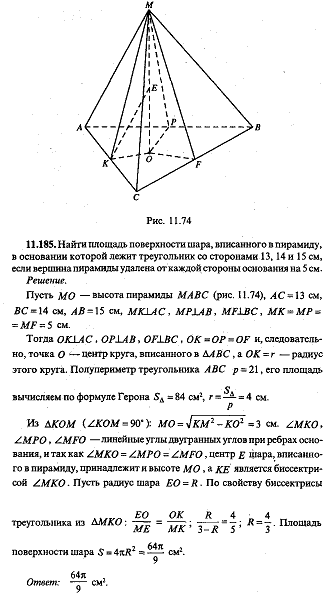
Найти площадь поверхности шара, вписанного в пирамиду, в основании которой лежит треугольник со сторонами, равными 13 см, 14 см, и 15 см , если вершина пирамиды удалена от каждой стороны основания на 5 см.
1 2 3 4 5 Категория: Задачи стереометрии \| Добавил: alexlat
Просмотров: 967 \| Загрузок: 0 \| Рейтинг: 0.0/0

Добавлять комментарии могут только зарегистрированные пользователи.

[

Регистрация

Вход

]

Источник

В правильной треугольной пирамиде отношение бокового ребра к высоте пирамиды равно 2. Найдите отношение радиуса вписанного в пирамиду шара к стороне основания пирамиды.

Спрятать решение

Решение.

Решение:

Задачу решим несколькими методами.

а)  Методом объемов.

Пусть   — высота заданной правильной пирамиды,

SM  — ее апофема,   — медианы основания,

Поскольку а это значит, что т. е.

Пусть Тогда

Замечание:

Поскольку центр вписанного шара равноудалена от всех граней заданной пирамиды, то это обстоятельство позволяет выразить радиус шара, вписанного в пирамиду, через объем пирамиды и площадь ее полной поверхности. Мы имеем возможность мысленно разбить заданную пирамиду на четыре пирамиды, основаниями которых будут служить грани заданной пирамиды, а высоты их будут равны радиусу искомого шара. Так как объем заданной пирамиды V будет равен сумме объемов пирамид, составляющих эту пирамиду, то понятно, что где r  — искомый радиус.

б)  Использование тангенса половинного угла.

Искомый центр вписанного шара будет лежать на SO (а это надо бы доказать!). Кроме того, центр вписанного шара есть точка пересечения биссектрис линейных углов двугранных углов, образуемых боковыми гранями и основанием заданной пирамиды. Таким образом, центр шара лежит на пересечении высоты пирамиды SO и биссектрисы угла SMC. Если это  — точка O_1, то OO_1 и есть искомый радиус.

Вычислив OM и SM, можно найти косинус угла SMО. Тогда по формуле тангенса половинного угла сможем вычислить и значение тангенса угла O_1.

в)  Метод площадей.

Пусть SO=1. Тогда SB=2,

В прямоугольном треугольнике SOD по теореме Пифагора имеем:

Будем иметь в виду, что центр вписанного шара (сферы) лежит на SO. Обозначим эту точку O_1. Опустим из нее перпендикуляр O_1P к грани ASC. Ясно, что где r  — радиус шара (сферы). Теперь соединим точку O_1 отрезком с точкой Треугольник SOD разбивается на два треугольника: и

г)  Координатный метод исследования.

Поместим пирамиду в декартову систему координат, как показано на рисунке. Пусть SO=1. Тогда AC=3.

Для дальнейшего исследования этих расстояний нам вполне достаточно.

Будем иметь в виду, что центр вписанного шара (сферы) лежит на SO. Обозначим эту точку O_1. Тогда радиус шара (сферы) равен z_0.

Зная, что точка O_1 удалена от грани ASCна то же расстояние, что и от основания ABC, для достижения цели найти искомый радиус, используем формулу расстояния от точки до плоскости.

Найдем координаты точек

В нашем случае очень легко составить уравнения плоскостей ASC и ABC. Ясно, что уравнение плоскости ABC заведомо имеет вид: z=0.

Составим уравнение плоскости ASC, имея в виду, что в этой же плоскости лежит также точка

В системе, приведенной ниже, первое уравнение учитывает принадлежность точки D, второе  — принадлежность точки S, а третье  — принадлежность точки

Таким образом, искомое уравнение имеет вид: или

Теперь нетрудно найти расстояние rho от точки до плоскости ASC.

Поскольку то

Очевидно, что 

Следовательно,

д)  Метод подобия.

Пусть  SO=1.

Тогда

В прямоугольном треугольнике SOD по теореме Пифагора имеем:

Будем иметь в виду, что центр вписанного шара (сферы) лежит на SO. Обозначим эту точку O_1. Опустим из нее перпендикуляр O_1 к грани ASC. Ясно, что где r  — радиус шара (сферы).

Теперь соединим точку O_1 отрезком с точкой

Прямоугольные треугольники SPO_1 и SOD подобны как имеющие общий острый угол. Значит, Будем иметь в виду, что В таком случае:

Ответ:

Спрятать критерии

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Обоснованно получен верный ответ.	2
Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено ИЛИ при правильном ответе решение недостаточно обосновано.	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0

Критерии оценивания выполнения задания

Баллы

Обоснованно получен верный ответ.

Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено

ИЛИ

при правильном ответе решение недостаточно обосновано.

Решение не соответствует ни одному из критериев, перечисленных выше.

Источник

Тип C10 № 30

Угол между высотой правильной треугольной пирамиды и боковой гранью равен 30°. Найдите площадь боковой поверхности пирамиды, если радиус вписанного в пирамиду шара равен 1 см.

Спрятать решение

Решение.

Шар с центром в точке O вписан в пирамиду PABC. PM  — апофема пирамиды, AM  — высота правильного треугольника ABC. Тогда MO  — биссектриса угла PMH.

Рассмотрим прямоугольный треугольник PHM. Пусть HM = a, тогда PM = 2a, так как угол HPM равен 30°. Тогда

HO = R = 1 см.

По теореме о биссектрисе треугольника значит, PO = 2 см, тогда PH = 3 см. Отсюда см, а см.