Как найти площадь шара описанного пирамидой - AvtoShod.ru

Тема: Найти площадь поверхности сферы, описанной вокруг пирамиды, подскажите (Прочитано 4283 раз)

0 Пользователей и 1 Гость просматривают эту тему.

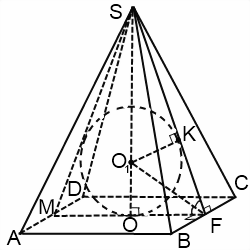
Боковое ребро правильной пирамиды равно b и наклонено к плоскости основания под углом α. Найти площадь поверхности сферы, описанной вокруг пирамиды.

С чего начинать? Центр сферы лежит на высоте пирамиды и равноудален от вершин. Заранее спасибо.

« Последнее редактирование: 21 Апреля 2010, 08:25:24 от Asix »

Рассмотрите осевое сечение пирамиды и, соответственно сферы. Выполучите равнобедренный треугольник, у которого все практически параметры известны с описанной вокруг него окружностью. Используйте теорему синусов и определите радиус описанной окружности. Ну а дальше арифметика. Удачи)

Пожалуйста не пишите голое условие! Сначало мы выслушаем Ваши мысли или хотябы вопросы, но конкретные и лишь потом дадим необходимые советы!
Но можете всего этого и не делать, если Вас не интересует результат
Если не хотите разбираться сами закажите решение на сайте.

Катет треугольника равен b×sinα R=b/2 Опять что-то не то!

Источник

В данной публикации представлены формулы, с помощью которых можно найти радиус сферы (шара), описанной около правильной пирамиды: треугольной, четырехугольной, шестиугольной и тетраэдра.

Формулы расчета радиуса сферы (шара)
- Правильная треугольная пирамида
- Правильная четырехугольная пирамида
- Правильная шестиугольная пирамида

Формулы расчета радиуса сферы (шара)

Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.

Правильная треугольная пирамида

На этом рисунке и чертежах далее:

a – ребро основания пирамиды;
h – высота фигуры.

Если эти величины даны, вычислить радиус (R) описанной вокруг пирамиды сферы/шара можно по формуле ниже:

Правильный тетраэдр является разновидностью правильной треугольной пирамиды. Формула для него:

Правильная четырехугольная пирамида

Радиус (R) описанной сферы/шара вычисляется следующим образом:

Правильная шестиугольная пирамида

Формула для нахождения радиус (R) сферы/шара выглядит так:

Источник

Опубликовано 11.06.2017 по предмету Геометрия от Гость
>> <<

Найдите площадь поверхности шара, описанного вокруг правильной треугольной пирамиды если ее высота равна h и образует угол гамма с ее боковым ребром

Ответ оставил Гость

Rшара =(R1²+h²)/2h,R1-радиус окружности описанной около основания,h-высота пирамиды
Рассмотрим прямоугольный треугольник с катетами h и R1,угол между
катетом (высотой)и гипотенузой (боковым ребром ) равен γ
R1=htgγ
R=(h²tg²γ+h²)/2h=h²(tg²γ+1)/2h=h/2*1/cos²γ=h/2cos²γ
S=4πR²
S=4π*h²/4cos^4γ=πh²/cos^4γ

Оцени ответ

Подпишись на наш канал в телеграм. Там мы даём ещё больше полезной информации для школьников!

Источник

Чтобы легко справиться с решением задач на шар, вписанный в пирамиду, полезно разобрать небольшой теоретический материал.

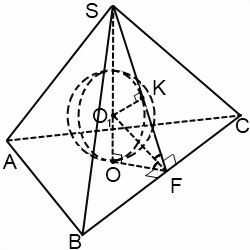
Шар вписан в пирамиду (или сфера вписана в пирамиду) — значит, шар (сфера) касаются каждой грани пирамиды. Плоскости, содержащие грани пирамиды, являются касательными плоскостями шара. Отрезки, соединяющие центр шара с точками касания, перпендикуляры к касательным плоскостям. Их длины равны радиусу шара. Центр вписанного в пирамиду шара — точка пересечения бисекторных плоскостей двугранных углов при основании (то есть плоскостей, делящих эти углы пополам).

Чаще всего в задачах речь идет о шаре, вписанном в правильную пирамиду. Шар можно вписать в любую правильную пирамиду. Центр шара в этом случае лежит на высоте пирамиды. При решении задачи удобно провести сечение пирамиды и шара плоскостью, проходящей через апофему и высоту пирамиды.

Если пирамида четырехугольная или шестиугольная, сечение представляет собой равнобедренный треугольник, боковые стороны которого — апофемы, а основание — диаметр вписанной в основание окружности.

Если пирамида треугольная или пятиугольная, достаточно рассмотреть лишь часть этого сечения — прямоугольный треугольник, катеты которого — высота пирамиды и радиус вписанной в основание пирамиды окружности, а гипотенуза — апофема.

В любом случае, в итоге приходим к рассмотрению соответствующего прямоугольного треугольника и других связанных с ним треугольников.

Итак, в прямоугольном треугольнике SOF катет SO=H — высота пирамиды, катет OF=r — радиус вписанной в основание пирамиды окружности, гипотенуза SF=l — апофема пирамиды. O1- центр шара и, соответственно, окружности, вписанной в треугольник, полученный в сечении (мы рассматриваем его часть). Угол SFO — линейный угол двугранного угла между плоскостью основания и плоскостью боковой грани SBC. Точки K и O — точки касания, следовательно, O1K перпендикулярен SF. OO1=O1K=R — радиусу шара.

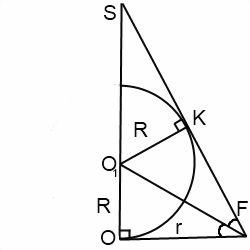
Прямоугольные треугольники OO1F и KO1F равны (по катетам и гипотенузе). Отсюда KF=OF=r.

Прямоугольные треугольники SKO1 и SOF подобны (по острому углу S), откуда следует, что

$[frac{{OF}}{{K{O_1}}} = frac{{SO}}{{SK}}, Rightarrow frac{r}{R} = frac{H}{{l - r}}.]$

В треугольнике SOF применим свойство биссектрисы треугольника:

$[frac{{SF}}{{S{O_1}}} = frac{{OF}}{{O{O_1}}}, Rightarrow frac{l}{{H - R}} = frac{r}{R}.]$

Из прямоугольного треугольника OO1F

$[tgangle OF{O_1} = frac{{O{O_1}}}{{OF}} = frac{R}{r}.]$

При решении задач на шар, вписанный в правильную пирамиду, будет полезным еще одно рассуждение.

$[frac{l}{{H - R}} = frac{r}{R}, Rightarrow Rl = (H - R)r, Rightarrow ]$

$[R = frac{{rH}}{{l + r}}.]$

Теперь найдем отношение объема пирамиды к площади ее поверхности:

$[frac{V}{{{S_{n.n/}}}} = frac{{frac{1}{3}{S_{ocn}} cdot H}}{{{S_{ocn}} + {S_{bok}}}} = frac{1}{3} cdot frac{{prH}}{{pr + pl}} = ]$

$[ = frac{1}{3} cdot frac{{rH}}{{r + l}} = frac{1}{3}R.]$

Таким образом, радиус вписанного шара выражается через объем пирамиды и ее полную поверхность:

$[R = frac{{3V}}{{{S_{n.n.}}}}.]$

Все эти рассуждения верны не только для правильной пирамиды, но и для пирамиды, основание высоты которой совпадает с центром вписанной в основание окружности (то есть для пирамиды, у которой все двугранные углы при основании равны).

Источник

Формулы расчета радиуса сферы (шара)

Правильная треугольная пирамида

Правильная четырехугольная пирамида

Правильная шестиугольная пирамида

Найдите площадь поверхности шара, описанного вокруг правильной треугольной пирамиды если ее высота равна h и образует угол гамма с ее боковым ребром

Не пропустите также: