Через какой параметр считать:
Радиус
Диаметр
Укажите размер:
r
Радиус
Округлить число Пи до 3,14
Площадь поверхности:
Решение:
Ссылка на страницу с результатом:
# Теория
Сфера — это геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки (центра сферы).
Диаметр сферы — это прямая линия соединяющая две точки поверхности сферы и проходящая через точку центра сферы.
Радиус сферы — это расстояние от точки центра сферы до её поверхности.
Формула площади сферы
Площадь сферы через радиус
r
S = 4 pi r^2
- S — площадь поверхности сферы
- π — число Пи ( ≈ 3.14 )
- r — радиус сферы
Площадь сферы через диаметр
d
S = pi d^2
- S — площадь поверхности сферы
- π — число Пи ( ≈ 3.14 )
- d — диаметр сферы
Похожие калькуляторы:
Войдите чтобы писать комментарии
В данной публикации мы рассмотрим, как можно найти площадь шара (сферы) и разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади шара/сферы
-
1. Через радиус
- 2. Через диаметр
-
1. Через радиус
- Примеры задач
Формула вычисления площади шара/сферы
1. Через радиус
Площадь (S) поверхности шара/сферы равняется произведению четырех его радиусов в квадрате и число π.
S = 4 π R2
Примечание: в расчетах значение числа π округляется до 3,14.
2. Через диаметр
Как известно, диаметр шара/сферы равен двум его радиусам: d = 2R. Следовательно, рассчитать площадь поверхности фигуры можно, используя такой вид формулы:
S = 4 π (d/2)2
Примеры задач
Задание 1
Вычислите площадь поверхности шара, если его радиус составляет 7 см.
Решение:
Воспользуемся первой формулой (через радиус):
S = 4 ⋅ 3,14 ⋅ (7 см)2 = 615,44 см2.
Задание 2
Площадь поверхности сферы равна 200,96 см2. Найдите ее диаметр.
Решение:
Выведем величину диаметра из соответствующей формулы расчета площади:
Калькулятор площади сферы
Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
Что известно
Длина
Размерность
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что такое калькулятор площади поверхности шара?
Калькулятор расчета площади шара (сферы) — это онлайн инструмент, который помогает определить площадь поверхности сферы на основе заданных параметров. Площадь поверхности сферы представляет собой сумму всех площадей ее точечных элементов.
Для использования калькулятора расчета площади шара (сферы) необходимо знать радиус сферы. Радиус — это расстояние от центра сферы до любой ее точки. Введите значение радиуса в соответствующее поле в калькуляторе и нажмите на кнопку «Рассчитать».
Какую формулу использует калькулятор?
Формула для расчета площади поверхности шара (сферы) выглядит следующим образом:
S = 4πr2
где S обозначает площадь поверхности, π (пи) — математическую константу, примерное значение которой равно 3,14159, а r — радиус сферы.
Калькулятор автоматически применяет эту формулу, используя введенное значение радиуса, и выводит площадь поверхности шара (сферы) в соответствующем поле.
Как определить радиус шара (сферы)
Радиус шара (сферы) можно определить несколькими способами, в зависимости от доступных данных:
- Измерение. Если у вас есть физический объект в форме шара, вы можете использовать линейку или мерную ленту для измерения расстояния от центра шара до его внешней поверхности. Полученное значение будет радиусом шара.
- Информация о диаметре. Если у вас есть информация о диаметре шара (расстояние между двумя точками на его внешней поверхности, проходящих через его центр), вы можете разделить значение диаметра на 2, чтобы получить радиус. Формула для этого: r = D/2, где r — радиус, D — диаметр.
- Заданная площадь поверхности. Если вам известна площадь поверхности шара, вы можете использовать обратную формулу, чтобы вычислить радиус. Формула для этого: r = √(S/4π), где r — радиус, S — площадь поверхности.
- Другие известные параметры. В некоторых случаях у вас может быть информация о других параметрах, таких как объем шара или площадь поперечного сечения. В таких случаях можно использовать соответствующие формулы, чтобы выразить радиус через эти данные.
В каких областях можно применить такой калькулятор?
Калькулятор расчета площади шара (сферы) может быть полезен в различных областях, где требуется работа со сферическими формами и расчеты их площади. Некоторые из таких областей включают:
- Геометрия. Калькулятор позволяет быстро и удобно рассчитать площадь поверхности сферы при известном радиусе. Это может быть полезно в учебных задачах, связанных с геометрией и сферическими формами.
- Физика. В физике сферические объекты могут встречаться в различных контекстах, таких как моделирование планет, атомов, молекул или капель жидкости. Расчет площади поверхности сферы может быть важным для определения поверхностных свойств или характеристик таких объектов.
- Инженерия. В инженерных расчетах может возникнуть необходимость в определении площади поверхности сферы, например, при проектировании шаровых резервуаров, сферических антенн или шаровых линз.
- Астрономия. В астрономии сферические формы широко присутствуют, начиная от планет и спутников до звезд и галактик. Расчет площади поверхности сферы может быть полезен при изучении этих объектов и астрономических явлений.
- 3D-моделирование и компьютерная графика. Когда создаются трехмерные модели объектов в компьютерной графике или игровой индустрии, площадь поверхности сферы может быть необходима для определения освещения, текстурирования или коллизий объекта.
Это лишь несколько примеров областей, в которых калькулятор расчета площади шара (сферы) может быть полезен. Его применение может быть более широким, в зависимости от конкретных потребностей и задачи.
Пример
Расчет площади поверхности Земли может быть интересным примером для применения калькулятора расчета площади шара. Земля приближенно является геоидом, то есть ее форма приближенно сферическая с некоторыми нерегулярностями.
Для расчета площади поверхности Земли можно использовать радиус, который обычно указывают в километрах. Приближенное значение радиуса Земли составляет около 6 371 километр.
Применяя формулу для расчета площади поверхности шара, получим:
- S = 4πr2
- S = 4 * 3.14159 * (6,371)2
- S ≈ 4 * 3.14159 * 40,518,241
- S ≈ 509,904,080 квадратных километров
Таким образом, приближенная площадь поверхности Земли составляет около 509,904,080 квадратных километров.
Отметим, что это приближенное значение, так как форма Земли не является точной сферой. В реальности форма Земли более сложная и неоднородная, и точное измерение ее поверхности требует более сложных геодезических методов.
❓ Вопросы и ответы
Вот некоторые вопросы, которые могут возникнуть при использовании калькулятора площади шара (сферы) и ответы на них.
Что такое площадь поверхности шара?
Площадь поверхности шара представляет собой сумму площадей всех его точечных элементов.
Какова формула для расчета площади поверхности шара?
Формула для расчета площади поверхности шара выглядит так: S = 4πr^2, где S — площадь поверхности, π — математическая константа (приблизительное значение 3.14159), r — радиус шара.
Как использовать калькулятор площади шара?
Введите значение радиуса шара в соответствующее поле на калькуляторе и нажмите кнопку «Рассчитать». Калькулятор автоматически применит формулу и выдаст результат — площадь поверхности шара.
Могу ли я использовать дробные значения радиуса?
Да, вы можете использовать дробные значения радиуса при расчете площади поверхности шара. Просто введите соответствующее десятичное число в поле радиуса.
В каких единицах измерения будет выведен результат площади?
Результат площади будет выведен в квадратных единицах измерения, соответствующих используемой системе измерения радиуса (например, квадратных метрах, квадратных сантиметрах и т.д.).
Можно ли использовать калькулятор для других форм, а не только для шара?
Нет, калькулятор расчета площади шара предназначен исключительно для расчета площади поверхности шара. Для расчета площади других форм (например, цилиндра, конуса и т.д.) вы можете использовать другие наши калькуляторы.
Можно ли использовать калькулятор для расчета объема шара?
Нет, калькулятор площади шара предназначен только для расчета площади его поверхности. Для расчета объема шара используется другая формула: V = (4/3)πr^3.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Как найти площадь сферы
Сферой называют поверхность шара. По-другому ее можно определить как трехмерную геометрическую фигуру, все точки которой находятся на одинаковом расстоянии от точки, называемой центром сферы. Чтобы выяснить размеры этой фигуры достаточно знать лишь один параметр — например, радиус, диаметр, площадь или объем. Их значения связаны между собой постоянными соотношениями, которые позволяют вывести простую формулу вычисления каждого из них.

Инструкция
Если известна длина диаметра сферы (d), то для нахождения площади ее поверхности (S) возводите этот параметр в квадрат и умножайте на число Пи (π): S=π∗d². Например, если длина диаметра составляет два метра, то площадь сферы составит 3,14∗2²=12,56 квадратных метров.
Если известна длина радиуса (r), то площадь поверхности сферы (S) будет составлять учетверенное произведение возведенного в квадрат радиуса на число Пи (π): S=4∗π∗r². Например, при длине радиуса сферы в три метра его площадь составит 4∗3,14∗3²=113,04 квадратных метров.
Если известен объем (V) пространства, ограниченного сферой, то сначала можно найти ее диаметр (d), а затем воспользоваться формулой, приведенной в первом шаге. Так как объем равен одной шестой части от произведения числа Пи на возведенную в куб длину диаметра сферы (V=π∗d³/6), то диаметр можно определить, как кубический корень из шести объемов, разделенных на число Пи: d=³√(6∗V/π). Подставив это значение в формулу из первого шага, получим: S=π∗(³√ (6∗V/π))². Например, при объеме ограниченного сферой пространства равном 500 кубометров вычисление ее площади будет выглядеть так: 3,14∗(³√(6∗500/3,14))² = 3,14∗(³√955,41)² = 3,14∗9,85² = 3,14∗97,02 = 304,64 квадратных метра.
Производить все эти расчеты в уме довольно затруднительно, поэтому придется воспользоваться каким либо из калькуляторов. Например, это может быть вычислитель, встроенный в поисковые системы Google или Nigma. Google отличается в лучшую сторону тем, что умеет самостоятельно определять порядок операций, а Nigma потребует от вас тщательно расставить все скобки. Для вычисления площади сферы по данным, например, из второго шага поисковый запрос, который надо ввести в Google, будет выглядеть так: «4*пи*3^2». А для наиболее сложного случая с вычислением кубического корня и возведением в квадрат из третьего шага запрос будет таким: «пи*(6*500/пи)^(2/3)».
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Площадь поверхности шара
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь поверхности шара
Чтобы посчитать площадь поверхности шара (площадь сферы) воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чему равна площадь поверхности шара, если:
=
S =
0
Округление числа π: Округление ответа:
Просто введите известный вам параметр, и узнаете площадь сферы шара.
Теория
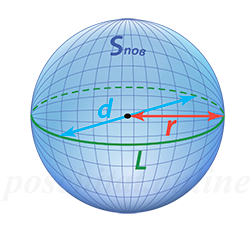
Ликбез: Поверхность шара — сфера.
Площадь поверхности шара через радиус
Чему равна площадь поверхности шара Sпов, если его радиус r:
Формула
Sпов = 4⋅π⋅r² , где π ≈ 3.14…
Пример
Для примера посчитаем какая площадь поверхности у шара, если его радиус r = 3 см:
Sпов = 4 ⋅ 3.14 ⋅ 3² = 12.56 ⋅ 9 = 113.04 см²
Площадь поверхности шара через диаметр
Чему равна площадь поверхности шара Sпов, если его диаметр d?
Формула
Sпов = π⋅d² , где π ≈ 3.14…
Пример
Для примера посчитаем какая площадь поверхности у шара, если его диаметр d = 6 см:
Sпов = 3.14 ⋅ 6² = 3.14 ⋅ 36 = 113.04 см²
Площадь поверхности шара через длину окружности
Чему равна площадь поверхности шара Sпов, если длина его окружности L?
Формула
Sпов = L²⁄π , где π ≈ 3.14…
Пример
Для примера посчитаем чему равна площадь поверхности шара, имеющего длину окружности L = 10 см:
Sпов = 10² ⁄ 3.14 ≈ 31.85 см²