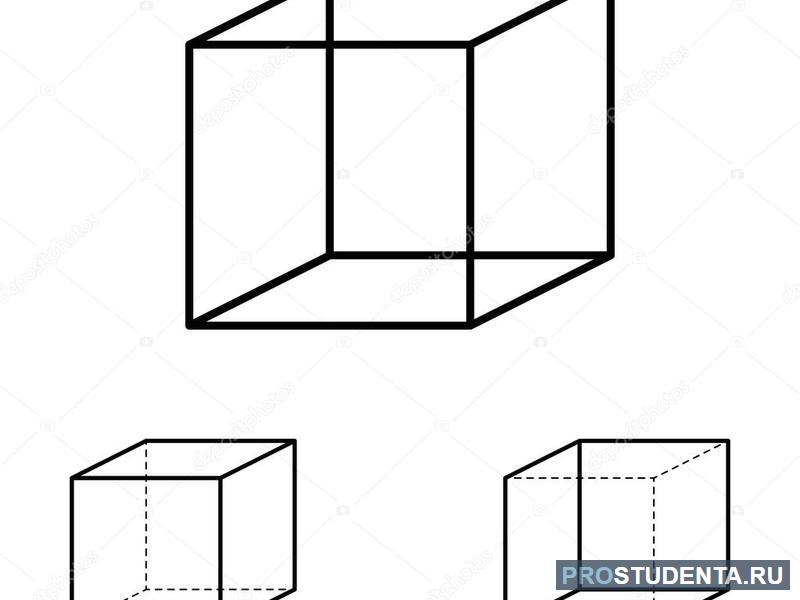
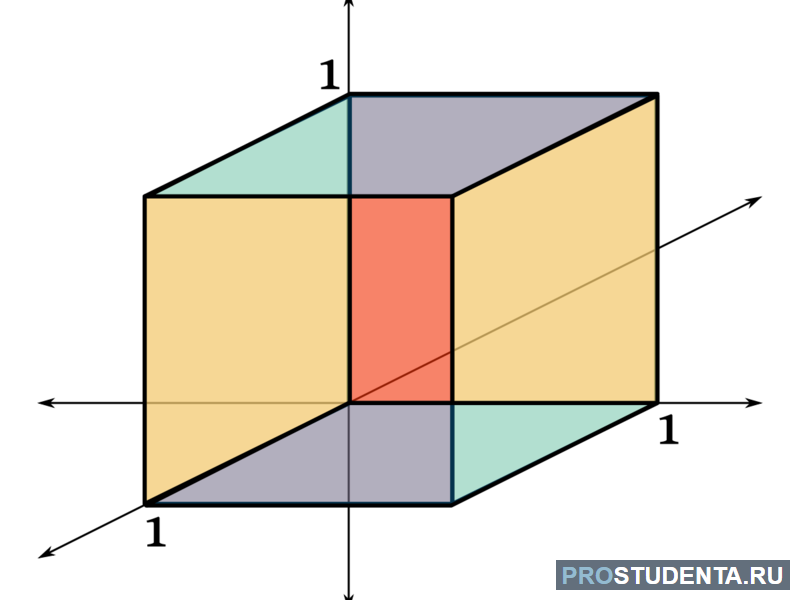
На практике часто возникают задачи, которые требуют умения строить сечения геометрических фигур различной формы и находить площади сечений. В данной статье рассмотрим, как строятся важные сечения призмы, пирамиды, конуса и цилиндра, и как рассчитывать их площади.
Объемные фигуры
Из стереометрии известно, что объемная фигура совершенно любого типа ограничена рядом поверхностей. Например, для таких многогранников, как призма и пирамида, этими поверхностями являются многоугольные стороны. Для цилиндра и конуса речь идет уже о поверхностях вращения цилиндрической и конической фигур.

Если взять плоскость и пересечь ею произвольным образом поверхность объемной фигуры, то мы получим сечение. Площадь его равна площади части плоскости, которая будет находиться внутри объема фигуры. Минимальное значение этой площади равно нулю, что реализуется, когда плоскость касается фигуры. Например, сечение, которое образовано единственной точкой, получается, если плоскость проходит через вершину пирамиды или конуса. Максимальное значение площади сечения зависит от взаимного расположения фигуры и плоскости, а также от формы и размеров фигуры.
Ниже рассмотрим, как рассчитывать площади образованных сечений для двух фигур вращения (цилиндр и конус) и двух полиэдров (пирамида и призма).
Цилиндр
Круговой цилиндр является фигурой вращения прямоугольника вокруг любой из его сторон. Цилиндр характеризуется двумя линейными параметрами: радиусом основания r и высотой h. Ниже схематически показано, как выглядит круговой прямой цилиндр.

Для этой фигуры существует три важных типа сечения:
- круглое;
- прямоугольное;
- эллиптическое.
Эллиптическое образуется в результате пересечения плоскостью боковой поверхности фигуры под некоторым углом к ее основанию. Круглое является результатом пересечения секущей плоскости боковой поверхности параллельно основанию цилиндра. Наконец, прямоугольное получается, если секущая плоскость будет параллельна оси цилиндра.
Площадь круглого сечения рассчитывается по формуле:
S1 = pi*r2
Площадь осевого сечения, то есть прямоугольного, которое проходит через ось цилиндра, определяется так:
S2 = 2*r*h
Сечения конуса
Конусом является фигура вращения прямоугольного треугольника вокруг одного из катетов. Конус имеет одну вершину и круглое основание. Его параметрами также являются радиус r и высота h. Пример конуса, сделанного из бумаги, показан ниже.

Видов конических сечений существует несколько. Перечислим их:
- круглое;
- эллиптическое;
- параболическое;
- гиперболическое;
- треугольное.
Они сменяют друг друга, если увеличивать угол наклона секущей плоскости относительно круглого основания. Проще всего записать формулы площади сечения круглого и треугольного.
Круглое сечение образуется в результате пересечения конической поверхности плоскостью, которая параллельна основанию. Для его площади справедлива следующая формула:
S1 = pi*r2*z2/h2
Здесь z — это расстояние от вершины фигуры до образованного сечения. Видно, что если z = 0, то плоскость проходит только через вершину, поэтому площадь S1 будет равна нулю. Поскольку z < h, то площадь изучаемого сечения будет всегда меньше ее значения для основания.
Треугольное получается, когда плоскость пересекает фигуру по ее оси вращения. Формой получившегося сечения будет равнобедренный треугольник, сторонами которого являются диаметр основания и две образующие конуса. Как находить площадь сечения треугольного? Ответом на этот вопрос будет следующая формула:
S2 = r*h
Это равенство получается, если применить формулу для площади произвольного треугольника через длину его основания и высоту.
Сечения призмы
Призма — это большой класс фигур, которые характеризуются наличием двух одинаковых параллельных друг другу многоугольных оснований, соединенных параллелограммами. Любое сечение призмы — это многоугольник. В виду разнообразия рассматриваемых фигур (наклонные, прямые, n-угольные, правильные, вогнутые призмы) велико и разнообразие их сечений. Далее рассмотрим лишь некоторые частные случаи.

Если секущая плоскость параллельна основанию, то площадь сечения призмы будет равна площади этого основания.
Если плоскость проходит через геометрические центры двух оснований, то есть является параллельной боковым ребрам фигуры, тогда в сечении образуется параллелограмм. В случае прямых и правильных призм рассматриваемый вид сечения будет представлять собой прямоугольник.
Пирамида
Пирамида — это еще один многогранник, который состоит из n-угольника и n треугольников. Пример треугольной пирамиды показан ниже.

Если сечение проводится параллельной n-угольному основанию плоскостью, то его форма будет в точности равна форме основания. Площадь такого сечения вычисляется по формуле:
S1 = So*(h-z)2/h2
Где z — расстояние от основания до плоскости сечения, So — площадь основания.
Если секущая плоскость содержит вершину пирамиды и пересекает ее основание, то мы получим треугольное сечение. Для вычисления его площади необходимо обратиться к использованию соответствующей формулы для треугольника.
Как найти площадь сечения призмы
Призма — это многогранник, основанием которого служат равные многоугольники, боковыми гранями — параллелограммы. Для того чтобы найти площадь сечения призмы, необходимо знать, какое сечение рассматривается в задании. Различают перпендикулярное и диагональное сечение.

Инструкция
Способ расчета площади сечения также зависит от данных, которые уже имеются в задаче. Кроме этого, решение определяется тем, что лежит в основании призмы. Если необходимо найти диагональное сечение призмы, найдите длину диагонали, которая равна корню из суммы (основания сторон в квадрате). Например, если основания сторон прямоугольника равны 3 см и 4 см, соответственно, длина диагонали равна корню из (4х4+3х3)= 5 см. Площадь диагонального сечения найдите по формуле: диагональ основания умножить на высоту.
Если в основании призмы находится треугольник, для вычисления площади сечения призмы используйте формулу: 1/2 часть основания треугольника умножить на высоту.
В случае, если в основании находится круг, площадь сечения призмы найдите умножением числа «пи» на радиус заданной фигуры в квадрате.
Различают следующие виды призм — правильные и прямые. Если необходимо найти сечение правильной призмы, вам нужно знать длину только одной из сторон многоугольника, ведь в основании лежит квадрат, у которого все стороны равны. Найдите диагональ квадрата, которая равна произведению его стороны на корень из двух. После этого перемножив диагональ и высоту, вы получите площадь сечения правильной призмы.
Призма имеет свои свойства. Так, площадь боковой поверхности произвольной призмы вычисляется по формуле, где — периметр перпендикулярного сечения, — длина бокового ребра. При этом перпендикулярное сечение перпендикулярно ко всем боковым ребрам призмы, а его углы — это линейные углы двугранных углов при соответствующих боковых ребрах. Перпендикулярное сечение перпендикулярно и ко всем боковым граням.
Источники:
- диагональное сечение призмы
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Оглавление:
- Как выглядит призма
- Площадь поверхности и объём
- Нахождение элементов призмы
- Примеры задач с решениями
- Как найти площадь куба

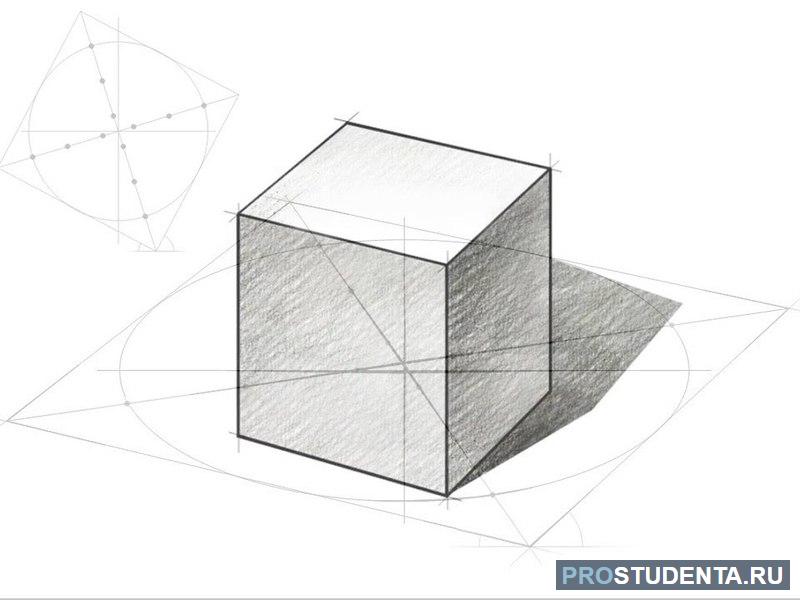
Как выглядит призма
Правильной четырёхугольной призмой называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками. Иное название для этой геометрической фигуры — прямой параллелепипед.
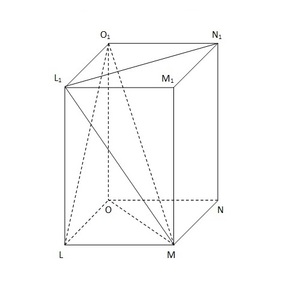
Рисунок, на котором изображена четырёхугольная призма, показан ниже.
На картинке также можно увидеть важнейшие элементы, из которых состоит геометрическое тело. К ним принято относить:
Основы призмы — квадраты LMNO и L₁M₁N₁O₁.
- Боковые грани — прямоугольники MM₁L₁L, LL₁O₁O, NN₁O₁O и MM₁N₁N, расположенные под прямым углом к основаниям.
- Боковые рёбра — отрезки, расположенные на стыке между двумя боковыми гранями: M₁M, N₁N, O₁O и L₁L. Также выполняют роль высоты (поскольку лежат в параллельной основаниям плоскости). В призме боковые рёбра всегда равны между собой — это одно из важнейших свойств этого геометрического тела.
- Диагонали, которые, в свою очередь, подразделяются ещё на 3 категории. К ним относится 4 диагонали основания (MO, N₁L₁), 8 диагоналей боковых граней (ML₁, O₁L) и 4 диагонали призмы, начала и концы которых являются вершинами 2 разных оснований и боковых сторон (MO₁, N₁L).
Иногда в задачах по геометрии можно встретить понятие сечения. Определение будет звучать так: сечение — это все точки объёмного тела, принадлежащие секущей плоскости. Сечение бывает перпендикулярным (пересекает рёбра фигуры под углом 90 градусов). Для прямоугольной призмы также рассматривается диагональное сечение (максимальное количество сечений, которых можно построить — 2), проходящее через 2 ребра и диагонали основания.
Если же сечение нарисовано так, что секущая плоскость не параллельна ни основам, ни боковым граням, в результате получается усечённая призма.
Для нахождения приведённых призматических элементов используются различные отношения и формулы. Часть из них известна из курса планиметрии (например, для нахождения площади основания призмы достаточно вспомнить формулу площади квадрата).
Площадь поверхности и объём
Чтобы определить объём призмы по формуле, необходимо знать площадь её основания и высоту:
V = Sосн·h
Так как основанием правильной четырёхгранной призмы является квадрат со стороной a, можно записать формулу в более подробном виде:
V = a²·h
Если речь идёт о кубе — правильной призме с равной длиной, шириной и высотой, объём вычисляется так:
V = a³
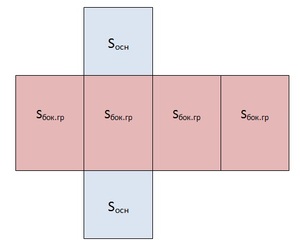
Чтобы понять, как найти площадь боковой поверхности призмы, необходимо представить себе её развёртку.
Из чертежа видно, что боковая поверхность составлена из 4 равных прямоугольников. Её площадь вычисляется как произведение периметра основания на высоту фигуры:
Sбок = Pосн·h
С учётом того, что периметр квадрата равен P = 4a, формула принимает вид:
Sбок = 4a·h
Для куба:
Sбок = 4a²
Для вычисления площади полной поверхности призмы нужно к боковой площади прибавить 2 площади оснований:
Sполн = Sбок + 2Sосн
Применительно к четырёхугольной правильной призме формула имеет вид:
Sполн = 4a·h + 2a²
Для площади поверхности куба:
Sполн = 6a²
Зная объём или площадь поверхности, можно вычислить отдельные элементы геометрического тела.
Нахождение элементов призмы
Часто встречаются задачи, в которых дан объём или известна величина боковой площади поверхности, где необходимо определить длину стороны основания или высоту. В таких случаях формулы можно вывести:
- длина стороны основания: a = Sбок / 4h = √(V / h);
- длина высоты или бокового ребра: h = Sбок / 4a = V / a²;
- площадь основания: Sосн = V / h;
- площадь боковой грани: Sбок. гр = Sбок / 4.
Sдиаг = ah√2
Для вычисления диагонали призмы используется формула:
dприз = √(2a² + h²)
Чтобы понять, как применять приведённые соотношения, можно попрактиковаться и решить несколько несложных заданий.
Примеры задач с решениями
Вот несколько заданий, встречающихся в государственных итоговых экзаменах по математике.
Задание 1.
В коробку, имеющую форму правильной четырёхугольной призмы, насыпан песок. Высота его уровня составляет 10 см. Каким станет уровень песка, если переместить его в ёмкость такой же формы, но с длиной основания в 2 раза больше?
Решение.
Следует рассуждать следующим образом. Количество песка в первой и второй ёмкости не изменялось, т. е. его объём в них совпадает. Можно обозначить длину основания за a. В таком случае для первой коробки объём вещества составит:
V₁ = ha² = 10a²
Для второй коробки длина основания составляет 2a, но неизвестна высота уровня песка:
V₂ = h (2a)² = 4ha²
Поскольку V₁ = V₂, можно приравнять выражения:
10a² = 4ha²
После сокращения обеих частей уравнения на a² получается:
10 = 4h
В результате новый уровень песка составит h = 10 / 4 = 2,5 см.
Задание 2.
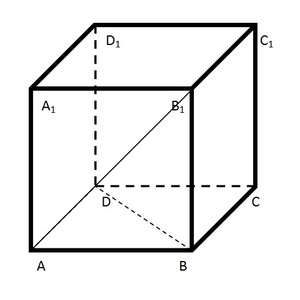
ABCDA₁B₁C₁D₁ — правильная призма. Известно, что BD = AB₁ = 6√2. Найти площадь полной поверхности тела.
Решение.
Чтобы было проще понять, какие именно элементы известны, можно изобразить фигуру.
Поскольку речь идёт о правильной призме, можно сделать вывод, что в основании находится квадрат с диагональю 6√2. Диагональ боковой грани имеет такую же величину, следовательно, боковая грань тоже имеет форму квадрата, равного основанию. Получается, что все три измерения — длина, ширина и высота — равны. Можно сделать вывод, что ABCDA₁B₁C₁D₁ является кубом.
Длина любого ребра определяется через известную диагональ:
a = d / √2 = 6√2 / √2 = 6
Площадь полной поверхности находится по формуле для куба:
Sполн = 6a² = 6·6² = 216
Задание 3.
В комнате производится ремонт. Известно, что её пол имеет форму квадрата с площадью 9 м². Высота помещения составляет 2,5 м. Какова наименьшая стоимость оклейки комнаты обоями, если 1 м² стоит 50 рублей?
Решение.
Поскольку пол и потолок являются квадратами, т. е. правильными четырёхугольниками, и стены её перпендикулярны горизонтальным поверхностям, можно сделать вывод, что она является правильной призмой. Необходимо определить площадь её боковой поверхности.
Длина комнаты составляет a = √9 = 3 м.
Обоями будет оклеена площадь Sбок = 4·3·2,5 = 30 м².
Наименьшая стоимость обоев для этой комнаты составит 50·30 = 1500 рублей.
Таким образом, для решения задач на прямоугольную призму достаточно уметь вычислять площадь и периметр квадрата и прямоугольника, а также владеть формулами для нахождения объёма и площади поверхности.
Как найти площадь куба
Для
решения большинства задач из раздела стереометрии необходимы знания и навыки в
построении сечения объёмных тел. Именно об этом мы сейчас с вами и поговорим.
Итак,
секущей плоскостью называют любую плоскость, по обе стороны от которой
имеются точки данной фигуры.
Секущая
плоскость пересекает грани многогранника по отрезкам.
Многоугольник,
сторонами которого являются эти отрезки, называется сечением
многогранника.
Построить
сечение многогранника плоскостью – это значит указать
точки пересечения секущей плоскости с рёбрами многогранника и соединить эти
точки отрезками, принадлежащими граням многогранника.
Теперь
давайте вспомним, что нам необходимо знать для построения плоскости.
Итак,
построить плоскость можно: с помощью трёх точек, не лежащих на одной прямой;
с
помощью двух пересекающихся прямых;
с
помощью прямой и точки, которая не лежит на прямой;
а
также с помощью двух параллельных прямых.
Метод
следов включает три важных пункта: сначала нужно построить
линию пересечения (след) секущей плоскости с плоскостью основания многогранника;
затем найти точки пересечения секущей плоскости с рёбрами многогранника, а
после этого построить и заштриховать сечение.
В
основе построения сечения методом следов лежат две теоремы:
1)
если две точки прямой принадлежат плоскости, то и вся прямая принадлежит
плоскости;
2)
если плоскость проходит через прямую, параллельную другой плоскости, и эти
плоскости пересекаются, то линия их пересечения параллельна первой прямой.
Метод
вспомогательных сечений применяется при построении сечений в
тех случаях, когда неудобно находить след секущей плоскости. Например, след
получается очень далеко от заданной фигуры.
Суть
комбинированного метода построения сечений многогранников состоит в
применении теорем о параллельности прямых и плоскостей в пространстве в
сочетании с методом следов или методом вспомогательных сечений.
Обратите
внимание: тетраэдр имеет четыре грани, поэтому его сечениями могут быть только
треугольники и четырёхугольники. А вот параллелепипед имеет шесть граней,
поэтому его сечениями могут быть треугольники, четырёхугольники, пятиугольники
и шестиугольники.
Основные
моменты мы с вами повторили, а теперь давайте перейдём к практической части
занятия.
Задача
первая. В основании прямой призмы лежит равнобедренная
трапеция с основаниями, равными см
и см,
и боковой стороной, равной см.
Боковое ребро призмы равно см.
Найдите площадь сечения призмы плоскостью, проходящей через большую сторону
основания и середину противоположного бокового ребра призмы.
Решение.
Задача
вторая. На ребре правильного
тетраэдра с
длиной ребра взята
точка такая,
что .
Найдите площадь сечения тетраэдра плоскостью, содержащей точку и
перпендикулярной ребру .
Решение.
Задача
третья. В основании четырёхугольной пирамиды лежит
квадрат ,
а две боковые грани и
представляют
собой прямоугольные треугольники с прямым .
Найдите площадь сечения пирамиды плоскостью, содержащей точку пересечения
диагоналей основания и параллельной грани ,
если .
Решение.
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности правильной призмы разных видов (треугольной, четырехугольной и шестиугольной), а также, разберем примеры решения задач для закрепления материала.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник. А прямой фигура является в том случае, если ее боковые грани перпендикулярны основаниям.
-
Формула площади правильной призмы
- 1. Общая формула
- 2. Площадь правильной треугольной призмы
- 3. Площадь правильной четырехугольной призмы
-
4. Площадь правильной шестиугольной призмы
-
Примеры задач
Формула площади правильной призмы
1. Общая формула
Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.
Sполн. = Sбок. + 2Sосн.
Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.
Sбок. = Pосн. ⋅ h
Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.
2. Площадь правильной треугольной призмы
Основание: равносторонний треугольник.
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 3ah |
| полная |  |
microexcel.ru
3. Площадь правильной четырехугольной призмы
Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 4ah |
| полная | Sполн. = 2a2 + 4ah |
microexcel.ru
Примечание: Если высота правильной четырехугольной призмы равняется длине стороны ее основания, значит мы имеем дело с кубом, площадь одной грани которого равна a2. А так как все шесть граней куба равны, то полная площадь его поверхности равняется 6a2.
4. Площадь правильной шестиугольной призмы
Основание: правильный шестиугольник
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 6ah |
| полная |  |
microexcel.ru
Примеры задач
Задание 1:
Сторона правильной треугольной призмы равна 6 см, а ее высота – 8 см. Найдите полную площадь поверхности фигуры.
Решение:
Воспользуемся подходящей формулой, подставив в нее известные нам значения:
Задание 2:
Площадь полной поверхности правильной шестиугольной призмы составляет 400 см2. Найдите ее высоту, если известно, что сторона основания равна 5 см.
Решение:
Выведем выражение для нахождения высоты призмы из формулы ее полной площади:

 Основы призмы — квадраты LMNO и L₁M₁N₁O₁.
Основы призмы — квадраты LMNO и L₁M₁N₁O₁.