Как найти площадь сечения призмы правильного треугольника - AvtoShod.ru

Ответ:Sсеч. =0,5
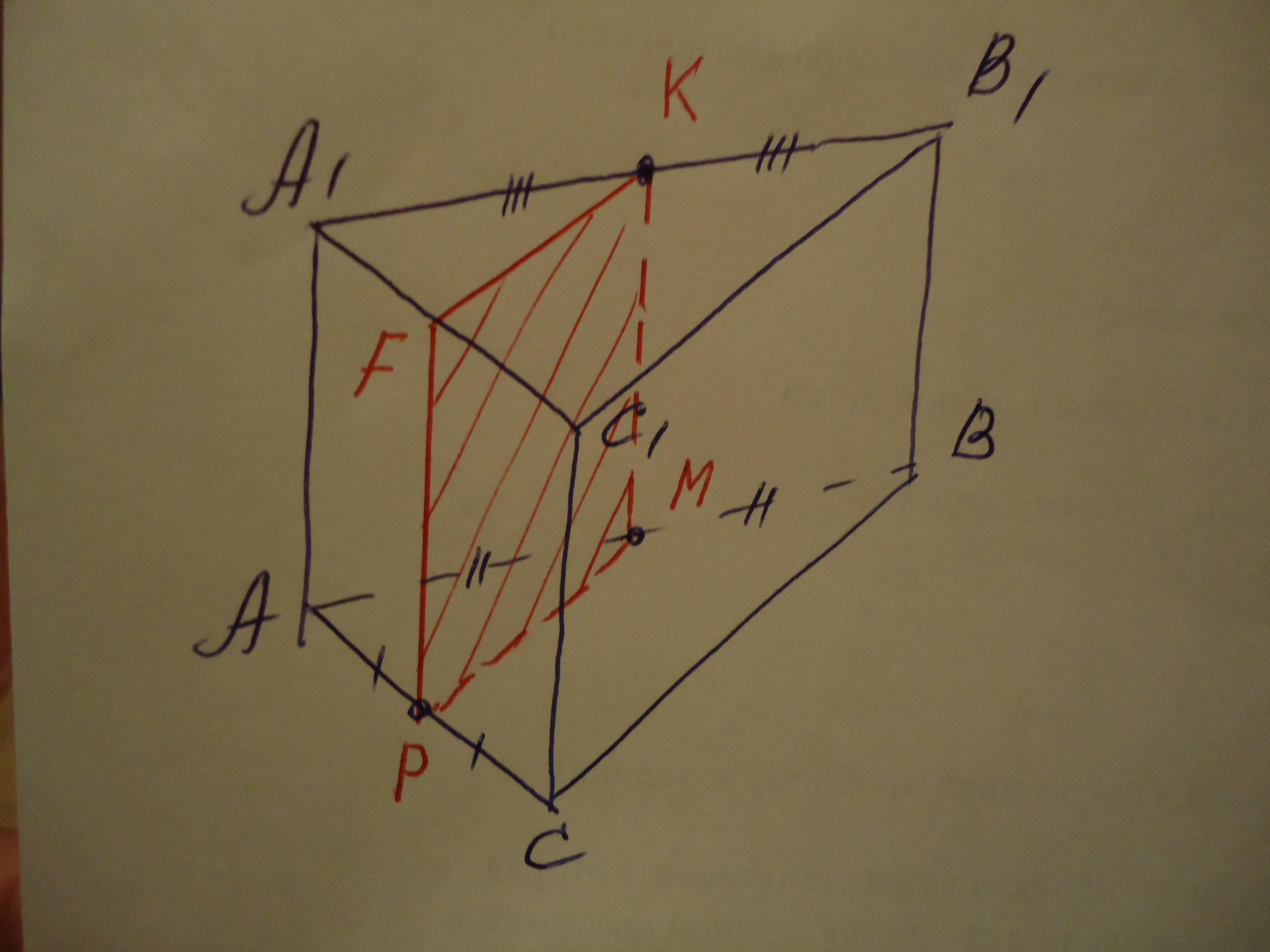
Объяснение: См. рисунок на фото.
Пл. сечения пересекает нижнее основание призмы по прямой РМ, являющейся средней линией ΔАВС по определению⇒ РМ= 0,5 по свойству средней линии.
А₁К=АМ и А₁К║АМ, ∠А₁АМ=90°⇒А₁АКМ- прямоугольник КМ= АА₁=1.
Пл. сечения ∩ пл. (АА₁В₁) = МК. Пл. ( А₁В₁С₁)║пл. (АВС) ⇒ КF║РМ.
Соединим точки F и Р. РМКF- искомое сечение.
АА₁ ⊥пл.(АВС), КМ║АА₁⇒КМ⊥ пл.(АВС), но РМ⊂пл.(АВС)⇒ КМ⊥РМ⇒
⇒РМКF-прямоугольник. S сеч.=РМ*КМ=0,5*1=0,5.

Источник

Как найти площадь сечения призмы

Призма — это многогранник, основанием которого служат равные многоугольники, боковыми гранями — параллелограммы. Для того чтобы найти площадь сечения призмы, необходимо знать, какое сечение рассматривается в задании. Различают перпендикулярное и диагональное сечение.

Инструкция

Способ расчета площади сечения также зависит от данных, которые уже имеются в задаче. Кроме этого, решение определяется тем, что лежит в основании призмы. Если необходимо найти диагональное сечение призмы, найдите длину диагонали, которая равна корню из суммы (основания сторон в квадрате). Например, если основания сторон прямоугольника равны 3 см и 4 см, соответственно, длина диагонали равна корню из (4х4+3х3)= 5 см. Площадь диагонального сечения найдите по формуле: диагональ основания умножить на высоту.

Если в основании призмы находится треугольник, для вычисления площади сечения призмы используйте формулу: 1/2 часть основания треугольника умножить на высоту.

В случае, если в основании находится круг, площадь сечения призмы найдите умножением числа «пи» на радиус заданной фигуры в квадрате.

Различают следующие виды призм — правильные и прямые. Если необходимо найти сечение правильной призмы, вам нужно знать длину только одной из сторон многоугольника, ведь в основании лежит квадрат, у которого все стороны равны. Найдите диагональ квадрата, которая равна произведению его стороны на корень из двух. После этого перемножив диагональ и высоту, вы получите площадь сечения правильной призмы.

Призма имеет свои свойства. Так, площадь боковой поверхности произвольной призмы вычисляется по формуле, где — периметр перпендикулярного сечения, — длина бокового ребра. При этом перпендикулярное сечение перпендикулярно ко всем боковым ребрам призмы, а его углы — это линейные углы двугранных углов при соответствующих боковых ребрах. Перпендикулярное сечение перпендикулярно и ко всем боковым граням.

Источники:

диагональное сечение призмы

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

В данной публикации мы рассмотрим, как можно вычислить площадь поверхности правильной призмы разных видов (треугольной, четырехугольной и шестиугольной), а также, разберем примеры решения задач для закрепления материала.

Правильная призма – это прямая призма, основанием которой является правильный многоугольник. А прямой фигура является в том случае, если ее боковые грани перпендикулярны основаниям.

Формула площади правильной призмы
- 1. Общая формула
- 2. Площадь правильной треугольной призмы
- 3. Площадь правильной четырехугольной призмы
- 4. Площадь правильной шестиугольной призмы
Примеры задач

Формула площади правильной призмы

1. Общая формула

Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.

S_полн. = S_бок. + 2S_осн.

Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.

S_бок. = P_осн. ⋅ h

Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.

2. Площадь правильной треугольной призмы

Основание: равносторонний треугольник.


Площадь	Формула
основание
боковая поверхность	S_бок. = 3ah
полная

microexcel.ru

3. Площадь правильной четырехугольной призмы

Основание: квадрат.


Площадь	Формула
основание	S_осн. = a²
боковая поверхность	S_бок. = 4ah
полная	S_полн. = 2a² + 4ah

microexcel.ru

Примечание: Если высота правильной четырехугольной призмы равняется длине стороны ее основания, значит мы имеем дело с кубом, площадь одной грани которого равна a². А так как все шесть граней куба равны, то полная площадь его поверхности равняется 6a².

4. Площадь правильной шестиугольной призмы

Основание: правильный шестиугольник


Площадь	Формула
основание
боковая поверхность	S_бок. = 6ah
полная

microexcel.ru

Примеры задач

Задание 1:
Сторона правильной треугольной призмы равна 6 см, а ее высота – 8 см. Найдите полную площадь поверхности фигуры.

Решение:
Воспользуемся подходящей формулой, подставив в нее известные нам значения:

Задание 2:
Площадь полной поверхности правильной шестиугольной призмы составляет 400 см². Найдите ее высоту, если известно, что сторона основания равна 5 см.

Решение:
Выведем выражение для нахождения высоты призмы из формулы ее полной площади:

Источник

Привет!

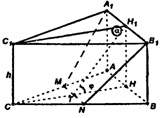
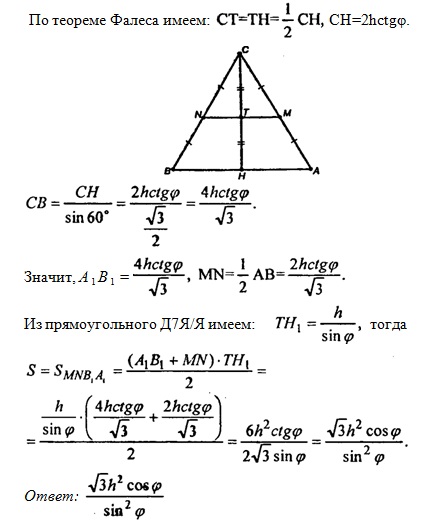
Пусть ΔАВС — правильный,ABC, CC₁=h.
Построим линейный угол двугранного угла с ребром MN.
Построим отрезки H₁H, TH₁
(раз MN || АВ) и(A₁H₁=AH, A₁H₁ || АН, поэтому A₁H₁HA — параллелограмм с прямым углом A₁AH, A₁H₁HA — прямо угольник) то по теореме о 3-х перпендикулярах имеем: Т₁Н₁┴ MN.
Тогда линейный угол двугранного данного угла.
4-угольник ABNM- трапеция (MN || A₁B₁).
Из ΔTHH₁ имеем: Н₁H:TH=tgα, или