Как рассчитать площадь ромба
На данной странице калькулятор поможет рассчитать площадь ромба онлайн. Для расчета задайте длину основания, высоту или длины диагоналей и угол между ними.
Ромб – четырёхугольник, у которого все стороны равны между собой. Ромб является частным случаем параллелограмма. Ромб с прямыми углами называется квадратом.
Через сторону и высоту
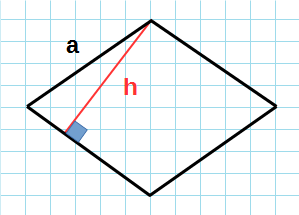
Формула для нахождения площади ромба через сторону и высоту:
a — сторона ромба; h — высота ромба.
Через диагонали
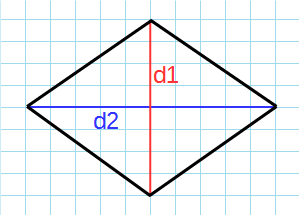
Формула для нахождения площади ромба через диагонали:
d1, d2 — диагонали ромба.
Через сторону и угол
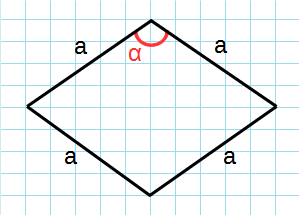
Формула для нахождения площади ромба через сторону и угол:
a — сторона ромба; α — угол между сторонами.
Через угол и диагональ из этого угла
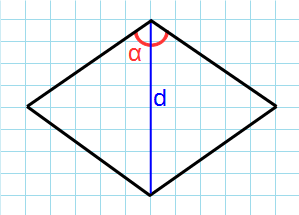
Формула для нахождения площади ромба через угол и диагональ выходящая из этого угла:
d — диагональ ромба; α — угол между сторонами.
Через угол и противолежащию диагональ
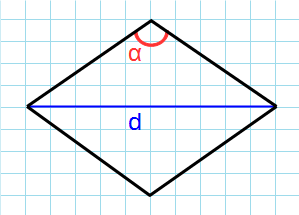
Формула для нахождения площади ромба через угол и диагональ противолежащая углу:
d — диагональ ромба; α — угол между сторонами.
Через угол и радиус вписанной окружности
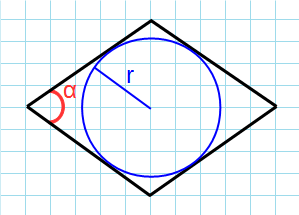
Формула для нахождения площади ромба через угол и радиус вписанной окружности:
r — радиус окружности; α — угол между сторонами.
Через сторону и радиус вписанной окружности
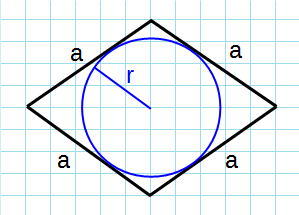
Формула для нахождения площади ромба через сторону и радиус вписанной окружности:
a — сторона ромба; r — радиус вписанной окружности.
Как считать:
через сторону и высоту
через диагонали
через сторону и угол
Укажите размеры:
Результат:
Решение:
Ссылка на страницу с результатом:
# Теория
Ромб — это параллелограмм у которого все стороны равны.
Расчёты площади ромба основааны непосредственно на данных свойствах ромба:
- Все стороны ромба равны;
- Диагонали ромба пересекаются под прямым углом и в месте пересечения делятся пополам;
- Сумма углов, прилежащих к одной стороне ромба, равна 180°
- Противоположные углы ромба равны.
Формула площади ромба
Площадь ромба через сторону и высоту
a
a
a
a
h
S = a cdot h
- S — площадь ромба
- a — сторона ромба
- h — высота
Площадь ромба через диагонали
d
1
d
2
S = dfrac{d_1 cdot d_2}{2}
- S — площадь ромба
- d1 и d2 — диагонали ромба
Площадь ромба через сторону и угол
При расчёте площади ромба через сторону и угол, значение для α можно брать у любого угла — как устрого так и тупого (синус у них будет одиноковый).
S = a^2 cdot sin alpha
- S — площадь ромба
- a — сторона ромба
- sin α — синус угла
Похожие калькуляторы:
Войдите чтобы писать комментарии
Онлайн калькулятор. Площадь ромба
Используя этот онлайн калькулятор, вы сможете найти площадь ромба.
Воспользовавшись онлайн калькулятором для вычисления площади ромба, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.
Найти площадь ромба
Выберите известные величины:
Введите данные:
a =
α =
Площадь в
Вводить можно числа или дроби (-2.4, 5/7, …). Более подробно читайте в правилах ввода чисел.
Онлайн калькулятор площади ромба может вычислить плошадь семью различными методами.
Сделав расчет на этом калькуляторе площади ромба Вы сможете получить детальное пошаговое решение с ответом. Также Вы сможете понять алгоритм нахождения площади ромба различными методами.Тем самым Вы усвоите пройденный материал и закрепите полученные знания.
Ромбом называется параллелограмм, у которого все стороны равны.
Так как ромб является параллелограммом, то он обладает всеми свойствами параллелограмма.
Свойства ромба.
1) Противоположные стороны ромба равны.
2) Противоположные углы ромба равны.
3) Диагонали ромба точкой пересечения делятся пополам.
4) Сумма углов, прилежащих к одной стороне ромба, равна 180 °.
5) Диагонали ромба взаимно перпендикулярны.
6) Диагонали ромба являются также биссектрисами его углов (делят углы ромба пополам).
7) Диагонали делят ромб на четыре равных прямоугольных треугольника.
Скачать все формулы нахождения площади ромба в формате Word
Так как ромб – это параллелограмм, у которого все стороны равны, то для него действуют все те же формулы, как и для параллелограмма, включая формулу нахождения площади через произведение высоты и стороны.
Площадь ромба можно найти, также зная его диагонали. Диагонали делят ромб на четыре абсолютно одинаковых прямоугольных треугольника. Если мы их рассортируем, так чтобы получить прямоугольник, то его длина и ширина будут равны одной целой диагонали и половине второй диагонали. Поэтому площадь ромба находится умножением диагоналей ромба, сокращенных на два (как площади получившегося прямоугольника).
Если в распоряжении только угол и сторона, то можно вооружиться диагональю в качестве помощника и начертить ее напротив известного угла. Тогда она разделит ромб на два конгруэнтных треугольника, площади которых в сумме дадут нам площадь ромба. Площадь каждого из треугольников будет равна половине произведения квадрата стороны на синус известного угла, как площадь равнобедренного треугольника. Поскольку таких треугольников два, то коэффициенты сокращаются, оставив только сторону во второй степени и синус:
Если внутри ромба вписать окружность, то его радиус будет относиться к стороне под углом 90°, что значит, что удвоенный радиус будет равен высоте ромба. Подставив вместо высоты h=2r в предыдущую формулу, получим площадь S=ha=2ra
Если же вместе с радиусом вписанной окружности, дана не сторона, а угол, то следует сначала найти сторону, проведя высоту таким образом, чтобы получить прямоугольный треугольник с заданным углом. Тогда сторона a может быть найдена из тригонометрических отношений по формуле 




