Как найти площадь равнобедренной трапеции задачи

Голикова Татьяна Валерьевна

Задачи пригодятся для отработки материала по теме, сдесь же имеются задачи для домашней работы.

Скачать:

Предварительный просмотр:

Площадь трапеции.

  1. В трапеции основания равны 6 см и 10 см, а высота равна полусумме длин оснований. Найдите площадь трапеции.
  2. В прямоугольной трапеции основания равны 6 см и 10см, меньшая боковая сторона- 5 см. Чему равна площадь трапеции?
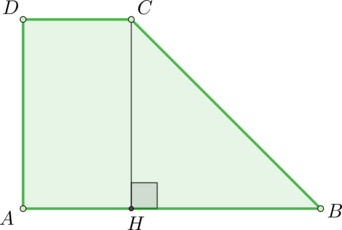
  3. В равнобедренной трапеции ABCM большее основание AM=20 см, высота BH отсекает от  AM отрезок AH=6 см, ∠BAM=45°. Найдите площадь трапеции.
  4. В трапеции ABCM одно из оснований в 3 раза меньше другого, а высота составляет 75% большего основания, площадь трапеции равна 72 см². Найдите основания и высоту трапеции.
  5. В трапеции ABCD    BC и AD-основания, BC÷AD=4÷5. Площадь треугольника ACD=35 см². Найдите площадь трапеции.

Домашнее задание.

  1. Найдите площадь трапеции ABCD, если основания AD и BC равны соответственно 12 см и 8 см, боковая сторона AB=6 см, ∠A=30°.
  2. В треугольнике ABC стороны AB и BC равны соответственно 14 см и 18 см. Сторона AB продолжена за точку A на отрезок AM=AB. Сторона BC продолжена за точку C на отрезок KC, равный половине BC. Найдите площадь треугольника MBK, если площадь треугольника ABC равна 126 см².

Площадь трапеции.

  1. В трапеции основания равны 6 см и 10 см, а высота равна полусумме длин оснований. Найдите площадь трапеции.
  2. В прямоугольной трапеции основания равны 6 см и 10см, меньшая боковая сторона- 5 см. Чему равна площадь трапеции?
  3. В равнобедренной трапеции ABCM большее основание AM=20 см, высота BH отсекает от  AM отрезок AH=6 см, ∠BAM=45°. Найдите площадь трапеции.
  4. В трапеции ABCM одно из оснований в 3 раза меньше другого, а высота составляет 75% большего основания, площадь трапеции равна 72 см². Найдите основания и высоту трапеции.
  5. В трапеции ABCD    BC и AD-основания, BC÷AD=4÷5. Площадь треугольника ACD=35 см². Найдите площадь трапеции.

Домашнее задание.

  1. Найдите площадь трапеции ABCD, если основания AD и BC равны соответственно 12 см и 8 см, боковая сторона AB=6 см, ∠A=30°.
  2. В треугольнике ABC стороны AB и BC равны соответственно 14 см и 18 см. Сторона AB продолжена за точку A на отрезок AM=AB. Сторона BC продолжена за точку C на отрезок KC, равный половине BC. Найдите площадь треугольника MBK, если площадь треугольника ABC равна 126 см².

По теме: методические разработки, презентации и конспекты

  • Мне нравится 

 

Источник

18. Площади геометрических фигур


1. Вспоминай формулы по каждой теме


2. Решай новые задачи каждый день


3. Вдумчиво разбирай решения

Площадь трапеции

Найдите площадь прямоугольной трапеции, основания которой равны (6) и (2), большая боковая сторона составляет с основанием угол (45^circ).

Проведем высоту (CH).

Так как (angle HBC=45^circ), то (angle HCB=45^circ). Следовательно, (triangle HBC) равнобедренный и (HB=HC).
(ADCH) – прямоугольник, следовательно, (AH=DC=2). Тогда (CH=HB=6-2=4). Тогда площадь трапеции равна [S=dfrac{AB+DC}2cdot CH=dfrac{2+6}2cdot 4=16]

Ответ: 16

Основания прямоугольной трапеции равны (12) и (4). Ее площадь равна (64). Найдите острый угол этой трапеции. Ответ дайте в градусах.

Проведем высоту (CH).

(ADCH) – прямоугольник, следовательно, (AH=DC=4). Тогда (HB=12-4=8). Площадь трапеции равна [64=dfrac{AB+DC}2cdot CH=dfrac{4+12}2cdot CHquadRightarrowquad
CH=8] Заметим, что мы получили, что (CH=HB=8). То есть (triangle
CHB) равнобедренный, значит, углы при основании равны, то есть (angle HCB=angle HBC). Так как сумма острых углов в прямоугольном треугольнике равна (90^circ), то (angle B=angle
HBC=90^circ:2=45^circ).

Ответ: 45

Основания трапеции равны (18) и (6), боковая сторона, равная (7), образует с одним из оснований угол (150^circ). Найдите площадь трапеции.

Пусть (AD=7), тогда (angle ADC=150^circ). По свойству трапеции (angle DAB=180^circ-150^circ=30^circ). Проведем (DHperp
AB).

Рассмотрим (triangle ADH). Катет, лежащий против угла (30^circ), равен половине гипотенузы, следовательно, (DH=AD:2=3,5). Тогда площадь трапеции равна [S=dfrac{AB+DC}2cdot DH=dfrac{18+6}2cdot 3,5=42]

Ответ: 42

Основания трапеции равны (27) и (9), боковая сторона равна (8). Площадь трапеции равна (72). Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ дайте в градусах.

Пусть (AD=8). Проведем (DHperp AB).

Тогда площадь трапеции равна [72=dfrac{AB+DC}2cdot DH=dfrac{27+9}2cdot DHquadRightarrowquad
DH=4] Рассмотрим прямоугольный (triangle ADH). Так как катет (DH) равен половине гипотенузы (AD), то угол (DAH) равен (30^circ).

Ответ: 30

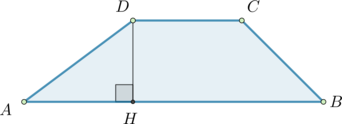
Основания равнобедренной трапеции равны (14) и (26), а ее боковые стороны равны (10). Найдите площадь трапеции.

Проведем высоту (BH). По свойству равнобедренной трапеции (AH=(AD-BC):2=(26-14):2=6).

Тогда из прямоугольного треугольника (ABH): [BH=sqrt{AB^2-AH^2}=sqrt{10^2-6^2}=8] Тогда площадь трапеции: [S=dfrac{AD+BC}2cdot BH=dfrac{26+14}2cdot 8=160]

Ответ: 160

Основания равнобедренной трапеции равны (7) и (13), а ее площадь равна (40). Найдите боковую сторону трапеции.

Проведем высоту (BH).

Площадь трапеции равна [40=dfrac{AD+BC}2cdot BH=dfrac{7+13}2cdot BHquadRightarrowquad BH=
4] Рассмотрим прямоугольный (triangle ABH). По свойству равнобедренной трапеции (AH=(AD-BC):2=(13-7):2=3). Следовательно, [AB=sqrt{AH^2+BH^2}=5]

Ответ: 5

Основания равнобедренной трапеции равны (14) и (26), а ее периметр равен (60). Найдите площадь трапеции.

Проведем высоту (BH). По свойству равнобедренной трапеции (AH=(AD-BC):2=(26-14):2=6).

Так как периметр трапеции равен (60), а боковые стороны равны, то [AB=dfrac{60-14-26}2=10] Тогда из прямоугольного треугольника (ABH): [BH=sqrt{AB^2-AH^2}=sqrt{10^2-6^2}=8] Тогда площадь трапеции: [S=dfrac{AD+BC}2cdot BH=dfrac{26+14}2cdot 8=160]

Ответ: 160

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Источник

Для начала найдем длины боковых сторон равнобедренной трапеции. Равнобедренная трапеция имеет две параллельные стороны (основания) и две равные не параллельные стороны (боковые стороны). Зная основания и периметр трапеции, мы можем найти длину каждой из боковых сторон.

Основания равны 8 и 18, а периметр равен 52. Обозначим длины боковых сторон трапеции как a и b.

Так как это равнобедренная трапеция, a = b.

Теперь найдем длины боковых сторон:

a + b + 8 + 18 = 52

a + a + 26 = 52

2a = 26

a = 13

Теперь, когда у нас есть длины боковых сторон, давайте найдем высоту трапеции. Высота трапеции опускается перпендикулярно к основаниям. Разделите трапецию на два равнобедренных треугольника. В таком случае, можно использовать теорему Пифагора для одного из этих треугольников.

Разность оснований равна 18 — 8 = 10. Таким образом, каждый из равнобедренных треугольников имеет основание, равное 10/2 = 5.

Теперь используем теорему Пифагора:

a^2 = h^2 + b^2

13^2 = h^2 + 5^2

169 = h^2 + 25

h^2 = 144

h = 12

Теперь, когда у нас есть высота и основания трапеции, мы можем найти её площадь. Формула для площади трапеции:

S = ((a + b) / 2) * h

S = ((8 + 18) / 2) * 12

S = (26 / 2) * 12

S = 13 * 12

S = 156

Площадь равнобедренной трапеции равна 156 квадратных единиц.

Источник

Выбирайте формулу в зависимости от известных величин.

1. Как найти площадь трапеции через основания и высоту

Посчитайте сумму оснований трапеции.

Умножьте результат на высоту и поделите на два.

Иллюстрация: Лайфхакер
  • S – искомая площадь трапеции.
  • a и b – основания трапеции (её параллельные стороны).
  • h – высота трапеции.

2. Как вычислить площадь трапеции через высоту и среднюю линию

Просто умножьте высоту трапеции на среднюю линию.

Иллюстрация: Лайфхакер
  • S – искомая площадь трапеции.
  • m – средняя линия трапеции (отрезок, соединяющий середины боковых сторон).
  • h – высота трапеции.

3. Как найти площадь трапеции через диагонали и угол между ними

Умножьте одну диагональ на другую, а затем — на синус любого угла между ними.

Поделите результат на два.

Иллюстрация: Лайфхакер
  • S – искомая площадь трапеции.
  • x и y – диагонали трапеции.
  • α – любой угол между диагоналями.

4. Как найти площадь трапеции через четыре стороны

Отнимите от большего основания меньшее.

Найдите квадрат полученного числа.

Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.

Поделите полученное число на удвоенную разность оснований.

Найдите квадрат результата и отнимите его от квадрата боковой стороны.

Найдите корень из полученного числа.

Умножьте результат на половину от суммы оснований.

Иллюстрация: Лайфхакер
  • S – искомая площадь трапеции.
  • a, b – основания трапеции.
  • c, d – боковые стороны.

5. Как вычислить площадь равнобедренной трапеции через четыре стороны

Отнимите от большего основания трапеции меньшее и поделите результат на два.

Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.

Найдите корень из результата.

Умножьте полученное число на сумму оснований и поделите на два.

Иллюстрация: Лайфхакер
  • S — искомая площадь трапеции.
  • a, b — основания трапеции.
  • c, d — боковые стороны (напомним, в равнобедренной трапеции они равны).

6. Как найти площадь равнобедренной трапеции через радиус вписанной окружности и угол

Найдите квадрат радиуса и умножьте его на четыре.

Поделите результат на синус известного угла.

Иллюстрация: Лайфхакер
  • r — радиус вписанной окружности.
  • α — любой угол трапеции.

Читайте также 📐✏️🎓

  • 8 способов найти длину окружности
  • 8 способов найти периметр треугольника
  • 7 способов найти площадь прямоугольника
  • Как перевести обычную дробь в десятичную
  • Как освоить устный счёт школьникам и взрослым
Источник

Тема 1.

Геометрия на плоскости (планиметрия)

1

.

12

Равнобедренная трапеция

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

геометрия на плоскости (планиметрия)

Решаем задачи

В равнобедренной трапеции основания равны 3 и 9 и угол между боковой стороной и одним из оснований равен ∘ 45 . Найдите
площадь этой трапеции.

PIC

Показать ответ и решение

PIC

Пусть ABCD — равнобедренная трапеция из условия, отрезок BH — высота трапеции. Тогда

1 9− 3 AH = 2 (AD − BC )=--2- = 3

Треугольник ABH — прямоугольный, причем ∠BAH = 45∘, то есть этот треугольник равнобедренный и
BH = AH = 3.

Тогда площадь трапеции равна

1 1 2(BC +AD )⋅BH = 2(3+ 9)⋅3= 18

Показать ответ и решение

PIC

Найдем угол BAD :

∘ ∘ ∘ ∠BAD = ∠BAC + ∠CAD =1 + 46 = 47

Так как ABCD — равнобедренная трапеция,

∘ ∘ ∘ ∘ ∠ABC = 180 − ∠BAD = 180 − 47 = 133

Значит больший угол равен 133∘.

Сумма двух углов равнобедренной трапеции при основании равна ∘ 50 . Найдите больший угол этой трапеции. Ответ дайте в
градусах.

PIC

Показать ответ и решение

PIC

Так как ABCD — равнобокая трапеция, то

∘ ∠ABC + ∠DAB =180 ∠BAD = ∠CDA ∠ABC = ∠BCD

Таким образом, можем считать, что сумма углов BAD и CDA равна 50∘. Так как они равны, каждый из них равен
25∘.

Тогда

∘ ∘ ∘ ∠BCD = ∠ABC = 180 − 25 = 155

Высота равнобедренной трапеции, проведенная из вершины C, делит основание AD на отрезки длиной 1 и 11. Найдите длину
основания BC.

PIC

Показать ответ и решение

PIC

Обозначим точки основания высот за H1, H2. Так как трапеция равнобедренная,

AH1 = DH2 = 1

Также BCH2H1 — прямоугольник, т.е. H1H2 = BC. Значит,

BC =H1H2 = AH2 − AH1 = 11− 1= 10

Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.

PIC

Показать ответ и решение

Обозначим боковую сторону трапеции через x. Опустим высоты BE и CF на большее основание AD.

PIC

Трапеция равнобокая, AB = CD, ∠EAB =∠CDF, следовательно, прямоугольные треугольники ABE и DCF равны и
AE = F D. BCF E — прямоугольник, значит, EF = BC = 7. Тогда

AE = FD = AD--− EF = 6= 3 2 2

Запишем площадь трапеции, чтобы найти BE :

1 2SABCD 2⋅40 SABCD = 2(AD + BC )⋅BE ⇒ BE = AD-+-BC- = 7+-13 = 4

По теореме Пифагора в треугольнике ABE

∘ ---------- x= AE2 +BE2 =5

Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

PIC

Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.

PIC

Показать ответ и решение

Обозначим боковую сторону трапеции через x. Опустим высоты BE и CF на большее основание AD.

PIC

Трапеция равнобокая, AB = CD, ∠EAB =∠CDF, следовательно, прямоугольные треугольники ABE и DCF равны и
AE = F D. BCF E — прямоугольник, значит, EF = BC = 7. Тогда

AD − EF 6 AE = FD = ----2--- = 2 = 3

Запишем площадь трапеции, чтобы найти BE :

SABCD = 1(AD + BC ) ⇒ BE = -2SABCD- = 2⋅40-= 4 2 AD + BC 7+ 13

По теореме Пифагора в треугольнике ABE :

∘ --2-----2- x= AE +BE = 5 ⇒ PABCD =7 +13 +2 ⋅5= 30

Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.

PIC

Показать ответ и решение

Обозначим боковую сторону трапеции через x. Тогда периметр равен

2x+ 14+ 26= 60 ⇔ x= 10

Опустим высоты BE и CF на большее основание AD.

PIC

Трапеция равнобокая, AB = CD, ∠EAB =∠CDF, следовательно, прямоугольные треугольники ABE и DCF равны и
AE = F D. BCF E — прямоугольник, значит, EF = BC = 14. Тогда

AD − EF 12 AE =F D = ---2----= -2 = 6

В прямоугольном треугольнике ABE по теореме Пифагора √ ---------- BE = AB2 − AE2 = 8. Тогда площадь трапеции

SABCD = 1 (AD +BC )⋅BE = 1 (14+ 26)⋅8= 160 2 2

В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними 60∘. Найдите меньшее
основание.

PIC

Показать ответ и решение

∠A = 60∘. Проведем высоту BH.

PIC

По свойству равнобедренной трапеции AH = (AD − BC) :2. В прямоугольном треугольнике ABH

∠ABH = 90∘ − 60∘ =30∘

Катет, лежащий против угла 30∘, равен половине гипотенузы:

AH = AB :2= 5

Следовательно,

5 = (25 − BC ):2 ⇒ BC = 15

Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.

PIC

Показать ответ и решение

Проведем высоту BH.

PIC

Площадь трапеции равна

AD-+-BC- 7+-13- 40 = 2 ⋅BH = 2 ⋅BH ⇒ BH = 4

Рассмотрим прямоугольный △ABH. По свойству равнобедренной трапеции AH = (AD − BC ):2 = (13− 7):2 =3.
Следовательно,

∘ ---------- AB = AH2 + BH2 = 5

Тогда периметр трапеции равен

5 +5 +7 +13 = 30

Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.

PIC

Показать ответ и решение

Проведем высоту BH. По свойству равнобедренной трапеции

AH = (AD − BC ):2= (26− 14) :2= 6

PIC

Так как периметр трапеции равен 60, а боковые стороны равны, то

AB = 60-− 14-− 26-= 10 2

Тогда из прямоугольного треугольника ABH :

BH = ∘AB2--−-AH2-= ∘102−-62 = 8

Тогда площадь трапеции:

AD-+-BC- 26+-14- S = 2 ⋅BH = 2 ⋅8= 160

Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.

PIC

Показать ответ и решение

Рассмотрим рисунок:

PIC

Проведем BH ⊥ AD. По свойству равнобедренной трапеции

1 AH = 2 (AD − BC )= 7

Тогда по теореме Пифагора из △ABH :

∘ ------- ∘ ------------- BH = 252− 72 = (25− 7)(25 +7)= √----- = 18 ⋅32 = 3⋅8= 24

Тогда из △ABH :

BH 24 sin ∠A = AB--= 25 = 0,96

В равнобедренной трапеции ABCD основание AD вдвое длиннее основания BC и вдвое длиннее боковой стороны. Найдите
острый угол трапеции.

PIC

Показать ответ и решение

PIC

Если опустить высоты BH и CK на основание AD, то они отсекут равные отрезки AH и KD. При этом

AD − HK HK AB AB =BC = HK ⇒ AH = ----2----= --2-= -2-

Отсюда ∠ABH = 30∘ как угол напротив катета, равного половине гипотенузы. Тогда искомый угол равен

∠BAK = 90∘ − 30∘ =60∘

Показать ответ и решение

PIC

Четырехугольник BCDK — параллелограмм, так как противоположные стороны попарно параллельны. Далее, ∠AKB = ∠KBC
как накрест лежащие при параллельных BC и AD и секущей BK. Тогда имеем:

∠BAK = ∠CDK = ∠KBC и ∠AKB = ∠KBC = ∠ABK

Тогда △ABK — равносторонний. Кроме того,

BC = KD =4 ⇒ AK = 2= AB = CD

Отсюда периметр трапеции равен:

PABCD =AB +BC + CD +KD + AK = = 2 +4 +2 +4 +2 = 14

Диагонали в равнобедренной трапеции ABCD перпендикулярны. O — точка пересечения диагоналей, причем AO :OC = 7:1.
Найдите периметр трапеции, если меньшее основание равно 1.

PIC

Показать ответ и решение

BC — меньшее основание, треугольники △BOC и △AOD подобны и их стороны относятся как 1 :7, следовательно,
BC :AD = 1:7. Значит, AD = 7; OB = OC. По теореме Пифагора

2 2 2 OB + OC = 1 ⇒ 1-- ⇒ OB =OC = √2 7 ⇒ AO = √2-

В △ABO :

AO2 + OB2 = AB2 ⇒ AB = 5

Тогда

PABCD = AB + BC + CD + AD = = 1+ 7+ 5+ 5= 18

Основания равнобедренной трапеции равны 15 и 9, один из углов равен 45∘. Найдите высоту трапеции.

PIC

Показать ответ и решение

∠A = 45∘. Проведем высоту BH.

PIC

По свойству равнобедренной трапеции

AH = (AD − BC ):2 = (15− 9):2 =3

В прямоугольном △ABH :

∠ABH = 90∘ − 45∘ =45∘

Следовательно, △ABH — равнобедренный и

BH =AH = 3

В равнобедренной трапеции основания равны 12 и 27, острый угол равен 60∘. Найдите ее периметр.

PIC

Показать ответ и решение

∠A = 60∘. Проведем высоту BH.

PIC

По свойству равнобедренной трапеции

AH =(AD − BC ):2= (27− 12):2= 7,5

В прямоугольном △ABH :

∠ABH = 90∘ − 60∘ =30∘

Катет, лежащий против угла 30∘, равен половине гипотенузы: AH =AB :2. Значит, AB = 2AH = 15. Следовательно,
периметр равен

P = 15+ 15+ 12+ 27= 69

Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.

PIC

Показать ответ и решение

Проведем высоту BH.

PIC

Площадь трапеции равна

AD-+-BC- 7+-13- 40 = 2 ⋅BH = 2 ⋅BH ⇒ BH = 4

Рассмотрим прямоугольный △ABH. По свойству равнобедренной трапеции

AH = (AD − BC ):2 = (13− 7):2 =3

Следовательно,

∘ ---------- AB = AH2 + BH2 = 5

Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

PIC

Показать ответ и решение

Проведем высоту BH. По свойству равнобедренной трапеции

AH = (AD − BC ):2= (26− 14) :2= 6

PIC

Тогда из прямоугольного треугольника ABH :

∘ ---------- ∘------- BH = AB2 − AH2 = 102− 62 = 8

Тогда площадь трапеции:

S = AD-+-BC-⋅BH = 26+-14-⋅8= 160 2 2

Проекция диагонали равнобедренной трапеции на ее большее основание равна 6, боковая сторона равна 3. Найдите площадь
трапеции, если угол при её меньшем основании равен 150∘.

PIC

Показать ответ и решение

PIC

AE — есть проекция диагонали AC на основание трапеции AD. Запишем формулу площади трапеции:

BC + AD S =CE ⋅---2----

Проведя вторую высоту BF, заметим, что треугольники AF B и DEC равны по двум углам и стороне между ними, т. к.
боковые стороны в равнобедренной трапеции равны, отсюда следует, что:

AF = ED ⇒ FE = AD − 2ED = BC

Подставим полученные данные в формулу площади трапеции:

CE ⋅ BC-+-AD-= CE ⋅ AD-− 2ED-+AD = 2 2 =CE ⋅ 2⋅(AE-+ED-)−-2ED--=CE ⋅AE 2

Чтобы найти высоту CE, заметим, что

∠ABC = 150∘ ⇒ ∘ ∘ ∘ ⇒ ∠ABF = 150 − 90 = 60 ⇒ ⇒ BF = CE = cos(60∘)⋅AB

Теперь подставим высоту в формулу и найдем площадь трапеции:

S =AE ⋅cos60∘⋅AB = 6⋅ 1 ⋅3= 9 2

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как найти повторения в ячейках
  • Как на карте найти дагестан
  • Как найти людей через архивы
  • Судебный приказ от налоговой как найти
  • Как найти ток утечки в проводке

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии