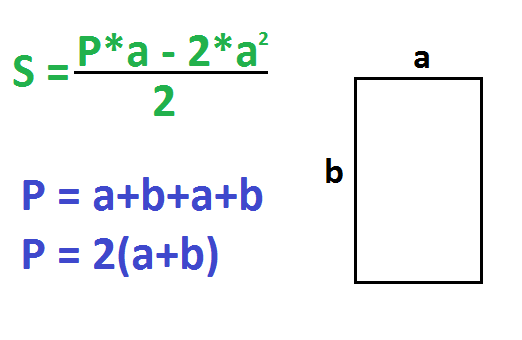Как найти площадь прямоугольника с высотой формула - AvtoShod.ru

Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.

11 439

Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.

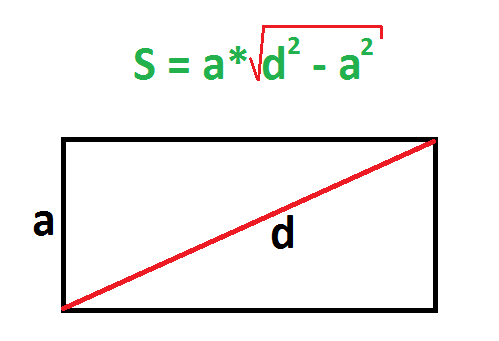
По диагонали и стороне

Должна быть известна диагональ и любая из сторон. Действия:

Найти квадрат диагонали, то есть умножить ее на саму себя.
Найти квадрат известной стороны.
Из квадрата диагонали вычесть квадрат стороны.
Найти квадратный корень получившейся разности.
Умножить его на известную сторону.

Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.

Квадрат стороны = 3*3 = 9 см.
Квадрат диагонали = 5*5 = 25 см.
Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
Умножаю корень разности на известную сторону: 16*9 = 144 см.

Ответ: 144 см.

Обратите внимание

Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.

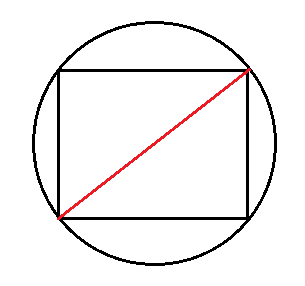
По стороне и диаметру описанной окружности

Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.

Действия:

Найдите квадрат диаметра – умножьте диаметр на диаметр.
Найдите квадрат известной стороны.
Отнимите от квадрата диаметра квадрат стороны.
Найдите квадратный корень разности.
Умножьте квадратный корень на известную сторону.

Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.

Квадрат диаметра: 10*10 = 100 см.
Квадрат стороны: 8*8 = 64 см.
Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
Умножаю сторону на корень из разности: 8*6 = 48 см.

Ответ: 48 см.

Лайфхак

Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:

А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.

Диаметр равен двум радиусам, потому что радиус – это половина диаметра.

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

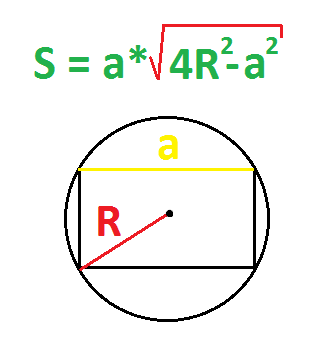
По радиусу описанной окружности и стороне

Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.

Другой способ:

Найти квадрат радиуса (умножьте радиус на радиус).
Умножить квадрат радиуса на 4.
Найти квадрат известной стороны.
Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
Найти квадратный корень разности.
Умножить корень на известную сторону.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.

Квадрат радиуса: 5*5=25 см.
Четыре квадрата радиуса: 4*25 = 100 см.
Квадрат стороны: 6*6 = 36 см.
Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
Нахожу квадратный корень разности. Корень из 64 равен 8 см.
Умножаю корень на сторону: 8*6 = 48 см.

Ответ: 48 см.

Помните

Радиус = половине диаметра.

Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.

По стороне и периметру – 1 способ

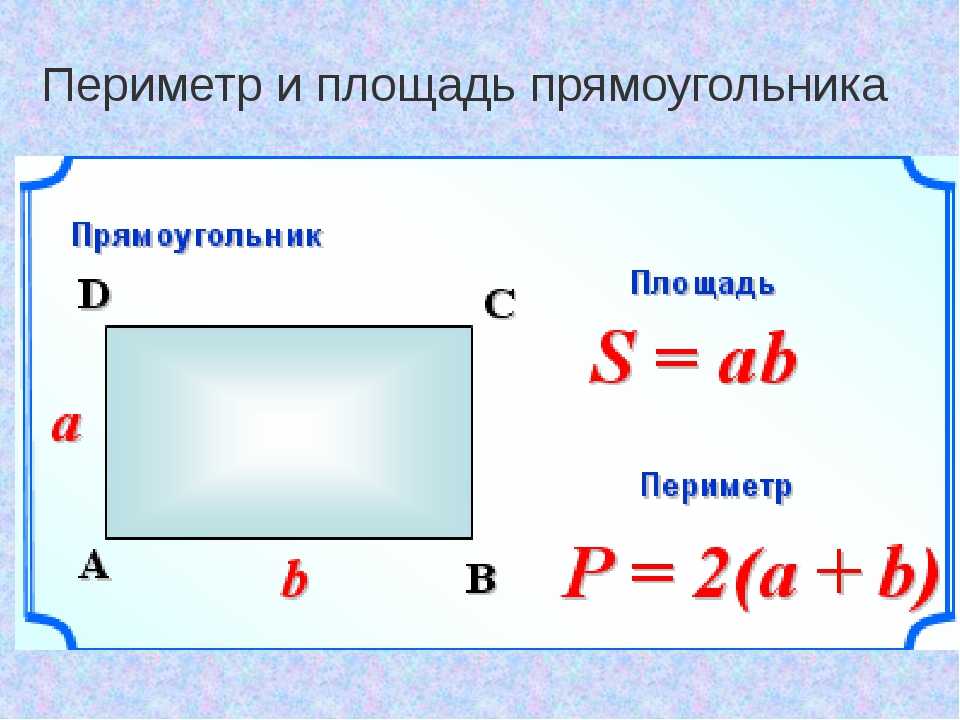
Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).

Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.

Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.

Нахожу вторую сторону прямоугольника:
1. P=2(a+b).
2. P=2a+2b.
3. 14= 2*3+2b.
4. 14 = 6+2b.
5. 2b = 14-6 = 8.
6. b = 8/2.
7. b = 4.
Нахожу площадь по основной формуле. S = 3*4 = 12 см.

Ответ: 12 см.

По стороне и периметру – 2 способ

Действия такие:

Умножьте периметр на сторону.
Найдите квадрат стороны.
Умножьте квадрат стороны на 2.
Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
Поделите на 2.

Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.

Умножаю периметр на сторону: 8*28 = 224 см.
Нахожу квадрат стороны: 8*8 = 64 см.
Умножаю квадрат стороны на два: 64*2 = 84 см.
Отнимаю из первого третье: 224-84 = 140 см.
Делю разность на два: 140/2 = 70 см.

Ответ: 70 см.

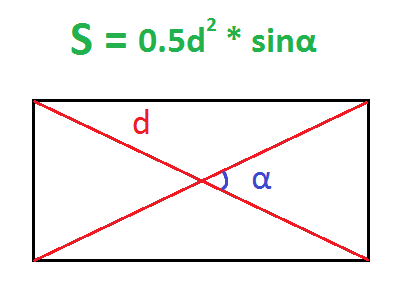
По диагонали и углу между диагоналями

Диагонали прямоугольника всегда равны.

Действия:

Найти квадрат диагонали (умножить диагональ на саму себя).
Найти половину этого квадрата – умножить его на 0,5.
Найти синус угла между диагоналями.
Умножить половину квадрата диагонали на синус угла между диагоналями.

Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.

Квадрат диагонали: 10*10 = 100 см.
Половина этого квадрата: 0,5*100 = 50 см.
Синус угла между диагоналями: sin 30 градусов = 0,5.
Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.

Ответ: 25 см.

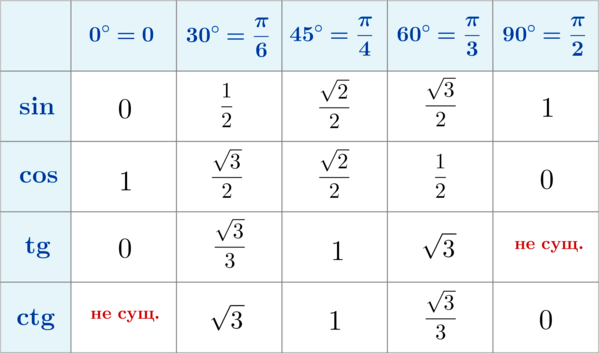
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).

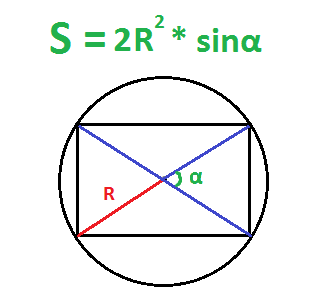
По радиусу описанной окружности и углу между диагоналями – первый способ

Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.

Находим длину диагонали: 6*2 =12 см.
Квадрат диагонали равен 144 см.
Половина квадрата: 72 см.
Синус 30 градусов равен 0,5.
Умножаем половину квадрата на синус: 72*0,5 = 36 см.

Ответ: 36 см.

По радиусу описанной окружности и углу между диагоналями – второй способ

Действия:

Найти квадрат радиуса (умножить радиус на радиус).
Умножить квадрат радиуса на два.
Найти синус угла между диагоналями.
Умножить синус угла на два радиуса в квадрате.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.

Квадрат радиуса: 6*6 = 36.
Два радиуса в квадрате: 36*2 = 72.
Синус 30 градусов равен 0,5.
Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.

Ответ: 36 см.

Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.

( 1 оценка, среднее 5 из 5 )

Оцените статью

ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА

Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети

Источник

Area of rectangle is the region covered inside the boundaries of the rectangle. A rectangle is a quadrilateral in which opposite sides are equal and parallel. The diagonals of a rectangle are equal and are perpendicular bisectors to each other. All the angles of the rectangles are 90°. A rectangle is similar to a parallelogram. We can say that all the rectangles are parallelograms but its converse is not true.

Table of Contents:

Definition

Units

Formula

How to Calculate the Area of Rectangle

Area by Diagonal

Area by perimeter

Derivation

Solved Examples

FAQS

What is the Area of a Rectangle?

Definition – The area of a Rectangle is the region occupied by a rectangle within its four sides or boundaries.

The area of a rectangle is the space enclosed by the boundaries of the rectangle. In general, the area of any shape is the space enclosed by the geometrical shape. We can also say that the space enclosed by the perimeter of the rectangle is the area of a rectangle. The perimeter of a rectangle is the sum of all the sides. For a rectangle, the area is the multiplication of its length by its breadth. The opposite sides of the rectangle are equal, and if the length and breadth are also equal, then the shape becomes a square. Therefore, every square is a rectangle. The below-given diagram shows the rectangle and its area,

Area of Rectangle

Unit of Area of Rectangle

The area of a rectangle is measured in square units and the standard unit for measuring the area of a rectangle is m². Other units widely used for measuring the area of the rectangle are cm², mm², and others.

Side	Area
meter(m)	m² or (meter)²
centimeter(cm)	cm^{2 or}(centimeter)²

Area of a Rectangle Formula

The formula for the area of a rectangle is the multiplication of length (L) and breadth (B).

The formula of the Area of a Rectangle
Area of Rectangle	A = L x B

where ,
L is the length of the rectangle
B is the breadth of the rectangle

Note:-

If the unit of length and breadth is not exact then it should be transformed into one unit. For e.g. If the length is in cm and breadth in m then both dimensions should be adjusted either to m or cm.

How to Find the Area of a Rectangle?

The area of the rectangle is defined as the product of its length and breadth. Following are the steps that help calculate the area of the rectangle,

Step 1: Note down the dimensions of the rectangle.

Step 2: Calculate the product of the length and breadth of the rectangle.

Step 3: Write the answer in respective square units.

Example: Find the area of a rectangle whose length is 20 inches and breadth is 50 inches.

Solution:

The formula for area of rectangle is given:

Area = L × B

Area = 20 × 50

Area = 1000 inches²

Thus, the required area is 1000 inches²

Area of a Rectangle with Diagonal

The area of the rectangle can be found by two methods which are:

Method 1:

We can find the value of the missing side using the Pythagoras theorem and then find the area. Let us understand this using an example.

The diagonal of the rectangle is the line joining opposite vertices. The diagonal of the rectangle is calculated using Pythagoras’s Theorem

Method 1 to find the Area of the Rectangle

(Diagonal)² = (Length)² + (Breadth)²

Length² = (Diagonals² – Breadth²)

Length = √(Diagonals² – Breadth²)

The formula for the area of a rectangle is calculated by:

Area = Length × Breadth

Area = √(Diagonals² – Breadth²) × Breadth

Area = Breadth √(Diagonals² – Breadth²)

Method 2:

If both the diagonals of the rectangle are given then its area can be found with the help of the area of the quadrilateral formula.

Let a rectangle ABCD have diagonals as AC and BD and their length is d₁ and d₂ then its area is given by,

Area of rectangle ABCD = 1/2 × d₁ × d₂

Example: Find the area of a rectangle whose length of the diagonals is 10 cm and 14 cm.

Solution:

The formula for area of rectangle is,

Area = 1/2 × d₁ × d₂

Area = 1/2 × 10 × 14

Area = 70 cm²

Thus, the area of required rectangle is 70 cm².

Area of Rectangle using Perimeter

To calculate the area of a rectangle using the perimeter and one dimension follow the following steps,

Step 1: Note the perimeter and the given dimension.

Step 2: Use the perimeter formula to find the other dimension.

Step 3: Use the area of the rectangle formula and substitute the required value obtained in Step 2

Step 4: Simplify the expression and add unit²to get the final answer.

The example given below explains the above concept.

Example: Find the area of a rectangle when the perimeter is 28 cm and the breadth is 8 cm.

Solution:

Given,

Perimeter of Rectangle = 28 cm

length = 8 cm

breadth(b) = ?

Using Perimeter of rectangle formula,

Perimeter of rectangle = 2 (l + b)

28 = 2 (8 + b)

14 = 8 + b

b = 6 cm

Thus the breadth of rectangle is 6 cm

Area of Rectangle = l × b

= 8 × 6 = 48 cm²

Thus, the area of the Rectangle is 48 cm²

Derivation of Area of a Rectangle

The area of a rectangle is the product of length and breadth. This can be derived by dividing the rectangle into two triangles. The triangles are equal as the base and height of the two triangles will be equal.

Let’s derive the formula for the area of a rectangle, the image given below shows that a rectangle is made by joining two equal right-angle triangles.

Area of a Rectangle Formula Derivation

Area of Rectangle = 2 (Area of Triangle)
Area of Rectangle = 2 (1/2 × Base × Height)
Area of Rectangle = 2 (1/2 × AB × BC)
Area of Rectangle = AB × BC
Area of Rectangle = Length × Breadth.

Thus, the area of the rectangle formula is derived.

Solved Examples on Area of Rectangle

Example 1: The length and width of a rectangle are 6 units and 3 units, respectively. Find the area of the rectangle.

Solution:

Given,

length = 6 unit
breadth = 3 units

Area of rectangle = length × breath
= 6 × 3
= 18 square units

Thus, the area of given rectangle is 18 square units

Example 2: Find the area of a rectangle whose height is 10 cm and width is 2 cm.

Solution:

Given,

Height = 10 cm
Width = 2 cm

Area of Rectangle = width × height

Area of Rectangle = 10 × 2 = 20

Therefore, the area of the rectangle is 20 cm².

Example 3: A rectangular panel has a width of 150 mm and a height of 99 mm. Find the area of this panel.

Solution:

Given,

Height = 99 mm
= 9.9 cm

Width = 150 mm = 15 cm

Area of Rectangle = width × height

Area of Rectangle = 15 × 9.9

Therefore, the area of the rectangle = 148.5 cm².

Example 4: The height of a rectangular net is seen to be 20 cm. Its area is seen to be 260 cm². Find the width of the provided net.

Solution:

Given,

Height = 20 cm
Area = 260 cm²

Area of Rectangle = width × height

Therefore,

width = Area / height

width = 260/20

width = 13 cm

Thus, the width of the rectangle is 13 cm

Example 5: The height and width of a rectangular desk are 40 m and 20 m, respectively. If a carpenter charges ₹ 2 per m² for his work, how much would it cost to make the whole desk?

Solution:

Given,

Height of Desk = 40 m
Width of Desk = 20 m

Area of top of Desk = width of desk × height of desk

Area of top of Desk = 40 × 20

Area of top of Desk = 800 m²

At the cost of ₹ 2 per m²,

The cost for making top of the desk is 800 × 2 = ₹ 1600

Example 6: A wall whose length and width are 60 m and 40 m respectively needs to be painted. Find the quantity of the paint required if 1 litre of paint can paint 400 m² of the wall.

Solution:

Given,

Length of wall = 60 m

Width of wall = 40 m

Area of wall = width × length

Area of wall = 60 × 40

Area of wall = 2400 m²

Paint required for 400 m² of wall = 1 litre (given)

Paint required for 2400 m² of wall = 2400 / 400 × 1 = 6 litre.

Thus, the paint required to paint the wall is 6 litre.

Q7: If the length and breadth of the rectangular glass slab are 6 m and 4 m respectively. Then finds its area.

Solution:

Length of the rectangular slab is 6 m

Breadth of the rectangular slab is 4 m

Area of rectangular slab = length × breadth

= 6 × 4
= 24 m²

Here, the area is measured in m².

Related Articles:

Area of Square

Area of a Triangle

Area of Circle

Area of Quadrilateral

Area of Rhombus

Area of Trapezium

Area of Parallelogram

FAQs on Area of Rectangle

Q1: What is the formula for the area of a rectangle?

Answer:

Area (A) of rectangle formula is the product of the length and breadth. It can be defined as the space occupied by its boundaries.

Q2: What is the unit of area of a rectangle?

Answer:

The unit of the area of rectangle are meter², centimeter², inches², etc. In general, it is unit².

Q3: What is the perimeter of a rectangle?

Answer:

The perimeter of rectangle is the sum of the length of all its boundaries. The formula for perimeter of rectangle is given as;

P = 2 (Length + Breadth)

Q4: How to find the area of a rectangle?

Answer:

For a rectangle whose length is l and breadth is b then its area can be calculated by using the formula,

Area = l × b

Q5: How to find the area of a rectangle with a diagonal?

Answer:

The area of the rectangle when its diagonal is given is calculated using the formula,

Area = 1/2 × d₁ × d₂

where
d₁ is the first diagonal.
d₂ is the second diagonal.

Q6: How to find the area of a rectangle when a perimeter is given?

Answer:

The area of a rectangle when its perimeter and any one side is given can be calculated by,

Step 1: Use the perimeter of the rectangle formula to find the relation between length (l) and breadth (b).

Step 2: One dimension is already given. Use the relation to find the other dimension.

Step 3: When both dimensions are known use the area formula to find the area.

Q7: How to calculate the area of a quadrilateral with 4 different sides?

Answer:

The area of a quadrilateral with all fours sides different and both diagonal given are,

Area = 1/2 × d₁ × d₂

where
d₁ is the first diagonal.
d₂ is the second diagonal.

Q8: Is the area of a rectangle equal to the area of a square?

Answer:

No, it is not necessary that the area of the rectangle is equal to the area of square. The condition where both the areas are equal is when the length and breadth in a rectangle are equal.

Источник

1. Формула площади равнобедренной трапеции через стороны и угол

b — верхнее основание

a — нижнее основание

c — равные боковые стороны

α — угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):

2. Формула площади равнобокой трапеции через радиус вписанной окружности

R — радиус вписанной окружности

D — диаметр вписанной окружности

O — центр вписанной окружности

H — высота трапеции

α, β — углы трапеции

Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d — диагональ трапеции

α, β — углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m — средняя линия трапеции

c — боковая сторона

α, β — углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

b — верхнее основание

a — нижнее основание

h — высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, (S):

Источник

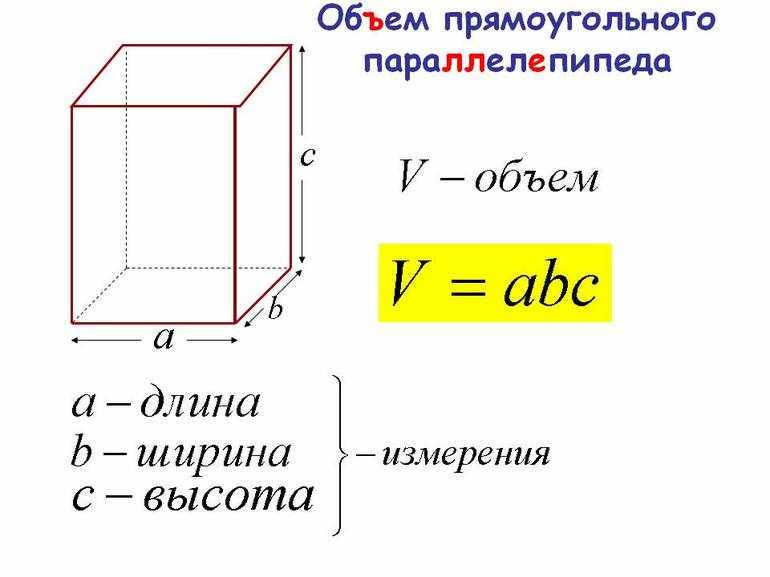
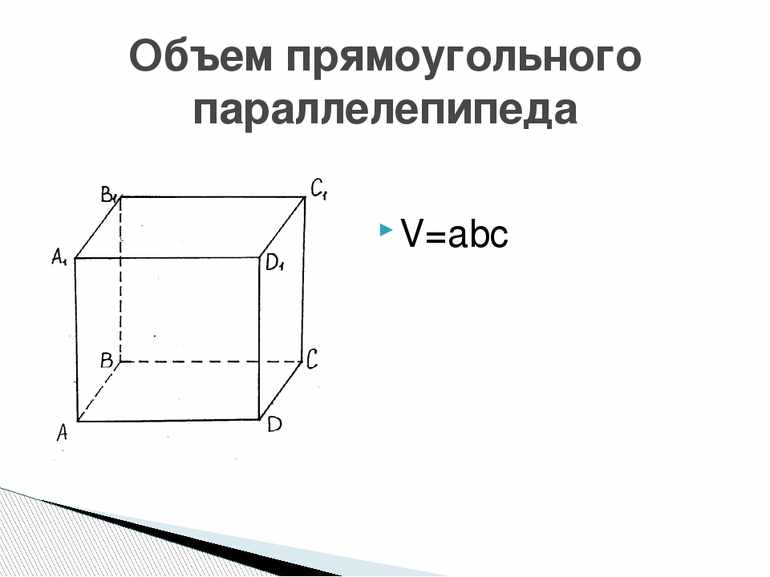
Форма объекта и его линейные размеры определяют один из важных с геометрической точки зрения параметров — объём. Формула для прямоугольника, позволяющая его вычислить, довольно проста и основана на знании стороны и высоты. Но при решении не всегда известны значения рёбер фигуры, поэтому приходится использовать свойства параллелограмма, а именно — способы нахождения площади.

Общие сведения

По своей сути объём является количественной характеристикой пространства, которое занимает тело или вещество. Простыми словами, этот параметр показывает вместимость. В качестве единицы измерения, согласно СИ, принят кубический метр. За обозначение же объёма взята латинская буква V.

У тел, имеющих простую форму, характеристики находятся путём перемножения площади на высоту. Например, для куба он равен a3, прямоугольной призмы — h * b * a, пирамиды — (S * b * h) / 3. В эллипсоидных фигурах при расчётах используется радиус. Так, для конуса объём равен (p * R2 * h) / 3, сферы — (4 * p * R3) / 3, тора — 2 * p2 * R1 * R22.

Объём плоских фигур, таких как треугольник, круг, квадрат, прямоугольник, равен нулю. Но если их стороны или окружности имеют связанные с ними попарно параллельные линии, то они уже являются объёмными фигурами. Например, прямоугольник в пространстве называют параллелепипедом. Таким образом, чтобы найти объём прямоугольника, необходимо, чтобы он представлял собой прямоугольный параллелепипед, иначе действие будет бессмысленным.

Определить объём — значит, знать две основные величины фигуры:

площадь — двумерная характеристика, определяющая размер фигуры,
высоту — это длина перпендикуляра, опущенного из вершины на основание в трёхмерном пространстве.

Так как площадь измеряется в метрах квадратных, а высота просто в метрах, то перемножение площади и высоты как раз и даст единицу измерения объёма — метр кубический.

Решение задач

На самом деле вычисление объёма не только выполняют на уроках математики. Это знание востребовано в довольно многих специальностях и науках. Например, при строительстве, в архитектуре, инженерии, физике, химии. Поэтому знание нахождения параметра может пригодиться не только в школе. Теорию обязательно необходимо закреплять на практике. Вот некоторые задачи, которые помогут усвоить рассматриваемый материал:

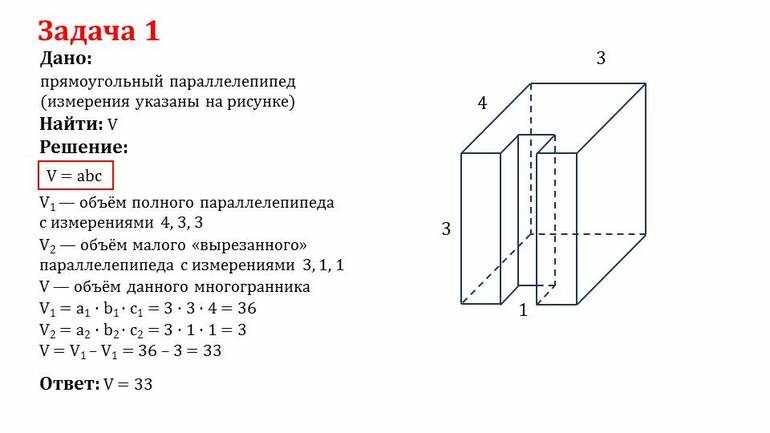
Пусть есть параллелепипед с прямыми сторонами. Его рёбра у основания равняются 19 и 20 сантиметрам. Размер же боковой грани составляет 10 сантиметров. Вычислить объём фигуры. Эта задача на одну формулу, все данные для подстановки в неё известны. Так, V = a * b * c = 19 * 20 * 10 = 3 800 см3 = 0,0038 м³.
Пусть имеется параллелепипед с основанием 1 см на 1,2 см и высотой 0,8 см. Из него был удалено другое прямоугольное тело с размерами 0,3 x 0,55 x 0,5. Найти объём получившейся фигуры. Так как искомый параметр новой фигуры равен разнице изначального и удалённого объёмов, то зная формулу найти ответ не составит труда: V = 0,8 * 1 * 1,2 — 0,3 * 0,5 * 0,55 = 0,877 см3.
Дан прямоугольный параллелепипед с вершинами ABCD и A1B1C1D1. Сравнить объём образованного в середине пирамиды AA1BD тела со значением фигуры. Для удобства решения стороны AB, AD, AA соответственно можно обозначить как x, y, z. Тогда объём прямоугольного тела будет равен Vп = Sп * AA1 = x * y * z. Если начертить условие на рисунке, то можно отметить, что площадь пирамиды вполовину меньше площади основания прямоугольника. То есть, Sabd = 0,5 * Sabd. Тогда V = Sabd * AA1 / 3 = x * y * z / 3 * 2 = x * y* z / 6. Значит, объём вписанной пирамиды меньше в шесть раз чем у фигуры.
В гальванической ванне помещается три тысячи литров раствора. Высота наполнения ёмкости при этом достигает 75 сантиметров. В ванную поместили заготовку, после чего уровень поднялся на два сантиметра. Найти объём заготовки в метрах кубических. Итак, в одном кубическом метре содержится тысяча литров. Поэтому изначально в ёмкости было 3 м³ раствора. Значит, изначально в ванне раствор занимал: 3 = S * 75. Отсюда s = 3/75 = 1/25 см2. Объём детали составляет: V = S * 2 = (1/25) * 2 = 2 / 25 = 0,08 м³.

Использование калькулятора

Конечно же, на обычном калькуляторе объём прямоугольника не подсчитаешь. Разве что известны три его грани и формула нахождения параметра. Тогда нужно будет просто перемножить три числа. В других же случаях, когда нужно решить сложную задачу, связанную с громоздкими вычислениями, можно использовать математические сайты, имеющие название онлайн-калькуляторы.

Это интернет-сервисы, предлагающие своим пользователям бесплатно воспользоваться услугами по вычислению объёма геометрических фигур и выполнить другие математические операции. Для того чтобы воспользоваться сайтами-решателями, нужно иметь любой гаджет с возможностью подключения его к интернету и установленным на него веб-обозревателем.

После загрузки онлайн-калькулятора все действия пользователя сводятся к заполнению специальной формы в которую вносится условие задания. Конечно же, такое решение не может называться самостоятельным, но для проверки полученного результата или выявления ошибок в расчёте подходит идеально. Кроме, непосредственно автоматического вычисления объёма большинство сайтов содержат на своих страницах теоретический материал, а также примеры решений типовых заданий. Так что при обучении учащихся их использование на первых порах вполне оправданно.

Источник

Формулы площади и программы для расчета площадей
- - Формулы площади треугольника
  - Формулы площади квадрата:
  - Формула площади прямоугольника:
  - Формула площади параллелограмма:
  - Формула площади трапеции:
  - Формулы площади ромба:
  - Формула площади круга:
  - Формула площади эллипса:
Площади фигур — Сайт учителя математики
исчисление — Рассчитать высоту или ширину прямоугольника, учитывая его площадь и высоту или ширину.
- - Зарегистрируйтесь или войдите в систему
  - Опубликовать как гость
  - Опубликовать как гость
геометрия — Почему площадь прямоугольника равна высоте, умноженной на ширину?

Формулы площади и программы для расчета площадей

Содержание:

Формулы площади треугольника
Формулы площади квадрата:
Формула площади прямоугольника:
Формула площади параллелограмма:
Формула площади трапеции:
Формулы площади ромба:
Формула площади круга:
Формула площади эллипса:

Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры.
Величина площади выражается числом заключающихся в него квадратных единиц.

Формулы площади треугольника

1-ая формула

S — площадь треугольника

a, b — длины 2-х сторон треугольника

С — угол между сторонами a и b

2-ая формула

S — площадь треугольника

a — длина стороны треугольника

h — длина высоты, опущенной на сторону a

3-ья формула

S — площадь треугольника

a, b, c — длины 3-х сторон треугольника

p — полупериметр треугольника

4-ая формула

S — площадь треугольника

r — радиус вписанной окружности

p — полупериметр треугольника

5-ая формула

S — площадь треугольника

a, b, c — длины 3-х сторон треугольника

R — радиус описанной окружности

См. также: Программа для расчета площади треугольника.

Формулы площади квадрата:

1) Площадь квадрата равна квадрату длины его стороны (a).

2) Площадь квадрата равна половине квадрата длины его диагонали (d).

S — площадь квадрата

a — длина стороны квадрата

d — длина диагонали квадрата

См. также: Программа для расчета площади квадрата.

Формула площади прямоугольника:

1) Площадь прямоугольника равна произведению длин двух его смежных сторон (a, b).

S — площадь прямоугольника

a — длина 1-ой стороны прямоугольника

b — длина 2-ой стороны прямоугольника

См. также: Программа для расчета площади прямоугольника.

Формула площади параллелограмма:

1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).

S — площадь параллелограмма

a — длина основания

h — длина высоты

См. также: Программа для расчета площади параллелограмма.

Формула площади трапеции:

1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).

S — площадь трапеции

a — длина 1-ого основания

b — длина 2-ого основания

h — длина высоты трапеции

См. также: Программа для расчета площади трапеции.

Формулы площади ромба:

1) Площадь ромба равна произведению длины его стороны на высоту (a, h).

2) Площадь ромба равна половине произведения его диагоналей.

S — площадь ромба

a — длина основания ромба

h — длина высоты ромба

d₁ — длина 1-ой диагонали

d₂ — длина 2-ой диагонали

См. также: Программа для расчета площади ромба.

Формула площади круга:

1) Площадь круга равна произведению квадрата радиуса на число пи (3. 1415).

2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.

S — площадь круга

π — число пи (3.1415)

r — радиус круга

См. также: Программа для расчета площади круга.

Формула площади эллипса:

1) Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи (3.1415).

S — площадь эллипса

π — число пи (3.1415)

a — длина большой полуоси

b — длина малой полуоси

См. также: Программа для расчета площади эллипса.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Площади фигур — Сайт учителя математики

Площади многоугольников
Друзья мои, легко найти
S параллелограмма:
Вы помножьте а на b
И на синус гамма.
(S=absin)
S трапеции ты знаешь.
Посчитай, я подожду.
Полусумму оснований
Ты умножь на высоту.
(S = (а+b/2)h)
Площадь треугольника
Знать, конечно, надо:
Мы умножим а на аш
И разделим на два.

С понятием площади нам
приходиться сталкиваться ежедневно. Для того, чтобы постелить новую
плитку в вашей квартире вам нужно приобрести определенное ее количество,
которое будет зависеть от площади вашей комнаты. Размер земельного
участка вашего дома также будет характеризоваться площадью. Обычно люди
забывают как найти площадь более сложных фигур, таких как треугольник,
трапеция, или круг, но если вы настолько закрутились в жизни, что забыли
как найти площадь прямоугольника, то мы вам это напомним в данной
статье.

Вычисление площади прямоугольника.
Площадь измеряют в квадратных единицах, миллиметрах, сантиметрах,
метрах и так далее. Сколько квадратов в данном прямоугольнике?

Совершенно верно. В нем пятнадцать квадратных единиц. Значит для того,
чтобы найти площадь прямоугольника нужно его ширину умножить на длину. В
виде формулы это можно представить как S = h*b, где S-площадь,
h-высота, b-ширина. Или так:
площадь прямоугольника = ширина х длину.
Вот еще несколько примеров определения площади прямоугольника.

	Площадь = Длина х Ширина Площадь = 9 х 5 = 45 квадратных единиц
	Площадь = Длина х Ширина Площадь = 8 х 6 = 48 квадратных единиц

Единицы измерения площади.
Как было сказано выше площадь измеряется в квадратных единицах. Они
будут различными в зависимости от размера измеряемой площади. Конечно,
можно измерять все в одних единицах, но в результате мы будем получать
либо слишком маленькие, либо слишком большие для восприятия цифры.

Пример	Единица измерения	Единица площади
Ноготь на пальце	Миллиметр	мм²
Лист бумаги	Сантиметр	см²
Комната	Метр	м²
Город	Километр	км²

Площадь земельных участков еще часто указывают в сотках.

Одна сотка —
это площадь участка размером 10х10 метров, которая составляет 100
квадратных метров и поэтому называется соткой. Вот несколько характерных
примеров размеров, которые может иметь земельный участок площадью 15
соток.

Ширина 15, длина 100	Площадь 1500 м²	Площадь 15 соток
Ширина 20, длина 75	Площадь 1500 м²	Площадь 15 соток
Ширина 25, длина 60	Площадь 1500 м²	Площадь 15 соток
ширина 30, длина 50	Площадь 1500 м²	Площадь 15 соток

В будущем, если вы вдруг забудете как найти площадь прямоугольника,
то вспоминайте очень старый анекдот, когда дедушка спрашивает у
пятиклассника как найти площадь Ленина, а тот отвечает что нужно ширину
Ленина умножить на длину Ленина.

Иногда в быту людям приходится вспоминать давно забытые школьные знания.
Например, когда при очередном ремонте в доме или квартире нужно
определить количество материала для какой-то поверхности треугольной
формы. Когда-то вы знали это на зубок, но теперь судорожно пытаетесь
вспомнить как найти площадь треугольника?

Не переживайте! Это нормально, когда человеческий мозг перекладывает уже
давно не используемую информацию в удаленные уголки, из которых ее не
вседа получается быстро извлечь. А чтобы вы не мучились этим вопросом,
мы напомним как найти площадь треугольника различными методами в данной
статье.

Как известно, треугольником называется плоская фигура, образованная
пересекающимися прямыми. Точки пересечения называют вершинами, а
противоположные им отрезки прямых ребрами. Встречаются частные виды
треугольников, такие как прямоугольный, равнобедренный и равносторонний
треугольники.

С самом общем случае площадь треугольника находится как половина
произведения длина основания треугольника на величину высоты, опущенной
на данное основание с противоположной вершины. Записывается это
следующим образом S = 1/2*b*h, где S-площадь треугольника, b-длина одной
из сторон треугольника, h-высота, опущенная к этой стороне.

Данную формулу можно хорошо понять, запомнить и вспоминать по частному
случаю нахождения площади прямоугольного треугольника. Посмотрите
внимательно на рисунок.

Как видите площадь такого треугольника легко определяется как половина
площади воображаемого прямоугольника образованного из двух таких
треугольников. Для непрямоугольного треугольника вы как бы добавляете
два треугольника до образования прямоугольника и находите его площадь.

Если известна длина трех сторон треугольника, то его площадь может быть
найдена по формуле Герона. Для упрощения ее использования вводят новую
величину, называемую полупериметром, который находиться как половина
суммы всех сторон треугольника и записывается в виде P = (a+b+c)/2, где
P-полупериметр, а,b,с-стороны (ребра) треугольника. После нахождения
полупериметра формула Герона принимает следующий вид: S =
√(p(p-a)(p-b)(p-c)), где S — площадь треугольника, √-квадратный корень,
p-полупериметр, a,b,c-стороны (ребра) треугольника.

Существуют также другие формулы того, как найти площадь треугольника, но
мы не станем их здесь приводить, так как в них используются такие
данные как синусы углов и которые больше подходят для задач по
математической практике, чем по бытовому использованию.

Как найти площадь
трапеции? Данная задача в быту возникает очень редко, но иногда
оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме
трапеции, которые все чаще применяют при строительстве современных
квартир, или в дизайн-проектах по ремонту.

Трапеция — это геометрическая фигура, образованная четырьмя
пересекающимися отрезками, два из которых параллельны между собой и
называются основаниями трапеции. Два других отрезка называются сторонами
трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение.
Это средняя линия трапеции, которая представляет собой отрезок,
соединяющий середины боковых сторон и высота трапеции, которая равна
расстоянию между основаниями.

Как и у треугольников, у трапеция есть частные виды в виде
равнобедренной (равнобокой) трапеции, у которой длина боковых сторон
одинаковы и прямоугольной трапеции, у которой одна из сторон образует с
основаниями прямой угол.

Трапеции обладают некоторыми интересными свойствами:

Средняя линия трапеции равна полусумме оснований и параллельна им.
У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
Если сумма углов, образованных сторонами трапеции у любого ее
основания равна 90, то длина отрезка, соединяющего середины оснований,
равна их полуразности.
Равнобедренную трапецию можно описать окружностью. И наоборот.
Если в трапеция вписывается в окружность, значит она равнобедренная.
Отрезок, проходящий через середины оснований равнобедренной
трапеции будет перпендикулярен ее основаниям и представляет собой ось
симетрии.

Как найти площадь трапеции.
Площадь трапеции будет равна полусумме ее оснований, умноженной на
высоту. В виде формулы это записывается как S = ((a+b)*h)/2, где
S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота
трапеции.

Понять и запомнить эту формулу можно следующим образом. Как следует из
рисунка ниже трапецию с использованием средней линии можно преобразовать
в прямоугольник, длина которого и будет равна полусумме оснований.

Можно также любую трапецию разложить на более простые фигуры:
прямоугольник и один, или два треугольника и если вам так проще, то
найти площадь трапеции, как сумму площадей составляющих ее фигур.

Есть еще одна простая формула для подсчета ее площади.

Согласно ней
площадь трапеции равна произведению ее средней линии на высоту трапеции и
записывается в виде: S = m*h, где S-площадь, m-длина средней линии,
h-высота трапеции. Данная формула больше подходит для задач по
математике, чем для бытовых задач, так как в реальных условиях вам не
будет известна длина средней линии без предварительных расчетов. А
известны вам будут только длины оснований и боковых сторон.

В этом случае площадь трапеции может быть найдена по формуле: S = ((a+b)/2)*√c²-((b-a)²+c²-d²/2(b-a))², где S-площадь, a,b-основания, c,d-боковые стороны трапеции.

Существуют еще несколько способов того, как найти площади трапеции. Но,
они примерно также неудобны как и последняя формула, а значит не имеет
смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться
первой формулой из статьи и желаем всегда получать точные результаты.

Мы знаем, что окружность
представляет собой множество точек равноудаленных от заданной точки и
лежащих с данной точкой, а также между собой в одной плоскости. Точка,
от которой равноудалены другие точки называется центром окружности.

Расстояние от любой точки окружности до его центра называется радиусом окружности и обычно обозначается заглавной английской буквой R.
Расстояние между двумя противолежащими точками, у которых соединяющий их отрезок проходит через центр окружности, называется диаметром окружности и по общепринятым стандартам обозначается английской заглавной буквой D.

Кругом называется часть плосткости, ограниченная окружностью.

Исходя из определения окружности можно понять, что диаметр равен двум радиусм окружности D=2R, а радиус наоборот равен половине диаметра R=D/2.

После того, как были определены все свойства и ключевые характеристики
кругов и окружностей можно приступить к определению площади круга, для
чего может быть использована следующая формула:

S = πR²

где, S — площадь круга, π — число пи (о нем мы расскажем ниже), R — радиус окружности.

π=3,14.

Формулу площади круга можно преобразовать с учетом того, что радиус равен полудиаметру круга. В этом случае она примет вид:

D = πD²/4

где, S — площадь круга, π — число пи, D — диаметр окружности.

исчисление — Рассчитать высоту или ширину прямоугольника, учитывая его площадь и высоту или ширину.

спросил
8 лет, 5 месяцев назад

Изменено
8 лет, 5 месяцев назад

Просмотрено
2к раз

$begingroup$

Думаю, это должно быть очень просто, но я застрял. 92 = 120 text{ см} cdot y$. Теперь разделите обе части на $120 text{ см}$.

$endgroup$

$begingroup$

Шаг 1: Вызов $ Area = x . 2}{cm}$, которую можно упростить до $Rightarrow cm = frac {см . cm}{cm}$ теперь, отменив, вы получите $Rightarrow cm = cm$ , вам не нужно извлекать квадратный корень ни на одном из шагов.

Если вы запутались с единицами измерения подобных задач, подставьте единицы измерения в формулу, которую вы используете, и упростите ее. Если ваш метод верен, единица измерения справа должна быть равна единице измерения слева.

$endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

геометрия — Почему площадь прямоугольника равна высоте, умноженной на ширину?

Задавать вопрос

спросил
2 года 3 месяца назад

Изменено
2 года, 3 месяца назад

Просмотрено
265 раз

$begingroup$

Я знаю, что здесь есть ответ на аналогичный вопрос, однако я ищу немного другое.

Время от времени друзья приходят ко мне с математическими задачами, которые им нужно решить, и я стараюсь предвидеть, какие вопросы они могут задать. Недавно одному другу нужно было найти площадь нескольких прямоугольников, чтобы узнать, сколько плиток нужно купить для стены, которую он облицовывал. Один из вопросов, который, как я думал, он мог бы задать, был вопросом заголовка, и я понял, что за все время, которое я потратил на изучение математики, я не думаю, что смогу дать достойное интуитивное объяснение этому основному факту. .

Итак, мой вопрос таков: если бы вам нужно было дать нестрогое интуитивное объяснение неспециалисту или молодому студенту, как бы вы это сделали?

Редактировать : Полезный комментарий и редактирование предложили использовать пример шариков в качестве объяснения, однако причина, по которой я не думаю, что это полностью отвечает на мой вопрос, заключается в том, что я могу предвидеть, что вызовет проблемы в чьей-то интуиции при столкновении с прямоугольник, который имеет десятичную высоту или ширину. Что бы значило, например, иметь шарики по 0,36$?

Редактировать: Для ясности, вопрос, который я здесь задаю, заключается в том, как бы вы объяснили неспециалисту с небольшим знанием математики, почему площадь прямоугольника равна произведению ширины на высоту. Я не спрашиваю, как бы я объяснил своему другу, сколько плиток ему нужно, чтобы заполнить его стену. Я упомянул эту проблему просто потому, что именно она побудила меня задуматься над этим вопросом.

геометрия
мягкий вопрос
область

$endgroup$

$begingroup$

Я думаю, что все сводится к тому, хорошо ли вы представляете себе, что такое область, а что нет. Площадь — это мера того, сколько места что-то занимает. 1 квадратная единица – это площадь квадрата, состоящая из одной единицы на одну единицу. Теперь прямоугольник длины $a$ и ширины $b$ можно разбить на $atimes b$ квадратов по одной единице.

Следовательно, площадь прямоугольника равна $atimes b$.

$endgroup$

$begingroup$

Вы, конечно, хотите, чтобы площадь была пропорциональна длине, а также пропорциональна высоте (поскольку, например, прямоугольник вдвое большей высоты может содержать две копии меньшего прямоугольника, поэтому он должен иметь двойную площадь). Отсюда следует, что площадь должна быть равна $cLH$, где $L$ — длина, $H$ — высота, а $c$ — константа. Теперь на самом деле не имеет ни малейшего значения, какое (положительное) значение вы берете для $c$ (при условии, что вы берете одно и то же значение $c$ для всех прямоугольников), поэтому мы принимаем соглашение, что оно равно самое простое число вокруг, которое составляет $ 1 $.

Источник

По диагонали и стороне

По стороне и диаметру описанной окружности

По радиусу описанной окружности и стороне

По стороне и периметру – 1 способ

По стороне и периметру – 2 способ

По диагонали и углу между диагоналями

По радиусу описанной окружности и углу между диагоналями – первый способ

По радиусу описанной окружности и углу между диагоналями – второй способ

What is the Area of a Rectangle?

Unit of Area of Rectangle

Area of a Rectangle Formula

How to Find the Area of a Rectangle?

Example: Find the area of a rectangle whose length is 20 inches and breadth is 50 inches.

Area of a Rectangle with Diagonal

Method 1:

Method 2:

Example: Find the area of a rectangle whose length of the diagonals is 10 cm and 14 cm.

Area of Rectangle using Perimeter

Example: Find the area of a rectangle when the perimeter is 28 cm and the breadth is 8 cm.

Derivation of Area of a Rectangle

Solved Examples on Area of Rectangle

Example 1: The length and width of a rectangle are 6 units and 3 units, respectively. Find the area of the rectangle.

Example 2: Find the area of a rectangle whose height is 10 cm and width is 2 cm.

Example 3: A rectangular panel has a width of 150 mm and a height of 99 mm. Find the area of this panel.

Example 4: The height of a rectangular net is seen to be 20 cm. Its area is seen to be 260 cm2. Find the width of the provided net.

Example 5: The height and width of a rectangular desk are 40 m and 20 m, respectively. If a carpenter charges ₹ 2 per m2 for his work, how much would it cost to make the whole desk?

Example 6: A wall whose length and width are 60 m and 40 m respectively needs to be painted. Find the quantity of the paint required if 1 litre of paint can paint 400 m2 of the wall.

Q7: If the length and breadth of the rectangular glass slab are 6 m and 4 m respectively. Then finds its area.

FAQs on Area of Rectangle

Q1: What is the formula for the area of a rectangle?

Q2: What is the unit of area of a rectangle?

Q3: What is the perimeter of a rectangle?

Q4: How to find the area of a rectangle?

Q5: How to find the area of a rectangle with a diagonal?

Q6: How to find the area of a rectangle when a perimeter is given?

Q7: How to calculate the area of a quadrilateral with 4 different sides?

Q8: Is the area of a rectangle equal to the area of a square?

Общие сведения

Решение задач

Использование калькулятора

Формулы площади и программы для расчета площадей

Формулы площади треугольника

Формулы площади квадрата:

Формула площади прямоугольника:

Формула площади параллелограмма:

Формула площади трапеции:

Формулы площади ромба:

Формула площади круга:

Формула площади эллипса:

Площади фигур — Сайт учителя математики

исчисление — Рассчитать высоту или ширину прямоугольника, учитывая его площадь и высоту или ширину.

Зарегистрируйтесь или войдите в систему

Опубликовать как гость

Опубликовать как гость

геометрия — Почему площадь прямоугольника равна высоте, умноженной на ширину?

Не пропустите также:

Example 4: The height of a rectangular net is seen to be 20 cm. Its area is seen to be 260 cm². Find the width of the provided net.

Example 5: The height and width of a rectangular desk are 40 m and 20 m, respectively. If a carpenter charges ₹ 2 per m² for his work, how much would it cost to make the whole desk?

Example 6: A wall whose length and width are 60 m and 40 m respectively needs to be painted. Find the quantity of the paint required if 1 litre of paint can paint 400 m² of the wall.