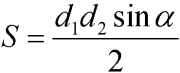Найти площадь четырехугольного участка неправильной формы — задача непростая. Когда стороны попарно равны (прямоугольник) — расчет площади простой: перемножить 2 соседние стороны.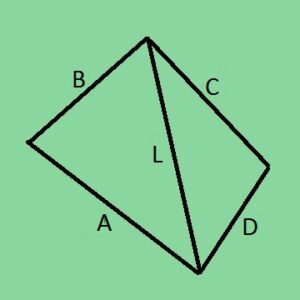 
Чтобы рассчитать площадь четыреугольника, у которого стороны не равны, надо использовать более сложные формулы (на которые имеются дополнительные ограничения, например, все углы располагаются на окружности). Один из способов требует, кроме измерения длин, и определения углов. А если из всех инструментов у вас только рулетка? Нельзя вычислить площадь участка в форме неправильного четырехугольника (даже трапеции), зная только длины сторон! Посчитать площадь можно, зная еще дополнительную информацию, например длину диагонали.
Наш онлайн калькулятор поможет по 5 замерам рулеткой определить площадь непрямоугольного участка. Измерите все стороны и диагональ — сможете вычислить его площадь! Обратите внимание на порядок ввода сторон относительно диагонали, в соответствии с рисунком. Вычисления основываются на формуле Герона, как здесь: «Расчет площади треугольника по трем сторонам«. Т.е. фактически используется тот факт, что диагональ делит четырехугольный участок на 2 треугольных.
In this platform, you have to learn about how to find the Perimeter and Area of irregular figures. An irregular shape will be of any size and length. We will see irregular shapes all around us, for example, a diamond shape, a kite, a leaf, a flower, etc. The Area of irregular shapes will be the space occupied by the shape which is measured in square units. The Perimeter of irregular shapes is by adding all the lengths of their sides. Any shape whose sides and angles are not of equal length is named an irregular shape.
On this page, you will learn about the definition of the area and the perimeter of irregular figures, how to find the area and perimeter of irregular figures, some solved example problems, and so on.
Read More:
- Area and Perimeter of Combined Figures
- Area of a Circular Ring
- Worksheet on Area of the Path
Irregular Figures – Definition
The Irregular Figures are defined as a figure that is not a standard geometric shape. An irregular shape is simply a shape where every single side is not the same length. But some irregular figures are made up of two or further standard geometric shapes. If the shape is irregular then it has some angles that are not all the same size. Based on the number of sides or corners we can decide that irregular figure.
How to find Perimeter and Area of Irregular Figures?
The following are the ways for finding the area and perimeter of irregular figures:
How to find Area of Irregular Shapes or Figures?
- Step 1: First, divide the compound shape into a basic regular shape.
- Step 2: Next, find each basic shape area separately.
- Step 3: Now Add all the areas of basic shapes together.
- Step 4: Now, write the final answer in square units.
How to find the Perimeter of Irregular Figures?
To find the perimeter of the irregular figure, we can simply add up each of its outer sides length of a shape. To find the perimeter of any shape like rectangle, square, and so on you have to add all the lengths of four sides. Consider ‘A’ is in this case the length of the rectangle and ‘B’ is the width of the rectangle.
See More:
- Plane Figures
- Solid Figures
- Rectilinear Figures
Perimeter and Area of Irregular Shapes Examples
Example 1:
The Irregular Figure is given below. Find the area of that figure?
Solution:
As given in the question, the irregular figure is given.
Now, we can break the given irregular figure. After separating the figure we have two rectangle blocks.
Next, we will find the area of those two rectangles. The area of the irregular figure is the sum of the areas of two rectangles.
The width of one block is 12 and the length of the block is 4.
Next, the width of the other rectangle is 2, but its length is not given. By using the upper rectangle length we can find the length of the lower rectangle. So the right side of the figure is the length of the upper rectangle block plus the length of the lower rectangle block.
Since the total length is 10 units, the right side of the upper rectangle is 4 units long. So the length of the lower rectangle will be 6 units.
So the area of the figure is,
The Area of the figure is the Area of the upper rectangle + Area of the lower rectangle
We know that the Area of the rectangle is, length x width (or) breadth.
So, the area of a figure is , lw + lw = 12(4) + 2(6).
Area of the figure is = 48 + 12 = 60sq.units.
Thus, the total area of the figure is 60 square units.
Example 2:
Find the area of the below-given irregular figure?
Solution:
As given in the question, the given figure is an irregular figure.
Now, we can break the given irregular figure. After separating the figure, we have two blocks one is a triangle block and another one is a rectangle.
Next, we will find the area of the irregular figure. The area of the irregular figure is the sum of the areas of two rectangles.
The rectangle has a length of 8 units and a width of 4 units. We need to find the base and height of the triangle.
On both sides of the rectangle 4units, the perpendicular side of the triangle is 3 units, which is 7- 4 = 3units.
Next, the length of the rectangle is 8units, so the base of the triangle is 3units, which is 8-5= 4units.
Now, we can add the areas then we get the area of the irregular figure.
So, the Area of the figure is the Area of the rectangle + the Area of the triangle.
We know the formulas, the area of the rectangle is, length x width (or) breadth.
The area of the triangle is 1/2bh.
So, the area of a figure is , lw + 1/2bh = 8(4) + 1/2(3)(3).
Area of the figure is = 32 + 4.5 = 36.5sq.units.
Hence, the total area of the given irregular figure is 36.5square units.
Example 3:
The figure is given below. Find the perimeter of the given Pentagon figure?
Solution:
As given in the question, the irregular shape figure is given.
This shape is a pentagon because it has five sides. Even though two of its sides are both 13m, it is an irregular pentagon because not all of its sides are the same length.
Now, we have to find the perimeter of the irregular figure.
To find the perimeter of this irregular shape, we add up the five side lengths.
We make the calculation easier by starting with the largest sides and also looking for number bonds to ten.
The two largest sides are 13m and 13m. These add together to make 26m.
The remaining three sides are 2m, 8m, and 9m. Now the value is 2m + 8m+ 9m = 19m.
Now, adding those two values are, 26m + 19m = 45m.
Thus, the perimeter of this given irregular pentagon is 45m.
Example 4:
Find the perimeter of the below-given figure?
Solution:
As given in the question, the figure is an irregular figure.
Now, we have to find the perimeter of the irregular figure.
To find the perimeter of this irregular shape, we add up all side lengths.
We make the mathematics easier by starting with the largest sides and also looking for number bonds to ten.
The largest sides is 10 cm. The remaining sides are 2cm, 2cm, 8cm, 8cm and 4 cm. Then the value is 2 cm + 2cm + 8 cm+ 8 cm + 4cm= 24cm.
Now, adding those two values are, 10 cm + 24 cm = 34 cm.
Thus, the perimeter of this given irregular figure is 34 cm.
FAQ’s on Perimeter and Area of Irregular Figures
1. What is meant by Irregular Figures?
An irregular figure is a figure that is not a standard geometric shape. Its area cannot be calculated using any of the standard area formulas. But some irregular figures are made up of two or further standard geometric shapes.
2. Define Area of Irregular Figures?
The area of irregular shapes is defined as the quantity of space that is covered by an irregular shape. Irregular shapes are those shapes that do not have equal sides or equal angles. The unit for the area of an irregular shape is expressed in terms of square units, for representative, m2, cm2, in2, or feet2.
3. How to find the perimeter of Irregular Figures?
In order to calculate the perimeter of an irregular polygon we use the following two steps:
- Step 1: Note the length of each side of the given polygon.
- Step 2: Once the length of all the sides is acquired, then the perimeter is adding all the sides length.
Когда вы впервые начинаете вычислять площадь, вы получаете простые формы с четко определенными формулами для нахождения их площади: например, круги, треугольники, квадраты и прямоугольники. Но что происходит, когда вы сталкиваетесь с формой, которая не вписывается легко в эти категории? Пока вы не войдете в дивный новый мир интегральных исчислений, лучший способ найти область неправильных форм — это разделить их на формы, с которыми вы уже знакомы.
TL; DR (слишком долго; не читал)
Самый простой способ вычислить площадь неправильной формы — это разделить ее на знакомые фигуры, вычислить площадь знакомых фигур, а затем сложить эти вычисления площади, чтобы получить площадь неправильной формы, которую они составляют.
-
Соберите свои инструменты
-
Подразделить неправильную форму
-
Найти размеры подразделенных фигур
-
Рассчитать площадь каждой подразделенной формы
-
Обратите внимание, как вы переносите единицы измерения — в данном случае, дюймы — на протяжении всех расчетов. Всегда записывайте свои единицы измерения. В противном случае это одна из самых распространенных ошибок, но также и одна из самых простых, которую можно избежать.
-
Всего областей подразделяемых форм
-
Вместо того, чтобы делить неправильную форму на что-то знакомое, можете ли вы добавить кусок, чтобы сделать его чем-то знакомым? Например, представьте, что ваша фигура выглядит как квадрат, но с одним углом, отрезанным под углом. Можете ли вы «добавить» треугольник в этот отрезанный угол, чтобы превратить его в аккуратный квадрат? Если да, вы можете рассчитать площадь всего квадрата, а затем вычесть площадь треугольника, который вы только что добавили. В результате вы получите площадь неправильной формы, с которой вы начали.
Соберите формулы для форм, с которыми вы уже знакомы. Наиболее распространенные формы и их формулы включают в себя:
Площадь квадрата или прямоугольника = l × w (где l — длина, а w — ширина)
Площадь треугольника = 1/2 ( b × h) (где b — основание треугольника, а h — его вертикальная высота)
Площадь параллелограмма = b × h (где b — основание параллелограмма, а h — его вертикальная высота)
Площадь круга = π_r_ 2 (где r — радиус круга)
Используйте свое воображение, чтобы разделить имеющуюся неправильную форму на более привычные формы. Иногда рисуя форму, затем добавляя линии для подразделений, вы можете визуализировать ее и отслеживать соответствующие измерения для каждого измерения. Например, представьте, что вам нужно найти область пятигранной формы, которая не является шестиугольником, но имеет три перпендикулярные стороны, противоположные «точке». Немного подумав, вы можете разделить это на прямоугольник, который упирается в треугольник, с треугольником, образующим «точку» фигуры.
Вернитесь к формулам площади, чтобы узнать размеры, необходимые для расчета площади каждой подразделенной фигуры. В этом случае вам понадобится базовая и вертикальная высота треугольника, а также длина и ширина (или две соседние стороны) прямоугольника. Если вы работаете над математической задачей в школе, вы, вероятно, получите хотя бы некоторые из этих измерений и, возможно, потребуется использовать некоторую базовую алгебру или геометрию, чтобы найти пропущенные измерения. Если вы работаете в реальном мире, вы можете заполнить некоторые измерения физическими измерениями.
Заполните размеры в формуле площади для каждой подразделенной фигуры. Например, если треугольник имеет основание 6 дюймов и высоту по вертикали 3 дюйма, его формула площади:
1/2 ( b × h ) = 1/2 (6 дюймов × 3 дюйма) = 1/2 (18 дюймов 2) = 9 дюймов 2
Если прямоугольник имеет длину 6 дюймов (что также является стороной, составляющей основание треугольника) и высоту 4 дюйма, его формула площади:
l × w = 6 в × 4 в = 24 в 2
подсказки
Добавьте области подразделенных форм; общая площадь неправильной формы, с которой вы начали. Чтобы завершить этот пример, площадь треугольника 9 в 2, а площадь прямоугольника 24 в 2. Итак, ваша общая площадь:
9 в 2 + 24 в 2 = 33 в 2
подсказки
С помощью данного калькулятора вы можете легко и быстро рассчитать площадь неправильного четырехугольника в условных единицах. Инструмент позволяет определить площадь выпуклой фигуры тремя разными способами: по сторонам, сторонам и углам, диагоналям и углам (первые два вычисления выполняются с ограничениями). Теоретическое обоснование расчета и формулы представлены ниже. Чтобы получить результат — выберите наиболее подходящий метод расчета, заполните поля калькулятора и нажмите кнопку «Рассчитать».
Как найти площадь неправильного четырехугольника?
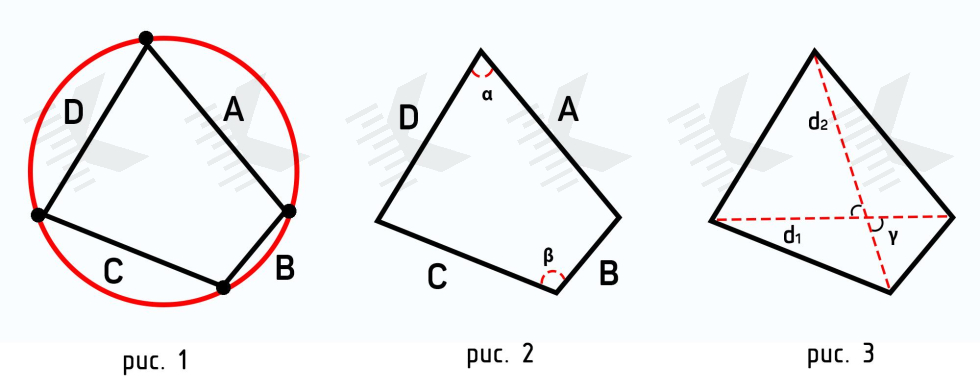
Первый способ расчета основан на формуле Брахмагупты (рис. 1), которая выражает площадь вписанного в окружность четырёхугольника как функцию длин его сторон. Эта формула является обобщением формулы Герона для площади треугольника.
где P — полупериметр, a, b, c, d — длины сторон четырехугольника.
Вторая формула также основывается на формуле Брахмагупты, но на ее расширенной версии (рис. 2), когда необходимо найти площадь произвольного четырехугольника.
где P — полупериметр, a, b, c, d — длины сторон, θ — полусумма противоположных углов четырёхугольника.
В формулах Брахмагупты есть одно ограничение — любая из сторон не может превышать полупериметр. В противном случае стороны четырехугольника не замкнутся. Математически, в формуле появится отрицательное значение.
Последняя формула позволяет найти площадь не самопересекающейся фигуры по проведенным диагоналям и синусу угла между ними (рис. 3). По сути, формула основывается на сумме площадей треугольников, которые образуются диагоналями четырехугольника.
где d1, d2 — диагонали четырехугольника, α — острый угол между диагоналями.
Как найти площадь неправильной фигуры
В школьном курсе геометрии ученики в основном считают площади правильных многоугольников. Между тем, для решения множества практических задач нередко приходится иметь дело с неправильными геометрическими фигурами. С этой проблемой человек сталкивается и при определении размеров дачного участка или придомовой территории, и при расчете количества ткани для шитья, и еще во многих случаях. Высчитать площадь неправильной фигуры можно несколькими способами.
Вам понадобится
- — неправильная геометрическая фигура;
- — измерительные инструменты;
- — прозрачный пластик;
- — линейка;
- — угольник;
- — шариковая ручка.
Инструкция
Рассмотрите геометрическую фигуру и определите, какие ее параметры вам известны. Это могут быть длины сторон или углы. В зависимости от заданных параметров и выберите способ определения площади. Например, разделите ее на несколько фигур, формулы вычисления площади которых вы знаете. Один из самых распространенных методов — провести диагонали из одного угла ко всем остальным вершинам. В этом случае вам нужно знать формулу вычисления площади произвольного треугольника. Но никто не запрещает разделить заданную фигуру и на другие многоугольники. Например, при расчете площади пола в комнате с нишей удобнее разделить неправильную фигуру на два прямоугольника или квадрата.
Для определения площади не слишком большой детали можно воспользуйтесь палеткой. Ее можно сделать самому. Отрежьте прямоугольный кусок любого прозрачного пластика. Разделите его на квадраты, площадь которых вам известна — например, 1х1 или 0,5х0,5 см. Линейка и угольник должны быть точными. Наложите палетку на деталь. Сосчитайте полные квадратики, затем — неполные. Количество неполных квадратов разделите на 2 и приплюсуйте результат к числу целых. Чем мельче деления на палетке — тем точнее будет результат. Аналогично можно посчитать и площадь участка. Роль палетки будет выполнять сетка из квадратов со стороной 1х1 м, начерченная на земле или отмеченная колышками с протянутыми между ними шнурами. Можно ограничиться и разметкой территории на полосы. .
С крупными площадями можно поступить и иначе. Возьмите максимально точный план участка или придомовой территории. Определите масштаб. Воспользуйтесь одним из предложенных способов. Затем полученное количество квадратных сантиметров переведите в нужный масштаб.
Полезный совет
При изготовлении плоских деталей из металла можно вычислить их площадь по эталону с помощью взвешивания. Вырежьте саму деталь и эталон — квадратик, площадь которого удобно рассчитать. Делать их необходимо из одного и того же материала, причем толщина листа должна быть одинаковой и при этом незначительной. Вычислите соотношение масс, а по ней — неизвестную площадь. Однако это не очень точный способ и применять его можно только в крайних случаях.
Любую неправильную фигуру можно представить в виде графика. Каждая точка имеет свои координаты. Представьте каждый отрезок как график функции. Площадь участка от абсциссы до него являет собой определенный интеграл. Высчитайте все интегралы. Площадь фигуры определите с помощью разности интегралов с большим и меньшим значением. Это довольно трудоемкий метод, но он дает наибольшую точность.
Источники:
- http://matemonline.com/rubrika/%D0%B8%D0%BD%D1%82%D0%B5%D0%B3%D1%80%D0%B0%D0%BB/
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.