Формула:
S
=
3
3
·
R2
4
Где: R — радиус описанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
3
3
·
D2
16
Где: D — диаметр описанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
3
3
·
S
4π
Где: S — площадь описанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
3
3
·
P2
16
π2
Где: P — периметр описанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
3
3
·
R2
Где: R — радиус вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
3
3
·
D2
4
Где: D — диаметр вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
3
3
·
S
π
Где: S — площадь вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
3
3
·
P2
4π
Где: P — периметр вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
3
·
a2
4
Где: a — сторона.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
h2
3
Где: h — высота.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано
Площадь треугольника равна произведению 3, квадратного корня из 3, квадрата периметра описанной окружности поделенному на произведение 16 и квадрата π.
Расчёт площади равностороннего треугольника по периметру
Калькулятор рассчитывает площадь равностороннего треугольника по периметру.
Формула площади равностороннего треугольника по периметру
Где P — периметр треугольника
Разберём пример
Дан равносторонний треугольник c периметром 6, необходимо найти его площадь
Как найти площадь равностороннего треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти площадь равностороннего треугольника
Чтобы найти площадь равностороннего (правильного, равноугольного) треугольника воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить площадь равностороннего треугольника вам нужно знать следующие параметры (либо-либо):
- длину равных сторон (a)
- высоту (h)
- радиус описанной окружности (R)
- радиус вписанной окружности (r)
- периметр треугольника (P)
Введите их в соответствующие поля и узнаете площадь равностороннего треугольника (S).
Как посчитать площадь равностороннего треугольника зная длину равных сторон
Чему равна площадь равностороннего треугольника если длина стороны
a =
?
Ответ:
S =
0
Какова площадь равностороннего треугольника (S) если известна длина сторон (a)?
Формула
S =√3/4 ⋅ a²
Пример
Если сторона a = 2 см, то:
S = √3/4 ⋅ 2² = 1.732/4 ⋅ 4 ≈ 1.732 см2
Как посчитать площадь равностороннего треугольника зная его высоту
Чему равна площадь равностороннего треугольника если его
высота h =
?
Ответ:
S =
0
Какова площадь равностороннего треугольника (S) если известна его высота (h)?
Формула
S =h² / √3
Пример
Если высота h = 3 см, то:
S = 3²/√3= 9/1.732 ≈ 5.19 см2
Как посчитать площадь равностороннего треугольника зная радиус описанной окружности
Чему равна площадь равностороннего треугольника если радиус описанной окружности
R =
?
Ответ:
S =
0
Какова площадь равностороннего треугольника (S) если известен радиус описанной окружности (R)?
Формула
S =3⋅√3/4 ⋅ R²
Пример
Если радиус описанной окружности R = 4 см, то:
S = 3 ⋅ √3/4 ⋅ 4² = 3 ⋅ 1.732/4 ⋅ 16 = 1.299 ⋅ 16 ≈ 20.784 см2
Как посчитать площадь равностороннего треугольника зная радиус вписанной окружности
Чему равна площадь равностороннего треугольника если радиус вписанной окружности
r =
?
Ответ:
S =
0
Какова площадь равностороннего треугольника (S) если известен радиус вписанной окружности (r)?
Формула
S =3⋅√3 ⋅ r²
Пример
Если радиус вписанной окружности r = 1 см, то:
S = 3⋅√3 ⋅ 1² = 3 ⋅ 1.732 ⋅ 1 ≈ 5.196 см2
Как посчитать площадь равностороннего треугольника зная его периметр
Чему равна площадь равностороннего треугольника если его периметр
P =
?
Ответ:
S =
0
Какова площадь равностороннего треугольника (S) если известен его периметр (P)?
Формула
S =√3/36 ⋅ P²
Пример
Если периметр P = 8 см, то:
S = √3/36 ⋅ 8² = 1.732/36 ⋅ 64 ≈ 3 см2
См. также
Содержание:
- Формула
- Примеры вычисления площади равностороннего треугольника
Формула
Чтобы найти площадь равностороннего треугольника (рис. 1), нужно квадрат его стороны умножить на
$sqrt{3}$ и поделить на четыре, то есть
$$mathrm{S}_{Delta}=frac{a^{2} sqrt{3}}{4}$$
Эту формулу легко получить из общей
формулы для площади треугольника
$$mathrm{S}_{Delta A B C}=frac{1}{2} a b sin alpha$$
при условии, что $a=b$ (так как треугольник равносторонний) и
$alpha=60^{circ}$ (угол равностороннего треугольника).
Напомним, что треугольник называется равносторонним, если все его стороны равны.
Примеры вычисления площади равностороннего треугольника
Пример
Задание. Найти площадь равностороннего треугольника
$ABC$, если известно, что его сторона равна 2 дм.
Решение. Подставив заданное значение в формулу, будем иметь:
$mathrm{S}_{Delta A B C}=frac{2^{2} cdot sqrt{3}}{4}=frac{4 cdot sqrt{3}}{4}=sqrt{3}$ (дм2)
Ответ. $mathrm{S}_{Delta A B C}=sqrt{3}$ (дм2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти площадь равностороннего треугольника
$ABC$, если его высота равна 3 м.
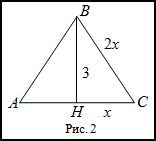
Решение. Сделаем чертеж (рис. 2).
Так треугольник равносторонний, то его высота $BH$ является и
медианой, а это означает, что $AH=HC$ .
Пусть $HC=x$, тогда $AC=2HC=2x=BC$. Рассмотрим прямоугольный треугольник
$BHC$. Записываем для него теорему Пифагора:
$$B C^{2}=B H^{2}+H C^{2}$$
$$(2 x)^{2}=2^{2}+x^{2}$$
Решаем полученное уравнение относительно $x$ :
$4 x^{2}-x^{2}=9 Rightarrow 3 x^{2}=9 Rightarrow x^{2}=3 Rightarrow H C=x=sqrt{3}$ (м)
Отсюда получаем, что
$A C=2 x=2 sqrt{3}$ (м)
А тогда искомая площадь
$mathrm{S}_{Delta A B C}=frac{(2 sqrt{3})^{2} cdot sqrt{3}}{4}=frac{12 sqrt{3}}{4}=3 sqrt{3}$ (м2)
Ответ. $mathrm{S}_{Delta A B C}=3 sqrt{3}$ (м2)
Остались вопросы?
Здесь вы найдете ответы.
Как можно вычислить площадь равсностороннего треугольника?
Согласно формуле, по которой вычисляется площадь S треугольника с равными
сторонами, она равна:
S = √3/4*а, в которой а – это длина стороны фигуры.
Площадь можно также найти следующим образом:
S = a*h/2, где h – это высота.
Высоту можно вычислить, используя теорему Пифагора:
h = а² — (а/2)².
Как можно рассчитать площадь равностороннего треугольника, если известно,
что площадь треугольной фигуры, отсекаемой от него средней линией,
составляет 6 см. кв.?
Обозначим имеющийся треугольник с равными сторонами как АВС. Обозначим
длину стороны как а, и получим, что АВ=ВС=АС=а. Среднюю линию обозначим
как МК. Тогда Sмвк = 6 см. кв.
В случае с равносторонним треугольником:
S = а²√3/4
Зная свойство средней линии треугольника, можно записать следующее
равенство:
МК = АС/2 = а/2.
В этом случае площадь отсекаемого треугольника равна:
Sмвк = (а/2)²*√3/4 = а²√3/16 см.кв.
В условии дано, что Sмвк = 6 см.кв., тогда:
а²√3/16 = 6
а² = 96/√3.
Площадь равностороннего треугольника:
S = а²√3/4 = (96√3)/(4√3) = 96/4 =24 см.кв.
Как можно вычислить площадь равностороннего треугольника при условии, что
его периметр составляет 24 см.?
Найдем сторону равносторонней треугольной фигуры, разделив его периметр на
3:
а = 24:3 = 8 см.
Тогда площадь этой фигуры равна:
S =1/2a²sin 60° = 1/2*64*√3/2 = 16√3 см.кв.
Что представляет собой формула площади равностороннего треугольника?
Обозначив одну из сторон равносторонней треугольной фигуры как а, а
высоту, проведенную к ней, — как h, то формула расчета площади этой фигуры
будет выглядеть так:
S=ah/2.
Принимая во внимание то, что все стороны данной треугольной фигуры равны,
то его высоту можно выразить через сторону и вычислить, используя теорему
Пифагора:
h² = а²-(а/2)² = h² = а²- а²/4 = 3а²/4
h = (а√3)/2
Тогда площадь данной фигуры равна:
S = ½ a* h = ½ a*(а√3)/2 = (a²√3)/4
Как выразить длину стороны а из формулы площади равностороннего
треугольника?
Для расчета площади треугольника, длины всех сторон которого равны,
используется формула:
S=a²√3/4
Перенесем 4 в правую часть равенства:
4S=a²√3.
Тогда:
a² = 4S/√3
а = √4S/√3.
Какая формула используется для вычисления площади равностороннего
треугольника с длиной стороны а?
Если известно, что сторона равносторонней треугольной фигуры равна а, то
его площадь рассчитывается так:
S = а²√3/4.
Каким образом можно привести доказательство теоремы о площади
равностороннего треугольника?
Треугольник имеет два катета – АВ и ВС. Его гипотенуза – ВС. Так как
фигура является равносторонней, то АВ = АС.
Требуется доказать, что площадь треугольной фигуры, стороны которой
одинаковы, равна произведению длин его катетов, разделенному на два.
Превратим имеющийся треугольник в квадрат, проведя перпендикуляр из его
углов, и получим что:
ΔВАС = ΔВСD.
Площадь квадрата равна:
S = а*b.
Диагональ квадрата ВС является гипотенузой треугольника, которая делит
квадрат на 2 равные части. Из этого следует, что площадь треугольника
равна половине площади квадрата. Что и требовалось доказать.
Как вычислить площадь равностороннего треугольника со стороной длиной 9 см.?
Имеется треугольник АВС с равным сторонами.
ВН = 9 см.
Площадь данной фигуры находится по формуле:
S=1/2*АС*ВН,
в которой АС – основание треугольной фигуре, по длине равное любой из
сторон (равносторонний Δ), ВН – высота.
Предположим, что АС = 2а см. Тогда:
АН = АС/2 = ½*2а = а см.
Согласно теореме Пифагора:
АВ² = ВН²+АН².
В данном случае:
(2а)² = 9²+а²
Переносим а² в правую часть уравнения:
4а²-а² = 81
Упрощаем:
3а² = 81.
Отсюда:
а² = 81/3 = 27
а=√27=√9×3=3√3 см.
Теперь можно найти площадь:
S=1/2*9*3√3=1/2*27/√3=27√3/2=13,5√3 см.кв.
Какому числу равна площадь равностороннего треугольника с основанием длиной
6 см.?
Известна формула расчета площади треугольника:
S=1/2*h*b.
Проведем высоту h, которая в равностороннем треугольнике представляет
собой также биссектрису и медиану.
Воспользуемся теоремой Пифагора для вычисления высоты:
h = √(36-9) = √27 см.
Тогда:
S = h*3 = 3√27 см.кв.
Возможно ли привести доказательство того, что площадь равностороннего
треугольника равна √3*a²/4, в которой длина его стороны обозначена как а?
Доказать, что приведенное в задании утверждение является верным, можно,
если превратить имеющуюся треугольную фигуру в параллелограмм/, площадь
которого равна произведению длины стороны и высоты.
Параллелограмм состоит из двух треугольников, которые равны. Это значит,
что площадь одной из треугольных фигур находится так:
S = a*h /2.
Высоту можно выразить через определение синуса.
Все углы в равносторонней треугольной фигуре равны и составляют 60
градусов (180/3).
sin(60) = V3/2.
Из определения синуса следует:
h/a = sin(60).
Это значит, что:
h = a*V3/2.
Значит:
S = a*a*V3/4.
Почему площадь равностороннего треугольника равна a^2√3/4?
Известно, что площадь любого треугольника можно найти по формуле:
S = 1/2*a*b*sinA,
в которой стороны треугольника обозначены как а и b, а угол, образованный
ими, — как А.
Доказано, что каждый угол равносторонней треугольной фигуры составляют 60
градусов (sin60 =sqrt(3)/2), а его стороны имеют одинаковые длины. Если
подставить эти значения в формулу, то получим:
S = a22√3/4.
Как найти площадь равностороннего треугольника при условии, что длина каждой
его стороны составляет 12 см.?
Площадь треугольника с равными сторонами вычисляется по формуле:
S = √3/4*a².
В данном случае:
S= √3/4*12²= √3*144 /4*1 = 36√3 ≈ 62,35 см.кв.
Согласно формуле Герона:
S = √(р(р-а)(р-a)(p-a))
Для данного треугольника:
Р = 12*3 = 36 см.
Р = р/2 = 36/2 = 18 см.
Тогда:
S = √ (18× (18-12)³) = √(18*6³) = √(18×216)=√3888 ≈ 62,35 см. кв.
Как вычислить площадь правильного равностороннего треугольника, зная радиус
круга R?
Площадь треугольника с одинаковыми сторонами считается как:
S = a²√3/4.
Радиус r окружности, которая вписана в данный Δ, равен a√3/6. Значит:
а = 2√3r.
Считаем площадь треугольника:
S = 4*3r²√3/4 = 3√3r².
Радиус R окружности, которая описана около правильной треугольной фигуры,
равен a/√3. Следовательно, а = R√3.
В этом случае:
S = R²*3√3/4 = 3√3R²/4.
Известно, что площадь правильного треугольника равна 100√3 м.кв. Как
вычислить его сторону?
Площадь треугольника равна:
(a²√3)/4.
В данном случае:
100√3=(a²√3)/4
Тогда:
a²√3=400√3.
Находим а:
a²√3 = 400√3
a² = 400
a = 20 см.
Чему равна площадь правильного треугольника при условии, что диаметр
окружности, вписанной в него, = 10 см.?
Если d = 10 см., то r = 10/2 = 5 см.
Известно, что:
r = а√3/6, где а – это длина стороны правильного Δ.
Значит:
5 = а√3/6.
Отсюда:
а = 30/√3 = 10√3 см.
Тогда:
SΔ = a²√3/4 =(10√3)³ *√3/4 = 75√3 см. кв.
Чему равна площадь правильного треугольника со стороной 4 дм.?
Известно, что:
S = 1/2 * a * a sin 60 = 1/2 * 4 * 4 * √3/2 = 4√3 дм.кв.
Площадь также можно найти так:
S = a²√3/4 = 16√3/4 = 4√3 дм.кв.
Как найти площадь правильного треугольника, зная, что длина описанной около
него окружности равна 4Пи см.?
Длина окружности через радиус находится так:
L=2πR.
Значит:
R=L/2π=4π/2π=2 у.е.
Имеем правильный треугольник, значит длина его стороны:
a=R*√3=2√3 у.е.
Можем найти SΔ:
S = √3/4a² = √3/43*3 = 3√3 у.е.кв.
Чему равна площадь правильного треугольника и его стороны, если его высота =
14 см.?
В правильном треугольнике длины всех сторон одинаковы. Это значит, что
каждую из них можно обозначить как х. Тогда:
Р (периметр) = х + х + х = 3х см.
Площадь будет равна:
S = 1/2 h * x = 14/2*x = 7х см.кв.
Как найти площадь правильного треугольника с равными сторонами при условии,
что радиус круга R?
Площадь треугольной фигуры с равными сторонами считается как:
S = a²√3/4.
Радиус окружности, вписанной в этот Δ, составляет a√3/6. Тогда а = 2√3r.
Находим площадь треугольника:
S = 4*3r²√3/4 = 3√3r².
Радиус R окружности, которая описана около правильного Δ, составляет a/√3.
Это означает, что а = R√3.
Теперь можем высчитать площадь треугольника:
S = R²*3√3/4 = 3√3R²/4.
Как найти площадь правильного треугольника при условии, что расстояние от
его центра до вершины составляет 2 м.?
Центр правильно треугольной фигуры также является центральной точкой
описанной около нее окружности. Ее радиус представляет собой расстояние от
центра до вершины фигуры:
а=R√3=2√3
Все углы в правильном треугольнике являются одинаковыми и равны по 60
градусов (180/3).
Площадь треугольной фигуры рассчитывается как:
а²sin60°/2=(2√3)²√3/2/2=6√3 м.кв.
Как найти площадь правильного треугольника, если определено, что сторона
имеет длину, аналогичную длине стороны ромба с диагоналями 10 см. и 12 см.?
Предположим, что BD = 10 см., а АС = 12 см.
Диагонали ромба перпендикулярны и делятся на две равные части, пересекаясь
в определенной точке.
ΔАВО: ∠АОВ = 90°, АО = АС/2 = 6, ВО = BD/2 = 5.
Согласно теореме Пифагора:
АВ = √(АО² + ВО²) = √(36 + 25) = √41.
Треугольник имеет равные стороны, длина каждой из которых аналогична длине
стороны ромба:
а = √41.
Тогда:
SΔ = a²√3/4 = 41√3/4 см.кв.
Как найти площадь правильного треугольника периметром 6 см.?
Если длина стороны правильного треугольника указана, то его площадь
вычисляется следующим образом:
S = a²√3/4.
Согласно определению правильного треугольника, длины всех его сторон
одинаковые. Исходя из этого можно найти его сторону, разделив периметр на
три:
а = 6/3 = 2 см.
Ищем площадь, подставив в равенство значение а:
S = 2²√3/4 = S 4√3/4 = √3 см.кв.
Как найти площадь правильного треугольника при условии, что окружность,
которая вписана в него, имеет радиус длиной 4 см.?
Площадь треугольника, имеющего стороны одинаковой длины, может быть
рассчитана через длину его стороны без применения формулы радиуса
окружности, которая вписана в него. Для данной фигуры верно утверждение о
том, что высота, биссектриса и медиана делятся в точке пересечения в
отношении 2:1. При схематичном изображении можно увидеть, что треугольная
фигура АВС включает 6 треугольников с прямыми углами, которые имеют
одинаковый катет (R) и гипотенузу (АО=ВО=СО). Следовательно, площадь
треугольника АВС будет представлять собой сумму площадей всех 6
треугольников, формирующих его.
Какова формула вычисления площади равностороннего треугольника со стороной
а?
Если сказано, что сторона равносторонней треугольной фигуры равна а, то
его площадь можно найти:
S = a²√3/4.
Как определить, чему равна длина стороны треугольника с равными сторонами,
зная формулу, по которой вычисляется площадь равностороннего треугольника
(S=√3/4 а²) и то, что она равна 9√3см²?
Если S=√3/4 а², то в данном случае S=9√3, что означает: 9√3=√3/4 а².
Выразим а²:
а² = 9√3:√3/4 = 9√3 x 4√3 = 36
а = +-√36 = +- 6.
Так как длина стороны не может быть отрицательным числом, то a = 6 см.
Какой вид имеет формула, которая отражает зависимость площади
равностороннего треугольника от длины его сторон?
Доказано, что равносторонний треугольник имеет равные углы по 60 градусов.
Также известна формула вычисления площади данной фигуры путем умножения
длин двух его сторон и синуса угла, который они образуют:
S = 1/2*a*a*sin 60 = a²√3/4 см.кв.
Чему равна площадь равностороннего треугольника и длина его медианы, если
известно, что его сторона составляет а?
Если указано, что длина стороны равностороннего треугольника составляет а,
то его площадь равна:
S=a²√3/4.
Медиана, проведенная в треугольнике с равными сторонами, также
представляет собой его биссектрису и высоту. Из этого следует, что:
h=a√3/2.
Ответ: Площадь треугольника = a²√3/4 см.кв., его медиана = a√3/2 см.
Как определить площадь равностороннего треугольника со стороной, длина
которой составляет 8√2 см?
В случае с треугольником с равными сторонами, высота представляет собой
также медиану, делящую на две равные части сторону, на которую она
опущена. Если применить в данном случае теорему Пифагора, то высота равна:
h = √((8√2)²-(4√2)²)=4√6 см.
Теперь есть возможность найти площадь:
S = (1/2)*8√2*4√6 = 32√3 см. кв.
Площадь также можно найти по формуле для треугольника с равными сторонами:
S =(√3/4)*a² или S =(√3/4)*128 = 32√3 см. кв.
Дано два равносторонних треугольника, площадь одного из которых превышает
площадь другого в три раза. Чему будет равна сторона второго равностороннего
треугольника, при условии, что сторона первого из них составляет 1 см.?
Для расчета площади треугольника с равными сторонами есть формула:
S = a²√3/4.
Найдем площадь меньшего из треугольников, подставив значение а:
S₁ = 12 √3/4 = √3/4 см.кв.
Известно, что площадь второго треугольника больше площади первой фигуры в
три раза. Тогда:
S₂ = 3√3/4.
Очевидно, что сторона большего треугольника составляет √3 см.
Сторона равностороннего треугольника равна 14 см. Чему будет равна его
площадь, умноженная на √3?
Формула площади для треугольника с равными сторонами:
S = а²*√3/4.
Подставляем значение а:
S = 14²*√3/4 = 49√3 см. кв.
Умножаем полученное число на √3:
49√3*√3 = 49*3 = 147 см.
Читать дальше: как найти площадь круга.
Фигура с 3 отрезками в геометрии определяется, как треугольник. Равносторонний тот, у которого все
стороны имеют одинаковый размер.
Чтобы произвести измерения площади геометрической фигуры, специалисты применяют универсальную
формулу, которая выглядит следующим образом: S = 1/2 * ah, где S — площадь фигуры, а — длина (чтобы
узнать величину, необходимо измерить расстояние от А до В, h — высота. Для определения переменной
необходимо провести медиану. Ее размер и будет высотой.
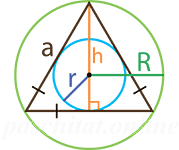
Также определить параметры равносторонней
фигуры можно другими способами: через радиус и диаметр вписанной и описанной окружности, площадь
описанного и вписанного круга, периметр описанной и вписанной окружности, сторону, высоту.
- Площадь равностороннего треугольника через радиус описанной
окружности - Площадь равностороннего треугольника через диаметр
описанной окружности - Площадь равностороннего треугольника через площадь
описанного круга - Площадь равностороннего треугольника через длину описанной
окружности (периметр) - Площадь равностороннего треугольника через радиус вписанной
окружности - Площадь равностороннего треугольника через диаметр
вписанной окружности - Площадь равностороннего треугольника через площадь
вписанного круга - Площадь равностороннего треугольника через длину вписанной
окружности (периметр) - Площадь равностороннего треугольника через сторону
- Площадь равностороннего треугольника через высоту
Через радиус описанной окружности
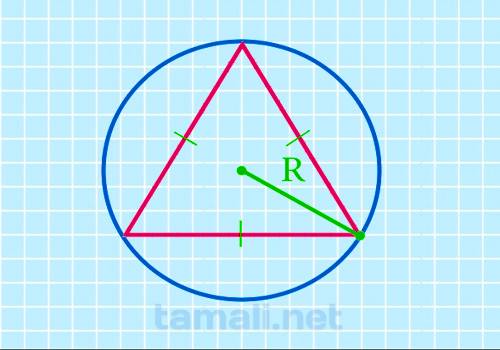
Треугольник может иметь лишь 1 описанную окружность. Для этого три отрезка геометрической фигуры
должны быть внутри круга. Зная радиус, который относится, к описанной окружности, можно применить
эту формулу для выполнения расчетов:
S = 3*√3 / 4*R²
где S — площадь фигуры, R — радиус описанной окружности.
Цифр после
запятой:
Результат в:
Это размеры отрезка от центра круга до любой вершины. Например, если R=5 см, то определение размеров
будет выполняться следующим образом:
S = 3√3/4*5²=3*1.732/4*25 = 32.476 м². Таким образом, применив формулу,
можно узнать искомую величину.
Через диаметр описанной окружности
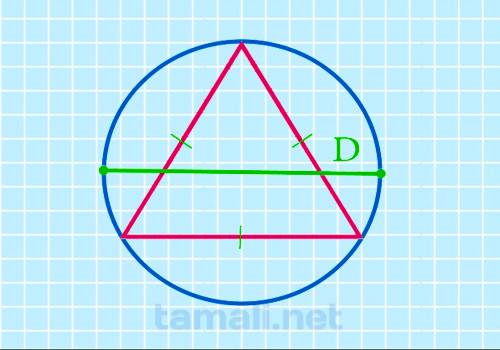
Под диаметром понимается отрезок, проходящий через центр окружности, а также соединяющий две точки.
Другими словами, длина упомянутой линии и будет значением диаметра. Если значение диаметра
неизвестно, но известен радиус, переменную можно рассчитать с помощью данного метода: D=2R, где R —
радиус, D — диаметр. Определив диаметр описанной фигуры, можно применить такую формулу для
расчетов:
S = 3 * √3 / 16 * D²
где S — площадь фигуры, D — диаметр описанного круга.
Цифр после
запятой:
Результат в:
То есть, длина луча, который начинается от 1 стороны круга. Также он проходит через центр окружности
и описанного геометрического объекта. Завершается отрезок на противоположной части круга. К примеру,
если D=6 м, то расчет размеров будет выполняться следующим образом: S = 3√3/16*6²=3*1.732/16*36 = 11.691 м²
Применив эту формулу, можно найти искомую величину.
Через площадь описанного круга
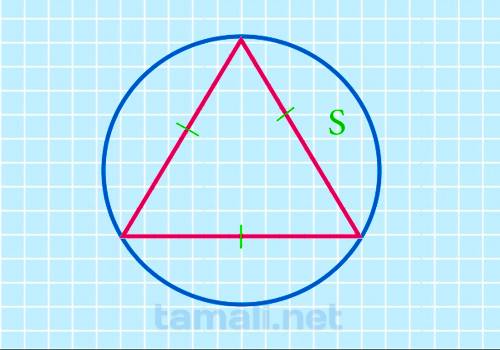
После того, как размеры круга станут известны, можно найти с помощью них площадь геометрической
фигуры. Для этого необходимо воспользоваться математической формулой:
S1 = 3 * √3 / 4 * π * S2
где S1 — площадь треугольника, S2 — площадь круга.
Цифр после
запятой:
Результат в:
Для вычисления потребуется знать радиус окружности, чтобы с помощью него определить размеры круга.
Она рассчитывается по данной формуле: S = π * R², где R — радиус, π — число Пи, значение величины
всегда остается неизменным и равно 3,1415926535. На практике расчет переменной круга проще показать
на конкретной задаче. Например, если R=5, π = 3,14, то следовательно S = 3,14*25 = 78,5
К примеру, если S2= 78,5, то расчет размеров будет выполняться следующим образом: S = 3 * √3 / 4π
*78,5=3*1.732/4π*78,5 = 32.459 м². Используя такой метод можно определить S равностороннего
объекта.
Через радиус вписанной окружности
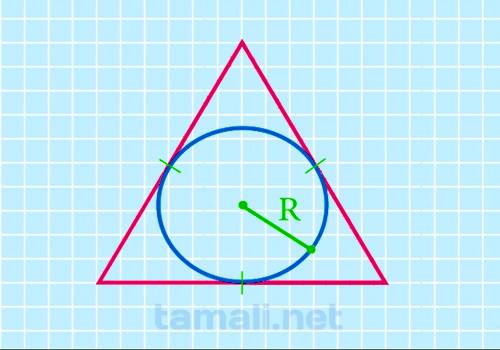
У треугольника может быть только одна вписанная окружность. Для этого круг должен быть внутри фигуры,
а также соприкасаться со всеми ее сторонами. Если указан радиус, который относится, к вписанной
окружности, можно использовать эту формулу для определения общих размеров искомой фигуры:
S = 3 * √3 * R² где S — площадь геометрической фигуры, R — радиус вписанного круга. Это длина
прямой от центра круга до любой стороны.
Цифр после
запятой:
Результат в:
К примеру, если R=5, то расчет будет осуществляться так: S = 3√3*5²=3*1.732*25 = 129.903 м². Таким
образом, следуя данной формуле, можно решить задачу.
Через длину описанной окружности (периметр)
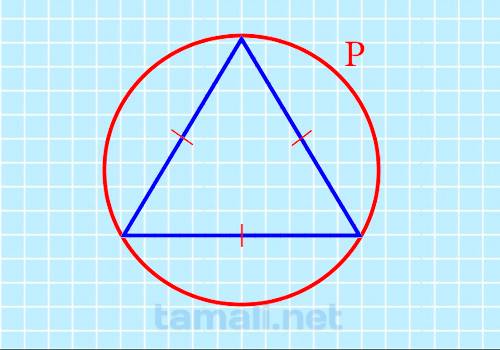
После того, как периметр круга будет подсчитан, можно определить с помощью него площадь
геометрического объекта. Для этого необходимо подставить полученное значение в формулу:
S = 3√3/16π² * P² где S — площадь треугольника, P — периметр или длина круга.
Цифр после
запятой:
Результат в:
Длина, а также периметр описанной окружности определяются как луч, охватывающий геометрическую фигуру
в 2 измерениях. Периметр рассчитывается по такой формуле: S = 2πR где R — радиус, π — число Пи.
Значение величины считается постоянным и равно 3,1415926535.
На практике расчет длины круга легче продемонстрировать на определенной задаче. Например, если R=5, π
= 3,14, то следовательно Р круга = 2 * 3,14 * 5 = 31,4. К примеру, если P= 31,4, то расчет
размеров будет производиться следующим образом: S = 3 * √3 / 16 π² * 31,4²=3 * 1.732 / 16 * 9,85 =
32.443 м². С помощью такой схемы можно рассчитать S искомой фигуры.
Через диаметр вписанной окружности
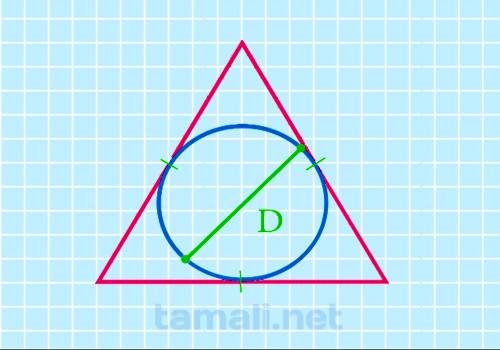
Зная диаметр вписанной окружности, рекомендуется использовать такую формулу для определения
площади:
S = 3 * √3 / 4 * D²
где S — площадь геометрической фигуры, D — диаметр вписанной окружности.
Цифр после
запятой:
Результат в:
Диаметр в геометрии определяется, как луч, который проходит через центр окружности и соединяет две
точки. Если сказать проще, то длина упомянутой линии и будет значением диаметра. В ситуации, когда
известен радиус, но нет данных о диаметре, необходимо рассчитать его с помощью этой формулы: D=2R, где R — радиус, D — диаметр. То есть, длина отрезка, который
начинается от стороны круга, а также пересекает центр и заканчивается на противоположной стороне.
К примеру, если D=6, то расчет размеров производится, как на представленном примере: S = 3 * √3 / 4 * 6²=3 * 1.732 / 4 * 36 = 32.475 м².
Через длину вписанной окружности (периметр)
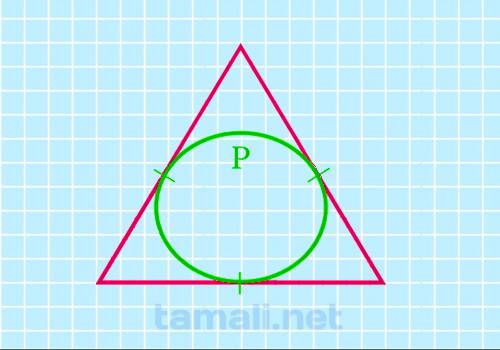
После нахождения значения периметра, можно определить с помощью него параметры требуемого объекта.
Для этого потребуется подставить полученное число в формулу:
S = 3√3/4π*P²
где S — площадь треугольника, P — длина вписанной окружности.
Цифр после
запятой:
Результат в:
Длина или периметр окружности определяются как луч, охватывающий геометрическую фигуру в 2
измерениях. Периметр рассчитывается по формуле: S = 2πR, где R — радиус, π
— число Пи. Значение величины считается постоянным и равно 3,1415926535. Чтобы было нагляднее, длину
круга легче продемонстрировать на конкретной задаче. Например, если R=5, π = 3,14, то следовательно
P круга = 2* 3,14*5 = 31,4.
К примеру, если P= 31,4, то расчет размеров будет производиться следующим образом: S = 3√3/4π*31,4²=3*1.732/4*3.14*985 = 407,691 м². С помощью такого
способа можно рассчитать S искомой фигуры.
Через сторону
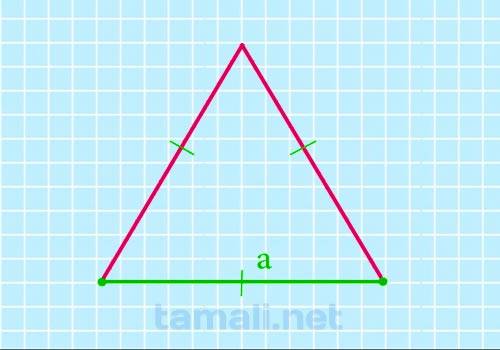
Все отрезки у этого геометрического объекта равны между собой. Поэтому, достаточно знать длину
любого. Определив сторону фигуры, можно применить следующую формулу для расчета размеров:
S = √3/4a²
где S — площадь геометрического объекта, a — длина отрезка.
Цифр после
запятой:
Результат в:
К примеру, если a =5, то расчет размеров будет выполняться следующим образом: S = √3/4*5²=3*1.732/4*25 = 10.825 м².
Через высоту
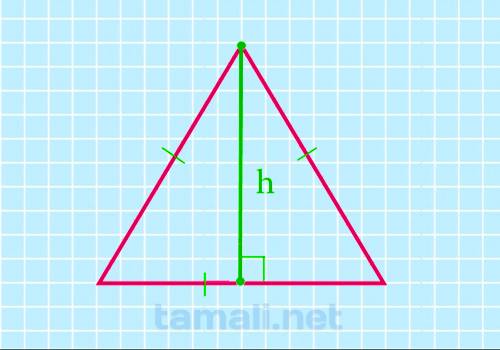
Медиана в такой фигуре является высотой и биссектрисой. По этой причине достаточно провести медиану,
чтобы узнать высоту объекта. Зная высоту, можно применить следующую формулу для расчета:
S = h²/√3
где S — площадь, h — высота.
Цифр после
запятой:
Результат в:
Например, если h =5, то расчет S будет осуществляться следующим способом: S = 5²/√3=25/1.732 = 14.433 м².
С помощью этой формулы можно узнать общие размеры равностороннего треугольника.
Через площадь вписанного круга
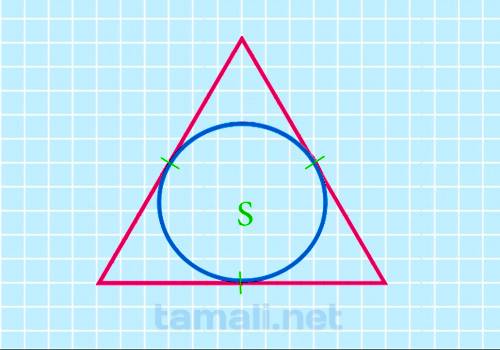
После того, как переменные круга найдены, предстоит вычислить с помощью них S фигуры. Для этого
потребуется применить формулу:
S1 = 3*√3/π*S2
где S1 — площадь треугольника, S2 — площадь вписанного круга.
Цифр после
запятой:
Результат в:
Для вычисления потребуется знать радиус окружности, чтобы с помощью него определить общие размеры
круга. Чтобы их рассчитать потребуется данная формула: S= π*R², где R —
радиус, π — число Пи. Константа, которая всегда равна 3,1415926535. На практике расчет площади круга
нагляднее продемонстрировать на конкретном упражнении. Например, если R=6, π = 3,14, то
следовательно S круга = 3,14*36 = 113
К примеру, если S2= 113, то расчеты будут выглядеть следующим образом: S = 3√3/π*113=3*1.732/π*113 = 186,900 м²
Практическое применение формулы для определения площади равностороннего треугольника
Чтобы было проще понять, рекомендуется начертить на листе бумаге объект с 3 равными отрезками. У него
необходимо обозначить каждую сторону латинскими буквами, например, «А» «B» «C». В результате должна
получиться фигура, у которой стороны АВ=ВС=АС.
Треугольник, который имеет стороны одного размера, обладает следующими есть свойствами:
- Все углы между собой равны. ∠А=∠B=∠C. Из курса геометрии известно, что у данной фигуры сумма
углов составляет 180°. Следовательно, = 60°. - Медиана считается биссектрисой, а также высотой. Медиана — линия, которая соединяет вершину
треугольника с противоположным отрезком. Биссектриса — отрезок, разделяющий угол пополам.
Правильно рассчитать размеры геометрической фигуры полезно не только для сдачи экзаменов, но и в
повседневной жизни. Например, есть задача — оформить грядку. Для нее потребуется земля. Чтобы
понимать, сколько купить материала, необходимо знать размеры участка. Если объект прямоугольной
формы все просто — достаточно умножить длину на ширину. Однако, в случае с треугольниками придется
использовать другую формулу.
Кроме того, необходимо понимать, какой тип фигуры представлен в задаче: равнобедренный или
равносторонний.
Таким образом, понимая, как правильно вычислить S геометрической фигуры с 3 сторонами, можно легко
решить задачу по геометрии или применить знания в реальной жизни.
Важно учитывать, что вышеперечисленные формулы подходят для вычисления размеров именно
равностороннего треугольника. К примеру, чтобы определить площадь прямоугольного треугольника
потребуется знать длину стороны «а» и «b», поскольку у них разное значение. Также необходимо
измерить или найти гипотенузу прямоугольной геометрической фигуры.
Умение вычисления S геометрического объекта по формуле будет полезно при выполнении математических
упражнений. Кроме того, такие знания пригодятся в реальной жизни, когда потребуется измерить размеры
объекта треугольной формы. Например, при копании грядок на огороде или для проведения строительных
работ по возведению здания в виде пирамиды.