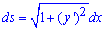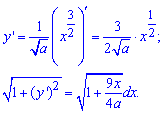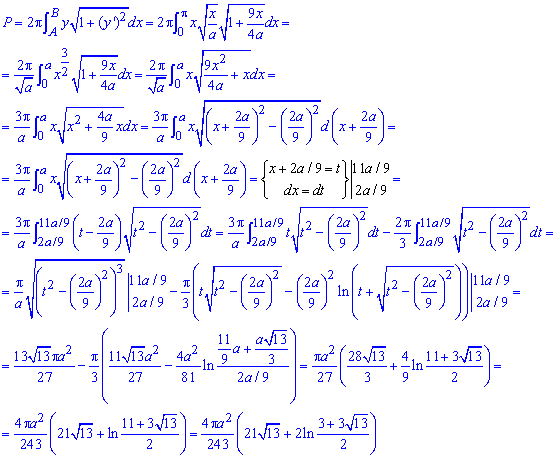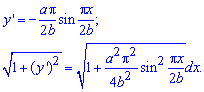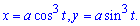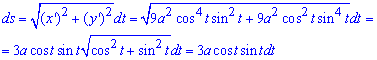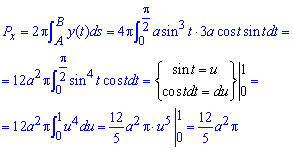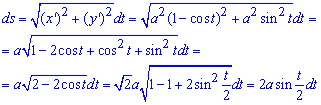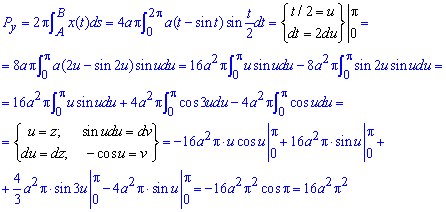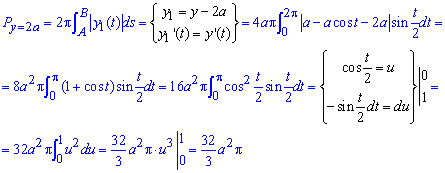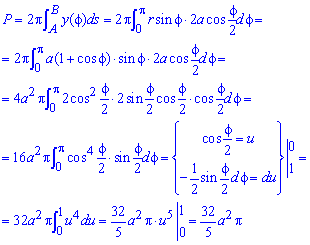Площадь поверхности вращения тела
Пусть даны прямая и кривая
, лежащая в одной плоскости с
и расположенная по одну сторону от этой прямой. При вращении кривой
вокруг оси
получается поверхность
, площадь которой мы и хотим сначала определить, а потом вычислить (см. 46).
Начнем со случая, когда — отрезок, один конец которого отстоит от
на
, а другой — на
(рис. 58). Тогда, как доказывается в школьном курсе геометрии, площадь поверхности вращения (боковой поверхности усеченного конуса) выражается формулой
. В этом случае при
имеем:
(1)
Таким образом, боковая поверхность конуса заключена между произведением длины образующей на длину наименьшей окружности и произведением длины образующей на длину наибольшей окружности.
То же самое неравенство будет иметь место и при вращении любой ломаной линии, расположенной по одну сторону от оси вращения:
(2)
где и
— наименьшее и наибольшее расстояния точек ломаной от оси
, и
— длина ломаной.
Для доказательства достаточно применить неравенство (1) к каждому звену ломаной, сложить полученные результаты и учесть что и для любого звена имеем
и
(здесь
и
— наименьшее и наибольшее расстояния точек k-ro звена от оси вращения).
Естественно потребовать, чтобы неравенства (2) выполнялись для любой спрямляемой кривой. Кроме того, потребуем, чтобы площадь поверхности вращения обладала свойством аддитивности: при разбиении дуги на части
должно выполняться равенство
(3)
где — поверхность, полученная при вращении всей дуги
, а
— при вращении части
.
Если применить к каждой части неравенства (2), то получим, что
где — длина дуги
, а
и
— наименьшее и наибольшее расстояния точек этой дуги
от оси вращения. Складывая эти неравенства и учитывая требование аддитивности, получаем, что
(4)
Иными словами, площадь поверхности вращения должна разделять множества
Именно это требование мы и примем за определение площади поверхности вращения.
Если — плоская спрямляемая кривая, лежащая по одну сторону от оси
, то площадью поверхности
, получаемой при вращении этой кривой вокруг оси
, называется число
, разделяющее множества
соответствующие всевозможным разбиениям дуги . Здесь
и
имеют указанный выше смысл.
Докажем сейчас, что это число существует и единственно, а затем выведем для него выражение в виде интеграла. Выберем на плоскости систему координат, такую, что ось абсцисс совпадает с осью вращения. Зададим параметризацию кривой , выбрав в качестве параметра длину
дуги
, соединяющей в заданном направлении фиксированную точку
кривой
с произвольной точкой
этой кривой (рис. 59). Тогда
и
будут наименьшими и наибольшими значениями ординаты для точек части
.
Поэтому суммы, стоящие в неравенствах (4) слева и справа, являются не чем иным, как суммами Дарбу для интеграла , где через
обозначена длина всей кривой
. Поскольку функция
непрерывна в силу непрерывности кривой
, то существование и единственность числа, разделяющего эти суммы Дарбу, вытекают из теоремы существования интеграла от непрерывной функции. При этом мы доказали, что площадь поверхности вращения, т. е. число
, разделяющее эти суммы, равняется интегралу:
(5)
Из формулы (5) получаются различные частные случаи в зависимости от того, как задана кривая . Если она задана параметрически:
, то
,
и формула (5) принимает вид:
(6)
(когда меняется от
до
, переменная
меняется от
до
).
В частности, если кривая задана явным уравнением
, то
(7)
Если кривая задана в полярных координатах уравнением
, где
, а функция
имеет непрерывную производную
на
, то, учитывая, что
, a
, получим:
(8)
Пример 1. Найдем площадь поверхности шара радиуса .
Решение. Поместим начало координат в центр шара. Будем рассматривать поверхность шара как поверхность, полученную в результате вращения полуокружности вокруг оси
. Тогда площадь поверхности шара найдется по формуле
Так как — функция четная, то
Найдя и вычислив сумму
, получим:
Пример 2. Вычислить площадь поверхности, образованной вращением одной арки циклоиды вокруг
Решение. Найдем . Тогда
Искомая площадь поверхности вращения равна
Пример 3. Найдем площадь поверхности, образованной вращением лемнискаты вокруг полярной оси.
Решение. Имеем: . Поэтому
Пользуясь формулой (8) для вычисления площади поверхности в полярных координатах, найдем сначала половину искомой площади поверхности:
Вся площадь данной поверхности будет равна
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
I Определения
Определение
1. Поверхность
вращения – это поверхность, которая
получается при вращении плоской линии
вокруг оси, лежащей в её плоскости и не
пересекающей её.
Ось вращения может
и пересекать линию, если это ось симметрии
линии. В этом случае рассматривают лишь
«половину» линии.
Впишем в кривую
произвольную ломанную и обозначим
длину наибольшего её звена. При вращении
этой ломанной вокруг оси мы получим
поверхность,
составленную из боковых поверхностей
усеченных конусов. Обозначим площадь
этой поверхности.
Определение
2. Конечный
предел
называют площадью поверхности вращения.
Можно показать,
что если линия
имеет длину, то поверхность, полученная
её вращением, имеет площадь.
II Общая формула
Линия
,
вращением которой вокруг оси абсцисс
получена поверхность, может быть задана
одним из следующих способов:
1) 2) 3)
Теорема.
Если функции, определяющие линию,
непрерывны вместе со своими производными,
то площадь поверхности вращения (вокруг
оси
)
определяется формулой:
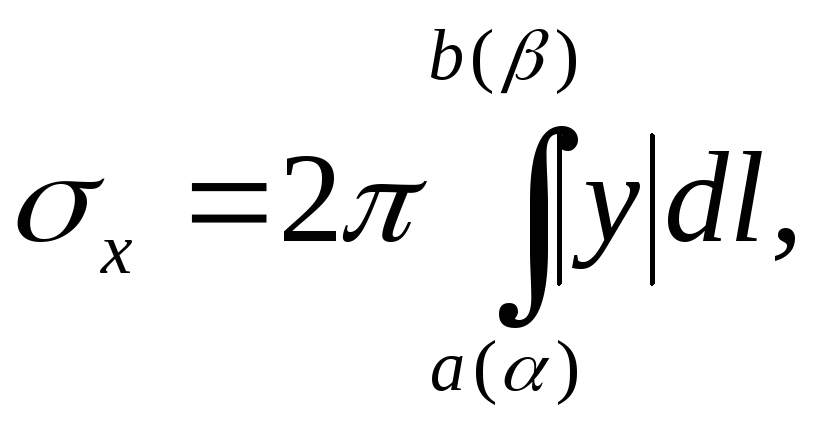
где
– подынтегральное выражение, фигурирующее
в соответствующей формуле для длины
дуги.
Идея
доказательства.
Пусть концы -го
звена ломанной имеют координаты
и .
Это звено при вращении вокруг оси
опишет
боковую поверхность усеченного конуса
с радиусами основанийи
и образующей
(длина
-го
звена). Для площади такой поверхности
известна формула
Вся ломанная даст
поверхность с площадью
Если, например,
имеющаяся кривая – это график функции
,
тогда
(см. §3, II). Также,
заменяя
на
получим
В этой сумме
нетрудно увидеть интегральную сумму,
которая в пределе даст интеграл из (1).
III Частные случаи и примеры
1) Найти площадь
сферического пояса, полученного вращением
дуги окружности ,
,
вокруг оси абсцисс.
Формула имеет вид
Проведём
предварительные вычисления:
,
.
Теперь вычисляем
площадь:
Сферический пояс
– это часть сферы, заключенная между
двумя параллельными плоскостями.
Полученный результат показывает, что
площадь сферического пояса зависит
лишь от расстояния между плоскостями,
и не зависит от их положения относительно
сферы.
2) Найти площадь
поверхности, полученной вращением
астроиды ,
вокруг оси
.
Общая формула
принимает вид
Астроида симметрична
относительно оси вращения. Поэтому
необходимо рассматривать лишь часть
её, например, для
.
Предварительные вычисления:
,
,
Так как
то, чтобы не «разбираться» с модулем,
воспользуемся симметрией астроиды
относительно оси
,
т.е. будем рассматривать:
3) Дуга кардиоиды
,
,
вращается вокруг полярной оси. Найти
объём тела вращения.
Формула (1) в этом
случае принимает вид:
Имеем для кардиоиды
Задачи
для самостоятельного решения.
1. Найти площадь
поверхности тора, полученного вращением
окруж-ности ,
,
вокруг оси
.
2. Круговой сегмент,
основание которого
,
высота,
вращается вокруг основания. Найти
площадь поверхности получающегося тела
вращения.
3. Первая арка
циклоиды
,
,
,
вращается: а) вокруг оси;
б) вокруг оси.
Найти площади получающихся поверхностей
вращения.
Соседние файлы в папке Лекции по мат.анализу
- #
- #
- #
- #
- #
- #
- #
Онлайн калькулятор для нахождения, вычисления площади поверхности вращения, рисунок тела вращения.
Например, вычислить площадь поверхности тора, полученного вращением окружности x^2+(y-3)^2=1 вокруг оси Ох.
Основные функции
модуль x: abs(x)
|
 : sin[x] или Sin[x] : sin[x] или Sin[x] : tan[x] или Tan[x] : tan[x] или Tan[x] : cot[x] или Cot[x] : cot[x] или Cot[x] : sec[x] или Sec[x] : sec[x] или Sec[x] : csc[x] или Csc[x] : csc[x] или Csc[x] : ArcCos[x] : ArcCos[x] : ArcSin[x] : ArcSin[x] : ArcTan[x] : ArcTan[x] : ArcCot[x] : ArcCot[x] : ArcSec[x] : ArcSec[x] : ArcCsc[x] : ArcCsc[x] : cosh[x] или Cosh[x] : cosh[x] или Cosh[x] |
 : sinh[x] или Sinh[x] : sinh[x] или Sinh[x] : tanh[x] или Tanh[x] : tanh[x] или Tanh[x] : coth[x] или Coth[x] : coth[x] или Coth[x] : sech[x] или Sech[x] : sech[x] или Sech[x] : csch[x] или Csch[е] : csch[x] или Csch[е] : ArcCosh[x] : ArcCosh[x] : ArcSinh[x] : ArcSinh[x] : ArcTanh[x] : ArcTanh[x] : ArcCoth[x] : ArcCoth[x] : ArcSech[x] : ArcSech[x] : ArcCsch[x] : ArcCsch[x] |
Скачать калькулятор
Рейтинг: 2.3 (Голосов 14)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Решение определенных интегралов | Решение неопределенных интегралов | Решение двойных интегралов | Решение интегралов |
| Объем тела вращения | Решение тройных интегралов | Графические построения | Решение задачи Коши |
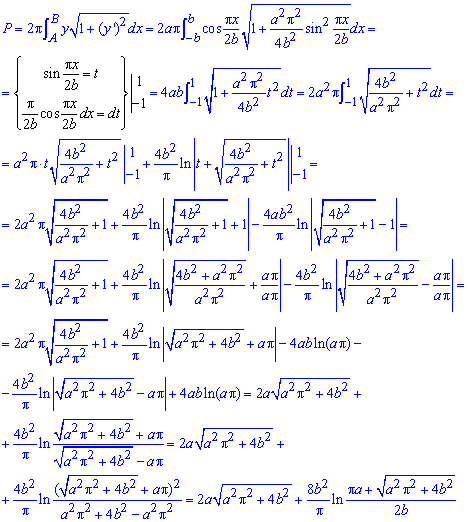
Площадь поверхности P, что образована вращением гладкой кривой AB вокруг оси Ox где y(x) — непрерывная гладкая функция равняется
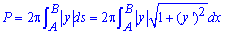
Основные формулы теории расчета площади поверхности Вы имеете, теперь перейдем к примерам, что Вас ожидают на практике и экзаменах.
Задание подобрано из учебной программы для студентов мех-мату Львовского национального университета имени Ивана Франко.
Другие Вузы имеют подобную программу учебы, задания похожие, а в ряде случаев те же.
Номера в примерах отвечает номеру из сборника Б. П. Демидовича. Для изучения основных моментов формулы интегрирования для вычисления площади поверхности вращения будут повторяться из примера в пример.
Часть заданий проиллюстрируем графиками кривых.
Пример 2486 Найти площадь поверхности вращения кривой 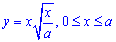
Решение: Найдем дифференциал дуги:
для этого вычисляем производную функции и, возведя к квадрату, подставляем в формулу
Запишем пределы интегрирования (известно за условием):
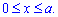
Интегрированием находим площадь поверхности вращения:
Как видите больше всего трудностей возникает при нахождении интеграла.
Здесь пришлось выделить полные квадраты под корнем, а дальше перейти к новой переменной под интегралом.
Не забывайте, что это приводит к изменению пределов интегрирования. Также здесь и в следующих примерах будем искать лишь интеграл, то что площадь измеряется в единицах квадратных Вы должны знать еще из школы.
Пример 2487 Найти площадь поверхности вращения кривой 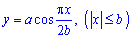
Решение: Вычисляем дифференциал дуги кривой:
За условием предела интегрирования: xє[-b;b].
За формулой находим площадь поверхности вращения:
Здесь также под интегралом переходим к новой переменной, дальше после возведения к табличным интегралам подставляем пределы и упрощаем логарифмы.
Пример 2492 Найти площадь поверхности вращения астроиды 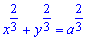
Решение: Записываем уравнение астроиды в параметрическом виде:
Находим дифференциал дуги параметрически заданной кривой по формуле:
Заметьте, что для параметрически заданной кривой формула несколько иная.
Запишем пределы интегрирования: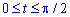
Вычислим площадь поверхности вращения:
Замена переменных упрощает интегрирование.
Пример 2495 Найти площадь поверхности вращения кривой, заданной параметрически x=a(t-sin (t)), y=a(1-cos(t)), t[0;2pi]
а) вокруг оси Ox;
б) вокруг оси Oy;
в) вокруг прямой y=2a.
Решение: Найдем дифференциал дуги параметрически заданной кривой:
При упрощении использовали известные тригонометрические зависимости.
Пределы интегрирования:
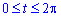
Найдем площадь поверхности вращения вокруг осей:
а) 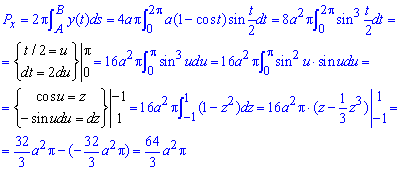
б)
в) площадь поверхности вращения вокруг прямой y=2a
Здесь использовали симметрию относительно прямой x1=a*Pi, поэтому результат умножили на 2.
Пример 2497 Найти площадь поверхности вращения кардиоиды 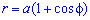

Решение: Для кривой заданной в полярных координатах дифференциал дуги находим по формуле:
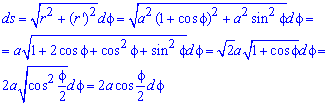
Пределы интегрирования:
Вычислим площадь поверхности вращения кардиоиды:
Здесь также использовали замену переменных под интегралом.
Использованная литература:
1. Практикум из математического анализа. Часть 2. Заболоцький М. В., Фединяк С. И., Филевич П. В. — Львов: Издательский центр ЛНУ имени Ивана Франко, 2006. — 68 с.
2. Демидович Б. П. Сборник задач и упражнений по математическому анализу. Учебное пособие для студентов физических и механико-математических специальностей ВУЗов.-9-е изд.-М.: Наука, главная редакция физико-математической литературы, 1977. — 528 с.
3. Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, том ІІ : — М.: Наука, главная редакция физико-математической литературы, 1966. — 800 с.
4. Справочное пособие по математическому анализу, часть И -К. : «Высшая школа», 1978. — 696 с.
Как найти площадь поверхности вращения с помощью интеграла
Прежде чем перейти к формулам площади поверхности вращения, дадим краткую формулировку самой поверхности вращения. Поверхность вращения, или, что то же самое — поверхность тела вращения — пространственная фигура, образованная вращением отрезка AB кривой вокруг оси Ox (рисунок ниже).
Представим себе криволинейную трапецию, ограниченную сверху упомянутым отрезком кривой. Тело, образованное вращением этой трапеции вокруг то же оси Ox, и есть тело вращения. А площадь поверхности вращения или поверхности тела вращения — это его внешняя оболочка, не считая кругов, образованных вращением вокруг оси прямых x = a и x = b .
Заметим, что тело вращения и соответственно его поверхность могут быть образованы также вращением фигуры не вокруг оси Ox, а вокруг оси Oy.
Вычисление площади поверхности вращения, заданной в прямоугольных координатах
Пусть в прямоугольных координатах на плоскости уравнением y = f(x) задана кривая, вращением которой вокруг координатной оси образовано тело вращения.
Формула для вычисления площади поверхности вращения следующая:
(1).
Пример 1. Найти площадь поверхности параболоида, образованную вращением вокруг оси Ox дуги параболы , соответствующей изменению x от x = 0 до x = a .
Решение. Выразим явно функцию, которая задаёт дугу параболы:
Найдём производную этой функции:
Прежде чем воспользоваться формулу для нахождения площади поверхности вращения, напишем ту часть её подынтегрального выражения, которая представляет собой корень и подставим туда найденную только что производную:
Далее по формуле (1) находим:
Ответ: длина дуги кривой равна
.
Пример 2. Найти площадь поверхности, образуемой вращением вокруг оси Ox астроиды .
Решение. Достаточно вычислить площадь поверхности, получающейся от вращения одной ветви астроиды, расположенной в первой четверти, и умножить её на 2. Из уравнения астроиды выразим явно функцию, которую нам нужно будет подставить в формулу для нахождения площади повержности вращения:
.
Производим интегрирование от 0 до a:
Ответ: площадь поверхности вращения равна .
Вычисление площади поверхности вращения, заданной параметрически
Рассмотрим случай, когда кривая, образующая поверхность вращения, задана параметрическими уравнениями
Тогда площадь поверхности вращения вычисляется по формуле
(2).
Пример 3. Найти площадь поверхности вращения, образованной вращением вокруг оси Oy фигуры, ограниченной циклоидой и прямой y = a . Циклоида задана параметрическими уравнениями
Решение. Найдём точки пересечения циклоиды и прямой. Приравнивая уравнение циклоиды и уравнение прямой y = a , найдём
Из этого следует, что границы интегрирования соответствуют
Теперь можем применить формулу (2). Найдём производные:
Запишем подкоренное выражение в формуле, подставляя найденные производные:
Найдём корень из этого выражения:
.
Подставим найденное в формулу (2):
.
И, наконец, находим
В преобразовании выражений были использованы тригонометрические формулы
Ответ: площадь поверхности вращения равна .
Вычисление площади поверхности вращения, заданной в полярных координатах
Пусть кривая, вращением которой образована поверхность, задана в полярных координатах:
Площадь поверхности вращения вычисляется по формуле:
(3).
Пример 4. Найти площадь поверхности, образованной вращением лемнискаты вокруг полярной оси.
Решение. Действительные значения для ρ получаются при , то есть при (правая ветвь лемнискаты) или при (левая ветвь лемнискаты).
Решение. Дифференциал корня из формулы площади поверхности вращения равен:
В свою очередь произведение функции, которой задана лемниската, на синус угла равно
.
Поэтому площадь поверхности вращения найдём следующим образом:
.
Площадь поверхности вращения тела
Пусть даны прямая и кривая , лежащая в одной плоскости с и расположенная по одну сторону от этой прямой. При вращении кривой вокруг оси получается поверхность , площадь которой мы и хотим сначала определить, а потом вычислить (см. 46).
Начнем со случая, когда — отрезок, один конец которого отстоит от на , а другой — на (рис. 58). Тогда, как доказывается в школьном курсе геометрии, площадь поверхности вращения (боковой поверхности усеченного конуса) выражается формулой . В этом случае при имеем:
Таким образом, боковая поверхность конуса заключена между произведением длины образующей на длину наименьшей окружности и произведением длины образующей на длину наибольшей окружности.
То же самое неравенство будет иметь место и при вращении любой ломаной линии, расположенной по одну сторону от оси вращения:
где и — наименьшее и наибольшее расстояния точек ломаной от оси , и — длина ломаной.
Для доказательства достаточно применить неравенство (1) к каждому звену ломаной, сложить полученные результаты и учесть что и для любого звена имеем и (здесь и — наименьшее и наибольшее расстояния точек k-ro звена от оси вращения).
Естественно потребовать, чтобы неравенства (2) выполнялись для любой спрямляемой кривой. Кроме того, потребуем, чтобы площадь поверхности вращения обладала свойством аддитивности: при разбиении дуги на части должно выполняться равенство
где — поверхность, полученная при вращении всей дуги , а — при вращении части .
Если применить к каждой части неравенства (2), то получим, что
где — длина дуги , а и — наименьшее и наибольшее расстояния точек этой дуги от оси вращения. Складывая эти неравенства и учитывая требование аддитивности, получаем, что
Иными словами, площадь поверхности вращения должна разделять множества
Именно это требование мы и примем за определение площади поверхности вращения.
Если — плоская спрямляемая кривая, лежащая по одну сторону от оси , то площадью поверхности , получаемой при вращении этой кривой вокруг оси , называется число , разделяющее множества
соответствующие всевозможным разбиениям дуги . Здесь и имеют указанный выше смысл.
Докажем сейчас, что это число существует и единственно, а затем выведем для него выражение в виде интеграла. Выберем на плоскости систему координат, такую, что ось абсцисс совпадает с осью вращения. Зададим параметризацию кривой , выбрав в качестве параметра длину дуги , соединяющей в заданном направлении фиксированную точку кривой с произвольной точкой этой кривой (рис. 59). Тогда и будут наименьшими и наибольшими значениями ординаты для точек части .
Поэтому суммы, стоящие в неравенствах (4) слева и справа, являются не чем иным, как суммами Дарбу для интеграла , где через обозначена длина всей кривой . Поскольку функция непрерывна в силу непрерывности кривой , то существование и единственность числа, разделяющего эти суммы Дарбу, вытекают из теоремы существования интеграла от непрерывной функции. При этом мы доказали, что площадь поверхности вращения, т. е. число , разделяющее эти суммы, равняется интегралу:
Из формулы (5) получаются различные частные случаи в зависимости от того, как задана кривая . Если она задана параметрически:
и формула (5) принимает вид:
(когда меняется от до , переменная меняется от до ).
В частности, если кривая задана явным уравнением , то
Если кривая задана в полярных координатах уравнением , где , а функция имеет непрерывную производную на , то, учитывая, что , a , получим:
Пример 1. Найдем площадь поверхности шара радиуса .
Решение. Поместим начало координат в центр шара. Будем рассматривать поверхность шара как поверхность, полученную в результате вращения полуокружности вокруг оси . Тогда площадь поверхности шара найдется по формуле
Так как — функция четная, то
Найдя и вычислив сумму , получим:
Пример 2. Вычислить площадь поверхности, образованной вращением одной арки циклоиды вокруг
Решение. Найдем . Тогда
Искомая площадь поверхности вращения равна
Пример 3. Найдем площадь поверхности, образованной вращением лемнискаты вокруг полярной оси.
Решение. Имеем: . Поэтому
Пользуясь формулой (8) для вычисления площади поверхности в полярных координатах, найдем сначала половину искомой площади поверхности:
Вся площадь данной поверхности будет равна .
4.4. Объемы и поверхности тел вращения
I. Объемы тел вращения. Предварительно изучите по учебнику Г. М. Фихтенгольца главу XII, п°п° 197, 198* Разберите подробно примеры, приведенные в п° 198.
508. Вычислить объем тела, образуемого вращением эллипса Вокруг оси Ох.
Решение. При вращении эллипса вокруг оси Ox образуется тело, называемое эллипсоидом вращении. Как известно, объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной сверху кривой у = f
Из уравнения эллипса видно, что большая его полуось равна 2, следовательно, . Разрешив уравнение
эллипса относительно , получим Объем
эллипсоида вращения равен:
509. Найти объем тора, образованного вращением круга
Вокруг оси Ox (рис. 18). Решение. Искомый объем тора равен разности объемов, полученных от вращения верхнего и нижнего полукругов. Так как для верхнего полукруга
, а для нижнего , то
Б10. Вычислить объем прямого конуса, высота которого h и радиус основания г, рассматривая конус как тело вращения прямоугольного треугольника около одного из катетов.
Решение. Выберем систему координат так, чтобы ось Ox совпала с высотой h (рис. 19), а вершину конуса
примем за начало координат. Тогда уравнение прямой OA
Следовательно, объем конуса
запишется так: будет равен:
511. Вычислить объемы тел, образованных вращением около осей Ox и Oy сегмента AOB параболы , от
секаемого хордой AFB, проходящей через фокус параболы перпендикулярно к оси Ox (рис. 20, а, б).
Решение I. Вычислим объем тела, получаемого при вращении сегмента AOB вокруг оси Ох, пользуясь формулой:
Найдем пределы интегрирования. Прямая AB параллельна оси Oy. Ее уравнение . Для того чтобы
найти точки пересечения этой прямой с параболой, решим совместно систему уравнений:
мя я AB проходит через фокус параболы, то координаты точки F будут Следовательно,
Получим точки . Так Kaw пря
2. Вычислим объем тела, получаемого при вращении сегмента AOB вокруг оси Oy. Учитывая симметрию сегмента относительно оси Oxi найдем сначала половину искомого объема. Она равна разности объемов тел, получаемых от вращения вокруг оси Oy прямоугольника OFBD и криволинейного тоеугольника OBD. Так как объем цилиндра равен , а объем Тела, полученного от вращения криволинейного треугольника OBD вокруг оси Oy, будет:
512. Фигура, ограниченная гиперболой И
то половина искомого объема равна:
Следовательно, весь искомый объем
прямыми , вращается вокруг оси
Ох. Найти объем тела вращения.
Решение. В результате вращения данной фигуры вокруг оси Ox образуются два тела вращения, имеющие равные объемы Тогда
Найдем объем V1 тела (рис. 21), сбразованного вращением площади, ограниченной правей ветвью гиперболы И прямей Пределы интегрирова
ния найдем из геометрических соображений:
513. Вычислить объем тела, образованного вращением вокруг оси Ox одной полуволны синусоиды у = sin х.
514. Найти объем конуса, производимого вращением вокруг оси Ox части прямой _ , содержащейся между осями координат.
515. Криволинейная трапеция, ограниченная срерху параболой ,с боков—ординатами х = — I и х—, снизу — осью Ох, вращается вокруг оси Ох. Найти объем полученного тела вращения.
516. Вычислить объем тела, образованного вращением вокруг оси Ox площади, ограниченной цепной линией
, ординатами X = — а, х = а и осью Ох.
517. Прямой параболический сегмент, основание которого а, а высота R, вращается вокруг основания. Определить объем полученного тела вращения.
518. Найти объем цирка, осевое сечение которого — парабола. Высота цирка 30 м. Диаметр основания 50 м.
519. Найти объем тела, образованного вращением кривой Вокруг оси абсцисс.
520. Вычислить объем тела, полученного вращением
астроиды Вокруг оси Oy.
521. На кривой Взяты две точки А и В, абсциссы которых соответственно а = I и Ь = 2. Найти объем тела, полученного вращением криволинейной трапеции аАВЬ вокруг оси Ох.
522. Найти объем тела, производимого вращением площади, ограниченной дугой циклоиды ,
И осью Ox вокруг ее основания.
523. Вычислить объем тела, образованного вращением вокруг оси ординат дуги OM циклоиды ,
, ограниченной точками О (0, 0) и M (та*, 2а).
524. Найти объем тела, ограниченного поверхностью, полученной при вращении линии
вокруг оси абсцисс.
2. Площадь поверхности тела вращения. Предварительно изучите по учебнику Г. М. Фихтенгольца главу XII, п° 205. В теоретическом курсе показано, что площадь поверхности тела вращения определяется по формуле:
52$. Определить площадь поверхности параболоида, образованного вращением дуги параболы у2 = 2х вокруг оси Ox от х = 0 до х = 2.
Решение. В нашем случае . Поэтому
526. Найти площадь поверхности шара радиуса R. Решение. Поместим начало координат в центре шара. Будем рассматривать поверхность шара как поверхность, полученную в результате вращения полуокружности Вокруг оси Ох. Тогда площадь поверхности шара найдется по формуле:
527. Найти площадь поверхности эллипсоида, образованного вращением эллипса Вокруг оси Ох.
Решение. Из уравнения эллипса имеем:
Тогда . Так как полуось эллипса
Если кривая задана параметрически, то, заменяя переменную под знаком определенного интеграла, получим для площади поверхности следующую формулу:
528 Вычислить площадь поверхности, сбразованной вращением одной арки циклоиды
Вокруг оси Ox (см. рис. 13).
Тогда . Искомая по
Решение. Построим данную кривую. Найдем точки пересечения ее с осями координат.
нием петли кривой х = /2, у
(/2— 3) вокруг оси Ох.
При у — 0 находим t = 0 и t = ±>/ 3 . Следовательно, X1 = 0 и X2 -= 3* т. е. кривая пересекает ось Ox в двух точках О (0, 0) и А (3, 0).
При х = 0 находим / = 0, следовательно, у = 0. Мы получили ту же точку О (0, 0).
При люб dx вещественных значениях параметра / будут вещественны х и у Так как х — четная функция параметра /, у — нечетная функция параметра /, то график расположен симметрично относительно оси Ох.
Исследуем данную функцию на экстремум. Находим производную:
Легко видеть, что у = 0 при / = + I и, следовательно^
у — + —; когда X= I; у’-* оо, когда / —> 0, следовательно,
когда х -> 0, то и у 0. Это значит, что в начале координат касательная к данной кривой вертикальна. В точке
А (3; 0) будет у’ = — J=, это значит, что касательная У з
к данной кривой в этой точке образует с положительным направлением оси Ox угол в 30°.
Полученных данных достаточно для построения графика данной функции (рис. 22).
Найдем площадь данной поверхности. Имеем: х’ = 21, y’ = f — I; х’% -(-y’z = (I +12 )а.
Р=2* Jyj/T^T |±( —sin ф), у = а (I — cos ф) вокруг оси Oy, равна 16 и2 о2.
539. Найти поверхность, полученную вращением кардиоиды Вокруг полярной оси.
540. Найти площадь поверхности, образованной вращением лемнискаты Вокруг полярной оси.
Дополнительные задачи к главе IV
Площади плоских фигур
541. Найтивсю площадь области, ограниченной кривой И осью Ох.
542. Найти площадь области, ограниченной кривой
543. Найти часть площади области, расположенной в первом квадранте и ограниченной кривой
л осями координат.
544. Найти площадь области, содержащейся внутри
545. Найти площадь области, ограниченной одной петлей кривой:
546. Найти площадь области, содержащейся внутри петли:
547. Найти площадь области, ограниченной кривой
548. Найти площадь области, ограниченной кривой
549. Найти площадь области, ограниченной осью Oxr
прямой И кривой
550. Найти площадь области, ограниченной кривыми.
Вычисление длины дуги
551. Найти длину дуги кривой От точки А(0: до точки В (I: 6).
552. Найти длину дуги CD кривой , где
Дать геометрическую иллюстрацию.
553. Найти длину дуги OA кривой Где
554. Найти длину дуги AB кривой у = еху где А (0; I), В (I; 2)
555. Нгйти длину дуги AB кривой , где
556. Нгйти длину дуги кривой , отсеченной прямей X = — I.
557. Нгйти длину дуги кривой От
Объем тела вращения
558. Нгйти объем тела, полученного вращением вокруг юси Ox п/ощоди, сграниченной крквой
559. Нййти объем тела, полученного от вращения рокруг сси Ox площади, ограниченной кривой
560. Найти объем тела, образованного вращением вокруг оси Oy площади, ограниченной кривой
561. Найти объем тела, образованного вращением вокруг оси Oy площади, ограниченней эллипсом
562. Нгйти объем тела, полученного вращением вокруг оси Oy плещади, ограниченной кривой
И отрезком оси Oy.
563. Найти объем тела, полученного вращением вокруг оси Ox площади, ограниченной кривой
564. Круг радиуса 2 с центром в точке (7; 0) вращается вокруг оси Oy. Определить объем полученного тела вращения.
565. Нлйти объем тела, полученного вращением вокруг оси Ox площади, расположенной в первом квадранте и
ограниченной кривой (эволюта
Площадь поверхности вращения
566. Найти площадь поверхности, образованной вращением дуги кривой , отсеченной прямой
567. Найти площадь поверхности шаоовой чаши, полученной при вращении круга Вокруг оси Ox в пределах от 0 до h.
568. Найти площадь поверхности катеноида, образованного вращением вокруг оси абсцисс цепной линии
От точки До точки
569. Найти площадь поверхности эллипсоида, образованного вращением эллипса Вокруг оси Oy.
570. Найти площадь поверхности, образованной вращением вокруг оси Ox петли кривой
571. Найти площадь поверхности, образованной вращением вокруг оси Ox кривой
572. Найти площадь поверхности, образованной вращением Вокруг полярной оси.
http://mathhelpplanet.com/static.php?p=ploshchad-poverkhnosti-vrashcheniya-tela
http://matica.org.ua/metodichki-i-knigi-po-matematike/a-z-ryvkin-i-e-s-kunitckaia-zadachnik-praktikum-po-matematicheskomu-analizu/4-4-obemy-i-poverkhnosti-tel-vrashcheniia


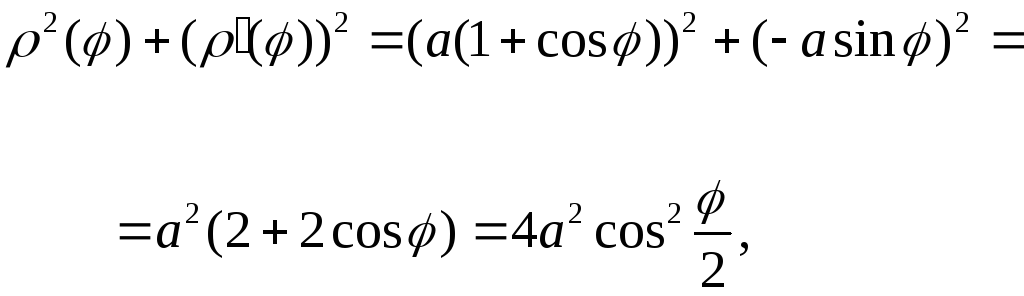
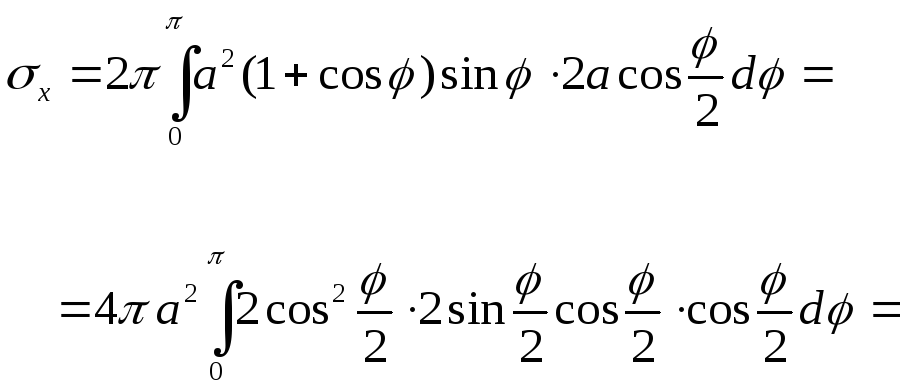

 : x^a
: x^a : Sqrt[x]
: Sqrt[x]![sqrt[n]{x}](https://upload.wikimedia.org/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) : x^(1/n)
: x^(1/n) : a^x
: a^x : Log[a, x]
: Log[a, x] : Log[x]
: Log[x] : cos[x] или Cos[x]
: cos[x] или Cos[x]