Как найти площадь поверхности части сферы - AvtoShod.ru

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности сегмента шара, а также разберем пример решения задачи для демонстрации их практического применения.

Определение сегмента шара
Формулы для нахождения площади сегмента шара
- Площадь основания
- Площадь сферической поверхности
- Площадь полной поверхности
Пример задачи

Определение сегмента шара

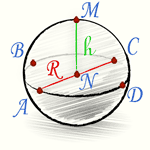
Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью. На чертеже ниже закрашен зеленым цветом.

R – радиус шара;
r – радиус основания сегмента;
h – высота сегмента; это длина перпендикуляра от центра его основания (точка O₂) до точки на поверхности шара.

Связь между радиусом основания сегмента, его высотой и радиусом шара:

Формулы для нахождения площади сегмента шара

Площадь основания

Основанием шарового сегмента является круг, площадь (S) которого находится по стандартной формуле (в расчетах число π округляется до 3,14):

S_осн. = πr²

Примечание: если известен диаметр круга (d), чтобы найти радиус (r), нужно первое разделить на второе, то есть: r = d/2.

Площадь сферической поверхности

Чтобы найти площадь (S) сферической/внешней поверхности шарового сегмента, необходимо знать его высоту и радиус самого шара.

S_{сфер. пов.} = 2πRh

Площадь полной поверхности

Чтобы найти площадь (S) полной поверхности сегмента шара, необходимо сложить площади его основания и внешней поверхности.

S_полн. = S_осн. + S_{сфер. пов.} = π (2Rh + r²)

Пример задачи

Дан шар радиусом 6 см. Найдите полную площадь шарового сегмента, если известно, что его высота равняется 2,4 см, а радиус основания – 4,7 см.

Решение

Воспользуемся формулами, приведенными выше, подставив в них известные по условиям задачи значения.

S_осн. = 3,14 ⋅ (4,7 см)² = 69,3626 см²

S_{сфер. пов.} = 2 ⋅ 3,14 ⋅ 6 см⋅ 2,4 см = 90,432 см²

S_полн. = S_осн. + S_{сфер. пов.} = 69,3626 см² + 90,432 см² = 159,7946 см²

Источник

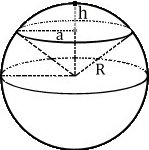
Площадь поверхности шарового сегмента

Часть шара, [шар, сфера] осекаемая от него какой-нибудь плоскостью, называется шаровым или сферическим сегментом. Основанием шарового сегмента называется круг ABCD. Высотой шарового сегмента называется отрезок NM, т.е. длина перпендикуляра, восстановленного из центра N основания до пересечения с поверхностью шара. Точка M называется вершиной шарового сегмента.

Площадь поверхности шарового сегмента равняется произведению его высоты на окружность большого круга шара.

[ S = 2 pi R h ]

(R — радиус большого круга шара, h=NM — высота шарового сегмента)

Формулы шара, сферы

Вычислить, найти площадь поверхности шарового сегмента по формуле (1)

Площадь поверхности шарового сегмента	стр. 318

Источник

Сегмент шара

Сферический сегмент

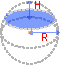
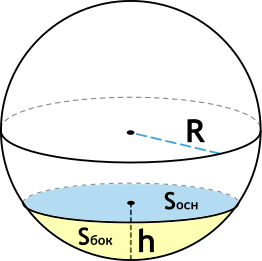
Шаровым сегментом называется часть шара, отсеченная от него плоскостью.

Формулы:
$S_{lateral}=2 pi R H$ — площадь боковой поверхности
— площадь основания
$V=pi H^2(R- frac{1} {3} H)$ — формула объема

Сегмент шара

Точность вычисления

Знаков после запятой: 5

Площадь боковой поверхности

Слой шара

Сферический слой

Шаровой слой — часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар.

Формулы:
$S_{lateral}=2 pi R (H_2-H_1)$ — площадь боковой поверхности
$V = pi left[ H_2^2 left( R - frac{1} {3} H_2 right) - H_1^2 left( R - frac{1} {3} H_1 right) right]$ — объем

Шаровой слой

Точность вычисления

Знаков после запятой: 5

Площадь боковой поверхности

Источник

Главная Учёба Площадь поверхности сферического сегмента

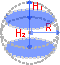
Площадь поверхности сферического сегмента

Сферический сегмент — часть сферы, что отсекается от сферы плоскостью.

Вам нужно указать радиус сферы (R), высоту (h) сферического сегмента.

Формула площади поверхности сферического сегмента: S = 2*π*R*h
Два умножается на число PI, на радиус и высоту.

Объем шарового сегмента

Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!

Нет комментариев.

Оставить комментарий

Заполните все поля.

Источник

{S_{бок} = 2pi Rh} newline
{S_{осн} = pi h(2R-h)} newline
{S_{полн} = S_{бок}+S_{осн}}

С помощью приведенных на странице онлайн калькулятора и формулы вы можете рассчитать площадь поверхности шарового сегмента, которая состоит из площади боковой поверхности и площади основания. Введите радиус шара и высоту шарового слоя и получите результат.

Шарово́й сегмент — часть шара, отсеченная от него плоскостью.

Содержание:

калькулятор площади поверхности шарового сегмента
формула площади боковой поверхности шарового сегмента
формула площади основания шарового сегмента
формула площади полной поверхности шарового сегмента

Формула площади боковой поверхности шарового сегмента

{S_{бок} = 2pi Rh}

R — радиус шара

h — высота шарового сегмента

Формула площади основания шарового сегмента

{S_{осн} = pi h(2R-h)}

R — радиус шара

h — высота шарового сегмента

Формула полной поверхности шарового сегмента

{S_{осн} = S_{бок} + S_{осн}}

S_бок — площадь боковой поверхности шарового сегмента

S_осн — площадь основания шарового сегмента

Источник

Определение сегмента шара

Формулы для нахождения площади сегмента шара

Площадь основания

Площадь сферической поверхности

Площадь полной поверхности

Пример задачи

Площадь поверхности шарового сегмента

Формулы шара, сферы

Вычислить, найти площадь поверхности шарового сегмента по формуле (1)

Площадь поверхности шарового сегмента

Сегмент шара

Шаровой слой

Площадь поверхности сферического сегмента

Оставить комментарий

Содержание:

Формула площади боковой поверхности шарового сегмента

Формула площади основания шарового сегмента

Формула полной поверхности шарового сегмента

Не пропустите также: