Как найти площадь полукруга шара - AvtoShod.ru - решение различных проблем

Скачать материал

Сейчас обучается 184 человека из 50 регионов

Сейчас обучается 41 человек из 29 регионов

Сейчас обучается 35 человек из 26 регионов

Описание презентации по отдельным слайдам:

1 слайд

Сфера и шар.
Сш №12 п. Осакаровка
2 слайд

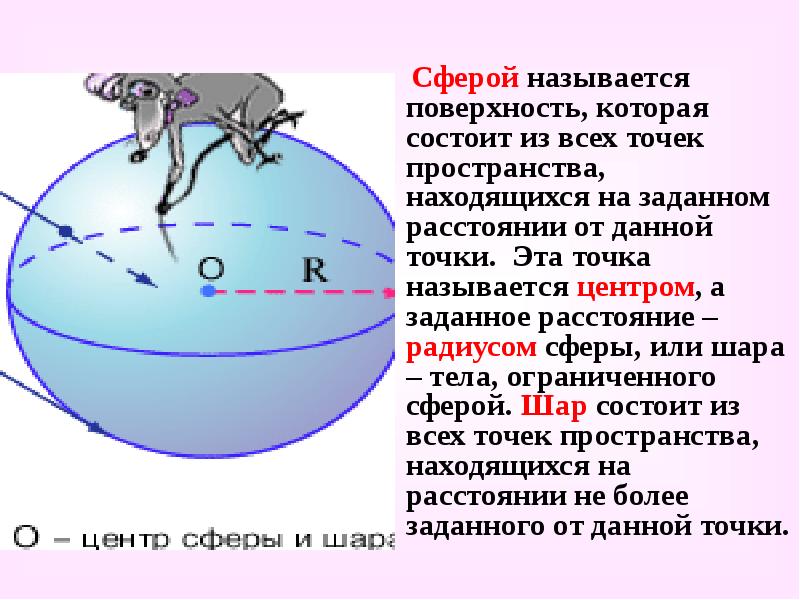
Сферой называется поверхность, которая состоит из всех точек пространства, находящихся на заданном расстоянии от данной точки. Эта точка называется центром, а заданное расстояние – радиусом сферы, или шара – тела, ограниченного сферой. Шар состоит из всех точек пространства, находящихся на расстоянии не более заданного от данной точки.
3 слайд

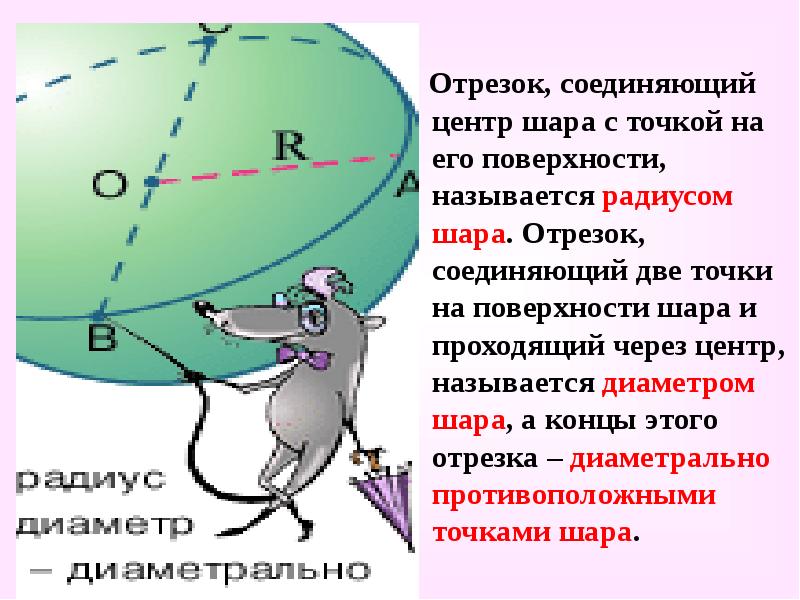
Отрезок, соединяющий центр шара с точкой на его поверхности, называется радиусом шара. Отрезок, соединяющий две точки на поверхности шара и проходящий через центр, называется диаметром шара, а концы этого отрезка – диаметрально противоположными точками шара.
4 слайд

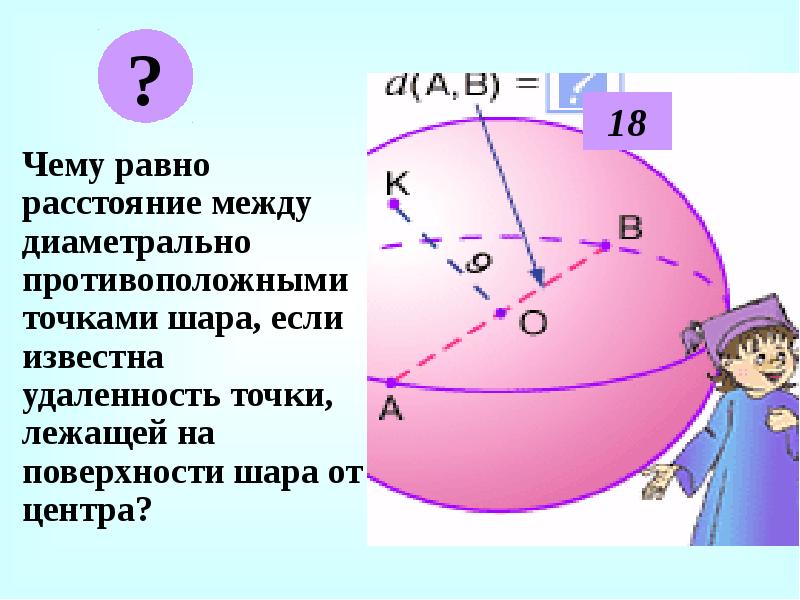
Чему равно расстояние между диаметрально противоположными точками шара, если известна удаленность точки, лежащей на поверхности шара от центра?
?
18
5 слайд

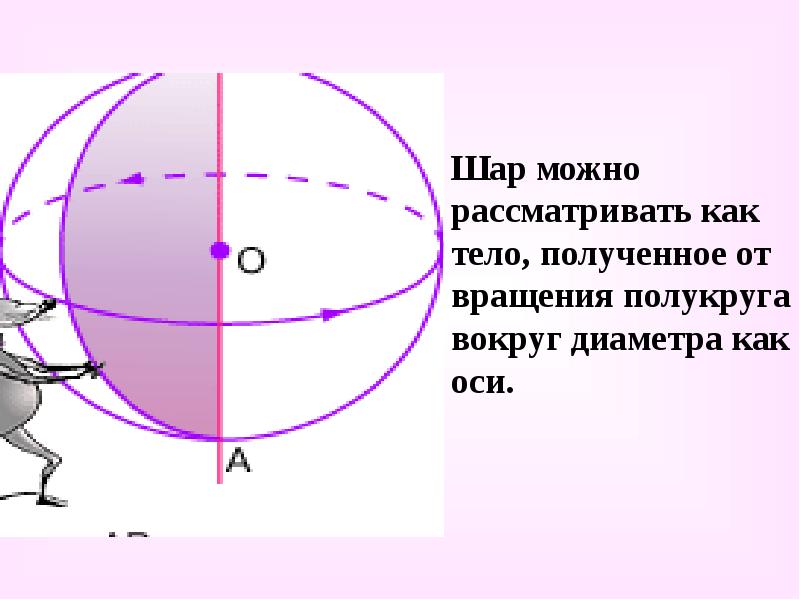
Шар можно рассматривать как тело, полученное от вращения полукруга вокруг диаметра как оси.
6 слайд

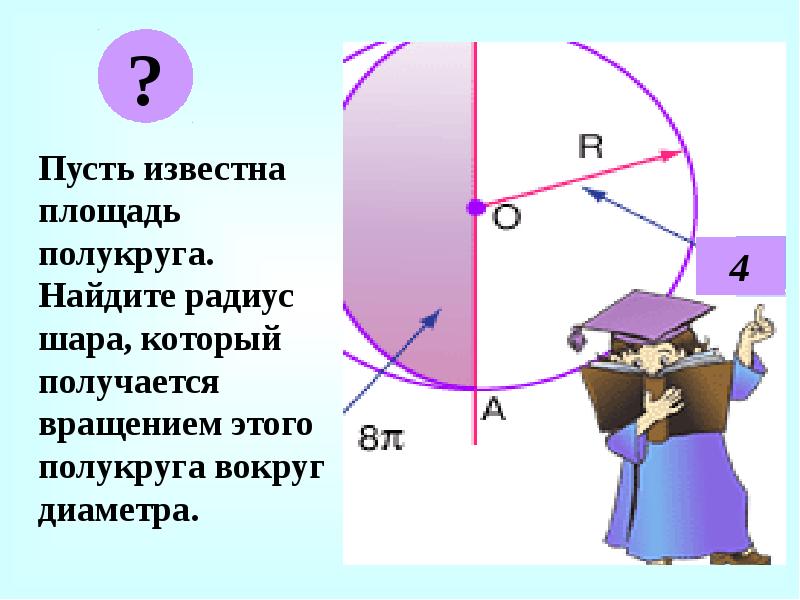
Пусть известна площадь полукруга. Найдите радиус шара, который получается вращением этого полукруга вокруг диаметра.
?
4
7 слайд

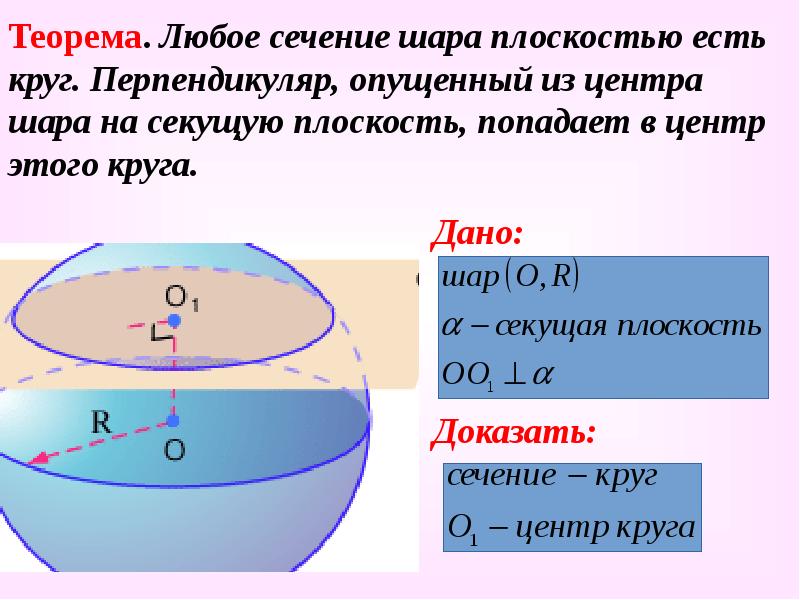
Теорема. Любое сечение шара плоскостью есть круг. Перпендикуляр, опущенный из центра шара на секущую плоскость, попадает в центр этого круга.
Дано:

Доказать:
8 слайд

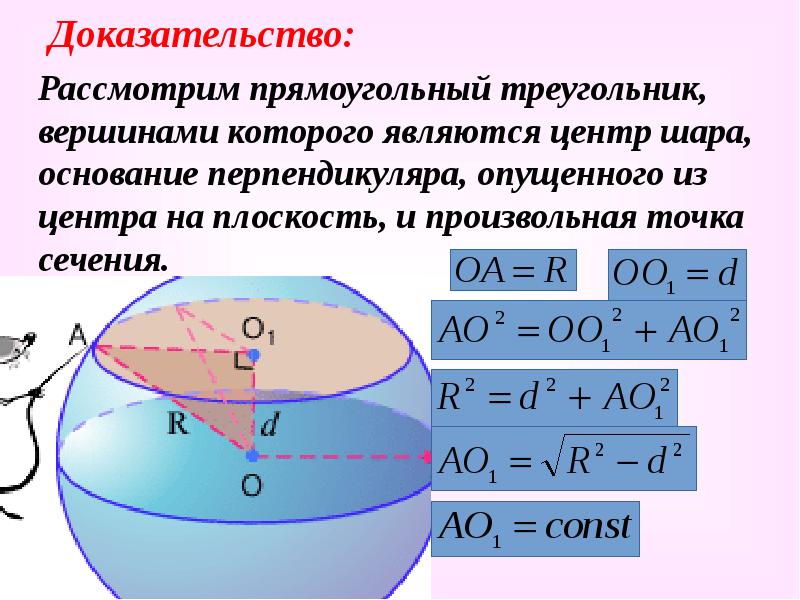
Доказательство:
Рассмотрим прямоугольный треугольник, вершинами которого являются центр шара, основание перпендикуляра, опущенного из центра на плоскость, и произвольная точка сечения.
9 слайд

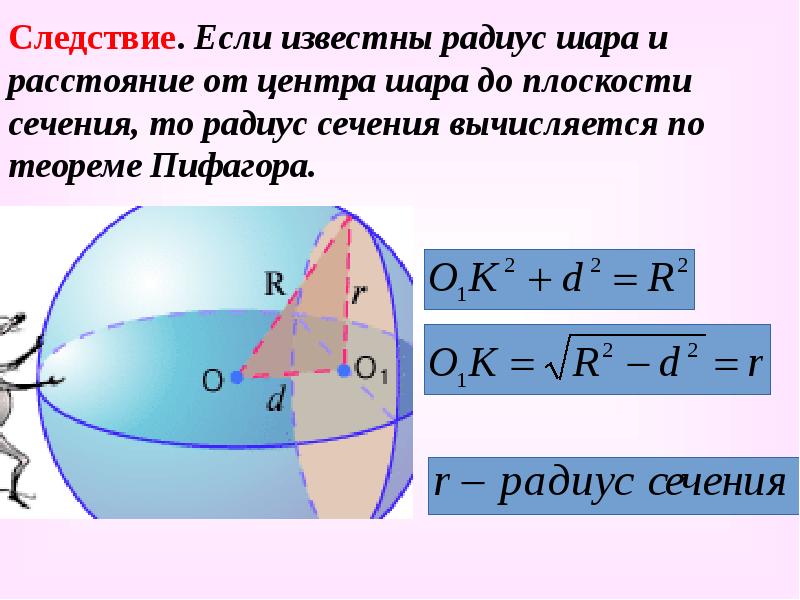
Следствие. Если известны радиус шара и расстояние от центра шара до плоскости сечения, то радиус сечения вычисляется по теореме Пифагора.
10 слайд

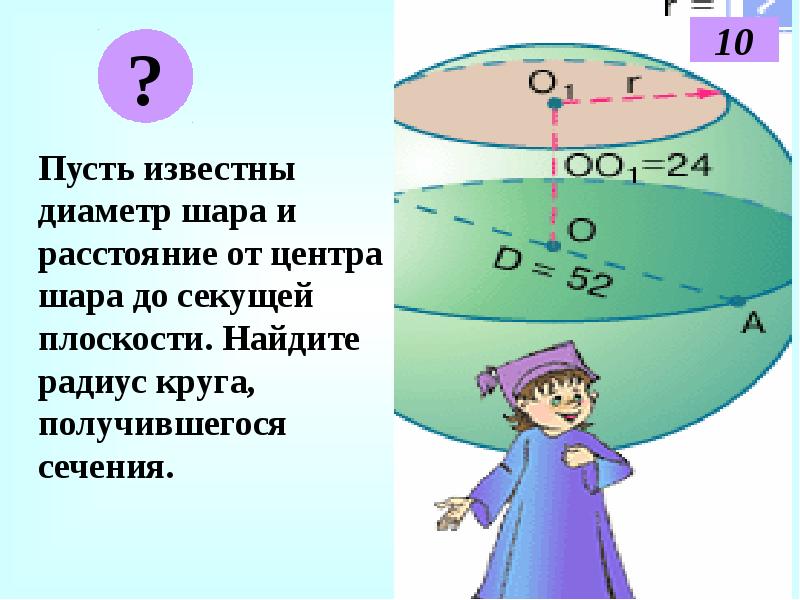
Пусть известны диаметр шара и расстояние от центра шара до секущей плоскости. Найдите радиус круга, получившегося сечения.
?
10
11 слайд

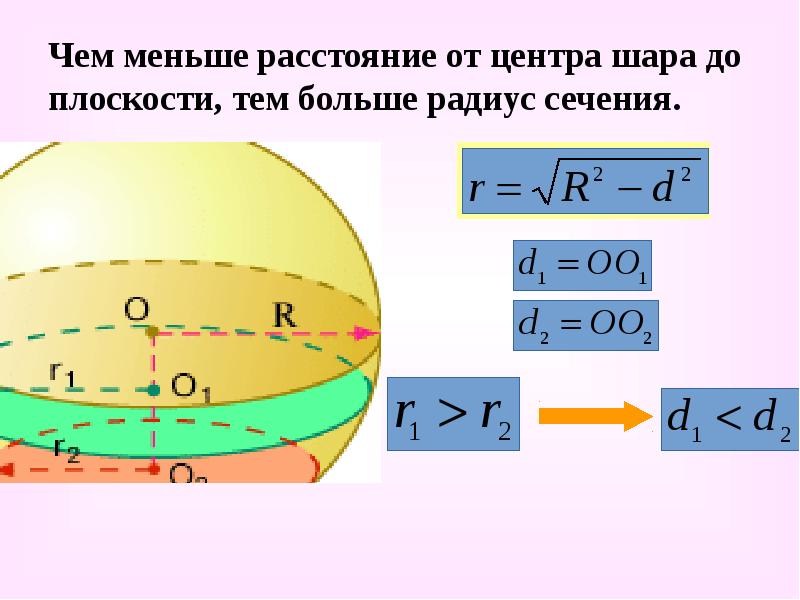
Чем меньше расстояние от центра шара до плоскости, тем больше радиус сечения.
12 слайд

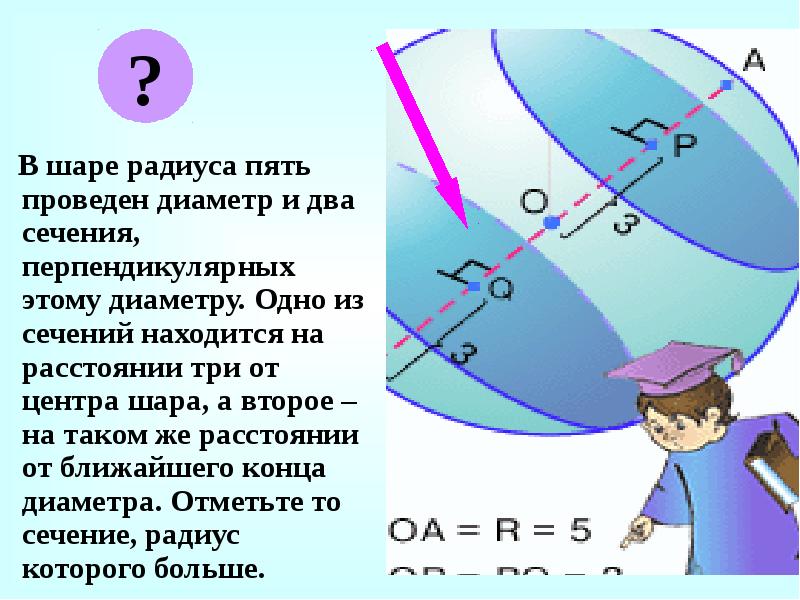
В шаре радиуса пять проведен диаметр и два сечения, перпендикулярных этому диаметру. Одно из сечений находится на расстоянии три от центра шара, а второе – на таком же расстоянии от ближайшего конца диаметра. Отметьте то сечение, радиус которого больше.
?
13 слайд

Задача.
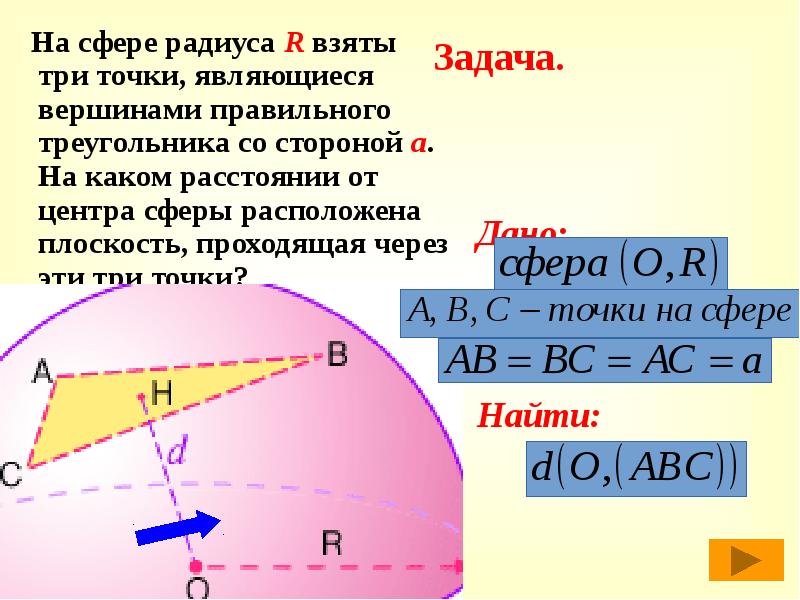
На сфере радиуса R взяты три точки, являющиеся вершинами правильного треугольника со стороной а. На каком расстоянии от центра сферы расположена плоскость, проходящая через эти три точки?
Дано:

Найти:
14 слайд

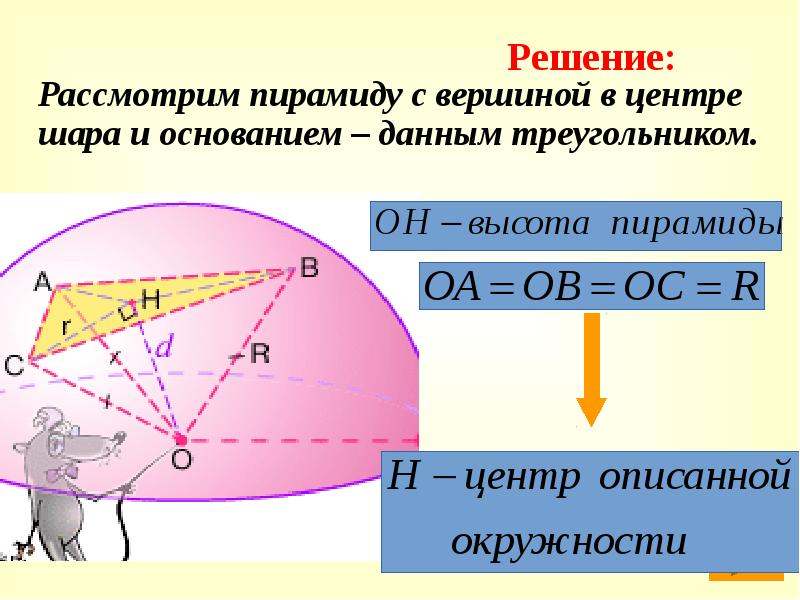
Рассмотрим пирамиду с вершиной в центре шара и основанием – данным треугольником.
Решение:
15 слайд

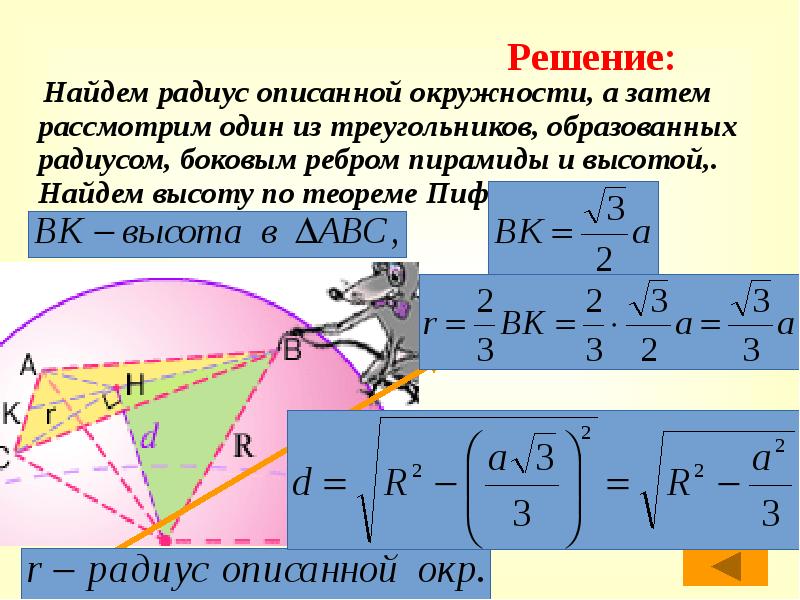
Найдем радиус описанной окружности, а затем рассмотрим один из треугольников, образованных радиусом, боковым ребром пирамиды и высотой,. Найдем высоту по теореме Пифагора.
Решение:
16 слайд

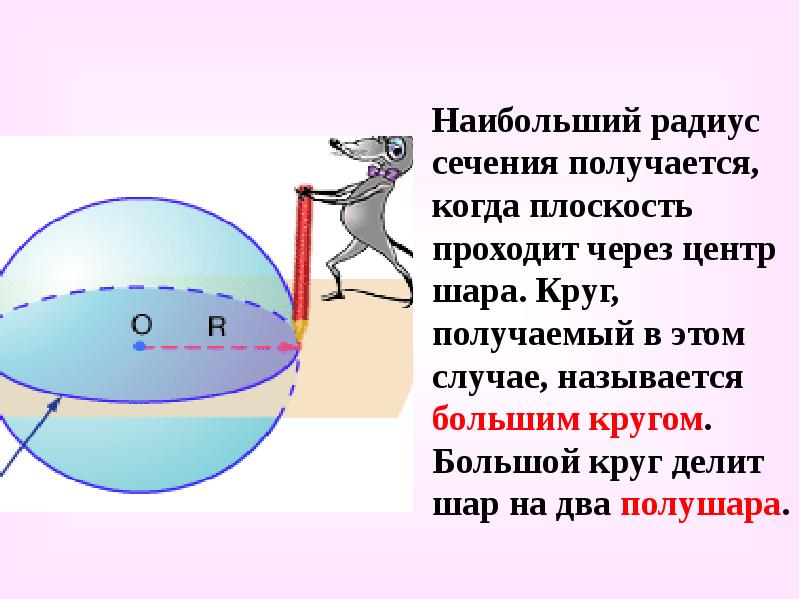
Наибольший радиус сечения получается, когда плоскость проходит через центр шара. Круг, получаемый в этом случае, называется большим кругом. Большой круг делит шар на два полушара.
17 слайд

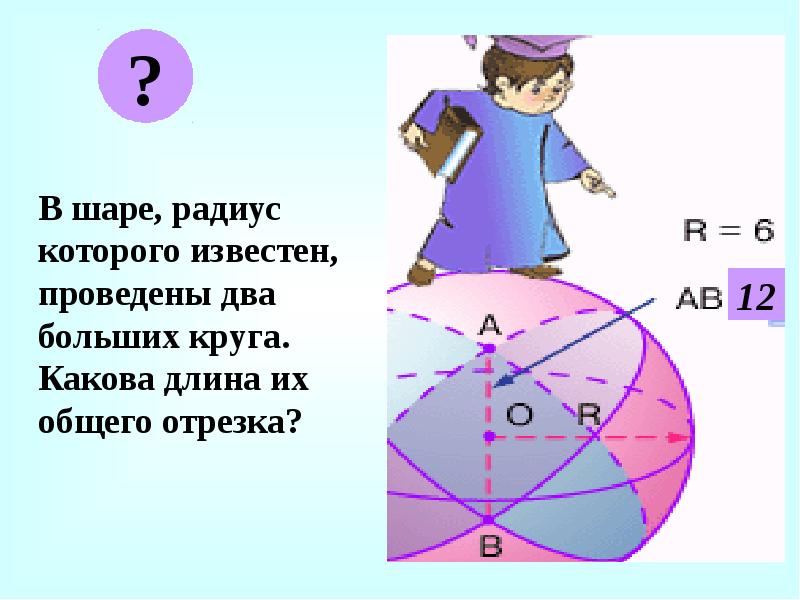
В шаре, радиус которого известен, проведены два больших круга. Какова длина их общего отрезка?
?
12
18 слайд

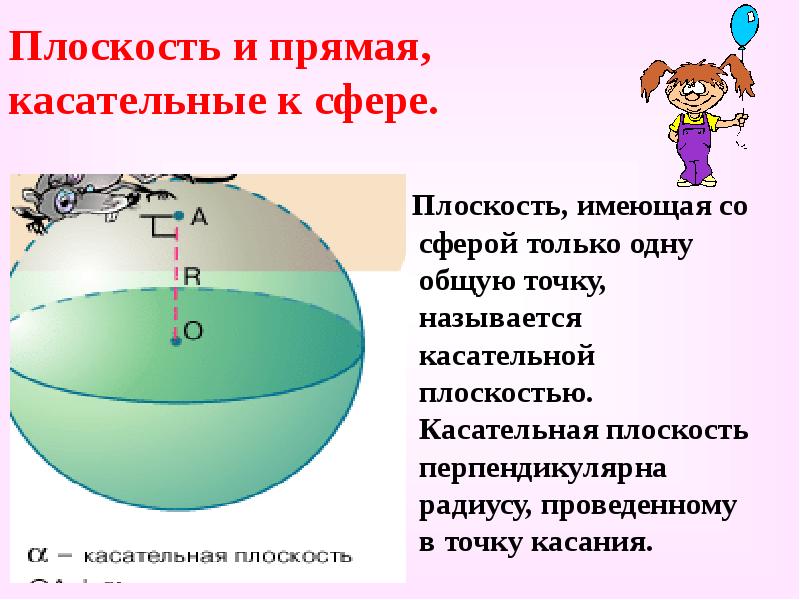
Плоскость и прямая, касательные к сфере.
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью. Касательная плоскость перпендикулярна радиусу, проведенному в точку касания.
19 слайд

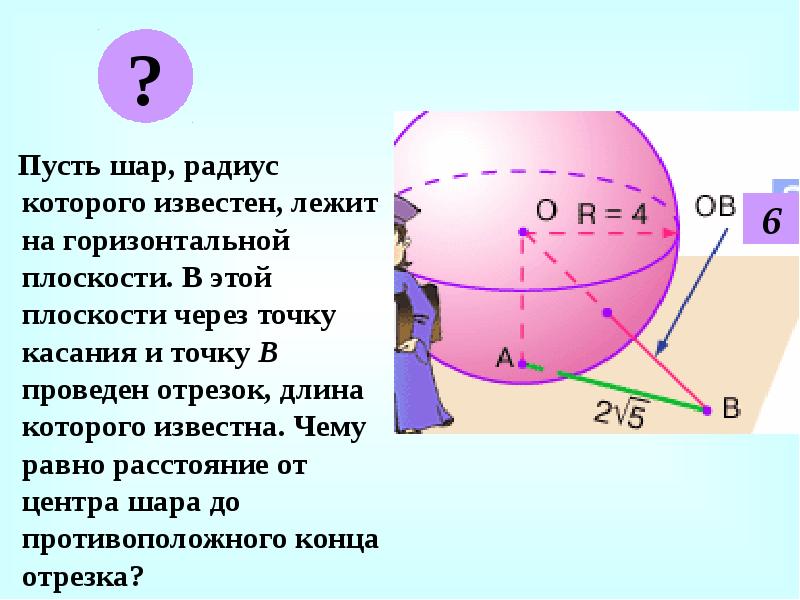
Пусть шар, радиус которого известен, лежит на горизонтальной плоскости. В этой плоскости через точку касания и точку В проведен отрезок, длина которого известна. Чему равно расстояние от центра шара до противоположного конца отрезка?
?
6
20 слайд

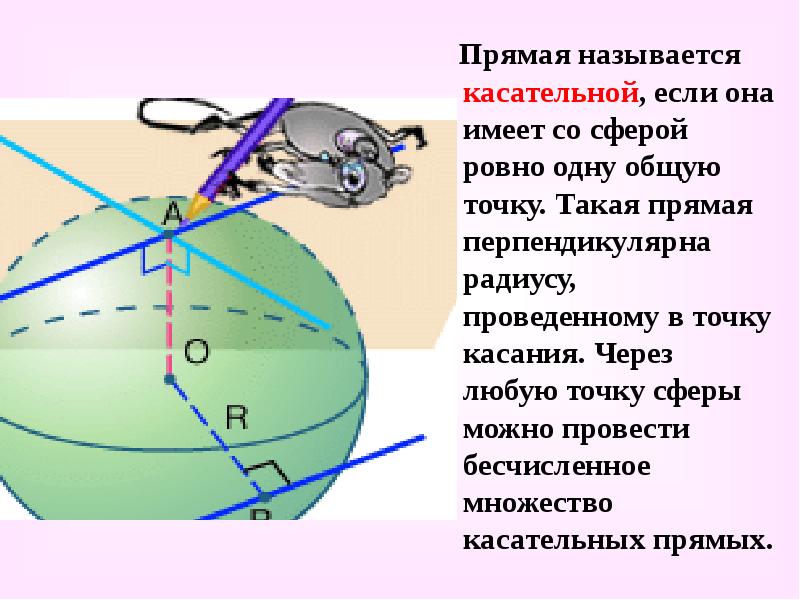
Прямая называется касательной, если она имеет со сферой ровно одну общую точку. Такая прямая перпендикулярна радиусу, проведенному в точку касания. Через любую точку сферы можно провести бесчисленное множество касательных прямых.
21 слайд

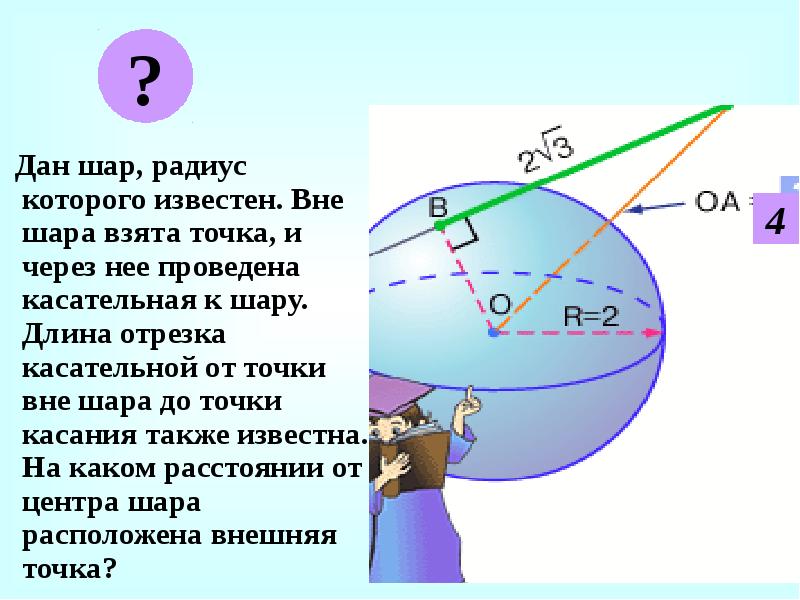
Дан шар, радиус которого известен. Вне шара взята точка, и через нее проведена касательная к шару. Длина отрезка касательной от точки вне шара до точки касания также известна. На каком расстоянии от центра шара расположена внешняя точка?
?
4
22 слайд

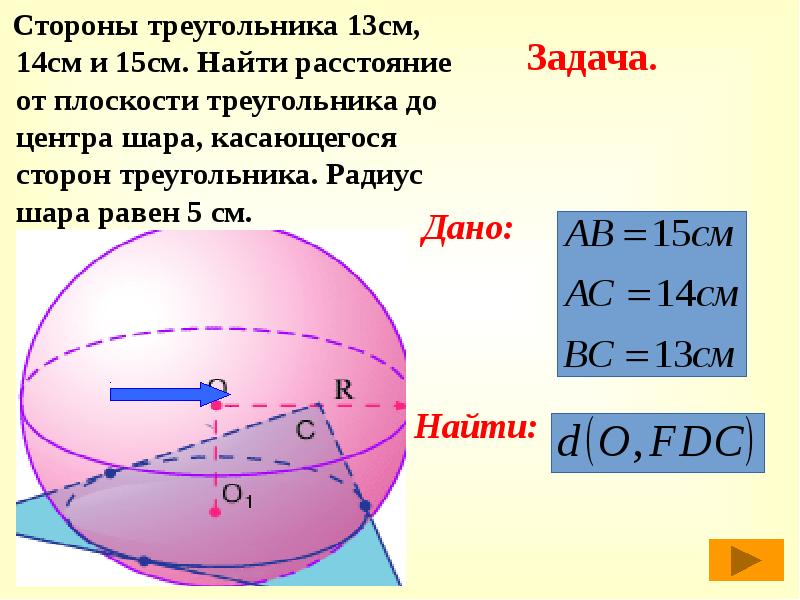
Стороны треугольника 13см, 14см и 15см. Найти расстояние от плоскости треугольника до центра шара, касающегося сторон треугольника. Радиус шара равен 5 см.
Задача.
Дано:

Найти:
23 слайд

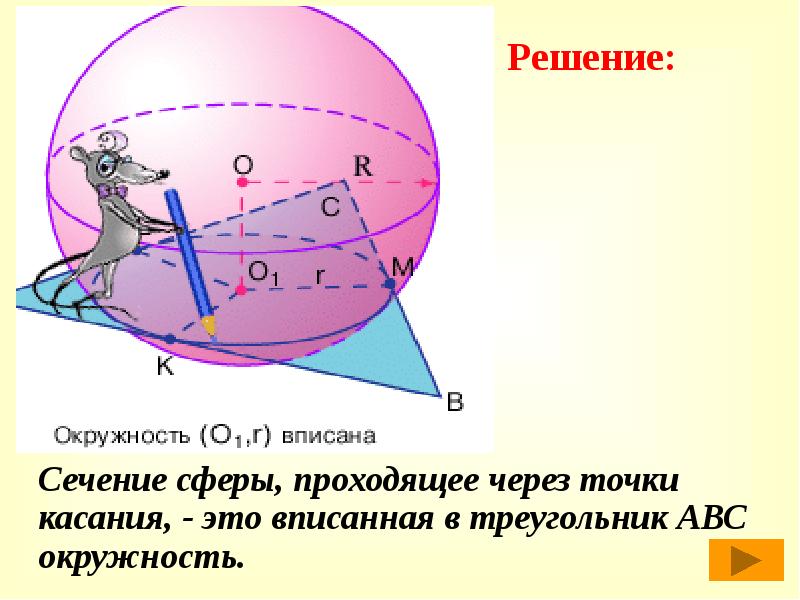
Сечение сферы, проходящее через точки касания, — это вписанная в треугольник АВС окружность.
Решение:
24 слайд

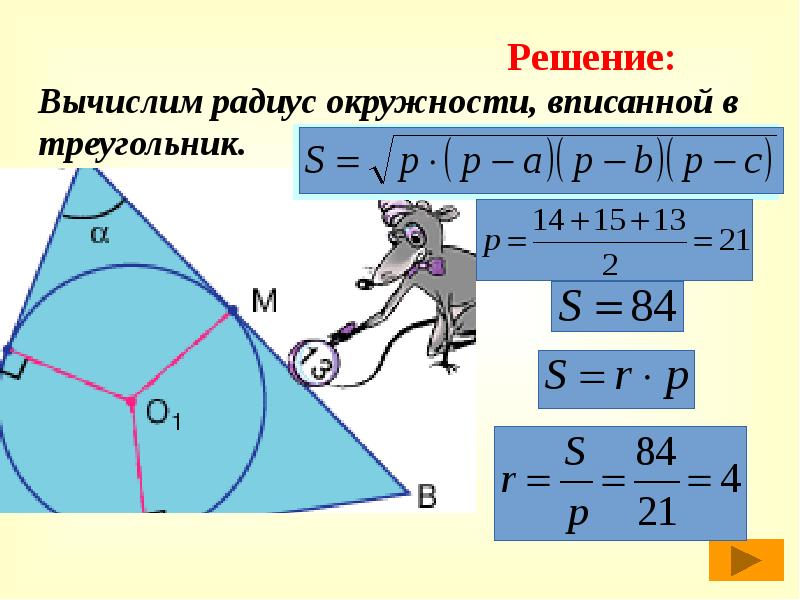
Вычислим радиус окружности, вписанной в треугольник.
Решение:
25 слайд

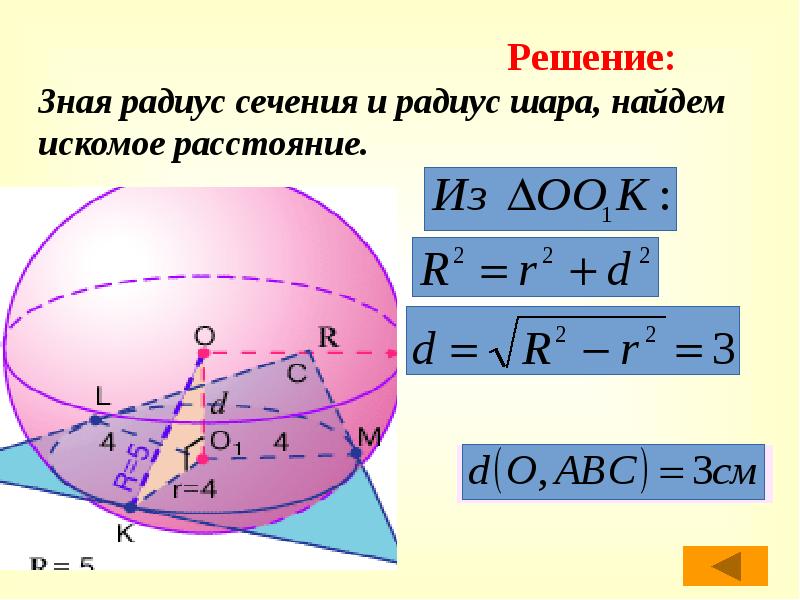
Зная радиус сечения и радиус шара, найдем искомое расстояние.
Решение:
26 слайд

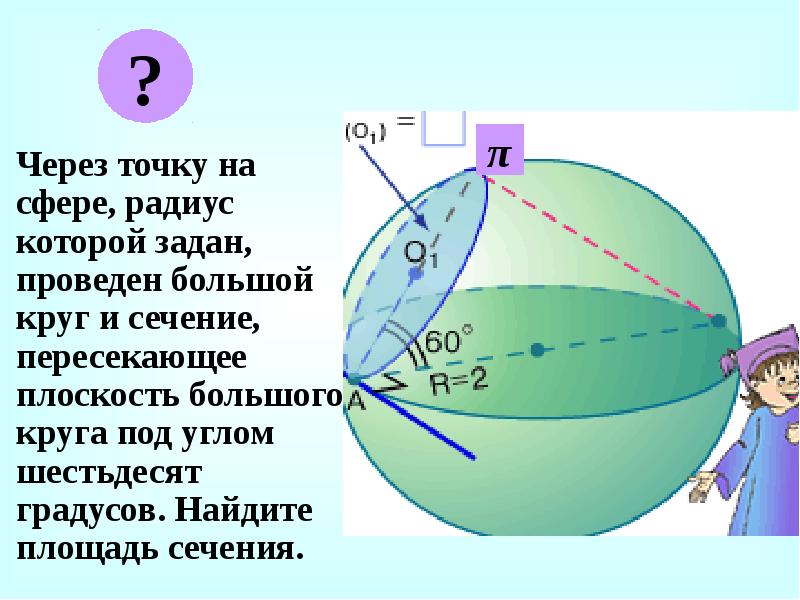
Через точку на сфере, радиус которой задан, проведен большой круг и сечение, пересекающее плоскость большого круга под углом шестьдесят градусов. Найдите площадь сечения.
?
π
27 слайд

Взаимное расположение двух шаров.
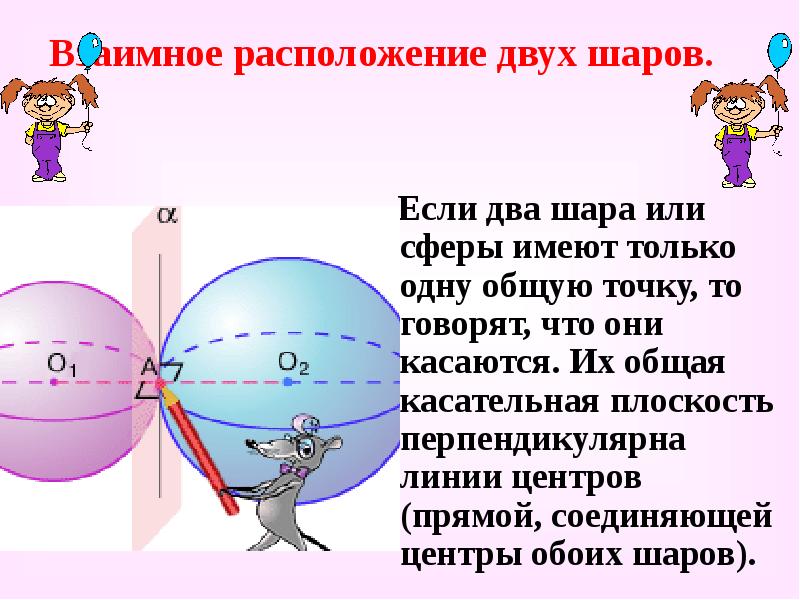
Если два шара или сферы имеют только одну общую точку, то говорят, что они касаются. Их общая касательная плоскость перпендикулярна линии центров (прямой, соединяющей центры обоих шаров).
28 слайд

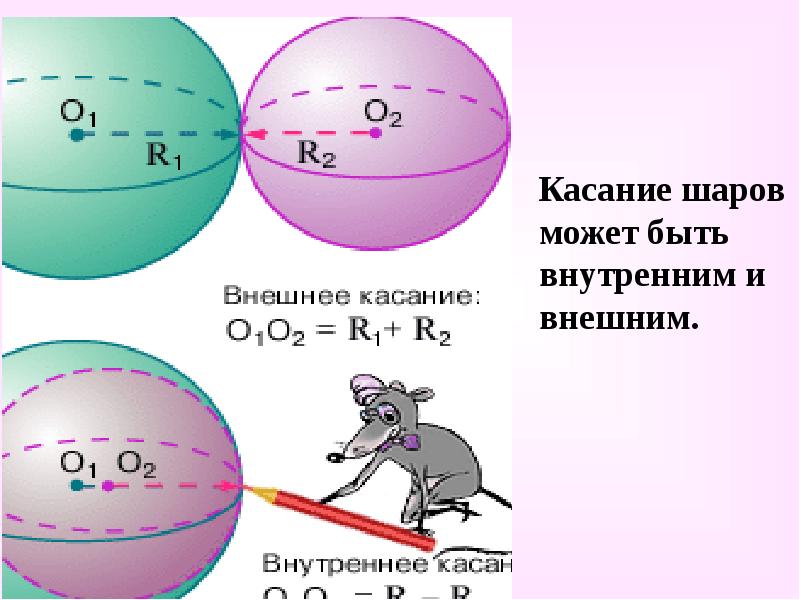
Касание шаров может быть внутренним и внешним.
29 слайд

Расстояние между центрами двух касающихся шаров равно пяти, а радиус одного из шаров равен трем. Найдите те значения, которые может принимать радиус второго шара.
?
2
8
30 слайд

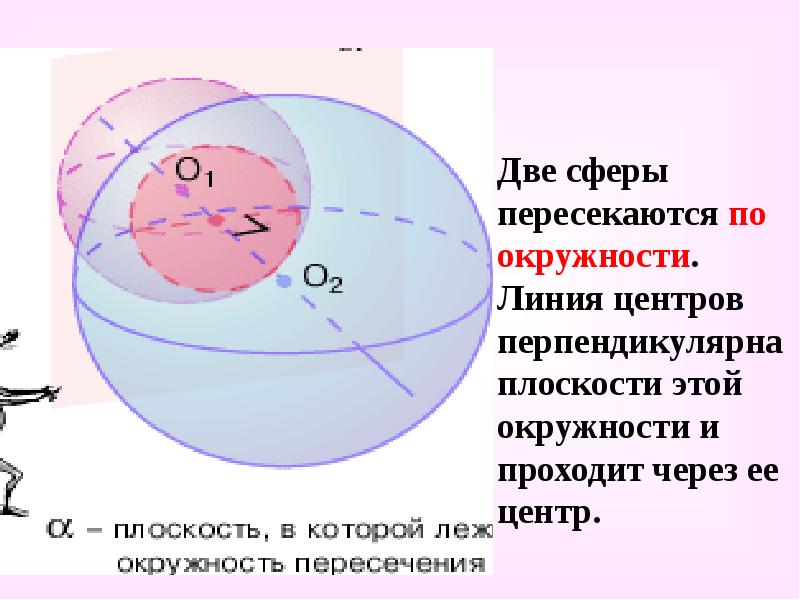
Две сферы пересекаются по окружности. Линия центров перпендикулярна плоскости этой окружности и проходит через ее центр.
31 слайд

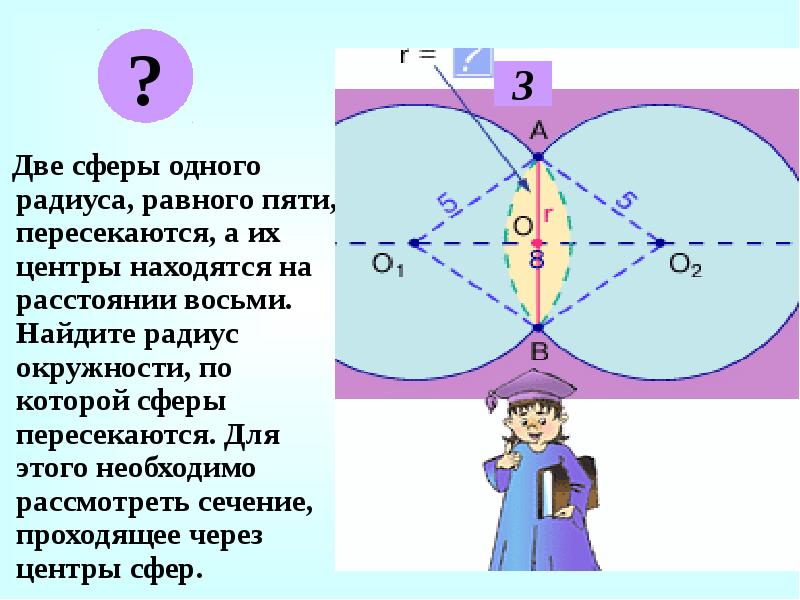
Две сферы одного радиуса, равного пяти, пересекаются, а их центры находятся на расстоянии восьми. Найдите радиус окружности, по которой сферы пересекаются. Для этого необходимо рассмотреть сечение, проходящее через центры сфер.
?
3
32 слайд

Вписанная и описанная сферы.
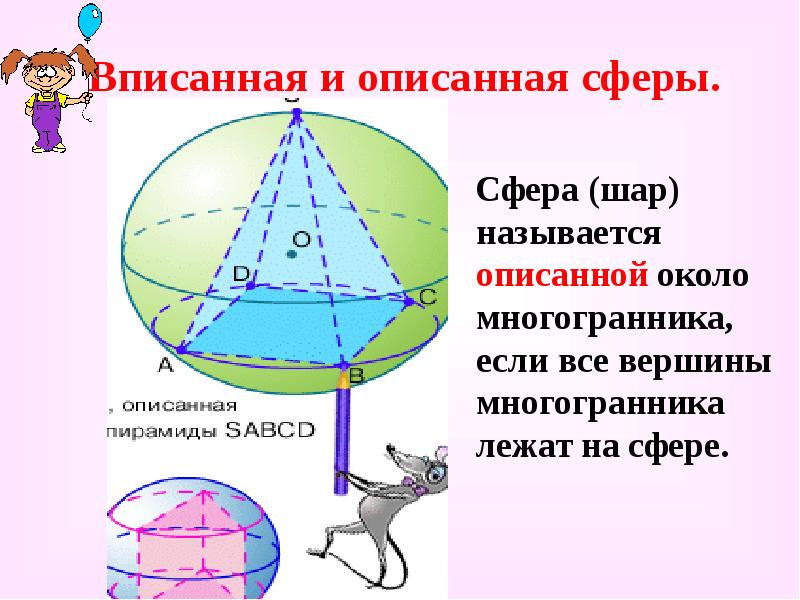
Сфера (шар) называется описанной около многогранника, если все вершины многогранника лежат на сфере.
33 слайд

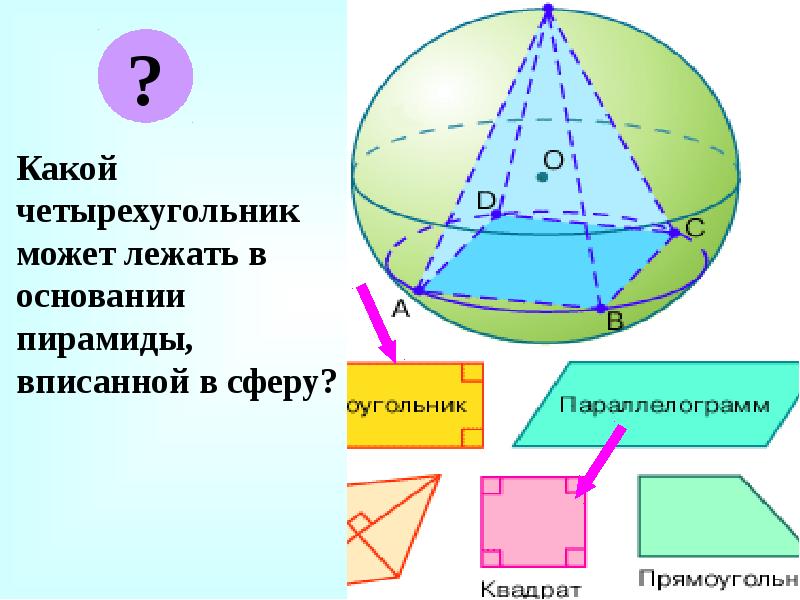
Какой четырехугольник может лежать в основании пирамиды, вписанной в сферу?
?
34 слайд

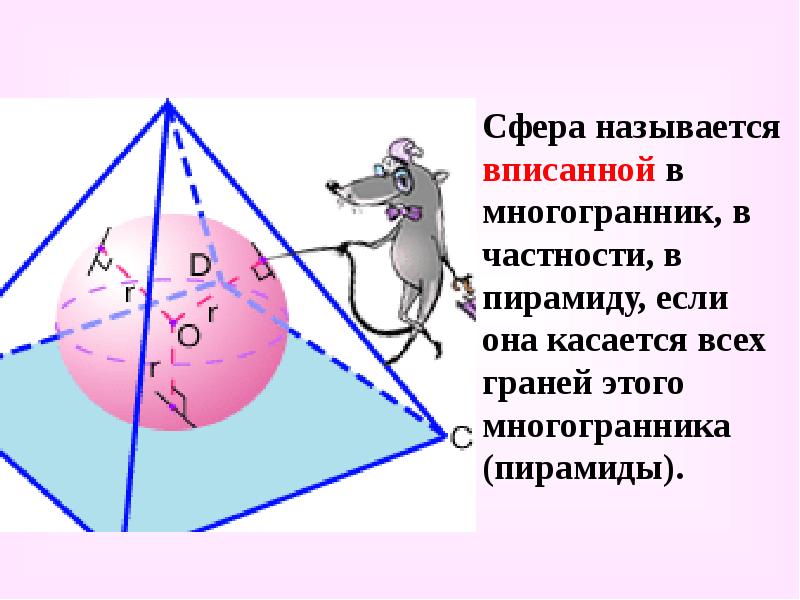
Сфера называется вписанной в многогранник, в частности, в пирамиду, если она касается всех граней этого многогранника (пирамиды).
35 слайд

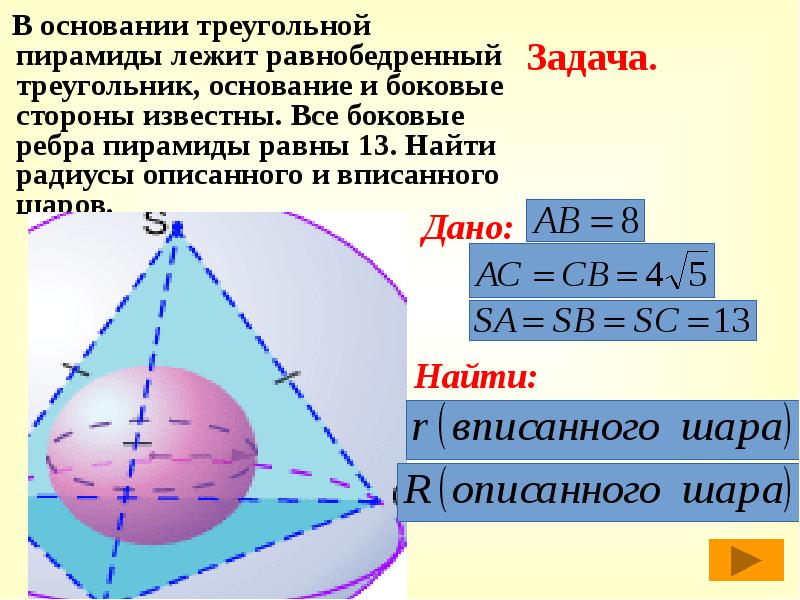
В основании треугольной пирамиды лежит равнобедренный треугольник, основание и боковые стороны известны. Все боковые ребра пирамиды равны 13. Найти радиусы описанного и вписанного шаров.
Задача.
Дано:

Найти:
36 слайд

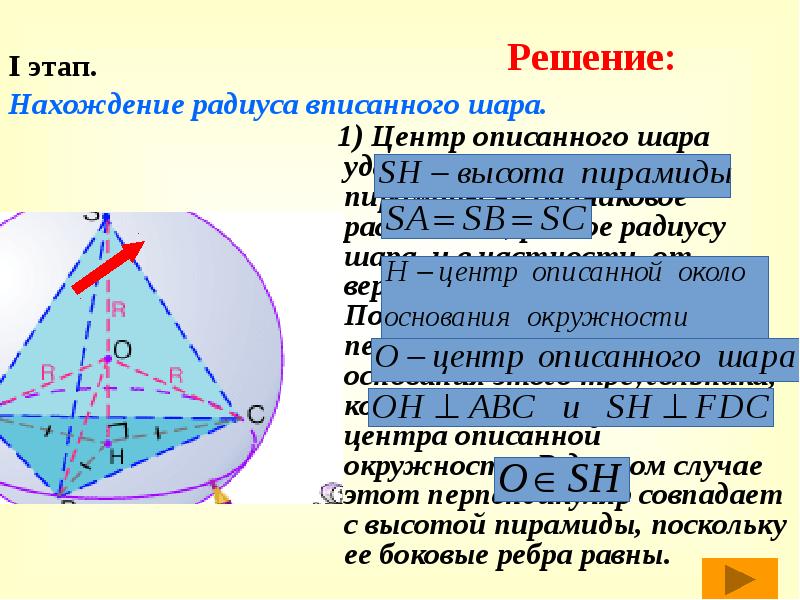
I этап.
Нахождение радиуса вписанного шара.
1) Центр описанного шара удален от всех вершин пирамиды на одинаковое расстояние, равное радиусу шара, и в частности, от вершин треугольника АВС. Поэтому он лежит на перпендикуляре к плоскости основания этого треугольника, который восстановлен из центра описанной окружности. В данном случае этот перпендикуляр совпадает с высотой пирамиды, поскольку ее боковые ребра равны.
Решение:
37 слайд

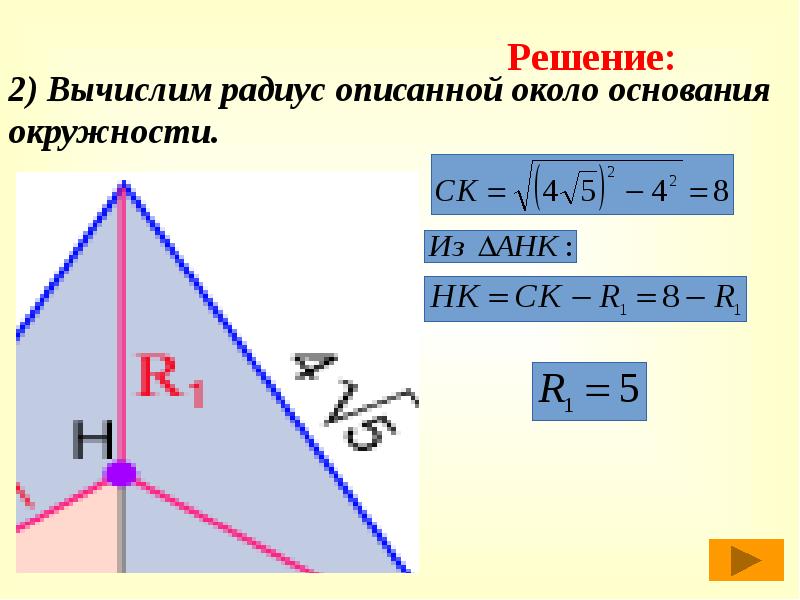
2) Вычислим радиус описанной около основания окружности.
Решение:
38 слайд

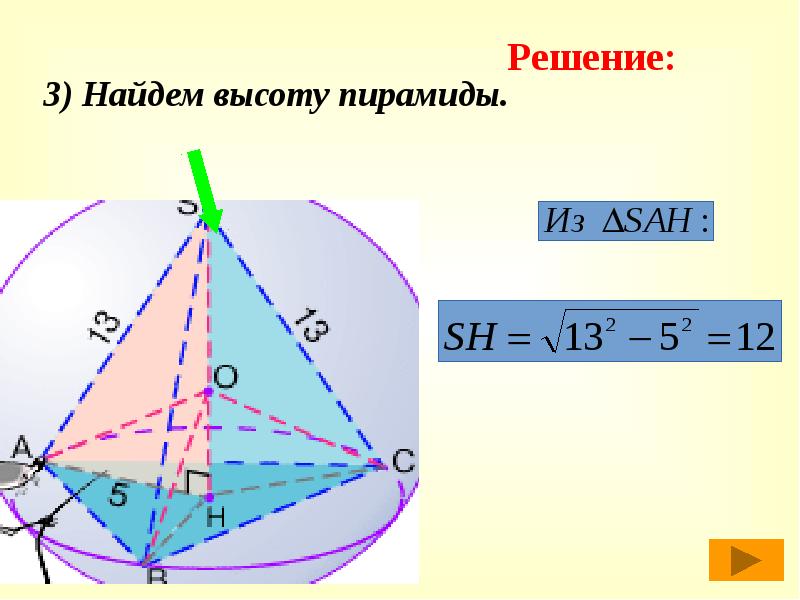
3) Найдем высоту пирамиды.
Решение:
39 слайд

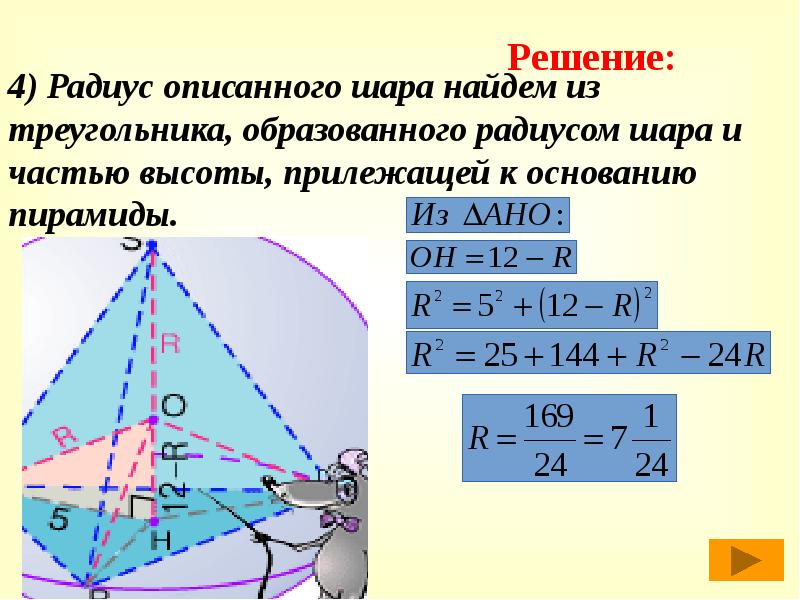
4) Радиус описанного шара найдем из треугольника, образованного радиусом шара и частью высоты, прилежащей к основанию пирамиды.
Решение:
40 слайд

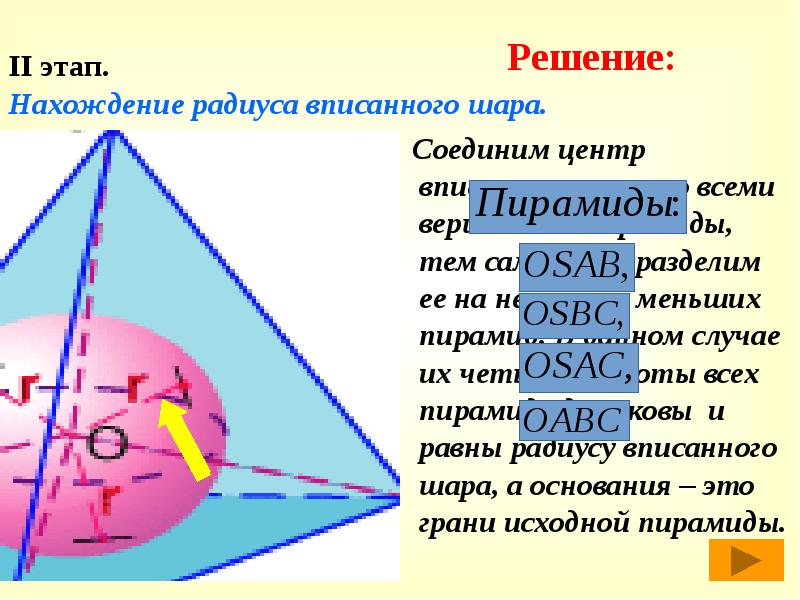
Соединим центр вписанного шара со всеми вершинами пирамиды, тем самым мы разделим ее на несколько меньших пирамид. В данном случае их четыре. Высоты всех пирамид одинаковы и равны радиусу вписанного шара, а основания – это грани исходной пирамиды.
Решение:
II этап.
Нахождение радиуса вписанного шара.
41 слайд

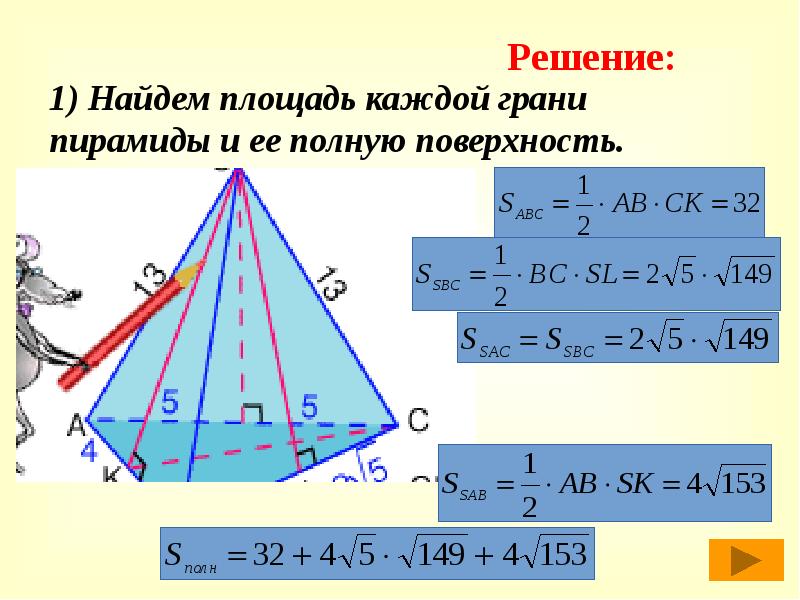
1) Найдем площадь каждой грани пирамиды и ее полную поверхность.
Решение:
42 слайд

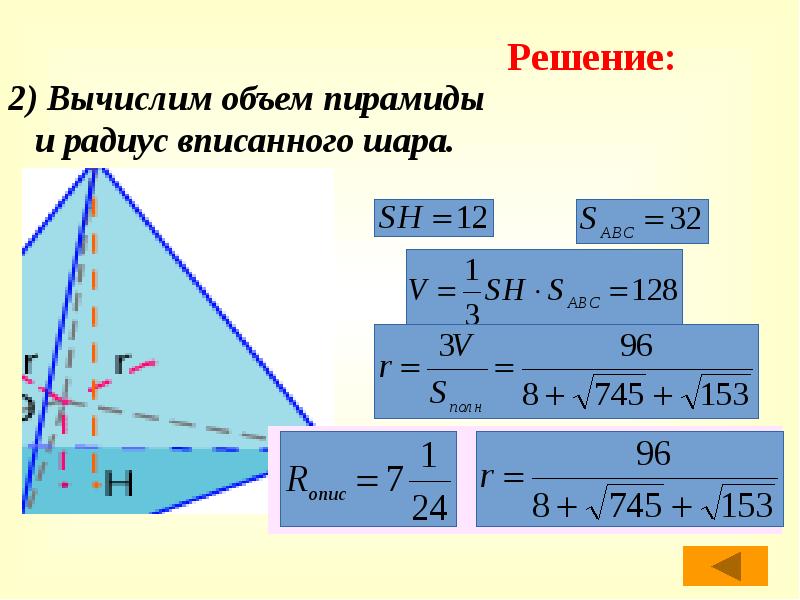
2) Вычислим объем пирамиды
и радиус вписанного шара.
Решение:
43 слайд

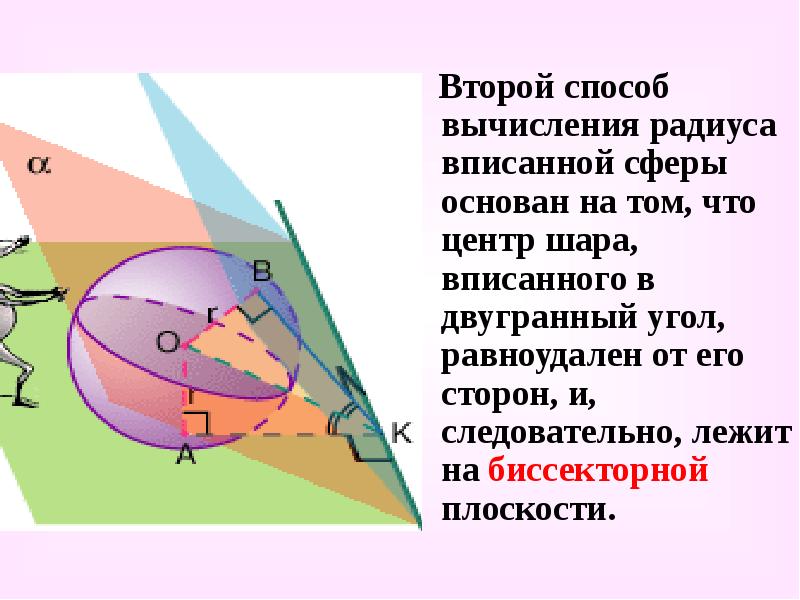
Второй способ вычисления радиуса вписанной сферы основан на том, что центр шара, вписанного в двугранный угол, равноудален от его сторон, и, следовательно, лежит на биссекторной плоскости.
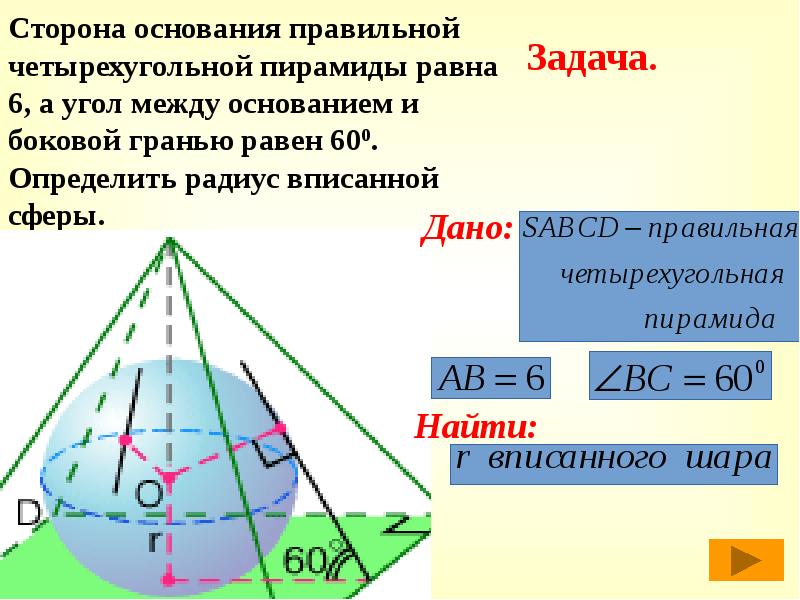
44 слайд

Сторона основания правильной четырехугольной пирамиды равна 6, а угол между основанием и боковой гранью равен 600. Определить радиус вписанной сферы.
Задача.
Дано:

Найти:
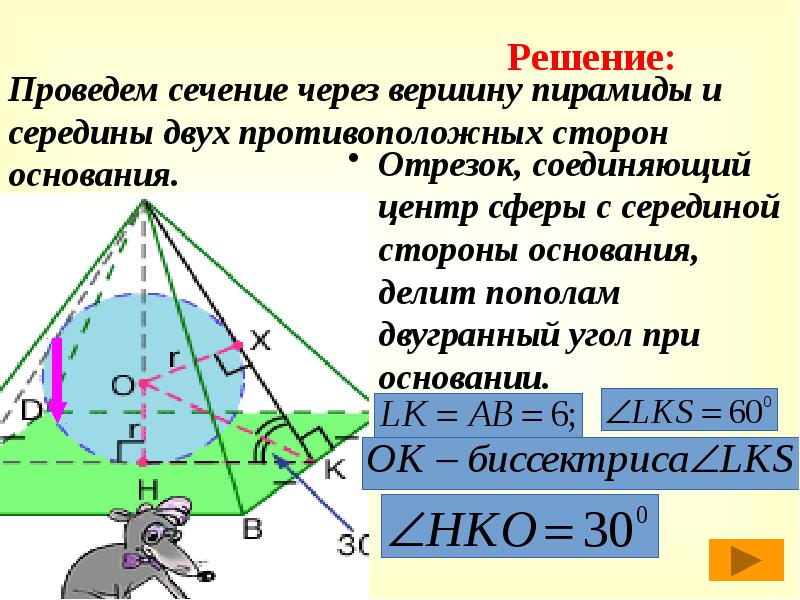
45 слайд

Проведем сечение через вершину пирамиды и середины двух противоположных сторон основания.
Отрезок, соединяющий центр сферы с серединой стороны основания, делит пополам двугранный угол при основании.
Решение:
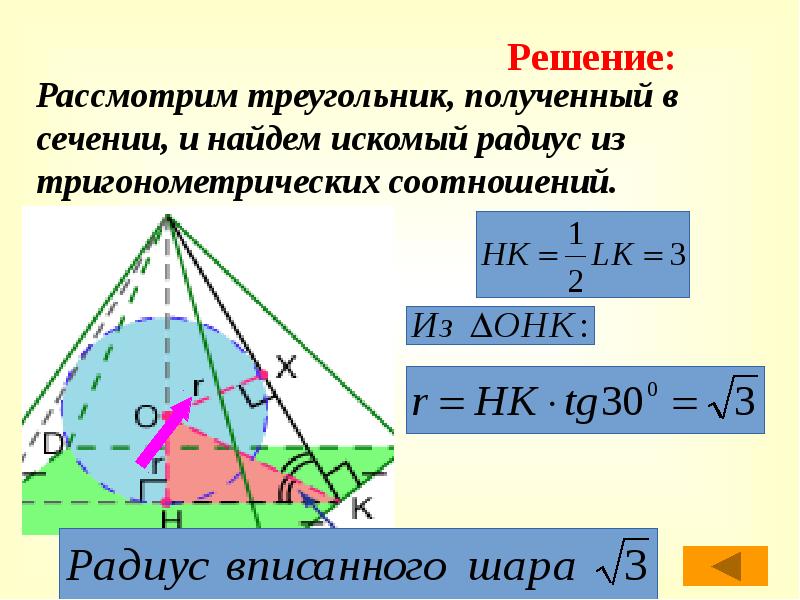
46 слайд

Рассмотрим треугольник, полученный в сечении, и найдем искомый радиус из тригонометрических соотношений.
Решение:

Краткое описание документа:

Сферой называется поверхность, которая состоит из всех точек
пространства, находящихся на заданном расстоянии от данной точки. Эта точка называется центром,
а заданное расстояние – радиусом сферы, или шара – тела, ограниченного сферой.
Шарсостоит из всех точек пространства, находящихся на расстоянии не более заданного от данной точки.

Чему равно расстояние между диаметрально противоположными точками шара, если известна удаленность точки, лежащей на поверхности шара от центра?

Шар можно рассматривать как тело, полученное от вращения полукруга вокруг диаметра как оси.

Пусть известна площадь полукруга. Найдите радиус шара, который получается вращением этого полукруга вокруг диаметра.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 267 196 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

14.01.2015
1178
2

14.01.2015
616
0

Рейтинг:
5 из 5

14.01.2015
6345
112

Рейтинг:
5 из 5

14.01.2015
1903
1

14.01.2015
975
0

Рейтинг:
1 из 5

14.01.2015
2402
7

14.01.2015
587
0

Источник

Площадь геометрической фигуры — это численная характеристика геометрической фигуры, показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Содержание:

Площади поверхностей круглых фигур
Площадь поверхности шара и его частей
Площадь поверхности цилиндра
Площадь поверхности конуса

Площадь поверхности шара и его частей

Пусть дана полуокружность AF с центром в а точке О (рис. 2.529). При вращении этой полуокружности вокруг диаметра AF мы получим поверхность шара (сферу с центром в точке О и диаметром AF).

Дадим следующее определение площади поверхности шара.

Определение. За площадь поверхности шара, полученного вращением полукруга вокруг диаметра, принимается предел, к которому стремится поверхность, получаемая вращением около того же диаметра правильной вписанной в полуокружность ломаной линии при неограниченном увеличении числа ее звеньев.

Формула поверхности шара такова:

где R — радиус шара.

Формула для нахождения площади поверхности шарового сегмента, получаемого при вращении дуги АС вокруг оси AF:

где R — радиус шара, h — высота шарового сегмента.

Пример:

Определите вес котла, поверхность которого состоит из цилиндрической поверхности и сферической поверхности двух шаровых сегментов (рис. 2.530).

Известно, что радиус цилиндрической поверхности r = 60 см, длина образующей этой поверхности h = 2 м, высота сегмента и котел сделан из листового железа, вес которого равен 12 кг.

Решение:

Для нахождения площади поверхности котла нужно найти площади поверхностей двух сферических сегментов, так как площадь поверхности цилиндрической части находится без труда.

1. Определим радиус сферы, частями которой служат поверхности сегментов, для чего построим центр сферы — точку О (рис. 2.530).

2. Из прямоугольного треугольника MON имеем: , или , откуда (1, теорема Пифагора).

3. Подставив в равенство п. 2 вместо r и данные значения, получим (2).

4. Площадь поверхности S всего котла будет: (данные задачи, формулы площади поверхности цилиндра и сегмента).

5. Заменив в последнем равенстве r, h и их данными значениями и R, получим:

6. Умножив вес листового железа на число квадратных метров поверхности котла, получаем его вес:

Площадь поверхности цилиндра

Если радиус цилиндра R, а высота Н, то его боковая поверхность развертывается в прямоугольник со сторонами и Н (рис. 2.531). Площадь этой развертки принимают за площадь боковой поверхности цилиндра.

Теорема 17. Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.

За площадь поверхности цилиндра, или за полную поверхность цилиндра, принимается площадь ее боковой поверхности, сложенной с удвоенной площадью основания. Она вычисляется по формуле

где R — радиус основания цилиндра, а Н — его высота.

Площадь поверхности конуса

Пусть нам дан конус с радиусом основания R и образующей .

Если посмотреть на рис. 2.531, то можно заметить, что площадь боковой поверхности конуса равна площади кругового сектора с радиусом и длиной дуги

Теорема 18. Площадь боковой поверхности конуса равна половине произведения длины окружности основания на образующую.

За площадь поверхности конуса, или за площадь полной поверхности конуса, принимается площадь его развертки . Она состоит из площади боковой поверхности и площади круга основания (рис. 2.532):

Формула для вычисления площади боковой поверхности усеченного конуса такова:

(рис. 2.533)

Выразим боковую поверхность усеченного конуса через длины окружностей оснований С и :

Итак, мы доказали теорему:

Теорема 19. Площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую.

За площадь поверхности усеченного конуса, или за полную поверхность усеченного конуса, принимается площадь его развертки. Она состоит из площади его боковой поверхности и площади кругов оснований.

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Математика решение заданий и задач

Смотрите также дополнительные лекции по предмету «Математика»:

Лекции:

Интегралы для чайников
Метод координат на прямой и его применение
Системы счисления
Смешанная производная
Предел функции
Механический смысл производной
Аналитическое решение уравнения
Полярные координаты
Найти общее решение уравнения
Значения случайной величины

Источник

Как найти площадь полукруга

Необходимость найти площадь полукруга или сектора возникает регулярно при проектировании архитектурных сооружений. Это может понадобиться и при расчете ткани, например, на рыцарский или мушкетерский плащ. В геометрии встречаются самые разные задания на вычисление этого параметра. В условиях может быть предложено определить площадь полкруга, построенного на определенной стороне треугольника или параллелепипеда. В этих случаях необходимы дополнительные вычисления.

Вам понадобится

— радиус полуокружности;
— линейка;
— циркуль;
— лист бумаги;
— карандаш;
— формула площади круга.

Инструкция

Постройте окружность с заданным радиусом. Центр ее обозначьте как О. Чтобы получить полукруг, достаточно провести через эту точку отрезок до пересечения с окружностью. Этот отрезок является диаметром данной окружности и равен двум ее радиусам. Вспомните, что такое окружность и что такое круг. Окружность — это линия, все точки которой удалены от центра на одинаковое расстояние. Круг — часть плоскости, ограниченная этой линией.

Вспомните формулу площади круга. Она равна квадрату радиуса, умноженному на постоянный коэффициент π, равный 3,14. То есть площадь круга выражается формулой S=πR2, где S – площадь, а R — радиус окружности. Вычислите площадь полукруга. Она равна половине площади круга, то есть S1= πR2/2.

В случае, когда вам в условиях дана только длина окружности, найдите сначала радиус. Длина окружности вычисляется по формуле P=2πR. Соответственно, чтобы найти радиус, необходимо длину окружности разделить на удвоенный коэффициент. Получается формула R=P/2π.

Полукруг можно представить и как сектор. Сектором называется часть круга, которая ограничена его двумя радиусами и дугой. Площадь сектора равна площади круга, умноженной на отношение центрального угла к полному углу окружности. То есть, в данном случае она выражается формулой S=π*R2*n°/360°. Угол сектора известен, он составляет 180°. Подставив его значение, вы снова получите ту же самую формулу — S1= πR2/2.

Обратите внимание

Встречаются задания, где угол дуги указан не в градусах, а в радианах. В этом случае необходимо воспользоваться формулой перевода Ar = Ad *π / 180°, где Ar — угол в радианах, а Ad — он же в градусах. Для вычисления площади полукруга это не особенно важно. Даже если вы представляете полукруг как сектор, в конечной формуле никаких градусов нет. Но это может оказаться нужным для вычисления площади сектора, имеющего другой центральный угол.

В некоторых задачах требуется найти площадь круга или полукруга, построенного на определенной стороне правильного или неправильного многоугольника. Без дополнительных построений в этом случае не обойтись. Необходимо разделить заданную фигуру на другие, параметры которых вам заданы или вы легко можете их найти. После этого вычислите нужную сторону, которая чаще всего и представляет собой диаметр круга или полукруга.

Источники:

формула как найти площадь

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

На этой странице представлена справочная информация с формулами для вычисления площадей простых фигур (сечений) с указанием положения их центров тяжестей.

Эта страничка будет полезна при расчёте более сложных фигур (составных поперечных сечений): определении положения центра тяжести, а также общей площади.

Центры тяжести

Для всех фигур, положение центра тяжести в статье обозначается буквой – C, это наиболее используемый вариант. Также иногда центр тяжести обозначают буквой – O.

Формулы для расчёта площадей

В сопромате площадь поперечного сечения обозначается буквой – A, однако, в некоторой литературе ты можешь встретить обозначения с буквой – F.

Другую справочную информацию, размещённую на сайте – ssopromat.ru, можешь найти, перейдя по указанной ссылке.

Источник

Слайды и текст этой презентации

Слайд 1
Тема урока:
«Сфера и шар.»
Цели: ввести понятие сферы, шара и их элементов; вывести уравнение сферы в заданной прямоугольной системе координат; исследовать взаимное расположение сферы и плоскости.
Развивающая: развивать логическое мышление, пространственное воображение; умение сравнивать, проводить аналогию; интерес к предмету; творческие способности учащихся.

Описание слайда:

Тема урока:
«Сфера и шар.»
Цели: ввести понятие сферы, шара и их элементов; вывести уравнение сферы в заданной прямоугольной системе координат; исследовать взаимное расположение сферы и плоскости.
Развивающая: развивать логическое мышление, пространственное воображение; умение сравнивать, проводить аналогию; интерес к предмету; творческие способности учащихся.

Слайд 2

Описание слайда:

Сферой называется поверхность, которая состоит из всех точек пространства, находящихся на заданном расстоянии от данной точки. Эта точка называется центром, а заданное расстояние – радиусом сферы, или шара – тела, ограниченного сферой. Шар состоит из всех точек пространства, находящихся на расстоянии не более заданного от данной точки.
Сферой называется поверхность, которая состоит из всех точек пространства, находящихся на заданном расстоянии от данной точки. Эта точка называется центром, а заданное расстояние – радиусом сферы, или шара – тела, ограниченного сферой. Шар состоит из всех точек пространства, находящихся на расстоянии не более заданного от данной точки.

Слайд 3

Описание слайда:

Отрезок, соединяющий центр шара с точкой на его поверхности, называется радиусом шара. Отрезок, соединяющий две точки на поверхности шара и проходящий через центр, называется диаметром шара, а концы этого отрезка – диаметрально противоположными точками шара.
Отрезок, соединяющий центр шара с точкой на его поверхности, называется радиусом шара. Отрезок, соединяющий две точки на поверхности шара и проходящий через центр, называется диаметром шара, а концы этого отрезка – диаметрально противоположными точками шара.

Слайд 4

Описание слайда:

Чему равно расстояние между диаметрально противоположными точками шара, если известна удаленность точки, лежащей на поверхности шара от центра?
Чему равно расстояние между диаметрально противоположными точками шара, если известна удаленность точки, лежащей на поверхности шара от центра?

Слайд 5

Описание слайда:

Шар можно рассматривать как тело, полученное от вращения полукруга вокруг диаметра как оси.
Шар можно рассматривать как тело, полученное от вращения полукруга вокруг диаметра как оси.

Слайд 6

Описание слайда:

Пусть известна площадь полукруга. Найдите радиус шара, который получается вращением этого полукруга вокруг диаметра.
Пусть известна площадь полукруга. Найдите радиус шара, который получается вращением этого полукруга вокруг диаметра.

Слайд 7

Описание слайда:

Теорема. Любое сечение шара плоскостью есть круг. Перпендикуляр, опущенный из центра шара на секущую плоскость, попадает в центр этого круга.
Дано:

Доказать:

Слайд 8
Доказательство:
Рассмотрим прямоугольный треугольник, вершинами которого являются центр шара, основание перпендикуляра, опущенного из центра на плоскость, и произвольная точка сечения.

Описание слайда:

Доказательство:
Рассмотрим прямоугольный треугольник, вершинами которого являются центр шара, основание перпендикуляра, опущенного из центра на плоскость, и произвольная точка сечения.

Слайд 9

Описание слайда:

Следствие. Если известны радиус шара и расстояние от центра шара до плоскости сечения, то радиус сечения вычисляется по теореме Пифагора.

Слайд 10

Описание слайда:

Пусть известны диаметр шара и расстояние от центра шара до секущей плоскости. Найдите радиус круга, получившегося сечения.
Пусть известны диаметр шара и расстояние от центра шара до секущей плоскости. Найдите радиус круга, получившегося сечения.

Слайд 11

Описание слайда:

Чем меньше расстояние от центра шара до плоскости, тем больше радиус сечения.

Слайд 12

Описание слайда:

В шаре радиуса пять проведен диаметр и два сечения, перпендикулярных этому диаметру. Одно из сечений находится на расстоянии три от центра шара, а второе – на таком же расстоянии от ближайшего конца диаметра. Отметьте то сечение, радиус которого больше.
В шаре радиуса пять проведен диаметр и два сечения, перпендикулярных этому диаметру. Одно из сечений находится на расстоянии три от центра шара, а второе – на таком же расстоянии от ближайшего конца диаметра. Отметьте то сечение, радиус которого больше.

Слайд 13
Задача.
На сфере радиуса R взяты три точки, являющиеся вершинами правильного треугольника со стороной а. На каком расстоянии от центра сферы расположена плоскость, проходящая через эти три точки?

Описание слайда:

Задача.
На сфере радиуса R взяты три точки, являющиеся вершинами правильного треугольника со стороной а. На каком расстоянии от центра сферы расположена плоскость, проходящая через эти три точки?

Слайд 14

Описание слайда:

Рассмотрим пирамиду с вершиной в центре шара и основанием – данным треугольником.
Рассмотрим пирамиду с вершиной в центре шара и основанием – данным треугольником.

Слайд 15

Описание слайда:

Найдем радиус описанной окружности, а затем рассмотрим один из треугольников, образованных радиусом, боковым ребром пирамиды и высотой,. Найдем высоту по теореме Пифагора.
Найдем радиус описанной окружности, а затем рассмотрим один из треугольников, образованных радиусом, боковым ребром пирамиды и высотой,. Найдем высоту по теореме Пифагора.

Слайд 16

Описание слайда:

Наибольший радиус сечения получается, когда плоскость проходит через центр шара. Круг, получаемый в этом случае, называется большим кругом. Большой круг делит шар на два полушара.
Наибольший радиус сечения получается, когда плоскость проходит через центр шара. Круг, получаемый в этом случае, называется большим кругом. Большой круг делит шар на два полушара.

Слайд 17

Описание слайда:

В шаре, радиус которого известен, проведены два больших круга. Какова длина их общего отрезка?
В шаре, радиус которого известен, проведены два больших круга. Какова длина их общего отрезка?

Слайд 18

Описание слайда:

Плоскость и прямая, касательные к сфере.
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью. Касательная плоскость перпендикулярна радиусу, проведенному в точку касания.

Слайд 19

Описание слайда:

Пусть шар, радиус которого известен, лежит на горизонтальной плоскости. В этой плоскости через точку касания и точку В проведен отрезок, длина которого известна. Чему равно расстояние от центра шара до противоположного конца отрезка?
Пусть шар, радиус которого известен, лежит на горизонтальной плоскости. В этой плоскости через точку касания и точку В проведен отрезок, длина которого известна. Чему равно расстояние от центра шара до противоположного конца отрезка?

Слайд 20

Описание слайда:

Прямая называется касательной, если она имеет со сферой ровно одну общую точку. Такая прямая перпендикулярна радиусу, проведенному в точку касания. Через любую точку сферы можно провести бесчисленное множество касательных прямых.
Прямая называется касательной, если она имеет со сферой ровно одну общую точку. Такая прямая перпендикулярна радиусу, проведенному в точку касания. Через любую точку сферы можно провести бесчисленное множество касательных прямых.

Слайд 21

Описание слайда:

Дан шар, радиус которого известен. Вне шара взята точка, и через нее проведена касательная к шару. Длина отрезка касательной от точки вне шара до точки касания также известна. На каком расстоянии от центра шара расположена внешняя точка?
Дан шар, радиус которого известен. Вне шара взята точка, и через нее проведена касательная к шару. Длина отрезка касательной от точки вне шара до точки касания также известна. На каком расстоянии от центра шара расположена внешняя точка?

Слайд 22

Описание слайда:

Стороны треугольника 13см, 14см и 15см. Найти расстояние от плоскости треугольника до центра шара, касающегося сторон треугольника. Радиус шара равен 5 см.
Стороны треугольника 13см, 14см и 15см. Найти расстояние от плоскости треугольника до центра шара, касающегося сторон треугольника. Радиус шара равен 5 см.

Слайд 23

Описание слайда:

Сечение сферы, проходящее через точки касания, — это вписанная в треугольник АВС окружность.
Сечение сферы, проходящее через точки касания, — это вписанная в треугольник АВС окружность.

Слайд 24

Описание слайда:

Вычислим радиус окружности, вписанной в треугольник.
Вычислим радиус окружности, вписанной в треугольник.

Слайд 25

Описание слайда:

Зная радиус сечения и радиус шара, найдем искомое расстояние.
Зная радиус сечения и радиус шара, найдем искомое расстояние.

Слайд 26

Описание слайда:

Через точку на сфере, радиус которой задан, проведен большой круг и сечение, пересекающее плоскость большого круга под углом шестьдесят градусов. Найдите площадь сечения.
Через точку на сфере, радиус которой задан, проведен большой круг и сечение, пересекающее плоскость большого круга под углом шестьдесят градусов. Найдите площадь сечения.

Слайд 27

Описание слайда:

Взаимное расположение двух шаров.
Если два шара или сферы имеют только одну общую точку, то говорят, что они касаются. Их общая касательная плоскость перпендикулярна линии центров (прямой, соединяющей центры обоих шаров).

Слайд 28

Описание слайда:

Касание шаров может быть внутренним и внешним.
Касание шаров может быть внутренним и внешним.

Слайд 29

Описание слайда:

Расстояние между центрами двух касающихся шаров равно пяти, а радиус одного из шаров равен трем. Найдите те значения, которые может принимать радиус второго шара.
Расстояние между центрами двух касающихся шаров равно пяти, а радиус одного из шаров равен трем. Найдите те значения, которые может принимать радиус второго шара.

Слайд 30

Описание слайда:

Две сферы пересекаются по окружности. Линия центров перпендикулярна плоскости этой окружности и проходит через ее центр.
Две сферы пересекаются по окружности. Линия центров перпендикулярна плоскости этой окружности и проходит через ее центр.

Слайд 31

Описание слайда:

Две сферы одного радиуса, равного пяти, пересекаются, а их центры находятся на расстоянии восьми. Найдите радиус окружности, по которой сферы пересекаются. Для этого необходимо рассмотреть сечение, проходящее через центры сфер.
Две сферы одного радиуса, равного пяти, пересекаются, а их центры находятся на расстоянии восьми. Найдите радиус окружности, по которой сферы пересекаются. Для этого необходимо рассмотреть сечение, проходящее через центры сфер.

Слайд 32
Вписанная и описанная сферы.
Сфера (шар) называется описанной около многогранника, если все вершины многогранника лежат на сфере.

Описание слайда:

Вписанная и описанная сферы.
Сфера (шар) называется описанной около многогранника, если все вершины многогранника лежат на сфере.

Слайд 33

Описание слайда:

Какой четырехугольник может лежать в основании пирамиды, вписанной в сферу?
Какой четырехугольник может лежать в основании пирамиды, вписанной в сферу?

Слайд 34

Описание слайда:

Сфера называется вписанной в многогранник, в частности, в пирамиду, если она касается всех граней этого многогранника (пирамиды).
Сфера называется вписанной в многогранник, в частности, в пирамиду, если она касается всех граней этого многогранника (пирамиды).

Слайд 35

Описание слайда:

В основании треугольной пирамиды лежит равнобедренный треугольник, основание и боковые стороны известны. Все боковые ребра пирамиды равны 13. Найти радиусы описанного и вписанного шаров.
В основании треугольной пирамиды лежит равнобедренный треугольник, основание и боковые стороны известны. Все боковые ребра пирамиды равны 13. Найти радиусы описанного и вписанного шаров.

Слайд 36

Описание слайда:

I этап.
Нахождение радиуса вписанного шара.
1) Центр описанного шара удален от всех вершин пирамиды на одинаковое расстояние, равное радиусу шара, и в частности, от вершин треугольника АВС. Поэтому он лежит на перпендикуляре к плоскости основания этого треугольника, который восстановлен из центра описанной окружности. В данном случае этот перпендикуляр совпадает с высотой пирамиды, поскольку ее боковые ребра равны.

Слайд 37

Описание слайда:

2) Вычислим радиус описанной около основания окружности.

Слайд 38

Описание слайда:

3) Найдем высоту пирамиды.

Слайд 39

Описание слайда:

4) Радиус описанного шара найдем из треугольника, образованного радиусом шара и частью высоты, прилежащей к основанию пирамиды.

Слайд 40

Описание слайда:

Соединим центр вписанного шара со всеми вершинами пирамиды, тем самым мы разделим ее на несколько меньших пирамид. В данном случае их четыре. Высоты всех пирамид одинаковы и равны радиусу вписанного шара, а основания – это грани исходной пирамиды.
Соединим центр вписанного шара со всеми вершинами пирамиды, тем самым мы разделим ее на несколько меньших пирамид. В данном случае их четыре. Высоты всех пирамид одинаковы и равны радиусу вписанного шара, а основания – это грани исходной пирамиды.

Слайд 41

Описание слайда:

1) Найдем площадь каждой грани пирамиды и ее полную поверхность.

Слайд 42
2) Вычислим объем пирамиды
и радиус вписанного шара.

Описание слайда:

2) Вычислим объем пирамиды
и радиус вписанного шара.

Слайд 43

Описание слайда:

Второй способ вычисления радиуса вписанной сферы основан на том, что центр шара, вписанного в двугранный угол, равноудален от его сторон, и, следовательно, лежит на биссекторной плоскости.
Второй способ вычисления радиуса вписанной сферы основан на том, что центр шара, вписанного в двугранный угол, равноудален от его сторон, и, следовательно, лежит на биссекторной плоскости.

Слайд 44

Описание слайда:

Сторона основания правильной четырехугольной пирамиды равна 6, а угол между основанием и боковой гранью равен 600. Определить радиус вписанной сферы.

Слайд 45

Описание слайда:

Проведем сечение через вершину пирамиды и середины двух противоположных сторон основания.
Отрезок, соединяющий центр сферы с серединой стороны основания, делит пополам двугранный угол при основании.

Слайд 46

Описание слайда:

Рассмотрим треугольник, полученный в сечении, и найдем искомый радиус из тригонометрических соотношений.

Слайд 47
Итог урока
Сегодня вы познакомились с:

определением сферы, шара;
взаимным расположением сферы и плоскости;
нахождением радиуса вписанного шара.