Как найти площадь полной поверхности усеченного конуса - AvtoShod.ru

Как рассчитать площадь усеченного конуса

На данной странице калькулятор поможет рассчитать площадь поверхности усеченного конуса онлайн. Для расчета задайте радиусы и образующую.

Усеченный конус — часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.

Образующая конуса — это отрезок, соединяющий вершину и границу основания.

Боковая поверхность

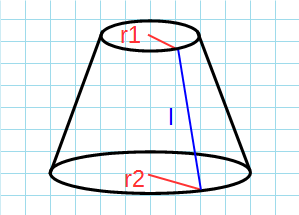
Формула площади боковой поверхности усеченного конуса через радиусы и образующую:

π — константа равная (3.14); r1 — радиус верхнего основания ; r2 — радиус нижнего основания; l — образующая усеченного конуса.

Полная поверхность

Формула площади полной поверхности усеченного конуса через радиусы и образующую:

Источник

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности прямого усеченного кругового конуса (боковую, полную и основания), а также разберем пример решения задачи для закрепления представленного теоретического материала.

Формулы вычисления площади усеченного конуса
- 1. Боковая поверхность
- 2. Основания
- 3. Полная площадь
Пример задачи

Формулы вычисления площади усеченного конуса

Примечание: иногда усеченный конус, также, называют коническим слоем.

1. Боковая поверхность

Чтобы найти площадь (S) боковой поверхности прямого усеченного кругового конуса, необходимо знать длину его образующей, а также радиусы двух оснований.

S_бок. = πRl + πrl = πl(R + r)

Примечание: в этой и других формулах ниже число π чаще всего округляется до 3,14.

2. Основания

Основаниями кругового усеченного конуса являются два круга, площади которых считаются таким образом:

S_осн.1 = πR²

S_осн.2 = πr²

Примечание: если вместо радиусов (R или r) даны соответсвующие им диаметры (d), их следует разделить на 2, чтобы получить нужные радиусы.

3. Полная площадь

Чтобы вычислить площадь полной поверхности усеченного конуса, требуется сложить площади его боковой поверхности и двух оснований.

S_полн. = πl(R + r) + πR² + πr² = π(lR + lr + R² + r²)

Пример задачи

Найдите площадь поверхности усеченного конуса, если известно, что радиусы его оснований равны 6 и 11 см, а длина образующей составляет 8 см.

Решение

Все известные значения для вычисления площади нам известны, так что остается лишь подставить их в формулы, приведенные выше.

S_бок. = 3,14 ⋅ 8 см ⋅ (6 см + 11 см) = 427,04 см²

S_осн.1 = 3,14 ⋅ (11 см)² = 379,94 см²

S_осн.2 = 3,14 ⋅ (6 см)² = 113,04 см²

S_полн. = 427,04 см² + 379,94 см² + 113,04 см² = 920,02 см²

Источник

Площадь поверхности усеченного конуса

Усечённый конус или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием.

Усечённый конус может быть получен вращением прямоугольной трапеции вокруг меньшей боковой стороны.

Формула площади боковой поверхности усеченного конуса: S = π l (R + r) ,

где R — радиус нижнего основания, r — радиус верхнего основания, l — образующая усеченного конуса.

Формула площади полной поверхности усеченного конуса: S = π (l R + l r + R² + r²) ,

где R — радиус нижнего основания, r — радиус верхнего основания, l — образующая усеченного конуса.

Образующая усеченного конуса рассчитывается по формуле:

,
где R — радиус нижнего основания, r — радиус верхнего основания, h — высота усеченного конуса.

Калькулятор пощади поверхности усеченного конуса позволяет найти площадь боковой поверхности усеченного конуса и полную площадь поверхности усеченного конуса.

Поделиться страницей в социальных сетях:

Источник

Площадь поверхности усеченного конуса, формула.

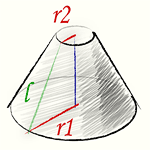Полная площадь поверхности усеченного конуса

Усеченный конус получится, если в конусе провести сечение, параллельное основанию. Тело ограниченное этим сечением, основанием и боковой поверхностью конуса называется усеченным конусом.
См. также Объем усеченного конуса

Боковая площадь поверхности усеченного конуса, формула.

Боковая площадь поверхности усеченного конуса вычисляется по формуле:

[S=pi (r_1 + r_2) l]

(r₁ — радиус нижнего основания усеченного конуса; r₂ — радиус верхнего основания усеченного конуса; l — образующая усеченного конуса)

Вычислить площадь боковой поверхности усеченного конуса по формуле (1).

Полная площадь поверхности усеченного конуса, формула.

Полная площадь поверхности усеченного конуса равна сумме площадей боковой поверхности усеченного конуса и его оснований. Основания усеченного конуса есть круги и их площадь вычисляется по формуле площади круга:

[S=pi (r_1^2 + (r_1 + r_2) l + r_2^2) ]

(r — радиус вращения усеченного конуса; l — образующая усеченного конуса)

Вычислить площадь полной поверхности усеченного конуса по формуле (2).

Ссылки по теме

Площадь поверхности усеченного конуса	стр. 314

Источник

Усеченный конус – это часть конуса, ограниченная между двумя параллельными основаниями перпендикулярными его оси симметрии.Основаниями конуса являются геометрические круги.

Усеченный конус может быть получен в результате вращения прямоугольной трапеции вокруг ее боковой стороны, которая является ее высотой. Границей конуса является круг радиуса R, круг радиуса r и боковая поверхность конуса. Боковую поверхность конуса описывает боковая сторона трапеции во время ее вращения.

Площадь боковой поверхности усеченного конуса через направляющую и радиусы его оснований

При нахождении площади боковую поверхность усеченного конуса целесообразней рассматривать как разность боковой поверхности конуса и боковой поверхности отсеченного конуса.

Пусть от данного конуса AMB отсекли конус A`MB`. Необходимо вычислить боковую площадь усеченного конуса AA`B`B. Известно, что радиусы его оснований AO=R, A`O`=r, образующая равна L.Обозначим MB` за x. Тогда боковая поверхность конуса A`MB` будет равна πrx. А боковая поверхность конуса AMB будет равна πR(L+x).
Тогда боковую поверхность усеченного конуса AA`B`B можно выразить через разность боковой поверхности конуса AMB и конуса A`MB`:
$S_bok={pi}R(L+x)-{pi}rx={pi}(RL+Rx-rx)={pi}(RL+x(R-r))$
Треугольники OMB и O`MB`– подобны по равенству углов ∠{MOB} = ∠{MO`B`} и ∠{OMB} = ∠{O`MB`}. Из подобия этих треугольников следует:
Воспользуемся производной пропорции. Имеем:
Отсюда находим x:
Подставив это выражение в формулу площади боковой поверхности, имеем: $S_bok={pi}(RL+{{rL}/{R-r}} (R-r) )={pi}(RL+rL)={pi}L(R+r)$
Таким образом, площадь боковой поверхности усеченного конуса равна произведению числа π на его направляющую и сумму радиусов его оснований.
Формула площади боковой поверхности усеченного конуса имеет следующий вид: $S_bok={pi}L(R+r)$

Пример расчета площади боковой поверхности усеченного конуса, если известны его радиус и образующая
Радиус большего основания, образующая и высота усеченного конуса равны 7, 5 и 4 см соответственно. Найдите площадь боковой поверхности конуса.
Осевое сечение усеченного конуса представляет собой равнобедренную трапецию, с основаниями 2R и 2r. Образующая усеченного конуса, являющаяся боковой стороной трапеции, высота, опушенная на большое основание и разность радиусов основания усеченного конуса, образуют египетский треугольник. Это прямоугольный треугольник с соотношением сторон 3:4:5. По условию задачи образующая равна 5, а высота – 4, тогда разность радиусов основания усеченного конуса будет равна 3.
Имеем:
L=5
R=7
R=4
Формула площади боковой поверхности усеченного конуса имеет следующий вид:
$S_bok={pi}L(R+r)$
Подставив значения, имеем:
$S_bok=5{pi}(7+4)=27{pi}$

Площади боковой поверхности усеченного конуса через направляющую и средний радиус

Средний радиус усеченного конуса равен половине суммы радиусов его оснований:
$R_sr={R+r}/2$

Тогда формула площади боковой поверхности усеченного конуса может быть представлена следующим образом:
$S_bok=2{pi}LR_sr$
Площадь боковой поверхности усеченного конуса равна произведению длины окружности среднего сечения на его образующую.

Площади боковой поверхности усеченного конуса через радиусы его основания и угол наклона образующей к плоскости основания

Если меньшее основание ортогонально спроектировать на большее основание, то тогда проекция боковой поверхности усеченного конуса будет иметь вид кольца, площадь которого вычисляется по формуле:
$S={pi}(R^2-r^2)={pi}(R-r)(R+r)$
Тогда: $S_bok={{pi}(R-r)(R+r)}/{cos{alpha}}$

Площади боковой поверхности усеченного конуса по Архимеду

$S_bok={pi}(sqrt{L(R+r)})^2$
Площадь боковой поверхности усеченного конуса равна площади такого круга, радиус которого является средней пропорциональной между образующей и суммой радиусов его оснований

Полная поверхность усеченного конуса

Полная поверхность конуса – это сумма площади его боковой поверхности и площади оснований конуса:

$S_poln=S_bok+S_{b.osn}+S_{m.osn}$

Основаниями конуса является круги с радиусом R и r. Их площадь равна произведению числа на квадрат их радиуса:
$S_{b.osn}={pi}R^2$
$S_{m.osn}={pi}r^2$
Площадь боковой поверхности вычисляется по формуле:
$S_bok={pi}L(R+r)$
Тогда площадь полной поверхности усеченного конуса равна:
$S_poln={pi}L(R+r)+{pi}R^2+{pi}r^2={pi}(R^2+(R+r)L+r^2)$
Формула имеет следующий вид:
$S_poln={pi}(R^2+(R+r)L+r^2)$

Пример расчета площади полной поверхности усеченного конуса, если известны его радиус и образующая
Радиус основания усеченного конуса 1 и 7 дм, а диагонали осевого сечения взаимно перпендикулярны. Найдите площадь полную площадь усеченного конуса
Осевое сечение усеченного конуса представляет собой равнобедренную трапецию, с основаниями 2R и 2r. То есть основания трапеции равны 2 и 14 дм соответственно. Так как диагонали трапеции взаимно перпендикулярны, то высота равна полусумме ее оснований. Тогда:

Образующая усеченного конуса, являющаяся боковой стороной трапеции, высота, опушенная на большое основание и разность радиусов основания усеченного конуса, образуют прямоугольный треугольник.
По теореме Пифагора найдем образующую усеченного конуса:
$L=sqrt{h^2+(R-r)^2}=sqrt{8^2+(7-1)^2}=sqrt{64+36}=sqrt{100}=10$
Формула площади полной поверхности усеченного конуса имеет следующий вид:
$S_poln={pi}(R^2+(R+r)L+r^2)$
Подставив значения из условия задачи и найденные значения, имеем:
$S_poln={pi}(7^2+(7+1)10+1^2)={pi}(49+80+1)=130{pi}$