Площадь под ROC-кривой – один из самых популярных функционалов качества в задачах бинарной классификации. На мой взгляд, простых и полных источников информации «что же это такое» нет. Как правило, объяснение начинают с введения разных терминов (FPR, TPR), которые нормальный человек тут же забывает. Также нет разборов каких-то конкретных задач по AUC ROC. В этом посте описано, как я объясняю эту тему студентам и своим сотрудникам…
Допустим, решается задача классификации с двумя классами {0, 1}. Алгоритм выдаёт некоторую оценку (может, но не обязательно, вероятность) принадлежности объекта к классу 1. Можно считать, что оценка принадлежит отрезку [0, 1].
Часто результат работы алгоритма на фиксированной тестовой выборке визуализируют с помощью ROC-кривой (ROC = receiver operating characteristic, иногда говорят «кривая ошибок»), а качество оценивают как площадь под этой кривой – AUC (AUC = area under the curve). Покажем на конкретном примере, как строится кривая.
Пусть алгоритм выдал оценки, как показано в табл. 1. Упорядочим строки табл. 1 по убыванию ответов алгоритма – получим табл. 2. Ясно, что в идеале её столбец «класс» тоже станет упорядочен (сначала идут 1, потом 0); в самом худшем случае – порядок будет обратный (сначала 0, потом 1); в случае «слепого угадывания» будет случайное распределение 0 и 1.
Чтобы нарисовать ROC-кривую, надо взять единичный квадрат на координатной плоскости, см. рис. 1, разбить его на m равных частей горизонтальными линиями и на n – вертикальными, где m – число 1 среди правильных меток теста (в нашем примере m=3), n – число нулей (n=4). В результате квадрат разбивается сеткой на m×n блоков.
Теперь будем просматривать строки табл. 2 сверху вниз и прорисовывать на сетке линии, переходя их одного узла в другой. Стартуем из точки (0, 0). Если значение метки класса в просматриваемой строке 1, то делаем шаг вверх; если 0, то делаем шаг вправо. Ясно, что в итоге мы попадём в точку (1, 1), т.к. сделаем в сумме m шагов вверх и n шагов вправо.
На рис. 1 (справа) показан путь для нашего примера – это и является ROC-кривой. Важный момент: если у нескольких объектов значения оценок равны, то мы делаем шаг в точку, которая на a блоков выше и b блоков правее, где a – число единиц в группе объектов с одним значением метки, b – число нулей в ней. В частности, если все объекты имеют одинаковую метку, то мы сразу шагаем из точки (0, 0) в точку (1, 1).
AUC ROC – площадь под ROC-кривой – часто используют для оценивания качества упорядочивания алгоритмом объектов двух классов. Ясно, что это значение лежит на отрезке [0, 1]. В нашем примере AUC ROC = 9.5 / 12 ~ 0.79.
Выше мы описали случаи идеального, наихудшего и случайного следования меток в упорядоченной таблице. Идеальному соответствует ROC-кривая, проходящая через точку (0, 1), площадь под ней равна 1. Наихудшему – ROC-кривая, проходящая через точку (1, 0), площадь под ней – 0. Случайному – что-то похожее на диагональ квадрата, площадь примерно равна 0.5.
Замечание. ROC-кривая считается неопределённой для тестовой выборки целиком состоящей из объектов только одного класса. Большинство современных реализаций выдают ошибку при попытки построить её в этом случае
Сетка на рис. 1 разбила квадрат на m×n блоков. Ровно столько же пар вида (объект класса 1, объект класса 0), составленных из объектов тестовой выборки. Каждый закрашенный блок на рис. 1 соответствует паре (объект класса 1, объект класса 0), для которой наш алгоритм правильно предсказал порядок (объект класса 1 получил оценку выше, чем объект класса 0), незакрашенный блок – паре, на которой ошибся.
Таким образом, AUC ROC равен доле пар объектов вида (объект класса 1, объект класса 0), которые алгоритм верно упорядочил, т.е. первый объект идёт в упорядоченном списке раньше. Численно это можно записать так:
Замечание. В формуле (*) все постоянно ошибаются, забывая случай равенства ответов алгоритма на нескольких объектах. Также эту формулу все постоянно переоткрывают. Она хороша тем, что легко обобщается и на другие задачи обучения с учителем.
Принятие решений на основе ROC-кривой
Пока наш алгоритм выдавал оценки принадлежности к классу 1. Ясно, что на практике нам часто надо будет решить: какие объекты отнести к классу 1, а какие к классу 0. Для этого нужно будет выбрать некоторый порог (объекты с оценками выше порога считаем принадлежащими классу 1, остальные – 0).
Выбору порога соответствует выбор точки на ROC-кривой. Например, для порога 0.25 и нашего примера – точка указана на рис. 4 (1/4, 2/3). см. табл. 3
Заметим, что 1/4 – это процент точек класса 0, которые неверно классифицированы нашим алгоритмом (это называется FPR = False Positive Rate), 2/3 – процент точек класса 1, которые верно классифицированы нашим алгоритмом (это называется TPR = True Positive Rate). Именно в этих координатах (FPR, TPR) построена ROC-кривая. Часто в литературе её определяют как кривую зависимости TPR от FPR при варьировании порога для бинаризации.
Кстати, для бинарных ответов алгоритма тоже можно вычислить AUC ROC, правда это практически никогда не делают, поскольку ROC-кривая состоит из трёх точек, соединёнными линиями: (0,0), (FPR, TPR), (1, 1), где FPR и TPR соответствуют любому порогу из интервала (0, 1). На рис. 4 (зелёным) показана ROC-кривая бинаризованного решения, заметим, что AUC после бинаризации уменьшился и стал равным 8.5/12 ~ 0.71.
В общем случае, как видно из рис. 5 AUC ROC для бинарного решения равна
(как сумма площадей двух треугольников и квадрата). Это выражение имеет самостоятельную ценность и является «честной точностью» в задаче с дисбалансом классов (но об этом надо писать отдельный пост).
Задача
На ответах алгоритма a(x) объекты класса 0 распределены с плотностью p(a)=2-2a, а объекты класса 1 – с плотностью p(a)=2a, см. рис. 6. Интуитивно понятно, что алгоритм обладает некоторой разделяющей способностью (большинство объектов класса 0 имеют оценку меньше 0.5, а большинство объектов класса 1 – больше). Попробуйте угадать, чему здесь равен AUC ROC, а мы покажем как построить ROC-кривую и вычислить площадь под ней. Отметим, что здесь мы не работаем с конкретной тестовой выборкой, а считаем, что знаем распределения объектов всех классов. Такое может быть, например, в модельной задаче, когда объекты лежат в единичном квадрате, объекты выше одной из диагоналей принадлежат классу 0, ниже – классу 1, для решения используется логистическая регрессия (см. рис. 7). В случае, когда решение зависит только от одного признака (при втором коэффициент равен нулю), получаем как раз ситуацию, описанную в нашей задаче.
Значение TPR при выборе порога бинаризации равно площади, изображённой на рис. 6 (центр), а FPR – площади, изображённой на рис. 6 (справа), т.е.
Параметрическое уравнение для ROC-кривой получено, можно уже сразу вычислить площадь под ней:
Но если Вы не любите параметрическую запись, легко получить:
Заметим, что максимальная точность достигается при пороге бинаризации 0.5 (почему?), и она равна 3/4 = 0.75 (что не кажется очень большой). Это частая ситуация: AUC ROC существенно выше максимальной достижимой точности (accuracy)!
Кстати, AUC ROC бинаризованного решения (при пороге бинаризации 0.5) равна 0.75! Подумайте, почему это значение совпало с точностью?
В такой «непрерывной» постановке задачи (когда объекты двух классов описываются плотностями) AUC ROC имеет вероятностный смысл: это вероятность того, что случайно взятый объект класса 1 имеет оценку принадлежности к классу 1 выше, чем случайно взятый объект класса 0.
Для нашей модельной задачи можно провести несколько экспериментов: взять конечные выборки разной мощности с указанными распределениями. На рис. 8 показаны значения AUC ROC в таких экспериментах: все они распределены около теоретического значения 5/6, но разброс достаточно велик для небольших выборок. Запомните: для оценки AUC ROC выборка в несколько сотен объектов мала!
Также полезно посмотреть, как выглядят ROC-кривые в наших экспериментах. Естественно, при увеличении объёма выборок ROC-кривые, построенные по выборкам, будут сходиться к теоретической кривой (построенной для распределений).
Замечание
Интересно, что в рассмотренной задаче исходные данные линейны (например, плотности – линейные функции), а ответ (ROC-кривая) нелинейная (и даже неполиномиальная) функция!
Замечание
Почему-то многие считают, что ROC-кривая всегда является ступенчатой функцией – лишь при построении её для конечной выборки, в которой нет объектов с одинаковыми оценками. Полезно посмотреть на интерактивную визуализацию ROC-кривых для нормально распределённых классов.
Максимизация AUC ROC на практике
Оптимизировать AUC ROC напрямую затруднительно по нескольким причинам:
- эта функция недифференцируема по параметрам алгоритма,
- она в явном виде не разбивается на отдельные слагаемые, которые зависят от ответа только на одном объекте (как происходит в случае log_loss).
Есть несколько подходов к оптимизации
- замена в (*) индикаторной функции на похожую дифференцируемую функцию,
- использование смысла функционала (если это вероятность верного упорядочивания пары объектов, то можно перейти к новой выборке, состоящей из пар),
- ансамблирование нескольких алгоритмов с преобразованием их оценок в ранги (логика здесь простая: AUC ROC зависит только от порядка объектов, поэтому конкретные оценки не должны существенно влиять на ответ).
Замечания
- AUC ROC не зависит от строго возрастающего преобразования ответов алгоритма (например, возведения в квадрат), поскольку зависит не от самих ответов, а от меток классов объектов при упорядочивании по этим ответам.
- Часто используют критерий качества Gini, он принимает значение на отрезке [–1, +1] и линейно выражается через площадь под кривой ошибок:
Gini = 2 ×AUC_ROC – 1
- AUC ROC можно использовать для оценки качества признаков. Считаем, что значения признака — это ответы нашего алгоритма (не обязательно они должны быть нормированы на отрезок [0, 1], ведь нам важен порядок). Тогда выражение 2×|AUC_ROC — 0.5| вполне подойдёт для оценки качества признака: оно максимально, если по этому признаку 2 класса строго разделяются и минимально, если они «перемешаны».
- Практически во всех источниках приводится неверный алгоритм построения ROC-кривой и вычисления AUC ROC. По нашему описанию легко эти алгоритмы исправить…
- Часто утверждается, что AUC ROC не годится для задач с сильным дисбалансом классов. При этом приводятся совершенно некорректные обоснования этого. Рассмотрим одно из них. Пусть в задаче 1 000 000 объектов, при этом только 10 объектов из первого класса. Допустим, что объекты это сайты интернета, а первый класс – сайты, релевантные некоторому запросу. Рассмотрим алгоритм, ранжирующий все сайты в соответствии в эти запросом. Пусть он в начало списка поставил 100 объектов класса 0, потом 10 – класса 1, потом – все остальные класса 0. AUC ROC будет довольно высоким: 0.9999. При этом ответ алгоритма (если, например, это выдача поисковика) нельзя считать хорошей: в верхней части выдачи 100 нерелевантных сайтов. Разумеется, нам не хватит терпения пролистать выдачу и добраться до 10 тех самых релевантных.
В чём некорректность этого примера?! Главное: в том, что он никак не использует дисбаланс классов. С таким же успехом объектов класса 1 могло быть 500 000 – ровно половина, тогда AUC ROC чуть поменьше: 0.9998, но суть остаётся прежней. Таким образом, этот пример не показывает неприменимость AUC ROC в задачах с дисбалансом классов, а лишь в задачах поиска! Для таких задач есть другие функционалы качества, кроме того, есть специальные вариации AUC, например AUC@k. - В банковском скоринге AUC_ROC очень популярный функционал, хотя очевидно, что он также здесь не очень подходит. Банк может выдать ограниченное число кредитов, поэтому главное требование к алгоритму – чтобы среди объектов, которые получили наименьшие оценки были только представители класса 0 («вернёт кредит», если мы считаем, что класс 1 – «не вернёт» и алгоритм оценивает вероятность невозврата). Об этом можно судить по форме ROC-кривой (см. рис. 10).
П.С.
Если Вы дочитали до конца — можете попробовать пройти тест по AUC ROC (авторский, публикуется впервые). Задачи теста можно обсуждать в комментариях. Любые замечание по тексту — смело пишите!
Что можно ещё почитать…
- Wiki (и там есть хорошие ссылки!)
- Логистическая регрессия и ROC-анализ — математический аппарат
- Задачки про AUC (ROC)
Площадь под ROC-кривой (Area Under Curve – площадь под кривой, Receiver Operating Characteristic – рабочая характеристика приёмника) – это метрика оценки для задач Бинарной классификации (Binary Classification). Площадь под кривой (AUC) является мерой способности классификатора различать классы и используется в качестве сводки кривой ROC:
Представьте: вы создали свою Модель (Model) Машинного обучения (ML), но что же дальше? Вам необходимо оценить ее и оценить качество, чтобы затем Вы могли решить, стоит ли она внедрения. Вот тут-то и пригодится кривая AUC ROC.
Название может показаться скучным, но оно просто говорит о том, что мы вычисляем «Площадь под кривой» (AUC) «рабочей характеристики приёмника (ROC). Пока много неясного, но мы подробно рассмотрим, что означают эти термины, и все встанет на свои места.
ROC-кривая помогает визуализировать, насколько хорошо работает классификатор машинного обучения. Хотя она работает только для задач двоичной классификации, ближе к концу мы увидим, как расширить его, чтобы решать проблемы Мультиклассовой классификации (Multi-Class Classification).
Мы также затронем такие темы, как Чувствительность (Sensitivity) и Специфичность (Specificity), поскольку это ключевые вспомогательные термины.
Матрица ошибок
Из Матрицы ошибок (Confusion Matrix) мы можем вывести некоторые важные показатели. Это показатель успешности классификации, где классов два или более. Это таблица с 4 различными комбинациями сочетаний прогнозируемых и фактических значений.
Давайте рассмотрим значения ячеек (истинно позитивные, ошибочно позитивные, ошибочно негативные, истинно негативные) с помощью «беременной» аналогии.
Истинно позитивное предсказание (True Positive, сокр. TP)
Вы предсказали положительный результат, и женщина действительно беременна.
Истинно отрицательное предсказание (True Negative, TN)
Вы предсказали отрицательный результат, и мужчина действительно не беременен.
Ошибочно положительное предсказание (ошибка типа I, False Positive, FN)
Вы предсказали положительный результат (мужчина беременен), но на самом деле это не так.
Ошибочно отрицательное предсказание (ошибка типа II, False Negative, FN)
Вы предсказали, что женщина не беременна, но на самом деле она беременна.
Чувствительность
Очевидно, желательны более высокий уровень TP и более низкий уровень FN. Чувствительность говорит нам, какая часть положительного класса была правильно классифицирована:
$$Чувствительность = frac{TP}{TP + FN}$$
$$TPspace{}{–}space{количество}space{истинно}space{позитивных}space{предсказаний,}$$
$$FNspace{}{–}space{количество}space{ошибочно}space{отрицательных}space{предсказаний}$$
Специфичность (TPR)
Специфичность говорит нам, какая часть отрицательного класса была правильно классифицирована:
$$Специфичность = frac{TN}{TN + FP}$$
$$TNspace{}{–}space{количество}space{истинно}space{негативных}space{предсказаний,}$$
$$FPspace{}{–}space{количество}space{ошибочно}space{позитивных}space{предсказаний}$$
Если взять тот же пример, что и в случае с чувствительностью, специфичность будет означать определение доли здоровых людей, которые были правильно идентифицированы моделью.
Доля неверно классифицированных негативных наблюдений
Доля ложных положительных классификаций (FPR) сообщает нам, какая часть отрицательного класса была неправильно классифицирована классификатором:
$$FPR = 1 — Специфичность$$
Из этих показателей чувствительность и специфичность, пожалуй, самые важные, и позже мы увидим, как они используются для построения оценочной метрики. Но перед этим давайте разберемся, почему вероятность предсказания лучше, чем предсказание целевого класса напрямую.
Вероятность прогнозов
Модель классификации может использоваться для непосредственного определения класса Наблюдения (Observation) или прогнозирования ее вероятности принадлежности к разным классам. Последнее, как ни странно, дает нам больше контроля над результатом. Мы можем задать наш собственный порог для интерпретации результата. Иногда это более благоразумно, чем просто построить совершенно новую модель!
Установка различных пороговых значений для классификации положительного класса непреднамеренно изменит чувствительность и специфичность модели. И один из этих пороговых значений, вероятно, даст лучший результат, чем другие, в зависимости от того, стремимся ли мы снизить количество ложноотрицательных или ложноположительных результатов. Взгляните на таблицу ниже:
Показатели меняются с изменением пороговых значений. Мы можем генерировать различные матрицы путаницы и сравнивать различные метрики, которые обсуждали в предыдущем разделе. Но это было бы неразумно. Вместо этого мы можем создать график между некоторыми из этих показателей, чтобы легко увидеть, какой порог дает наилучший результат. Кривая AUC-ROC решает именно эту проблему!
ROC-кривая – это кривая вероятности, которая отображает отношение TPR к FPR при различных пороговых значениях и по существу отделяет «сигнал» от «шума». Площадь под кривой (AUC) является мерой способности классификатора различать классы. Чем выше площадь под кривой, тем лучше производительность модели.
Когда AUC равен единице, тогда классификатор может правильно различать все положительные и отрицательные точки класса:
Однако, если бы AUC была равна 0, тогда классификатор предсказывал бы все отрицательные значения как положительные, а все положительные – как отрицательные.
Когда 0,5 < AUC < 1, высока вероятность, что классификатор сможет различить положительные и отрицательных значения класса. Это так, потому что классификатор может обнаруживать больше истинно положительных и истинно отрицательных результатов, чем ложно отрицательных и ложно положительных результатов:
Когда AUC = 0,5, тогда классификатор не может различать положительные и отрицательные баллы класса. Это означает, что либо классификатор предсказывает случайный класс, либо существует один постоянный класс для всех точек данных:
Таким образом, чем выше значение AUC для классификатора, тем лучше его способность различать положительные и отрицательные классы.
Как работает кривая AUC-ROC?
На ROC-кривой более высокое значение по оси X указывает на бо́льшее количество ложных, чем истинно отрицательных «срабатываний». В то время как более высокое значение по оси Y указывает на большее количество истинно положительных, чем ложно отрицательных результатов. Итак, выбор порога зависит от способности балансировать между «ложными срабатываниями» и «ложными отрицаниями».
Давайте копнем немного глубже и поймем, как наша кривая будет выглядеть для разных пороговых значений и как будут меняться специфичность и чувствительность.
Мы можем попытаться понять этот график, сгенерировав матрицу путаницы для каждой точки, соответствующей порогу, и поговорим о производительности нашего классификатора:
В точке А графика выше чувствительность самая высокая, а специфичность – самая низкая. Это означает, что все представители положительного класса классифицируются правильно, а все представители отрицательного – неправильно. Фактически, любая точка на синей линии соответствует ситуации, когда TPR равен FPR.
Все точки над этой линией соответствуют ситуации, когда доля правильно классифицированных точек, принадлежащих к положительному классу, больше, чем доля неправильно классифицированных точек, принадлежащих к отрицательному классу.
Хотя точка B имеет ту же чувствительность, что и точка A, у нее более высокая специфичность. Это означает, что количество баллов ложно отрицательного класса ниже по сравнению с предыдущим порогом. Это указывает на то, что данный порог лучше предыдущего.
Чувствительность в точке C выше, чем в D при той же специфичности. Это означает, что для того же количества неправильно классифицированных представителей отрицательного класса классификатор предсказал большее количество баллов положительного класса. Следовательно, порог в точке C лучше, чем в точке D.
Теперь, в зависимости от того, сколько неправильно классифицированных очков мы хотим допустить для нашего классификатора, мы будем выбирать между точкой B или C.
Точка E – это место, где специфичность становится самой высокой:
Это означает, что модель не содержит ложных срабатываний. Модель может правильно классифицировать все отрицательные записи! Мы бы выбрали эту точки, если бы наша задача заключалась в генерации рекомендации Spotify.
Следуя этой логике, можете ли вы угадать, где на графике будет находиться точка, соответствующая идеальному классификатору? Да! Она будет в верхнем левом углу графика ROC, соответственно координатам (0, 1). Именно здесь чувствительность и специфичность будут наивысшими, и классификатор правильно классифицирует все положительные и отрицательные наблюдения.
AUC-ROC: Scikit-learn
Давайте посмотрим, как кросс-валидация реализована в SkLearn. Для начала импортируем необходимые библиотеки:
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_scoreСгенерируем игрушечный Датасет (Dataset) из 1000 наблюдений, каждое из которых принадлежит одному из двух классов. Разделим его на Тренировочные данные (Train Data) и Тестовые данные (Test Data) в пропорции 3 к 7:
X, y = make_classification(n_samples = 1000, n_classes = 2, n_features = 20, random_state = 27)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = 27)Инициируем модели Логистической регрессии (Logistic Regression) и Метода K-ближайших соседей (kNN). Затем обучим модели и сгенерируем предсказания классов для тестовой выборки:
model1 = LogisticRegression()
model2 = KNeighborsClassifier(n_neighbors = 4)
model1.fit(X_train, y_train)
model2.fit(X_train, y_train)
pred_prob1 = model1.predict_proba(X_test)
pred_prob2 = model2.predict_proba(X_test)Конечно, мы можем вручную проверить чувствительность и специфичность для каждого порога, однако предпочту дать scikit-learn сделать всю работу за нас. В этой прекрасной библиотеке есть очень мощный метод roc_curve(), который вычисляет ROC для классификатора за считанные секунды! Он возвращает значения FPR, TPR и пороговые значения:
fpr1, tpr1, thresh1 = roc_curve(y_test, pred_prob1[:, 1], pos_label = 1)
fpr2, tpr2, thresh2 = roc_curve(y_test, pred_prob2[:, 1], pos_label = 1)
random_probs = [0 for i in range(len(y_test))]
p_fpr, p_tpr, _ = roc_curve(y_test, random_probs, pos_label = 1)Дело за малым: рассчитаем площади под кривой:
auc_score1 = roc_auc_score(y_test, pred_prob1[:, 1])
auc_score2 = roc_auc_score(y_test, pred_prob2[:, 1])
print(auc_score1, auc_score2)Модель логистической регрессии более эффективна в данной ситуации, чем метод K-ближайших соседей:
0.9762374461979914 0.9233769727403157Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: Aniruddha Bhandari
Материал из MachineLearning.
(Перенаправлено с ROC-кривая)
Перейти к: навигация, поиск
Содержание
- 1 Задача классификации
- 2 TPR и FPR
- 3 ROC-кривая
- 4 Площадь под ROC-кривой AUC
- 5 Алгоритм построения ROC-кривой
- 6 Чувствительность и специфичность
- 7 История
- 8 См. также
- 9 Ссылки
Кривая ошибок или ROC-кривая – графичекая характеристика качества бинарного классификатора, зависимость доли верных положительных классификаций от доли ложных положительных классификаций при варьировании порога решающего правила. Преимуществом ROC-кривой является её инвариантность относительно отношения цены ошибки I и II рода.
Задача классификации
Рассмотрим задачу классификации в случае двух классов, называемых «положительным» и «отрицательным». Обозначим множество классов через . Большинство известных классификаторов могут быть представлены в виде
где
— произвольный объект,
— дискриминантная функция,
— вектор параметров, определяемый по обучающей выборке,
— порог.
Уравнение определяет разделяющую поверхность.
Примером является линейный классификатор, в котором дискриминантная функция имеет вид скалярного произведения вектора описания объекта на вектор параметров:
.
Пусть – цена ошибки (штраф за ошибку) на объекте класса
.
Для байесовского классификатора при достаточно общих предположениях доказано, что оптимальное значение порога зависит только от соотношения цены ошибок:
тогда как оптимальное значение вектора параметров , наоборот, зависит от выборки и не зависит от цены ошибок.
Таким образом, варьирование порога для многих классификаторов эквивалентно варьированию отношения цены ошибок на отрицательных и положительных объектах.
На практике цены ошибок зависят от особенностей конкретной задачи (например, от различных экономических соображений или экспертных оценок) и могут многократно пересматриваться.
Заметим, что частным случаем линейного байесовского классификатора является логистическая регрессия.
ROC-кривая наглядно представляет, каким будет качество классификации при различных и фиксированном
.
TPR и FPR
Пусть задана выборка объектов с соответствующими им верными ответами
.
Тогда для классификатора можно определить две характеристики качества:
- Доля ложных положительных классификаций (False Positive Rate, FPR):
- Доля верных положительных классификаций (True Positive Rate, TPR):
ROC-кривая
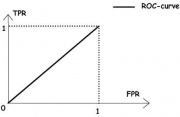
Рис.1. «Случайное гадание».
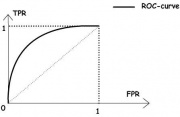
Рис.2. «Хороший» классификатор.
ROC-кривая показывает зависимость TPR от FPR при варьировании порога .
Она проходит из точки , соответствующей максимальному значению
, в точку
, соответствующую минимальному значению
.
При все объекты классифицируются как отрицательные, и ошибки возникают на всех положительных объектах,
,
.
При все объекты классифицируются как положительные, и ошибки возникают на всех отрицательных объектах,
,
.
ROC-кривая монотонно не убывает.
Чем выше лежит кривая, тем лучше качество классификации.
На рисунке 1 приведена ROC-кривая, соответствующая худшему случаю — алгоритму «случайного гадания».
На рисунке 2 изображён общий случай.
Лучший случай — это кривая, проходящая через точки
ROC-кривая может быть вычислена по любой выборке. Однако ROC-кривая, вычисленная по обучающей выборке, является оптимистично смещённой влево-вверх вследствие переобучения. Величину этого смещения предсказать довольно трудно, поэтому на практике ROC-кривую всегда оценивают по независомой тестовой выборке.
Площадь под ROC-кривой AUC
Площадь под ROC-кривой AUC (Area Under Curve) является агрегированной характеристикой качества классификации, не зависящей от соотношения цен ошибок.
Чем больше значение AUC, тем «лучше» модель классификации.
Данный показатель часто используется для сравнительного анализа нескольких моделей классификации.
Алгоритм построения ROC-кривой
Следующий алгоритм строит ROC-кривую за обращений к дискриминантной функции.
Входные данные:
Результат:
1. вычислить количество представителей классови
в выборке:
; 2. упорядочить выборку
по убыванию значений
; 3. установить начальную точку ROC-кривой:
;
; 4. для всех
если
, то сместиться на один шаг вправо:
;
; 5. иначе сместиться на один шаг вверх:
;
Чувствительность и специфичность
Наряду с FPR и TPR используют также показатели чувствительности и специфичности, которые также изменяются в интервале :
Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры). Если рассуждать в терминах медицинской диагностики, где модель классификации пациентов на больных и здоровых называется диагностическим тестом, то получится следующее:
- чувствительный диагностический тест проявляется в гипердиагностике – максимальном предотвращении пропуска больных;
- специфичный диагностический тест диагностирует только доподлинно больных. Это важно в случае, когда, например, лечение больного связано с серьезными побочными эффектами и гипердиагностика пациентов нежелательна.
История
Термин операционная характеристика приёмника (Receiver Operating Characteristic, ROC) пришёл из теории обработки сигналов.
Эту характеристику впервые ввели во время II мировой войны, после поражения американского военного флота в Пёрл Харборе в 1941 году, когда была осознана проблема повышения точности распознавания самолётов противника по радиолокационному сигналу. Позже нашлись и другие применения: медицинская диагностика, приёмочный контроль качества, кредитный скоринг, предсказание лояльности клиентов, и т.д.
См. также
- Линейный классификатор
- Логистическая регрессия
Ссылки
- Логистическая регрессия и ROC-анализ
- RoC-curve (english wikipedia)
This topic describes the performance metrics for classification, including the receiver
operating characteristic (ROC) curve and the area under a ROC curve (AUC), and introduces the
Statistics and Machine Learning Toolbox™ object rocmetrics, which you can
use to compute performance metrics for binary and multiclass classification problems.
Introduction to ROC Curve
After training a classification model, such as ClassificationNaiveBayes or ClassificationEnsemble, you can examine the
performance of the algorithm on a specific test data set. A common approach is to compute a
gross measure of performance, such as quadratic loss or accuracy, averaged over the entire test
data set. You can inspect the classifier performance more closely by plotting a ROC curve and
computing performance metrics. For example, you can find the threshold that maximizes the
classification accuracy, or assess how the classifier performs in the regions of high
sensitivity and high specificity.
Receiver Operating Characteristic (ROC) Curve
A ROC curve shows the true positive rate (TPR, or sensitivity) versus the false positive
rate (FPR, or 1-specificity) for different thresholds of classification scores.
Each point on a ROC curve corresponds to a pair of TPR and FPR values for a specific
threshold value. You can find different pairs of TPR and FPR values by varying the threshold
value, and then create a ROC curve using the pairs.
For a multiclass classification problem, you can use the one-versus-all coding design and find a ROC curve for each class. The one-versus-all
coding design treats a multiclass classification problem as a set of binary classification
problems, and assumes one class as positive and the rest as negative in each binary
problem.
A binary classifier typically classifies an observation into a class that yields a larger
score, which corresponds to a positive adjusted score for a one-versus-all
binary classification problem. That is, a classifier typically uses 0 as a threshold and
determines whether an observation is positive or negative. For example, if an adjusted score
for an observation is 0.2, then the classifier with a threshold value of 0 assigns the
observation to the positive class. You can find a pair of TPR and FPR values by applying the
threshold value to all observations, and use the pair as a single point on a ROC curve. Now,
assume you use a new threshold value of 0.25. Then, the classifier with a threshold value of
0.25 assigns the observation with an adjusted score of 0.2 to the negative class. By applying
the new threshold to all observations, you can find a new pair of TPR and FPR values and have a
new point on the a ROC curve. By repeating this process for various threshold values, you find
pairs of TPR and FPR values and create a ROC curve using the pairs.
Area Under ROC Curve (AUC)
The area under a ROC curve (AUC) corresponds to the integral of a ROC curve
(TPR values) with respect to FPR from FPR = 0 to FPR = 1.
The AUC provides an aggregate performance measure across all possible thresholds. The AUC
values are in the range 0 to 1, and larger AUC values
indicate better classifier performance.
-
A perfect classifier always correctly assigns positive class observations to the
positive class and has a true positive rate of1for any threshold values.
Therefore, the line passing through[0,0],[0,1], and
[1,1]represents the perfect classifier, and the AUC value is
1. -
A random classifier returns random score values and has the same values for the false
positive rate and true positive rate for any threshold values. Therefore, the ROC curve for
the random classifier lies on the diagonal line, and the AUC value is
0.5.
Performance Curve with MATLAB
You can compute a ROC curve and other performance curves by creating a rocmetrics object. The
rocmetrics object supports both binary and multiclass classification problems
and provides the following object functions:
-
plot— Plot ROC or
other classifier performance curves.plotreturns a
ROCCurvegraphics object for each curve. You can modify the properties of
the objects to control the appearance of each curve. For details, see ROCCurve Properties. -
average— Compute
performance metrics for an average ROC curve for multiclass problems. -
addMetrics—
Compute additional classification performance metrics.
You can also compute the confidence intervals of performance curves by providing
cross-validated inputs or by bootstrapping the input data.
After training a classifier, use a performance curve to evaluate the classifier performance
on test data. Various measures such as mean squared error, classification error, or exponential
loss can summarize the predictive power of a classifier in a single number. However, a
performance curve offers more information because it lets you explore the classifier performance
across a range of thresholds on the classification scores.
Plot ROC Curve for Binary Classifier
Compute the performance metrics (FPR and TPR) for a binary classification problem by creating a rocmetrics object, and plot a ROC curve by using plot function.
Load the ionosphere data set. This data set has 34 predictors (X) and 351 binary responses (Y) for radar returns, either bad ('b') or good ('g').
Partition the data into training and test sets. Use approximately 80% of the observations to train a support vector machine (SVM) model, and 20% of the observations to test the performance of the trained model on new data. Partition the data using cvpartition.
rng("default") % For reproducibility of the partition c = cvpartition(Y,Holdout=0.20); trainingIndices = training(c); % Indices for the training set testIndices = test(c); % Indices for the test set XTrain = X(trainingIndices,:); YTrain = Y(trainingIndices); XTest = X(testIndices,:); YTest = Y(testIndices);
Train an SVM classification model.
Mdl = fitcsvm(XTrain,YTrain);
Compute the classification scores for the test set.
[~,Scores] = predict(Mdl,XTest); size(Scores)
The output Scores is a matrix of size 70-by-2. The column order of Scores follows the class order in Mdl. Display the class order stored in Mdl.ClassNames.
ans = 2x1 cell
{'b'}
{'g'}
Create a rocmetrics object by using the true labels in YTest and the classification scores in Scores. Specify the column order of Scores using Mdl.ClassNames.
rocObj = rocmetrics(YTest,Scores,Mdl.ClassNames);
rocObj is a rocmetrics object that stores the AUC values and performance metrics for each class in the AUC and Metrics properties. Display the AUC property.
For a binary classification problem, the AUC values are equal to each other.
The table in Metrics contains the performance metric values for both classes, vertically concatenated according to the class order. Find the rows for the first class in the table, and display the first eight rows.
idx = strcmp(rocObj.Metrics.ClassName,Mdl.ClassNames(1)); head(rocObj.Metrics(idx,:))
ClassName Threshold FalsePositiveRate TruePositiveRate
_________ _________ _________________ ________________
{'b'} 15.545 0 0
{'b'} 15.545 0 0.04
{'b'} 15.105 0 0.08
{'b'} 11.424 0 0.16
{'b'} 10.077 0 0.2
{'b'} 9.9716 0 0.24
{'b'} 9.9417 0 0.28
{'b'} 9.0338 0 0.32
Plot the ROC curve for each class by using the plot function.
For each class, the plot function plots a ROC curve and displays a filled circle marker at the model operating point. The legend displays the class name and AUC value for each curve.
Note that you do not need to examine ROC curves for both classes in a binary classification problem. The two ROC curves are symmetric, and the AUC values are identical. A TPR of one class is a true negative rate (TNR) of the other class, and TNR is 1-FPR. Therefore, a plot of TPR versus FPR for one class is the same as a plot of 1-FPR versus 1-TPR for the other class.
Plot the ROC curve for the first class only by specifying the ClassNames name-value argument.
plot(rocObj,ClassNames=Mdl.ClassNames(1))
Plot ROC Curves for Multiclass Classifier
Compute the performance metrics (FPR and TPR) for a multiclass classification problem by creating a rocmetrics object, and plot a ROC curve for each class by using the plot function. Specify the AverageROCType name-value argument of plot to create the average ROC curve for the multiclass problem.
Load the fisheriris data set. The matrix meas contains flower measurements for 150 different flowers. The vector species lists the species for each flower. species contains three distinct flower names.
Train a classification tree that classifies observations into one of the three labels. Cross-validate the model using 10-fold cross-validation.
rng("default") % For reproducibility Mdl = fitctree(meas,species,Crossval="on");
Compute the classification scores for validation-fold observations.
[~,Scores] = kfoldPredict(Mdl); size(Scores)
The output Scores is a matrix of size 150-by-3. The column order of Scores follows the class order in Mdl. Display the class order stored in Mdl.ClassNames.
ans = 3x1 cell
{'setosa' }
{'versicolor'}
{'virginica' }
Create a rocmetrics object by using the true labels in species and the classification scores in Scores. Specify the column order of Scores using Mdl.ClassNames.
rocObj = rocmetrics(species,Scores,Mdl.ClassNames);
rocObj is a rocmetrics object that stores the AUC values and performance metrics for each class in the AUC and Metrics properties. Display the AUC property.
ans = 1×3
1.0000 0.9636 0.9636
The table in Metrics contains the performance metric values for all three classes, vertically concatenated according to the class order. Find and display the rows for the second class in the table.
idx = strcmp(rocObj.Metrics.ClassName,Mdl.ClassNames(2)); rocObj.Metrics(idx,:)
ans=13×4 table
ClassName Threshold FalsePositiveRate TruePositiveRate
______________ _________ _________________ ________________
{'versicolor'} 1 0 0
{'versicolor'} 1 0.01 0.7
{'versicolor'} 0.95455 0.02 0.8
{'versicolor'} 0.91304 0.03 0.9
{'versicolor'} -0.2 0.04 0.9
{'versicolor'} -0.33333 0.06 0.9
{'versicolor'} -0.6 0.08 0.9
{'versicolor'} -0.86957 0.12 0.92
{'versicolor'} -0.91111 0.16 0.96
{'versicolor'} -0.95122 0.31 0.96
{'versicolor'} -0.95238 0.38 0.98
{'versicolor'} -0.95349 0.44 0.98
{'versicolor'} -1 1 1
Plot the ROC curve for each class. Specify AverageROCType="micro" to compute the performance metrics for the average ROC curve using the micro-averaging method.
plot(rocObj,AverageROCType="micro")
The filled circle markers indicate the model operating points. The legend displays the class name and AUC value for each curve.
ROC Curve for Multiclass Classification
For a multiclass classifier, the rocmetrics function
computes the performance metrics of a one-versus-all ROC curve for each class, and the average function
computes the metrics for an average of the ROC curves. You can use the plot function to plot
a ROC curve for each class and the average ROC curve.
One-Versus-All (OVA) Coding Design
The one-versus-all (OVA) coding design reduces a multiclass classification
problem to a set of binary classification problems. In this coding design, each binary
classification treats one class as positive and the rest of the classes as negative.
rocmetrics uses the OVA coding design for multiclass classification and
evaluates the performance on each class by using the binary classification that the class is
positive.
For example, the OVA coding design for three classes formulates three binary classifications:
Each row corresponds to a class, and each column corresponds to a binary
classification problem. The first binary classification assumes that class 1 is a positive
class and the rest of the classes are negative. rocmetrics evaluates the
performance on the first class by using the first binary classification problem.
rocmetrics applies the OVA coding design to a binary classification
problem as well if you specify classification scores as a two-column matrix.
rocmetrics formulates two one-versus-all binary classification problems each
of which treats one class as a positive class and the other class as a negative class, and
rocmetrics finds two ROC curves. You can use one of them to evaluate the
binary classification problem.
Average of Performance Metrics
You can compute metrics for an average ROC curve by using the average function.
Alternatively, you can use the plot function to
compute the metrics and plot the average ROC curve. For examples, see Find Average ROC Curve (example for
average) and Plot Average ROC Curve for Multiclass Classifier (example for
plot).
average and plot support three algorithms for
computing the average false positive rate (FPR) and average true positive rate (TPR) to find
the average ROC curve:
-
Micro-averaging — The software combines all one-versus-all binary classification problems into one binary classification
problem and computes the average performance metrics as follows:-
Convert the values in the
Labelsproperty
of arocmetricsobject to logical values where logical
1(true) indicates a positive class for each binary
problem. -
Stack the converted vectors of labels, one vector from each binary problem, into a
single vector. -
Convert the matrix that contains the adjusted values of the
classification scores (theScoresproperty)
into a vector by stacking the columns of the matrix. -
Compute the components of the confusion matrix for
the combined binary problem for each threshold (each distinct value of adjusted scores). A
confusion matrix contains the number of instances for true positive (TP), false negative
(FN), false positive (FP), and true negative (TN). -
Compute the average FPR and TPR based on the components of the confusion
matrix.
-
-
Macro-averaging — The software computes the average values for FPR and TPR by averaging
the values of all one-versus-all binary classification problems.The software uses three metrics—threshold, FPR, and TPR—to compute the average values
as follows:-
Determine a fixed metric. If you specify
FixedMetricof
rocmetricsas"FalsePositiveRate"or
"TruePositiveRate", then the function holds the specified metric
fixed. Otherwise, the function holds the threshold values fixed. -
Find all distinct values in the
Metrics
property for the fixed metric. -
Find the corresponding values for the other two metrics for each binary
problem. -
Average the FPR and TPR values of all binary problems.
-
-
Weighted macro-averaging — The software computes the weighted average values for FPR
and TPR using the macro-averaging algorithm and using the prior class probabilities (the
Priorproperty) as
weights.
Performance Metrics
The rocmetrics object supports these built-in performance metrics:
-
Number of true positives (TP)
-
Number of false negatives (FN)
-
Number of false positives (FP)
-
Number of true negatives (TN)
-
Sum of TP and FP
-
Rate of positive predictions (RPP)
-
Rate of negative predictions (RNP)
-
Accuracy
-
True positive rate (TPR), recall, or sensitivity
-
False negative rate (FNR), or miss rate
-
False positive rate (FPR), fallout, or 1-specificity
-
True negative rate (TNR), or specificity
-
Positive predictive value (PPV), or precision
-
Negative predictive value (NPR)
-
Expected cost
rocmetrics also supports a custom metric specified as a function
handle. For details, see the AdditionalMetrics
name-value argument of the rocmetrics function.
rocmetrics computes performance metric values for various thresholds for
each one-versus-all binary classification problem using a confusion matrix, scale vector,
and misclassification cost matrix. Each performance metric is a function of a confusion matrix
and scale vector. The expected cost is also a function of the misclassification cost matrix, as
is a custom metric.
-
Confusion matrix — A confusion matrix contains the number of instances for true positive
(TP), false negative (FN), false positive (FP), and true negative (TN).
rocmetricscomputes confusion matrices for various threshold values for
each binary problem. -
Scale vector — A scale vector is defined by the prior class probabilities and the number
of classes in true labels.rocmetricsfinds the probabilities and number of
classes for each binary problem from the prior class probabilities specified by thePriorname-value
argument and the true labels specified by theLabelsinput
argument. -
Misclassification cost matrix —
rocmetricsconverts the
misclassification cost matrix specified by theCostname-value
argument to the values for each binary problem.
By default, rocmetrics uses all distinct adjusted score values as threshold values for each binary problem. For more details on
threshold values, see Thresholds, Fixed Metric, and Fixed Metric Values.
Confusion Matrix
A confusion matrix is defined as
where
-
Pstands for «positive». -
Nstands for «negative». -
Tstands for «true». -
Fstands for «false».
For example, the first row of the confusion matrix defines how the classifier
identifies instances of the positive class: TP is the count of correctly identified positive
instances, and FN is the count of positive instances misidentified as negative.
rocmetrics computes confusion matrices for various threshold values for
each one-versus-all binary classification. The one-versus-all binary classification model
classifies an observation into a positive class if the score for the observation is greater
than or equal to the threshold value.
Prior Class Probabilities
By default, rocmetrics uses empirical probabilities, which are class
frequencies in the true labels.
rocmetrics normalizes the 1-by-K
prior probability vector π to a 1-by-2
vector for each one-versus-all binary classification, where K is the number
of classes.
The prior probabilities for the kth binary classification in which the
positive class is the kth class is [πk,1−πk], where πk is the prior probability
for class k in the multiclass problem.
Scale Vector
rocmetrics defines a scale vector
sk of size
2-by-1 for each one-versus-all binary classification
problem:
where P and N represent the total
instances of positive class and negative class, respectively. That is, P is
the sum of TP and FN, and N is the sum of FP and TN. sk(1) (first element of sk) and sk(2) (second element of sk) are the
scales for the positive class (kth class) and negative class (the rest),
respectively.
rocmetrics applies the scale values as multiplicative factors to the
counts from the corresponding class. That is, the function multiplies counts from the positive
class by sk(1) and counts from the negative class by sk(2). For example, to compute the positive predictive value (PPV =) for the kth binary problem,
TP/(TP+FP)
rocmetrics scales PPV as follows:
Misclassification Cost Matrix
By default, rocmetrics uses a
K-by-K cost matrix C, where C(i,j) = 1 if i ~= j, and C(i,j) = 0 if i = j. C(i,j) is the cost of classifying a point into class
j if its true class is i (that is, the rows correspond
to the true class and the columns correspond to the predicted class).
rocmetrics normalizes the K-by-K
cost matrix C to a 2-by-2 matrix for
each one-versus-all binary classification:
Ck is the cost matrix for the
kth binary classification in which the positive class is the
kth class, where costk(N|P) is
the cost of misclassifying a positive class as a negative class, and
costk(P|N) is the cost of misclassifying a negative
class as a positive class.
For class k, let
πk+ and
πk— be
K-by-1 vectors with the following values:
πki+
and πki— are the
ith elements of
πk+ and
πk—,
respectively.
The cost of classifying a positive-class (class k) observation into the
negative class (the rest) is
Similarly, the cost of classifying a negative-class observation into the
positive class is
Classification Scores and Thresholds
The rocmetrics function
determines threshold values from the input classification scores or the FixedMetricValues
name-value argument.
Classification Score Input for rocmetrics
rocmetrics accepts classification scores (Scores) in a matrix
of size n-by-K or a vector of length
n, where n is the number of observations and
K is the number classes. For cross-validated data,
Scores can be a cell array of vectors or a cell array of matrices.
-
Matrix of size n-by-K — Specify
Scoresusing the second output argument of the
predictfunction of a classification model object (such aspredictofClassificationTree). Each row of the output
contains classification scores for an observation for all classes, and the column order of
the output matches the class order in theClassNamesproperty of the
classification model object. You can specifyScoresas a matrix for
both binary classification and multiclass classification problems.If you use a matrix format,
rocmetricsadjusts the classification
scores for each class relative to the scores for the rest of the classes. Specifically, the
adjusted score for a class given an observation is the difference between the score for the
class and the maximum value of the scores for the rest of the classes. For more details, see
Adjusted Scores for Multiclass Classification Problem. -
Vector of length n — Specify
Scoresusing a
vector when you have classification scores for one class only. A vector input is also
suitable when you want to use a different type of adjusted scores for a multiclass problem.
As an example, consider a problem with three classes,A,
B, andC. If you want to compute a performance curve
for separating classesAandB, with
Cignored, you need to address the ambiguity in selecting
AoverB. You can use the score ratio
s(A)/s(B)or score differences(A)–s(B)and pass the
vector torocmetrics; this approach can depend on the nature of the scores
and their normalization.
You can use rocmetrics with any classifier or any function that returns a
numeric score for an instance of input data.
-
A high score returned by a classifier for a given instance and class signifies that the
instance is likely from the respective class. -
A low score signifies that the instance is not likely from the respective class.
For some classifiers, you can interpret the score as the posterior probability
of observing an instance of a class given an observation. An example of such a score is the
fraction of observations for a certain class in a leaf of a decision tree. In this case, scores
fall into the range from 0 to 1, and scores from all classes add up to 1. Other functions can
return scores ranging between minus and plus infinity, without any obvious mapping from the
score to the posterior class probability.
rocmetrics does not impose any requirements on the input score range.
Because of this lack of normalization, you can use rocmetrics to process
scores returned by any classification, regression, or fit functions.
rocmetrics does not make any assumptions about the nature of input
scores.
rocmetrics is intended for use with classifiers that return scores, not
those that return only predicted classes. Consider a classifier that returns only
classification labels, 0 or 1, for data with two classes. In this case, the performance curve
reduces to a single point because the software can split classified instances into positive and
negative categories in one way only.
Adjusted Scores for Multiclass Classification Problem
For each class, rocmetrics adjusts the classification scores (input argument
Scores of rocmetrics) relative to the scores for the rest
of the classes if you specify Scores as a matrix. Specifically, the
adjusted score for a class given an observation is the difference between the score for the
class and the maximum value of the scores for the rest of the classes.
For example, if you have [s1,s2,s3] in a row of Scores for a classification problem with
three classes, the adjusted score values are [s1—max(s2,s3),s2—max(s1,s3),s3—max(s1,s2)].
rocmetrics computes the performance metrics using the adjusted score values
for each class.
For a binary classification problem, you can specify Scores as a
two-column matrix or a column vector. Using a two-column matrix is a simpler option because
the predict function of a classification object returns classification
scores as a matrix, which you can pass to rocmetrics. If you pass scores in
a two-column matrix, rocmetrics adjusts scores in the same way that it
adjusts scores for multiclass classification, and it computes performance metrics for both
classes. You can use the metric values for one of the two classes to evaluate the binary
classification problem. The metric values for a class returned by
rocmetrics when you pass a two-column matrix are equivalent to the
metric values returned by rocmetrics when you specify classification scores
for the class as a column vector.
Model Operating Point
The model operating point represents the FPR and TPR corresponding to the
typical threshold value.
The typical threshold value depends on the input format of the Scores argument (classification scores) specified when you create a
rocmetrics object:
-
If you specify
Scoresas a matrix,rocmetricsassumes that the values in
Scoresare the scores for a multiclass classification
problem and uses adjusted score values.
A multiclass classification model classifies an observation into a class that
yields the largest score, which corresponds to a nonnegative score in the
adjusted scores. Therefore, the threshold value is0. -
If you specify
Scoresas a column vector,
rocmetricsassumes that the values in
Scoresare posterior probabilities of the class
specified inClassNames. A binary classification model
classifies an observation into a class that yields a higher posterior
probability, that is, a posterior probability greater than
0.5. Therefore, the threshold value is
0.5.
For a binary classification problem, you can specify Scores as a
two-column matrix or a column vector. However, if the classification scores are not
posterior probabilities, you must specify Scores as a matrix. A binary
classifier classifies an observation into a class that yields a larger score, which is
equivalent to a class that yields a nonnegative adjusted score. Therefore, if you specify
Scores as a matrix for a binary classifier,
rocmetrics can find a correct model operating point using the same
scheme that it applies to a multiclass classifier. If you specify classification scores that
are not posterior probabilities as a vector, rocmetrics cannot identify a
correct model operating point because it always uses 0.5 as a threshold
for the model operating point.
The plot function displays a filled circle marker at the model
operating point for each ROC curve (see ShowModelOperatingPoint). The function chooses a point corresponding to the
typical threshold value. If the curve does not have a data point for the typical threshold
value, the function finds a point that has the smallest threshold value greater than the
typical threshold. The point on the curve indicates identical performance to the performance
of the typical threshold value.
For an example, see Find Model Operating Point and Optimal Operating Point.
Thresholds, Fixed Metric, and Fixed Metric Values
rocmetrics finds the ROC curves and other metric values that correspond
to the fixed values (FixedMetricValues
name-value argument) of the fixed metric (FixedMetric
name-value argument), and stores the values in the Metrics property as a
table.
The default FixedMetric value is "Thresholds", and
the default FixedMetricValues value is "all". For each
class, rocmetrics uses all distinct adjusted score values as threshold values, computes the components of the confusion matrix for each
threshold value, and then computes performance metrics using the confusion matrix
components.
If you use the default FixedMetricValues value
("all"), specifying a nondefault FixedMetric value
does not change the software behavior unless you specify to compute confidence intervals. If
rocmetrics computes confidence intervals, then it holds
FixedMetric fixed at FixedMetricValues and computes
confidence intervals for other metrics. For more details, see Pointwise Confidence Intervals.
If you specify a nondefault value for FixedMetricValues,
rocmetrics finds the threshold values corresponding to the specified fixed
metric values (FixedMetricValues for FixedMetric) and
computes other performance metric values using the threshold values.
-
If you set the
UseNearestNeighbor
name-value argument tofalse, thenrocmetricsuses the
exact threshold values corresponding to the specified fixed metric values. -
If you set
UseNearestNeighbortotrue, then
among the adjusted scores,rocmetricsfinds a value that is the nearest to
the threshold value corresponding to each specified fixed metric value.
The Metrics property includes an additional threshold value that
replicates the largest threshold value for each class so that a ROC curve starts from the
origin (0,0). The additional threshold value represents the
reject-all threshold, for which
TP = FP = 0 (no
positive instances, that is, zero true positive instances and zero false positive
instances).
Another special threshold in Metrics is the
accept-all threshold, which is the smallest threshold value for which
TN = FN = 0 (no
negative instances, that is, zero true negative instances and zero false negative
instances).
Note that the positive predictive value (PPV = TP/(TP+FP)) is
NaN for the reject-all threshold, and the negative predictive value
(NPV = TN/(TN+FN)) is NaN for the accept-all
threshold.
NaN Score Values
rocmetrics processes NaN values in the classification
score input (Scores) in one of two
ways:
-
If you specify
NaNFlag="omitnan"rocmetrics
discards rows withNaNscores. -
If you specify
NaNFlag="includenan", then
rocmetricsadds the instances ofNaNscores to false
classification counts in the respective class for each one-versus-all binary classification.
That is, for any threshold, the software counts instances withNaNscores
from the positive class as false negative (FN), and counts instances with
NaNscores from the negative class as false positive (FP). The software
computes the metrics corresponding to a threshold of1by setting the
number of true positive (TP) instances to zero and setting the number of true negative (TN)
instances to the total count minus theNaNcount in the negative
class.
Consider an example with two rows in the positive class and two rows in the
negative class, each pair having a NaN score:
| True Class Label | Classification Score |
|---|---|
| Negative | 0.2 |
| Negative | NaN |
| Positive | 0.7 |
| Positive | NaN |
If you discard rows with NaN scores
(NaNFlag="omitnan"), then as the score threshold varies,
rocmetrics computes performance metrics as shown in the following table. For
example, a threshold of 0.5 corresponds to the middle row where rocmetrics
classifies rows 1 and 3 correctly and omits rows 2 and 4.
| Threshold | TP |
FN |
FP |
TN |
|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 1 |
| 0.5 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
If you add rows with NaN scores to the false category in
their respective classes (NaNFlag="includenan"), rocmetrics
computes performance metrics as shown in the following table. For example, a threshold of 0.5
corresponds to the middle row where rocmetrics counts rows 2 and 4 as
incorrectly classified. Notice that only the FN and FP
columns differ between these two tables.
| Threshold | TP |
FN |
FP |
TN |
|---|---|---|---|---|
| 1 | 0 | 2 | 1 | 1 |
| 0.5 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 2 | 0 |
Pointwise Confidence Intervals
rocmetrics computes pointwise confidence intervals for the performance
metrics, including the AUC values and score thresholds, by using either bootstrap samples or
cross-validated data. The object stores the values in the Metrics and AUC properties.
-
Bootstrap — To compute confidence intervals using bootstrapping, set the
NumBootstraps
name-value argument to a positive integer.rocmetricsgenerates
NumBootstrapsbootstrap samples. The function creates each bootstrap
sample by randomly selectingnout of thenrows of
input data with replacement. For an example, see Compute Confidence Intervals Using Bootstrapping. -
Cross-validation — To compute confidence intervals using cross-validation, specify
cross-validated data for true class labels (Labels),
classification scores (Scores), and
observation weights (Weights) using cell
arrays.rocmetricstreats elements in the cell arrays as cross-validation
folds. For an example, see Compute Confidence Intervals with Cross-Validated Input Data.
You cannot specify both options. If you specify a custom metric in AdditionalMetrics, you
must use bootstrap to compute confidence intervals. rocmetrics does not support
cross-validation for a custom metric.
rocmetrics holds FixedMetric
(threshold, FPR, TPR, or a metric specified in AdditionalMetrics) fixed at
FixedMetricValues and
computes the confidence intervals on AUC and other metrics for the points corresponding to the
values in FixedMetricValues.
-
Threshold averaging (TA) (when
FixedMetricis
"Thresholds"(default)) —rocmetricsestimates
confidence intervals for performance metrics at fixed threshold values. The function takes
samples at the fixed thresholds and averages the corresponding metric values. -
Vertical averaging (VA) (when
FixedMetricis a performance metric)
—rocmetricsestimates confidence intervals for thresholds and other
performance metrics at the fixed metric values. The function takes samples at the fixed
metric values and averages the corresponding threshold and metric values.
The function estimates confidence intervals for the AUC value only when
FixedMetric is "Thresholds",
"FalsePositiveRate", or "TruePositiveRate".
References
[1] Fawcett, T. “ROC Graphs: Notes and
Practical Considerations for Researchers”, Machine Learning 31, no. 1
(2004): 1–38.
[2] Zweig, M., and G. Campbell.
“Receiver-Operating Characteristic (ROC) Plots: A Fundamental Evaluation Tool in Clinical
Medicine.” Clinical Chemistry 39, no. 4 (1993): 561–577 .
[3] Davis, J., and M. Goadrich. “The Relationship Between Precision-Recall and ROC Curves.” Proceedings of ICML ’06, 2006, pp. 233–240.
[4] Moskowitz, C. S., and M. S. Pepe.
“Quantifying and Comparing the Predictive Accuracy of Continuous Prognostic Factors for Binary
Outcomes.” Biostatistics 5, no. 1 (2004): 113–27.
[5] Huang, Y., M. S. Pepe, and Z. Feng.
“Evaluating the Predictiveness of a Continuous Marker.” U. Washington Biostatistics
Paper Series, 2006, 250–61.
[6] Briggs, W. M., and R. Zaretzki. “The
Skill Plot: A Graphical Technique for Evaluating Continuous Diagnostic Tests.”
Biometrics 64, no. 1 (2008): 250–256.
[7] Bettinger, R. “Cost-Sensitive Classifier Selection Using the ROC Convex Hull Method.” SAS Institute, 2003.
See Also
rocmetrics | addMetrics | average | plot | ROCCurve Properties
Я думаю, что большинство людей слышали о ROC-кривой или о AUC (площади под кривой) раньше. Особенно те, кто интересуется наукой о данных. Однако, что такое ROC-кривая и почему площадь под этой кривой является хорошей метрикой для оценки модели классификации?
Полное название ROC — Receiver Operating Characteristic (рабочая характеристика приёмника). Впервые она была создана для использования радиолокационного обнаружения сигналов во время Второй мировой войны. США использовали ROC для повышения точности обнаружения японских самолетов с помощью радара. Поэтому ее называют рабочей характеристикой приемника.
AUC или area under curve — это просто площадь под кривой ROC. Прежде чем мы перейдем к тому, что такое ROC-кривая, нужно вспомнить, что такое матрица ошибок.
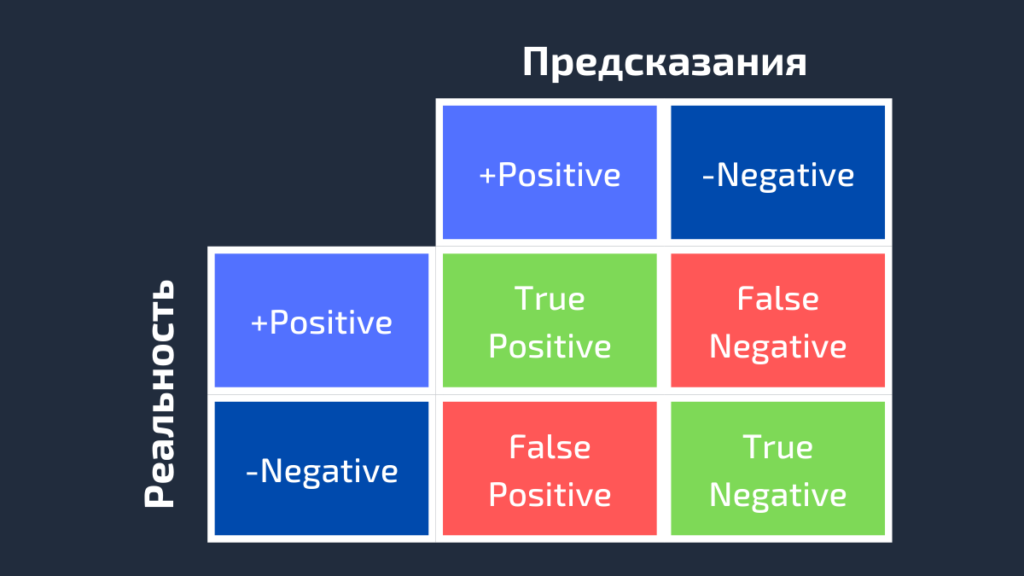
Как видно из рисунка выше, матрица ошибок — это комбинация вашего прогноза (1 или 0) и фактического значения (1 или 0). В зависимости от результата предсказания и того, корректна ли была проведена классификация, матрица разделена на 4 части. Например, true positive (истинно положительный) результат — это количество случаев, в которых вы правильно классифицируете семпл как положительный. А false positive (ложноположительный) — это число случаев, в которых вы ошибочно классифицируете семпл как положительный.
Матрица ошибок содержит только абсолютные числа. Однако, используя их, мы можем получить множество других метрик, основанных на процентных соотношениях. True Positive Rate (TPR) и False Positive Rate (FPR) — две из них.
True Positive Rate (TPR) показывает, какой процент среди всех positive верно предсказан моделью.
TPR = TP / (TP + FN).
False Positive Rate (FPR): какой процент среди всех negative неверно предсказан моделью.
FPR = FP / (FP + TN).
Хорошо, давайте теперь перейдем к кривой ROC!
Что такое ROC-кривая?
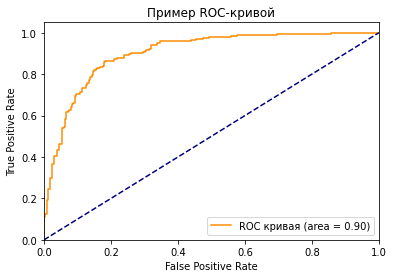
Как вы можете видеть на графике, кривая ROC — это просто отношение TPR к FPR. Теперь вам все понятно, в заключение…
Поверили?
Если серьезно, вы можете прочитать намного больше информации из диаграммы. Первый вопрос, который я хочу здесь обсудить: у нас же есть только один набор TPR, FPR, посчитанный на основе сделанных моделью предсказаний. Так откуда взялось такое количество точек для построения целого графика?
Все следует из того, как работает модель классификации. Когда вы строите классификационную модель, такую как дерево решений, и хотите определить, будут ли акции расти в цене или падать на основе входных данных. Модель сначала рассчитает вероятность увеличения или уменьшения, используя предоставленные вами исторические данные. После этого, основываясь на пороговом значении, она решит, будет ли результат увеличиваться или уменьшаться.
Да, ключевое слово здесь — порог. Разные пороговые значения создают разные TPR и FPR. Они представляют те самые точки, что образуют кривую ROC. Вы можете выбрать «Увеличение» в качестве предсказания модели, если полученная на основе исторических данных вероятность роста акций больше 50%. Также можете изменить пороговое значение и отобразить «Увеличение», только если соответствующая вероятность больше 90%. Если вы установите 90% порог вместо 50%, вы будете более уверены в том, что выбранные для «Увеличения» акции действительно вырастут. Но так вы можете упустить некоторые потенциально выгодные варианты.
Что значит синяя пунктирная линия на графике?
Как мы знаем, чем больше площадь под кривой (AUC), тем лучше классификация. Идеальная или наилучшая кривая — это вертикальная линия от (0,0) до (0,1), которая тянется до (1,1). Это означает: модель всегда может различить положительные и отрицательные случаи. Однако, если вы выбираете класс случайным образом для каждого семпла, TPR и FPR должны увеличиваться с одинаковой скоростью. Синяя пунктирная линия показывает кривую TPR и FPR при случайном определении positive или negative для каждого случая. Для этой диагональной линии площадь под кривой (AUC) составляет 0.5.
Что произойдет с TPR, FPR и ROC-кривой, если изменить пороговое значение?
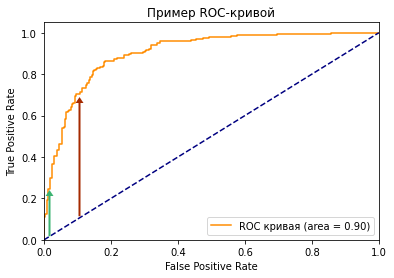
Посмотрите на две точки на ROC-кривой. Зеленая точка имеет очень высокий порог, это означает, что только если вы уверены на 99%, можете классифицировать случай как positive. Красная точка имеет относительно более низкий порог. Это означает, что вы можете классифицировать случай как positive, если вы уверены на 90%.
Как изменяются TPR и FPR при движении от зеленой точки к красной?
И TPR, и FPR увеличиваются. Когда вы уменьшаете порог, модель будет определять больше положительных случаев. Таким образом, TP увеличивается, как и TP/(TP + FN). С другой стороны, вы неизбежно ошибочно классифицируете некоторые отрицательные случаи как положительные из-за снижения порога, и поэтому FP и FP/(FP + TN) также увеличиваются.
Мы видим, что TPR и FPR положительно коррелируют. Вам нужно балансировать между максимальным охватом positive случаев и минимизацией неправильной классификации negative случаев.
Как выбрать оптимальную точку на кривой ROC?
Трудно определить оптимальную точку, потому что нужно выбрать наиболее подходящее пороговое значение, учитывая сферу применения модели. Однако общее правило — максимизировать разницу (TPR-FPR), которая на графике представлена вертикальным расстоянием между оранжевой и синей пунктирной линией.
Почему площадь под кривой ROC – хорошая метрика для оценки модели классификации?
Хорошая метрика модели машинного обучения должна отображать истинную и постоянную способность модели к прогнозированию. Это означает, что, если я изменю тестовый набор данных, он не должен давать другой результат.
ROC-кривая учитывает не только результаты классификации, но и вероятность предсказания всех классов. Например, если результат корректно классифицирован на основе 51% вероятности, то он, скорее всего, будет классифицирован неверно, если вы воспользуетесь другим тестовым датасетом. Кроме того, ROC-кривая также учитывает эффективность модели при различных пороговых значениях. Она является комплексной метрикой для оценки того, насколько хорошо разделяются случаи в разных группах.
Какое значение AUC является приемлемым для модели классификации?
Как я показал ранее, для задачи двоичной классификации при определении классов случайным образом, вы можете получить 0.5 AUC. Следовательно, если вы решаете задачу бинарной классификации, разумное значение AUC должно быть > 0.5. У хорошей модели классификации показатель AUC > 0.9, но это значение сильно зависит от сферы ее применения.
Как рассчитать AUC и построить ROC-кривую в Python?
Если вы просто хотите рассчитать AUC, вы можете воспользоваться пакетом metrics библиотеки sklearn (ссылка).
Если вы хотите построить ROC-кривую для результатов вашей модели, вам стоит перейти сюда.
Вот код для построения графика ROC, который я использовал в этой статье.
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_curve, auc
from sklearn.metrics import roc_auc_score
from matplotlib import pyplot as plt
# генерируем датасет на 2 класса
X, y = make_classification(n_samples=1000, n_classes=2, random_state=1)
# разделяем его на 2 выборки
trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2)
# обучаем модель
model = LogisticRegression(solver='lbfgs')
model.fit(trainX, trainy)
# получаем предказания
lr_probs = model.predict_proba(testX)
# сохраняем вероятности только для положительного исхода
lr_probs = lr_probs[:, 1]
# рассчитываем ROC AUC
lr_auc = roc_auc_score(testy, lr_probs)
print('LogisticRegression: ROC AUC=%.3f' % (lr_auc))
# рассчитываем roc-кривую
fpr, tpr, treshold = roc_curve(testy, lr_probs)
roc_auc = auc(fpr, tpr)
# строим график
plt.plot(fpr, tpr, color='darkorange',
label='ROC кривая (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Пример ROC-кривой')
plt.legend(loc="lower right")
plt.show()
Вам нужны следующие входные данные: фактическое значение y и вероятность предсказания. Обратите внимание, что функция roc_curve требует только вероятность для положительного случая, а не для обоих классов. Если вам нужно решить задачу мультиклассовой классификации, вы также можете использовать этот пакет, и в приведенной выше ссылке есть пример того, как построить график.