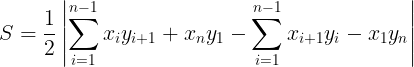Как найти площадь по координатам геодезия

С помощью этого калькулятора Вы сможете рассчитать площадь земельного участка по координатам его углов. При расчете используется формула
Гаусса (формула землемера) для определения площади многоугольника, вершины которого заданы декартовыми координатами на плоскости

где

S — площадь

n — количество углов

x, y — координаты вершин

Примечание: если в кадастровом плане Вашего участка не указаны координаты поворотных точек, то для расчета площади можно воспользоваться
методом треугольников, в основе которого лежит формула Герона.

Калькулятор площади по координатам

Площадь
полигона S
по координатам его вершин вычисляется
по формулам (1.14):

(1.14)

где
x_i
, y_i
– координаты i
– ой вершины полигона;

x_i+1
, y_i+1
– координаты последующей i+1
вершины полигона;

x_i-1
, y_i-1
– координаты предыдущей i
– 1 вершины полигона;

n
– число вершин в полигоне.

Таблица 1.4

Определение площади
полигона по координатам

1.5 Определение площадей участков на планах.

Наиболее
распространенным и достаточно точным
способом определения площадей участков,
имеющих криволинейные контуры, является
измерение площадей планиметром.

Перед измерением
площадей планиметр поверяют и, если
есть необходимость, юстируют.

Затем
определяют цену деления каретки
планиметра. Для этого, на листе плана
устанавливают иглу планиметра в любую
точку замкнутого контура, площадь
которого известна: полигона, квадрата
сетки квадратов, окружности известного
радиуса и т д. берут отсчет по каретке
( если у планиметра одна каретка) или
по обеим кареткам планиметра. Затем
обводят контур по часовой стрелке,
возвращая иглу в исходную точку, и вновь
берут отсчеты.

При работе с
однокареточным планиметром площадь
контура обводят дважды, а при работе с
двухкареточным планиметром один раз.
Цену деления у однокареточного планиметра
р определяют по формуле (1.15):

Р=
S_изв/(n_к-n_н)ср
; (1.15)

Где
S_изв
– известная площадь контура ;

n_к
, n_н—
соответственно конечный и начальный
отсчеты по каретке ;

(n_к-n_н)ср
– среднее значение разности отсчетов
из первого и второго обводов контура.

Цена
деления у двухкаретного планиметра
определяется как, среднее арифметическое
из цены деления по первой и второй
кареткам. Для измерения площади контура
полюс планиметра устанавливают вне
контура, а иглу в любую точку контура.
Затем берут начальный отсчет (при
однокареточном планиметре) по каретке,
обводят контур по часовой стрелке.
Возвращая иглу в исходную точку, и снова
берут отсчет по каретке. Затем повторно
обводят этот же контур, записывая отсчеты
в таблицу. Площадь контура вычисляют
по формуле (1.16):

S_i=p*(n_ik
—
n_iн)ср,
(1.16),

где
(n_ik
— n_iн)ср
–среднее значение разности отсчетов
из первого и второго обводов i-го
контура.

При измерении
площадей планиметром необходимо
выполнять следующие требования:

• не
  допускать, чтобы угол между рычагами
  планиметра был меньше 30° или больше
  150°,

• не
  допускать схода обводного колесика с
  листа бумаги.

Таблица 1.7

Ведомость вычисления
площадей участков угодий

двухкаретным
планиметром ПП-2К

Сумма
измеренных площадей должна равняться
теоретической сумме площади полигона.
Из-за неизбежных погрешностей будет
невязка:

ΔS
=S_план
—
S_коор,

Где
S_план
–сумма площадей участков, вычисленная
по показаниям планиметра;

S_коор
– площадь полигона, вычисленная по
координатам;

Относительная
невязка вычисляется по формуле (1.17):

ΔS
=( ΔS/S_коор)
=

Если
Δ не превышает 1/120, то считают точность
измерения площадей планиметром
удовлетворительной. В этом случае
находят поправку на измеренные планиметром
площади участков, для чего невязку
распределяют на площади участков
пропорционально их площадям. Если же
относительная ошибка больше допустимой,
измерение площадей участков повторяют
заново.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Инструкция по использованию калькулятора

Координаты вершин полигона (широту и долготу) следует указывать в градусах в виде десятичной дроби. Координаты вершин указываются последовательно и в одном направлении (по часовой или против часовой стрелки).

При наличии прямоугольных координат X и Y вершин n -угольника его площадь можно вычислить по формулам аналитической геометрии; выведем одну из таких формул.

Пусть в треугольнике ABC координаты вершин равны X1 , Y1 (A), X2, Y2 (B) и X3, Y3 (C) – рис.6.2.

Рис.6.2

Из вершин треугольника опустим перпендикуляры на оси координат и обозначим их длину, как показано на рис.6.2.

Площадь треугольника P будет равна сумме площадей двух трапеций I(aABc) и II(bBCc) за вычетом площади трапеции III(aACc)

P=PI+PII-PIII.                                          (6.9)

Выразим площадь каждой трапеции через ее основания и высоту:

PI=0.5(X1+X2)*(Y1-Y2);
PI=0.5(X2+X3)*(Y3-Y2);                      (6.10)
PI=0.5(X3+X1)*(Y1-Y3);

Чтобы избавиться от множителя 0.5, будем вычислять удвоенную площадь треугольника. Выполним умножение, приведем подобные члены, вынесем общие множители за скобки и получим:

2*P=X1*(Y2-Y3)+X2*(Y3-Y1)+X3*(Y1-Y2)

или в общем виде:

(6.11)

В этой формуле индекс “i” показывает номер вершины треугольника; индекс “i” означает, что нужно брать следующую или предыдущую вершину (при обходе фигуры по часовой стрелке).

Если при группировке членов выносить за скобки Y1, то получится формула:

(6.12)

Вычисления по обоим формулам дают одинаковый результат, поэтому на практике можно пользоваться любой из них.

Хотя формулы (6.11) и (6.12) выведены для треугольника, нетрудно показать, что они пригодны для вычисления площади любого n – угольника.

Оценка точности площади. В большинстве случаев участки на местности имеют форму неправильного n – угольника, причем количество вершин многоугольника n может быть от 30 до 20 и более. Площадь таких участков вычисляют аналитическим способом по прямоугольным координатам вершин, которые, в свою очередь, определяют в результате обработки геодезических измерений. При этом для каждой вершины многоугольника получают координаты и ошибку ее положения относительно исходных пунктов, задающих систему координат на местности.

Выведем формулу для оценки площади многоугольника по известным внутренним углам, длинам его сторон и ошибкам положения mti его вершин.

На рис.6.3 изображен фрагмент многоугольника с вершинами i-1, i, i+1, i+2 и сторонами li-1,li,li+1.

Проведем на вершинах i и i+1 окружности радиусами mti и mt(i+1) и построим биссектрисы углов βi и βi+1. Затем восстановим перпендикуляры к стороне li и найдем проекции отрезков mti и mt(i+1) на эти перпендикуляры:

(6.13)

(6.14)

Рис.6.3

Построим трапецию, основаниями которой являются отрезки mi и mi+1, а высотой – сторона li и найдем площадь этой трапеции ΔPi. Как известно, площадь трапеции равна произведению полусуммы оснований на высоту, а поскольку основаниями трапеции являются проекции ср.кв. ошибок, то вместо полусуммы нужно взять квадратичную полусумму оснований; таким образом,

(6.15)

где

c = Sin( β/2 ) .

Площадь трапеции, построенной на одной стороне многоугольника, является частью ошибки площади всего многоугольника; выполнив квадратичное суммирование площадей ΔPi по всем сторонам, получим:

или

(6.16)

Из формулы (6.16) можно получить формулу средней квадратической ошибки площади правильного многоугольника с одинаковой ошибкой положения mt всех его вершин:

mP=an * mt * L,                    (6.17)

где: L – периметр многоугольника,
an – коэффициент, зависящий от n – количества вершин;

его значения:

n    3    4     5    6    7     8    9    10
an    0.204     0.250    0.256     0.250     0.243    0.231     0.222     0.212
n    11    12     15    20    24     30    60    120
an    0.205     0.197    0.179     0.156     0.143    0.128     0.091     0.065

Формула (6.17) является базовой и при оценке площади неправильных n-угольников, для которых ошибка площади mp оказывается лишь на несколько процентов больше, чем для правильного n – угольника. Так, если площадь неправильного n – угольника при том же периметре в два раза меньше площади правильного n-угольника, то ошибка его площади увеличивается лишь на 20 %.

При неодинаковых ошибках положения вершин многоугольника в формуле (6.17) достаточно вместо mt поставить mt(ср).

Примером применения формулы (6.17) является оценка площади участков, координаты вершин которых получены с топографических планов. Например, для плана масштаба 1:2000 ошибку положения точек можно принять равной mt = 0.50 мм * M = 1 м (при условии, что основа плана достаточно жесткая и ее деформацией можно пренебречь). При площади участка 0.12 га и количестве вершин n=4 (5 или 6) средняя квадратическая ошибка его площади при правильной форме (периметр L = 140 м) будет равна 35 кв.м, а при неправильной форме (периметр L>140 м) она может достигать 40 кв.м.

Другим примером применения формулы (6.17) может служить оценка площади многоугольника, координаты вершин которого получены из полярной засечки, выполненной с одного пункта-станции.

При использовании точных приборов (электронных тахеометров или систем GPS) доля ошибок измерений в ошибке положения точек значительно меньше доли ошибки их фиксации mф на местности. Приняв mti= mф, можно использовать формулу (6.17) для любых способов получения координат вершин многоугольника.

Площадь правильного n-угольника можно выразить через его периметр:

(6.18)

И из формулы (6.17) получить формулу относительной ошибки площади:

(6.19)

где

(6.20)

Например:

для треугольника (n=3) mp/P = 4.24* mt/L,
для четырехугольника (n=4) mp/P = 4.00* mt/L,
для пятиугольника (n=5) mp/P = 3.72 mt/L,
для шестиугольника (n=6) mp/P = 3.46 mt/L.

Таким образом, для приближенной оценки площади 3-4-5-6- угольника в аналитическом способе можно применять формулу:

mp/P=4* mt/L;           (6.21)

ошибка этой формулы может достигать 15% – 20% для участков, форма которых заметно отличается от формы правильного n -угольника.