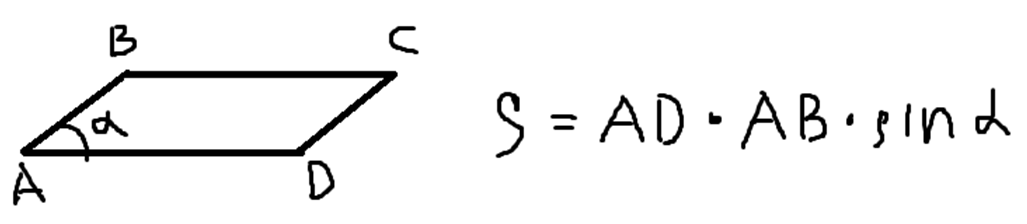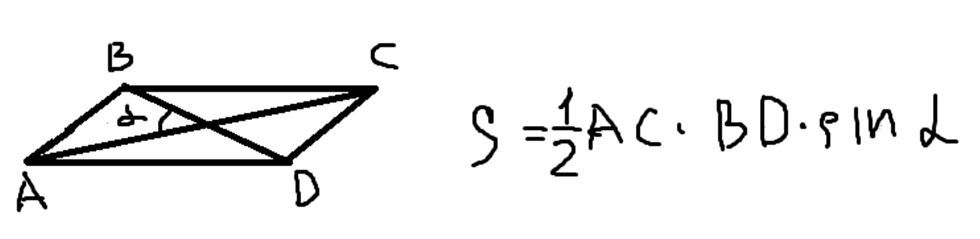{S = a cdot h}
Найти площадь параллелограмма
На этой странице вы можете рассчитать площадь параллелограмма с помощью калькулятора по трем формулам. Просто введите известные вам данные — основание, высоту, стороны, диагонали и углы между ними и получите ответ.
Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).
Содержание:
- калькулятор площади параллелограмма
- формула площади параллелограмма через сторону и высоту
- формула площади параллелограмма через две стороны и угол между ними
- формула площади параллелограмма через диагонали и угол между ними
- примеры задач
Формула площади параллелограмма через сторону и высоту
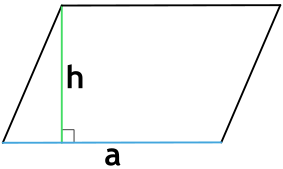
{S = a cdot h}
a — сторона параллелограмма
h — высота параллелограмма
Формула площади параллелограмма через две стороны и угол между ними
{S=a cdot b cdot sin(alpha)}
a, b — стороны параллелограмма
α — угол между сторонами a и b
Формула площади параллелограмма через диагонали и угол между ними
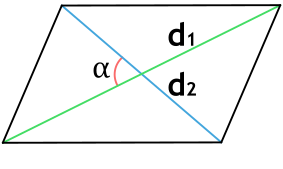
{S = dfrac{1}{2} cdot d_1 cdot d_2 cdot sin(alpha)}
d1, d2 — диагонали параллелограмма
α — угол между диагоналями
Примеры задач на нахождение площади параллелограмма
Задача 1
Найдите площадь параллелограмма, стороны которого равны 9 см и 12 см, а угол между ними 60 градусов.
Решение
Для решения задачи нам подойдет вторая формула, так как из условия нам известны стороны параллелограмма и угол между ними. Подставим значения в формулу и произведем расчет.
S = a cdot b cdot sin(alpha) = 9 cdot 12 cdot sin(60) = 108 cdot sin(60) = 108 cdot 0.866 approx 93.53074 : см^2
Ответ: 108 cdot 0.866 approx 93.53074 : см^2
Мы можем проверить ответ с помощью калькулятора .
Задача 2
Найдите площадь параллелограмма, если две его стороны равны 8 см и 12 см, а угол между ними равен 30 градусов.
Решение
Задача похожа на предыдущую, поэтому ее решение будет выглядеть аналогично.
S = a cdot b cdot sin(alpha) = 8 cdot 12 cdot sin(30) = 96 cdot sin(30) = 96 cdot 0.5 = 48 : см^2
Ответ: 48 см²
И снова проверить ответ нам поможет калькулятор .
Задача 3
Найдите площадь параллелограмма, сторона которого равна 12 см, а высота проведенная к ней 8 см.
Решение
В этом случае нам известны сторона параллелограмма и высота, поэтому воспользуемся первой формулой.
S = a cdot h = 12 cdot 8 = 96 : см^2
Ответ: 96 см²
И снова проверить ответ нам поможет калькулятор .
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам
Формула Герона
S = √
p
(
p — a
)(
p — b
)(
p — c
)
- Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон, умноженного на синус угла между ними. - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
где S — площадь треугольника,
a, b, c
— длины сторон треугольника,
h
— высота треугольника,
γ
— угол между сторонами
a
и
b
,
r
— радиус вписанной окружности,
R — радиус описанной окружности,
|
p = |
a + b + c |
— полупериметр треугольника. |
| 2 |
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
a, b
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади параллелограмма по диагоналям и углу между ними Площадь параллелограмма равна половине произведения длин его диагоналей, умноженному на синус угла между ними.
S = 1/2d1 · d2 · sin
γ
- Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон, умноженному на синус угла между ними.
где S — Площадь параллелограмма,
a, b
— длины сторон параллелограмма,
h
— длина высоты параллелограмма,
α
— угол между сторонами параллелограмма,
- γ — угол между диагоналями параллелограмма,
- d1, d2 — длины диагоналей параллелограмма.
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
Формулы площади ромба
где S — Площадь ромба,
a
— длина стороны ромба,
h
— длина высоты ромба,
α
— угол между сторонами ромба,
d
1,
d
2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
S = a
+
b
√( p — a
)(
p — b
)(
p — a — c
)(
p — a — d
)
4| a
—
b
|
- Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высоту
где S — Площадь трапеции,a, b
— длины основ трапеции,
c, d
— длины боковых сторон трапеции,
p
=
a
+
b
+
c
+
d
— полупериметр трапеции. 2
Загрузить PDF
Загрузить PDF
Параллелограмм определяется как простой четырехугольник с двумя парами параллельных сторон. Если вы занимаетесь геометрией, то вам может понадобиться найти площадь параллелограмма. Вот несколько указаний как именно это сделать.
Шаги
-
1
Найдите основание параллелограмма. Основание – это длина нижней стороны параллелограмма.
-
2
Найдите высоту параллелограмма. Высота параллелограмма – это перпендикулярная линия, проведенная из произвольной точки верхней стороны к нижней стороне параллелограмма.
-
3
Умножьте основание на высоту.
Реклама
Об этой статье
Эту страницу просматривали 9149 раз.
Была ли эта статья полезной?
Как рассчитать площадь параллелограмма
На данной странице калькулятор поможет рассчитать площадь параллелограмма онлайн. Для расчета задайте длину основания, высоту или длины диагоналей и угол между ними.
Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Через основание и высоту
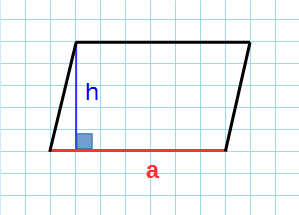
Формула для нахождения площади параллелограмма через основание и высоту:
a — длина основания; h — высота.
Через основания и угол между ними
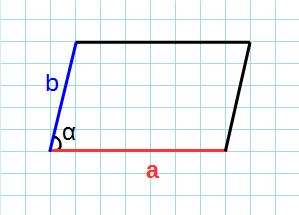
Формула для нахождения площади параллелограмма через основания и угол между ними:
a, b — длина основания; α — угол между основаниями.
Через диагонали и угол между ними
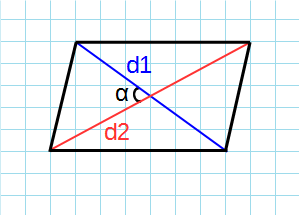
Формула для нахождения площади параллелограмма через диаганали и угол между ними:
d1, d2 — диагонали; α — угол между диагоналями.
Немного из истории
Необходимость нахождения площади параллелограммов и их частных случаев – прямоугольников, возникла очень давно. С древних времен человеку необходимо было находить площади земельных участков для сельскохозяйственных нужд и градостроительства.
Площадь параллелограмма: основные формулы
Существует несколько формул нахождения площади параллелограмма. Каждая из них подходит для решения соответствующего круга задач.
Рассмотрим основные формулы.
Площадь параллелограмма
Площадь параллелограмма через одну из его сторон и высоту, проведенную к этой стороне:
Площадь параллелограмма через две его стороны и синус угла между ними:
Площадь параллелограмма через его диагонали и угол между ними:
Давайте разберем задачу, иллюстрирующую применение одной из этих формул:
Задача
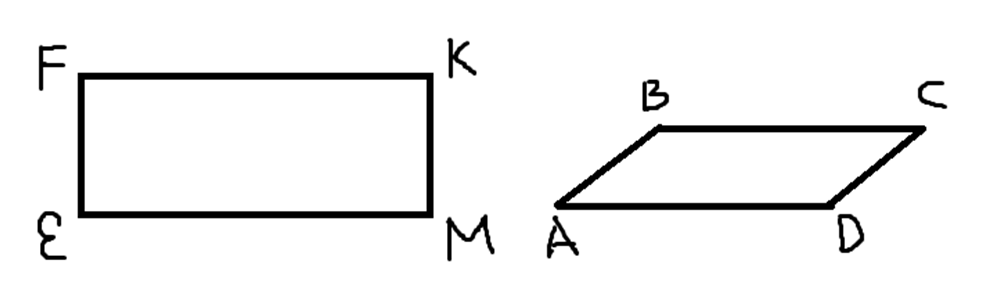
Даны параллелограмм АВСD и прямоугольник EFKM, которые имеют одинаковую длину соответствующих сторон (см. рисунок ниже). Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Решение
На первый взгляд, это очень сложная задача, так как мы не знаем ни одного конкретного параметра ни одной из этих геометрических фигур. Давайте попробуем разобраться.
По условию задачи, стороны FE = АВ, КМ = СD, ЕМ = АD, FК = ВС.
Площадь параллелограмма в данном случае удобно найти через две стороны и синус угла между ними (2-я формула). Площадь прямоугольника в классическом прочтении равна произведению длины на ширину. Но так как прямоугольник – это частный случай параллелограмма, то его площадь также можно представить через две стороны и синус угла между ними. Только в этом случае угол будет равен 90 градусов, а синус 90 градусов равен «1». Поэтому значительно проще при нахождении площади прямоугольников обходится без синусов.
Так как по условию задачи соответствующие стороны прямоугольника и параллелограмма равны, мы можем их обозначить одной буквой:
FE = АВ = Х
ЕМ = АD = У
Острый угол, например, ВАD обозначим одной буквой А.
Тогда площадь параллелограмма равна:
Sпар = ХУsinA
а площадь прямоугольника равна:
Sпрям = ХУ
Также по условию площадь прямоугольника вдвое больше площади параллелограмма:
Sпрям = 2 Sпар
Следовательно, мы можем записать следующее уравнение:
ХУ = 2 ХУ sinA
Сокращаем обе части этого уравнения на «Х У», получаем:
1 = 2 sinA
Откуда:
sinA = 0,5
По таблице синусов находим, что если sinA = 0,5, то угол А = 30 градусов
Ответ: 30
Как видите, иногда, зная только один сравнительный параметр, связывающий две геометрические фигуры, мы можем вычислить некоторые параметры одной из фигур, опираясь только на знание формул для нахождения площади этих фигур.
Часто задаваемые вопросы
✅ Что такое параллелограмм?
↪ Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны и равны по длине.
✅ Какие свойства параллелограмма?
↪ Важными свойствами параллелограмма являются равенство противоположных сторон, противоположных углов и диагоналей, а также равенство площадей параллелограмма и прямоугольника, основание и высоту которого образуют две параллельные стороны параллелограмма.
✅ Какие виды параллелограмма существуют?
↪ Ромб, прямоугольник и квадрат являются разновидностями параллелограмма.
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!