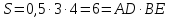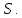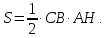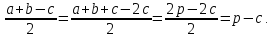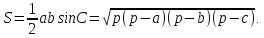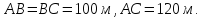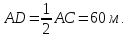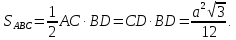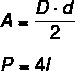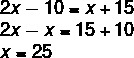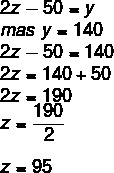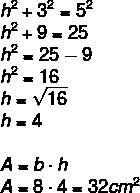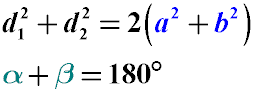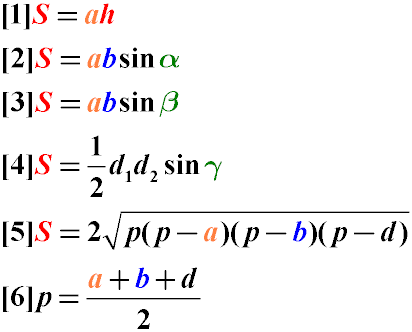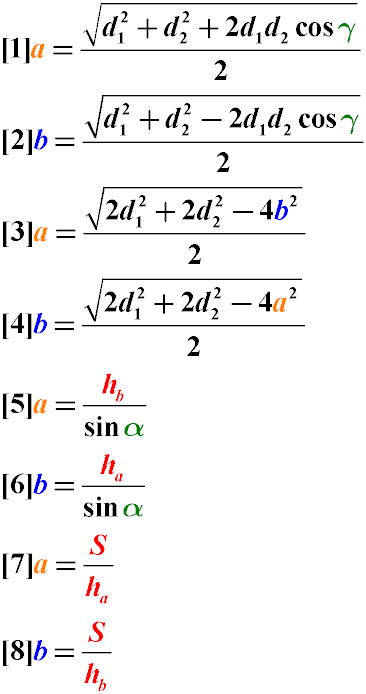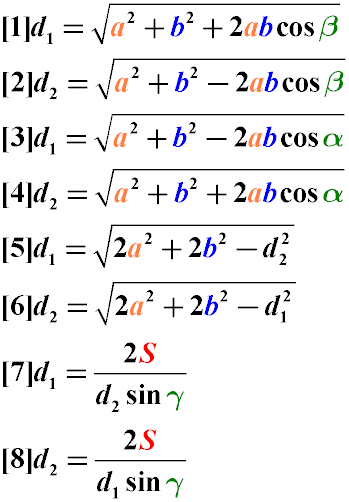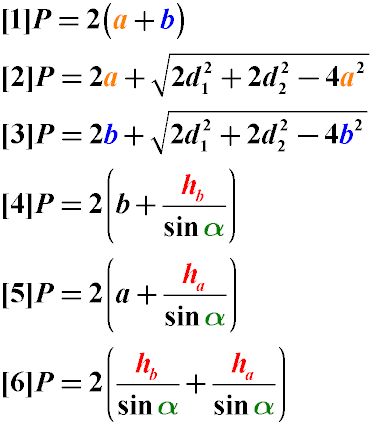Вывод
формулы площади параллелограмма сводится
к построению прямоугольника, равного
данному параллелограмму по площади.
Примем одну сторону параллелограмма
за основание, а перпендикуляр, проведенный
из любой точки противолежащей стороны
на прямую, содержащую основание будем
называть высотой параллелограмма. Тогда
площадь параллелограмма будет равна
произведению его основания на высоту.
[4, c.
254]
Теорема.
Площадь
параллелограмма равна произведению
его основания на высоту.
Доказательство.
Рассмотрим параллелограмм


Примем сторону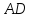
основание и проведем высоты


Рисунок
2.3.1
Докажем
сначала, что площадь прямоугольника


Трапеция


С другой стороны, она составлена из
прямоугольника НВСК и треугольника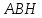
Но прямоугольные треугольники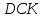
равны
по гипотенузе и острому углу (их
гипотенузы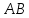
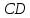
параллелограмма, а углы 1 и 2 равны как
соответственные углы при пересечении
параллельных прямых


поэтому их площади равны. Следовательно,
площади параллелограмма



По теореме о площади прямоугольника,
но так как
то
Теорема
доказана.
Пример
2.3.1.
В
ромб со стороной

вписана окружность. Определить площадь
четырёхугольника, вершинами которого
являются точки касания окружности со
сторонами ромба.[5, c.
150]
Решение:
Радиус
вписанной в ромб


поскольку


углы опираются на диаметр окружности.
Его площадь
где

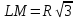
Рисунок
2.3.2
Итак,
Ответ:
Пример
2.3.2.
Дан
ромб

диагонали которого равны 3 см и 4 см. Из
вершины тупого угла

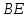

Решение:
Площадь
ромба
(рисунок 2.3.3).
Рисунок
2.3.3
Далее,
из





Итак,
Ответ:
Пример
2.3.3.
Площадь
четырёхугольника равна
Найти площадь параллелограмма, стороны
которого равны и параллельны диагоналям
четырёхугольника.
Решение:
Так
как




Рисунок
2.3.4
Аналогично
получаем
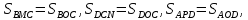

Ответ:

2.4 Площадь треугольника
Существует
несколько формул для вычисления площади
треугольника. Рассмотрим те, что изучаются
в школе.
Первая
формула вытекает из формулы площади
параллелограмма и предлагается учащимся
в виде теоремы. [4, c.
254]
Теорема.
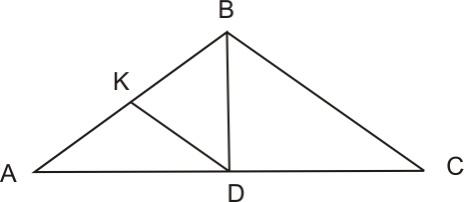
Площадь треугольника равна половине
произведения его основания на высоту.
Доказательство.
Пусть


Примем сторону
высоту
Докажем что:
Рисунок
2.4.1
Достроим
треугольник


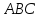


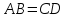
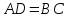

поэтому их площади равны. Следовательно,
площадь S треугольника АВС равна половине
площади параллелограмма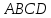
т.е.
Теорема
доказана.
Важно
обратить внимание учащихся на два
следствия, вытекающих из данной теоремы.
А именно:
-
площадь
прямоугольного треугольника равна
половине произведения его катетов. -
если
высоты двух треугольников равны, то их
площади относятся как основания.
Эти
два следствия играют важную роль в
решении разного рода задач. С опорой на
данную доказывается еще одна теорема,
имеющая широкое применение при решении
задач.
Теорема.
Если
угол одного треугольника равен углу
другого треугольника, то их площади
относятся как произведения сторон,
заключающих равные углы.
Доказательство.
Пусть




у которых углы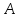

Рисунок
2.4.2
Докажем,
что:

Наложим
треугольник
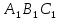
на треугольник
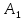
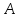
а стороны



Рисунок
2.4.3
Треугольники



поэтому

Треугольники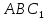


поэтому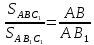

Перемножая полученные равенства, получим
Теорема
доказана.
Вторая
формула. Площадь
треугольника равна половине произведения
двух его сторон на синус угла между
ними.
Существует несколько способов
доказательства этой формулы, и я
воспользуюсь одним из них.
Доказательство.
Из
геометрии известна теорема о том, что
площадь треугольника равна половине
произведения основания на высоту,
опущенную на это основание:
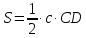
В
случае остроугольного треугольника

В случае тупого угла
Ho
а поэтому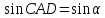
Итак, в обоих случаях
Подставив вместо
треугольника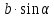
получим тригонометрическую формулу
площади треугольника:
Теорема
доказана.
Третья
формула
для площади треугольника – формула
Герона
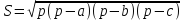
названа так в честь древнегреческого
ученого Герона Александрийского, жившего
в первом веке нашей эры. Эта формула
позволяет находить площадь треугольника,
зная его стороны. Она удобна тем, что
позволяет не делать никаких дополнительных
построений и не измерять углов. Ее вывод
основывается на второй из рассмотренных
нами формул площади треугольника и
теореме косинусов:
и

Далее
мы должны из второй формулы (теоремы
косинусов) выразить через


а затем и
Прежде
чем перейти к реализации этого плана,
заметим, что
Точно
так же имеем:
Теперь
выразим косинус через
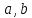

Так
как любой угол в треугольнике больше


то

Теперь
отдельно преобразуем каждый из
сомножителей в подкоренном выражении.
Имеем:
Значит,
Подставляя
это выражение в формулу для площади,
получаем:
Тема
«Площадь треугольника» имеет большое
значение в школьном курсе математики.
Треугольник – простейшая из геометрических
фигур. Он является «структурным элементом»
школьной геометрии. Подавляющее
большинство геометрических задач
сводятся к решению треугольников. Не
исключение и задача о нахождении площади
правильного и произвольного
n-угольника.[6,c.238]
Пример
2.4.1.
Чему
равна площадь равнобедренного
треугольника, если его основание

а боковая сторона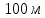
Решение:

Рисунок
2.4.4
Проведём
по свойству равнобедренного треугольника

медиана и высота. Тогда
В

теореме Пифагора:

площадь треугольника:
Ответ:
Пример
2.4.2.
В
прямоугольном треугольнике биссектриса
острого угла делит противоположный
катет на отрезки длиной 4 и 5 см. Определить
площадь треугольника.[7, c.
78]
Решение:
Пусть


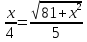
–
биссектриса). Отсюда имеем

то есть
Значит,
Рисунок
2.4.5
Ответ:
Пример
2.4.3.
Найти
площадь равнобедренного треугольника,
если его основание равно
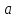
а длина высоты, проведённой к основанию,
равна длине отрезка, соединяющего
середины основания и боковой стороны.
Решение:
По
условию,
–
средняя линия
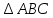
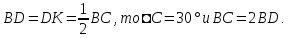
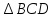


откуда
Рисунок
2.4.6
Ответ:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Параллелограмм и его свойства
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства параллелограмма:
(blacktriangleright) Противоположные стороны попарно равны;
(blacktriangleright) Диагонали точкой пересечения делятся пополам;
(blacktriangleright) Противоположные углы попарно равны, а сумма соседних равна (180^circ).
Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:
(blacktriangleright) если противоположные стороны попарно равны;
(blacktriangleright) если две стороны равны и параллельны;
(blacktriangleright) если диагонали точкой пересечения делятся пополам;
(blacktriangleright) если противоположные углы попарно равны.
Площадь параллелограмма
Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.
Задание
1
#1783
Уровень задания: Легче ЕГЭ
Периметр параллелограмма равен (100), его большая сторона равна (32). Найдите меньшую сторону параллелограмма.
Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна (100 : 2 = 50), значит, меньшая сторона параллелограмма равна (50 — 32 = 18).
Ответ: 18
Задание
2
#1784
Уровень задания: Равен ЕГЭ
Периметр параллелограмма равен (15). При этом одна сторона этого параллелограмма на (5) больше другой. Найдите меньшую сторону параллелограмма.
У параллелограмма противоположные стороны равны. Пусть (BC = AB +
5), тогда периметр параллелограмма (ABCD) равен (AB + BC + CD + AD =
AB + AB + 5 + AB + AB + 5 = 4cdot AB + 10 = 15), откуда находим (AB
= 1,25). Тогда меньшая сторона параллелограмма равна (1,25).
Ответ: 1,25
Задание
3
#273
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (BE) – высота, (BE = ED = 5). Площадь параллелограмма (ABCD) равна 35. Найдите длину (AE).
Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда (35 = BE cdot AD = 5cdot(5 + AE)), откуда находим (AE = 2).
Ответ: 2
Задание
4
#1785
Уровень задания: Равен ЕГЭ
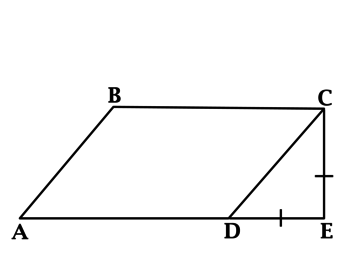
Из точки (C) параллелограмма (ABCD) опустили перпендикуляр на продолжение стороны (AD) за точку (D). Этот перпендикуляр пересёк прямую (AD) в точке (E), причём (CE = DE). Найдите (angle B) параллелограмма (ABCD). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle EDC = angle DCE). Так как (angle DEC = 90^{circ}), а сумма углов треугольника равна (180^{circ}), то (angle EDC =
45^{circ}), тогда (angle ADC = 180^{circ} — 45^{circ} =
135^{circ}). Так как в параллелограмме противоположные углы равны, то (angle B = angle ADC = 135^{circ}).
Ответ: 135
Задание
5
#1686
Уровень задания: Равен ЕГЭ
Диагональ (BD) параллелограмма (ABCD) перпендикулярна стороне (DC) и равна (4). Найдите площадь параллелограмма (ABCD), если (AD=5).
По теореме Пифагора находим: (AB^2=AD^2 — BD^2 = 25 — 16 = 9) (Rightarrow) (AB = 3). (S_{ABCD} = 4cdot3 = 12).
Ответ: 12
Задание
6
#1685
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (P_{triangle AOB} = 
(P_{triangle AOB} = AO + OB + AB), (P_{triangle AOD} = AO + OD + AD), (BO = OD) (Rightarrow) (P_{triangle AOD} — P_{triangle AOB} = AD — AB = 1), но (AD + AB = 7) (Rightarrow) (AD = 4), (AB = 3) (Rightarrow) (ADcdot AB = 12).
Ответ: 12
Задание
7
#3617
Уровень задания: Равен ЕГЭ
Стороны параллелограмма равны (9) и (15). Высота, опущенная на первую сторону, равна (10). Найдите высоту, опущенную на вторую сторону параллелограмма.
Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена. Следовательно, с одной стороны, площадь (S=9cdot 10), с другой стороны, (S=15cdot h), где (h) – высота, которую нужно найти.
Следовательно, [9cdot 10=15cdot hquadLeftrightarrowquad h=6]
Ответ: 6
Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.
Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».
Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

УСТАЛ? Просто отдохни
Ты параллелограммы многоугольники плоская геометрия широко изучается как обычные геометрические фигуры в нашей повседневной жизни. Мы определяем параллелограмм как многоугольник, имеющий противоположные стороны параллельны, характеристика, которая приводит к исключительным свойствам.
Частными случаями параллелограммов являются квадраты, прямоугольники и ромбы. Для каждого из этих многоугольников есть свои формулы для расчета площади и периметра.
Читайте тоже: Круг и окружность — геометрические фигуры с множеством особенностей
Элементы параллелограмма
Чтобы быть параллелограммом, многоугольник должны иметь параллельные противоположные стороны. В качестве специфических особенностей мы должны:
-
Каждый параллелограмм состоит из четырех сторон, а противоположные стороны равны параллели.

-
Каждый параллелограмм имеет четыре внутренних угла, а сумма этих углов всегда равен 360º.

-
У каждого параллелограмма две диагонали.

Помните, что параллелограммы частные случаи четырехугольники, поэтому есть особенности, унаследованные от этих геометрических фигур, такие как наличие двух диагоналей, четыре стороны и четыре угла, а также сумма внутреннего и внешнего углов всегда равна 360º.
Свойства параллелограмма
-
1-й объект: Противоположные стороны параллелограмма равны, то есть имеют одинаковую меру.

-
2-е свойство: Противоположные углы параллелограмма равны, а два последовательных угла всегда являются дополнительными (сумма равна 180 °).
Зная, что AB и CD параллельны, тогда стороны BC и AD поперечны AB и CD; следовательно, углы сформированные (w и x) являются дополнительными, поскольку они являются внутренними боковыми углами. Кроме того, можно показать, что углы x и z совпадают.
- 3-е свойство: Диагонали параллелограмма разрезаются пополам.
Когда мы рисуем две диагонали параллелограмма, их точка встречи делит каждую на ее середины.
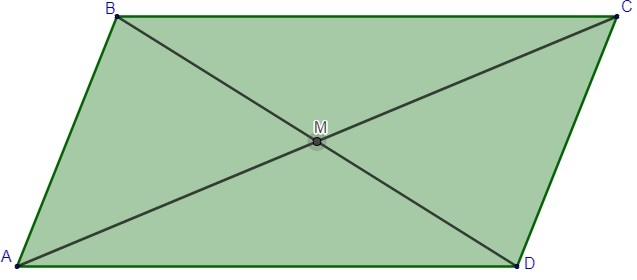
AM = см
BM = DM
Смотрите также: Точка, линия, плоскость и пространство: основные понятия геометрии
Площадь параллелограмма
Площадь параллелограмма, в общем, рассчитывается как произведение основания и высоты. Есть частные случаи (прямоугольники, ромбы и квадраты), которые имеют определенные формулы — они будут представлены в этом тексте — но вытекают из общей формы.
А = b.h
b: база
h: высота
Периметр параллелограмма
О периметр дан кем-то сумма со всех сторон. Поскольку параллелограмм обычно имеет две равные стороны, его периметр можно определить следующим образом:
п = 2 (а + б)
Частные случаи параллелограммов
Как мы знаем, по определению, чтобы быть параллелограммом, многоугольник должен иметь параллельные стороны. Есть три четырехугольника, которые рассматриваются как частные случаи параллелограмма: прямоугольник, ромб и квадрат.
-
Квадратный
мы называем квадратный четырехсторонний многоугольник с четырьмя сторонами и четырьмя равными углами — каждый угол равен точно 90 градусам. Поскольку квадрат является параллелограммом, все свойства действительны для квадрата.
Площадь квадрата и его периметр рассчитываются аналогично тому, как это делается с параллелограммом, но поскольку все стороны квадрата равны, мы можем представить площадь и периметр квадрата следующим образом:
A = l²
P = 4,1
-
Прямоугольник
О прямоугольник это параллелограмм, у которого есть все совпадающие углы. Он получил такое название, потому что все твои углы прямые, то есть четыре угла составляют 90º. Область прямоугольника идентична области параллелограмма, но мы можем рассматривать вертикальную сторону как высоту, в конце концов, она перпендикулярна основанию.
А =а.б
P = 2 (а + б)
-
Алмаз
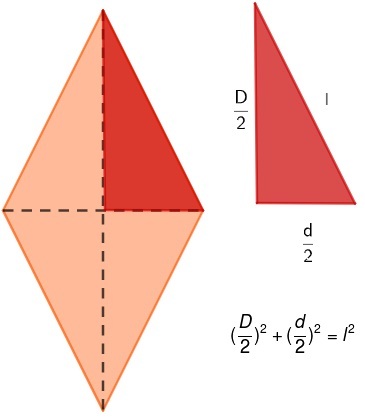
О алмаз это параллелограмм, у которого все стороны равны. Учтите, что ограничений по углам нет, они могут быть разными или нет. В отличие от предыдущих примеров, Расчет площади алмаза производится по его диагоналям. Также существует очень важная взаимосвязь между диагоналями алмаза и его стороной.
D: большая диагональ
d: малая диагональ
l: сторона
Для любого ромба мы знаем, что диагонали пересекаются в средней точке, образуя четыре прямоугольных треугольника. Анализируя один из этих треугольников, можно увидеть Пифагорейские отношения между стороной и половиной каждой из диагоналей.
Также доступ: длина окружности и площадь круга
Связь параллелограммов
Важно понимать определение параллелограмма, чтобы не было никаких сложностей при классификации. Всегда полезно помнить, что каждый параллелограмм — четырехугольник, но не каждый четырехугольник — параллелограмм.
Мы также можем утверждать, что каждый прямоугольник, каждый квадрат и каждый ромб являются параллелограммами. Более того, сравнивая частные случаи параллелограммов, мы можем увидеть другую взаимосвязь, потому что квадрат он имеет конгруэнтные углы, что является определением прямоугольника, а также конгруэнтные стороны, что является определением алмаз. Как следствие, можно сказать, что каждый квадрат — это прямоугольник, а также ромб.

решенные упражнения
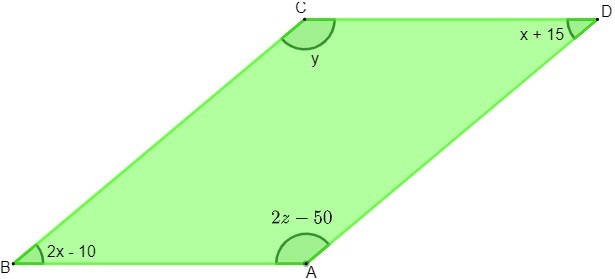
Вопрос 1 — Зная, что рисунок ниже представляет собой параллелограмм, каковы будут значения x, y и z соответственно?
а) 40,140 и 180
б) 30, 100 и 100
в) 25, 140 и 95
г) 30, 90 и 145
д) 45, 55 и 220
разрешение
1 шаг: Используя свойство параллелограмма, мы знаем, что противоположные углы равны. При анализе изображения удобнее использовать это свойство при углах при вершинах B и D, так как они имеют одно и то же неизвестное.
2-й шаг: Зная, что последовательные углы являются дополнительными и что x = 25, можно найти значение y.
3 шаг: Поскольку углы вершин C и A противоположны, они совпадают, поэтому мы можем найти значение z.
Альтернатива C.
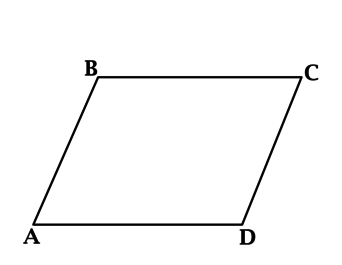
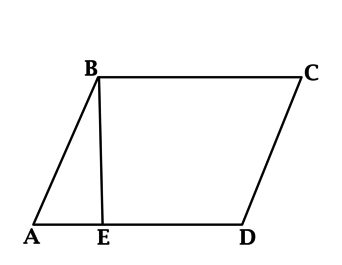
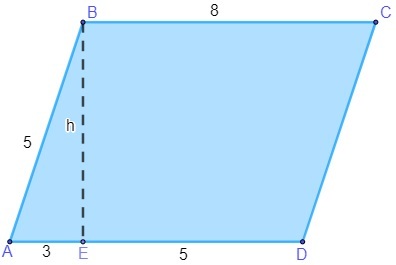
Вопрос 2 — Вычислите площадь параллелограмма (стороны, измеренные в сантиметрах) ниже.
а) 16 см²
б) 32 см²
в) 8 см²
г) 64 см²
д) 40 см²
разрешение
Чтобы найти площадь параллелограмма, сначала необходимо найти значение h. Обратите внимание, что треугольник AEB — это прямоугольник гипотенузы, равный 5, поэтому мы можем применить теорему Пифагора, чтобы найти значение h.
Альтернатива Б.
Рауль Родригес де Оливейра
Учитель математики
Источник: Бразильская школа — https://brasilescola.uol.com.br/matematica/paralelogramos.htm
| Учебный курс | Решаем задачи по геометрии |
|
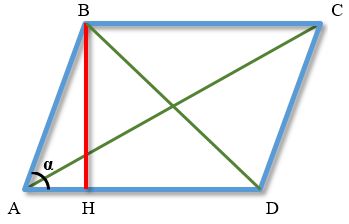
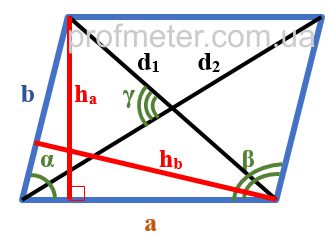
Параллелограмм — четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб. Как выглядит параллелограмм На приведенном рисунке параллелограмм обозначен синими линиями. Элементы параллелограмма, указанные на рисунке: Свойства параллелограмма
Признаки параллелограммаЧетырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий:
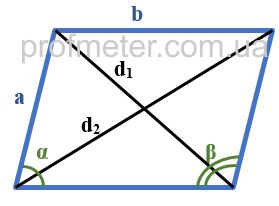
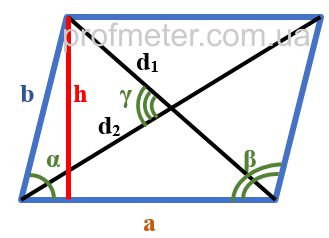
Как найти площадь параллелограмма
Как найти стороны параллелограмма
Как найти диагонали параллелограмма
Как найти периметр параллелограмма
Задачи с решениями про параллелограмм смотрите в уроках ниже:
Трапеция, описанная вокруг окружности | Описание курса | Параллелограмм. Задачи про площадь и стороны |
Обсудить на форуме
Записаться на курсы
Обратиться к консультанту
Пройти тест
Полный список курсов обучения
Бесплатные видеоуроки
Нужна информация!
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам
Формула Герона
S = √
p
(
p — a
)(
p — b
)(
p — c
)
- Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон, умноженного на синус угла между ними. - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
где S — площадь треугольника,
a, b, c
— длины сторон треугольника,
h
— высота треугольника,
γ
— угол между сторонами
a
и
b
,
r
— радиус вписанной окружности,
R — радиус описанной окружности,
|
p = |
a + b + c |
— полупериметр треугольника. |
| 2 |
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
a, b
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади параллелограмма по диагоналям и углу между ними Площадь параллелограмма равна половине произведения длин его диагоналей, умноженному на синус угла между ними.
S = 1/2d1 · d2 · sin
γ
- Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон, умноженному на синус угла между ними.
где S — Площадь параллелограмма,
a, b
— длины сторон параллелограмма,
h
— длина высоты параллелограмма,
α
— угол между сторонами параллелограмма,
- γ — угол между диагоналями параллелограмма,
- d1, d2 — длины диагоналей параллелограмма.
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
Формулы площади ромба
где S — Площадь ромба,
a
— длина стороны ромба,
h
— длина высоты ромба,
α
— угол между сторонами ромба,
d
1,
d
2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
S = a
+
b
√( p — a
)(
p — b
)(
p — a — c
)(
p — a — d
)
4| a
—
b
|
- Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высоту
где S — Площадь трапеции,a, b
— длины основ трапеции,
c, d
— длины боковых сторон трапеции,
p
=
a
+
b
+
c
+
d
— полупериметр трапеции. 2