Рассмотрим несколько задач на данную тему.
| #1 | #2 | #3 | #4 | #5 |
Задача #1
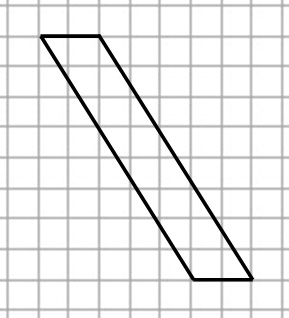
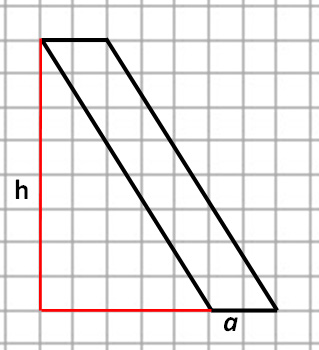
(Номер задачи на fipi.ru — 71E23E). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Прежде чем приступать к решению задачи, вспомним теорию >>
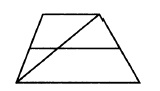
Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Площадь параллелограмма вычисляется по формуле:
где a — основание параллелограмма, h — высота параллелограмма.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 7, а высота: h = 4.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 28 ед. кв.
Задача #2
(Номер задачи на fipi.ru — 3BD9B6). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 5. Из рисунка также находим высоту параллелограмма: h = 3.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 15 ед. кв.
Задача #3
(Номер задачи на fipi.ru — 5C5046). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 5. Из рисунка также находим высоту параллелограмма: h = 4.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 20 ед. кв.
Задача #4
(Номер задачи на fipi.ru — 566A4E). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 6. Из рисунка также находим высоту параллелограмма: h = 3.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 18 ед. кв.
Задача #5
(Номер задачи на fipi.ru — 0275CC). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 6. Из рисунка также находим высоту параллелограмма: h = 6.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 36 ед. кв.
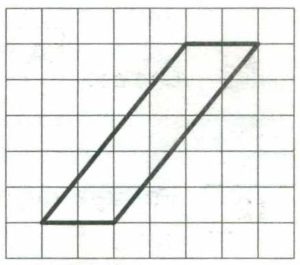
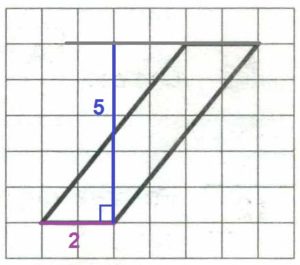
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Источник: ОГЭ 2021 Ященко 36 вариантов.
Решение:
Основание параллелограмма а = 2, высота h = 5:
Найдём его площадь:
S = a·h = 2·5 = 10
Ответ: 10.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 28
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Треугольники, четырёхугольники, многоугольники и их элементы
В 18 задании нас ждут задачи с четырехугольниками, а именно трапецией, ромбами и произвольными параллелограммами. Необходимо знать формулы вычисления площади всех вышеперечисленных четырехугольников, а также их свойства.
В демонстрационном варианте ОГЭ предлагается задание, связанное с нахождением площади фигуры.
Как найти площадь треугольника, трапеции, параллелограмма, круга и сектора?
С одной стороны, мы знаем соответствующие формулы. Для выполнения большинства заданий этого будет вполне достаточно, но иногда надо проявить и определенную сообразительность. В некоторых случаях будет разумно представить
заданную геометрическую фигуру как сумму или как разность более простых фигур. Безусловно, площадь измеряется в соответствующих единицах. Например, если длины сторон фигуры заданы в сантиметрах, то вычисляемая площадь автоматически измеряется в квадратных сантиметрах. Чтобы не загромождать условие задачи информацией, которая при ее решении фактически не используется, единицы измерения, если они не существенны, не указаны.
Ответом в задании 16 является целое число или конечная десятичная дробь.
Теория к заданию №18
Приступим к разбору теории.
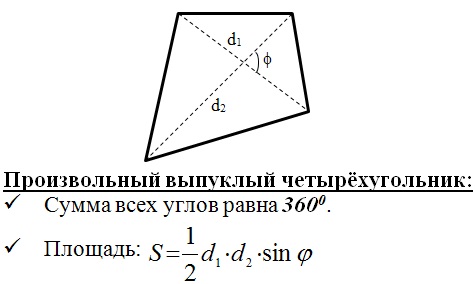
Выпуклый четырехугольник:
Правильный многоугольник:
- Правильным многоугольником называется многоугольник, у которого все стороны и углы равны между собой.
- Около всякого правильного многоугольника можно описать окружность и в него вписать окружность, причём центры этих окружностей совпадают.
Ниже я привожу формулы для вычисления элементов произвольного правильного многоугольника:
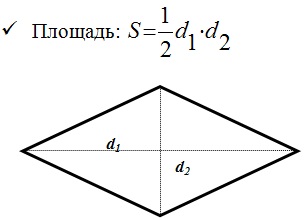
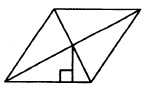
Разберем пример четырехугольника — ромб.
Параллелограмм, все стороны которого равны называется ромбом.
- Диагональ ромба является его осью симметрии.
- Диагонали взаимно перпендикулярны.
- Диагонали являются биссектрисами углов.
Трапеция:
Четырёхугольник, у которого две стороны параллельны, а другие не параллельны, называется трапецией.
Ниже я разобрал типовые примеры 11 задания. Давайте приступим к их рассмотрению.
Разбор типовых вариантов задания №18 ОГЭ по математике
Первый вариант задания
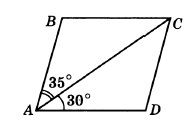
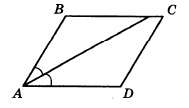
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите меньший угол параллелограмма.
Решение:
Найдем угол BAD — это сумма углов, на которые диагональ делит этот угол, поэтому:
∠BAD = 35° + 30° = 65°
Вспоминаем, что в параллелограмме противоположные углы равны, а соседние в сумме дают 180°.
Значит:
∠ABC = ∠ADC = 180 — 65 = 115°
∠BAD = ∠BCD = 65°
Так как нас просят найти меньший угол, то это 65.
Ответ: 65
Второй вариант задания
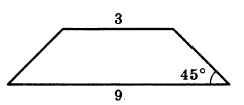
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основаниям равен 45°. Найдите площадь трапеции.
Решение:
Площадь трапеции равна произведению полусуммы оснований, умноженную на высоту. Основания нам известны из условия, необходимо самим найти высоту:
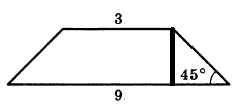
После проведения высоты, у нас получается прямоугольный треугольник. Прямоугольный — потому что высота проводится к основанию под углом 90 градусов. Один из углов равен 45°, значит, и второй тоже, так как сумма острых углов в прямоугольном треугольнике равна 90°. Следовательно, треугольник равнобедренный.
Проведя еще одну высоту, мы получим прямоугольник в центре, та с противоположной стороной, равной основанию 3.
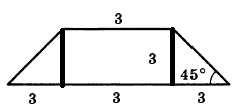
Так как трапеция равнобедренная, то и треугольники равны, значит оставшаяся длина делится пополам:
( 9 — 3 ) / 2 = 3
А так как треугольники равнобедренные, то и высота равна 3.
Отсюда можем найти площадь:
S = ( a + b ) • h / 2 = ( 3 + 9 ) • 3 / 2 = 18
Ответ: 18
Третий вариант задания
Основания трапеции равны 10 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Решение:
Средняя линия трапеции является еще и средней линией для треугольников, на которые трапецию поделила её диагональ. Средняя линия треугольника равна половине основания, поэтому отрезки, на которые делит диагональ среднюю линию, будут равны:
10 / 2 = 5
11 / 2 = 5,5
Так как нас просят найти больший из отрезков, то ответ 5,5.
Ответ: 5,5
Демонстрационный вариант ОГЭ 2019
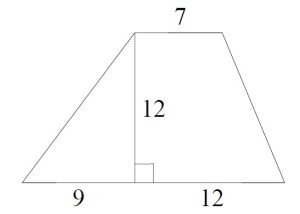
Найдите площадь трапеции, изображённой на рисунке.
Решение:
Для решения необходимо помнить и знать формулу для вычисления площади трапеции, а это
«полусумма оснований умноженная на высоту»
Непонятно, зачем нам дана информация о значениях длин отрезков, тем не менее решение выглядит так:
- Верхнее основание равно 7
- Нижнее основание равно 9 + 12 = 21
- Полусумма (21 + 7) / 2 = 14
- Высота равна 12
Таким образом, площадь равна 14 • 12 = 168 см²
Ответ: 168
Четвертый вариант задания
Сторона ромба равна 4, а расстояние от точки пересечения диагоналей ромба до неё равно 1. Найдите площадь ромба.
Решение:
Площадь ромба будем искать по формуле:
S=ah,
где a – сторона ромба, h– высота, опущенная на сторону а.
По условию а=4.
Найдем h. Для этого рассмотрим ∆ОКС и ∆АРС:
Здесь ОК || АР, причем ОК проходит через середину АС (т.к. АВСD ромб, то его диагонали в т.О делятся пополам). Значит, ОК – ср.линия ∆АРС. Поэтому АР=2ОК. Т.к. пор условию ОК=1, то АР=2·1=2. Т.о., h=АР=2.
Отсюда получаем:
S=4·1=4.
Ответ: 4
Пятый вариант задания
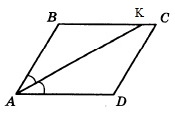
Найдите величину острого угла параллелограмма АВСD, если биссектриса угла А образует со стороной ВС угол, равный 410. Ответ дайте в градусах.
Решение:
Т.к. АК биссектриса, то углы ВАК и КАD равны. Обозначим ∠ВАК через х.
Поскольку АВСD параллелограмм, то ∠В+∠А=1800. Т.к. АК биссектриса, то ∠А=2х. Тогда ∠В=1800–2х.
Рассм. ∆АВК:
По теореме о сумме углов треуг-ка ∠ВАК+∠В+∠ВКА=1800.
По условию ∠ВКА = 410.
Отсюда получаем:
х+ 1800–2х+410=1800
х–2х=1800–1800–410
–х=–410
х=410
Значит, искомый (острый) ∠А=2·410=820
Ответ: 82
Рубрика Задание 3, Решаем ЕГЭ по математике Комментарии (0)
Задание. На клетчатой бумаге с размером клетки 1 × 1 изображен параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению его основания на высоту:
S = a·h, где a – основание, h – высота.
Длину основания и длину высоты легко подсчитать по клеточкам:
a = 2, h = 8
S = 2 · 8 = 16
Ответ: 16
Понравилось? Нажмите
Для получения максимального балла задание нужно оформлять разборчивым почерком с подробным решением. Обязательно должны присутствовать чертёж, дано и решение.
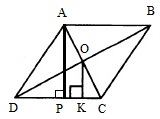
Рис. (1). Чертёж
1) Построим параллелограмм (ABCD), проведём диагональ (AC), построим окружность, вписанную в треугольник (ABC). Расстояния от точки (O) до точки (A) и прямых (AD) и (AC) соответственно равны 25, 9 и 7.
2) Сделаем дополнительные построения. Центр вписанной окружности — это точка пересечения биссектрис, поэтому (AO), (BO), (CO) — биссектрисы. Проведём касательные — (OK), (OM), (OL). Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
3) Из прямоугольного треугольника (AOK) по теореме Пифагора найдём (AK):
AK=AO2−OK2=252−72=625−49=576=24.
4) Отрезки (OK), (OM) и (OL) равны как радиусы вписанной в треугольник (ABC) окружности, то есть
OK=OM=OL=7
. Рассмотрим треугольники (ALO) и (AOK), они прямоугольные, углы (LAO) и (OAK) равны, (AO) — общая, следовательно, треугольники равны, откуда (AL=AK=) 24. Аналогично из равенства треугольников (COM) и (COK) получаем (MC=CK), а из равенства треугольников (BOL) и (BOM) — (BL=BM).
5) Площадь треугольника (ABC) можно найти как произведение радиуса вписанной окружности на полупериметр:
SABC=AB+BC+AC2⋅OK=AL+LB+BM+MC+CK+AK2⋅OK;
так как (AL=AK), (BM=LB), (MC=CK), то
SABC=2⋅AL+2BM+2MC2⋅7=2⋅24+2BM+2MC2⋅7=24+BM+MC⋅7.
6) Площадь параллелограмма равна произведению высоты на основание:
SABCD=MH⋅BC=MO+OH⋅BM+MC=16BM+MC.
7) Рассмотрим треугольники (ABC) и (ACD): (AB) равно (CD), (AD) равно (BC), углы (ABC) и (ADC) равны, следовательно, треугольники (ABC) и (ACD) равны. Поэтому площадь треугольника (ABC) равна половине площади параллелограмма:
7⋅24+BM+MC=12⋅16BM+MC⇔BM+MC=168.

SABCD=MH⋅BC=16⋅168=2688.
Ответ: 2688.
Источники:
Рис. 1. Чертёж. © ЯКласс.