Содержание:
- § 1 Понятие прямоугольного параллелепипеда
- § 2 Площадь прямоугольного параллелепипеда
§ 1 Понятие прямоугольного параллелепипеда
В этом уроке Вы познакомитесь с новым понятием – прямоугольный параллелепипед, кроме того научитесь вычислять площадь его поверхности.
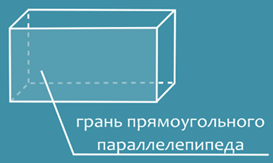
Итак, что же такое прямоугольный параллелепипед? Это такая объемная фигура, которая состоит из 6 прямоугольников, каждый из которых называют гранью прямоугольного параллелепипеда.
Многие предметы окружающие нас в повседневной жизни имеют форму параллелепипеда. Например, кирпич, спичечный коробок, дом – небоскреб прямоугольной формы, коробка из-под телевизора или системный блок компьютера, все они служат примерами прямоугольного параллелепипеда.
Таким образом:
1.Прямоугольный параллелепипед имеет 6 граней – прямоугольников.
2.Противоположные грани его попарно равны.
3.стороны граней называют ребрами параллелепипеда, а вершины граней – вершинами параллелепипеда. Всего у параллелепипеда имеется 12 ребер и 8 вершин.
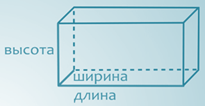
4.Любой прямоугольный параллелепипед имеет три измерения – длину, ширину, высоту. Обычно за них принимают длины трех рёбер прямоугольного параллелепипеда, имеющих общий конец, то есть выходящих из одной вершины.
Так вот, если все три измерения равны, то такой прямоугольный параллелепипед называют кубом. Поэтому, не трудно догадаться, что поверхность куба состоит из 6 равных квадратов, кроме того все 12 рёбер куба также равны.
§ 2 Площадь прямоугольного параллелепипеда
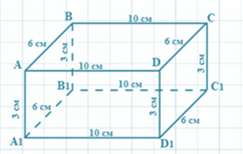
Давайте решим такую задачу. Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 3 см, 6 см и 10 см.
Решение:
Т.к. прямоугольный параллелепипед имеет 6 граней – прямоугольников, причем противоположные грани его попарно равны, то площадь поверхности прямоугольного параллелепипеда будет равна сумме площадей его 6 граней, при этом площади противоположных друг другу граней будут равны.
Поэтому найдем сначала площади граней, начнем с прямоугольника, у которого стороны равны 3 см и 6 см (помним, что таких граней в параллелепипеде две).
Для этого 3 умножим на 6, получим 18 квадратных сантиметров. Теперь перейдем к двум другим одинаковым граням – прямоугольникам, со сторонами 3 см и 10 см. Площадь каждой из них равна 3 умножить на 10, будет 30 квадратных сантиметров. Теперь осталось найти площадь каждой из двух последних одинаковых граней со сторонами 6 см и 10 см. Умножим 6 на 10, получим 60 квадратных сантиметров. Значит, площадь всей поверхности прямоугольного параллелепипеда равна 2 умножить на 18 плюс 2 умноженное на 30 плюс 2 умноженное на 60, равно 36 + 60 + 120, получится 216.
Ответ: площадь поверхности прямоугольного параллелепипеда равна двести шестнадцать квадратных сантиметров.
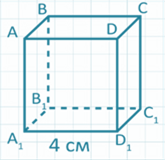
Выполним следующее задание: найти площадь поверхности куба с ребром 4 см.
Решение: так как у куба 6 граней, каждая из которых является квадратом со стороной 4 см, значит, найдем сначала площадь одной грани. Для этого 4 умножим на 4, или 4 возведем в квадрат, получим 16.
А затем 16 умножим на 6, будет 96. Ответ: площадь поверхности куба 96 квадратных сантиметров.
Таким образом, на этом уроке Вы познакомились с таким понятием как прямоугольный параллелепипед, его элементами – гранями, ребрами, вершинами. Узнали, что куб – это прямоугольный параллелепипед, у которого все измерения равны. А также научились находить площади поверхностей прямоугольного параллелепипеда и куба.
Список использованной литературы:
- Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. — М: 2013.
- Дидактические материалы по математике 5 класс. Автор — Попов М.А. – 2013г.
- Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор — Минаева С.С. – 2014г.
- Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. – 2010г.
- Контрольные и самостоятельные работы по математике 5 класс. Авторы — Попов М.А. – 2012г.
- Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009. — 270 с.:
Введение
Что общего у кирпича, коробки из-под телевизора и дома? (Рис. 1.)
Рис. 1. Кирпич, дом и коробка из-под телевизора
Можно ли понять что-то про них такое, что относится к каждому из этих предметов?
В этом и состоит задача математики: изучать нечто общее у совершенно разных вещей.
Например, мяч и глобус – шары и Земля – почти шар. (Рис. 2.)

Но вернемся к кирпичу, зданию и коробке. Как их возможно описать?
Это фигуры, ограниченные плоскостями (рис. 3). Каждая грань является прямоугольником. Все такие фигуры называются прямоугольными параллелепипедами.
Рис. 3. Грани прямоугольного параллелепипеда
По названию видно, что бывают и непрямоугольные параллелепипеды. Действительно, гранями параллелепипеда могут быть не только прямоугольники, а и произвольные параллелограммы (рис. 4).
Рис. 4. Произвольный параллелограмм
Так же, как из прямоугольника можно сделать обычный параллелограмм, так и из прямоугольного параллелепипеда легко сделать «косой параллелепипед» (рис. 5).
Рис. 5. Косой параллелепипед
Как начертить прямоугольный параллелепипед?
Сначала необходимо нарисовать ближнюю к нам сторону, стенку, грань (это прямоугольник) затем верхнюю. Рисовать надо ее чуть-чуть под углом, как будто бы смотришь на нее немного сбоку.
Теперь необходимо нарисовать правую грань. Так как все грани – это прямоугольники, то нужно следить, чтобы противоположные стороны этих граней были параллельны друг другу.
Понятно, что, глядя на настоящую объемную фигуру, невозможно увидеть ее сразу со всех сторон.
Остальные, «невидимые», стороны тоже нужны. Поэтому договорились те линии, которые не видны, рисовать пунктиром. Необходимо дорисовать их, соблюдая параллельность. (Рис. 6.)
Рис. 6. Чертеж прямоугольного параллелепипеда
Все, изображение прямоугольного параллелепипеда готово.
Элементы прямоугольного параллелепипеда
У любого прямоугольного параллелепипеда есть 8 вершин. Зачастую их обозначают ,
,
,
снизу,
,
,
,
– сверху. (Рис. 7.)
Рис. 7. Прямоугольный параллелепипед
6 прямоугольников, вершины которых совпадают с вершинами параллелепипеда, называются гранями:
На рисунке они не все выглядят как прямоугольники, это происходит потому что, мы смотрим на них не прямо, а под углом.
Еще есть отрезки ,
,
и так далее. Они являются сторонами прямоугольников, то есть граней, и называются ребрами. У любого параллелепипеда 12 ребер.
Итак, у любого параллелепипеда всегда 8 вершин, 6 граней и 12 ребер.
Многогранники. Теорема Эйлера для многогранников.
Разберемся подробнее с элементами, о которых мы поговорили: гранями, ребрами, вершинами.
Отрезок ограничен точками. Граница области на плоскости – линия или несколько отрезков.
Из отрезков и их границ (точек) на плоскости мы собираем многоугольники (треугольники, четырехугольники, … 100-угольники).
В пространстве имеем плоскости, их границы – ребра, кроме того, у ребер тоже есть граница – точки под названием вершины.
Из них можно собирать пространственные аналоги многоугольников – многогранники (рис. 1). Параллелепипед – один из примеров многогранников.
Рис. 1. Отрезок, многоугольник и многогранник
Самый «маленький» многогранник – треугольная пирамида (или тетраэдр) (рис. 2), по аналогии с самым «маленьким» многоугольником – треугольником.
Рис. 2. Тетраэдр
Интересный факт: в любом многограннике выполняется следующее свойство, где
– количество граней,
– количество вершин,
– количество ребер.
Давайте посчитаем:
1) Тетраэдр: 4 вершины, 4 грани и 6 ребер.
Рис. 3. Тетраэдр
2) Параллелепипед: 8 вершин, 6 граней и 12 ребер.
Рис. 4. Параллелепипед
3) Пятиугольная призма: 10 вершин, 7 граней и 15 ребер
Рис.5. Пятиугольная призма
Количество вершин и граней вместе всегда на 2 больше, чем количество ребер. И это свойство выполняется для всех многогранников. Это свойство сформулировал Леонард Эйлер в свое время. Свойство так и назвали: Теорема Эйлера.
,
где:
– количество граней,
– количество вершин,
– количество рёбер.
Грани прямоугольного параллелепипеда
У прямоугольного параллелепипеда все грани (их 6) являются прямоугольниками. Все ли эти прямоугольники разные? Конечно, нет.
Держа коробку в руках, можно заметить, что противоположные грани равны, то есть это совершенно одинаковые прямоугольники.
Например, передняя грань равна задней. Точно так же равны друг другу верхняя и нижняя грани, левая и правая.
А есть ли равные ребра?
Да, конечно, можно увидеть, что вертикальные ребра, их 4, все равны друг другу. Аналогично есть еще две четверки равных ребер.
Площадь поверхности прямоугольного параллелепипеда
Вопрос: если нужно склеить такой параллелепипед из бумаги, то сколько бумаги необходимо? И как необходимо клеить прямоугольный параллелепипед или другой многогранник?
Сначала нужно сделать развертку прямоугольного параллелепипеда (рис. 8).
Рис. 8. Развертка прямоугольного параллелепипеда
Уже видно на ней 6 граней, попарно равных друг другу. Если согнуть ее по линиям, то получится прямоугольный параллелепипед.
Площадь этой развертки – это то количество бумаги, которое необходимо. Она называется площадью поверхности. Очевидно, она равна сумме площадей всех шести граней.
Теперь можно вывести формулу площади поверхности прямоугольного параллелепипеда.
Три ребра, исходящих из одной вершины, могут иметь разную длину. Пусть они будут обозначены ,
, и
. (Рис. 9.)
Рис. 9. Прямоугольный параллелепипед со сторонами ,
, и
Все остальные ребра равны какому-нибудь из этих значений. Необходимо найти площади всех граней и сложить.
Площадь нижней грани равна , так это прямоугольник. Верхняя грань точно такая же, ее площадь тоже равна
. Правая и левая грани имеют площади
каждая. Передняя и задняя –
каждая.
Складывая все эти площади, получаем площадь поверхности:
Задача
Сколько необходимо краски для покраски картонной коробки, если высота, ширина и длина коробки составляют 20, 30 и 60 см соответственно? Расход краски составляет 1 г на каждые 100 см2.
Решение
Какую площадь надо покрасить? Очевидно, это площадь поверхности коробки, ведь красить мы будем ее поверхность.
Найдем площадь поверхности коробки. Коробка – это прямоугольный параллелепипед. Площадь поверхности – это сумма площадей всех граней, причем грани попарно равны.
Расход краски – 1 г на 100 см2. Чтобы найти необходимое количество краски, делим общую площадь на 100:
Получается, что необходимо 72 грамма краски, чтобы покрасить коробку.
Вывод
На данном уроке был изучен прямоугольный параллелепипед, его основные свойства и элементы. Кроме того, была выведена формула его поверхности и решена задача на применение данной формулы.
Список литературы
1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия, 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс – ЗШ МИФИ, 2011.
5) Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. – ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. – Просвещение, 1989.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Портал «Знайка» (Источник)
2. Портал «Первое сентября» (Источник)
3. Портал «Презентации для школьников» (Источник)
Домашнее задание
1. Сколько краски надо, чтобы покрасить кубик с высотой, шириной и длиной 20, 45 и 60 см соответственно? Расход краски составляет 5 грамм на каждые 100 см2.
На этом уроке мы узнаем, какую фигуру называют
прямоугольным параллелепипедом. Рассмотрим, какими измерениями обладает данная
фигура. А также рассмотрим некоторые свойства прямоугольного параллелепипеда.
Нас окружают тела. Они имеют самую разнообразную
форму. В математике, прежде всего, изучают некоторый определённый набор тел
стандартной формы. Посмотрите на экран.
Это такие фигуры как призма, цилиндр, шар,
пирамида и конус. Каждую из этих фигур мы рассмотрим в будущем, а
сегодня же мы остановимся на рассмотрении призмы, или конкретно – прямоугольного
параллелепипеда.
Представление о прямоугольном параллелепипеде
дают, например,
Обратите внимание на экран.
Здесь на первом рисунке изображён прямоугольный
параллелепипед, а на втором рисунке – его математическое
представление – изображение.
Определение
Поверхность прямоугольного параллелепипеда состоит
из 6 прямоугольников, каждый из которых
называют гранью прямоугольного параллелепипеда. Стороны этих
прямоугольников называются рёбрами, а вершины прямоугольников – вершинами
прямоугольного параллелепипеда.
Заметьте, прямоугольный параллелепипед
имеет 6 граней, 12
рёбер и 8 вершин.
Посмотрите, на экран.
Здесь изображён прямоугольный параллелепипед, его
противоположные грани не имеют общих точек, они равны между собой. Запомните,
противоположные грани прямоугольного параллелепипеда равны.
Определение
Нижнюю и верхнюю грани прямоугольного
параллелепипеда называют его основаниями, остальные грани – боковыми
гранями.
Названия «нижняя грань», «верхняя грань», «боковая
грань» условны.
Например
На экране изображён один и тот же параллелепипед, а
его верхние грани на рисунках различны.
В каждой вершине прямоугольного параллелепипеда
сходятся 3 ребра. Такие рёбра называют длиной,
шириной и высотой прямоугольного параллелепипеда.
Вместе их называют измерениями параллелепипеда.
Названия «длина», «ширина» и «высота»
также условны.
На рисунке изображён один и тот же прямоугольный
параллелепипед, а его высотой, например, названы разные рёбра.
Определение
Прямоугольный параллелепипед, у которого все рёбра
равны, называется кубом.
Все грани куба – равные между собой квадраты.
Поэтому поверхность куба состоит из 6 равных
квадратов.
Тело имеет разные свойства. Одним из них
является масса, которую находят с помощью весов. Другим свойством тела является
площадь поверхности.
Обозначим измерения прямоугольного
параллелепипеда таким образом: a –
его длина, b – ширина и c –
высота. Тогда с помощью этих обозначений запишем формулу площади поверхности
прямоугольного параллелепипеда:
Что хорошо видно из развёртки поверхности
прямоугольного параллелепипеда на плоскость.
Если ребро куба равно а,
то его поверхность состоит из 6 одинаковых
квадратов, каждый из которых имеет сторону длиной а.
Поэтому площадь поверхности куба можно записать так:
Итоги
Итак, сегодня на уроке мы узнали, какую фигуру
называют прямоугольным параллелепипедом. Рассмотрели, какими измерениями
обладает данная фигура, а также рассмотрели его свойства.
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.
- Формула вычисления площади
- Пример задачи
Формула вычисления площади
Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:
S = 2 (ab + bc + ac)
Формула получена следующим образом:
- Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
- два основания: со сторонами a и b;
- четыре боковые грани: со стороной a/b и высотой c.
- Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).
Пример задачи
Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.
Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см2.