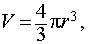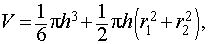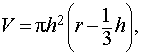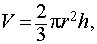Содержание
- Сфера и шар. Площади сферы и ее частей. Объемы шара и его частей
- Шар, сфера и их части
- Площади сферы и ее частей. Объемы шара и его частей
- Шар и сфера, их сечения
- Урок 40. Подготовка к ЕГЭ по математике
- В данный момент вы не можете посмотреть или раздать видеоурок ученикам
- Получите невероятные возможности
- Конспект урока «Шар и сфера, их сечения»
Сфера и шар. Площади сферы и ее частей. Объемы шара и его частей
Шар, сфера и их части
Введем следующие определения, связанные с шаром, сферой и их частями.
Определение 1. Сферой с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O равно r (рис. 1).
Определение 2. Шаром с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).
Таким образом, сфера с центром в точке O и радиусом r является поверхностью шара с центром в точке O и радиусом r.
Замечание. Радиусом сферы ( радиусом шара ) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы ( радиусом шара ).
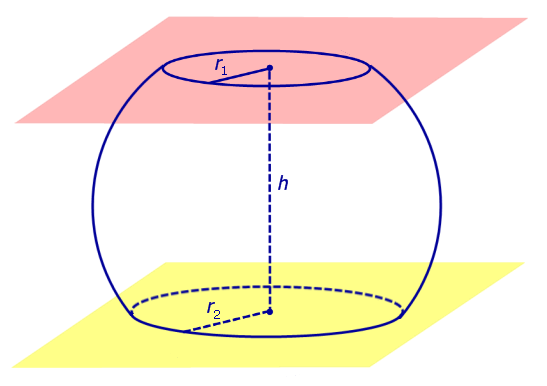
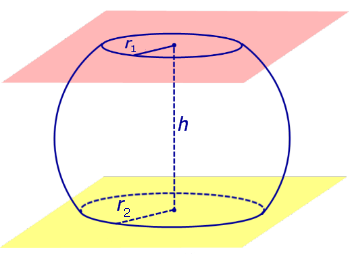
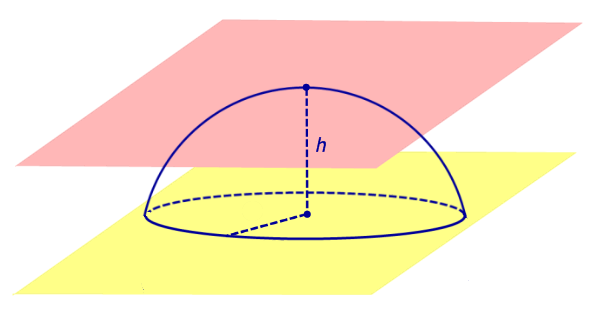
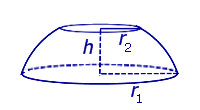
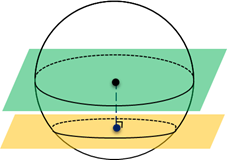
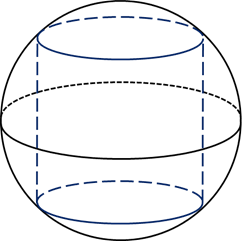
Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Определение 4. Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.
Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.
Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.
Высотой шарового слоя называют расстояние между плоскостями расстояние между плоскостями оснований шарового слоя .
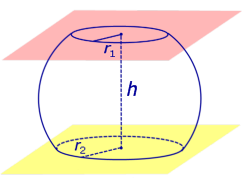
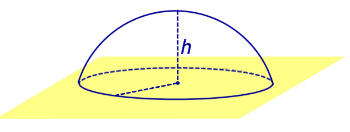
Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).
Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).
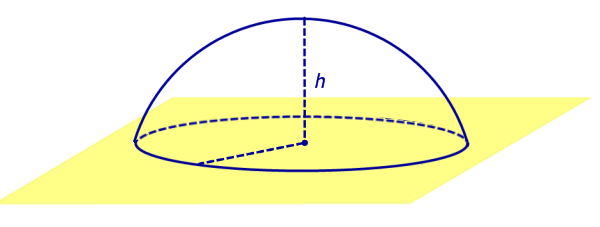
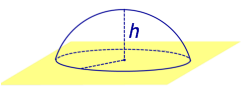
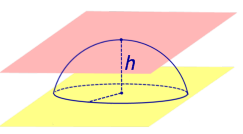
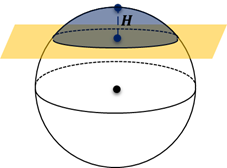
Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс, у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.
Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4). Высоту такого шарового слоя называют высотой шарового сегмента .
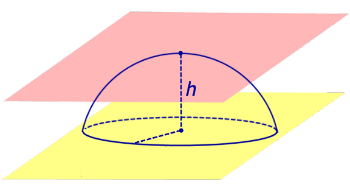
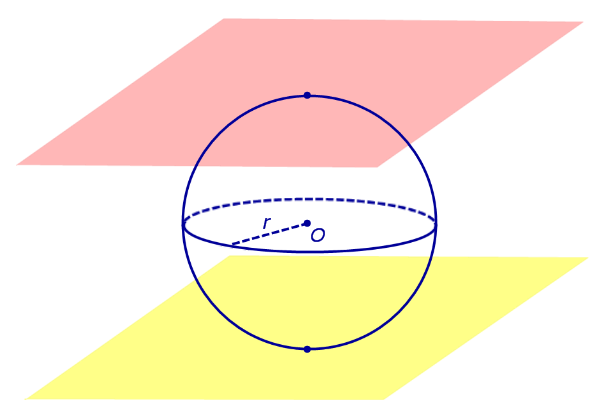
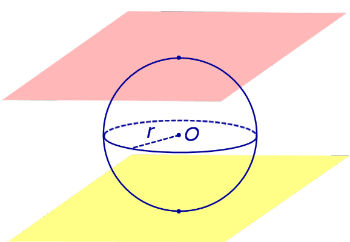
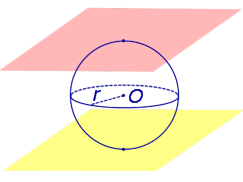
По той же причине всю сферу можно рассматривать как сферический пояс, у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).
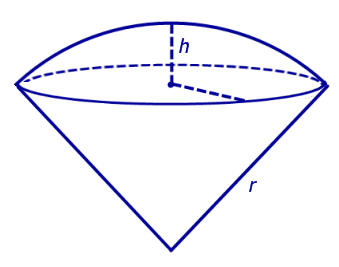
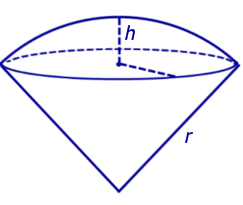
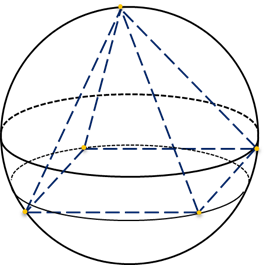
Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).
Площади сферы и ее частей. Объемы шара и его частей
В следующей таблице приведены формулы, позволяющие вычислить объем шара и объемы его частей, а также площадь сферы и площади ее частей.
Площадь сферического пояса не зависит от радиусов r1 и r2 !
Шар
Сферический пояс
Площадь сферического пояса:
Площадь сферического пояса не зависит от радиусов r1 и r2 !
Источник
Шар и сфера, их сечения
Урок 40. Подготовка к ЕГЭ по математике
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет.
Получите невероятные возможности
Конспект урока «Шар и сфера, их сечения»
Напомним, что шаром называется тело, состоящее из всех точек пространства, находящихся на расстоянии не большем заданного от некоторой данной точки. Эта точка – центр шара, а заданное расстояние – радиус шара.
Шар так же, как цилиндр и конус, является телом вращения. Он получается в результате вращения полукруга вокруг его диаметра.
Поверхность, образуемая при этом вращении полуокружности, называется сферой. Можно сказать, что сфера – это как бы оболочка, или граница, шара. Как окружность есть граница круга, так и сфера – это граница шара.
Назовём элементы сферы и шара.
Радиус сферы – это отрезок, соединяющий центр сферы и любую её точку.
Хорда сферы – отрезок, соединяющий две точки сферы.
Диаметр сферы – хорда сферы, проходящая через её центр.
Радиус, хорда, диаметр шара – это радиус, хорда, диаметр его сферы.
Любое сечение шара плоскостью есть круг. Центром этого круга является основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Плоскость, которая проходит через центр шара, называется диаметральной плоскостью. Сечение ею шара – большим кругом, а сечение сферы – большой окружностью.
Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.
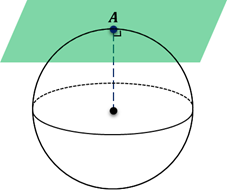
Плоскость, проходящая через точку А сферы и перпендикулярно радиусу, проведённому в эту точку, называется касательной плоскостью. Точка А называется точкой касания.
Свойство касательной плоскости к сфере: радиус сферы, проведённый в точку касания, перпендикулярен касательной плоскости.
Признак касательной плоскости к сфере: плоскость, перпендикулярная радиусу сферы в конечной его точке на сфере, является касательной к сфере.
Касательная плоскость пересекается с шаром в единственной точке – в точке касания.
Касательной прямой к сфере (шару) называется прямая, имеющая со сферой единственную общую точку.
Отрезки касательных к сфере, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр сферы.
Линией пересечения двух сфер является окружность.
Площадь сферы радиуса 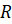
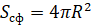
Объём шара радиуса 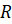
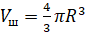
Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Площадь боковой поверхности шарового сегмента:
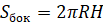
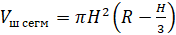
где 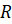
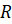
Шаровым сектором называется тело, которое получается из шарового сегмента и конуса, основанием которого является сечение плоскостью данного шара.
Площадь боковой поверхности шарового сектора:
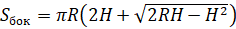
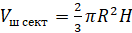
где 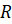
Шар называется вписанным в многогранник, а многогранник – описанным около шара, если поверхность шара касается всех граней многогранника.
Шар называется описанным около многогранника, а многогранник – вписанным в шар, если поверхность шара проходит через все вершины многогранника.
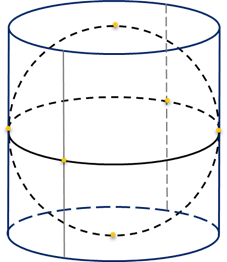
Шар называется вписанным в цилиндр, а цилиндр – описанным около шара, если поверхность шара касается оснований цилиндра и всех образующих.
Шар называется описанным около цилиндра, если окружности оснований цилиндра принадлежат поверхности шара.
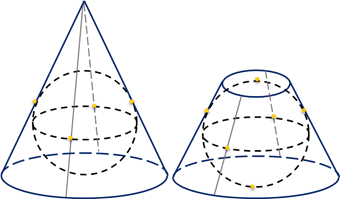
Шар называется вписанным в конус (усечённый конус), а конус (усечённый конус) – описанным около шара, если поверхность шара касается основания (оснований) конуса и всех образующих.
Шар называется описанным около конуса (усечённого конуса), если окружность основания и вершина (окружности оснований) конуса принадлежат поверхности шара.
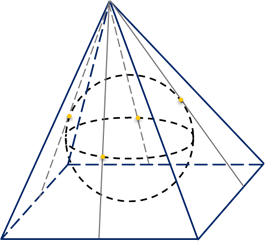
Если боковые грани пирамиды одинаково наклонены к плоскости основания, то в такую пирамиду можно вписать шар.
Около пирамиды можно описать шар тогда и только тогда, когда около её основания можно описать окружность.
Если боковые рёбра пирамиды равны между собой (или одинаково наклонены к плоскости основания), то около такой пирамиды можно описать шар.
В призму можно вписать шар тогда и только тогда, когда в перпендикулярное сечение этой призмы можно вписать окружность, а высота призмы равна диаметру окружности, вписанной в это перпендикулярное сечение.
Описать шар около призмы можно тогда и только тогда, когда призма прямая и около её основания можно описать окружность.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задача первая. Радиус шара увеличили в 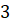
Задача вторая. Объём шара равен 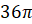
Задача третья. Шар пересечен плоскостью. Площадь сечения равна 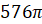
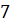
Задача четвёртая. В конус с радиусом основания, равным 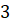
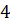
Задача пятая. Найдите объём шарового сектора, если радиус окружности его основания равен 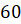
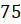
Задача шестая. Шар с радиусом 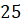
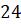
Источник
Как найти площадь сечения шара
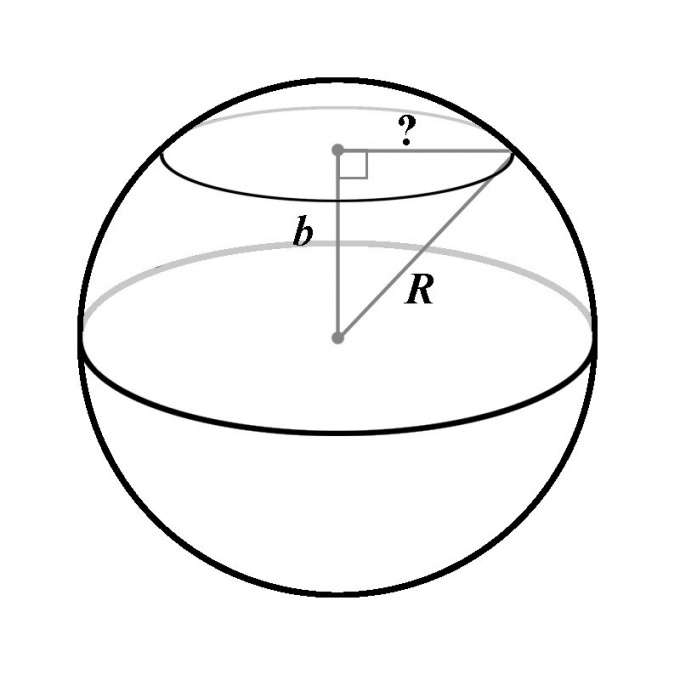
Пусть дан шар с радиусом R, который на некотором расстоянии b от центра пересекает плоскость. Расстояние b меньше или равно радиусу шара. Требуется найти площадь S получающегося при этом сечения.
Инструкция
Очевидно, что если расстояние от центра шара до плоскости равно радиусу плоскости, то плоскость касается шара только в одной точке, и площадь сечения будет равна нулю, то есть если b = R, то S = 0. Если b = 0, то секущая плоскость проходит через центр шара. В этом случае сечение будет представлять собой круг, радиус которого совпадает с радиусом шара. Площадь этого круга будет, согласно формуле, равна S = πR^2.
Эти два крайних случая дают границы, между которыми всегда будет лежать искомая площадь: 0 < S < πR^2. При этом любое сечение шара плоскостью всегда является кругом. Следовательно, задача сводится к тому, чтобы найти радиус окружности сечения. Тогда площадь этого сечения вычисляется по формуле площади круга.
Поскольку расстояние от точки до плоскости определяется как длина отрезка, перпендикулярного плоскости и начинающегося в точке, второй конец этого отрезка будет совпадать с центром окружности сечения. Такой вывод вытекает из определения шара: очевидно, что все точки окружности сечения принадлежат сфере, а следовательно, лежат на равном расстоянии от центра шара. Это значит, что каждая точка окружности сечения может считаться вершиной прямоугольного треугольника, гипотенузой которого служит радиус шара, одним из катетов — перпендикулярный отрезок, соединяющий центр шара с плоскостью, а вторым катетом — радиус окружности сечения.
Из трех сторон этого треугольника заданы два — радиус шара R и расстояние b, то есть гипотенуза и катет. По теореме Пифагора длина второго катета должна быть равна √(R^2 — b^2). Это и есть радиус окружности сечения. Подставляя найденное значение радиуса в формулу площади круга, легко прийти к выводу, что площадь сечения шара плоскостью равна:S = π(R^2 — b^2).В частных случаях, когда b = R или b = 0, выведенная формула полностью согласуется с уже найденными результатами.
Видео по теме
Источники:
- сечение шара плоскостью
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Площадь сечения шара
Шар — это геометрическое тело, представляющее собой совокупность всех точек пространства, находящихся от его центра на заданном расстоянии. Основной математической характеристикой шара является его диаметр.
Сечение шара — это изображение фигуры, образованной рассечением шара плоскостью в поперечном или продольном направлении.
Формула для расчета площади осевого сечения шара:
S = π * d 2 / 4, где
d — осевой диаметр шара.
Формула для расчета площади сечения шара плоскостью:
S = π * d 2 / 4, где
d — диаметр окружности шара в этой плоскости.
Смотрите также статью о всех геометрических фигурах (линейных 1D, плоских 2D и объемных 3D).
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета площади сечения шара, если известен диаметр шара. С помощью этого калькулятора вы в один клик сможете рассчитать площадь сечения шара через любую плоскость сечения (площадь осевого сечения шара и площадь сечения шара плоскостью).
Формула площади сечения шара плоскостью
Шар – это геометрическое тело, представляющее собой совокупность всех точек пространства, находящихся от его центра на заданном расстоянии. Основной математической характеристикой шара является его диаметр.
Сечение шара – это изображение фигуры, образованной рассечением шара плоскостью в поперечном или продольном направлении.
Формула для расчета площади осевого сечения шара:
S = π * d 2 / 4, где
d – осевой диаметр шара.
Формула для расчета площади сечения шара плоскостью:
S = π * d 2 / 4, где
d – диаметр окружности шара в этой плоскости.
Смотрите также статью о всех геометрических фигурах (линейных 1D, плоских 2D и объемных 3D).
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета площади сечения шара, если известен диаметр шара. С помощью этого калькулятора вы в один клик сможете рассчитать площадь сечения шара через любую плоскость сечения (площадь осевого сечения шара и площадь сечения шара плоскостью).
- Попроси больше объяснений
- Следить
- Отметить нарушение
Что ты хочешь узнать?
Ответ
Проверено экспертом
Ответ: πR²cos²α
Объяснение:
Отрезок, соединяющий центр шара с центром сечения, перпендикулярен плоскости сечения, значит
О₁А = ОА · cosα = R · cosα
O₁A – радиус сечения. Сечение – круг. Площадь сечения:
Sсеч = π · O₁A² = πR²cos²α
Урок 40. Подготовка к ЕГЭ по математике
Конспект урока «Шар и сфера, их сечения»
Напомним, что шаром называется тело, состоящее из всех точек пространства, находящихся на расстоянии не большем заданного от некоторой данной точки. Эта точка – центр шара, а заданное расстояние – радиус шара.
Шар так же, как цилиндр и конус, является телом вращения. Он получается в результате вращения полукруга вокруг его диаметра.
Поверхность, образуемая при этом вращении полуокружности, называется сферой. Можно сказать, что сфера – это как бы оболочка, или граница, шара. Как окружность есть граница круга, так и сфера – это граница шара.
Назовём элементы сферы и шара.
Радиус сферы – это отрезок, соединяющий центр сферы и любую её точку.
Хорда сферы – отрезок, соединяющий две точки сферы.
Диаметр сферы – хорда сферы, проходящая через её центр.
Радиус, хорда, диаметр шара – это радиус, хорда, диаметр его сферы.
Любое сечение шара плоскостью есть круг. Центром этого круга является основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Плоскость, которая проходит через центр шара, называется диаметральной плоскостью. Сечение ею шара – большим кругом, а сечение сферы – большой окружностью.
Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.
Плоскость, проходящая через точку А сферы и перпендикулярно радиусу, проведённому в эту точку, называется касательной плоскостью. Точка А называется точкой касания.
Свойство касательной плоскости к сфере: радиус сферы, проведённый в точку касания, перпендикулярен касательной плоскости.
Признак касательной плоскости к сфере: плоскость, перпендикулярная радиусу сферы в конечной его точке на сфере, является касательной к сфере.
Касательная плоскость пересекается с шаром в единственной точке – в точке касания.
Касательной прямой к сфере (шару) называется прямая, имеющая со сферой единственную общую точку.
Отрезки касательных к сфере, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр сферы.
Линией пересечения двух сфер является окружность.
Площадь сферы радиуса Объём шара радиуса 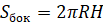
Объём шарового сегмента:
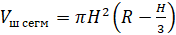
где
Шаровым сектором называется тело, которое получается из шарового сегмента и конуса, основанием которого является сечение плоскостью данного шара.
Площадь боковой поверхности шарового сектора:
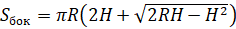
Объём шарового сектора:
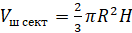
где
Шар называется вписанным в многогранник, а многогранник – описанным около шара, если поверхность шара касается всех граней многогранника.
Шар называется описанным около многогранника, а многогранник – вписанным в шар, если поверхность шара проходит через все вершины многогранника.
Шар называется вписанным в цилиндр, а цилиндр – описанным около шара, если поверхность шара касается оснований цилиндра и всех образующих.
Шар называется описанным около цилиндра, если окружности оснований цилиндра принадлежат поверхности шара.
Шар называется вписанным в конус (усечённый конус), а конус (усечённый конус) – описанным около шара, если поверхность шара касается основания (оснований) конуса и всех образующих.
Шар называется описанным около конуса (усечённого конуса), если окружность основания и вершина (окружности оснований) конуса принадлежат поверхности шара.
Если боковые грани пирамиды одинаково наклонены к плоскости основания, то в такую пирамиду можно вписать шар.
Около пирамиды можно описать шар тогда и только тогда, когда около её основания можно описать окружность.
Если боковые рёбра пирамиды равны между собой (или одинаково наклонены к плоскости основания), то около такой пирамиды можно описать шар.
В призму можно вписать шар тогда и только тогда, когда в перпендикулярное сечение этой призмы можно вписать окружность, а высота призмы равна диаметру окружности, вписанной в это перпендикулярное сечение.
Описать шар около призмы можно тогда и только тогда, когда призма прямая и около её основания можно описать окружность.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задача первая. Радиус шара увеличили в 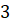
Задача вторая. Объём шара равен 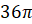
Задача третья. Шар пересечен плоскостью. Площадь сечения равна 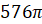
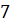
Задача четвёртая. В конус с радиусом основания, равным
Задача пятая. Найдите объём шарового сектора, если радиус окружности его основания равен
Урок 26 Бесплатно Шар
Обратите внимание на предметы, изображенные на рисунке:
Давайте подумаем, что же их может объединять?
Очевидно, что цвет и фактура у этих объектов различна, но если вы обратите внимание на форму, то заметите явное сходство.
В математике (геометрии) важную роль при описании и представлении тела играет его геометрическая форма.
Все представленные объекты на рисунке объемные тела (т.е. их в реальности можно посмотреть и потрогать со всех сторон).
Отметим еще одну важную общую черту: у всех изображенных объектов отсутствуют углы (т.е. в действительности они шарообразной, или еще называют: сферической формы, их свободно можно покатать в любые стороны).
Давайте же разберемся, что такое шар, а что называют сферой.
Определим, какими элементами описывают данные геометрические фигуры, какими они свойствами обладают.
Узнаем, как определить площадь сферы, объем круга и рассмотрим примеры решения задач.
Шар и сфера
Шар — это множество точек пространства, равноудаленных от некоторой заданной точки — центра шара.
Сфера — это поверхность шара (оболочка). Сфера внутри полая.
Примеры сфер: мыльный пузырь, мяч, глобус. Эти тела состоят из оболочки, но внутри пустые.
Можно сказать, что шар — это геометрическое тело, ограниченное сферой (шаровой поверхностью).
Шар внутри заполнен.
Примеры шаров: арбуз, пушечное ядро, бильярдный шар. Эти тела заполненные внутри.
Центр шара (сферы) — это точка, которая находится на одинаковом расстоянии (равноудаленная) от любой точки, находящейся на шаровой поверхности.
Центр шара (сферы) обозначают обычно заглавной буквой О.
Сфера и шар пространственные фигуры, но определяются такими же элементами, что и окружность, и круг на плоскости.
Радиус шара— это отрезок, соединяющий точку поверхности шара (шаровой поверхности) с его центром.
Радиус обозначается строчной латинской буквой r или заглавной R.
Для шара можно провести столько же радиусов, сколько точек имеет поверхность шара, при этом все эти радиусы равны.
Диаметром шара называют отрезок, проходящий через центр шара и соединяющий две точки шаровой поверхности.
Обычно диаметр обозначают строчной латинской буквой d или заглавной D.
По величине диаметр равен двум радиусам, лежащим на одной прямой.
d = 2r
Следовательно, радиус — это половина диаметра.
r = d : 2
Точки сферы, являющиеся концами диаметра сферы, называют диаметрально противоположными.
Для сферы характерны те же элементы, которые используют для описания шара.
При построении изображений пространственных (объемных) фигур на листе бумаги или иной плоской поверхности, приходится рисовать рисунок так, чтобы он казался объемным- для этого линии, которые не видны глазу человека, изображают штрихпунктирной линией.
Рассмотрим, как выглядят шар, сфера и элементы, их характеризующие, на плоскости.
Сфера и шар- это фигуры вращения.
Подобно секущей прямой для круга, для шара существует секущая плоскость.
Рассмотрим, как могут быть расположены по отношению друг к другу плоскость и шар (сфера) в пространстве:
1. Если расстояние от центра шара (сферы) до плоскости больше длины радиуса шара (сферы), то шар (сфера) и плоскость не имеют ни одной общей точки.
Отрезок ОМ = r — это радиус шара.
Отрезок ОА = m — это расстояние от центра шара (сферы) до плоскости
Для данного случая m > r
2. Если расстояние от центра шара (сферы) до плоскости равно длине радиуса шара (сферы), то шар (сфера) и плоскость имеют единственную общую точку.
Отрезок ОМ = r — это радиус шара.
Отрезок ОА = m — это расстояние от центра шара (сферы) до плоскости
Для данного случая m = r
Точка А общая для плоскости сечения и шара
3. Если расстояние от центра шара (сферы) до плоскости меньше длины радиуса, то плоскость пересекает шар (сферу).
Отрезок ОМ = r — это радиус шара.
Отрезок ОА = m — это расстояние от центра шара (сферы) до плоскости (mathbf)
Для данного случая m < r
Сечение шара плоскостью представляет круг.
Представить мы можем это на примере апельсина, разрезанного на две части.
Сечением сферы плоскостью является окружность.
Такое сечение мы можем представить, если разрезать теннисный мяч
Отсеченная плоскостью часть шара называется шаровым сегментом.
Отсеченную плоскостью часть сферы называют сферическим сегментом.
Если плоскость сечения проходит через центр шара (сферы), то сечением шара (сферы) является самый большой круг (окружность), а радиус круга (окружности) является радиусом самого шара (сферы).
В таком случае шар (сфера) делится на два равных сегмента (две равные части).
Чем дальше проходит секущая плоскость от центра шара (сферы), тем меньше радиус сечения.
Обратите внимание на рисунок:
Сечение шара с радиусом сечения r является самым большим кругом, а радиус круга является радиусом самого шара.
Сечение шара с радиусом сечения r1 находится дальше от центра шара, чем сечение шара с радиусом сечения r2 Мы можем заметить на рисунке что r2 > r1
Сечения шара (сферы), удаленные на равные расстояния от центра, имеют равные радиусы:
Сечение шара с радиусом сечения r2 и сечение шара с радиусом сечения r3 удаленные на равные расстояния от центра шара, имеют равные радиусы (r2 = r3)
Сфера и шар- фигуры вращения
Шар образуется вращением полукруга около его неподвижного диаметра- оси шара.
Сфера является фигурой вращения, образованной при вращении полуокружности вокруг своего неподвижного диаметра.
АВ— это ось вращения шара (сферы).
У меня есть дополнительная информация к этой части урока!
Во все времена к шару и сфере относились с большим интересом.
Удивительно совершенные формы шара и сферы издавна привлекали ученых, философов, мыслителей, которые с помощью сферы и шара пытались объяснить гармонию создания и существования окружающего мира.
Так, например, поражало то, что шар имеет точку равновесия в любой точке своей поверхности, в отличие от других пространственных геометрических фигур.
А при равных объемах площадь сферической поверхности меньше площади любого другого отличного по форме геометрического тела.
Многие ученые, философы, астрономы занимались изучением объектов сферической и шарообразной формы и объяснением их свойств.
В XI веке древнегреческий математик Евклид в знаменитом теоретическом трактате по математике «Начала» в своих рассуждениях открыл многое об объемных телах. Так, например, он определил и описал шар как фигуру вращения, образованную вращением полукруга вокруг неподвижного диаметра.
Позже древнегреческий физик-математик Архимед вычислил площадь поверхности шара, объем шара и его сегментов
Пройти тест и получить оценку можно после входа или регистрации
Площадь сферы, объем шара
Если посмотреть вокруг, мы можем заметить множество объектов, имеющих или принимающих форму шара (сферы).
Так, например, падающая микроскопическая капля дождя или капля жидкости, находящаяся в невесомости, принимают форму шара.
Это происходит потому, что давление вокруг жидкости и в самой жидкости примерно равны (т.е. со всех сторон давление на каплю одинаковое), в результате получается шарообразная форма.
Сферической формой обладают мыльные пузыри или пузыри в воде.
Происходит это благодаря поверхностному натяжению, свойственному жидкостям (своего рода, «невидимая» оболочка жидкости).
Силы поверхностного натяжения стремятся придать мыльному пузырю оптимальную форму, а этой формой и является шар, так как в шарообразной форме воздух внутри пузыря равномерно давит на все участки его внутренней стенки.
Многие ягоды и фрукты, икринки рыбы, жемчужины и др. в природе являются обладателями шарообразных и сферических форм.
Представления о планетах и небесных телах, молекулах и некоторых элементарных частицах в связи с определенными свойствами и поведением сводятся к модели шара и сферы.
Существует множество примеров использования свойств и характеристик шара (сферы) в науке, технике и производстве.
У меня есть дополнительная информация к этой части урока!
Например, резервуары для хранения легковоспламеняющихся жидкостей, различных видов газа и т.п. имеют сферическую форму.
Шаровая форма емкостей является наиболее экономически выгодной для хранения легковоспламеняющихся продуктов, так как сферическая форма резервуара обеспечивает равномерное распределение напряжения внутреннего давления на стенки металлической сферы, минимизируя опасность взрыва.
Преимущество шаровых резервуаров еще в том, что они имеют минимальную площадь поверхности, по сравнению с цилиндрическими резервуарами такого же объема.
Сферические формы применяют в шаровых подшипниках, используемых для обеспечения свободного вращения, качения, перемещения с минимальным сопротивлением, без последствий износа деталей и их разрушений (например, в автомобилях, бытовой технике, спортивном инвентаре).
Металлические шарики в этом устройстве самый основной элемент, сферическая форма позволяет им вращаться свободно во всевозможных направлениях.
Так как они идеально гладкой сферической формы, то у них очень маленькая площадь контакта, что обеспечивает беспрепятственное вращение.
Подобные свойства шарообразных тел применяется в шариковой ручке.
Она состоит из стержня, откуда поступают густые чернила. На конце рцучкинаходится наконечник (пишущий узел).
Пишущий узел состоит из маленького металлического шарика, который благодаря идеальной гладкой форме (подобно шаровому подшипнику) свободно вращается в разные стороны.
Прикасаясь к бумаге, шарик с попадающими на него чернилами, оставляет след на бумаге.
Еще один распространенный пример сферического тела — это надутый мяч.
Благодаря своей шарообразной форме, обладает хорошими аэродинамическими свойствами.
Мяч хорошо катится, летит в любом направлении на большие расстояния и легко закручивается в разные стороны, позволяя тем самым искривлять траекторию полета.
Благодаря сферической форме у мяча отсутствуют углы и выступы, что снижает риск травм.
Сферических и шарообразных форм в жизни огромное множество, они прекрасно демонстрируют в своих закономерностях и проявлениях законы физики и математики.
Приводя примеры объектов сферической и шарообразной формы, мы много говорили о площади и объеме этих тел.
Давайте посмотрим, как определить площадь поверхности сферы и объем шара.
Площадь поверхности сферы (площадь поверхности шара) находят по формуле:
S— площадь поверхности сферы (шара)
r— радиус сферы (шара)
(mathbf)- постоянная величина, равная приблизительно 3,14
Задача 1
Найдите площадь поверхности сферы, радиус которой равен 8 см.
Решение:
Число (mathbf) округлить до десятых.
r = 8 см
Площадь поверхности сферы S — ?
Площадь поверхности сферы, зная радиус сферы, определяют по формуле:
Подставим известные значения радиуса сферы и постоянной величины (mathbf), получим
Ответ: S = 793,6 (см 2 ).
Задача 2
Найдите площадь поверхности сферы, диаметр которой равен 6 см.
Решение:
Число (mathbf) округлить до десятых.
d = 6 см
Площадь поверхности сферы S — ?
Площадь поверхности сферы, зная диаметр этой сферы, определяют по формуле:
Подставим известные значения радиуса сферы и постоянной величины , получим
Ответ: S = 111,6 (см 2 ).
Объем шара определяется по формуле:
V— объем шара
r— радиус шара
(mathbf)- постоянная величина, равная приблизительно 3,14
Вспомним, что означает r 3
Задача 3
Найдите объем шара, если радиус шара 5 м.
Решение:
Число (mathbf) округлить до целых.
r = 5 м
Объем шара V — ?
Объем шара определяется по формуле:
Подставим известные значения радиуса шара и постоянной величины , получим:
Содержание
- — Что представляет собой Диаметральное Сечение шара?
- — Что является осевым сечением сферы?
- — Как найти плоскость сечения шара?
- — Что такое Диаметральное сечение?
- — Что такое сечение шара?
- — Что представляет собой сечение шара плоскостью что такое большой круг шара?
- — Какой фигурой является осевое сечение?
- — Как называется Цилиндр осевое сечение которого квадрат?
- — Что представляет собой осевое сечение цилиндра?
- — Как рассчитать сечение цилиндра?
- — Как вычислить площадь сечения?
- — Как найти осевое сечение конуса?
- — Что такое диаметр круга?
- — Сколько общих точек с шаром имеет касательная плоскость?
- — Что такое сфера и чем отличается от шара?
Всякое сечение шара плоскостью есть круг (или точка, если плоскость касается шара). При решении заданий удобнее вместо шара чертить один из больших кругов, а плоскость сечения заменить хордой этого круга.
Что представляет собой Диаметральное Сечение шара?
Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы — большой окружностью Любая диаметральная плоскость шара являются его плоскостью симметрии.
Что является осевым сечением сферы?
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии ( R ) от данной точки (центра сферы О ). Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара.
Как найти плоскость сечения шара?
S = π * d 2 / 4, где
d — диаметр окружности шара в этой плоскости.
Что такое Диаметральное сечение?
Секущая плоскость — это плоскость, которая пересекает сферу. Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг.
Что такое сечение шара?
Плоскость, проходящая через центр сферы (шара) называется диаметральной плоскостью. Сечение сферы (шара) диаметральной плоскостью называется большой окружностью (большим кругом).
Что представляет собой сечение шара плоскостью что такое большой круг шара?
Сечение шара, проходящее через центр, называется большим кругом, не проходящее — малым кругом. Центр большого круга совпадает с центром шара, а центр малого круга является основанием перпендикуляра, опущенного из центра шара на плоскость этого круга.
Какой фигурой является осевое сечение?
Объяснение: Осевое сечение цилиндра — прямоугольник. Оно выполняется плоскостью, которая проходит по оси цилиндра.
Как называется Цилиндр осевое сечение которого квадрат?
Цилиндр, осевое сечение которого — квадрат, называют равносторонним цилиндром (рис. 149). Так как все образующие цилиндра равны и параллельны друг другу, то любое сечение цилиндра плоскостью, параллельной его оси, есть прямоугольник, высота которого равна образующей цилиндра (рис.
Что представляет собой осевое сечение цилиндра?
Сечения цилиндра
Определение 2. Сечением цилиндра называют пересечение цилиндра с плоскостью. Если сечение проходит через ось цилиндра, то такое сечение называют осевым сечением цилиндра (рис. 3).
Как рассчитать сечение цилиндра?
Площадь сечения цилиндра
- S = π * d 2 / 4, где d — диаметр цилиндра. Формула для расчета площади осевого сечения цилиндра:
- S = d * h, где d — диаметр цилиндра; h — высота цилиндра. …
- S = a * h, где a — хорда основания цилиндра; h — высота цилиндра.
Как вычислить площадь сечения?
Площадь сечения круга или шара можно найти по формуле:
- S = πR2 …
- c = S*q*r*t*(a2 + b2) …
- S= c*h. …
- S=a*b. …
- S =2R*h. …
- S =2а*h.
Как найти осевое сечение конуса?
Формула для расчета площади основания конуса:
- S = π * d 2 / 4, где d — диаметр конуса. Формула для расчета площади осевого сечения конуса:
- S = d * h / 2, где d — диаметр конуса; h — высота конуса. …
- S = a * h / 2, где a — хорда основания конуса; h — высота конуса.
Что такое диаметр круга?
Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), проходящая через центр этой окружности (сферы). … Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет наибольшую длину. По величине диаметр равен двум радиусам.
Сколько общих точек с шаром имеет касательная плоскость?
1) Касательная прямая и сфера имеют только одну общую точку; 2) касательная прямая перпендикулярна к радиусу сферы, проведенному в точку касания. Касательные к сфере, проведенные из внешней точки, равны.
Что такое сфера и чем отличается от шара?
Сфера имеет свою площадь, но при этом у нее нет объема. … Поэтому главным отличием является то, что сфера полая, а шар – тело с содержимым внутри. Еще одно отличие кроется в радиусе. Например, радиусом сферы называется не только расстояние точек до центра.
Интересные материалы:
Что значит друзья не разлей вода?
Что значит духи селектив?
Что значит думать абстрактно?
Что значит два пальца на вене?
Что значит две октавы?
Что значит две Скобочки в переписке?
Что значит две трети от числа?
Что значит двери под ключ?
Что значит двойное полнолуние?
Что значит двойной интервал в ворде?
§ 19. Шар и сфера
19.1. Определения шара, сферы и их элементов
С шаром и сферой мы уже знакомы. Напомним их определения.
Определение. Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не большем данного R (R > 0). Данная точка называется центром шара, а данное расстояние R — радиусом шара.
Определение. Сферой называется множество всех точек пространства, находящихся от данной точки на расстоянии, равном данному R. Данные точка и расстояние R называются соответственно центром и радиусом сферы.
Рис. 193
На рисунке 193 изображён шар с центром О и радиусом R = OА.
Из определений шара и сферы следует, что шар с центром О и радиусом R является объединением двух множеств точек: 1) множества точек M пространства, для которых OM < R (они называются внутренними точками шара и образуют его внутренность); 2) множества всех М, для которых ОМ = R (эти точки являются граничными точками шара, а их объединение составляет границу шара, которая называется шаровой поверхностью и является сферой c центром О и радиусом R).
Радиусом шара называют также всякий отрезок, соединяющий центр шара с точкой шаровой поверхности. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара. Концы любого диаметра шара называются диаметрально nротивоположными точками шара. Отрезок, соединяющий две любые точки шаровой поверхности и не являющийся диаметром шара, называют хордой шара (сферы). На рисунке 193 отрезки ОА, ОВ, ON, OS — радиусы шара; отрезки АВ, NS — диаметры шара; A и B — диаметрально противоположные точки шара. Из определения диаметра шара следует, что он равен удвоенному радиусу шара.
Рис. 194
Покажем, что шар — тело вращения. Для этого рассмотрим полукруг F с центром О и радиусом R (рис. 194, а). При вращении полукруга F вокруг прямой, содержащей его диаметр NS, образуется некоторое тело F1 (рис. 194, б). Так как вращение вокруг прямой — движение и точка О принадлежит оси l вращения, то каждая точка тела F1 удалена от точки O на расстояние, не большее R (движение сохраняет расстояния между точками). Это означает, что тело F1 есть шар с центром О и радиусом R. Кроме того, при вращении границы полукруга — полуокружности — вокруг прямой l образуется сфера. Прямая, содержащая любой диаметр шара, может быть рассмотрена как ось вращения. Следовательно, сечением шара плоскостью, перпендикулярной его оси вращения l и пересекающей шар, является круг, а сечением сферы такой плоскостью — окружность этого круга; центр круга (окружности) есть точка пересечения секущей плоскости с осью l.
Плоскость, проходящая через центр шара (сферы), называется диаметральной плоскостью шара (сферы). Сечением шара диаметральной плоскостью является круг, радиус которого равен радиусу шара. Такой круг называется большим кругом, а его окружность — большой окружностью; большая окружность является пересечением сферы и её диаметральной плоскости.
19.2. Изображение сферы
Рис. 195
Рассмотрим сферу, диаметр NS которой проведён вертикально (рис. 195, а). Большая окружность, по которой сферу пересекает диаметральная плоскость, перпендикулярная диаметру (оси) NS, называется экватором, а точки N и S — полюсами сферы. Окружность, ограничивающая круг — изображение сферы, — называется абрисом или очерковой линией.
Типичная ошибка (!) при изображении сферы (рис. 195, б) в том, что, изображая её экватор эллипсом, полюсы изображают расположенными на абрисе.
Для верного и наглядного изображения сферы вспомним, как в курсе черчения изображают фигуру на комплексном двухкартинном чертеже (эпюре) посредством ортогонального её проектирования на две взаимно перпендикулярные плоскости, одну из которых называют фронтальной (обозначают V), а другую — профильной (обозначают W) плоскостями проекций.
Сферу расположим так, чтобы её ось N′S′ была параллельна профильной (W), но не параллельна фронтальной (V) плоскостям проекций. Тогда ортогональные проекции сферы на плоскости V и W имеют вид, изображённый на рисунке 196. На нём: равные круги — проекции сферы на плоскости V и W; отрезки A1B1 и N1S1 — профильные проекции соответственно экватора и оси сферы; точки N, S — фронтальные проекции полюсов (строятся с помощью линий связи); точки А, В — фронтальные проекции концов диаметра экватора, параллельного фронтальной плоскости (строятся с помощью линий связи); отрезок CD — фронтальная проекция диаметра C′D′ сферы, перпендикулярного профильной плоскости; эллипс с осями АВ и CD — фронтальная проекция экватора. При таком расположении относительно плоскостей проекций сфера изображается так, как показано на рисунках 195, a; 196, a.
Рис. 196
Рис. 197
Обратите внимание! Полюсы N и S не лежат на абрисе, и экватор изображается эллипсом. При этом положение полюсов N и S и положение вершин А и В эллипса-экватора взаимосвязаны.
Действительно, из равенства △ ОBF = △ ЕNО (см. рис. 196, а) следует: OВ = EN, BF = NO. Это означает: а) если изображены полюсы N и S сферы, то вершины А и В эллипса — изображения экватора определяются из равенств OВ = ОА = NE, где NE || OD; б) если изображён экватор (т. е. дана малая ось AB эллипса-экватора), то положение полюсов N и S определяется из равенств ON = OS = BF, где BF || OD.
На рисунке 197, а — верное и наглядное изображение сферы, на рисунке 197, б — изображение сферы верное (почему?), но не наглядное; на рисунке 197, в — неверное изображение (почему?).
ЗАДАЧА (3.106). Найти в пространстве множество вершин всех прямых углов, опирающихся на данный отрезок АВ.
Решение. Если ∠ АМВ = 90°, то точка М принадлежит окружности с диаметром АВ (рис. 198, a).
Рис. 198
Проведём произвольную плоскость α, содержащую отрезок АВ. В этой плоскости множество всех точек М, из которых отрезок AB виден под прямым углом, есть окружность, для которой отрезок AB — диаметр. Точки А и В этому множеству точек не принадлежат. (Почему?) Таким образом, искомое множество вершин прямых углов, опирающихся на отрезок AB, есть сфера с диаметром AB. Точки А и В этому множеству точек-вершин не принадлежат.
19.3. Уравнение сферы
Составим уравнение сферы с центром А (a; b; с) и радиусом R в декартовой прямоугольной системе координат Oxyz.
Пусть М(x; у; z) — любая точка этой сферы (рис. 199). Тогда MA = R или MA2 = R2. Учитывая, что MA2 = (x – a)2 + (у – b)2 + (z – c)2, получаем искомое уравнение cферы
(x – a)2 + (у – b)2 + (z – c)2 = R2.
Если начало системы координат совпадает с центром A сферы, то a = b = c = 0, а сфера в такой системе координат имеет уравнение
x2 + y2 + z2 = R2.
Из полученных уравнений следует, что сфера — поверхность второго порядка.
Так как для любой точки М(х; у; z) шара с центром А (a; b; с) и радиусом R выполняется МА ⩽ R, то этот шар может быть задан неравенством
(x – a)2 + (у – b)2 + (z – c)2 ⩽ R2.
При этом для всех внутренних точек М шара выполняется условие МА2 < R2, т. е.
Рис. 199
(х – a)2 + (у – b)2 + (z – c)2 < R2,
для точек М шаровой поверхности — условие
МА = R,
т. е. (х – a)2 + (у – b)2 + (z – c)2 = R2,
для точек М вне шара — условие
МА > R,
т. е. (х – a)2 + (у – b)2 + (z – c)2 > R2.
19.4. Пересечение шара и сферы с плоскостью
Рассмотрим подробнее вопрос о пересечении шара и сферы с плоскостью. Имеет место следующая теорема.
Теорема 30 (о пересечении шара и сферы с плоскостью). 1) Если расстояние от центра шара до данной плоскости меньше радиуса шара, то пересечением шара с плоскостью является круг. Центром этого круга является основание перпендикуляра, проведённого из центра шара на плоскость, или сам центр шара, если плоскость проходит через этот центр. Пересечением сферы с плоскостью является окружность указанного круга. Радиус r сечения в этом случае равен r = 
Доказательство. Пусть точка О — центр шара, R — его радиус; α — данная плоскость, точка A — основание перпендикуляра, проведённого из центра O на плоскость α. Обозначим ρ(О; α) = | ОА | = d — расстояние от центра шара до плоскости α.
Рассмотрим каждый из случаев взаимного расположения шара и данной плоскости α.
Рис. 200
1) ρ(O; α) = d < R и плоскость α не проходит через центр О шара (рис. 200). Докажем, что пересечение шара и плоскости есть круг с центром А и радиусом r = 

Действительно, пусть М — произвольная точка шара, принадлежащая плоскости α (см. рис. 200). В прямоугольном треугольнике AOM по теореме Пифагора ОM2 = ОА2 + АМ2, откуда AM = 



Обратно, пусть М — произвольная точка плоскости α, принадлежащая кругу с центром А и радиусом r = 
Если неравенства, которые использовались в предыдущем доказательстве, заменить равенствами, то, рассуждая аналогично, можно доказать, что при d < R пересечением сферы и плоскости является окружность с центром А и радиусом r = 
Рис. 201
Если плоскость α проходит через центр O шара, то d = 0, значит, r = R, т. е. сечением шара такой плоскостью является большой круг, а сечением сферы — большая окружность (см. рис. 200).
2) ρ(O; α) = d = OA = R (рис. 201).
Так как ОА = ρ(O; α) = R, то точка А, являющаяся основанием перпендикуляра из центра О шара на плоскость α, принадлежит шаровой поверхности, ограничивающей данный шар.
Рис. 202
Пусть M — произвольная точка плоскости α, отличная от точки A (см. рис. 201). Тогда длины наклонной ОМ и перпендикуляра OA, проведённых из точки О к плоскости α, удовлетворяют неравенству OM > ОА = R. Значит, точка М не принадлежит шару. Следовательно, плоскость α имеет только одну общую точку с шаром — точку А.
3) ρ(О; α) = ОА = d > R (рис. 202). Для любой точки М плоскости α выполняется (почему?) ОМ ⩾ d > R. Это означает, что на плоскости α нет точек шара. Теорема доказана. ▼
ЗАДАЧА (3.161). Через середину радиуса шара проведена перпендикулярная к нему плоскость. Радиус шара равен R. Найти: а) площадь получившегося сечения; б) площади боковой и полной поверхностей конуса, основанием которого служит получившееся сечение шара, а вершиной — центр шара; в) площади боковой и полной поверхностей правильной треугольной пирамиды, вписанной в этот конус.
Решение. а) Пусть точка O — центр шара, OD — его радиус, точка С — середина радиуса OD; α — секущая плоскость, проходящая через точку С перпендикулярно OD.
Рассмотрим сечение шара диаметральной плоскостью, проходящей через его радиус OD. Этим сечением является большой круг с центром О и радиусом R (рис. 203); АВ — диаметр круга — сечения данного шара плоскостью α.
Так как АВ ⟂ OD и точка С — середина радиуса OD, то отрезок AB равен стороне правильного треугольника, вписанного в окружность радиуса R, значит, АВ = R
Рис. 203
АС = r = 

б) Найдём площадь поверхности конуса с вершиной О и радиусом основания r = 
Рис. 204
Образующая ОЕ конуса (рис. 204) равна радиусу R данного шара. Поэтому площадь боковой поверхности этого конуса равна
πr•R = π•

а площадь его полной поверхности — 



в) Найдём площадь поверхности правильной треугольной пирамиды OEFK, вписанной в конус, радиус основания которого СK = r = 
Так как △ ЕFK — правильный, вписанный в окружность радиуса r = 




Площадь боковой поверхности пирамиды равна 3S△ EOF = 
ОН = 


Тогда 

Следовательно, площадь полной поверхности пирамиды равна





Ответ: a) 






19.5. Плоскость, касательная к сфере и шару
Из теоремы 30 следует, что плоскость может иметь со сферой (с шаром) только одну общую точку.
Определение. Плоскость, имеющая только одну общую точку со сферой (с шаром), называется касательной плоскостью к сфере (шару), а их единственная общая точка называется точкой касания (рис. 205).
Рис. 205
Также говорят, что плоскость касается сферы (шара).
Любая прямая, лежащая в касательной плоскости к сфере и проходящая через точку их касания, называется касательной прямой к сфере; эта прямая имеет со сферой единственную общую точку — точку касания, и радиус сферы, проведённый в точку касания, перпендикулярен касательной прямой.

Справедливо и обратное: если прямая a касается окружности большого круга сферы в точке М, то эта прямая касается в точке М самой сферы.
Более того, так как прямая a, касающаяся сферы в точке М, имеет со сферой лишь одну общую точку — точку М, то эта прямая касается любой окружности, по которой пересекаются данная сфера и любая (не только диаметральная) плоскость, проходящая через прямую a. А поскольку радиус, проведённый в точку касания прямой и окружности, перпендикулярен касательной прямой, то центры всех этих окружностей — полученных сечений сферы — лежат в плоскости, проходящей через точку М перпендикулярно касательной прямой a. При этом, если точка О — центр данной сферы радиуса R, точка А — центр окружности радиуса r, по которой пересекает сферу одна (любая) из плоскостей, проходящих через касательную в точке М прямую к данной сфере, ϕ — величина угла между этой секущей плоскостью и проходящей через точку М диаметральной плоскостью данной сферы, то справедливо равенство r = R•cos ϕ (△ ОАМ — прямоугольный, так как отрезок ОА перпендикулярен секущей плоскости (почему?)).
Для плоскости, касательной к сфере, справедливы теоремы, аналогичные теоремам о прямой, касательной к окружности на плоскости.
Теорема 31. Если плоскость касается сферы, то она перпендикулярна радиусу, проведённому в точку касания.
Доказательство. Пусть дана сфера с центром O и радиусом R. Рассмотрим плоскость α, касающуюся данной сферы в точке M (см. рис. 205) и докажем, что ОM ⟂ α.
Предположим, что радиус ОM — не перпендикуляр, а наклонная к плоскости α. Значит, расстояние от центра сферы до плоскости α, равное длине перпендикуляра, проведённого из центра О на плоскость α, меньше радиуса. Тогда по теореме 30 плоскость α пересекает сферу по окружности. Но по условию теоремы плоскость α касается сферы и имеет с ней единственную общую точку M. Пришли к противоречию, которое и доказывает, что OM ⟂ α. Теорема доказана. ▼
Справедлива обратная теорема.
Теорема 32. Если плоскость проходит через точку сферы и перпендикулярна радиусу, проведённому в эту точку, то она касается сферы.
Доказательство. Пусть плоскость α проходит через точку M сферы и перпендикулярна радиусу ОM (см. рис. 205). Значит, расстояние от центра сферы до плоскости равно радиусу ОM. Тогда по теореме 30 плоскость α и сфера имеют единственную общую точку M, следовательно, плоскость α касается сферы (в точке M). Теорема доказана.▼
Так как сечение шара плоскостью есть круг, то можно доказать, что для шара выполняются следующие метрические соотношения:
—диаметр шара, делящий его хорду пополам, перпендикулярен этой хорде;
—отрезки всех касательных прямых, проведённых к шару из одной расположенной вне шара точки, равны между собой (они образуют поверхность конуса с вершиной в данной точке, а точки касания этих прямых — окружность основания этого конуса);
—произведение длин отрезков хорд шара, проходящих через одну и ту же внутреннюю точку шара, есть величина постоянная (равная R2 – a2, где R — радиус шара, a — расстояние от центра шара до данной точки);
—если из одной и той же точки вне шара проведены к нему секущая и касательная, то произведение длины отрезка всей секущей на длину отрезка её внешней части равно квадрату длины отрезка касательной (и равно a2 – R2, где R — радиус шара, a — расстояние от центра шара до данной точки).
19.6. Вписанные и описанные шары и сферы
Определение. Шар называется вписанным в цилиндр, если основания и каждая образующая цилиндра касаются шара (рис. 206).
Рис. 206
Рис. 207
Цилиндр в таком случае называется описанным около шара. В цилиндр можно вписать шар тогда и только тогда, когда он равносторонний.
Определение. Шар называется описанным около цилиндра, если основания цилиндра служат сечениями шара (рис. 207).
Цилиндр при этом называют вписанным в шар. Около любого цилиндра можно описать шар. Центром шара служит середина оси цилиндра, а радиус шара равен радиусу круга, описанного около осевого сечения цилиндра.
Рис. 208
Рис. 209
Определение. Шар называется описанным около конуса, если основание конуса — сечение шара, а вершина конуса принадлежит поверхности шара (рис. 208).
Конус при этом называют вписанным в шар.
Центр шара, описанного около конуса, совпадает с центром круга, описанного около осевого сечения конуса, а радиус шара равен радиусу этого круга.
Определение. Шар называется вписанным в конус, если основание и все образующие конуса касаются шара.
Конус при этом называют описанным около шара (рис. 209). Центр вписанного в конус шара совпадает с центром круга, вписанного в осевое сечение конуса, а радиус шара равен радиусу этого круга.
Определение. Шар называется вписанным в многогранник, если он касается всех граней многогранника.
Многогранник в таком случае называют описанным около шара (рис. 210).
Не во всякий многогранник можно вписать шар. Например, вписать шар можно в любую треугольную или правильную пирамиду. А в прямую призму, в основании которой лежит прямоугольник, не являющийся квадратом, шар вписать нельзя.
Рис. 210
При нахождении радиуса r вписанного в многогранник шара (если таковой существует) удобно пользоваться соотношением
Vмногогр = 
Шар называется вписанным в двугранный угол, если он касается его граней. Центр вписанного в двугранный угол шара лежит на биссекторной плоскости этого двугранного угла. При этом для радиуса r шара, вписанного в двугранный угол, величины α этого угла и расстояния m от центра шара до ребра двугранного угла справедлива формула: r = m•sin 
Шар называется вписанным в многогранный угол, если он касается всех граней многогранного угла. При решении задач, в которых рассматриваются вписанные в многогранный угол шары, удобно пользоваться соотношением: r = m•sin 
Если все плоские углы трёхгранного угла равны по 60°, то расстояние от вершины угла до центра вписанного в этот угол шара радиуса r равно 3r; если все плоские углы трёхгранного угла прямые, то расстояние от вершины угла до центра вписанного в этот угол шара радиуса r равно r
Определение. Шар называется описанным около многогранника, если все вершины многогранника принадлежат поверхности шара (рис. 211). Многогранник при этом называют вписанным в шар.
Рис. 211
Не около всякого многогранника можно описать шар. Например, около любой правильной или любой треугольной пирамиды шар описать можно, а около четырёхугольной пирамиды, в основании которой лежит ромб, не являющийся квадратом, шар описать нельзя (около ромба нельзя описать окружность). Более того, нельзя описать шар около любой наклонной призмы.
Вообще, для того чтобы около многогранника можно было описать шар, необходимо, чтобы около любой его грани можно было описать круг. При этом центр описанного шара может лежать как внутри многогранника, так и вне его или на его поверхности (даже на ребре многогранника), и проектируется в центр описанного около любой грани круга. Кроме того, перпендикуляр, опущенный из центра описанного около многогранника шара на ребро многогранника, делит это ребро (как хорду шара) пополам.
Мы уже говорили о пирамидах, все рёбра которых одинаково наклонены к основанию. Около таких пирамид всегда можно описать шар, центр которого лежит на луче, содержащем высоту пирамиды.
Высота h пирамиды, радиус Rк описанного около основания пирамиды круга и радиус R описанного около этой пирамиды шара связаны соотношением:
(R – h)2 + 
Приведём формулы для вычисления радиусов вписанных и описанных шаров для правильных многогранников с ребром a.
В задачах иногда ещё рассматривают шары, касающиеся всех рёбер данного многогранника. Для куба, например, такой шар существует и его радиус равен 
19.7. Площади поверхностей шара и его частей
Часть шара, заключённая между секущей плоскостью и одной из двух частей его сферической поверхности, называется шаровым сегментом (рис. 212 и 214). Поверхность шарового сегмента называется сегментной поверхностью: она представляет собой часть шаровой поверхности, отсекаемую какой-нибудь плоскостью. Круг АВ, по которому плоскость пересекает шар, называется основанием шарового сегмента, а окружность этого круга — основанием сегментной поверхности. Отрезок ОС радиуса, перпендикулярного секущей плоскости, называется высотой шарового сегмента (сегментной поверхности).
Рис. 212
Часть шара, заключённая между двумя параллельными секущими плоскостями, называется шаровым слоем (см. рис. 212, 214). Поверхность шарового слоя называется шаровым поясом. Шаровой пояс — часть шаровой поверхности, заключённая между двумя параллельными секущими плоскостями. Перпендикуляр, проведённый из точки одного основания к плоскости другого, называется высотой шарового слоя (шарового пояса).
Сегментную поверхность и шаровой пояс можно рассматривать как поверхности вращения: в то время, как при вращении полуокружности CAA1D (см. рис. 212) вокруг диаметра CD образуется шаровая поверхность (сфера), при вращении дуги СА этой полуокружности вокруг того же диаметра образуется сегментная поверхность, а при вращении дуги AA1 — шаровой пояс.
Тело, образованное при вращении кругового сектора с углом ϕ (ϕ < 180°) вокруг прямой, которая содержит диаметр круга, не имеющий с круговым сектором общих внутренних точек, называется шаровым сектором.
Рис. 213
Из этого определения следует, что поверхность шарового сектора состоит из сегментной поверхности и боковой поверхности конуса (рис. 213, а, б) или из поверхности шарового пояса и боковых поверхностей двух конусов (рис. 213, в, г).
На рисунке 214 изображены различные элементы шара и сферы (шаровой сектор имеет простейший вид).
Рассмотрим вопрос о вычислении площадей сферы, сегментной поверхности, шарового пояса и шарового сектора.
Рис. 214
Рис. 215
а) Площадь сферы. Пусть ABCDEF — правильная ломаная линия, вписанная в данную полуокружность; a — длина её апофемы (рис. 215). При вращении полуокружности вокруг её диаметра AF образуется сфера, а при вращении ломаной ABCDEF вокруг этого же диаметра AF образуется некоторая поверхность Ф.
За площадь сферы, образованной вращением полуокружности вокруг её диаметра, принимают предел, к которому стремится площадь поверхности Ф, образованной вращением вокруг того же диаметра правильной n-звенной ломаной линии, вписанной в полуокружность, при n → +∞ (число сторон неограниченно возрастает).
Поверхность Ф является объединением поверхностей, образованных вращением звеньев ломаной линии, вписанной в полуокружность, вокруг её диаметра. Этими поверхностями являются боковые поверхности либо конуса (для первого и последнего звеньев ломаной), либо цилиндра (для звеньев, параллельных оси вращения; их может и не быть), либо усечённого конуса (для всех остальных звеньев ломаной).
При вычислении площадей получившихся поверхностей воспользуемся следствиями из теорем 26, 27, 29. Площадь Si (i = 1, 2, …, n) поверхности, образованной вращением любого звена, равна произведению 2π, расстояния bi от середины звена до центра сферы и длины mi проекции этого звена на ось вращения, т. е. Si вращ = 2π•bi•mi.
Так как ломаная — правильная, то все bi равны апофеме an данной n-звенной ломаной, а m1 + m2 + m3 + … + mn = 2R и S1 + S2 + S3 + … + Sn = 4π•an•R. Причём an = 

Следовательно, предел площади поверхности Ф при n → ∞ равен 4πR•R = 4πR2. Этот предел и принимается за величину площади сферы радиуса R:
Sсферы = 4πR2.
б) Площади сегментной поверхности и шарового пояса. Если правильная ломаная вписана не в полуокружность, а в некоторую её часть, например в дугу AD (см. рис. 215), при вращении которой образуется сегментная поверхность, то рассуждения, аналогичные предыдущим, приводят к выводу:
Sсегм. поверх = 2πRh,
где h — высота сферического сегмента.
Если же ломаная вписана в дугу ВЕ (см. рис. 215), при вращении которой образуется шаровой пояс, то получим:
Sшар. пояса = 2πRh,
где h — высота шарового пояса.
Проделайте эти рассуждения самостоятельно.
в) Площадь поверхности шарового сектора. Эта площадь может быть получена как сумма площадей поверхности сферического сегмента и боковой поверхности одного конуса (см. рис. 213, а, б) или как сумма площадей поверхности сферического слоя и боковых поверхностей двух конусов (см. рис. 213, в, г).
Рассмотрим частный случай (см. рис. 213, а, б). Если R — радиус сферы, h — высота шарового сегмента, то площадь боковой поверхности конуса с вершиной в центре сферы, образующей R, и радиусом основания 

Sшар. сект = πR(2h + 
ЗАДАЧА (3.418). Основанием треугольной пирамиды SABC является равносторонний треугольник АВС, сторона которого равна 4. Известно также, что AS = BS = 
Рис. 216
Решение. Решим эту задачу двумя методами.
Первый метод (геометрический). Пусть точка О — центр сферы, описанной около данной пирамиды; D — точка пересечения медиан правильного △ АВС; точка Е — середина отрезка АВ (рис. 216).
Центр О сферы равноудалён от всех вершин △ АBС, поэтому принадлежит прямой, проходящей через точку D перпендикулярно плоскости АВС.
Так как точка Е — середина отрезка АВ, то SE ⟂ АВ (AS = BS) и СЕ ⟂ АВ (△ АВС — правильный). Значит, по признаку перпендикулярности прямой и плоскости AB ⟂ (CSE), поэтому (CSE) ⟂ (ABC) (по признаку перпендикулярности двух плоскостей). Это означает, что прямая OD, а следовательно, и точка О — центр сферы — лежат в плоскости CSE.
Точка D является центром окружности, описанной около △ АВС. (По этой окружности плоскость АВС пересекает сферу, описанную около данной пирамиды.) Если L — точка пересечения прямой СЕ и упомянутой окружности, то CL — её диаметр. Найдём длину диаметра CL.
В правильном △ AВС имеем: CE = 




Далее △ BSE (∠ BES = 90°): SE2 = SB2 – BE2 = 19 – 4 = 15 (по теореме Пифагора); △ SEC (по теореме косинусов):
cos C = 


△ SLC (по теореме косинусов):
SL2 = SC2 + CL2 – 2SC•CL•cos C = 

Плоскость CSL проходит через центр О сферы, следовательно, пересекает сферу по большой окружности, которая описана около △ CSL. Значит, радиус R этой окружности равен радиусу сферы, описанной около данной пирамиды. Найдём длину радиуса R.
В треугольнике CSL имеем 







Находим площадь Q сферы:
Q = 4πR2 = 4π•

Второй метод (координатный). Введём в пространстве декартову прямоугольную систему координат так, чтобы её начало совпадало с вершиной А данной пирамиды, направление оси абсцисс — с направлением луча АС, ось аппликат была перпендикулярна плоскости основания АВС пирамиды (рис. 217).
В этой системе координат вершины основания пирамиды имеют координаты: А(0; 0; 0), B(2; 2 
Обозначив через х, у, z координаты вершины S пирамиды, найдём их из условий: AS = BS = 
Имеем
AS2 = x2 + y2 + z2 = 19,
ВS2 = (x – 2)2 + (y – 2 
CS2 = (x – 4)2 + y2 + z2 = 9.
Решая систему уравнений


находим: х = 


Рис. 217
Таким образом, вершина S имеет следующие координаты:
S 
Пусть центр O сферы имеет координаты a, b, с, а её радиус равен R. Так как сфера описана около пирамиды SABC, то OA2 = OB2 = OC2 = OS2 = R2. Это соотношение в координатном виде равносильно системе уравнений





Вычитая из первого уравнения четвёртое, получаем a = 2, после чего, вычитая из первого уравнения второе, получаем b = 
После вычитания третьего уравнения системы из первого её уравнения получаем:

Подставив в это уравнение вместо a и b найденные их значения, получаем с = 



Q = 4πR2 = 
Ответ: 
19.8. Объёмы шара и его частей
Рис. 218
Рассмотрим фигуру, образованную вращением равнобедренного прямоугольного треугольника с гипотенузой 2R вокруг прямой, проходящей через вершину прямого угла параллельно гипотенузе (рис. 218, а). Объём этой фигуры равен разности объёма цилиндра с высотой 2R, радиусом основания R и удвоенного объёма конуса высоты R, радиуса основания R:
V = π•R2•2R – 2•

Шар радиуса R (рис. 218, б) и образованную выше фигуру вращения расположим между двумя параллельными плоскостями, расстояние между которыми равно 2R. Шар при этом будет касаться каждой из данных плоскостей, а фигуру вращения расположим так, чтобы её ось вращения была перпендикулярна этим плоскостям (см. рис. 218). (Плоскость, которая содержит верхнее основание цилиндра и касается сферы в точке N, на рисунке не изображена.)
Будем пересекать наши фигуры плоскостями, параллельными данным плоскостям и удалёнными от центра шара на расстояние x (0 ⩽ x ⩽ R).
При х = 0 площади сечений обеих фигур равны π•R2; при х = R площади сечений равны нулю. В остальных случаях площадь сечения шара равна π•(
Vшара = 
гдe R — радиус шара.
Рис. 219
Для получения объёма шарового сегмента высоты h рассмотрим предыдущую ситуацию для R – h ⩽ x ⩽ R (при h < R) (рис. 218, 219). Применяя принцип Кавальери, получим: объём шарового сегмента равен разности объёма цилиндра высоты h и радиуса основания R и объёма усечённого конуса высоты h и радиусов оснований R и R – h, т. е.
V = π•h•R2 – 
= 
При h > R объём шарового сегмента можно найти как разность объёма шара и объёма шарового сегмента высоты 2R – h (рис. 220): V = 




Рис. 220
Мы показали, что в шаре радиуса R объём любого шарового сегмента высоты h может быть вычислен по формуле:
Vшар. сегм = 
или в другом виде
Vшар. сегм = π•h2•
Рис. 221
Рис. 222
Рис. 223
Выведем теперь формулу для вычисления объёма шарового сектора.
Сначала рассмотрим шаровой сектор, состоящий из шарового сегмента высоты h и конуса высоты (R – h) с вершиной в центре шара радиуса R (рис. 221). Для него имеем:
Vшар. сект = Vсегм + Vкон = 
+ 

Докажите самостоятельно, что и для других шаровых секторов (рис. 222, 223) их объём вычисляется по формуле:
Vшар. сект = 
Отметим, что объём шарового слоя с радиусами оснований r1 и r2 и высотой Н вычисляется по формуле
Vшар. слоя = 


ЗАДАЧА (3.457). Четыре шара радиуса R и четыре шара радиуса r расположены так, что каждый касается трёх шаров одного радиуса и трёх шаров другого радиуса. Найти отношение объёма шара радиуса R к объёму шара радиуса r (R > r).
Решение. Обозначим V1, V2 — объёмы шаров с радиусами соответственно R и r. Тогда V1 = 



Пусть А, В, С, Р — центры шаров радиуса R; A1, B1, С1, P1 — центры шаров радиуса r. Тогда:
1) AB = BC = CA = AP = BP = CP = 2R ⇒ РАВС — правильный тетраэдр с ребром 2R;
2) A1B1 = B1C1 = C1A1 = A1P1 = B1P1 = C1P1 = 2r ⇒ Р1А1В1С1 — правильный тетраэдр с ребром 2r.
Рис. 224
Обозначим точки A2, B2, C2, P2 — центры граней тетраэдра РАВС (рис. 224) и докажем, что все четыре высоты АA2, BB2, CC2, PP2 пересекаются в одной точке и делятся этой точкой в отношении 3 : 1, считая от вершин.
В самом деле, если М = AА2 ∩ PP2, то из подобия треугольников НАР и НР2А2 следует HP : НA2 = AP : A2P2 = 3 : 1, тогда из подобия треугольников APM и A2P2M следует, что AP : A2P2 = PM : MP2 = AM : MA2 = 3 : 1, т. е. PM = 
Аналогично доказывается, что высоты BB2 и CC2 делятся точкой M в отношении BM : MB2 = CM : MC2 = 3 : 1 и, таким образом, точки A2, B2, C2, P2 равноудалены от точки М.
Далее, так как шар с центром P1 и радиусом r касается шаров с центрами А, В, C и радиусами R, то P1А = P1B = P1С = R + r, т. е. точка P1 равноудалена от вершин А, В и С правильного тетраэдра РАВС. Так как (R + r) < 2R, то P1 принадлежит высоте РP2 этого тетраэдра: P1 ∈ PP2. Аналогично доказывается, что A1 ∈ АA2, B1 ∈ ВB2, C1 ∈ СC2.
Найдём дважды длину высоты РP2 тетраэдра РАВС: с одной стороны, как длину катета прямоугольного треугольника АPP2, с другой стороны, как сумму длин отрезков РМ, МР1 и P1P2.
В правильном △ AВС со стороной 2R имеем:
AP2 = 



Тогда в прямоугольном △ AРP2 :
РР2 = 


Найдём длину отрезка PP2 иначе. В прямоугольном △ AP1P2 имеем:
Аналогично можно убедиться, что A1A2 = B1B2 = C1C2 = P1P2 = 
Так как в правильном тетраэдре РАВС с ребром 2R для расстояния РМ от вершины Р до центра М этого тетраэдра выполняется РМ = 




Подставляя в равенство PP2 = РM + MP1 + P1P2 найденные значения длин отрезков РР2, РM, МP1 и P1P2, получаем:




или после элементарных преобразований:
R2 – 6Rr + r2 = 0.
Разделив это уравнение на r2 и введя новую переменную t = 








Ответ: (3 + 2 
Задания для работы с интернет-ресурсами
1. Посмотрите в Интернете и отберите рисунки по темам: «Тело вращения», «Поверхность вращения». Они помогут вам при построении рисунков к решению задач.
2. Сравните материалы Интернета и учебника по темам: «Цилиндр», «Конус», «Цилиндрическая и коническая поверхности вращения», «Касательная плоскость к цилиндру и конусу», «Формулы для вычисления площадей боковой и полной поверхностей цилиндра и конуса», «Формулы для вычисления объёма цилиндра и конуса», «Развёртки цилиндра и конуса», «Модели цилиндра и конуса». Что нового вы узнали из Интернета?
3. Вы узнаете много нового и интересного о замечательных кривых, сделав запрос в Интернете по темам: «Сечения цилиндра и конуса плоскостью», «Кривые второго порядка», «Конические сечения».
4. Найдите рисунки по темам: «Призма, вписанная в цилиндр и описанная около цилиндра», «Пирамиды, вписанные в конус и описанные около конуса». Удачные рисунки скопируйте в «Избранное» или в «Картотеку», чтобы можно было ими пользоваться при решении задач.
5. Найдите в Интернете теоремы о параллельных сечениях конуса. Посмотрите рисунки усечённых конусов. Найдите формулы для вычисления площадей боковой и полной поверхностей усечённого конуса и его объёма.
6. В Интернете посмотрите материал по темам: «Сфера», «Шар», «Изображение сферы», «Уравнение сферы», «Взаимное расположение сферы и плоскости», «Пересечение шара и сферы с плоскостью», «Плоскость, касательная к сфере и шару», «Шаровой сегмент, его основание и высота; сегментная поверхность», «Шаровой слой, его основания и высота», «Шаровой пояс», «Шаровой сектор и его поверхность».
7. Найдите в Интернете формулы для вычисления площадей сферы, сегментной поверхности, шарового пояса, поверхности шарового сектора, объёмов шара, шарового сегмента, шарового сектора, шарового слоя.
8. Обратите особое внимание на материал: «Шары и сферы, вписанные в двугранный угол и многогранный угол», «Шары и сферы, вписанные в многогранники (особенно в правильные многогранники) и описанные около них», «Шары и сферы, вписанные в цилиндр, конус и описанные около них».
9. Посмотрите рисунки и материалы по темам: «Комбинации геометрических тел», «Комбинации геометрических фигур в окружающем нас мире, в архитектуре». Тем, кто интересуется черчением и графикой, предлагаем найти статьи: «Техническое черчение: цилиндр и конус», «Пересечение двух цилиндров с перпендикулярными осями», «Резьбы и резьбовые соединения», «Цилиндрическая винтовая линия».
Вопросы для самооценки
1. Оцените результаты изучения этой главы. Довольны ли вы ими?
2.Что нового вы узнали в этой главе?
3.Как могут пригодиться вам эти знания в повседневной жизни?
4.Какие задания в этой главе были для вас самыми трудными? Почему?
5.Использовали ли вы при выполнении заданий дополнительные источники: справочники, пособия, интернет-ресурсы?
6.Обращались ли вы за помощью к одноклассникам, родителям, учителю?