Параллелограмм представляет собой четырехугольную фигуру, у которой противолежащие стороны попарно параллельны и попарно равны. Равны у него также и противоположные углы, а точка пересечения диагоналей параллелограмма делит их пополам, являясь при этом центром симметрии фигуры. Частными случаями параллелограмма являются такие геометрические фигуры как квадрат, прямоугольник и ромб. Площадь параллелограмма может быть найдена различными способами, в зависимости от того, какими исходными данными сопровождается постановка задачи.
Ключевой характеристикой параллелограмма, очень часто используемой при нахождении его площади, является высота. Высотой параллелограмма принято называть перпендикуляр, опущенный из произвольной точки противоположной стороны к отрезку прямой, образующей данную сторону.
- В самом простом случае площадь параллелограмма определяется как произведение его основания на высоту.
S = DC ∙ hгде S — площадь параллелограмма; a — основание; h — высота, проведенная к данному основанию.
Данную формулу очень легко понять и запомнить, если взглянуть на следующий рисунок.
Как видно из данного изображения, если слева от параллелограмма отрезать воображаемый треугольник и присоединить его справа, то в результате мы получим прямоугольник. А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону.
- Площадь параллелограмма может быть также найдена в результате перемножения длин двух смежных оснований и синуса угла между ними:
S = AD∙AB∙sinαгде AD, AB — смежные основания, образующие точку пересечения и угол а между собой; α — угол между основаниями AD и AB.
- Также площадь параллелограмма можно найти разделив пополам произведение длин диагоналей параллелограмма на синус угла между ними.
S = ½∙AC∙BD∙sinβгде AC, BD — диагонали параллелограмма; β — угол между диагоналями.
- Существует также формула для нахождения площади параллелограмма через радиус вписанной в него окружности. Она записывается следующий образом:
Поперечное сечение образуется под прямым углом по отношению к продольной оси. Причем, сечение разных геометрических фигур представлено может быть различными формами. К примеру, у параллелограмма сечение по внешнему виду напоминает прямоугольник или квадрат, у цилиндра – прямоугольник или круг и т.д.
Инструкция
Чтобы найти сечения параллелограмма, нужно знать значение его основания и высоту. Если, к примеру, известна лишь длина и ширина основания, то найдите диагональ, используя для этого теорему Пифагора (квадрат длины гипотенузы в прямоугольном треугольнике равен сумме квадратов катетов: a2 + b2 = c2). Ввиду этого, c = sqrt (a2 + b2).
Найдя значение диагонали, подставьте его в формулу S= c*h, где h – высота параллелограмма. Полученный результат и будет величиной площадью поперечного сечения параллелограмма.
Если же сечение проходит вдоль двух оснований, то его площадь рассчитывайте по формуле: S=a*b.
Для вычисления площади осевого сечения цилиндра, проходящей перпендикулярно основаниям (при условии, что одна сторона этого прямоугольника равна радиусу основания, а вторая – высоте цилиндра), используйте формулу S =2R*h, в которой R – величина радиуса окружности (основания), S – площадь поперечного сечения, а h – высота цилиндра.
Если по условиям задачи сечение не проходит через ось вращения цилиндра, но при этом параллельно его основаниям, значит, сторона прямоугольника не будет равна диаметру окружности основания.
Самостоятельно вычислите неизвестную сторону путем построения окружности основания цилиндра, проведения перпендикуляров от стороны прямоугольника (плоскости сечения) к окружности и расчета размера хорды (по теореме Пифагора). После этого подставьте в S =2а*h полученное значение (2а – значение хорды) и рассчитайте площадь поперечного сечения.
Площадь сечения шара определяется по формуле S = R2. Обратите внимание на то, что, если расстояние от центра геометрической фигуры до плоскости будет совпадать с плоскостью, то площадь сечения равна будет нулю, потому как шар касается плоскости лишь в одной точке.
Обратите внимание
Дважды пересчитывайте полученный результат: так вы не допустите ошибки в расчетах.
Внимание, только СЕГОДНЯ!
Все интересное
Призма — это многогранник с двумя параллельными основаниями и боковыми гранями в форме параллелограмма и в количестве, равном числу сторон многоугольника основания. Инструкция 1В произвольной призме боковые ребра расположены под углом к плоскости…
При вращении прямоугольного треугольника вокруг одного из его катетов образуется фигура вращения, называемая конусом. Конус — геометрическое тело с одной вершиной и круглым основанием. Инструкция 1Расположите чертежный угольник, совместив один из…
У цилиндра имеется высота, которая перпендикулярна двум его основаниям. Способ определения ее длины зависит от набора исходных данных. Таковыми могут быть, в частности, диаметр, площадь, диагональ сечения. Инструкция 1Для любых фигур существует…
Призма — это многогранник, основанием которого служат равные многоугольники, боковыми гранями — параллелограммы. Для того чтобы найти площадь сечения призмы, необходимо знать, какое сечение рассматривается в задании. Различают перпендикулярное и…
Цилиндр является пространственной фигурой и состоит из двух равных оснований, которые представляют собой круги и боковой поверхности, соединяющей линии, ограничивающие основания. Чтобы вычислить площадь цилиндра, найдите площади всех его…
Цилиндрическая геометрическая форма используется при производстве автомобильных двигателей, других технических и бытовых устройств, и не только. Чтобы определить площадь цилиндра, нужно найти его полную поверхность. Инструкция 1Согласно…
Если по обе стороны некоторой плоскости есть точки, принадлежащие объемной фигуре (например, многограннику), эту плоскость можно назвать секущей. А двухмерная фигура, образованная общими точками плоскости и многогранника, в этом случае называется…
Цилиндр представляет собой тело, ограниченное цилиндрического поверхностью с основаниями в форме круга. Эта фигура образуется путем вращения прямоугольника вокруг своей оси. Осевое сечение — есть сечение, проходящее через цилиндрическую ось, оно…
При решении задач по геометрии приходится вычислять площади и объемы фигур. Если сделать в любой фигуре сечение, обладая информацией о параметрах самой фигуры, можно найти и площадь этого сечения. Для этого необходимо знать специальные формулы и…
Множество задач в геометрии основаны на определении площади сечения геометрического тела. Одним из наиболее встречающихся геометрических тел является шар, и определение площади его сечения может подготовить к решению задач самых разных уровней…
Параметры труб определяются согласно расчётам, сделанным при помощи специальных формул. Сегодня большинство вычислений производится посредством онлайн сервисов, однако в большинстве случаев требуется индивидуальный подход к вопросу, поэтому важно понимать, каким образом производится расчёт площади сечения трубы.
Что такое золотое сечение и как его понимать
Часто мы сталкиваемся с домами, предметами, строениями, растениями, которые нас чем-то завораживают. Люди издавна пытались понять, почему одно нам кажется красивым, другое нет, искали закономерности. И вроде нашли. Это некоторое соотношение частей, которое назвали золотым сечением.
О том, кто и когда придумал золотое сечение никто не знает точно. Кто-то приписывает открытие Пифагору, но первое упоминание нашли еще в «Началах» Евклида, а жил он в 3 веке до нашей эры. Так что находка явно давняя. Именно по этому принципу построены древнегреческие и римские храмы. Конечно, это могут быть совпадения, но очень уж странные и очень их много. Так что, скорее всего, они были в курсе идеальных пропорций.
Сохранившиеся постройки древности тоже подчинены правилу золотого сечения
Совершенно точно то, что Леонардо да Винчи искал подтверждение этому принципу в строении человеческого тела. И, что самое интересное, нашел. Те лица и тела, которые кажутся нам красивыми, имеют пропорции, которые как раз и подчиняются закону золотого сечения.
Формальное определение звучит и просто, и сложно. Его связывают с двумя разными по размеру отрезками. Звучит этот принцип примерно так: если отрезок разделить на две неравные части, то это деление будет пропорциональным, если большая часть отрезка относится к целому так же, как и меньшая часть к большему. Будет понятнее, если посмотреть на иллюстрацию и формулу.
Принцип и формула золотого сечения
На рисунке целый отрезок разделен так, что если а разделить на b, получим 1,1618, та же цифра получается, если целый отрезок разделить на большую часть — a. Это число и есть воплощением идеальной пропорции. Теперь, если посмотрите на картинку с Парфеноном, пропорции этого строения также подчиняются указанному соотношению.
Ту же закономерность можно представить в виде процентов. Может, кому-то так проще. Для того, чтобы деление целого было пропорциональным, части должны составлять 62% и 38%. Возможно, так будет проще запомнить.
Последовательность Фибоначчи — не только математическая формула
Эту закономерность развил дальше математик Фибоначчи. Он разработал числовую последовательность, элементы которой, начиная с девятого, подчиняются тому же закону. Графическое изображение этой последовательности — спираль. Если присмотреться, и в природе, и в архитектуре, и в человеческом теле пропорции красоты присутствуют.
Как делаются вычисления?
Как известно, труба – это цилиндр. Следовательно, площадь её сечения рассчитывается по простым формулам, известным нам из курса геометрии. Основная задача – вычислить площадь круга, диаметр которого равен наружному диаметру изделия. При этом толщина стенок вычитается для получения истинного значения.
Как мы знаем из курса общеобразовательной школы, площадь круга равна произведению числа π на квадрат радиуса:
- R – радиус вычисляемой окружности. Он равен половине её диаметра;
- Π – постоянная равная 3,14;
- S – вычисляемая площадь поперечного сечения трубы.
Как построить прямоугольник с идеальными пропорциями
Чтобы применять на практике полученную информацию, надо каким-то образом научиться делить пространство или строить его согласно этому закону. Для начала давайте научимся строить прямоугольник с идеальными пропорциями. За основу берем квадрат.
Построение прямоугольника с золотым сечением
Квадрат делим пополам, в одном из полученных прямоугольников проводим линию, которая соединяет противоположные углы. Дальше берем циркуль, ставим иголку в центр нижней стороны квадрата, откладываем длину полученной диагонали и отмечаем ее на линии, которая будет продолжением нижней стороны квадрата. Полученный прямоугольник имеет соотношение сторон 1,62 (это как раз то соотношение, которое и дает 62% и 38%).
Это явно неспроста. Хотя далеко не все подчиняется этой закономерности
Что еще интересно, что если вы начнете делить прямоугольник с соотношением сторон 1,62 на квадрат и прямоугольник, вы получите снова прямоугольник с идеальными пропорциями, но меньшего размера. Если вы его снова разделите по тому же принципу, будет еще одна пара квадрат+прямоугольник со сторонами, соотношение которых будет соответствовать золотому сечению. И так до тех пор, пока вы сможете проводить деление. Но что еще интереснее, в это деление отлично вписывается ряд Фибоначчи, который имеет вид раскручивающейся спирали. Иллюстрация на рисунке выше.
Приступаем к расчёту
Так как задача – найти истинную площадь, то из полученного значения необходимо вычесть величину толщины стенки. Следовательно, формула приобретает вид:
- S = π (D/2 – N) 2 ;
- В этой записи D – внешний диаметр окружности;
- N – толщина стенки трубы.
Чтобы вычисления были максимально точными, следует вписать больше знаков после запятой в числе π (пи).
D = 1 м.; N = 0,01 м.
Для упрощения возьмём π = 3,14. Подставляем значения в формулу:
S = π (D/2 – N) 2 = 3,14 (1/2 – 0,01) 2 = 0,754 м 2 .
Идеальный треугольник и пентаграмма
Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.
Золотой треугольник, правило его построения и применение в создании интерьера, например
Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.
Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.
- Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
- Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D.
Построение пентаграммы
- Соединяем точки E и D. При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
- Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.
Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.
Некоторые физические особенности
От площади сечения трубы зависит скорость движения жидкостей и газов, которые по ней транспортируются. Надо выбрать оптимальный диаметр. Не менее важным является и внутреннее давление. Именно от его величины зависит целесообразность выбора сечения.
При расчёте учитывается не только давление, но и температура среды, её характер и свойства. Знание формул не освобождает от необходимости изучения теории. Расчёт труб канализации, водоснабжения, газоснабжения и отопления опирается на информацию справочников. Важно, чтобы выполнялись все необходимые условия при выборе сечения. Его величина также зависит и от характеристик используемого материала.
О чём стоит помнить?
Площадь сечения трубы – один из важных параметров, который следует учитывать при расчёте системы. Но наравне с тем высчитываются параметры прочности, определяется, какой материал выбрать, изучаются свойства системы в целом и пр.
Произвести расчет сечения трубы довольно просто, ведь для этого есть ряд стандартных формул, а также многочисленные калькуляторы и сервисы в интернете, которые могут выполнить ряд простых действий. В данном материале мы расскажем о том, как рассчитать площадь сечения трубы самостоятельно, ведь в некоторых случаях нужно учитывать ряд конструкционных особенностей трубопровода.
Как разделить отрезок по правилу золотого сечения
Это умение пригодится, например, при создании проекта дома, планировки, при разработке дизайна квартиры, расстановке мебели и т.д. Точно также может понадобиться при планировке участка, клумб, высадке растений и т.д. В общем, применяться может практически везде.
Ничего особенного, но взгляд не оторвать. Знаете почему?
Итак, порядок деления отрезка по правилу золотого сечения:
- Берем отрезок, делим его пополам.
- Из одного из концов восстанавливаем перпендикуляр (прямая под углом 90°), который длиной равен половине отрезка. На рисунке это отрезок BC.
- Полученную точку C соединяем прямой с другим концом отрезка (A).
- На отрезке AC ставим точку D. Она находится на расстоянии, равном длине отрезка BС. Проще всего это сделать при помощи циркуля, но можно и линейкой.
- Замеряем длину отрезка AD (снова циркулем, либо линейкой). Такую же длину откладываем на отрезке AB. Получаем точку E.
- Теперь, если измерить длины отрезков AE и EB и разделить их, получим то самое заветное число — 1,62.
Деление отрезка на участки с идеальным соотношением
Пару раз повторив процедуру, вы научитесь делать все буквально за считанные минуты. Если же вам надо, например, определить высоту окна, его форму, также можно воспользоваться данными пропорциями. По тому же принципу можно определять местоположение всех архитектурных элементов, их размеры. При планировании уже имеющихся объектов, деление проще проводить при помощи процентного соотношения. Тут уже либо считаете в уме, либо используете калькулятор.
Формулы вычислений
При проведении вычислений нужно учитывать, что по существу трубы имеют форму цилиндра. Поэтому для нахождения площади их сечения можно воспользоваться геометрической формулой площади окружности. Зная внешний диаметр трубы и значение толщины его стенок, можно найти показатель внутреннего диаметра, который понадобится для вычислений.
Стандартная формула площади окружности такова:
S=π×R 2 , где
π – постоянное число, равное 3,14;
R – величина радиуса;
S – площадь сечения трубы, вычисленная для внутреннего диаметра.
Порядок расчета
Поскольку главная задача – это найти площадь проходного сечения трубы, основная формула будет несколько видоизменена.
В результате вычисления производятся так:
S=π×(D/2-N) 2 , где
D – значение внешнего сечения трубы;
N – толщина стенок.
Примите к сведению, что, чем больше знаков в числе π вы подставите в расчеты, тем точнее они будут.
Приведем числовой пример нахождения поперечного сечения трубы, с наружным диаметром в 1 метр (N). При этом стенки имеют толщину в 10 мм (D). Не вдаваясь в тонкости, примем число π равным 3,14.
Итак, расчеты выглядят следующим образом:
S=π×(D/2-N) 2 =3,14×(1/2-0,01) 2 =0,754 м 2 .
Применение в строительстве
Как уже говорили, неизвестно кто открыл золотое сечение, но все, что кажется нам красивым, имеет именно такое соотношение сторон. Примеров в природе очень много. Если рассматривать известные здания, то и там тоже есть та же закономерность.
Исаакиевский собор — можете посчитать ради интереса
Если вы хотите, чтобы ваш дом внутри и снаружи был привлекательным, запоминался и нравился, при создании или выборе проекта можно просчитать хотя бы основные пропорции. Внести корректировки в пропорции, возможно, не всегда легко, часто связано с дополнительными расходами. Но, если при создании проекта сразу держать в уме золотое сечение, вопросы сами по себе отпадают. На самом деле не так уж это сложно.
Например, вы хотите дом площадью около 100 квадратных метров. Длинную сторону можно принять за 12 метров. Тогда короткая находится как 62% от длинной и составит 7,44 метра. Можно сделать 7 метров или 7,5, можно увеличить до 8. Точное, до сантиметра соблюдение размеров совсем не обязательно. Важно соотношение. А «на глаз» даже в приближении смотрится гармонично. Площадь застройки в таком случае получается несколько меньше — 90-96 квадратов. Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно.
Если основные параметры строения имеют правильную пропорцию, в любом стиле здание смотрится интересно
Высота этажа в таком случае принимается как 32% от длинной части. Она составит 12*0,32 = 3,84 метра. В принципе, это соответствует нынешним представлениям о комфортных габаритах помещения, но при желании можно сделать высоту меньше. Примерно также рассчитываются, подбираются все остальные фрагменты дома.
Не стоит забывать, что дом должен вписываться также в ландшафт. Если есть какая-то доминанта — высокий холм, например, то просчитывать надо и соотношение с холмом, и с пропорциями участка. В общем, для создания гармоничной усадьбы очень многие факторы надо учитывать.
Не только прямые линии можно использовать. Правда с изогнутыми поверхностями работать сложнее, да и обходятся они дороже — нестандартное устройство всегда более затратное
По такому же принципу разрабатывают внутреннюю планировку, стараясь по возможности соблюдать требуемое соотношение. Но еще раз повторим: по возможности. Не зацикливайтесь на точном соответствии до сантиметра. Важна общая тенденция.
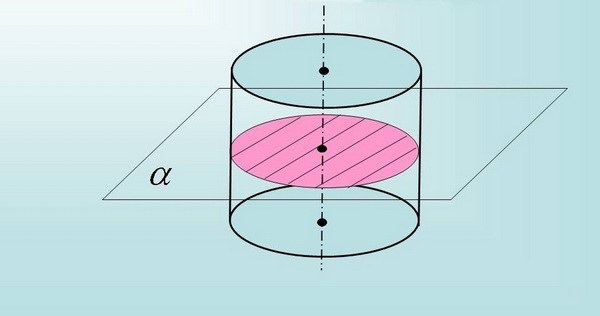
Как вычислить площадь поперечного сечения
Поперечное сечение образуется под прямым углом по отношению к продольной оси. Причем, сечение разных геометрических фигур представлено может быть различными формами. К примеру, у параллелограмма сечение по внешнему виду напоминает прямоугольник или квадрат, у цилиндра – прямоугольник или круг и т.д.
Вам понадобится
- — калькулятор;
- — исходные данные.
Инструкция
Чтобы найти площадь сечения параллелограмма, нужно знать значение его основания и высоту. Если, к примеру, известна лишь длина и ширина основания, то найдите диагональ, используя для этого теорему Пифагора (квадрат длины гипотенузы в прямоугольном треугольнике равен сумме квадратов катетов: a2 + b2 = c2). Ввиду этого, c = sqrt (a2 + b2).
Найдя значение диагонали, подставьте его в формулу S= c*h, где h – высота параллелограмма. Полученный результат и будет величиной площадью поперечного сечения параллелограмма.
Если же сечение проходит вдоль двух оснований, то его площадь рассчитывайте по формуле: S=a*b.
Для вычисления площади осевого сечения цилиндра, проходящей перпендикулярно основаниям (при условии, что одна сторона этого прямоугольника равна радиусу основания, а вторая – высоте цилиндра), используйте формулу S =2R*h, в которой R – величина радиуса окружности (основания), S – площадь поперечного сечения, а h – высота цилиндра.
Если по условиям задачи сечение не проходит через ось вращения цилиндра, но при этом параллельно его основаниям, значит, сторона прямоугольника не будет равна диаметру окружности основания.
Самостоятельно вычислите неизвестную сторону путем построения окружности основания цилиндра, проведения перпендикуляров от стороны прямоугольника (плоскости сечения) к окружности и расчета размера хорды (по теореме Пифагора). После этого подставьте в S =2а*h полученное значение (2а – значение хорды) и рассчитайте площадь поперечного сечения.
Площадь сечения шара определяется по формуле S = πR2. Обратите внимание на то, что, если расстояние от центра геометрической фигуры до плоскости будет совпадать с плоскостью, то площадь сечения равна будет нулю, потому как шар касается плоскости лишь в одной точке.
Обратите внимание
Дважды пересчитывайте полученный результат: так вы не допустите ошибки в расчетах.
Полезный совет
Чтобы рассчитать площадь сечения любой другой геометрической фигуры, воспользуйтесь математическим справочником, в котором подобраны формулы для расчета и даны подробные рекомендации.
Источники:
- Стереометрия. Теория
- поперечное сечение
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как найти площадь поперечного сечения прямоугольника?
Как найти площадь поперечного сечения прямоугольника?
Площадь сечения профилированной трубы считается по формуле площади прямоугольника: S = a * b, где a и b — длины сторон прямоугольника.
Как считать площадь поперечного сечения?
Площадь сечения круга или шара можно найти по формуле:
- S = πR2 …
- c = S*q*r*t*(a2 + b2) …
- S= c*h. …
- S=a*b. …
- S =2R*h. …
- S =2а*h.
Как найти площадь поперечного сечения стержня?
S = π * d 2 / 4, где На этой странице представлен самый простой онлайн калькулятор расчета площади поперечного сечения стержня, если известен диаметр стержня.
Как найти длину трубы зная диаметр?
Внутренний и наружный диаметр, толщина стенки, радиус Имея эти два значения, легко высчитать внутренний диаметр — от наружного отнять удвоенную толщину стенки: d = D — 2*S. Если у вас наружный диаметр 32 мм, толщина стенки 3 мм, то внутренний диаметр будет: 32 мм — 2 * 3 мм = 26 мм.
Как рассчитать объем трубы зная диаметр и длину?
Для расчета необходимо знать данные диаметра трубы. Его обозначают буквой D и рассчитывают по формуле R x 2. Определяется также длина окружности….Сама формула расчета, имеет следующий вид:
- V = S x L.
- Объем трубы – V;
- Площадь сечения – S;
- Длина – L.
Как рассчитать длину трубы по весу?
Расчет ведется по формуле m = ro / 7850 * 0.
Сколько весит 1 метр трубы?
Вес и сортамент стальных магистральных труб по ГОСТ’у /div>
| Наружный диаметр трубы, мм | Толщина стенки, мм | Масса 1 метра погонного, кг |
|---|---|---|
| 377 | 8,5 | 77,25 |
| 9 | 81,68 | |
| 426 | 5 | 51,9 |
| 5,5 | 57,04 |
Сколько весит метр трубы таблица?
Вес трубы стальной
| диаметр трубы, мм | Стенка, мм | Масса 1 метра, кг |
|---|---|---|
| Ø30 | 1,0 мм. |
0,715кг |
| Ø30 | 1,2мм | 0,852кг |
| Ø30 | 1,4мм | 0,987кг |
| Ø30 | (1,5)мм | 1,165кг |
Сколько весит метр трубы 57х3?
Теоретический вес труб стальных круглых
| Наружный диаметр, мм | Толщина стенки, мм | Теоретический расчёт Массы 1м, кг |
|---|---|---|
| Труба 57 | 2,0 | 57х2 вес метра 2,713 |
| Труба 57 | 2,5 | 57х2,5 вес метра 3,360 |
| Труба 57 | 3,0 | 57 х3 вес метра 3,995 |
| Труба 57 | 3,5 | 57х3,5 вес метра 4,618 |
Сколько весит 1 метр трубы диаметром 57 мм?
Вес метра трубы 57 с толщиной стенки 1.
Сколько стоит метр 57 трубы?
Труба электросварная 57 мм — от 100 руб/м купить в Сталь-Эксперт (цена)
Сколько метров в тонне трубы 57?
Теоретический вес горячедеформированных (г/д) бесшовных труб (ГОСТ 8732-78 и ГОСТ 8731-74)
| Наружный диаметр, мм | Толщина стенки, мм | Метров в тонне |
|---|---|---|
| 108 | 5 | 78,7 |
| 5,5 | 71,9 | |
| 6 | 66,3 | |
| 7 | 57,4 |
Сколько метров в тонне трубы?
| Наружный диаметр, мм | Толщина стенки, мм | Ориентировочное количество метров в тонне |
|---|---|---|
| 12 | 1,0 | 3690,04 |
| 1,2 | 3125,00 | |
| 1,4 | 2732,24 | |
| 1,5* | 2577,32 |
Сколько метров профильной трубы в тонне?
Теоретический удельный вес квадратных профильных труб (ГОСТ 8639-82)
| Размеры профильной трубы, мм | Толщина стенки профильной трубы, S, мм | Метров в тонне |
|---|---|---|
| 25 | 1 | 1351,4 |
| 1,5 | 934,6 | |
| 2 | 719,4 | |
| 2,5 | 595,2 |
Как найти 1 погонный метр трубы?
Как посчитать погонный метр? Вам нужно точное значение плотности материала, из которого сделано изделие.
Сколько будет 1 погонный метр?
Это очень упрощает учет. Погонный метр равен одному метру. Это единица измерения длины, без учёта ширины, или толщины. Можно взять в руки рулетку измерить длину в один метр, это и будет тот самый погонный метр.
Как рассчитать цену за погонный метр трубы?
Стоимость 1 погонного метра металлопроката можно определить по универсальной формуле: Цпм = Sпр х ρст х Цт / 1000, где
Как рассчитать цену погонного метра?
При необходимости можно перевести полученную площадь в погонные метры. Формула перевода такова – Pm = S/a, где a – это ширина линолеума. Например, имеется комната шириной 3 м и длиной 7 м.
Как рассчитать цену за квадратный метр?
Для расчета средней стоимости квадратного метра по абсолютному значению нам достаточно суммировать цены, суммировать метры и разделить суммированную цену на суммированную площадь.
Как считается погонный метр?
Погонный метр — это и есть метр, равный 100 см в длину. … Погонный метр — это величина, единица измерения длины или расстояния чего либо в метрах. Погонный метр = метр. В погонных метрах считают определенные отрезки поверхностей, для уточнения, измерения длинны, расстояния.
Расчет прямоугольного сечения балки по условию прочности
Пример решения задачи по подбору минимальных размеров балки прямоугольного поперечного сечения, обеспечивающих её необходимую прочность.
Задача
Для заданной стальной балки подобрать размеры прямоугольного поперечного сечения по условию прочности.
Соотношение сторон сечения h=2b (h – высота, b – ширина).
Полученные размеры принять согласно ГОСТ 6636.
Допустимые напряжения для материала балки [σ]=160МПа.
Другие примеры решений >
Помощь с решением задач >
Решение
Предыдущие пункты решения задачи:
- Определение опорных реакций
- Построение эпюр внутренних поперечных сил и изгибающих моментов
- Расчет момента сопротивления сечения балки по условию прочности
Минимально необходимый расчетный момент сопротивления сечения балки составил
В случаях, когда система изгибающих нагрузок действующих на балку расположена в вертикальной плоскости сечение тоже следует располагать вертикально.
По справочнику находим формулу осевого момента сопротивления прямоугольного сечения
Используя заданное соотношение сторон (h=2b), уменьшим количество переменных в выражении
и запишем необходимое неравенство
откуда находим расчетную высоту прямоугольного сечения
Из заданного соотношения сторон определяем расчетную ширину сечения
Отметим, что полученные размеры являются минимально необходимыми для обеспечения прочности заданной балки.
При отсутствии дополнительных условий расчетные размеры можно округлить до целого значения в миллиметрах исключительно в большую сторону (h=153мм, b=77мм).
По ГОСТ 6636 нормальных линейных размеров выбираются ближайшие значения в сторону увеличения.
Следовательно, за окончательные размеры прямоугольного сечения балки принимаем: h=155мм, b=80мм.
После принятия размеров согласно ГОСТ заданное соотношение сторон может несколько измениться. Это нормально.
Оценка экономичности сечений >
Построение эпюры нормальных напряжений >
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Подробнее
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
На нашем сайте можно бесплатно скачать:
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Сохранить или поделиться с друзьями
Помощь с решением
ВЫБЕРИТЕ РАЗДЕЛ МЕХАНИКИ
- Техническая механика (техмех)
- Теоретическая механика (теормех)
- Сопротивление материалов (сопромат)
- Строительная механика (строймех)
- Теория механизмов и машин (ТММ)
- Детали машин и ОК (ДМ)
Поиск формул и решений задач
Свойства прямоугольного сечения | Calcresource
Соглашение
-Геометрия
-Момент инерции
-Момент инерции и изгиба
-Полярный момент инерции
-Эластичный модуль
-Эластичные напряжения
-пластиковый модул
-около
-эластичные напряжения
-пластик
-около
-Эластичные напряжения
-пластик
-около
-Эластичные напряжения
-пластик
-около ось x
— Вокруг оси y
— Радиус вращения
— Формулы прямоугольного сечения
— Связанные страницы
93}{12}
Момент инерции и изгиб
Момент инерции (секундный момент или площадь) используется в теории балок для описания жесткости балки при изгибе.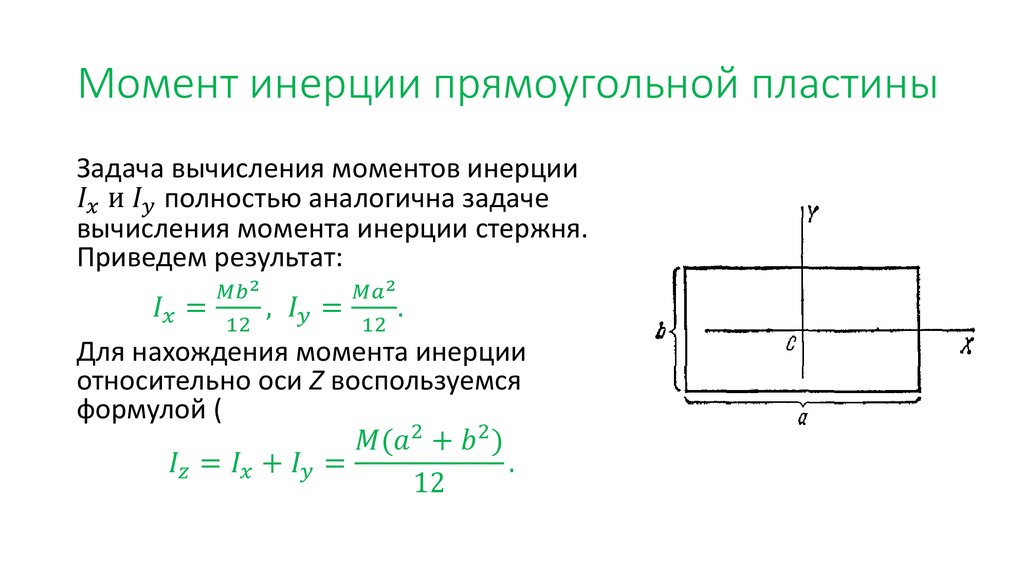
M = Etimes I times kappa
где E — модуль Юнга, свойство материала , а kappa — кривизна балки из-за приложенной нагрузки. Следовательно, из предыдущего уравнения видно, что когда к поперечному сечению балки приложен определенный изгибающий момент М, результирующая кривизна обратно пропорциональна моменту инерции I.94 .
Полярный момент инерции
Полярный момент инерции описывает жесткость поперечного сечения по отношению к крутящим моментам, так же как описанные выше плоские моменты инерции связаны с изгибом. Расчет полярного момента инерции I_z вокруг оси z (которая перпендикулярна плоскости сечения) можно выполнить с помощью теоремы о перпендикулярных осях:
I_z = I_x + I_y
, где I_x и I_y — моменты инерция вокруг осей x и y, которые взаимно перпендикулярны оси z и сходятся в одном начале координат.
Модуль упругости
Модуль упругости S_x любого поперечного сечения вокруг оси x (в центре) описывает реакцию сечения на упругий изгиб.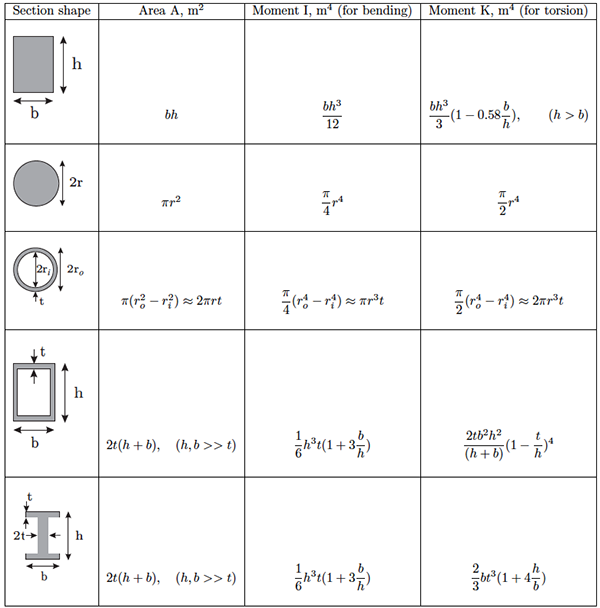
S_x = frac{I_x}{Y}
, где I_x — момент инерции секции вокруг оси x, а Y — расстояние от центра тяжести волокна секции, параллельное оси x и измеренное перпендикулярно от него. Как правило, представляют интерес более удаленные волокна. Для прямоугольника а наиболее удаленными от оси x волокнами являются волокна на верхнем и нижнем краях b на расстоянии, равном h/2. Таким образом, применение приведенной выше формулы для прямоугольного поперечного сечения приводит к следующему выражению для модуля упругого сечения вокруг оси x: 92}{6}
Можно заметить, что формула для S_y становится идентичной формуле для S_x, если заменить b на h и наоборот.
Упругие напряжения
Если к оси x приложен изгибающий момент M_x, сечение будет реагировать нормальными напряжениями, линейно изменяющимися с расстоянием от нейтральной оси (которая в упругом режиме совпадает с центроидальной осью x-x). Над нейтральной осью напряжения равны нулю. Абсолютный максимум сигма будет иметь место на самом удаленном волокне, величина которого определяется формулой: 93 .
Модуль пластичности
Модуль пластичности аналогичен упругому модулю, но определяется с допущением полной пластической текучести поперечного сечения вследствие изгибного изгиба. В этом случае все сечение разделено на две части, одну на растяжение и одну на сжатие, каждая из которых находится под однородным полем напряжений. Для материалов с равными напряжениями текучести при растяжении и сжатии это приводит к разделению сечения на две равные области, A_t, при растяжении, и A_c, при сжатии, разделенные нейтральной осью. Это результат уравновешивания внутренних сил в поперечном сечении при пластическом изгибе. В самом деле, общая сжимающая сила по всей сжимаемой площади будет равна A_cf_y, если предположить условия пластичности (т. е. материал будет деформироваться везде) и что предел текучести при сжатии равен f_y. Точно так же растягивающая сила будет равна A_t f_y, если использовать те же предположения. Обеспечение равновесия:
A_cf_y = A_t f_yRightarrow
A_c= A_t
Ось называется пластической нейтральной осью , а для несимметричных сечений она не совпадает с упругой нейтральной осью (которая снова является центроидальной).
Вокруг оси x
Модуль пластичности при изгибе вокруг оси x определяется по общей формуле:
Z = A_c Y_c + A_t Y_t
где Y_c, расстояние от центра масс области сжатия до пластика нейтральная ось и Y_t — соответствующее расстояние от центра тяжести области растяжения.
В случае прямоугольного поперечного сечения пластическая нейтральная ось проходит через центр тяжести, разделяя всю площадь на две равные части. Область сжатия будет прямоугольником с размерами b и h/2. Его центроид будет находиться на расстоянии, равном h/4, от оси x, как показано на следующем рисунке. То же самое относится и к области растяжения. Следовательно, модуль пластического сечения прямоугольного сечения при изгибе x-x находится следующим образом: 92}{4}
Еще раз, это последнее уравнение может быть получено из модуля пластичности Z_x, если мы заменим h на b и наоборот.
Радиус вращения
Радиус вращения R_g поперечного сечения относительно оси определяется по формуле:
R_g = sqrt{frac{I}{A}}
где I момент инерции поперечного сечения вокруг той же оси и A его площади. Размеры радиуса вращения [Длина]. Он описывает, насколько далеко от центра тяжести распределена область. Малый радиус указывает на более компактное сечение. Для прямоугольного сечения замена приведенного выше выражения дает следующие радиусы вращения вокруг центральных осей x и y соответственно:
R_{gx} = frac{h}{2sqrt{3}}
R_{gy} = frac{b}{2sqrt{3}}
Круг – это фигура с минимальным радиусом вращения по сравнению с любым другим сечением той же площади A.
Формулы для прямоугольного сечения
В следующей таблице приведены формулы, которые можно использовать для расчета основных механических свойств прямоугольного сечения.
Свойства прямоугольного сечения |
|
|---|---|
| Количество 92}{4} | |
| Радиус вращения |
R_{gx} = frac{h}{2sqrt{3}} R_{gy} = frac{b}{2sqrt {3}} |
Связанные страницы
Понравилась эта страница? Поделись с друзьями!
Площадь прямоугольника с калькулятором.
Открытый математический справочник
Главная
Контакт
О
Предметный указатель
Количество квадратных единиц, необходимое для полного заполнения прямоугольника.
Формула: Ширина × Высота
Попробуйте это Перетащите оранжевые точки, чтобы переместить и изменить размер прямоугольника. По размеру прямоугольника
изменяется, площадь пересчитывается.
Формула площади
Площадь прямоугольника находится путем умножения ширины на высоту. Как формула:
где
w это ширина
h это высота
Калькулятор
| Сторона 1 | прозрачный | |
| Сторона 2 | прозрачный | |
| Район: | ||
| Периметр: | ||
| Диагональ: | ||
Используйте калькулятор выше, чтобы вычислить свойства прямоугольника.
На практике часто возникают задачи, которые требуют умения строить сечения геометрических фигур различной формы и находить площади сечений. В данной статье рассмотрим, как строятся важные сечения призмы, пирамиды, конуса и цилиндра, и как рассчитывать их площади.
Объемные фигуры
Из стереометрии известно, что объемная фигура совершенно любого типа ограничена рядом поверхностей. Например, для таких многогранников, как призма и пирамида, этими поверхностями являются многоугольные стороны. Для цилиндра и конуса речь идет уже о поверхностях вращения цилиндрической и конической фигур.

Если взять плоскость и пересечь ею произвольным образом поверхность объемной фигуры, то мы получим сечение. Площадь его равна площади части плоскости, которая будет находиться внутри объема фигуры. Минимальное значение этой площади равно нулю, что реализуется, когда плоскость касается фигуры. Например, сечение, которое образовано единственной точкой, получается, если плоскость проходит через вершину пирамиды или конуса. Максимальное значение площади сечения зависит от взаимного расположения фигуры и плоскости, а также от формы и размеров фигуры.
Ниже рассмотрим, как рассчитывать площади образованных сечений для двух фигур вращения (цилиндр и конус) и двух полиэдров (пирамида и призма).
Цилиндр
Круговой цилиндр является фигурой вращения прямоугольника вокруг любой из его сторон. Цилиндр характеризуется двумя линейными параметрами: радиусом основания r и высотой h. Ниже схематически показано, как выглядит круговой прямой цилиндр.

Для этой фигуры существует три важных типа сечения:
- круглое;
- прямоугольное;
- эллиптическое.
Эллиптическое образуется в результате пересечения плоскостью боковой поверхности фигуры под некоторым углом к ее основанию. Круглое является результатом пересечения секущей плоскости боковой поверхности параллельно основанию цилиндра. Наконец, прямоугольное получается, если секущая плоскость будет параллельна оси цилиндра.
Площадь круглого сечения рассчитывается по формуле:
S1 = pi*r2
Площадь осевого сечения, то есть прямоугольного, которое проходит через ось цилиндра, определяется так:
S2 = 2*r*h
Сечения конуса
Конусом является фигура вращения прямоугольного треугольника вокруг одного из катетов. Конус имеет одну вершину и круглое основание. Его параметрами также являются радиус r и высота h. Пример конуса, сделанного из бумаги, показан ниже.

Видов конических сечений существует несколько. Перечислим их:
- круглое;
- эллиптическое;
- параболическое;
- гиперболическое;
- треугольное.
Они сменяют друг друга, если увеличивать угол наклона секущей плоскости относительно круглого основания. Проще всего записать формулы площади сечения круглого и треугольного.
Круглое сечение образуется в результате пересечения конической поверхности плоскостью, которая параллельна основанию. Для его площади справедлива следующая формула:
S1 = pi*r2*z2/h2
Здесь z — это расстояние от вершины фигуры до образованного сечения. Видно, что если z = 0, то плоскость проходит только через вершину, поэтому площадь S1 будет равна нулю. Поскольку z < h, то площадь изучаемого сечения будет всегда меньше ее значения для основания.
Треугольное получается, когда плоскость пересекает фигуру по ее оси вращения. Формой получившегося сечения будет равнобедренный треугольник, сторонами которого являются диаметр основания и две образующие конуса. Как находить площадь сечения треугольного? Ответом на этот вопрос будет следующая формула:
S2 = r*h
Это равенство получается, если применить формулу для площади произвольного треугольника через длину его основания и высоту.
Сечения призмы
Призма — это большой класс фигур, которые характеризуются наличием двух одинаковых параллельных друг другу многоугольных оснований, соединенных параллелограммами. Любое сечение призмы — это многоугольник. В виду разнообразия рассматриваемых фигур (наклонные, прямые, n-угольные, правильные, вогнутые призмы) велико и разнообразие их сечений. Далее рассмотрим лишь некоторые частные случаи.

Если секущая плоскость параллельна основанию, то площадь сечения призмы будет равна площади этого основания.
Если плоскость проходит через геометрические центры двух оснований, то есть является параллельной боковым ребрам фигуры, тогда в сечении образуется параллелограмм. В случае прямых и правильных призм рассматриваемый вид сечения будет представлять собой прямоугольник.
Пирамида
Пирамида — это еще один многогранник, который состоит из n-угольника и n треугольников. Пример треугольной пирамиды показан ниже.

Если сечение проводится параллельной n-угольному основанию плоскостью, то его форма будет в точности равна форме основания. Площадь такого сечения вычисляется по формуле:
S1 = So*(h-z)2/h2
Где z — расстояние от основания до плоскости сечения, So — площадь основания.
Если секущая плоскость содержит вершину пирамиды и пересекает ее основание, то мы получим треугольное сечение. Для вычисления его площади необходимо обратиться к использованию соответствующей формулы для треугольника.
Площадь боковой поверхности цилиндра
Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:






Видео
Формула площади поверхности цилиндра
Полная площадь поверхности цилиндра является суммой его боковой площади поверхности и площади оснований.
S=Sосн+SбокS=S_{text{осн}}+S_{text{бок}}S=Sосн+Sбок
SоснS_{text{осн}}Sосн — площадь оснований; SбокS_{text{бок}}Sбок — площадь боковой поверхности.
При вычислении площади поверхности цилиндра важным фактором является вид цилиндра. От него зависит и конкретная формула для площади.
Сечения конуса
Конусом является фигура вращения прямоугольного треугольника вокруг одного из катетов. Конус имеет одну вершину и круглое основание. Его параметрами также являются радиус r и высота h. Пример конуса, сделанного из бумаги, показан ниже.

Видов конических сечений существует несколько. Перечислим их:
- круглое;
- эллиптическое;
- параболическое;
- гиперболическое;
- треугольное.
Они сменяют друг друга, если увеличивать угол наклона секущей плоскости относительно круглого основания. Проще всего записать формулы площади сечения круглого и треугольного.
Круглое сечение образуется в результате пересечения конической поверхности плоскостью, которая параллельна основанию. Для его площади справедлива следующая формула:
S1 = pi*r2*z2/h2
Здесь z — это расстояние от вершины фигуры до образованного сечения. Видно, что если z = 0, то плоскость проходит только через вершину, поэтому площадь S1 будет равна нулю. Поскольку z < h, то площадь изучаемого сечения будет всегда меньше ее значения для основания.
Треугольное получается, когда плоскость пересекает фигуру по ее оси вращения. Формой получившегося сечения будет равнобедренный треугольник, сторонами которого являются диаметр основания и две образующие конуса. Как находить площадь сечения треугольного? Ответом на этот вопрос будет следующая формула:
S2 = r*h
Это равенство получается, если применить формулу для площади произвольного треугольника через длину его основания и высоту.
Геометрическая фигура
Сначала дадим определение фигуре, о которой пойдет речь в статье. Цилиндр представляет собой поверхность, образованную параллельным перемещением отрезка фиксированной длины вдоль некоторой кривой. Главным условием этого перемещения является то, что отрезок плоскости кривой принадлежать не должен.
На рисунке ниже показан цилиндр, кривая (направляющая) которого является эллипсом.
Здесь отрезок длиной h является его образующей и высотой.
Видно, что цилиндр состоит из двух одинаковых оснований (эллипсы в данном случае), которые лежат в параллельных плоскостях, и боковой поверхности. Последней принадлежат все точки образующих линий.
Задания для самостоятельной работы
Имеется некий сосуд цилиндрической формы. Емкость заполнили водой объемом 2000см3. После этого вода поднялась до уровня в 12 см. Затем в жидкость опустили предмет, что привело к ее подъему на 9 см. Требуется вычислить объем предмета, погруженного в воду, в см3.
Сосуд цилиндрической формы заполнен водой до уровня в 16 см. Жидкость перелили в другой сосуд аналогичной формы, диаметр которого в два раза больше по сравнению с диаметром первого. Нужно определить, на какой высоте будет находиться уровень воды во втором сосуде.
Имеется два цилиндра. Объем первой фигуры составляет 12м3. Высота второй фигуры в три раза больше по сравнению с первой, а радиус ее основания в два раза меньше, чем у первого цилиндра. Требуется определить, чему равен объем второго цилиндра.
Емкость в форме цилиндра заполнили водой в количестве 6см3. В жидкость опустили какой-то предмет, что привело к подъему уровня воды в 1,5 раза. Необходимо вычислить объем погруженного в жидкость предмета.
При сравнении двух кружек в форме цилиндра выяснили, что первая в два раза выше, чем вторая. Вместе с тем вторая кружка в 1,5 раза шире по сравнению с первой. Требуется найти отношение объема второй кружки к объему первой.




















