|
Площадь диагонального сечения куба очень легко найти, если известна величина его ребра или площадь одной грани. Если известна величина ребра куба, тогда площадь сечения находим по формуле S(диагонального сечения) = 1,414*а*а* Если известна площадь одной из граней куба, тогда формула площади сечения куба будет выглядеть так S(диагонального сечения) = 1,414*S(грани куба) Примечание — для удобства вместо корень из двух написано его числовое значение округленное до тысячных. модератор выбрал этот ответ лучшим Степан-16 5 лет назад Осевым сечением куба будет прямоугольник, одна сторона которого равна длине ребра, а другая — диагонали грани. Если ребро известно и равно а. То диагональ грани будет одновременно гипотенузой равностороннего прямоугольного треугольника, катеты которого — это два смежных ребра куба или две стороны квадрата грани. Отсюда диагональ (гипотенузу) можно вычислить по теореме Пифагора или отношением длина ребра а к синусу (или косинусу) 45град (половины прямого угла). Синус 45град равен половине кв. корня из 2, или 0.707. Поэтому диагональ b = a/0.707. И площадь диагонального сечения квадрата: S = а*b = (а^2)/0.707(где а^2 — это а в квадрате, или во второй степени). Ксарфакс 4 года назад Куб — это правильный многогранник, у которого каждая грань (всего их 6) является квадратом и все ребра равны между собой. Диагональное сечение куба — это прямоугольник, у него меньшая сторона совпадает с ребром, а большая — с диагональю грани (основания). Таким образом, чтобы найти площадь диагонального сечения куба, нужно воспользоваться формулой площади прямоугольника: S(пр) = a * b. Пусть ребро куба равно a. Тогда длину диагонали основания можно высчитать с помощью теоремы Пифагора. Это гипотенуза в прямоугольном треугольнике, у которого катеты равны между собой. Длина диагонали будет равняться a√2. Получаем формулу площади диагонального сечения: Нужно возвести ребро куба в квадрат и умножить полученное значение на √2 (корень из 2 равен приблизительно 1,41). ** Пример Если длина ребра куба составляет 10 см, то площадь сеч. будет такой: S = a²√2 ≈ 10 * 10 * 1,41 = 141 см. Марина Вологда 4 года назад Если в условии задачи необходимо найти площадь диагонального сечения куба, значит нам известно либо площадь одной грани или величина его ребра. Формула для нахождения площади диагонального сечения куба с известной величиной ребра: S=а*a * квадратный корень из 2 (где a — величина ребра). Пример: Длина ребра куба равна 5 см, высчитываем площадь сечения: S = axa умноженное на квадратный корень из 2 = 5 х 5 х 1,41 = 35,25 см. А вот здесь один из примеров решения по нахождению площади диагонального сечения куба: А вот еще одно решение, которое Вам поможет разобраться и подставить в формулу значения: Нахождение площади диагонального сечения куба задача не сложная, ведь у куба все его стороны равны между собой, а грани представляют собой квадраты. Поэтому если построить сечение куба проходящее через диагонали противоположных граней мы получим прямоугольник, у которого меньшие стороны кажутся равными стороне куба, пусть это классически будет А, а большие стороны будут равны диагоналям квадрата со стороной А. Формула для нахождения диагоналей квадрата вот: D=a*√2 Площадь прямоугольника — это произведение его сторон и тогда формула площади диагонального сечения куба принимает вид: S=D*a Или: S=а*a*√2 Бархатные лапки 4 года назад Куб — это геометрическая фигура, правильный многогранник, все его грани (а их шесть) представляют собой квадраты. Диагональное сечение куба представляет собой прямоугольник, меньшая из сторон будет равняться длине ребра куба, а другая сторона равняется — диагонали грани. Для начала нам нужно найти площадь прямоугольника, ее можно найти по формуле: S(пр) = a * b. Ребро обозначим — а. Другую сторону прямоугольника (б) можно вычислить по формуле Пифагора. Тогда у нас получается длина диагонали — a√2. Далее выводим формулу площади диагонального сечения — S=а*a*√2. Рассчитаем площадь диагонального сечения куба на примере: Допустим у нас длина ребра — 4 см. Подставляем по формуле: 4*4*1,41=22,56. IrinaKn 9 лет назад Если я правильно поняла, при диагональном сечение вы получите поверхность — прямоугольник, две стороны которого будут равные сторонам куба, а другие две — диагонали на любой из поверхностей куба (т.е. любого квадрата). Т.о., если у куба сторона = а, то вы получите прямоугольник со сторонами а и а*корень из 2 Т.о. искомая площадь = а*(а * корень из 2)= (а в квадрате) * (корень из 2). Помощни к 7 лет назад Достаточно узнать длину любого ребра объемной фигуры, в которой находится диагональное сечение. Если найдете длину ребра, то сможете найти площадь по формуле: длина ребра в квадрате помножить на корень двух. Вот формула: Валерий Альбертович 4 года назад Площадь диагонального сечения куба можно найти несколькими способами, в зависимости от того, какие данные нам известны. Если в нашем распоряжении информация о площади одного из граней куба, то диагональное сечение куба будет находиться по формуле: S (диагонального сечения) = S (грани куба) * √2 Если же в нашем распоряжении информация о величине ребра куба, то в таком случае формула будет выглядеть так: S (диагонального сечения) = a² * √2 88SkyWalker88 4 года назад Чтобы найти площадь диагонального сечения куба, необходимо воспользоваться формулой: S=а*a*√2 S — так обозначается площадь. а — это сторона куба (ее значение нам известно). √2 равно 1,41. Предположим, что по условию задачи сторона куба (то есть а) равна 5. Подставляем в формулу: S=5*5*1,41=25*1,41=35,25 Знаете ответ? |
Площадь куба, формула площади куба, найти площадь куба онлайн. Площадь сечения куба, формула площади сечения куба.
Формула площади куба
Для того, чтобы перейти к теме «формулы площади куба» — давайте нарисуем или предоставим, что такое куб.
Куб — это фигура с одинаковыми сторонами, угол между которыми равен 90°.
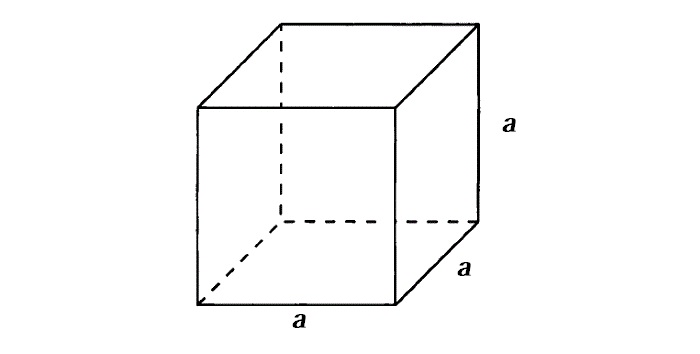
Формула площади куба звучит так :
Если сторона куба — «а».
Площадь куба равна 6 умноженное на а²
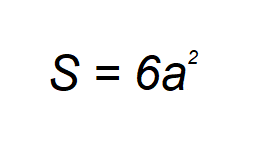
Доказательство формулы площади куба
Для того, чтобы доказать формулу «площади куба» Вам потребуется
Взглянуть на куб и вы увидите, что количество сторон куба — 6. И каждая сторона куба состоит из квадрата, со стороной «а».
Вы знаете площадь квадрата, которая выражается формулой:
S = a²
Выше вы уже сказали, что сторон у куба 6, то нужно площадь одного квадрата умножить на 6.
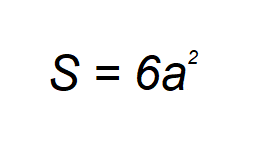
Вывод доказательства формулы куба:
Вы доказали, что «Площадь куба равна 6 умноженное на а²«
Задача : найдите площадь куба, если известна сторона.
Условие задачи :
Найдите площадь куба. если известна сторона куба, которая равна 5см.
Вспоминаем уже приведенную формулу куба :
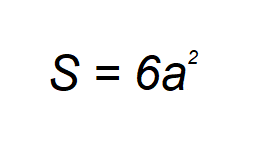
И букву a — сторону куба заменяем на наше значение — 5см
S = 6a² = 6 * 5² = 6 * 25 = 150
Ответ:
Если сторона куба равна 5см, то площадь куба равна 150см²
Для проверки правильности решения задачи «найдите площадь куба, если известна сторона» — воспользуйтесь онлайн калькулятором «подсчета площади куба» — см. ниже:
Найти площадь куба онлайн
Для того чтобы найти площадь куба онлайн, вам потребуется :
Форма для подсчета площади куба онлайн
Сторона куба — заполнить значением стороны куба.
И нажать кнопку найти площадь куба.
Формула площади сечения куба
Сформулируем «формулу площади сечения куба» начнем…
Если сторона куба — — «а».
То формула площади сечения куба звучит так:
Сечение площади куба равно произведению квадрата стороны на корень из двух.
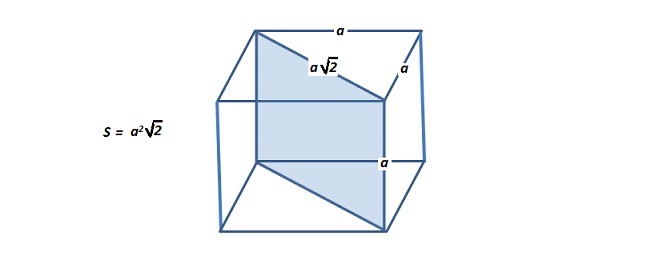
Доказательство формулы площади сечения куба
Выше Вы рассмотрели формулу «площади сечения куба«, теперь… давайте докажем «формулу площади сечения куба«.
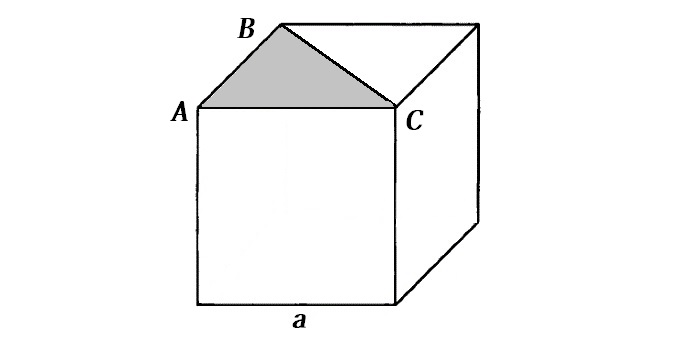
Нам нужно найти диагональ треугольника ABC — что будет одной из сторон сечения куба.
Вспоминаем теорию Пифагора
с² = а² + b²
Если мы переведем в наши буквенные обозначения, для нашего треугольника, то:
BC² = AB² + AC²
В нашем случае «AB = AC= a» — из чего получаем :
BC² = а² + а² = 2а²
Теперь извлекаем корень с двух сторон:
√BC² = √2а²
Мы нашли одну сторону сечения куба:
BC = а√2
Мы нашли сторону сечения куба это — BC
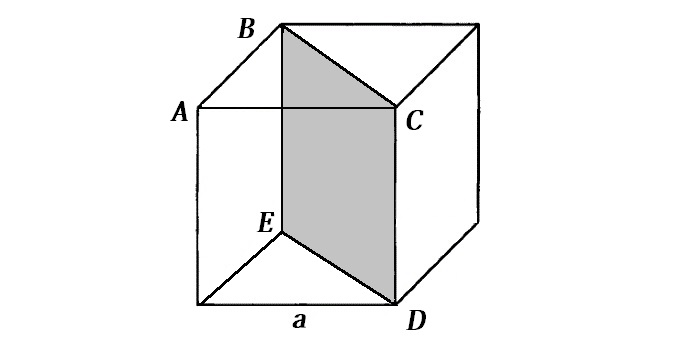
Теперь мы можем построить сечение куба:
Т.е нам нужно найти площадь прямоугольника BCDE.
Площадь прямоугольника равна :
S = BC * CD
Выше, мы уже нашли BC = а√2
Как мы знаем из условия, что это куб, а у куба все стороны равны, то CD = «a».
Заменяем BC и CD.
S = а√2 * a = a²√2
Найти площадь сечения куба онлайн
Для того, чтобы найти площадь сечения куба онлайн нам понадобится формула площади сечения куба и немного вернуться к теории, чтобы…
добавить ясности, как видим, что в формуле присутствует корень из 2, что равно:
1.4142135623731
И далее к форме:
Форма для подсчета площади сечения куба
Для того, чтобы подсчитать «площадь сечения куба» вам понадобится:
В первом поле выбираем диапазон числа(см. выше), диапазон от 1 до 13, который будет показывать ваш выбор сколько чисел после запятой оставить!
Во втором поле вбиваем размер стороны куба.
И далее вам остается подсчитать площадь сечения куба онлайн! Нажимаем кнопку — «найти площадь сечения куба«.
Задача: площадь сечения куба
Условие задачи :
Задача : найдите площадь сечения куба.
Найдите площадь сечения куба, если известна сторона, которая равна 10см.
Для решения данной задачи, нам потребуется знать формулу сечения площади куба
Вспоминаем площадь сечения куба:
S = a²√2
Заменяем а на 10, корень квадратный из 2 округлим до 1.4 :
S = 10²√2 = 100 * 1.4 = 140см².
Более точные вычисления «площади сечения куба » вы можете произвести в форме выше пунктом!
Так… 48, значит. Во-первых, что такое «Боковая поверхность куба»? где у куба бока?… Ну да ладно, это еще не все. Что такое «Осевое сечение»? У куба есть несколько способов сечения через оси его симметрии. Куб — не сфера, не конус и не цилиндр, чтобы однозначно можно было сказать «осевое сечение» Поэтому вот такое решение 🙂
У куба одинаковых 6 граней, поэтому площадь каждой грани 1, то есть и ребро куба равно 1. А «осевое сечение» куба просто равно грани. То есть его площадь тоже 1.
На самом деле куб можно рассечь еще через два противоположных ребра и диагонали противоположных граней, это сечение тоже проходит через ось симметрии куба, площадь такого сечения √2;
-
Комментариев (0)
Как вычислить площадь сечения
При решении задач по геометрии приходится вычислять площади и объемы фигур. Если сделать в любой фигуре сечение, обладая информацией о параметрах самой фигуры, можно найти и площадь этого сечения. Для этого необходимо знать специальные формулы и обладать пространственным мышлением.
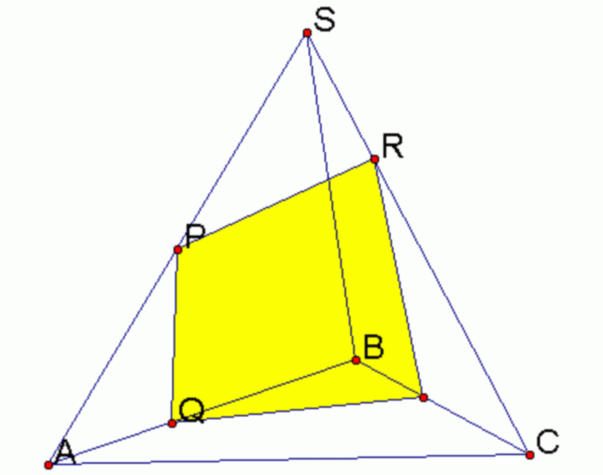
Вам понадобится
- Линейка, карандаш, ластик.
Инструкция
Шар является частным случаем простейшей объемной фигуры. Через него можно провести бесконечное количество сечений, и любое из них окажется кругом. Это произойдет независимо от того, насколько близко сечение расположено к центру шара. Вычислить площадь получившегося сечения проще всего в том случае, если оно проведено точно через центр шара, радиус которого известен. В таком случае площадь сечения равна:S=πR^2.
Другой фигурой, площадь сечения которой требуется найти в задачах по геометрии, является параллелепипед. Он имеет ребра и грани. Гранью называется одна из плоскостей параллелепипеда (куба), а ребром — сторона. Параллелепипед, у которого ребра и грани равны, называется кубом. Все сечения куба — квадраты. Зная это свойство, вычислите площадь сечения-квадрата:S=a^2, где a — ребро куба и сторона сечения.
Если в условиях задачи приведен обычный параллелепипед, у которого все грани являются разными, сечение может быть как квадратом, так и прямоугольником с различными сторонами. Сечение, проведенное параллельно двум квадратным граням, является квадратом, а сечение, проведенное параллельно двум прямоугольным — прямоугольником. Если сечение проходит через диагонали параллелепипеда, оно также является прямоугольником.
умножения диагонали нижнего основания на высоту параллелепипеда:S=d*h, где d — диагональ основания, h — высота основания.
Конус — одна из тех фигур вращения, сечения которой могут иметь различную форму. Если рассечь конус параллельно нижнему основанию, сечением будет круг, а если провести сечение параллельно пополам через вершину конуса, получится треугольник. В других случаях сечениями будут трапециевидные фигуры.Если сечением является круг, вычисляйте его площадь по следующей формуле:S=πR^2.Площадь сечения, представляющего собой треугольник, равно произведению половины основания на высоту:S=1/2f*h , где f — основание треугольника, h — высота треугольника.
Источники:
- как найти площадь получившейся фигуры
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Слайд 1
Построение сечения куба, нахождение его координат и площади

Ларионова Н.Е.
учитель математики МАОУ ЛМИ
г. Саратов
Слайд 2
ЗАДАЧА
по нахождению сечения куба,
его координат и

площади
Слайд 3
Задача №1
Построить сечение куба, проходящего через

точки P, Q, R, найти координаты точек сечения и
площадь сечения,
если P-середина BB1,
Q-середина B1C1,
R=D.
Слайд 4
B
C
D
C¹
B¹
A
A¹
D¹
Q
P
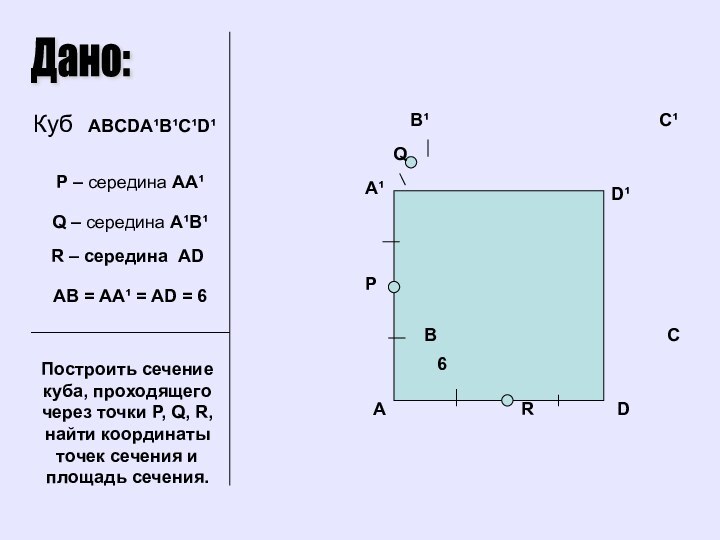
Дано:
Куб ABCDA¹B¹C¹D¹
P – середина BB¹
Q – середина
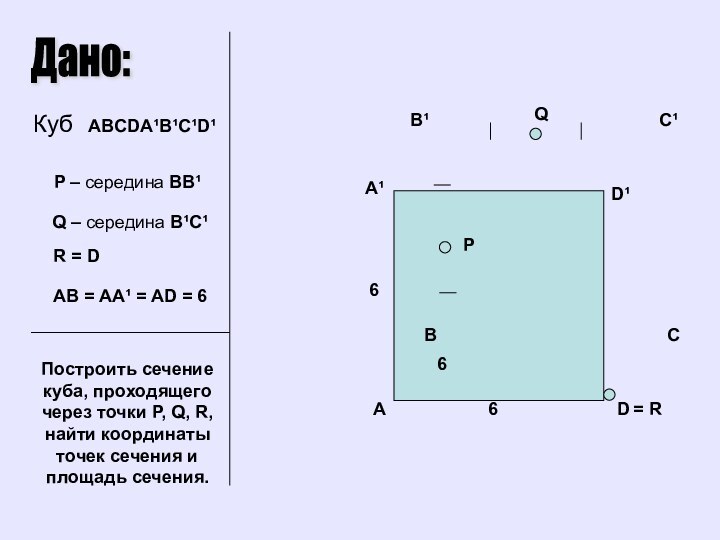
B¹C¹
R = D
Построить сечение куба, проходящего через точки P,
Q, R, найти координаты точек сечения и площадь сечения.
AB = AA¹ = AD = 6
6
6
6
= R
Слайд 5
Рассмотрим заднюю плоскость BB¹CC¹
B
B¹
C
C¹
P
Q
A²
C²
3
3
3
3
3
3
BB¹ = B¹C¹ = 6
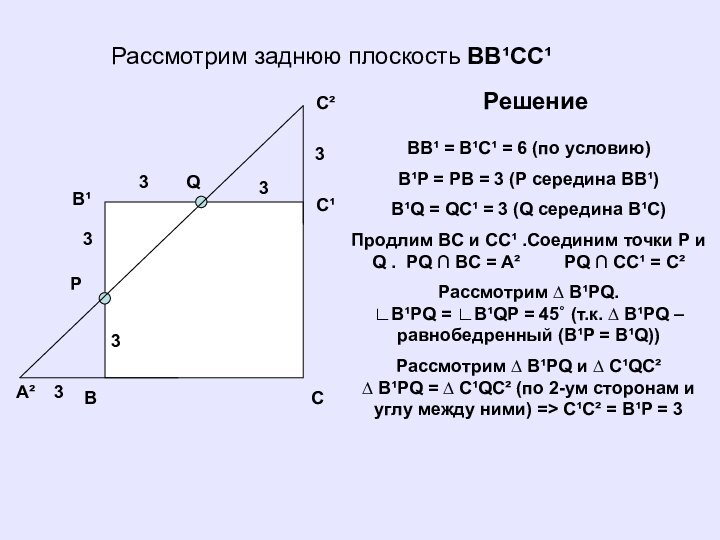
(по условию)
B¹P = PB = 3 (P середина BB¹)
B¹Q
= QC¹ = 3 (Q середина B¹C)
Продлим BC и CC¹ .Соединим точки P и Q . PQ ∩ BC = A² PQ ∩ CC¹ = C²
Рассмотрим ∆ B¹PQ. ∟B¹PQ = ∟B¹QP = 45˚ (т.к. ∆ B¹PQ – равнобедренный (B¹P = B¹Q))
Рассмотрим ∆ B¹PQ и ∆ C¹QC² ∆ B¹PQ = ∆ C¹QC² (по 2-ум сторонам и углу между ними) => C¹C² = B¹P = 3
Решение
Слайд 6
Рассмотрим боковую плоскость DD¹CC¹
D = R
D¹
C
C¹
C²
F
DC =
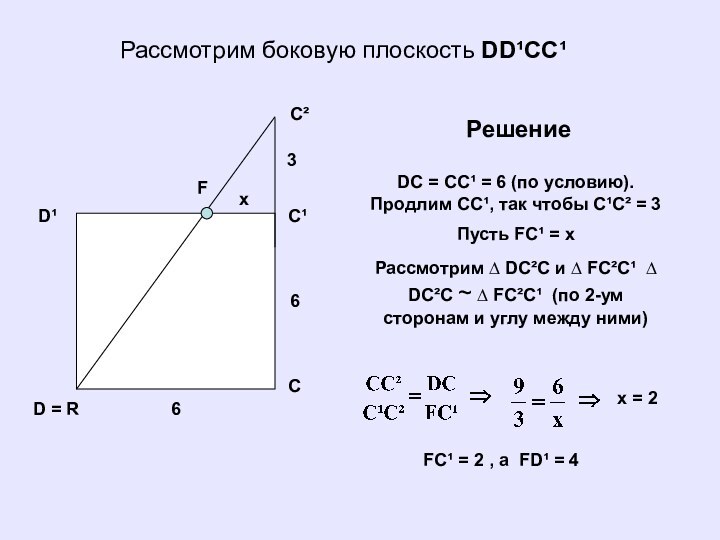
CC¹ = 6 (по условию). Продлим СC¹, так чтобы
C¹C² = 3
Пусть FC¹ = x
Рассмотрим ∆ DC²C и ∆ FC²C¹ ∆ DC²C ~ ∆ FC²C¹ (по 2-ум сторонам и углу между ними)
Решение
3
6
6
x
x = 2
FC¹ = 2 , a FD¹ = 4
Слайд 7
Рассмотрим нижнюю плоскость ABCD
A
B
C
E
D
A²
6
6
3
y
Решение
BC = CD =
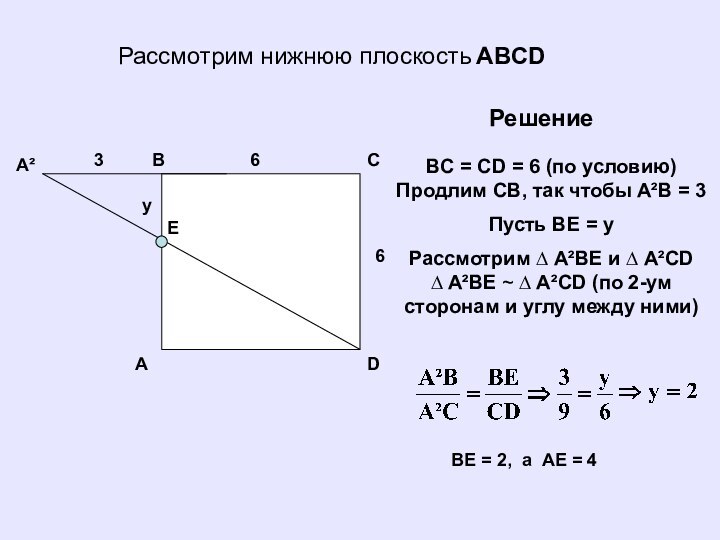
6 (по условию) Продлим СB, так чтобы A²B =
3
Пусть BE = y
Рассмотрим ∆ A²BE и ∆ A²CD ∆ A²BE ~ ∆ A²CD (по 2-ум сторонам и углу между ними)
BE = 2, а AE = 4
Слайд 8
Q
P
D = R
A
A¹
B¹
C¹
C
D¹
B
F
E
A²
C²
Q
F
R
E
P
Сечение куба (PQFRE)
Сечение куба, проходящей через
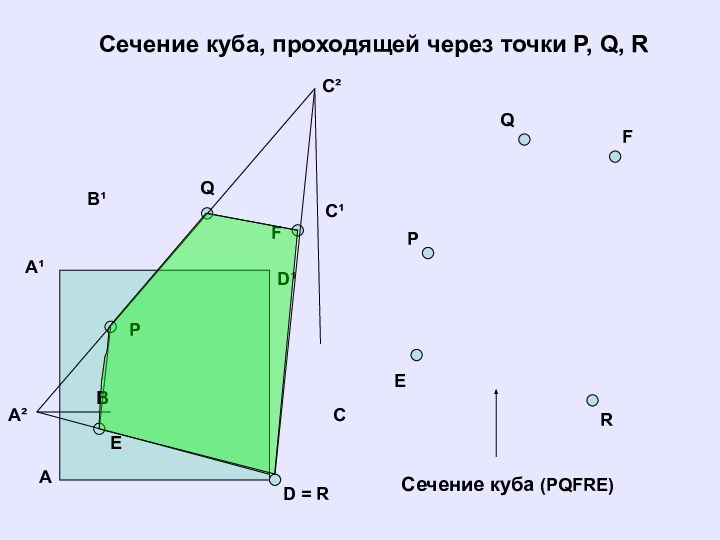
точки P, Q, R
Слайд 9
Q
P
D = R
A
A¹
B¹
C¹
C
D¹
B
F
E
Координаты точек сечения куба
x
y
z
3
3
3
3
6
2
2
P (0, 0,
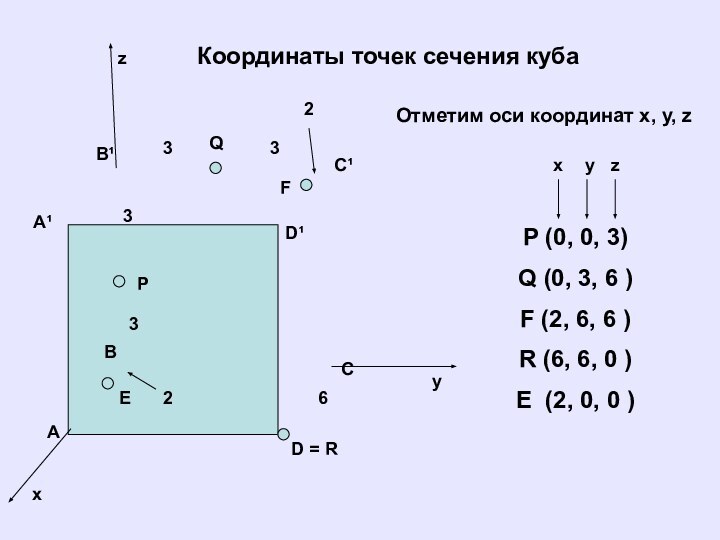
3)
Q (0, 3, 6 )
F (2, 6, 6 )
R
(6, 6, 0 )
E (2, 0, 0 )
x
y
z
Отметим оси координат x, y, z
Слайд 10
Нахождение площади сечения куба
Q
P
E
F
R
Разобьём плоскость сечения куба на
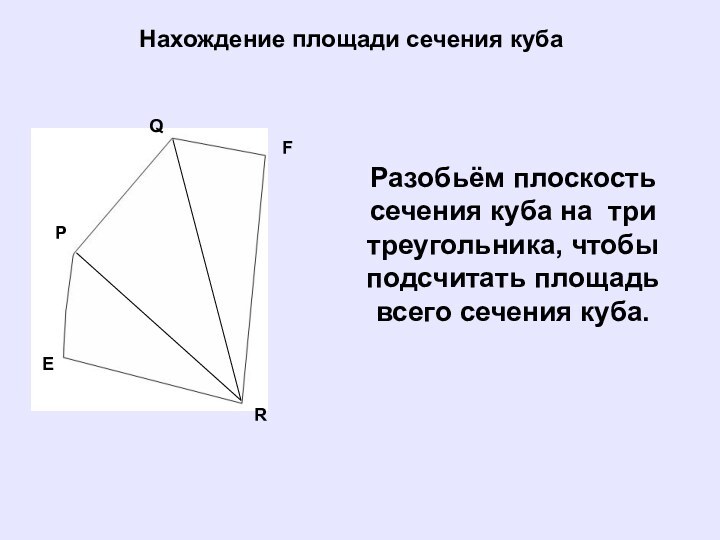
три треугольника, чтобы подсчитать площадь всего сечения куба.
Слайд 11
S ∆ EPR =
Рассмотрим ∆ EPR
E (2, 0,

0 )
Q (0,
3, 6 ) R (6, 6, 0 )
S ∆ EPR =
Q
F
P
E
R
Слайд 12
Рассмотрим ∆ QPR
S ∆ QPR =
P (0, 0,

3)
Q (0, 3,
6 ) R (6, 6, 0 )
S ∆ QPR =
Q
E
R
F
P
Слайд 13
Рассмотрим ∆ FQR
F (2, 6, 6 )

Q (0, 3, 6 )
R (6, 6, 0 )
S ∆ FQR =
S ∆ FQR =
Q
P
F
E
R
Слайд 14
Q
P
E
F
R
Нахождение площади сечения куба
∆ QPR +
+ ∆ QPR
+
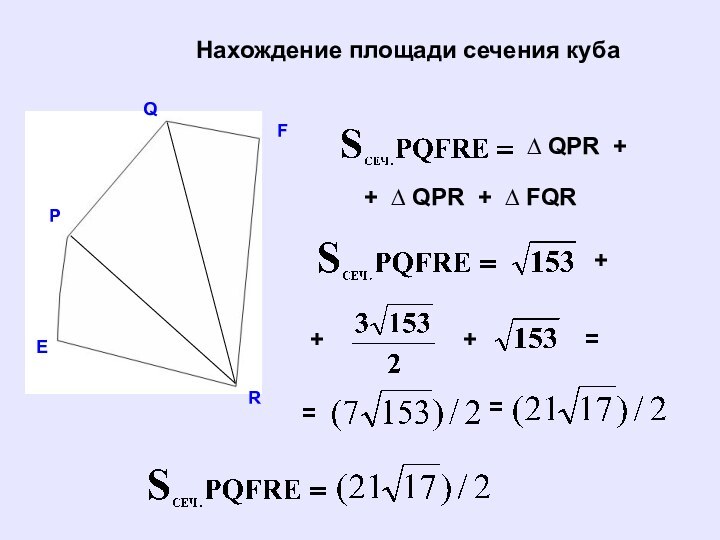
∆ FQR
+
+
+
=
=
=
Слайд 15
Q
F
R
E
P
Сечение куба (PQFRE)
P (0, 0, 3)
Q (0, 3,
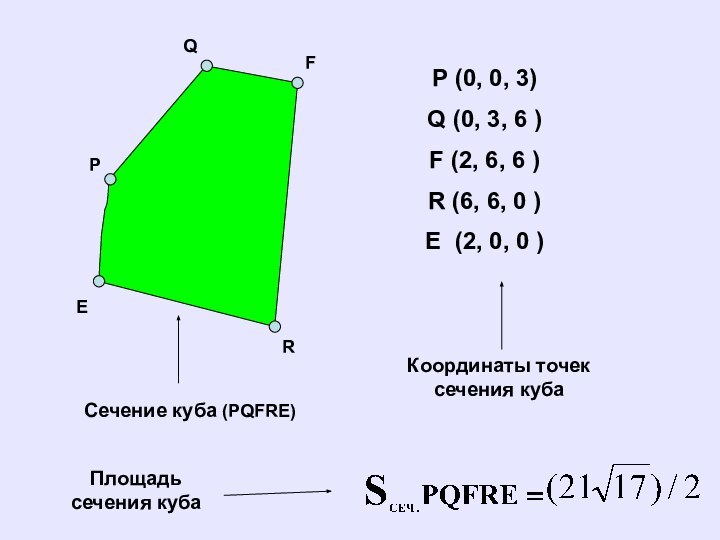
6 )
F (2, 6, 6 )
R (6, 6, 0
)
E (2, 0, 0 )
Координаты точек сечения куба
Площадь сечения куба
Слайд 16
Задача №2
Построить сечение куба, проходящего через

точки P, Q, R, найти координаты точек сечения и
площадь сечения,
если P-середина AA1,
Q-середина A1B1,
R- серединаAD.
Слайд 17
B
C
D
C¹
B¹
A
A¹
D¹
Q
P
Дано:
Куб ABCDA¹B¹C¹D¹
P – середина АА¹
Q – середина
А¹В¹
R – середина АD
Построить сечение куба, проходящего через точки
P, Q, R, найти координаты точек сечения и площадь сечения.
AB = AA¹ = AD = 6
6
Слайд 18
B
C
D
C¹
B¹
A
A¹
D¹
Q
P
6
R
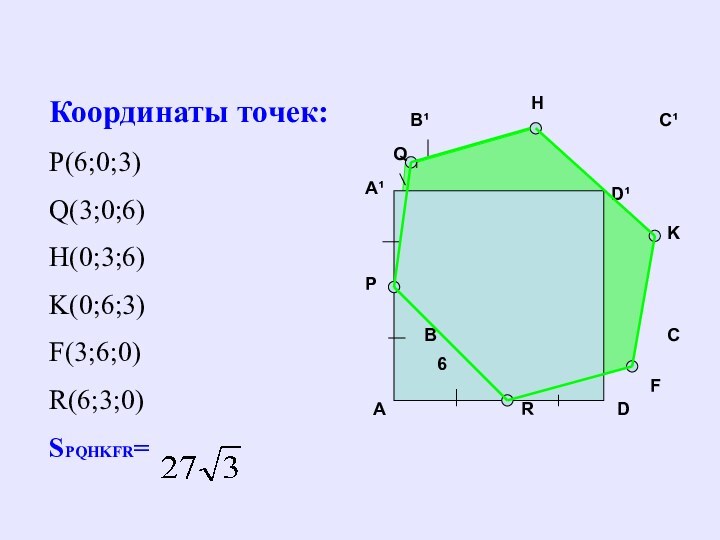
Координаты точек:
Р(6;0;3)
Q(3;0;6)
H(0;3;6)
K(0;6;3)
F(3;6;0)
R(6;3;0)
SPQHKFR=
H
K
F
Слайд 19
Задача №3
Построить сечение куба плоскостью, проходящей

через точки P, Q, R, найти координаты точек сечения,
если P принадлежит AA1,
AP=2,
Q принадлежит A1D1,
D1Q=2,
R=B.
Слайд 20
B
C
D
C¹
B¹
A
A¹
D¹
Q
P
6
R
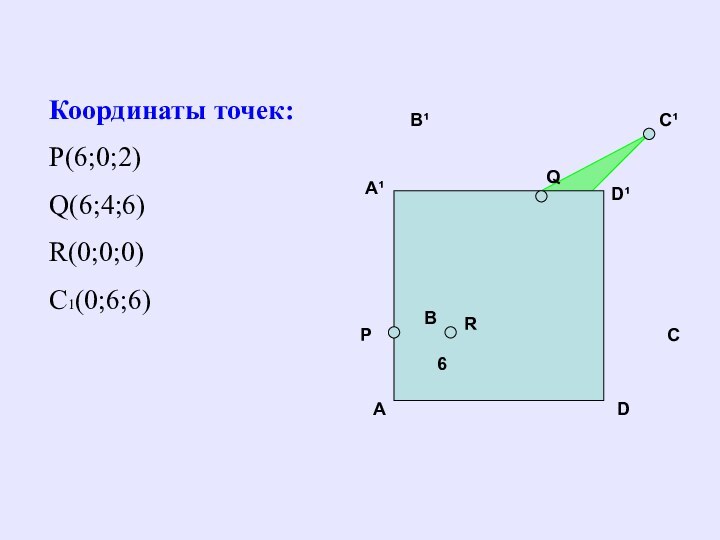
Координаты точек:
Р(6;0;2)
Q(6;4;6)
R(0;0;0)
C1(0;6;6)
Слайд 21
Задача №4
Построить сечение куба плоскостью, проходящей

через точки P, Q, R, найти координаты точек сечения,
если P принадлежит AA1,
AP=2,
Q –середина B1C1,
R принадлежит DD1,
D1R=2.
Слайд 22
B
C
D
C¹
B¹
A
A¹
D¹
Q
P
6
R
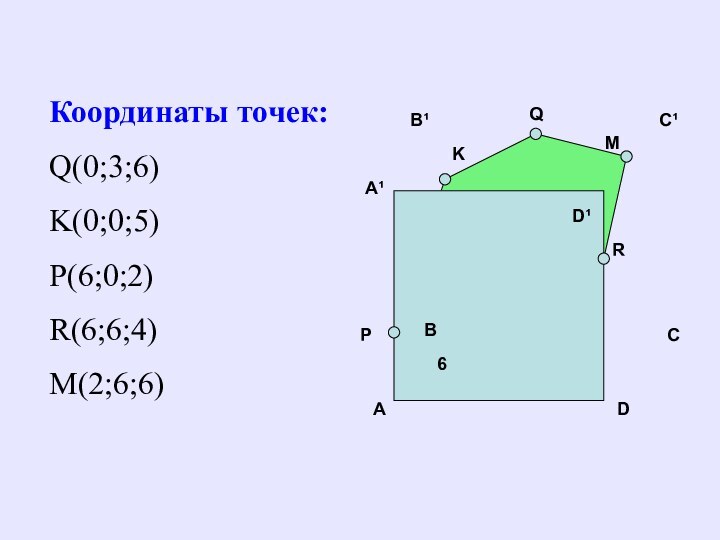
Координаты точек:
Q(0;3;6)
K(0;0;5)
Р(6;0;2)
R(6;6;4)
M(2;6;6)
K
M
Слайд 23
Задача №4
Построить сечение куба плоскостью, проходящей

через точки P, Q, R, найти координаты точек сечения
и площадь сечения,
если P принадлежит BB1,
BP=2,
Q –середина CC1,
C1Q=2,
R принадлежит DD1,
D1R=2.
Слайд 24
B
C
D
C¹
B¹
A
A¹
D¹
Q
M
6
R
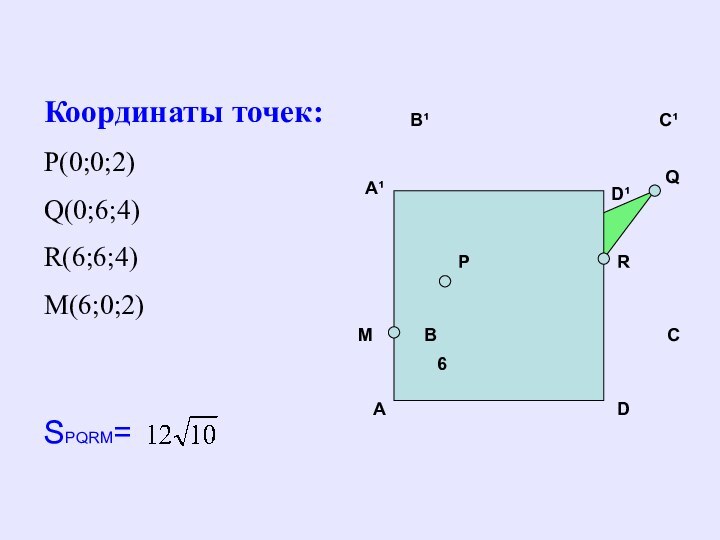
Координаты точек:
Р(0;0;2)
Q(0;6;4)
R(6;6;4)
M(6;0;2)
SPQRM=
P
Слайд 25
Задачи для самостоятельного решения:
Построить сечение куба плоскостью, проходящей

через точки P, Q, R, найти координаты точек сечения
и площадь сечения, если:
P принадлежит CC1,C1P=2,
Q- середина AD,R-середина A1B1.
2. P принадлежит CC1,C1P=1,
Q- середина AD,R-середина AA1.
Слайд 26
3. P принадлежит DD1,D1P=1,
Q-

середина AD,R-середина AB.
4. P принадлежит AA1, A1P=1,
Q- середина D1D, R принадлежит CC1, CR=1.
5. P принадлежит BB1,BP=2,
Q- середина C1D1,R-середина AA1.