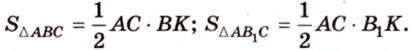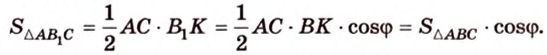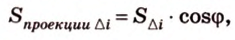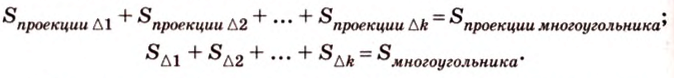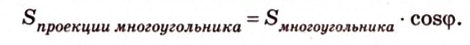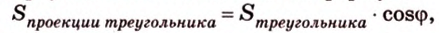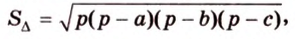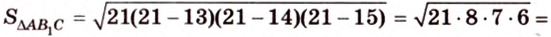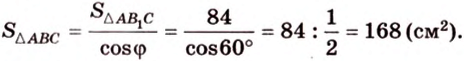Как найти площадь ортогональной проекции многоугольника - AvtoShod.ru

19
Фев 2014

Категория: Справочные материалы

Площадь ортогональной проекции многоугольника

2014-02-19
2014-02-19

Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекций.

Докажем теорему для треугольника. Поскольку многоугольник разбивается на треугольники, сумма площадей которых есть площадь многоугольника, то и для многоугольника теорема будет верна.

Доказательство:

Пусть треугольник – проекция треугольника на проецируемую плоскость.

Докажем, что

$S_{A_1B_1C_1}=S_{ABC}cdot cosalpha$ ,

где – угол между плоскостями

Для этого разобьем треугольник на два треугольника c общей стороной , параллельной прямой пересечения плоскостей . (Частный случай, когда одна из сторон треугольника параллельна линии пересечения плоскостей , можно рассмотреть отдельно (самостоятельно)).

Проекция треугольника – треугольник . Причем .

Пусть – перпендикуляр к . Тогда по т. о трех перпендикулярах и – перпендикуляр к . Стало быть, – угол между плоскостями треугольников (проецируемого и проекции).

Пусть – точка пересечения и , – проекция т. на плоскость . Очевидно, – высота треугольника ( – высота треугольника ).

Из треугольника

$cosalpha =frac{B_1H}{BH}$

Но и

$frac{HT_1}{HT}=cosalpha$

Тогда $BT=BH-HT=frac{1}{cosalpha }(BH_1-HT_1)=frac{B_1T_1}{cosalpha}.$

Имеем: $S_{ABM}=frac{1}{2}BTcdot AM=frac{1}{2}cdot frac{B_1T_1}{cosalpha}cdot AM=frac{S_{A_1B_1M_1}}{{cosalpha}}.$

Аналогичные рассуждения – для пары треугольников и :

$S_{AMC}=frac{1}{2}CRcdot AM=frac{1}{2}cdot frac{C_1R_1}{cosalpha}cdot AM=frac{S_{A_1M_1C_1}}{{cosalpha}}$

(где – высота треугольника , – ее проекция)

Итак, суммируя площади треугольников и соответственно, получаем

$S_{ABC}=frac{S_{A_1B_1C_1}}{cosalpha}$

или

$S_{A_1B_1C_1}=S_{ABC}cdot cosalpha$

Что и требовалось доказать.

Пример.

Ребро куба равно 2 см. Через диагональ основания под углом $45^{circ}$ к плоскости основания проведена плоскость, пересекающая боковое ребро. Найти площадь сечения.

Решение:

Пусть плоскость сечения проведена через диагональ и пересекает боковое ребро () в точке .

По вышеуказанной теореме

$S_{BDT}=frac{S_{BCD}}{cosalpha},$

где треугольник – проекция треугольника на плоскость основания, – угол между плоскостями

$S_{BDT}=frac{2}{frac{sqrt2}{2}}=2sqrt2.$

Ответ:

Применение теоремы можно также посмотреть, например, в этой задаче.

Автор: egeMax |

Нет комментариев

Печать страницы

Источник

§ 17.Площадь ортогональной проекции многоугольника

Из свойств параллельного проектирования (§ 12) следует, что если фигура лежит в плоскости, параллельной плоскости проекций, то ортогональной проекцией этой фигуры является равная ей фигура.

Рис. 109

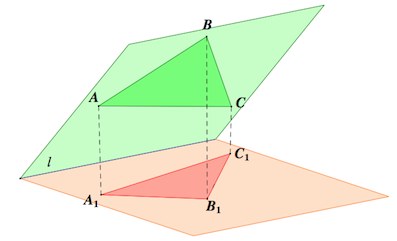
Рассмотрим вопрос о площади ортогональной проекции многоугольника, расположенного в плоскости α, которая образует угол ϕ (0° < ϕ < 90°) с плоскостью проекций π и пересекает её по прямой l (см. рис. 109). Предварительно рассмотрим ортогональное проектирование отрезка, лежащего в плоскости α, выделив два случая расположения этого отрезка относительно прямой l = α ∩ π.

Случай 1. AB ‖ l (см. рис. 109). Отрезок A1B1, являющийся ортогональной проекцией отрезка AB, равен и параллелен отрезку AB (§ 12).

Случай 2. CD ⊥ l (см. рис. 109). По теореме о трёх перпендикулярах прямая C1D1, являющаяся ортогональной проекцией прямой CD, также перпендикулярна прямой l. Следовательно, ∠ CEC1 — угол между плоскостью α и плоскостью проекций π, т. е. CEC1 = ϕ = (α; π) = (CD; C1D1) = CDC0 , где C0D ‖ C1D1. Поэтому

| C1D1 | = | CD|•cos ϕ.(1)

Теперь рассмотрим вопрос об ортогональном проектировании многоугольника.

Теорема 32. Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекций.

Рис. 110

Рис. 111

Доказательство. 1. Площадь проекции треугольника. а) Пусть одна из сторон, например AC, проектируемого треугольника ABC параллельна прямой l = α ∩ π (рис. 110) или лежит на ней. Тогда его высота BH перпендикулярна прямой l, а площадь равна AC•BH, т. е. S_⧌_ABC = AC•BH.

На основании выше рассмотренных свойств ортогональной проекции отрезка имеем:

AC ‖ l ⇒ A1C1 ‖ l; AC = A1C1; B1H1 = BH•cos ϕ.

По теореме о трёх перпендикулярах прямая B1H1 — ортогональная проекция прямой BH — перпендикулярна прямой l, следовательно, отрезок B1H1 — высота треугольника A1B1C1. Поэтому

S_⧌_A1_B1_C1 = A1C1•B1H1 = AC•BH•cos ϕ =S_⧌_ABC•cos ϕ.

Таким образом,

S_⧌_A1_B1_C1 = S_⧌_ABC•cos φ.(2)

б) Ни одна из сторон проектируемого треугольника ABC не параллельна прямой l (рис. 111).

Проведём через каждую вершину треугольника прямую, параллельную прямой l. Одна из этих прямых лежит между двумя другими (на нашем рисунке — это прямая m), и, следовательно, разбивает треугольник ABC на треугольники ABD и ACD с высотами соответственно BH и CE, проведёнными к их общей стороне AD (или её продолжению), которая параллельна l.

Рис. 112

Прямая m1 — ортогональная проекция прямой m — также разбивает треугольник A1B1C1 — ортогональную проекцию треугольника ABC — на треугольники A1B1D1 и A1C1D1, где A1D1 ‖ l, B1H1 ⊥ A1D1, C1E1 ⊥ A1D1. Принимая во внимание (1) и (2), получаем:

S⧌_A1_B1_C1 = S⧌_A1_B1_D1 + S⧌_A1_C1_D1 =

= S⧌_ABC•cos ϕ + S⧌_ACD•cos ϕ =

= (S⧌_ABD + S⧌_ACD)•cos ϕ = S⧌_ABC•cos ϕ.

Итак, для произвольно расположенного в плоскости α треугольника ABC выполняется

S_⧌_A1_B1_C1 = S_⧌_ABC•cos φ.(3)

2. Площадь проекции многоугольника. Пусть Ф — данный выпуклый многоугольник ABCDEF (рис. 112), расположенный в плоскости α. Его ортогональную проекцию — многоугольник A1B1C1D1E1F1 — обозначим Ф1.

Проведя из вершины A многоугольника Ф все его диагонали, разобьём этот многоугольник в объединение непересекающихся треугольников ABC, ACD, ADE и AEF и обозначим их площади соответственно S1, S2, S3 и S4. Тогда для площади SФ многоугольника Ф выполняется

SФ = S1 + S2 + S3 + S4.(4)

Аналогичным образом многоугольник Ф1 разобьём в объединение треугольников A1B1C1, A1C1D1, A1D1E1 и A1E1F1, площади которых обозначим соответственно , , и .

Тогда для площади многоугольника Ф1 выполняется

= + + + .

Принимая во внимание (2), (3) и (4), находим

= + + + = S1•cos ϕ + S2•cos ϕ + S3•cos ϕ + S4•cos ϕ = (S1 + S2 + S3 + S4)•cos ϕ = SФ•cos ϕ.

Разбивая указанным способом на треугольники любой n-угольник Ф, получим аналогичное соотношение между площадью S(Ф) этого n-угольника и площадью S(Ф1) его проекции Ф1:

S(Ф1) = S(Ф)•cos ϕ,

где ϕ — угол между плоскостью данного n-угольника и плоскостью проекций. Теорема доказана. ▼

В школьном курсе геометрии изучаются выпуклые многоугольники. Вместе с тем заметим, что доказанная теорема справедлива и для невыпуклых многоугольников.

Задания для работы с интернет-ресурсами

1. Распечатайте рисунки по теме «Плоскости в пространстве», «Параллельные плоскости», «Пересечение плоскостей», на них найдите параллельные и пересекающиеся плоскости, постройте прямые, по которым пересекаются пары плоскостей. На изображениях куба, призмы, параллелепипеда, пирамиды найдите две параллельные плоскости, каждая из которых проходит через одну из двух изображённых скрещивающихся прямых.

2. Наберите в поисковой системе слова «Три плоскости в пространстве» и найдите рисунки, на которых изображены различные случаи расположения трёх плоскостей в пространстве. Обратите внимание на различное расположение трёх плоскостей, среди которых нет пар параллельных плоскостей. Найдите материал об отрезках, образованных при пересечении двух прямых тремя параллельными плоскостями, вы получите пространственный аналог теоремы Фалеса. Найдите материал о жизни и творчестве Фалеса Милетского.

3. Найдите и рассмотрите рисунки по темам «Угол между плоскостями», «Двугранный угол», «Линейный угол двугранного угла», «Перпендикулярные плоскости», «Две плоскости, перпендикулярные третьей», «Отвес», «Отвесная стена», они помогут вам для построения рисунков к задачам.

4. Найдите материал по темам «Общий перпендикуляр двух скрещивающихся прямых», «Расстояние между двумя скрещивающимися прямыми». Посмотрите рисунки на сайтах:

http://school-collection.edu.ru/,

webmath.exponenta.ru/.

5. Посмотрите в Интернете материалы по теме «Теорема о площади ортогональной проекции многоугольника». Обратите внимание на рисунки и решения наиболее типичных задач по этой теме. Попытайтесь некоторые из этих задач решить самостоятельно.

6. а) Распечатайте рисунок правильного тетраэдра из Интернета. Проведите через ребро основания этого тетраэдра сечение, перпендикулярное двум его боковым граням.

б) На распечатанном рисунке куба найдите две плоскости, одна из которых проходит через концы трёх рёбер куба, имеющих общую вершину, а другая — через концы трёх рёбер, исходящих из противоположной его вершины. Определите угол между этими плоскостями.

Вопросы для самооценки

1. Оцените результаты изучения этой главы. Довольны ли вы ими?

2. Что нового вы узнали в этой главе?

3. Как могут пригодиться вам эти знания в повседневной жизни?

4. Какие задания в этой главе были для вас самыми трудными? Почему?

5. Использовали ли вы при выполнении заданий дополнительные источники: справочники, пособия, интернет-ресурсы?

6. Обращались ли вы за помощью к одноклассникам, родителям, учителю?

Источник

Преподаватель который помогает студентам и школьникам в учёбе.

Ортогональное проецирование — определение и вычисление с примерами решения

Ортогональное проецирование:

Параллельное проецирование, направление которого перпендикулярно плоскости проекции, называется ортогональным проецированием. Проекция фигуры, образующаяся при ортогональном проецировании, называется ортогональной проекцией, или просто проекцией этой фигуры.

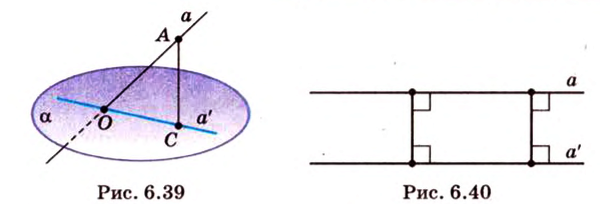
Поскольку ортогональное проецирование является особым видом параллельного проецирования, то для него выполняются все свойства последнего. Ортогональной проекцией прямой

Отметим, что прямые, перпендикулярные одной из параллельных плоскостей, перпендикулярны и остальным, поэтому ортогональное проецирование на одну из таких плоскостей будет ортогональным и на остальные плоскости. Очевидно, что ортогональные проекции фигуры на параллельные плоскости равны между собой.

Ортогональное проецирование также имеет только ему присущие свойства. Одно из них выражает теорема о площади ортогональной проекции многоугольника.

Площадь ортогональной проекции

Теорема 5

Площадь ортогональной проекции произвольного многоугольника на плоскость равна произведению площади самого многоугольника на косинус угла между плоскостью многоугольника и плоскостью проекции.

Доказательство:

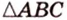
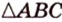
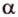
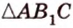
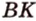
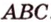
Как пример многоугольника возьмем (рис. 6.41). Проекцией на плоскость является . Проведем высоту треугольника . По теореме
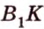
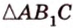
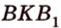
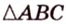
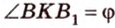
о трех перпендикулярах — высота . Угол — угол между плоскостью и плоскостью проекции. Пусть . Тогда

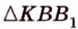
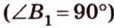
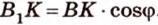
Учитывая, что прямоугольный , имеем:. Поэтому

Итак, . Теорема доказана.

Чтобы доказать теорему для произвольного многоугольника, его разбивают на треугольники. Тогда для каждого треугольника и его проекции можно записать равенство

где 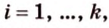поскольку угол между плоскостями этих треугольников и плоскостью их проекций будет один и тот же. Все эти равенства сложим почленно:

Получим в левой части равенства площадь проекции многоугольника, а в правой — площадь самого многоугольника, умноженную на косинус угла между их плоскостями. Отсюда

Т.е. и для этого случая теорема истинна.

Пример:

Ортогональной проекцией треугольника является треугольник со сторонами 13 см, 14 см и 15 см. Плоскость треугольника образует с плоскостью проекции угол 60°. Вычислите площадь данного треугольника.

Решение:

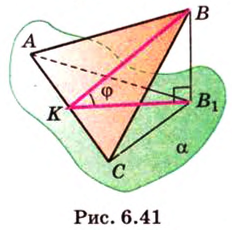
Воспользуемся рисунком 6.41. Известно, что площадь проекции треугольника вычисляют по формуле:

где 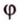— угол между плоскостью треугольника и плоскостью проекции.
По формуле Герона найдем площадь :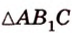

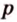
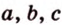
где — полупериметр треугольника, — его стороны.

Тогда

Ответ: 168 см².

Декартовы координаты на плоскости
Декартовы координаты в пространстве
Геометрические преобразования в геометрии
Планиметрия — формулы, определение и вычисление
Параллельность прямых и плоскостей
Перпендикулярность прямой и плоскости
Взаимное расположение прямых в пространстве, прямой и плоскости
Перпендикулярность прямых и плоскостей в пространстве

Источник

Теорема о площади ортогональной проекции многоугольника (с доказательством).

Теорема

Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции.

Доказательство.

Пусть есть треугольник ABC и его проекция ABC1 на плоскость α. Проведем высоту CD треугольника ABC. По теореме о трех перпендикулярах отрезок C1D – высота треугольника ABC1. Угол CDC1 равен углу φ между плоскостью треугольника ABC и плоскостью проекции α.

Следовательно, для треугольника теорема верна.
Пусть теперь есть многоугольник ABCD. Разобьем его на треугольники. Каждый треугольник, у которого нет стороны, параллельной плоскости проекции, разобьем на два треугольника с общей стороной, параллельной плоскости проекции. Получаем что для каждого треугольника Δ и его проекции Δ` в плоскости α верно равенство