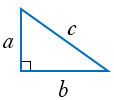Площадь квадрата можно найти с помощью двух основных формул:
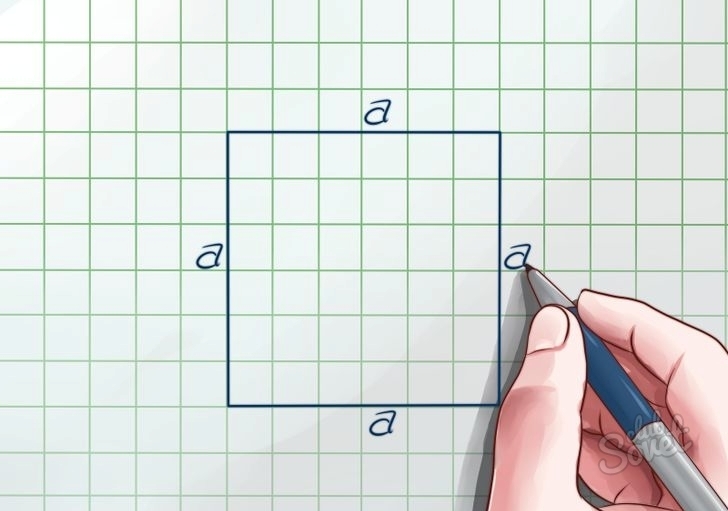
1) Через сторону.
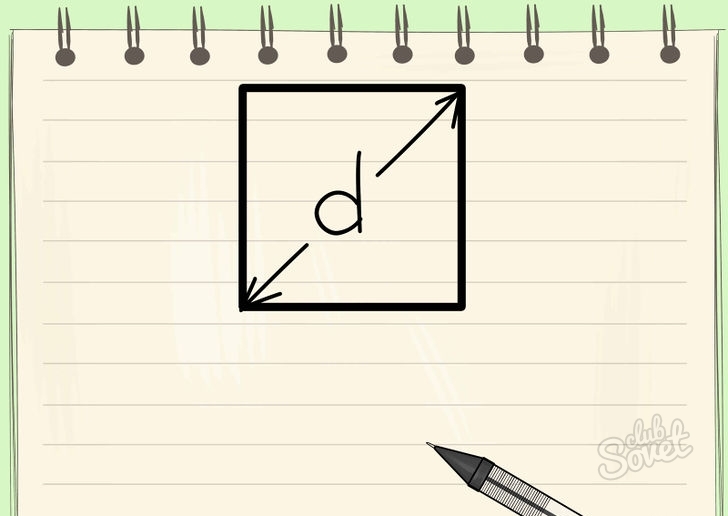
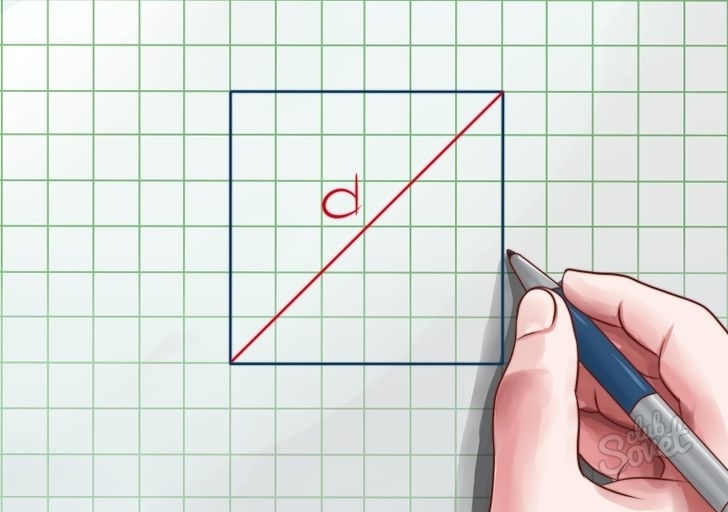
2) Через диагональ.
Как найти площадь квадрата, если известна его сторона.
Как известно, квадрат — это частный случай прямоугольника, у которого все стороны равны.
Площадь прямоугольника равна произведению 2 его сторон:
Sпр = a * b, a и b — стороны прямоугольника.
В случае с квадратом a = b.
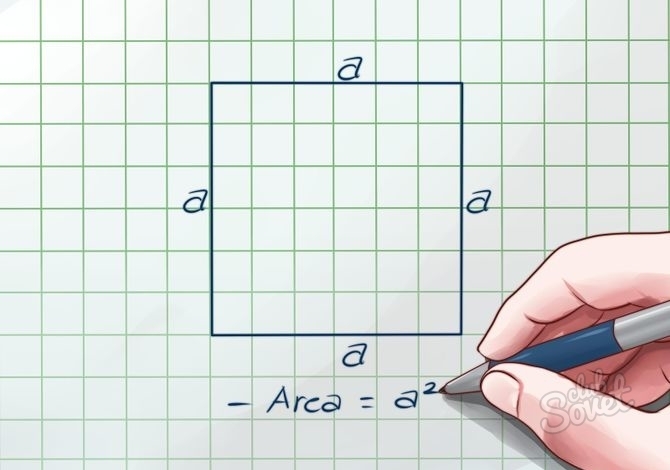
Таким образом, площадь квадрата будет находиться по формуле:
Sкв = a².
Например, если сторона квадрата равна 10 см., то его площадь = 10 * 10 = 100 см².
Как найти площадь квадрата, если известна его диагональ.
Диагональ делит квадрат на 2 прямоугольных треугольника. При этом диагональ является гипотенузой, а стороны квадрата — катетами.
Нам нужно выразить квадрат стороны через теорему Пифагора. Согласно данной теореме:
a*a + b*b = c*c.
a и b — катеты, c — гипотенуза.
В нашем случае a = b, а гипотенуза — это диагональ d.
Перепишем формулу в виде:
2a² = d².
a² = d² / 2.
Таким образом, если известна диагональ квадрата, то его площадь равна половине квадрата этой диагонали.
Например, если диагональ равна 10 см., то площадь квадрата = 10 * 10 / 2 = 50 см².
Пифагор ((570)–(490) года до н. э.) – древнегреческий математик, мыслитель и философ.
Рис. (1). Пифагор.
Факты биографии Пифагора достоверно не известны. О его жизненном пути можно судить лишь по произведениям других древнегреческих философов. По их мнению, математик Пифагор общался с известнейшими мудрецами, учёными того времени.
Известно, что долгое время Пифагор пробыл в Египте, изучая местные таинства.
Философия Пифагора, его образ жизни привлекли многих последователей, но у философа и учёного было и много противников.
Как математик Пифагор достиг больших успехов. Одна из самых известных геометрических теорем — теорема Пифагора, ему приписывают открытие и доказательство теоремы, создание таблицы Пифагора.
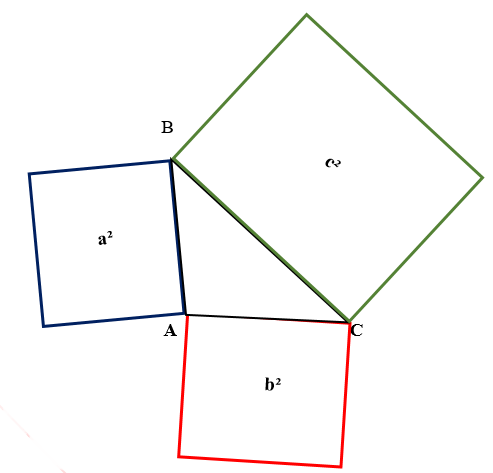
Рис. (2). Теорема Пифагора.
Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
В истории математики находим утверждения, что эту теорему знали за много лет до Пифагора, например, древние египтяне знали о том, что треугольник со сторонами (3), (4) и (5) является прямоугольным.
В наше время теорема звучит так (подразумевая не только площади, но и длины сторон прямоугольного треугольника):
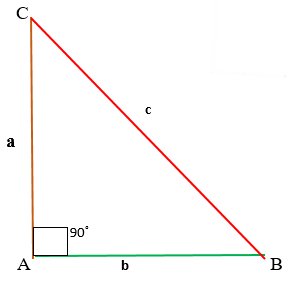
Рис. (3). Прямоугольный треугольник.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
c2=a2+b2
.
Известны очень многие доказательства теоремы разными математическими методами, но одни из самых наглядных связаны с площадями.
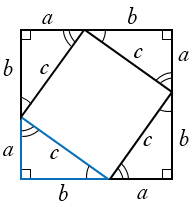
1. Построим квадрат, сторона которого равна сумме катетов данного треугольника
a+b
. Площадь квадрата равна
a+b2
:
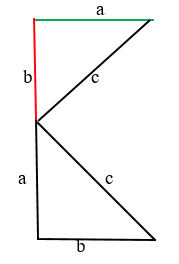
Рис. (4). Первое доказательство теоремы Пифагора.
2. Если провести гипотенузы (c), очевидно, что они образовали квадрат внутри построенного квадрата.
Стороны четырёхугольника равны (c), а углы — прямые, так как острые углы прямоугольного треугольника в сумме дают
90°
, то угол четырёхугольника также равен
90°
, потому что вместе все три угла дают
180°
.
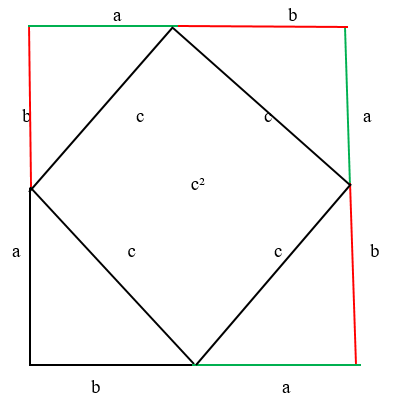
Следовательно, площадь квадрата состоит из четырёх площадей равных прямоугольных треугольников и площади квадрата, образованного гипотенузами.
Рис. (5). Второе доказательство теоремы Пифагора.
3. На двух сторонах квадрата поменяем местами отрезки (a) и (b), при этом длина стороны квадрата не меняется.
Теперь площадь квадрата можем сложить из двух площадей квадратов, образованных катетами (a) и (b), и двух площадей прямоугольников:
Рис. (6). Третье доказательство теоремы Пифагора.
4. Из этого следуют выводы:
c2+4⋅ab2=(a+b)2;c2+2ab=a2+2ab+b2;
Обрати внимание!
Если находим длину гипотенузы (c), то выполняем сложение квадратов длин катетов (a) и (b) и определяем квадратный корень:
c2=a2+b2;c=a2+b2.
Если находим длину одного катета, то выполняем вычитание длины квадрата другого катета из квадрата длины гипотенузы и определяем квадратный корень:
a2=c2−b2;a=c2−b2.
Обратная теорема используется как признак прямоугольного треугольника.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник является прямоугольным.
Пример:
является ли треугольник со сторонами (6) см, (7) см и (9) см прямоугольным?
Выбираем большую сторону и проверяем, выполняется ли теорема Пифагора:
— значит, этот треугольник не прямоугольный.
Является ли треугольник со сторонами (5) см, (12) см и (13) см прямоугольным?
Выбираем большую сторону и проверяем, выполняется ли теорема Пифагора:
— значит, этот треугольник прямоугольный.
Чтобы не тратить много времени на решение, полезно запомнить наиболее часто используемые числа Пифагора:
катет, катет, гипотенуза
(3), (4), (5);
(6), (8), (10);
(12), (16), (20);
(5), (12), (13).
Посмотри ещё одно своеобразное доказательство теоремы Пифагора:
Рис. (7). Четвёртое доказательство теоремы Пифагора.
Источники:
Рис. 2. Теорема Пифагора. Указание авторства не требуется, 2021-06-05, Наука/Технологии, бесплатно для коммерческого использования, https://clck.ru/VK55r.
Рис. 4, 5, 6. Доказательства теоремы Пифагора, © ЯКласс.
Рис. 7. Четвёртое доказательство теоремы Пифагора, http://linguaggio-macchina.blogspot.com
Как найти площадь квадрата
Квадрат – это геометрическая фигура, имеющая четыре стороны одинаковой длины, которые расположены под углом 90 градусов по отношению друг ко другу. Другими словами – это разновидность правильного прямоугольника. В некоторых случаях квадрат называют одним из вариантов ромба.
Диагональ квадрата – это отрезок, пересекающий центральную точку квадрата и соединяющий его противоположные углы. На одном квадрате размещаются 2 диагонали одинаковой длины.
1
Расчет площади квадрата с учетом длины диагонали
- Длина диагонали квадрата участвует в формуле расчета площади квадрата. Обозначим длину диагонали d, а площадь квадрата S, тогда S = d^2/2.
- Длину диагонали квадрата можно рассчитать при помощи теоремы Пифагора. Учитывая тот факт, что диагональ квадрата – это гипотенуза прямоугольного равнобедренного треугольника, имеем следующую формулу расчета длины гипотенузы: a^2 + a^2 = d^2, где a – длина одной стороны равнобедренного треугольника или квадрата. Тогда d = a√2.
- Например, если принять длину диагонали квадрата равной 4 см, то его площадь будет равна: S = 4^2/2 = 8 кв. см.
- Если квадрат вписан в окружность, и известна длина диаметра окружности, то стоит уточнить, что длина диаметра круга и длина диагонали квадрата равны между собой. Поэтому, в этом случае снова выходим на расчет площади квадрата через его диагональ.
2
Расчет площади квадрата с учетом длины стороны квадрата
- Из рассмотренной выше теоремы Пифагора следует, что при подстановке выражения d = a√2 в формулу подсчета площади квадрата S = d^2/2 мы выходим на возможность расчета площади квадрата через длину его стороны: S = (a√2)^2/2, тогда S = a^2.
- Вычислим длину стороны квадрата, исходя из рассчитанной нами ранее площади, равной 16 см. A = √S = √8 = 2,83 см.
3
Расчет площади квадрата с учетом длины периметра квадрата
- Если нам известна длина периметра квадрата, и требуется рассчитать площадь фигуры, тогда нужно уточнить, что представляет собой периметр квадрата. Периметр – это значение, полученное путем суммирования всех длин сторон геометрической фигуры.
- Обозначим периметр P, тогда P = 4a. Тогда длина стороны квадрата будет равна a = P/4. Это выражение подставляем в формулу расчета площади квадрата S = a^2 и получаем S = (P/4)^2, то есть S = P^2/16.
- Например, если периметр квадрата равен 20, тогда S = 20^2/16 = 25 кв. см.
Теорема Пифагора – в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Вы узнаете, как доказать теорему, формула Пифагора и как решать задачи.
История теоремы
Однако название получено в честь учёного только по той причине, что он первый и, даже единственный человек, который смог доказать теорему.
Немецкий историк математики Кантор утверждал, что о теореме было известно ещё египтянами приблизительно в 2300 году до н. э. Он считал, раньше строили прямые углы благодаря прямоугольным треугольникам со сторонами 3, 4 и 5.
Известный учёный Кеплер говорил, что у геометрии есть незаменимое сокровище – это теорема Пифагора, благодаря которой можно вывести большинство теорем в геометрии.
Раньше теорему Пифагора называли “теоремой невесты” или “теоремой нимфы”. А всё дело в том, что её чертёж был очень похож на бабочку или нимфу. Арабы же, когда переводили текст теоремы, решили, что нимфа означает невеста. Так и появилось интересное название у теоремы.
Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Подробнее
Теорема Пифагора, формула
Теорема Пифагора – в прямоугольном треугольнике сумма квадратов катетов () равна квадрату гипотенузы (
). Это одна из основополагающих теорем эвклидовой геометрии.
Формула:
Как уже говорилось, есть много разнообразных доказательств теоремы с разносторонними математическими подходами. Однако, более часто используют теоремы, связанные с площадями.
Построим на треугольнике квадраты (синий, зеленый, красный)
То есть сумма площадей квадратов, построенных на катетах равняется площади квадрата, построенном на гипотенузе. Соответственно, площади этих квадратов равны – . Это и есть геометрическое объяснение Пифагора.
Доказательство теоремы методом площадей: 1 способ
Докажем, что .
Рассмотрим всё тот же треугольник с катетами a, b и гипотенузой c.
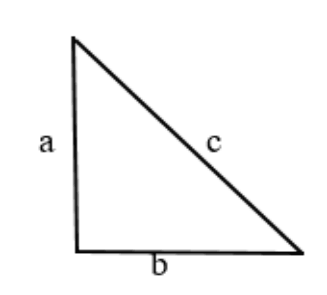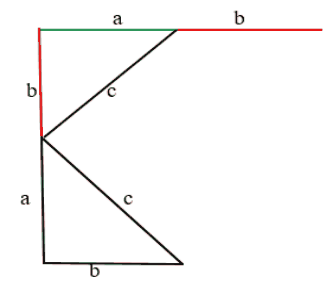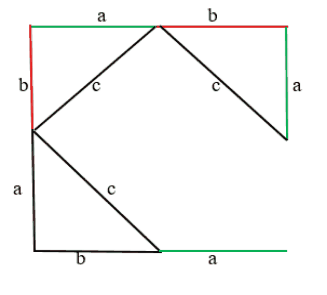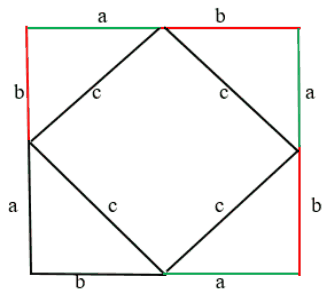
- Достраиваем прямоугольный треугольник до квадрата. От катета “а” продолжаем линию вверх на расстояние катета “b” (красная линия).
- Далее ведём линию нового катета “а” вправо (зелёная линия).
- Два катета соединяем гипотенузой “с”.
Получается такой же треугольник, только перевёрнутый.
Аналогично строим и с другой стороны: от катета “а” проводим линию катета “b” и вниз “а” и “b” А снизу от катета “b” проводим линию катета “а”. В центре от каждого катета провели гипотенузы “с”. Таким образом гипотенузы образовали квадрат в центре.
Этот квадрат состоит из 4-х одинаковых треугольников. А площадь каждого прямоугольного треугольника = половина произведения его катетов. Соответственно, . А площадь квадрата в центре =
, так как все 4 гипотенузы со стороной
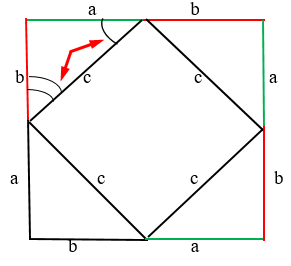
. Стороны четырёхугольника равны, а углы прямые. Как нам доказать, что углы прямые? Очень просто. Возьмём всё тот же квадрат:
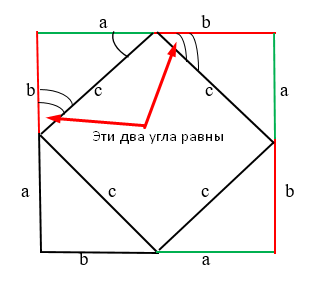
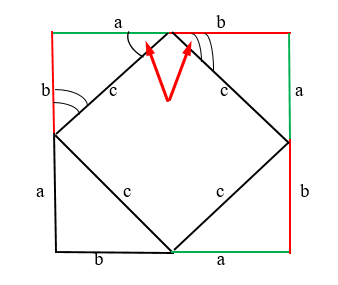
Мы знаем, что эти два угла, показаны на рисунке, являются 90 градусам. Так как треугольники равны, значит следующий угол катета “b” равен предыдущему катету “b”:
Сумма этих двух углов = 90 градусов. Соответственно, предыдущий угол тоже 90 градусов. Конечно же, аналогично и с другой стороны. Соответственно, у нас действительно квадрат с прямыми углами.
Так как острые углы прямоугольного треугольника в общей сложности равняются 90 градусам, то угол четырёхугольника так же будет равен 90 градусов, ведь 3 угла в сумме = 180 градусов.
Соответственно, площадь квадрата складывается из четырёх площадей одинаковых прямоугольных треугольников и площади квадрата, который образован гипотенузами.
Таким образом, получили квадрат со стороной . Мы знаем, что площадь квадрата со стороной
– это будет квадрат его стороны. То есть
. Этот квадрат состоит из четырёх одинаковых треугольников.
- Запишем:
.
- Далее смотрим, что площадь прямоугольного треугольника – это половина произведения его катетов. Поэтому дальше записываем:т
- Также надо прибавить площадь квадрата, который находится в центре между треугольниками со стороной “с”. И теперь получим:
- Раскрываем скобки и получаем:
- Сокращаем
. Получается:
И это значит, что мы доказали теорему Пифагора.
ВАЖНО!!! Если находим гипотенузу, тогда складываем два катета, а затем ответ выводим из корня. При нахождении одного из катетов: из квадрата длины второго катета вычитаем квадрат длины гипотенузы и находим квадратный корень.
Примеры решения задач
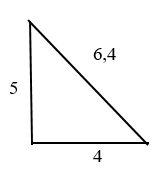
Задача
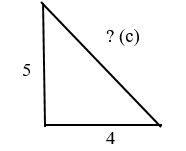
Дано: прямоугольный треугольник с катетами 4 и 5.
Найдите гипотенузу. Пока её обозначим “с”
Решение
Сумма квадратов катетов равняется квадрату гипотенузы. В нашем случае –
.
Воспользуемся теоремой Пифагора:
Итак, , а
. Катеты в сумме получают 41.
Тогда . То есть квадрат гипотенузы равен 41.
Квадрат числа 41 = 6,4.
Мы нашли гипотенузу.
Ответ
Гипотенуза = 6,4
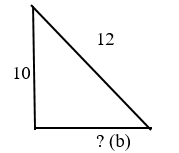
Задача
Дано: прямоугольный треугольник, где гипотенуза = 12, один катет = 10
Найдите второй катет.
Решение
Обозначим неизвестный катет – b.
Воспользуемся теоремой Пифагора:
, а
Запишем:
Находим
Если , тогда просто
Ответ
Второй катет (b) равен 6,6.
Заключение
Итак, мы рассмотрели теорему Пифагора, смогли привести ее доказательство и привели несколько примеров задач и их решений.
Запомните раз и навсегда: квадраты гипотенузы равен суммы квадратов катетов: (это вся теорема Пифагора).
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Площадь
- Теорема Пифагора
Теорема
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Доказательство
Дано: прямоугольный треугольник, 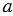
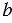
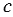
Доказать: 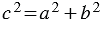
Доказательство:
Достроим данный треугольник до квадрата со стороной 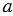
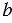
Площадь этого квадрата 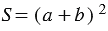
Также, по свойству 20 площадей, площадь этого же квадрата 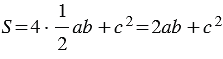
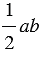
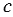
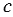
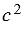
Итак, 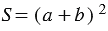
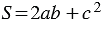
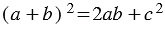
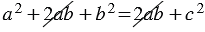
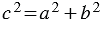
Советуем посмотреть:
Понятие площади многоугольника
Площадь квадрата
Площадь прямоугольника
Площадь параллелограмма
Площадь треугольника
Площадь трапеции
Теорема, обратная теореме Пифагора
Формула Герона
Площадь
Правило встречается в следующих упражнениях:
7 класс
Задание 492,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 9,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 521,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 578,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 725,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 763,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1057,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1174,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1247,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1276,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник