Почему бы просто не считать клеточки?
Возможно, вы читаете всё это и думаете: зачем все эти сложности? Формулы запоминать. Дорисовывать. Тут ведь сразу видно, сколько клеточек в фигуре.
Вот, например, трапеция:
Посчитаем клеточки: их всего 46, верно?
Но стоп, там же некоторые из них только наполовину внутри фигуры. Отметим их – всего таких 10. Итого, 36 полных (красные точки) и 10 половинчатых, вместе ( 36+frac{10}{2} = 41)
Вроде бы всё верно. Но, если присмотреться, можно заметить ещё маленькие треугольнички, которые попали внутрь. А также, что «синие» клеточки слева на самом деле разрезаны не ровно пополам – какие-то чуть больше, какие-то меньше…
Как всё это учитывать?
Попробуем рассуждать так: заметно, что тот маленький розовый треугольник дополняет серый кусок клетки.
А жёлтые сколько занимают? Постарайтесь ответить сами.
Если всё сделать правильно, то увидите, что жёлтые кусочки можно сложить вместе в одну целую клетку.
Итак, 2 жёлтых куска = 1 клетка.
Розовый треугольник + серый кусок = 1 клетка. Всего у нас две таких пары (розовый+серый) – это 2 полных клетки.
Всё остальное как было: 36 полных клеток и 6 половинок у правой стороны – это ( 36+frac{6}{2}=39) клетки.
Итого клеток: ( 1 + 2 + 39 = 42).
Проверим результат по формуле площади трапеции: нижнее основание 11, верхнее основание 3, высота 6. Полусумма оснований равна 7, умножаем на высоту – получилось 42. Всё совпало.
Но! Настолько ли проще был наш способ подсчёта клеточек? Не сказал бы. А если там будет несколько косых линий, то вообще можно замучиться собирать этот паззл (искать, какие кусочки друг друга дополняют).
Вычислите площадь простых фигур тремя способами
Стороны клеток равны 1. Вычислите самостоятельно площадь фигуры всеми тремя способами. Сравните результаты.
Вычислите площадь произвольных фигур по формуле Пика
Вычислите самостоятельно площади фигур с помощью формулы Пика:
Посчитайте площадь корабля и котика по формуле Пика
Посчитайте самостоятельно для тренировки и чтобы запомнить формулу Пика!
Фигуры с отверстиями — посчитайте площади двумя способами
Ну и напоследок фигуры с «дырками». Как думаешь, здесь придётся вычислять сначала площадь целой фигуры, а потом площадь дырки?
Или достаточно просто посчитать точки внутри закрашенной области и на её границах (в том числе, на границе с дыркой)?
Проверим на простом примере: это квадрат ( 4times 4), и в нём вырезан прямоугольник ( 1times 2), значит, его площадь ( 16-2=14).
А теперь по точкам. На границах (включая внутренние) ( Г = 22). Внутри ( В = 3). Тогда площадь по формуле Пика
( S = frac{22}{2} + 3 -1 = 13.)
Хм, близко, но не совпало. Может, я где-то ошибся? Давай ещё одну фигуру, для верности.
Сосчитай сам и проверь.
Что получилось?
У меня снова на 1 меньше.
Так может быть просто формулу немного «подкрутить»? Нет!
Очень и очень не рекомендую вам запоминать несколько похожих формул для похожих случаев, потому что придёт время, и вы обязательно перепутаете формулу.
Даже если вы уверены, что не перепутаете, оно всё равно того не стоит. В общем, наилучший вариант – это запомнить одну формулу. А если попалась фигура с дыркой, вычислить всю фигуру, а потом дырку. И вычесть.
Площадь поверхности пирамиды
Для пирамиды тоже действует общее правило:
Площадь полной поверхности пирамиды – это сумма площадей всех граней.( displaystyle {{S}_{полн. пов. }}={{S}_{боков.пов. }}+{{S}_{основания }})
Теперь давай посчитаем площадь поверхности самых популярных пирамид.
Площадь поверхности правильной треугольной пирамиды
Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b). Нужно найти ( displaystyle {{S}_{осн}}) и ( displaystyle {{S}_{ASB}}).
И тогда
( displaystyle {{S}_{полн. пов. }}=3{{text{S}}_{ASB}}+{{text{S}}_{text{осн}.}})
Вспомним теперь, что
( displaystyle {{S}_{осн}}) — это площадь правильного треугольника ( displaystyle ABC).
И еще вспомним, как искать эту площадь.
Используем формулу площади:
( displaystyle S=frac{1}{2}abcdot sin gamma ).
У нас «( displaystyle a)» — это ( displaystyle a), а «( displaystyle b)» — это тоже ( displaystyle a), а ( displaystyle sin gamma =sin 60{}^circ =frac{sqrt{3}}{2}).
Значит, ( displaystyle {{S}_{ABC}}=frac{1}{2}{{a}^{2}}frac{sqrt{3}}{2}=frac{{{a}^{2}}sqrt{3}}{4}).
Теперь найдем ( displaystyle {{S}_{Delta ASB}}).
Пользуясь основной формулой площади и теоремой Пифагора, находим
( displaystyle {{S}_{Delta ASB}} = frac{1}{2}asqrt{b^2-frac{a^2}{4}})
Внимание: если у тебя правильный тетраэдр (т.е. ( displaystyle b=a)), то формула получается такой:
( displaystyle S={{a}^{2}}sqrt{3}).
Проектирование корпусов судов, удовлетворяющих требованиям прочности и долговечности, осуществляется методами обобщенного прототипа (правилами Российского Речного Регистра) и расчетными. В учебном пособии для стандартных судов внутреннего и смешанного плавания предлагается использовать Правила РРР. Расчет площади судна начинается еще на этапе проектирования, поэтому ошибки в исчислениях недопустимы.
СодержаниеСвернуть
- Определение изгибающих моментов и перерезывающих сил, действующих на судно на тихой воде
- Дополнительные изгибающие моменты
- Дополнительные изгибающие моменты для судов класса “М-СП”, “М-ПР”, “О-ПР”
- Дополнительные изгибающие моменты для судов классов “М”, “О”, “Р”, “Л”
- Оценка прочности судов длиной менее 50 м
- Определение фактического момента сопротивления
- Расчет нормальных напряжений
- Расчеты общей предельной прочности
- Определение дополнительных волновых изгибающих моментов для судов, эксплуатирующихся с ограничениями, не ответствующими классу
В общем случае для оценки прочности судового корпуса решаются проблемы по определению внешних продольных нагрузок, внутренних усилий и необходимых запасов прочности. Связанные с проектированием конструкций расчеты носят проверочный характер.
Расчетные внешние нагрузки, действующие на корпус судна, представляются состоящими из двух частей: сил и моментов, действующих на тихой воде и дополнительных усилий на волнении. Волновое воздействие на судно реализуется в виде волновых нагрузок, изменяющихся с периодом, близким к периоду волн, ударов волн в днище и развалы бортов (слеминг), а также в виде волновой вибрации.
В расчетах общей прочности, когда корпус моделируется в виде пустотелой коробчатой балки, нагрузки представляются в виде интегральных характеристик – перерезывающих сил и изгибающих моментов. В частности, изгибающий момент представляется состоящим из изгибающих моментов на тихой воде, волнового и ударного. В Правилах РРР сумма волнового и ударного моментов называется дополнительным волновым моментом.
Читайте также: Конструкция судовых перекрытий
Суда внутреннего и смешанного плавания, в отличие от морских судов, подвергаются многочисленным эксплуатационным нагрузкам при посадке на мель, швартовке, шлюзовании, погрузке и выгрузке. При плавании в весенний – осенний период их корпуса подвергаются воздействию ледовых нагрузок.
По Правилам РРР за расчетные принимаются полные значения изгибающих моментов и перерезывающих сил при продольном изгибе путем суммирования моментов и сил на тихой воде и на волнении.
У речных низкобортных судов при L/H > 25 за счет изгиба корпуса существенно изменяются силы поддержания воды по длине судна, что приводит к уменьшению изгибающих моментов на тихой воде на 20-30 %.
Величина ударного изгибающего момента в большой степени зависит от осадки носом. Удары волн могут увеличить дополнительный момент на волнении в два раза. В связи с этим Правилами РРР ограничивается минимальная осадка носом для судов класса М-СП, М-ПР, О-ПР.
В частности, осадка носом судна класса М-СП во всех случаях нагрузки должна быть не менее 1,7 м для судов L ≥ 60 м и не менее 0,9 м для судов L ≤ 25 м. Осадка судов класса М-ПР должна быть не менее 1,4 м для судов L ≥ 60 м и не менее 0,75 м для судов L ≤ 25 м.
Осадка судов класса О-ПР должна быть не менее 0,9 м для всех случаев нагрузки при L ≥ 60 м и не менее 0,75 м при L ≤ 25 м. В формировании эквивалентного бруса и определении напряжений от общего изгиба корпуса морских и речных судов принципиальных отличий нет. Общая и местная прочность проверяется по нормальным и касательным напряжениям, а также по предельным моментам для вновь построенного судна и по предельным моментам в конце срока службы с учетом износа и остаточных деформаций.
Расчетные значения изгибающих моментов для прогиба и перегиба в расчетном сечении корпуса необходимо вычислять алгебраическим суммированием изгибающих моментов на тихой воде с дополнительным волновым изгибающим моментом в этом сечении:
Mp = Mтв+Mдв Форм. 1
Расчетные значения перерезывающих сил для прогиба и перегиба в расчетном сечении необходимо определять суммированием абсолютных значений перерезывающих сил на тихой воде и на волнении:
Np = Nтв+Nдв Форм. 2
В курсовом проекте за расчетное сечение принимается мидель-шпангоут.
Определение изгибающих моментов и перерезывающих сил, действующих на судно на тихой воде
Плавающее судно находится под действием сил тяжести и сил поддержания, которые в целом уравновешены. Корпус судна представляет собой упругую непризматическую балку, у которой распределение сил тяжести и сил поддержания непостоянны и распределены по длине неодинаково. Это приводит к появлению перерезывающих сил и изгибающих моментов:
N = ∫0xq(x)dx M = ∫0x∫0xq(x)dxdx, Форм. 3
где:
- N, M – перерезывающая сила и изгибающий момент;
- q(x) – нагрузка представляющая собой алгебраическую сумму сил тяжести и сил поддержания в каждом поперечном сечении по длине судна x.
Для вычисления изгибающих моментов и перерезывающих сил на тихой воде следует интегрировать кривую нагрузки по 21-й равноотстоящей ординате для наиболее неблагоприятных случаев нагрузки.
В курсовом проекте допускается определять искомые величины для одного случая – судно в полном грузу и 100 %-ными запасами. Кроме этого, допускается определять максимальные значения изгибающих моментов и перерезывающих сил по формулам
Mтв = DgLk Nтв = 4MтвL, Форм. 4
где:
- k – коэффициент, определяемый по прототипу или по статистическим дан ным (табл. 1).
| Таблица 1. Эмпирические коэффициенты kтв | ||||||||
|---|---|---|---|---|---|---|---|---|
| Класс судна | L, м | |||||||
| 40 | 50 | 60 | 70 | 80 | 100 | 120 | 140 | |
| М-СП | 90-105 | |||||||
| М | 83 | 95 | 110 | 170 | 260 | 370 | ||
| О | 74 | 76 | 81 | 120 | 160 | 200 | ||
| Р | 116 | |||||||
| Л | 75 |
Для судов с отношением L/H > 25 изгибающий момент и перерезывающую силу на тихой воде надо определять с учетом гибкости корпуса.
Тогда
Mтв = βMтв0, Nтв = βNтв0, Форм. 5
где:
- Mтв0, Nтв0
– изгибающий момент и перерезывающая сила на тихой воде без учета влияния гибкости корпуса;
- β – коэффициент, учитывающий гибкость корпуса, определяемый по формуле
β = 11+1,226·10–2L4BEIα2, Форм. 6
где:
- I — момент инерции площади поперечного сечения корпуса;
- Е – модуль упругости материала корпуса;
- α – коэффициент полноты расчетной ватерлинии.
В заключение следует отметить, что для сухогрузного суднаСпециализированные суда для перевозки сухих грузов на тихой воде при ходе порожнем, как правило, возникает перегиб судна (в палубе возникают напряжения растяжения, в днище – сжатия). При ходе в грузу картина меняется: возникает отрицательный изгибающий момент, вызывающий прогиб судна.
Дополнительные изгибающие моменты
Наибольшие дополнительные моменты возникают когда длина волны λ примерно равна длине судна, а мидель-шпангоут совпадает с вершиной или подошвой волны. Эти расчетные случаи называются постановкой на вершину или подошву волны. При этом при постановке на вершину волны возникает дополнительный момент, вызывающий перегиб судна, а на подошву волны – прогиб. Очевидно, что наиболее опасным будет случай, когда момент на тихой воде и дополнительный момент имеют одинаковый знак, так как величина суммарного момента получается наибольшей. Так, если судно на тихой воде испытывает перегиб, для него следует выполнить постановку на вершине волны.
Для речных судов, имеющих гибкий корпус и большое отношение L/H, частоты собственных изгибных колебаний первого тона не велики и часто оказываются близкими к частотам волн. Этот весьма опасный случай для речных судов называют волновой вибрацией. Волновая вибрация в околорезонансной зоне может привести к значительным дополнительным моментам и поэтому должна учитываться в расчетах.
Для судов класса «М-СП», корпуса которых более жесткие, такой учет не обязателен, поэтому рассмотрим отдельно учет дополнительных моментов в соответствии с «Правилами» для судов класса «М-СП» и других.
Дополнительные изгибающие моменты для судов класса “М-СП”, “М-ПР”, “О-ПР”
В качестве нормативной расчетной характеристики волнового режима принимается волна высотой 3,5 м 3 %-ной обеспеченности.
Дополнительный волновой изгибающий момент (кНм) определяется по следующей зависимости:
Mд = ±9,81k0k1k2δBL2h, Форм. 7
где:
- k0 – коэффициент, вычисляемый по формуле:
k0 = 1,24–1,7BL≤1,0,
- k1 – коэффициент, значения которого определяются по формуле:
k1 = 0,042+0,124·10–3L–0,391·10–2L,
- k2 – коэффициент, определяемый по формуле:
k2 = 2–20TнL≥1,0,
- h – расчетная высота волны, м.
Значения L, T и δ принимаются, исходя из расчетного случая нагрузки при определении изгибающего момента на тихой воде.
Для судов класса “М-ПР” в качестве нормативной расчетной характеристики волнового режима принимается высота волны 3 %-ной обеспеченности 3,0 м.
Дополнительный волновой изгибающий момент должен определяться в соответствии с формулой 6. Значения коэффициента k определяется по табл. 2.
| Таблица 2. Значения коэффициентов k1 | ||||
|---|---|---|---|---|
| Длина судна, м | 25 | 60 | 100 | 140 |
| Коэффициент k1 | 0,0224 | 0,0172 | 0,0136 | 0,0116 |
Для судов класса “О-ПР” в качестве нормативной расчетной характеристики волнового режима принимается высота волны 3 %-ной обеспеченности высотой 2,0 м.
Дополнительный волновой изгибающий момент должен определяться в соответствии с формулой 7. Значения коэффициента k1 определяется по табл. 3.
| Таблица 3. Значения коэффициентов k1 | |||
|---|---|---|---|
| Длина судна, м | 60 | 100 | 140 |
| Коэффициент k1 | 0,0154 | 0,0114 | 0,0089 |
Если длина судна в табл. 2 и 3 не совпадает с расчетной, определение коэффициента k1 проводится линейной интерполяцией.
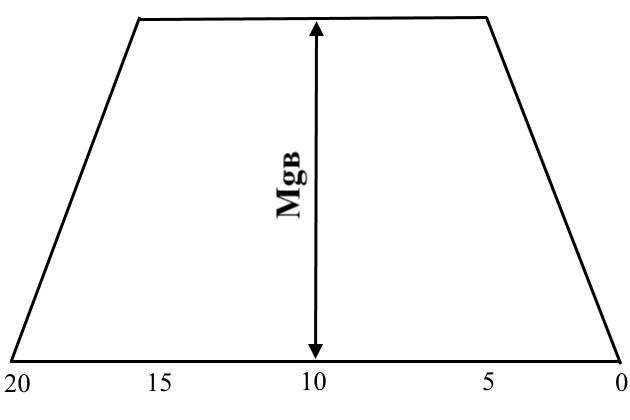
Дополнительный волновой изгибающий момент принимают постоянным в средней части судна на длине 0,5L, так как показано на рис. 1.
Дополнительные изгибающие моменты для судов классов “М”, “О”, “Р”, “Л”
Дополнительный волновой изгибающий момент на миделе судна (кНм) определяется по формуле:
Mдв = ±kpMв+Mу, Форм. 8
где:
- Мв – изгибающий момент, вызванный непосредственно действием волн;
- Му – изгибающий момент, вызванный ударом волн в носовую оконечность;
- kр – коэффициент, учитывающий влияние волновой вибрации (коэффициент динамичности).
Волновой изгибающий момент, кНм, определяется по формуле:
Mв = 0,255εkδkтkвBL2h, Форм. 9
где:
- h – расчетная высота волны, м;
- ε – коэффициент, определяемый по табл. 4.
Коэффициенты kδ, kт, kв определяются по формулам:
kδ = e–1,61–δ,
kт = e–1,14Тηh·δ2δ+1,
kв = 1–e–0.19δBηhηh0,19δB,
где:
- η – коэффициент, принимаемый по табл. Конструкция судовых перекрытий“Значения коэффициента k2“.
- Коэффициент kp рассчитывается по формуле:
kp = 1+ωк2/σ21–ωк2σ22+2kμωкσ2, Форм. 10
где:
- ωк = ωср+1,92kν vтв/L, c–1
– средняя частота волнения,
σ = ksI1,2+B/3ТgDL3,
kμ = 0,0611–0,047σ–0,008σ2≥0,
где:
- I – момент инерции поперечного сечения эквивалентного бруса на миделе, м4.
Собственная частота изгибных колебаний корпуса ωср определяется по табл. 3.
Коэффициент kv вычисляется по формулам:
kv = 1+1,1810ηhL–28,010ηhL2+61,710ηhL3,
если
10ηhL≤0,3;
kv = 0,5–0,810ηhL–0,3+10ηhL–0,32,
если
10ηhL>0,3.
- vтв – скорость хода судна на тихой воде, км/ч;
- kδ = 123 · 104 – для грузовых судов;
- kδ = 117 · 104 – для пассажирских судов;
- kδ = 104 · 104 – для буксиров и толкачей.
Ударный изгибающий момент определяется по формуле:
Mу = kуφ1DgL, Форм. 11
где:
- kу = 5,33·10–4φ0σv0,
- φ1 = 1,0 при Тн≤Тн0,
- φ1 = 3–2ТнТн0 при Тн0<Тн<1,5Тн0,
- φ1 = 0 при Тн≥1,5Тн0,
- Tн – осадка носом для расчетного случая нагрузки, м,
- Тн0
– пороговая осадка носом, м, равная
Tн0 = 0,68+0,21kvvтвLηh,
- φ0 – коэффициент, равный
φ0 = 1–1,03b0–b02–0,417b03,
b0 = 4,32δB/LT/L,
- величина v0 вычисляется по формуле:
v0 = 0,336+0,104kvvтвLv1+0,024kvvтв,
- величина v1 принимается по табл. 5.
Максимальное значение дополнительной волновой перерезывающей силы, кН, определяется по формуле:
Nдв = 4MдвL. Форм. 12
Поскольку ее максимальное значение наблюдается в районах ±0,25L от оконечностей, на миделе следует принимать значение
Nдв⊗ = 0,7Nдв. Форм. 13
Расчетные значения изгибающих моментов для прогиба и перегиба в миделевом сечении корпуса необходимо вычислять алгебраическим суммированием моментов на тихой воде с дополнительным моментом (Формула 1).
Расчетные значения перерезывающих сил необходимо определять суммированием абсолютных значений перерезывающих сил на тихой воде и дополнительной волновой перерезывающей силы (Формула 2).
| Таблица 4. Значения величин при определении дополнительных моментов | |||||
|---|---|---|---|---|---|
| Класс судна | Высота волн h, м | ε | η | ωср, c–1 | v, м/с |
| “М” | 3,0 | 0,920 | 1,00 | 1,11 | 5,42 |
| 2,5 | 0,970 | 1,00 | 1,22 | 4,95 | |
| 2,0 | 1,00 | 1,00 | 1,36 | 4,43 | |
| “О” | 2,0 | 0,805 | 0,874 | 1,46 | 4,14 |
| 1,5 | 0,857 | 0,874 | 1,69 | 3,57 | |
| “Р” | 1,2 | 0,848 | 0,874 | 1,88 | 3,21 |
| “Л” | 0,6 | 0,874 | 0,874 | 2,68 | 2,26 |
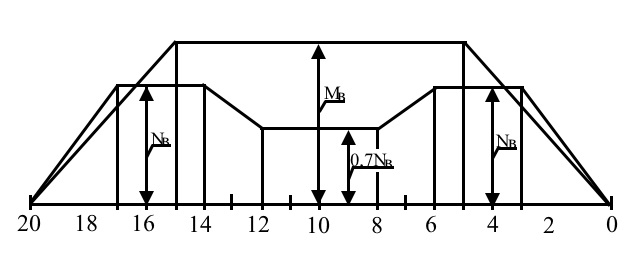
Форма распределения дополнительных волновых моментов и перерезывающих сил, рекомендуемая Правилами РРР, приведена на рис. 2.
Оценка прочности судов длиной менее 50 м
Для судов длиной 50 м и менее Правилами РРР регламентируется суммарное значение площади поперечного сечения палубы или днищевого пояса в зависимости от того, что меньше.
Эта площадь, см², должна быть не менее
F = DLH0,1L/T–1k1+k2η, Форм. 14
где:
- D – водоизмещение судна в полном грузу;
- k1 – коэффициент, определяемый по табл. 6;
- k2 – коэффициент, равный для самоходных судов 1,0/L;
- для несамоходных 0,67/L;
- η – коэффициент, равный для связей палубного пояса, не несущих местной нагрузки, 0,65;
- для связей днищевого и палубного пояса, несущего местную нагрузку, 0,75.
Значение выражения, стоящего в скобках формулы 13, не должно приниматься более 0,125.
| Таблица 5. Значения коэффициента k1 | ||
|---|---|---|
| Класс судна | Длина, м | |
| 25 | 50 | |
| “М” | 13 | 47 |
| “О” | 25 | 93 |
| “Р” | 50 | 193 |
| “Л” | 132 | 483 |
При вычислении площади поперечного сечения палубы включаются:
- 65 % площади настила палубы при продольной системе набора;
- полная площадь участков настила шириной 0,25 шпации с каждой стороны каждой продольной связи при поперечной системе набора;
- 10 % остальной площади сечения настила при поперечной системе набора;
- непрерывные продольные ребра жесткости, непрерывные комингсы и карлингсы;
- верхний участок ширстрека, возвышающийся над палубой, а также участок ширстрека ниже палубы высотой 0,25 шпации при поперечной системе набора и 0,25 шпации при продольной.
Если полученное фактическое значение площади палубы превышает нормированное (Формула 18) значение, расчет общей прочности можно не проводить.
Определение фактического момента сопротивления
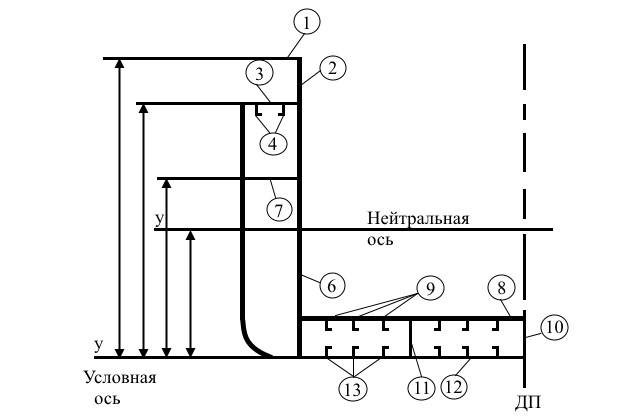
Для расчета фактического момента сопротивления и момента инерции поперечного сечения необходимо изобразить в масштабе на формате А4 поперечное полусечение со всеми продольными связями, участвующими в общем изгибе судна (рис. 3). Здесь же представляются размеры связей и их порядковый номер.
Расчет удобно вести в табл. 6.
| Таблица 6. Расчет геометрических характеристик корпуса | ||||||
|---|---|---|---|---|---|---|
| № п/п | Наименование и размеры связи | Площадь сечения связей Fi, см2 | Отстояние от оси сравнения, zi, м | Статический момент площади, Fizi, см2·м2 |
Переносный момент инерции Fizi2, см2·м2 |
Собственный момент инерции Iс, см2·м2 |
| 1 | Полка комингса | F1 | z1 | F1z1F2z2 | F1z12, | I1 |
| 2 | Стенка комингса | F2 | z2 | ···· | F2z22, | I2 |
| 3 | Настил палубы | ···· | ···· | ···· | ···· | |
| 4 | РЖ | |||||
| 5 | Наружный бор | |||||
| 6 | Внутренний борт | |||||
| 7 | Платформа | |||||
| 8 | Настил двойного дна | |||||
| 9 | РЖ настила | |||||
| 10 | Диаметральный кильсон | |||||
| 11 | Боковой кильсон | |||||
| 12 | Днище | |||||
| 13 | РЖ днища | F13 | z13 | F13z13 | F13z132, | I13 |
| Суммы | ΣFi | ΣFizi | ΣFizi2 | ΣIс |
При заполнении таблицы продольные одноименные связи, имеющие одинаковые размеры и расположенные на одном уровне, обычно объединяют в группы. В первый столбец заносят номера групп продольных связей, во второй – наименования и размеры листовых связей или номера профилей по сортаменту для каждой группы, в третий столбец – площади поперечных сечений каждой группы связей, Fi, (для профилей без присоединенного пояска), в четвертый – отстояние центра тяжести этих связей от оси сравнения – zi.
Предлагается к прочтению: Дополнительные или усиленные конструкции корпуса судна
Ось сравнения выбирается произвольно. Удобно принять ее, например, на основной плоскости. В пятый столбец заносят произведения Fizi (статические моменты), а в шестой – произведения
Fizi2
(переносные моменты инерции площади связей). В седьмой столбец записывают собственные моменты инерции связей Ic, которые определяются или по характеристикам в сортаменте (для профилей), или по формуле
Ic = sh3/12
(s – толщина связи, h – ее высота).
Отстояние нейтральной оси от оси сравнения, м, определяют по формуле:
e = ΣFiziΣFi Форм. 15
Учитывая, что момент инерции относительно нейтральной оси сечения равен моменту инерции относительно оси сравнения за вычетом площади сечения на квадрат расстояния между ними, получим:
Iф = 2ΣFizi2+ΣI0–e2ΣFi. Форм. 16
Фактический момент сопротивления:
- днища
Wg = I/e; Форм. 17
- палубы
Wn = I/H–e. Форм. 18
Нормальные и касательные напряжения, действующие в связях эквивалентного бруса при общем изгибе вычисляются по формулам:
σi = MpIzi, Форм. 19
τi = NpSIt, Форм. 20
где:
- σi, τi – нормальные и касательные напряжения в связях эквивалентного бруса;
- S – статический момент относительно нейтральной оси части площади сечения, отсекаемой по линии, нормальной к площади сечения;
- t – толщина стенки эквивалентного бруса.
Расчет нормальных напряжений
Обычно рассчитывают для прогиба и перегиба, однако в курсовом проекте допускается расчет выполнить один раз – для максимальных значений расчетного изгибающего момента. Расчет удобно делать в таблице форма которой приведена ниже.
| Таблица 7. Расчет нормальных и касательных напряжений в первом приближении | ||||
|---|---|---|---|---|
| № п/п | Наименование связи | Отстояние от НО, м2 | σi | τi |
| 1 | Комингс люка | |||
| 2 | Настил палубы | |||
| 3 | ||||
| 4 | ||||
| 5 | Настил двойного дна | |||
| 6 | Днище |
Отстояние от нейтральной оси и расчетные моменты необходимо вычислять со своими знаками.
Полученные фактические значения нормальных и касательных напряжений необходимо сравнить с допускаемыми, нормы которых в долях от предела текучести приведены в табл. 9.
За опасные нормальные и касательные напряжения принимаются
σ = Reн,
τ = 0,57Reн. Форм. 21
Если нормальные напряжения в связях корпуса не превышают критических, связи не теряют устойчивость и расчет эквивалентного бруса не требуется. Для проверки необходимо вычислить критические напряжения пластин.
| Таблица 8. Нормы допускаемых напряжений | ||
|---|---|---|
| Наименование и характеристика связей корпуса | Характеристика расчетных напряжений от нагрузок | Нормируемые значения допускаемых напряжений в долях предела текучести |
| 1. Жесткие связи эквивалентного бруса, участвующие только в общем изгибе и не несущие местной нагрузки (продольные непрерывные комингсы, связи ненагруженных палуб и т. п.) | Нормальные напряжения от общего изгиба | См. примечание 1 |
| 2. Жесткие связи эквивалентного бруса, участвующие в общем изгибе и несущие местную нагрузку (связи днища всех судов, нагруженных палуб и нагруженных продольных непрерывных комингсов, за исключением комингсов судов с двойными бортами классов “Л”, “Р” и “О”) | Нормальные напряжения от общего изгиба | 0,60 |
| 3. Продольные непрерывные комингсы и карлингсы судов, перевозящих грузы на люковых крышках и на палубе, а также кильсоны судов всех типов | Суммарные нормальные напряжения от общего изгиба и от изгиба перекрытий: | |
| в пролете | 0,75 | |
| на опоре | 0,95 | |
| 4. Продольные балки (неразрезные ребра жесткости) | Суммарные нормальные напряжения от общего и местного изгиба: | |
| в пролете | 0,85 | |
| на опоре | 0,95 | |
| 5. обшивка корпуса и настилы при поперечной системе набора | Нормальные напряжения от местной нагрузки: | |
| в пролете | 0,80 | |
| на опоре | 0,95 | |
| 6. Обшивка и настилы при продольной системе набора | Нормальные напряжения от местной нагрузки: | |
| в пролете | 0,80 | |
| на опоре | 0,95 | |
| 7. Связи корпуса, воспринимающие действие перерезывающей силы при общем изгибе (обшивка бортов и продольных переборок) | Касательные напряжения | 0,30 |
| 8. Поперечный рамный набор корпуса: флоры, рамные шпангоуты и бимсы | Нормальные напряжения от местной нагрузки: | |
| в пролете | 0,75 | |
| на опоре | 0,85 | |
| 9. Поперечный холостой набор корпуса: днищевые и бортовые шпангоуты, бимсы и связи внутреннего дна при поперечной системе набор | Нормальные напряжения от местной нагрузки: | |
| в пролете | 0,85 | |
| на опоре | 0,95 | |
| 10. Продольные и поперечные переборки (в том числе и стенки цистерн): | Нормальные напряжения от местной нагрузки: | |
| рамные стойки | в пролете | 0,85 |
| на опоре | 0,90 | |
| холостые стойки (ребра жесткости) | в пролете | 0,85 |
| на опоре | 0,95 | |
| листы переборок | в пролете | 0,85 |
| на опоре | 0,95 | |
| 11. Стенки балок рамного набора | Касательные напряжения в сплошных сечениях | 0,45 |
| Нормальные напряжения в районе вырезов | 0,95 | |
| Касательные напряжения в районе вырезов | 0,45 |
Примечания:
1 Для связей, указанных в п. 1 табл. 8, нормируемые значения допускаемых напряжений в долях предела текучести должны приниматься равными для судов:
- класса «М»
- 0,70 – при Reн = 235 МПа,
- 0,65 – при Reн = 315 МПа,
- 0,62 – при Reн = 355 МПа,
- 0,60 – при Reн = 390 МПа;
- классов «О», «Р» и «Л»
- 0,75 – при Reн = 235 МПа,
- 0,70 – при Reн = 315 МПа,
- 0,67 – при Reн = 355 МПа,
- 0,64 – при Reн = 390 МПа.
2 В расчетах прочности корпуса судна при подъеме из воды и спуске на воду, при испытании на непроницаемость и герметичность, а также при затопленном отсеке судна нормируемые значения допускаемых суммарных напряжений (от общего изгиба и от местной нагрузки) необходимо принимать равными 0,95 предела текучести материала связей.
3 Для изолированно работающих связей (пиллерсы и раскосы), проверяемых на устойчивость, нормируемые значения допускаемых напряжений при сжатии должны приниматься равными 0,50, для пересекающихся раскосов – 0,75 критического напряжения, но не более 0,50 предела текучести материала связей.
Критические напряжения пластин, сжатых вдоль длинной кромки, МПа, должны вычисляться по формуле:
σкр = σэ при σэ≤0,6Reн Форм. 22
σкр =1,63–0,8Reнσэ
при
0,6Reн≺σэ≺Reн Форм. 23
где:
-
σэ – Эйлеровы напряжения;
σэ = 78,5100t/a2
- t – толщина пластины, см;
- а – длина короткой кромки пластины, см.
Если
σж.с≻σкр
, то дальнейший расчет эквивалентного бруса надо вести с учетом редукционного коэффициента, представляющего собой отношение критического напряжения к напряжению в жестких связях
φ = σкр/σж.с. Форм. 24
Если
σэ≻σж.с φ≻1,0
, явления потери устойчивости нет. В этом случае редукционный коэффициент принимают равным 1. Если
σэ≺σж.с
, то
φ≺1
и пластина теряет устойчивость. Коэффициент φ показывает, какая часть пластины воспринимает такие же напряжения, как и смежная с ней жесткая связь.
Для расчетов вводят понятие приведенной площади сечения пластины к нередуцируемой площади относят относят ширину 0,25b с каждой стороны продольного опорного контура. В этом случае приведенная площадь пластины
Fпр = b21+φt, Форм. 25
где:
- b – ширина пластины.
Если некоторые пластины в сжатой зоне эквивалентного бруса теряют устойчивость, то проводят расчет эквивалентного бруса во втором приближении. Цель второго приближения вычислить исправленные площади пластин, потерявших устойчивость, ввести их в таблицу расчета эквивалентного бруса и для уменьшенной площади вновь определить напряжения в продольных связях корпуса при общем изгибе.
Определение напряжений от общего изгиба во втором приближении производят раздельно для положения судна на вершине и на подошве волны, так как в этих случаях разные связи теряют устойчивость и редукционные коэффициенты связей различны.
Будет интересно: Листовые конструкции корпуса судна
Подсчитав исправленные площади сечения, статические моменты и моменты инерции площадей относительно оси сравнения, определяют отстояние нейтральной оси во втором приближении (раздельно для изгиба на вершине волны и на подошве волны).
Напряжения во втором приближении определяют вполне аналогично первому.
Если напряжения от общего изгиба судна, вычисленные во втором приближении отличаются от напряжений первого не более чем на 5 %, дальнейшие уточнения не производят.
Расчеты общей предельной прочности
Во всех случаях должна быть проверена общая прочность корпуса судна по предельным моментам. Под предельным понимается момент, изгибающий корпус судна и вызывающий в наиболее удаленной кромке напряжения, равные пределу текучести материала.
Определению подлежат два предельных момента Mпр (кНм), один при прогибе, другой при перегибе судна:
Mпр = ±10–3ReнW, Форм. 26
где:
- Reн – предел текучести материала, МПа;
- W – фактический момент сопротивления эквивалентного бруса (днища или палубы), определяемый по формуле 16 или 17.
Однако в курсовом проекте допускается предельный момент вычислять один раз.
При вычислении момента сопротивления необходимо редуцировать гибкие связи корпуса (пластины), принимая напряжения на одной из кромок эквивалентного бруса, равными пределу текучести. Редукционные коэффициенты при поперечной системе набора можно назначать по табл. 9.
| Таблица 9. Редукционные коэффициенты при поперечной системе набора | ||||
|---|---|---|---|---|
| Виды деформации | Редукционные коэффициенты φ при толщине пластины, мм | |||
| 4 | 6 | 8 | 12 | |
| Растяжение | 0,08 | 0,24 | 0,40 | 0,60 |
| Сжатие | 0,03 | 0,07 | 0,12 | 0,28 |
При продольной системе набора редукционные коэффициенты сжатых пластин определяются по формуле:
φ = Reн/σж, Форм. 27
где:
-
σж
– абсолютное значение сжимающего напряжения жестких связях, МПа, полученное при расчете эквивалентного бруса.
Редукционный коэффициент не должен быть более 1.
Для обеспечения прочности корпуса по предельному моменту должно выполняться условие:
Mпр≥kMp, Форм. 28
где:
- k – коэффициент запаса прочности по предельному моменту;
- Мр – расчетный изгибающий момент при прогибе и перегибе, кНм.
Значения коэффициента k, независимо от марки применяемой стали, определятся следующим образом:
- если палуба или непрерывный комингс (за исключением судов с двойными бортами классов «О», «Р», «Л») загружены поперечной нагрузкой k = 1,5;
-
если поперечная нагрузка на палубу и непрерывный комингс отсутствуют, k = 1,35. Здесь предполагается, что напряжение в предельном со стоянии и днище не превышает
σд.пр≤0,9Reн
;
-
если поперечная нагрузка на палубу и непрерывный комингс отсутствуют, а
0,9Reн<σд.пр≤Reн, то k = 1,5σд.прReн.
Для грузовых судов прочность корпуса по предельному моменту должна быть дополнительно проведена по условию:
Mпр≥kпрDLg Форм. 29
где:
- kпр — коэффициент предельного момента, определяемый по табл. 10;
- D – водоизмещение судна, т.
| Таблица 10. Коэффициент предельного момента | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| b/a | 1,0 | 101 | 1,2 | 1,3 | 1,4 | 1,6 | 1,8 | 2,0 | 2,5 | 3,0 | ∞ |
| k | 9,34 | 8,56 | 8,0 | 7,60 | 7,30 | 6,92 | 6,70 | 6,56 | 6,07 | 5,86 | 5,35 |
Примечание:
- а – длина меньшей,
- b – длина большей стороны пластины.
Определение дополнительных волновых изгибающих моментов для судов, эксплуатирующихся с ограничениями, не ответствующими классу
Судам, длительное время находящимся в эксплуатации, может быть понижен класс РРР, а некоторым судам при переоборудовании или модернизации может быть повышен класс РРР. При этом изменяются дополнительные волновые моменты, что должно быть учтено в расчетах прочности.
Предлагаемая методика Методика определения дополнительн6ых волновых изгибающих моментов для судов, эксплуатирующихся с ограничениями, не соответствующему классу РРР.x регламентирует назначение величин расчетных дополнительных изгибающих моментов при введении дополнительных ограничений условий эксплуатации судов с классом РРР.
Действие методики распространяется на грузовые и пассажирские суда классов “Р”, “О” и “М” длиной от 50 до 140 м и соотношениями главных размеренийОпределение главных размерений и водоизмещения буксирных судов, приведенными в табл. Общие вопросы проектирования судовых конструкций“Максимальные соотношения главных размерений судов” и на грузовые суда классов “О-ПР”, “М-ПР” и “М-СП” длиной от 50 до 140 м.
При введении ограничений по волнению допускается устанавливать следующие высоты волн для судов класса:
- “М-СП” – 3,0 и 2,5 м;
- “М-ПР” – 2,0 м;
- “О-ПР” – 1,5 м;
- “М” – 2,5 и 2,0 м;
- “О” – 1,5 и 1,2 м;
- “Р” – 0,9 и 0,6 м.
Здесь для всех судов, кроме класса “О” и “Р”, указана высота волн 3 %-ной обеспеченности. Для судов класса “О” и “Р” принимается высота волн 1 %-ной обеспеченности.
Дополнительный волновой изгибающий момент с учетом дополнительных ограничений условий эксплуатации определяется по формуле:
Mдвогр = k3Mдв, Форм. 30
где:
- Mдв — дополнительный волновой изгибающий момент, определяемый в зависимости от класса судна;
- k3 — коэффициент, учитывающий уменьшения момента при введении дополнительных ограничений.
Величина k3 определяется по табл. 11. Промежуточные значения определяются линейной интерполяцией.
| Таблица 11. Значения коэффициента k3 | |||||||
|---|---|---|---|---|---|---|---|
| Класс судна | Ограничения по высоте волны, м | Длина судна L, м | |||||
| 50 | 60 | 80 | 100 | 120 | 140 | ||
| “М-СП” | 3,0 | – | 0,977 | 0,961 | 0,949 | 0,936 | 0,927 |
| 2,5 | – | 0,973 | 0,952 | 0,939 | 0,924 | 0,913 | |
| “М-ПР” | 2,0 | – | 0,960 | 0,942 | 0,924 | 0,904 | 0,890 |
| “О-ПР” | 1,5 | – | 0,932 | 0,906 | 0,885 | 0,863 | 0,842 |
| “М” | 2,5 | 0,910 | 0,895 | 0,865 | 0,840 | 0,815 | 0,785 |
| 2,0 | 0,810 | 0,770 | 0,720 | 0,650 | 0,600 | 0,550 | |
| “О” | 1,5 | 0,780 | 0,720 | 0,665 | 0,605 | 0,605 | 0,605 |
| 1,2 | 0,735 | 0,585 | 0,520 | 0,520 | 0,520 | 0,520 | |
| “Р” | 0,9 | 0,665 | 0,630 | 0,630 | 0,630 | 0,630 | 0,630 |
| 0,6 | 0,540 | 0,470 | 0,470 | 0,470 | 0,470 | 0,470 |
Суда внутреннего и смешанного плавания с дополнительными ограничениями по волнению могут быть допущены к эксплуатации в бассейнах, разряд которых соответствует классу судна.
Сноски
Площади фигур (плоских и объемных)
Слышал ты что-нибудь про формулу Пика? Когда ее можно применять, а когда нельзя?
Сколько ты знаешь способов нахождения площади фигур на клетчатой бумаге? А их на самом деле три! И хотя задачу по нахождению площади фигур на клетчатой бумаге убрали из ЕГЭ, сам навык очень полезен для понимания планиметрии!
Во второй части мы рассмотрим как находить площади объемных фигур (призмы и пирамиды)
ПЛОЩАДИ ПЛОСКИХ ФИГУР
Способы нахождения площади фигур на клетчатой бумаге:
Способ 1. Считай клетки и применяй формулы
Удобен для стандартных фигур: треугольника, трапеции и т.д.
- Подсчитывая клеточки и применяя простые теоремы, найти те стороны, высоту, диагонали, которые требуются для применения формулы площади;
- Подставить найденные значения в уравнение площади.
Способ 2. Дострой до прямоугольника и вычти лишнее
Очень удобен для сложных фигур, но и для простых неплох
- Достроить искомую фигуру до прямоугольника;
- Найти площадь всех получившихся дополнительных фигур и площадь самого прямоугольника;
- Из площади прямоугольника вычесть сумму площадей всех лишних фигур.
Способ 3. Формула Пика
Работает только для многоугольников без дырок, все вершины которых попадают в узлы сетки.
- Назовём «узлами» точки пересечения линий сетки нашей клетчатой бумаги.
Подсчитаем, сколько узлов попадает в нашу фигуру. Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.
В примере на рисунке получилось ( Г = 22) на границе и ( В = 32) внутри.
Формула Пика. Делим границу пополам, прибавляем внутренности и вычитаем 1:( S = Г/2 + В – 1 )
В примере на рисунке:
( S = Г/2 + В – 1 = 22/2 + 32 — 1 = 42.)
Способ 1. Считай клетки и применяй формулы
Удобен для стандартных фигур: треугольника, трапеции и т.д.
- Подсчитывая клеточки и применяя простые теоремы, найти те стороны, высоту, диагонали, которые требуются для применения формулы площади;
- Подставить найденные значения в уравнение площади.
Пусть нужно найти площадь трапеции, построенной на листе в клетку.
Просто считаем клеточки и видим, что в нашем случае ( displaystyle a=17), ( displaystyle b=6) и ( displaystyle h=6). Подставляем в формулу:
( displaystyle S=fraccdot h=fraccdot 6=69)
Но бывает, что не так-то просто рассчитать, сколько клеток в нужном отрезке. Вот смотри, треугольник:
Вроде бы даже прямоугольный и ( displaystyle S=fraccdot ab), но чему тут равно ( displaystyle a), и чему равно ( displaystyle b)?
Найдем ( displaystyle a) по теореме Пифагора из ( displaystyle Delta ADC), а ( displaystyle b) по теореме Пифагора из ( displaystyle Delta BCE).
Благо на листе в клетку легко посчитать длину катетов.
Значит, ( displaystyle a=sqrt=2sqrt)
Подставляем в формулу:
( displaystyle S=fraccdot ab=fraccdot 2sqrtcdot sqrt=13).
Способ 2. Дострой до прямоугольника и вычти лишнее
Очень удобен для сложных фигур, но и для простых неплох
- Достроить искомую фигуру до прямоугольника;
- Найти площадь всех получившихся дополнительных фигур и площадь самого прямоугольника;
- Из площади прямоугольника вычесть сумму площадей всех лишних фигур.
Давай посчитаем площадь того же треугольника вторым способом.
Нужно окружить нашу фигуру прямоугольником. Вот так:
Получился один (нужный) треугольник внутри и целых три ненужных треугольника снаружи. Но зато площади этих ненужных треугольников легко считаются на листе в клетку!
Вот мы их посчитаем, а потом просто вычтем из целого прямоугольника:
( displaystyle _>=fraccdot 6cdot 4=12)
( displaystyle _>=fraccdot 7cdot 4=14)
( displaystyle _>=fraccdot 3cdot 2=3)
( displaystyle Rightarrow S=42-12-14-3=13)
Почему бы просто не считать клеточки?
Возможно, вы читаете всё это и думаете: зачем все эти сложности? Формулы запоминать. Дорисовывать. Тут ведь сразу видно, сколько клеточек в фигуре.
Вот, например, трапеция:
Посчитаем клеточки: их всего 46, верно?
Но стоп, там же некоторые из них только наполовину внутри фигуры. Отметим их – всего таких 10. Итого, 36 полных (красные точки) и 10 половинчатых, вместе ( 36+frac = 41)
Вроде бы всё верно. Но, если присмотреться, можно заметить ещё маленькие треугольнички, которые попали внутрь. А также, что «синие» клеточки слева на самом деле разрезаны не ровно пополам – какие-то чуть больше, какие-то меньше…
Как всё это учитывать?
Попробуем рассуждать так: заметно, что тот маленький розовый треугольник дополняет серый кусок клетки.
А жёлтые сколько занимают? Постарайтесь ответить сами.
Если всё сделать правильно, то увидите, что жёлтые кусочки можно сложить вместе в одну целую клетку.
Итак, 2 жёлтых куска = 1 клетка.
Розовый треугольник + серый кусок = 1 клетка. Всего у нас две таких пары (розовый+серый) – это 2 полных клетки.
Всё остальное как было: 36 полных клеток и 6 половинок у правой стороны – это ( 36+frac=39) клетки.
Итого клеток: ( 1 + 2 + 39 = 42).
Проверим результат по формуле площади трапеции: нижнее основание 11, верхнее основание 3, высота 6. Полусумма оснований равна 7, умножаем на высоту – получилось 42. Всё совпало.
Но! Настолько ли проще был наш способ подсчёта клеточек? Не сказал бы. А если там будет несколько косых линий, то вообще можно замучиться собирать этот паззл (искать, какие кусочки друг друга дополняют).
Способ 3. Формула Пика
Существует довольно удобная формула, которая использует клеточки для вычисления площади. А то, что мы только что проделали, – очень полезное упражнение, которое поможет эту формулу понять.
Назовём «узлами» точки пересечения линий сетки нашей клетчатой бумаги.
Теперь вместо клеточек или их частей подсчитаем, сколько узлов попадает в нашу фигуру. Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.
У меня получилось ( Г = 22) на границе и ( В = 32) внутри.
Ну а теперь сама формула:
Делим границу пополам, прибавляем внутренности и вычитаем 1:
Называется она формулой Пика, поскольку доказал её математик Георг Пик 120 лет назад (да, она не специально для ЕГЭ была придумана, но очень нам помогает)
Как запомнить формулу Пика
Всё, что внутри, берём целиком (клетки внутри фигуры целые).
Граница режет клетки надвое, поэтому берём половину узлов границы.
Минус 1 – это надо просто запомнить. Очень легко себя проверить на квадрате 1×1. Его площадь равна 1. Сколько там точек на границе? ( Г = 4.) А сколько внутри? ( В = 0) (нисколько)
Границу делим пополам, получаем 2. Прибавляем внутренности (+0) – ничего не поменялось.
Очевидно, что осталось вычесть 1, чтобы получить 1.
Проверьте эту формулу на других простых фигурах, чтобы убедиться и закрепить.
Вычислите площадь простых фигур тремя способами
Стороны клеток равны 1. Вычислите самостоятельно площадь фигуры всеми тремя способами. Сравните результаты.
Вычислите площадь произвольных фигур по формуле Пика
Вычислите самостоятельно площади фигур с помощью формулы Пика:
Посчитайте площадь корабля и котика по формуле Пика
Посчитайте самостоятельно для тренировки и чтобы запомнить формулу Пика!
Фигуры с отверстиями — посчитайте площади двумя способами
Ну и напоследок фигуры с «дырками». Как думаешь, здесь придётся вычислять сначала площадь целой фигуры, а потом площадь дырки?
Или достаточно просто посчитать точки внутри закрашенной области и на её границах (в том числе, на границе с дыркой)?
Проверим на простом примере: это квадрат ( 4times 4), и в нём вырезан прямоугольник ( 1times 2), значит, его площадь ( 16-2=14).
А теперь по точкам. На границах (включая внутренние) ( Г = 22). Внутри ( В = 3). Тогда площадь по формуле Пика
Хм, близко, но не совпало. Может, я где-то ошибся? Давай ещё одну фигуру, для верности.
Сосчитай сам и проверь.
У меня снова на 1 меньше.
Так может быть просто формулу немного «подкрутить»? Нет!
Очень и очень не рекомендую вам запоминать несколько похожих формул для похожих случаев, потому что придёт время, и вы обязательно перепутаете формулу.
Даже если вы уверены, что не перепутаете, оно всё равно того не стоит. В общем, наилучший вариант – это запомнить одну формулу. А если попалась фигура с дыркой, вычислить всю фигуру, а потом дырку. И вычесть.
Когда формулу Пика применять нельзя?
Естественно, эта формула не работает для окружностей и любых других фигур с «кривыми» границами.
Также она не сработает, если хотя бы одна из вершин не попадает на узел, например, вот для такой, как на рисунке.
Почему я уверен, что не сработает? Ведь можно взять и не учитывать эту вершину, раз она не в узле. То есть
( Г = 10, В = 2, S = frac + 2 – 1 = 6.)
А очень просто: я возьму и «отрежу» эту вершину. Тогда будет не треугольник, а трапеция, и площадь, очевидно, станет меньше на тот отрезанный кусочек.
Но по формуле она останется такой же, ведь количество узлов не изменилось ни на границе, ни внутри. То есть мы получим, что площадь уменьшенного треугольника равна площади целого, чего, конечно же, не может быть.
Итак, формула Пика работает только для многоугольников без дырок, все вершины которых попадают в узлы сетки.
Какой способ лучше?
Второй и третий способы универсальные. Они помогут посчитать площадь даже самых замысловатых фигур. Вернемся еще раз ко второму способу.
Вот смотри, нужно посчитать площадь такой фигуры:
Окружаем ее прямоугольником и снова получаем одну нужную, но сложную площадь и много ненужных, но простых.
А теперь чтобы найти площадь ( displaystyle S) просто находим площадь прямоугольника и вычитаем из него оставшуюся площадь фигур на клетчатой бумаге ( displaystyle _>+_>+_>+_>).
( displaystyle _>=fraccdot 6cdot 4=12)
( displaystyle _>=fraccdot acdot h=fraccdot 5cdot 4=10) (обрати внимание, ( displaystyle _>) площадь НЕ прямоугольного треугольника, но все равно легко считается по основной формуле).
( displaystyle _>=fraccdot 5cdot 2=5)
( displaystyle _>=fraccdot 1cdot 11=5,5).
Вот и ответ: ( displaystyle S=33,5).Ну как тебе этот способ?
Вот смотри. С одной стороны, когда фигура занимает много клеточек, их замучаешься считать и можно ошибиться.
С другой стороны, когда мы дорисуем до прямоугольника, нужно считать много площадей.
Поэтому использование того или иного способа зависит лишь от конкретной задачи.
ПЛОЩАДИ ОБЪЕМНЫХ ФИГУР
Площадь поверхности призмы
Есть ли общая формула? Нет, в общем случае нет. Просто нужно искать площади боковых граней и суммировать их.
Площадь полной поверхности призмы – это сумма площадей всех граней.
Формулу можно написать для прямой призмы:
( displaystyle >_>=textcdot text
), где ( displaystyle P) — периметр основания.
Но всё-таки гораздо проще в каждом конкретном случае сложить все площади, чем запоминать дополнительные формулы. Для примера посчитаем полную поверхность правильной шестиугольной призмы.
Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b).
Все боковые грани – прямоугольники. Значит ( displaystyle >_>>=6cdot text).
Площадь поверхности пирамиды
Для пирамиды тоже действует общее правило:
Площадь полной поверхности пирамиды – это сумма площадей всех граней.( displaystyle _>=_>+_>)
Теперь давай посчитаем площадь поверхности самых популярных пирамид.
Площадь поверхности правильной треугольной пирамиды
Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b). Нужно найти ( displaystyle _>) и ( displaystyle _>).
Вспомним теперь, что
( displaystyle _>) — это площадь правильного треугольника ( displaystyle ABC).
И еще вспомним, как искать эту площадь.
Используем формулу площади:
( displaystyle S=fracabcdot sin gamma ).
У нас «( displaystyle a)» — это ( displaystyle a), а «( displaystyle b)» — это тоже ( displaystyle a), а ( displaystyle sin gamma =sin 60^circ =frac>).
Теперь найдем ( displaystyle _>).
Пользуясь основной формулой площади и теоремой Пифагора, находим
Внимание: если у тебя правильный тетраэдр (т.е. ( displaystyle b=a)), то формула получается такой:
Площадь поверхности правильной четырехугольной пирамиды
Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b).
В основании – квадрат, и поэтому ( displaystyle _>=>).
Осталось найти площадь боковой грани
Площадь поверхности правильной шестиугольной пирамиды
Пусть сторона основания равна ( displaystyle a), а боковое ребро ( displaystyle b).
Как найти ( displaystyle _>)?
Шестиугольник ( displaystyle ABCDEF) состоит ровно из шести одинаковых правильных треугольников. Площадь правильного треугольника мы уже искали при подсчете площади поверхности правильной треугольной пирамиды, здесь используем найденную формулу.
Ну, и площадь боковой грани мы уже искали аж два раза
Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике
Этот вебинар посвящен заданию №3 из ЕГЭ на нахождение площади фигур, длин отрезков и т.д на клетчатой бумаге.
И хотя эту задачу убрали из ЕГЭ в 2021 году, сам навык очень полезен для того, чтобы начать учить геометрию, для понимания планиметрии!
Ну и просто этот вебинар легкий и классный! Послушайте его и получите удовольствие!
Теорема Пика или формула для ленивых
Каждому из нас нередко приходилось считать площадь решётчатого многоугольника (изображённого, например, на клетчатой бумаге). В основном, это делают ещё по известным со школы формулам. Но в этом случае для каждой фигуры приходится помнить выражение её площади.
Не легче ли использовать одну формулу для всех многоугольников?
— Сказка? — Нет, теорема Пика!
• Названа она в честь Георга Пика (нет, не оружия или покемона), доказавшего её в 1899 году.
Формулировка звучит так:
S = В + Г / 2 − 1, где S — площадь многоугольника, В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
• Важное замечание: формула справедлива только для многоугольников, у которых вершины расположены в узлах решетки.
Например, для многоугольника на рисунке, В=7 (красные точки), Г=8 (зелёные точки), поэтому S = 7 + 8/2 — 1 = 10 квадратных единиц.
Докажем теорему Пика:
• Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны a и b. Имеем в этом случае В = (a-1)(b-1), Г = 2a+2b и, по формуле Пика, S = (a-1)(b-1)+a+b-1 = ab .
• Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами a и b, рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат c целочисленных точек. Тогда для этого случая В = ((a-1)(b-1)-c+2)/2, Г = (2a+2b)/2+c-1 и получаем, что S = ab/2.
• Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников (см. рисунок). Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.
• Остается сделать последний шаг: перейти от треугольников к многоугольникам. Любой многоугольник можно триангулировать, т.е. разбить на треугольники (например, диагоналями). Отсюда по индукции следует, что формула Пика верна для любого многоугольника. чтд
К сожалению, эта столь простая и красивая формула плохо обобщается на высшие размерности.
Наглядно показал это Рив, предложив в 1957 г. рассмотреть тетраэдр (называемый теперь тетраэдром Рива) со следующими вершинами:
A(0,0,0), B(1,0,0), C(0,1,0), D(1,1,k)
Тогда этот тетраэдр ABCD при любых k не содержит внутри ни одной точки с целочисленными координатами, а на его границе — лежат только четыре точки A, B, C, D. Таким образом, объём и площадь поверхности этого тетраэдра могут быть разными, в то время как число точек внутри и на границе — неизменны; следовательно, формула Пика не допускает обобщений даже на трёхмерный случай.
Тем не менее, некоторое подобное обобщение на пространства большей размерности всё же имеется, — это многочлены Эрхарта, но они весьма сложны, и зависят не только от числа точек внутри и на границе фигуры.
Площади многоугольников и тающий лёд
Как найти площадь многоугольника на клетчатой бумаге? Можно подсчитать число клеток, которые полностью накрыты фигурой, и ещё как-то учесть клетки, накрытые фигурой частично, — скажем, прибавить половину от числа этих клеток. И сказать, что площадь фигуры (в клеточках) приблизительно равна полученной сумме.
А можно вместо клеток, полностью или частично накрытых многоугольником, считать узлы сетки (вершины клеток) строго внутри многоугольника или на его границе.
Действительно, вокруг каждого узла сетки можно нарисовать по единичному квадратику. И если узел лежит на границе многоугольника, то этот квадратик накрыт многоугольником только частично. А если узел лежит внутри, то обычно и квадратик накрыт многоугольником полностью. впрочем, иногда всё же не полностью — но мы и считаем площадь только приближённо.
Но чудесным образом последний рецепт всегда даёт почти правильный ответ! А именно, верна Формула Пика. Площадь S многоугольника с вершинами в узлах сетки можно найти по формуле
где i — число узлов сетки строго внутри многоугольника, b — число узлов сетки на его границе.
Подчеркнём, что это уже не приближённая, а точная формула!
Интересно, что хотя длины сторон у многоугольников обычно совершенно не целые, формула Пика гарантирует, что площадь всегда получится целой или полуцелой.
Тающий лёд
Формула Пика известна с XIX века, и с тех пор у неё появилось много доказательств, но большинство из них не такие уж простые. Мы обсудим предложенный в 1997 году швейцарским математиком Кристианом Блаттером мысленный эксперимент с тающим льдом, который сразу объясняет формулу Пика.
Поставим на каждый узел сетки по одинаковому цилиндрическому столбику изо льда. Каждый столбик очень тонкий (пересекается только с теми сторонами многоугольника, которые проходят через центр столбика) и весит 1 грамм.
Построим вокруг каждого столбика забор в виде единичного квадратика, после чего растопим весь лёд (во всех квадратиках вода растекается одинаково и симметрично относительно центра своего квадратика). Вся клетчатая плоскость будет равномерно залита водой, и в каждой ячейке площади 1 будет по 1 грамму воды. То есть количество воды в нашем многоугольнике (в граммах) будет равно его площади (в клетках).
С другой стороны, задумаемся, откуда эта вода попала в наш многоугольник. Посмотрим на какую-нибудь конкретную сторону многоугольника. Если через неё внутрь многоугольника втекла вода из какого-то столбика, то точно столько же воды из симметричного столбика (симметричного относительно середины этой стороны) через неё из многоугольника вытекло.
То есть внутри многоугольника ровно столько воды, сколько в нём было льда! А сколько в нём было льда? Каждый из узлов сетки внутри многоугольника даёт вклад 1 грамм, общий вес получается i граммов. Узлы на сторонах обычно дают по 1 2 грамма, но только если это не вершина, для вершины этот вес меньше — так что и общий вес узлов на границе получается не b 2 граммов, а меньше.
Насколько меньше? Продлим немного каждую сторону, обходя многоугольник вдоль сторон по часовой стрелке. На рисунке ниже красная часть дополняет каждую из синих частей до половины круга. Но красные части в сумме дают ровно один круг! Ведь, обходя многоугольник по контуру, мы в каждой вершине поворачиваемся на угол, соответствующий красной части, пока не вернёмся в исходную точку, сделав как раз полный оборот.
То есть суммарный вес льда внутри многоугольника равен i + b 2 − 1 , и мы получили формулу Пика!
Упражнение
В рассуждении выше мы рисовали выпуклый многоугольник. А изменится ли что-то, если многоугольник станет невыпуклым? А если рассматривать «многоугольники с дырками»?
Вычислить площадь каркаса кораблика.

Вы зашли на страницу вопроса Вычислить площадь каркаса кораблика?, который относится к
категории Математика. По уровню сложности вопрос соответствует учебной
программе для учащихся 10 — 11 классов. В этой же категории вы найдете ответ
и на другие, похожие вопросы по теме, найти который можно с помощью
автоматической системы «умный поиск». Интересную информацию можно найти в
комментариях-ответах пользователей, с которыми есть обратная связь для
обсуждения темы. Если предложенные варианты ответов не удовлетворяют,
создайте свой вариант запроса в верхней строке.
Ответ:Общая площадь корабля будет 7440 кв.м.
1 — 1/2 = 1/2(остаток площади,не занятой под взлетно-посадочную площадь)
1/2 — 1/3 = 3/6 — 2/6 = 1/6 (остаток площади,не отведенный на зону отдыха и ожидания)
1 — 1/4 = 3/4(это оставшиеся 930 кв.м.)
найдем 1/6 часть всей площади:
930:3/4=930*4/3 = 1240 кв.м (это 1/6 часть всей площади корабля)
Для того чтобы найти всю площадь строящегося корабля,надо 1240 поделить на 1/6:
1240 : 1/6 = 1240*6/1 = 7440 кв.метров
Пошаговое объяснение: