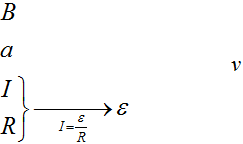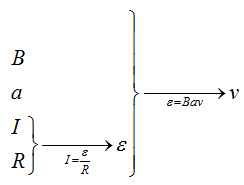Как найти площадь контура формула

16.
Способы определения площадей контуров,
их точность.

1.
Аналитический способ
— когда площадь вычисляется по

результатам
измерений линий на местности или по их
функциям

(координатам
вершин участка);

2.
Графический способ
— когда площадь вычисляется по результатам

измерений
линий на плане (карте);

3.
Механический способ
— когда площадь определяется по плану
при помощи специальных приборов
(планиметров).

Иногда
эти способы применяются комбинированно.

• Аналитический
  способ определения площадей

Вычисление
площади этим способом производится по
формулам

геометрии,
тригонометрии и аналитической геометрии.
Исходными

данными
для вычисления служат измеренные в
натуре углы или их

функции
– координаты. Если участок представляет
собой простейшую геометрическую фигуру
(треугольник, трапецию и др.), то площадь
его вычисляют по общеизвестным формулам
геометрии или тригонометрии .Площади
многоугольников вычисляют обычно по
координатам вершин.

Точность
аналитического способа 1/1000. При
определении площади этим способом на
точность влияют только погрешности
измерений на местности.

• Графический
  способ определения площадей

Площади
участков, имеющих форму геометрических
фигур

треугольника,
прямоугольника или трапеции, вычисляют
по известным формулам геометрии.

Если
участок представляет многоугольник,
то его делят на элементарные геометрические
фигуры – треугольники и трапеции.

Точность
определения площади графическим методом
зависит от графической ошибки измерений
линий плана. Известно, что линия плана
определяется циркулем – измерителем
с ошибкой 0,1 мм, которая не зависит от
длины линии. Из этого следует, что
относительная ошибка короткой линии
больше, чем длинной. Поэтому при построении

элементарных
фигур надо стремиться к фигурам больших
размеров и по возможности с одинаковыми
длинами оснований и высот

Определение
площади способом палетки

Квадратная
палетка представляет собой прозрачный
лист, на котором нанесена сеть квадратов
со сторонами 2 – 10 мм. Зная длину стороны
одного квадрата и масштаб плана, можно
вычислить площадь квадрата. Например,
масштаб карты (плана) 1:10 000 следовательно,
площадь одного квадрата со стороной
1см будет равна 10 000 м2 или 1га.

Для
определения площади палетку накладывают
на замкнутый

контур
(рис.3). Площадь подсчитывается как сумма
полных и неполных

квадратов.
Недостаток графического способа
заключается в том, что

количество
неполных квадратов приходится оценивать
на глаз. На рисунке

3
число полных квадратов 15, а неполных
примерно равно 8,5 для каждого неполного
квадрата глазомерно определяют, какую
часть он составляет от полного.
Следовательно, отсюда относительная
ошибка определения площади палеткой
составляет 1/100.

Механический
способ определения площадей

1.
Перед измерением площади участка план
или карта закрепляются

на
гладкой горизонтальной плоскости.

2.
Планиметр устанавливается так, чтобы
его полюс располагался вне

измеряемого
участка, а полюсный и обводной рычаги
образовывали

примерно
прямой угол.

3.
Совместив обводную точку планиметра с
исходной точкой контура,

снимают
по счетному механизму начальный отсчет
n1 и плавно

обводят
весь контур по ходу часовой стрелки.

4.
Вернувшись в исходную точку, берут
конечный отсчет n2.

5.
Разность отсчетов (n2 – n1) выражает
величину площади фигуры в

делениях
планиметра.

6.
Итоговая площадь контура рассчитывается
по формуле:

Измерение
площади полярным планиметром

S
= O·
(n2
– n1),

где
О – цена деления планиметра

Определение
цены деления полярного планиметра

1.
Для определения цены деления планиметра
измеряют фигуру,

площадь
которой Sо заранее известна (например,
квадрат

координатной
сетки, Sо = 1км· 1км = 1км2).

2.
Вычисляют цену деления планиметра по
формуле:

3.
Цена деления зависит от масштаба карты
и от длины

обводного
рычага (расстояние от обводной точки
до полюсного

рычага).

где
(m2 – m1) – разность отсчетов, полученных
при измерении

контура
с известной площадью.

(m2
– m1)

S
O
= о

Определение
площади электронным планиметром

Объект,
на котором определяют

площадь
контура, должен быть

расположен
на горизонтальной

поверхности;

• Установить
планиметр необходимо

так,
чтобы роликовый механизм и

рамка
трассера располагались под

прямым
углом друг к другу, а линза

трассера
при этом находилась

примерно
на середине контура

снимаемого
объекта.

Магнитная сила между параллельными проводниками

Магнитная сила между параллельными проводниками

Магнитная постоянная

Напряжённость магнитного поля

Индукция магнитного поля

Максимальный момент магнитного поля

Магнитная индукция

Момент однородного магнитного поля

Магнитное поле прямолинейного проводника конечной длины с током

Индукция магнитного поля, созданного бесконечно длинным прямым проводником с током

Магнитная индукция поля в центре кругового тока (витка)

Напряжённость магнитного поля: бесконечной прямой провод

Напряжённость магнитного поля в центре витка

Магнитная индукция соленоида

Напряжённость магнитного поля соленоида

Магнитный поток и угол

Магнитный поток

Сила Ампера

Магнитная индукция и сила Ампера

Сила Лоренца

Сила Лоренца и сила Ампера

Сила электромагнитного поля

Радиуса движения заряженной частицы в магнитном поле

Период вращения заряженной частицы в магнитном поле

Тема 2.3. Определение площадей

1.
Методы определения  площадей

1.1.
Аналитический метод определения площадей.

1.2.
Графический метод определения площадей.

1.3.
Способ палетки.

1.4.
Механический метод определения площадей.

ПЛОЩАДЬ
ЛЮБОЙ ФИГУРЫ ЛЮБЫМ СПОСОБОМ ВЫЧИСЛЯЕТСЯ НЕ МЕНЕЕ ДВУХ РАЗ

Определение
площадей в землеустроительном производстве имеет большое практическое значение.
Размеры площадей надо знать с большой точностью при составлении 
землеустроительных проектов, при выделении участков в пользование, а так же для
учета и использования земель в различных отраслях с/х и промышленного
производства. В зависимости от способа получения данных, с помощью которых
вычисляются площади, существует несколько методов определения площадей.

1.1.
Аналитический метод определения площадей.

Аналитический
метод состоит в определении площади участка по результатам непосредственных
измерений линий и углов в натуре или по координатам вершин (граничных точек). Точность
величины площади участка при этом зависит только от ошибок измерения длин и
углов на местности и характеризуется относительной ошибкой 1/500 – 1/1000.
Однако в условиях большой контурности и вкрапливаний одних контуров в другие,
площади которых определяются менее точными способами, аналитический метод становится
нецелесообразен.

А)
Определение площади участка по результатам измерения в натуре.

Площади
небольших участков, имеющих форму элементарных геометрических фигур, вычисляют
математически по формулам геометрии.

            
а                  S = a²

     
в

                     а       
S = a*в

                               
2 S = a*h; или S
= a*h/2

        
a

           
 a

                                      
S = ((a+в)/2)*h 
или  S = m*h

         
в

Б)
Вычисление площади полигона по координатам его вершин.

Площадь
любой фигуры ограниченной прямыми линиями можно вычислить по двум формулам.

Удвоенная
площадь полигона равна сумме произведений абсциссы каждой точки на разность
ординат последующей и предыдущей точек.

Она
же (удвоенная площадь) равна сумме произведений каждой ординаты на разность абсцисс
предыдущей и последующей точек.

2S
= x₁(y₂-y₃)+x₂(y₃-y₁)+x₃(y₁-y₂)

2S
= y₁(x₃-x₂)+y₂(x₁-x₃)+y₃(x₂-x₁)

                                               
2 (x₂,
y₂)

               
1(x₁,
y₁)                                            
3 (x₃,
y₃)

1.2.
Графический метод определения площадей.

Графический
метод заключается в том, что данные для вычисления площадей берутся с плана,
графически, и площади отдельных геометрических фигур вычисляются с помощью
геометрических формул.

Если
участок представляет собой многоугольник, то его делят на треугольники,
прямоугольники или трапеции. С помощью измерителя и масштабной линейки
определяют те величины, которые нужны для получения площадей отдельных фигур.
Сумма площадей элементарных геометрических фигур даст общую площадь участка.

Точность
определения площади графическим способом зависит от графической ошибки
измерения отрезка на плане. Отрезок на плане циркулем — измерителем
определяется с ошибкой +0,1мм, которая не зависит от длины линии. Из этого
следует, что относительная ошибка короткой линии больше, а длинной – меньше.

Правила
для определения площади графическим способом:

1.      Площади
определяются дважды (либо участок разбивается на другие элементарные фигуры,
либо в треугольниках изменяются основания и высота).

2.      План
берется в наиболее крупном масштабе.

3.      Фигуры
должны быть как можно крупнее и не очень вытянуты, то есть основание и высота
должны быть примерно равны.

4.      Если
в геометрических фигурах есть линии, величины которых известны из
непосредственных измерений, то их надо использовать для вычисления площадей.

5.      Предельное
расхождение двукратных определений не должно превышать1:200 величины площади
участка.

При
работе по этому способу применяют специальные палетки для проведения высот.

Графически
вычисляют площади контуров  имеющих вытянутую форму (дорога, канал, ручей и
т.д.), ширина которых не всегда выражается в масштабе плана, но она должна быть
известна или подписана на плане.

1.3.
Определение площади палеткой

Квадратная
палетка. Квадратная палетка представляет собой
прозрачный лист целлулоида, стекла или восковки, на котором нанесена сеть
квадратов со сторонами от 1 до 10 мм (рис. 180). Зная сторону квадрата, легко
подсчитать площадь его применительно к любому масштабу плана. Для определения
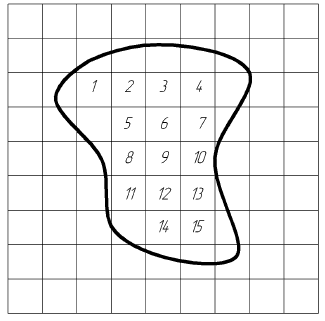
площади палетку накладывают на контур ABCD, имеющийся на плане. Вначале
подсчитывают число полных квадратов. На рис. 180 их оказалось 22, а затем
неполные квадраты объединяют и глазомерно заменяют некоторым числом полных.
Пусть таких квадратов девять. Общее число полных квадратов на площади ABCD
будет 31. Произведение площади одного квадрата на число их даст площадь
определяемого участка. Точность определения площади квадратной палеткой не
превышает 1:100.

Палетки
с параллельными линиями. Палетка с параллельными
линиями отличается от квадратной тем, что вместо квадратов на ней наносятся
параллельные линии. Она также делается из прозрачного целлулоида, на котором
нанесены параллельные линии с интервалом в 2 мм. Система таких линий с нужными
интервалами может быть нанесена на восковку. Это будет тоже палетка (рис. 181).
Для определения площади участка палетку накладывают на контур плана так, чтобы наиболее
удаленные друг от друга точки, например MN, приходились на середину расстояния
между какими-либо параллельными линиями. В результате этого площадь
определяемого контура будет разбита на трапеции, у которых сплошные линии а₁
в₁; а₂ в₂; а₃ в₃  и
т. д. будут средними линиями трапеций, а пунктирные (на палетке отсутствуют) —
основаниями трапеций.

Так
как высоты трапеций одинаковы и заранее известны, то для получения площади
контура надо измерить циркулем средние линии трапеций а₁ в₁;
а₂ в₂; а₃ в₃ т. д. Произведение
суммы средних линий на расстояние между нитями даст общую площадь контура.
Конечно, при этом надо учитывать масштаб плана.

Чтобы
не производить вычислений, ниже палетки наносят шкалу в виде простого линейного
масштаба. Ее строят с учетом следующих соображений. При масштабе плана 1:10 000
расстоянию между нитями на палетке в 2 мм соответствует 20 м на местности,
следовательно, каждому сантиметру длины полосы на плане будет в натуре
соответствовать площадь в 0,2 га. Если на прямой отложить несколько отрезков по
1 см, сделать соответствующие подписи и один отрезок разделить на мелкие
части        (см. рис. 181), то достаточно к такой шкале приложить раствор
циркуля, соответствующий сумме средних линий трапеций. Прочитанный отсчет по
шкале даст площадь в гектарах.

Аналогично
этому может быть построена шкала и для другого масштаба. Так, для масштаба 1 :
25 000 целесообразно за основание шкалы взять отрезок в 0,8 см, что будет
соответствовать 1 га.

Для
квадратной палетки пример:

Палетка
2х2мм,

Масштаб
плана 1:1000 – в 1мм – 1м, значит:

1квадрат
= 2м * 2м = 4м²,

Если
занято контуром 60 квадратов, то 60 *4 м² = 240 м²

1.4.
Механический метод.

Механический
способ заключается в измерении площадей плоских произвольных фигур на плане
(карте) с помощью специаль­ных приборов — планиметров,
относящихся к семейству механико-­математических интеграторов. Они бывают самых
разнообразных систем: от очень простых до очень сложных. Примером простейшего
планиметра может служить планиметр А. Амслера (1854г.). В это же время нашим
соотечественником Зарубиным П.А. был изобретен такой же по идее планиметр, но
более сложной конструкции. Подобные планиметры в настоящее время не применяют.

По
конструктивным
особенностям современные планиметры различают: полярные и роликовые (линейные).
 К полярным отно­сят планиметры, у которых одна точка (полюс) во
время обвода фи­гуры неподвижна, а к роликовым (линейным) — у
которых все точки прибора во время обвода фигуры подвижны.

По
способу фиксации результатов измерений на счетных уст­ройствах различают механические
и электронные устройства и в связи с этим появились термины:
механические планиметры и электронные (цифровые) планиметры.

1.4.1.
Полярный планиметр.

Планиметрами
называются приборы, при помощи которых можно получать площади криволинейных и
прямолинейных фигур по плану или топографической карте механически. Наиболее
часто

пользуются
полярным, или круговым, планиметром, представляющим собой соединение двух
рычагов R и
R₁
(рис. 71). Рычаг R₁
называется полюсным. Он имеет на одном
конце достаточно тяжелую гирьку  Г, имеющую форму цилиндра. В нижнем основании
цилиндра имеет­ся острая иголочка (полюс), при помо­щи которой планиметр
закрепляется на бумаге плана (иголочка вонзается в бумагу, и вокруг нее
вращается вся система планиметра). На другом конце рычага есть отросток с
шариком, кото­рый вкладывается в соответствующее углубление в раме М со
счетным меха­низмом (рис. 72) и служит вертикальной осью вращения рычагов.

В
указанной раме с одной стороны в двух выступах имеются отверстия,
в которые  вставляется   одним  концом о б водный рычаг R,
имеющий на другом конце обводный шпиль S.
Рычаг можно в раме передвигать и тем изменять  его
длину. В выступах рамы с другой стороны расположен счет­ный механизм, состоящий
из счетного ролика (колеса) к, вращающегося в на горизонтальной оси,
параллельной обводному рычагу. Эта ось посредством бесконечного (червячного)
винта сопряжена с шестеренкой циферблата  z, который разделен по окружности на
10 равных частей.

Цилиндрическая
поверхность счетного ролика разделена на 100 равных частей. На несколько
выступающем над цилиндрической поверхностью ободке счетного ролика нанесены
мелкие рубчики — рифельные  штрихи, параллельные оси вращения ролика, а
следовательно, и обводному рычагу. Благодаря этому движение по бумаге обводного
рычага, опирающе­гося на обводный шпиль и ролик, передается вследствие силы
трения (как говорят — по принципу фрикционного сцепления) ролику. При движении
обводного рычага перпендикулярно к своей оси ролик будет только вращать­ся
(предполагается, что плоскость ободка ролика перпендикулярна к оси его
вращения), а при движении по направлению вдоль оси рычага ролик будет только
скользить; при движении по любому иному направлению ролик час­тично будет
скользить, частично вращаться. По длине дуги, на которую ролик повернется при
обводе шпилем по всему контуру, и определяют пло­щадь контура. Длина дуги
выражается числом делений ролика. Таким образом, при работе планиметром дело
сводится к определению числа делений ролика, на которое оно повернется при
обводе контура шпилем. Для этого по ролику производятся отсчеты перед началом
движения и по его окончании. Разность этих отсчетов и выразит искомое число
делений. Отсчеты произво­дятся: тысячи делений по индексу циферблата, сотни и
десятки — на цилин­дрической поверхности ролика по нулевому штриху (индексу)
верньера и единицы — по верньеру.

Таким
образом планиметр имеет три основные части:

1.Полюсный
рычаг.

2.Обводной
рычаг.

3.Счетный
механизм, который состоит из:

a)     Счетчик
оборотов счетного ролика.

b)    Счетный
ролик с червяком.

c)     Верньер.

1.4.2.  Верньер (нониус).

Верньер,
называемый также иногда нониусом, представляет собой построение, позволяющее
более или менее точно отсчиты­вать доли делений, нанесенных на инструменте. На
ролике планиметра нанесены штрихи через интервалы, которые считаются за 10
делений плани­метра. Чтобы увереннее отсчитывать десятые доли этих интервалов,
т. е число единичных делений, и устраивается верньер.

Верньер
строится на небольшой части поверхности такого же цилиндра, как и  ролик, и плотно
прилегает к нему по линии .4-5 (рис. 73, деления изображены в увеличенном
виде), но так, чтобы при вращении ролика между ними не возникало трения. Для
построения верньера берется расстояние в 9 интервалов ролика и делится на 10
частей. Значит один интервал верньера составляет 0,9 интервала ролика, т. е.
меньше последнего на 0,1 его величины, что является одним делением планиметра.
Если нулевой штрих (индекс) верньера совместить с каким-либо штрихом ролика (т.
е. установить их так, чтобы они образовали одну прямую линяю), то первый штрих
верньера не дойдет до следующего штриха ролика на 1 деление, второй — на 2
деления и т. д. Если, наоборот, первый штрих верньера совпадает с каким-либо
штрихом ролика, то индекс верньера прошел за предыдущий штрих ролика на 1
деление: если совпадает второй штрих верньера с каким-либо штрихом ролика, то
индекс верньера прошел за предыдущий штрих ролика на 2 деле­ния, и  т. д.

Пусть
с каким-то (безразлично с каким) штрихом ролика совпал четвер­тый штрих
верьньера (рис. 74). Это значит, что индекс верньера прошел за предыдущий штрих
ролика на 4 деления. Цифры 4 и 5, написанные против штрихов ролика, означают
сотни его делений. Следовательно, отсчет по ролику на рисунке будет
400+10+4=414 делений. Если при этом еще было отсчи­тано по циферблату 3, то
общий отсчет составит 3414 делений.

Точностью
верньера называется величина (t),
которая выражает собой ту наименьшую долю делений
инструмента, которую можно отсчитать при помощи данного верньера. Для
определения точности данного вернье­ра практически нужно сосчитать число
делений на верньере и разделить на него цену деления инструмента.

При
отсчете по верньеру следует номер совпадающего штриха его умно­жать на
точность. В действительности, однако, штрихи верньера подписы­ваются
числами, выражающими произведения номеров штрихов на точность, так что
отсчеты читаются непосредственно.

Отсчет
по планиметру состоит из четырех цифр:

1.     1-я
цифра записывается со счетчика оборотов, (как меньшая по стрелке).

2.     2-я
цифра записывается со счетного ролика, (подписанная на нем ниже нуля верньера).

3.     3-я
цифра записывается со счетного ролика по количеству неподписанных делений ниже
нуля верньера.

4.     4-я
цифра представляет собой десятую часть неподписанного деления ниже нуля
верньера, берется по номеру совпадающего на верньере штриха.

1.4.3. 
Цена деления планиметра, ее определение и изменение.

 Обвод
контуров планиметром можно выполнять двумя способами, устанавливая полюс
планиметра вне контура или (для слишком больших контуров) внутри него.
На практике обычно применяют первый способ, предпочитая его даже и при
больших контурах, для чего последние расчленяют карандашными линиями на мелкие
части и площадь контура находят как сумму площадей таких частей.

Обозначим
отсчет по верньеру в начале обвода буквой а и в конце обвода буквой в.
Если обвод производится по ходу часовой стрелки, то последний отсчет будет
больше первого и, следовательно, число всех делений, на кото­рое повертывается
ролик, составит в—а  

Разность
отсчетов по верньеру выражает площадь контура в делениях планиметра;

Площадь,
соответствующая одному делению планиметра называется ценой деления планиметра

Цена
деления планиметра определяется в следующей последовательности:

1.     Вычисляют
теоретически площадь правильной геометрической фигуры (квадрата, прямоугольника
или круга). Можно воспользоваться сеткой координат.

М 1:2 000   

В
1см – 20м

Сторона
квадрата 10см с учетом масштаба 200м

Площадь
квадрата Sкв=а² =200²=40 000м²=4га

Площадь
фигуры =4га*3кв=12га

2.     Устанавливают
планиметр на план (на лист). Выбирают место полюсу так. Чтобы при обводке
фигуры угол между рычагами был в пределах 30-150^о, а при установке
иглы над начальной точкой – 90^о. При обводке фигуры счетному
механизму не должно быть помех.

3.     Ставят
иглу на начальную точку и записывают отсчет а равный показаниям на
счетчике.

4.     Обводят
фигуру по часовой стрелке не отклоняясь от ее границ и возвращаются в начальную
точку.

5.     Записывают
конечный отсчет, который увеличится (в-а)  (если
обводить контур по часовой стрелке) или уменьшиться (а-в) (если
обводить контур против часовой стрелки).

6.     Изменив
отсчет, обводят контур еще раз и вычисляют разность отсчетов (в₁-а₁).
Можно не менять отсчет, а принять за начальный отсчет второй обводки  конечный
отсчет первой обводки.

7.     Расхождение
между результатами первой и второй обводки зависит от величины обводимой
площади, но не должно превышать 5 делений планиметра.

8.     Вычисляют
цену деления планиметра:

                      
   Спл = S фигуры/
(в — а)среднее = цена деления планиметра

1.4.4.
 Поверки планиметра.

 Теория
полярного планиметра основана на том, что при движении обводного рычага в
направлении, перпендикуляр­ном к плоскости ободка ролика, последний только
скользит по бумаге, не вращаясь и, следовательно, не изменяя отсчета на
верньере, а при движении обводного рычага в направлении, совпадающем или
параллельном с плоско­стью ободка, он только вращается. Все это выполняется при
условии, если,

во-первых,
на движение ролика не влияют никакие другие причины, кроме трения его ободка о
бумагу плана,

во-вторых,
если плоскость ободка пер­пендикулярна к оси его вращения, а последняя
параллельна оси обводного рычага.

Таким
образом, к планиметру должны предъявляться следующие требо­вания.

1.Счетное
колесо должно вращаться свободно, без трения, не иметь коле­баний по оси и
близко прилегать к верньеру, но без соприкосновения с ним.

2.Плоскость
ободка ролика должна быть перпендикулярна к его оси, а последняя параллельна
оси обводного рычага.

При
вращении колеса происходит трение в концах его оси о подшипники. Поэтому, прежде
всего, следует добиться, чтобы ось не была сильно зажа­та в подшипниках. Это
достигается удалением подшипников от концов оси при помощи вывинчивания
регулирующих винтиков (причем не следует забы­вать, предварительно откреплять
зажимные винты последних). Однако чрез­мерное удаление подшипников может
привести к тому, что концы оси будут колебаться в них — появятся так называемые
боковые колебания оси ролика, чего не должно быть (ось ролика во время работы
должна занимать одно определенное положение, параллельное оси обводного
рычага). Соответствующей осторожной регулировкой следует добиться, чтобы ролик
вращался совершенно свободно, но без боковых колебаний. Эта регулировка
производится на глаз и на ощупь. Удерживая рычаг в воздухе, сообщают ролику
легким ударом пальца вращательное движение. При правильной установке это
движение должно быть быстрым и довольно продолжи­тельным.

Кроме
трения в подшипниках, возможно еще трение ролика о верньер, если плоскости не
будут соприкасаться. С другой стороны, для уверенных и более точных отсчетов по
верньеру необходимо, чтобы плоскости эти были расположены, возможно, ближе одна
от другой (чтобы совпадающие штрихи колеса и верньера казались одной
неразрывной линией). Таким образом, здесь выявляется необходимость выполнения
двух противоречащих друг другу условий. Это достигается также действием
регулирующих винтиков, при­чем одному из них сообщается положительное, а
другому отрицательное вращение.

Что
касается перпендикулярности плоскости ободка ролика к его оси вращения, то это
достаточно точно выполняется на заводах, где изготовляются планиметры. На
роликах планиметров, выпускаемых нашими заво­дами, уклонение конца радиуса
ободка от перпендикулярного к оси положе­ния не превышает 0,01 мм. Это при
длине радиуса 10 мм дает угол 3′,4, что па обводе контура отражается незаметно.

Поверка
параллельности оси вращения колеса с осью рычага может быть произведена методом
обвода одного и того же контура при двух различ­ных положениях рычагов
планиметра (или, как иногда выражаются, счет­ного механизма) относительно
линии, соединяющей полюс и конец обводного шпиля, один раз — вправо от нее
(если, например, смотреть от полюса шпиль), другой раз — влево.

Этот
метод будем называться  полным приемом; обвод же при одном только положении
рычагов будет называться п о л у п р и е м о м. При обведении контура полным
приемом, с одинаковой установ­кой полюса относительно контура в полуприем а х,
ошибка будет иметь в полуприемах разные знаки с одинаковой абсо­лютной
величиной, что и скажется на результатах обвода. Если расхождение между
площадями, выраженными в делениях планиметра, в полуприемах не превышает 2—3
делений, то условие считается выполненным. В противном случае условие не
выполнено, но среднее арифметическое из обоих полуприемов даст правильную
величину площади контура: при работе полным прие­мом ошибки компенсируются, что
и послужило причиной названия таких планиметров  компенсационными.

Если
полюс планиметра установить так, чтобы при обводе одной поло­вины контура углы
между рычагами все время были тупые, а в другой поло­вине — острые, то ошибка
от не параллельности оси колеса с осью рычага более или менее компенсируется и
при работе одним полуприемом.

В
планиметрах для урегулирования параллельности оси колеса с осью обводного рычага
имеется приспособление в виде исправи­тельного винта, упирающегося концом в
одну из плоскостей обводного рыча­га, к противоположной плоскости которого
прилегает пружина. Регулиро­вание обычно производится многократным повторением
поверки (методом последовательных приближений).

Заметим,
что при обводах для проверки параллельности оси колеса с осью обводного рычага
лучше использовать контрольную линеечку, которая прилагается к планиметру и
представляет собой металлическую линейку с иглой-полюсом вблизи одного конца и
с индексом на другом конце. На линейке на определенных расстояниях от иглы
расположены углубления для обводного шпиля. Воткнув иглу в бумагу и поместив в
одно из углубле­ний шпиль, обводят полную окружность (с радиусом, равным
расстоянию от иглы до углубления), для чего в начале обвода отмечают против
индекса точ­ку, на которой и заканчивают обвод. При таком обводе на колесе не
отража­ются сотрясения руки и площадь обведенного круга в делениях получается
точнее.

1.4.5.
 Правила работы планиметром.

Наиболее
благоприятные условия для обвода площади планиметром будут в случае, когда
бумага наклеена на ровную фанеру или на мензульную доску, которые располагаются
на гори­зонтальной поверхности стола.

Обводный
шпиль следует поместить для начала обвода в конце примерной линии симметрии А
В данного контура (рис. 75), а полюс — на перпен­дикуляре, восстановленном
из середины М этой линии и притом так, чтобы рычаги образовали между
собой прямой угол. Тогда при прохождении шпиля в верхней половине фигуры угол
между рычагами все время будет тупой, а при прохождении в нижней половине— все
время ост­рый, благодаря чему ошибки  будут более или менее компенсироваться.

Перед
окончательной установкой полюса следует сделать примерный быстрый обвод всего
контура, чтобы убедиться, что при обводе не образуется слишком острых и тупых
углов между рычагами планиметра и что ролик все время вращается свободно и не

сходит
с бумаги. Сам обвод должен производиться равномерно, не быстро, но и не слишком
медленно, причем глаз должен быть расположен по направлению движения шпиля
(впереди или сзади него), что необходимо для удержания острия шпиля на контуре.
В планиметрах МШ13 шпиль обводного рычага заменен стеклом, на нижней
сферической поверхности которого отмечена точка, которой и ведут по кон­туру,
глядя сверху. Совмещение такой точки с контуром выполняется легче и точнее.

Рукоятку
шпиля следует держать свободно, без напряжения, чтобы рычаг давил на бумагу
только своей тяжестью, потому что иначе под дей­ствием прилагаемой силы
возможно ослабление давления колеса на бумагу и даже его поднятие, т. е.
проскоки в его вращении, приводящие к грубым ошибкам в числе делений.

Для
контроля обвода и уточнения результата каждый контур должен обводиться не менее
двух раз. При этом второй обвод лучше производить в направлении,
противоположном первому, чтобы по возможности компен­сировать ошибки, зависящие
от напряжений планиметра, которые при таком методе будут иметь различные знаки.
Полезно также между обводами несколько перемещать полюс планиметра на новое
место, чтобы дать возмож­ность ролику катиться по другому пути и тем избавиться
от накопления оди­наковых ошибок, зависящих от шероховатости бумаги, а также,
чтобы избе­жать влияния изношенности гнезда полюса.

После
двух обводов вычисляют разности отсчетов, которые не должны превышать:

При
допустимой разности берут среднее арифметическое из обоих отсче­тов. В
противном случае обводы повторяют.

Если
нуль циферблата при обводе пройдет мимо индекса (указателя), то последующий
отсчет получится меньше предыдущего. В этом случае для образования разности
нужно к последующему отсчету прибавить 10 000.

Отсчеты,
разности и вычисленные площади следует аккуратно записы­вать в особую
ведомость, форма которой может иметь вид, приведенный в таблице 13.

Площадь
контура вычисляют по формуле:       

Sконтура= Спл (в-а)ср

1.4.6.
Постоянное число планиметра.

 Если
контур, площадь которого подлежит определению, большой, то полюс планиметра
можно устанавли­вать внутри контура. В этом случае к разности отсчетов f_l прибавляется
постоянное число q,
так что формула планиметра принимает вид

Для
определения постоянного числа одну и ту же фигуру со значитель­ной площадью
тщательно обводят планиметром как с полюсом вне фигуры, так и с полюсом внутри
нее.

Обозначим
разность отсчетов при полюсе вне фигуры через f, и при полю­се внутри нее через
f₁,. Тогда

Число
q определяется
многократными обводами при разных положениях планиметра.

1.4.7.
 Точность измерения площадей полярными планиметрами.

 Точ­ность
определения площадей полярными планиметрами зависит от многих причин: от
величины площади, конфигурации участка, длины обводного рычага (или величины
зависящей от него цены деления), от методов работы, качества бумаги плана и т.
д.

При
двойных обводах съемочных контуров величиной в среднем 50 см² и
средней вытянутостью  примерно 1:4, планиметром с абсолютной ценой деления
около 0,1 см², средняя относительная ошибка получается примерно ¹/₄₀₀.
Большие контуры обводятся точнее, меньшие — менее точно.

Особенно
низкая точность получается при обводе малых контуров, величиной менее 10 см².
Это происходит главным образом потому, что ошибка отсчета по верньеру, не
зависящая от величины контуров, на малых конту­рах отражается значительно
сильнее. Для повышения точности определения площадей малых контуров их следует
обводить методом повторений, т. е. обводить каждый контур несколько раз, причем
отсчет брать только в нача­ле первого и в конце последнего обводов, благодаря
чему обводка отсчета уменьшается в число раз, равное количеству обводов.
Полезно также при этом устанавливать и меньшую цену деленной, т. е. увеличивать
обводный рычаг примерно в два раза. При двух обводах с двумя повторениями в каж­дом
обводе и при укороченном в два раза рычаге (т. е. с ценой деления око­ло 0,05
см²) относительная ошибка малых контуров получается не грубее ¹/₁₀₀.

1.4.8.
Применение современной вычислительной техники для определения площадей.

Определение
площадей землепользований, земельных участков и сельскохозяйственных угодий
является одним из трудоемких видов работ в комплексе топографо-геодезических
изысканий для землеустройства и кадастра недвижимости.

Последние
десятилетия прошлого века ознаменовались тем, что в мировой и отечественной
практике наметились частичная и полная автоматизация определения площадей.

Частичная
автоматизация — применение различных видов электронных приборов: цифровых
планиметров, дигитайзеров, позволяющих автоматизировать процесс измерений и
вычислений. В этом случае обвод контуров осуществляется оператором, но  нет
необходимости производить отсчеты до и после обвода, т. к. значение площади
сразу после обвода выводится на жидко-кристаллическом дисплее счетного
механизма.

Электронные
планиметры имеются двух видов: полярные компенсационные (рис. 4.17) и линейные
(роликовые) (рис. 4.18).

Существуют
различные модификации электронных планиметров, например, полярные планиметры
моделей: КР-82Ы, РЬАМХ-5.6 (Япония) и др.

 Планиметры
позволяют выполнять измерения в делениях планиметра; устанавливать единицы
измерений; накапливать результаты измерений нескольких контуров. Площадь,
измеренная повторно (не более 9 раз), может быть осреднена для получения более
точного результата. При обводе вкрапленных контуров против хода часовой стрелки
их площадь автоматически вычитается из площади основного контура.

Следует
отметить, что линейные планиметры типа Х-РLAN
360 d
(рис. 4.19) позволяют быстро измерять площади участков, длины линий и контуров
по планам (картам). Длины прямых линий определяются путем фиксации двух точек —
начала и конца прямой, криволинейные контуры определяются путем их
отслеживания. Имеется встроенный калькулятор, позволяющий производить различные
операции над результатами измерений. При наличии программного обеспечения можно
дополнительно определять координаты точек на плане. Режимы измерений: точечный
— измерение только поворотных точек контура при прямолинейных границах между
ними; непрерывный — измерение криволинейных контуров путем их отслеживания.

При
обводе контура обводным индексом (курсором) прибора по ходу часовой стрелки
координаты могут регистрироваться только при нажатии клавиши на поворотных
точках или по всей границе через выбранный интервал времени, например через 1
с, либо через шаг расстояния, например через 1 мм.

В
алгоритме планиметра типа Х-РLAN
360d
может быть предусмотрено уравнивание площадей с учетом деформации бумаги,
обобщения контура в пределах шага регистрации координат, погрешностей
вторичного измерения координат на линии смежных участков (контуров).

Продолжительность
непрерывной работы разных моделей от 15 до 30 часов, а продолжительность
перезарядки аккумуляторной батареи — от 8 до 15 часов.

Точность
работы электронных планиметров в % при различных значениях площади на плане
приведена в табл. 4.1.

Таблица
4.1

Полная
автоматизация — автоматическое отслеживание контура, процесса измерения и
вычисления площадей, которые реализуется в различных ГИС-технологиях. В этом
случае предполагается, что оператор работает с электронным планом (картой). При
этом точность определения площади участков по плану будет зависеть оттого,
какой точностью обладала исходная геодезическая информация в базе данных. Если
она получена в результате полевых работ, то точность определения площади будет
соответствовать точности измерений на местности (аналитическому способу). Когда
база данных формировалась путем сканирования (дигитализации) планово-картографического
материала, то точность площади будет соответствовать графическому способу.

Магнитный поток, проходящий через площадь S равен:

Ф = BScosα;

где:

Ф ― величина магнитного потока [Вб],

S ― площадь контура [м2],

B ― индукция магнитного поля [Тл],

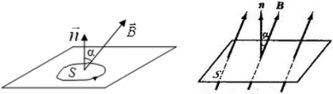
α ― угол между нормалью $overrightarrow{n}$ к площади контура и вектором индукции магнитного поля $overrightarrow{B}$.

Если вектор индукции магнитного поля $overrightarrow{B}$ перпендикулярен площади контура, то магнитный поток равен:

Ф = BScos90° = BS;

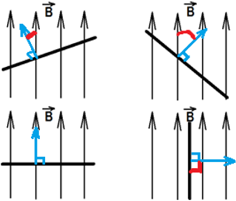
Максимальное значение потока будет тогда, когда косинус будет максимальным (cosα = 1), то есть угол между вектором $overrightarrow{B}$ и вектором нормали к пластинке равен 0°, чему соответствует картинка 3. Наименьшее же значение потока будет тогда, когда косинус будет равен нулю (cosα = 0), то есть угол между нормалью к пластинке и вектором индукции равен 90°, чему соответствует картинка 4.

Электромагнитная индукция ― явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через контур. Если контур разомкнут, то на его концах наблюдается разносность потенциалов, равная ЭДС индукции.

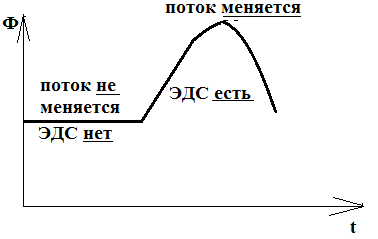
ЭДС электромагнитной индукции возникает только тогда, когда изменяется магнитный поток.

Закон Фарадея об электромагнитной индукции и гласит, что индуцируемая ЭДС прямо пропорциональна скорости изменения магнитного потока:

$varepsilon_i = -frac{Delta text{Ф}}{Delta t}$

где:

$varepsilon_i $ ― ЭДС электромагнитной индукции [B],

$frac{Delta text{Ф}}{Delta t}$ ― скорость изменения магнитного потока [Вб/с],

∆Ф ― изменение магнитного потока [Вб],

∆t ― время, за которое происходит это изменение [c].

Кроме того, ЭДС индукции равна производной магнитного потока по времени:

$varepsilon_i = -text{Ф}_t’$

где:

• ― ЭДС электромагнитной индукции [B],
• ― производная магнитного потока по времени [Вб/с].

Задача 1

Замкнутый контур площадью S из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. В контуре возникают колебания тока с амплитудой iм = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой B = acos (bt), где a = 6 · 10-3Тл, b = 3500 c-1. Электрическое сопротивление контура R = 1,2 Ом. Чему равна площадь контура?

Решение:

Обратите внимание на величины, данные в условии. Они здесь совсем не такие, к которым вы привыкли, потому что не дано значение магнитного поля, а дана зависимость магнитного поля от времени. Посмотрим, как это скажется на решении задачи.

Поскольку магнитное поле, а вместе с ним и поток меняются, то будет возникать ЭДС индукции, именно это ЭДС и вызовет электрический ток, поэтому запишем закон электромагнитной индукции.

По закону электромагнитной индукции $varepsilon_i = -frac{Delta text{Ф}}{Delta t}$

ЭДС — это изменение магнитного потока за время. Ничего в определении ЭДС не сказано про это самое время. Дело в том, что изменение какой-то величины за небольшой промежуток времени называется производной по времени. То есть наше ЭДС, которое является изменением магнитного потока за небольшой промежуток времени, это просто производная магнитного потока по времени $varepsilon_i = -text{Ф}_t’$

И это очень важный момент, без которого мы не сможем решить такого рода задачу.

Теперь посчитаем ЭДС индукции.

Напишем, чему равен магнитный поток Ф = BS = acos (bt) · S.

ЭДС индукции — это производная магнитного потока по времени. Теперь придётся вспомнить немного математики. Множители “a” и “S” перед косинусом не зависят от времени, поэтому производная их не трогает, а вот у косинуса в скобках стоит зависимость от времени, поэтому именно от косинуса производную и нужно взять.

Обратите внимание на полученную формулу магнитного потока. В ней стоит просто множитель aS перед сложной функцией косинуса

$text{Ф} underset{text{множитель}}{underbrace{aS}} ;; cdot ;; underset{text{сложная функция}}{underbrace{cos(bt)}}$.

Взяв производную от этой функции, получаем Ф´ = –abS · sin (bt). А теперь, раз мы знаем производную магнитного потока, значит, знаем и ЭДС индукции, потому что $varepsilon_i = -text{Ф}_t’$

Подставив сюда значение производной, получим $varepsilon_i = -text{Ф}_t’$ = abS · sin (bt).

Мы получили значение ЭДС. Кроме этого, мы знаем сопротивление и максимальную силу тока, поэтому запишем закон Ома.

По закону Ома $I = frac{varepsilon}{R}$ , подставив сюда значение ЭДС, получаем $I = frac{abScdot sin(bt)}{R}$.

Мы получили зависимость силы тока от времени.

Из-за синуса, который стоит в этой формуле, ток постоянно меняет свое значение, то он становится больше, то меньше, поскольку синус меняет своё значение от -1 до 1.

В условии дано максимальное значение силы тока, которое протекает по контуру. Когда эта величина будет максимальной? В тот момент, когда синус будет максимальным, то есть равный единице. Поэтому запишем sin (bt) = 1.

Максимальное значение тока будет в тот момент, когда будет максимальным значение ЭДС индукции, то есть когда, $I_{max} = frac{abS}{R}$.

Отсюда можно легко выразить площадь контура $S = frac{I_{max}R}{ab}$, подставив сюда все значения, получим $S = frac{I_{max}R}{ab} = frac{35cdot 10^{-3} Acdot 1,2text{Ом}}{6cdot 10^{-3}text{Тл} cdot 35000c^{-1}} = 0,002text{м}^2$

Ответ: 0,002

Как видно из формулы магнитного потока Ф = BScosα, изменение магнитного потока может быть вызвано разными факторами:

• увеличением или уменьшением модуля индукции магнитного поля (т. е. величины $frac{Delta B}{Delta t}$);
• изменением направления вектора магнитного поля (т. е. изменением угла α);
• деформацией контура, причем такой деформацией, при которой изменяется площадь контура (т. е. изменением величины $frac{Delta S}{Delta t}$ );
• изменением нескольких из этих величин одновременно.

Таким образом, изменение модуля или направление вектора магнитной индукции или площади контура неизбежно приводят к тому, что в контуре возникает электродвижущая сила.

Если нарисовать график зависимости магнитного потока, то он может выглядеть либо так: тогда поток не будет менятьсяи ЭДС не возникает.

Либо так, тогда будет меняться поток и возникать ЭДС:

Знак «минус» перед скоростью изменения магнитного потока в формуле отражает правило Ленца: индуцированный ток всегда направлен так, чтобы магнитное поле, которое он создает, препятствовало изменению магнитного потока.

Если магнитный поток, проходящий через площадь контура, уменьшается, то магнитное поле индуцированных токов будет стремиться его увеличить.

Если поток увеличивается ― магнитное поле индуцированных токов будет стремиться его уменьшить.

Задача 2

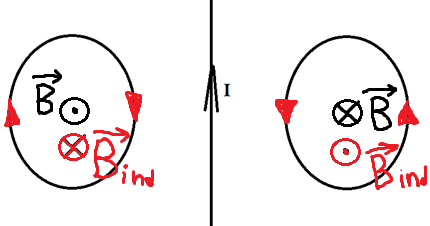
Два проводящих кольца расположены относительно проводника с током в одной плоскости, как это показано на рисунке. В каком направлении будет индуцироваться ток в этих кольцах, если начать двигать их в направлении проводника?

Решение:

Первым делом необходимо понять, как вообще может возникать индуцированный ток, если даже магнитного поля нет?

Его направление мы можем определить по правилу правого винта. Отметим это на рисунке.

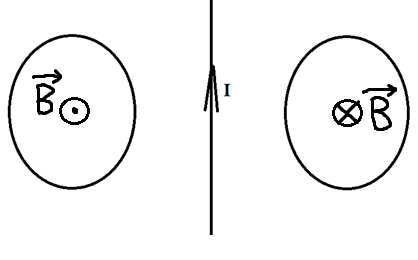
Теперь эти два проводника начинают двигать. Разве от этого меняется поток? Ведь площадь остаётся та же самая, угол между нормалью и вектором тоже не меняется. Однако, чем ближе к проводнику с током, тем сильней поле, а чем дальше от него, тем слабее! Поэтому, когда мы двигаем кольца к проводнику, мы увеличиваем поток, ведь ближе поле сильнее. Значит, будет появляться ток, а его направление можно определить по правилу Ленца. Что нам говорит правило Ленца?

Раз поток увеличивается, то по правилу Ленца ток будет индуцироваться так, чтобы уменьшить поток, то есть магнитное поле в левом кольце будет направлено от нас, а в правом ─ на нас. А значит, по правилу правого винта мы можем определить, что ток будет течь по часовой стрелке слева и против часовой стрелки справа.

Движение проводников

Если к концам проводника, движущегося в магнитном поле, подключить вольтметр, то прибор покажет наличие разности потенциалов на концах проводника. Таким образом, когда проводник перемещается в области с магнитным полем, в нем возникает электромагнитная движущая сила (ЭДС).

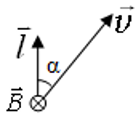
Согласно закону Лоренца, в проводнике, движущемся в магнитном поле, создается ЭДС $|varepsilon_i| = Blvsinalpha$;

где:

$varepsilon_i$― ЭДС электромагнитной индукции [B],

B ― индукция магнитного поля [Тл],

l ― длина проводника [м],

v ― скорость движения проводника [м/с],

α ― угол между направлением вектора скорости $overrightarrow{v}$ и длиной проводника $overrightarrow{l}$ , если вектор индукции магнитного поля $overrightarrow{B}$перпендикулярен проводнику и вектору скорости его движения: $overrightarrow{B} perp overrightarrow{v}, overrightarrow{B} perp overrightarrow{l}$

Используя силу Лоренца, можно получить это определение ЭДС. Сила Лоренца ― это проявленное действие магнитного поля на заряженную частицу.

В проводнике присутствует большое количество свободных зарядов (именно это отличает проводники от диэлектриков), и на каждый из зарядов действует сила Лоренца, перемещая их по проводнику так, что в одной его части скапливается отрицательный заряд, а в другой, соответственно, положительный. Это распределение зарядов и является физической основой для возникновения электродвижущей силы.

На рисунке показано как сила Лоренца, действующая на каждый из зарядов проводника, создаёт ЭДС в проводнике. Если одиночный отрицательный заряд попадает в магнитное поле, направленное от нас, то, согласно правилу левой руки, направление его движения изменяется так, как показано на рисунке. Если в область с таким же магнитным полем входит проводник, суммарный заряд которого равен нулю, но внутри которого находятся электроны, способные свободно перемещаться в проводнике, то электроны стекаются в один конец проводника. Так как электроны переместились в один конец проводника, то этот конец приобретает отрицательный заряд, а противоположный ему ― положительный. Таким образом, в проводнике возникает разность потенциалов и электродвижущая сила.

В некоторых случаях удобно решать задачи, используя определение ЭДС через закон Лоренца (обычно это задачи о движении прямолинейного проводника в поле), в других ― через закон Фарадея.

В проводнике, движущемся в магнитном поле, образуется разность потенциалов U = lvBsinα;

где:

U — разность потенциалов [В],

l — длина проводника [м],

v — скорость движения проводника $big[ frac{text{м}}{c} big]$

B — индукция магнитного поля [Тл],

α — угол между направлением скорости и длиной проводника.

В случае, если есть какой-то замкнутый контур, то ЭДС в нем возникает только тогда, когда меняется магнитный потокчерез этот контур. В случае же тонкого стержня, для которого нельзя применить понятия магнитного потока, потому что у него просто нет площади, ЭДС возникает при движении в постоянном магнитном поле.

В случае, если в задаче дана проводящая рамка или контур, для определения ЭДС (напряжения) используем формулу $varepsilon_i = — frac{Delta text{Ф}}{Delta t}$

В случае, если в задачи дан проводник, движущейся в поле, для определения ЭДС (напряжения) используем формулу $varepsilon$ =U= lvBsinα.

Задача 3

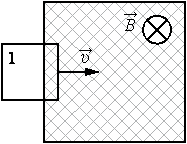
В заштрихованной области на рисунке действует однородное магнитное поле, перпендикулярное плоскости рисунка с индукцией В = 0,1 Тл. Квадратную проволочную рамку, сопротивление которой 10 Ом и длина стороны 10 см, перемещают в этом поле в плоскости рисунка поступательно равномерно с некоторой скоростью υ. При попадании рамки в магнитное поле в положении 1 в ней возникает индукционный ток, равный 1 мА. Какова скорость движения рамки?

Решение:

Составим цепочку.

Зная силу тока и сопротивление, что можно найти? Мы сможем найти напряжение, то есть ЭДС, а ЭДС, уже можно легко связать со скоростью движения рамки.

Составим цепочку. Мы знаем магнитное поле (В), длину стороны (a), сопротивление (R) и силу тока (I), а найти нужно скорость(v).

Зная ток и сопротивление, что сразу можно найти? Напряжение, то есть ЭДС, которое мы сможем найти по закону Ома.

А связать ЭДС с индукцией поля, стороной рамки и скоростью движения очень легко, воспользовавшись той формулой, которую мы получили в прошлой задаче.

Пройдёмся вдоль этой цепочки.

Запишем закон Ома $I = frac{varepsilon}{R}$, подставив сюда формулу для ЭДС, которую мы получили в прошлой задаче, отбросив знак «минус» получим $I = frac{varepsilon}{R} = frac{Bav}{R}$отсюда выразим скорость, и, подставив все величины, получим $v = frac{IR}{Ba} = frac{1cdot 10^{-3} Acdot 10text{Ом}}{0,1 text{Тл} cdot 0,1 text{м}} = 1 frac{text{м}}{c}$

Ответ: 1

Электромагнитная индукция

Явление электромагнитной индукции

Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

Опыты Фарадея

• На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
• Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
• Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.

Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Объяснения возникновения индукционного тока

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.

Свойства вихревого электрического поля:

• источник – переменное магнитное поле;
• обнаруживается по действию на заряд;
• не является потенциальным;
• линии поля замкнутые.

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.

Магнитный поток

Магнитным потоком через площадь ​( S )​ контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ​( B )​, площади поверхности ​( S )​, пронизываемой данным потоком, и косинуса угла ​( alpha )​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Обозначение – ​( Phi )​, единица измерения в СИ – вебер (Вб).

Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м², расположенную перпендикулярно вектору магнитной индукции:

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​( alpha )​ магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Закон электромагнитной индукции Фарадея

Закон электромагнитной индукции (закон Фарадея):

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​( N )​ витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​( R )​:

При движении проводника длиной ​( l )​ со скоростью ​( v )​ в постоянном однородном магнитном поле с индукцией ​( vec{B} )​ ЭДС электромагнитной индукции равна:

где ​( alpha )​ – угол между векторами ​( vec{B} )​ и ( vec{v} ).

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

• магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
• вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

• в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
• в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца

Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Алгоритм решения задач с использованием правила Ленца:

• определить направление линий магнитной индукции внешнего магнитного поля;
• выяснить, как изменяется магнитный поток;
• определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
• по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Самоиндукция

Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.

При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.

В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.

При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.

Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.

При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.

ЭДС самоиндукции ​( varepsilon_{is} )​, возникающая в катушке с индуктивностью ​( L )​, по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.

Индуктивность

Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ​( Phi )​ через контур из этого проводника пропорционален модулю индукции ​( vec{B} )​ магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.

Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Индуктивность – коэффициент пропорциональности ​( L )​ между силой тока ​( I )​ в контуре и магнитным потоком ​( Phi )​, создаваемым этим током:

Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.

Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:

Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.

Энергия магнитного поля

При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.

Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:

1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.

2. Записать формулу:

• закона электромагнитной индукции;
• ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.

3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.

4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).

5. Решить полученную систему уравнений относительно искомой величины.

6. Решение проверить.